Кинетика и катализ, 2020, T. 61, № 6, стр. 888-892

ВВЕДЕНИЕ

Реакторы со стационарным слоем катализатора широко используются как в промышленности, так и в лабораторной практике [1]. Например, при разработке процесса получения моторных топлив путем гидрирования растительных масел большая часть экспериментов проведена в реакторах со стационарным слоем катализатора [2].

Одним из факторов, снижающих эффективность использования катализатора, является внутридиффузионное торможение. При рассмотрении влияния внутренней диффузии на химический процесс в зерне катализатора используют квазигомогенную модель [3]. Уравнение для сферического зерна в рамках данной модели в случае реакции первого порядка А → В и постоянства коэффициента диффузии имеет вид

где c – концентрация реагента А, R – расстояние от центра зерна до выбранной точки, D – эффективный коэффициент диффузии, k – константа скорости реакции, скорость реакции отнесена к единице объема зерна.

Для уравнения ставятся граничные условия: ограниченность решения при R = 0 и с(b) = c₀, где b – радиус зерна, с₀ – концентрация реагента во внешнем потоке.

Для решения уравнения используют безразмерные переменные: y = c/c₀, x = R/b, в которых уравнение и граничные условия принимают вид

где ψ – параметр Тиле,

Общее решения уравнения имеет вид

Второй член, как неограниченный при х → 0, отбрасывают и, используя граничное условие y(1) = 1, окончательное решение записывают в виде

При выводе данной зависимости предполагалось, что концентрация реагента на внешней поверхности зерна в каждой точке одна и та же. Но если зерно находится в реакторе, например, в реакторе со стационарным слоем катализатора, то концентрация реагента уменьшается вдоль реактора и не является постоянной. На поверхности катализатора концентрация реагента также падает в направлении потока, т.е. она выше на лобовой поверхности зерна и ниже на тыльной. В кинетических экспериментах из-за малости размера зерна (менее 1 мм) изменением концентрации реагента на зерне пренебрегают. Но в промышленных реакторах, в которых используются зерна размером 2–50 мм, оно может быть заметным. Относительное изменение концентрации реагента на зерне можно оценить на основе уравнения и решения для реактора идеального вытеснения в случае реакции первого порядка, которые имеют вид

где u – среднерасходная скорость реакционной смеси в стационарном слое, z – продольная координата реактора, скорость реакции отнесена к единице объема слоя катализатора.

Относительное изменение концентрации реагента на зерне оценивается как отношение диаметра зерна d к характерному размеру изменения концентрации, равному u/k:

Например, по данным работы [4], посвященной кинетике гидрирования рапсового масла на Ni–Cu/CeO₂–ZrO₂-катализаторе, можно оценить значение Δc/c₀. Принимая следующие значения параметров: диаметр частиц катализатора 0.75 мм, температура 360°С, константа скорости реакции 3.3 ч^–1, объем катализатора 5 см³, время контакта 0.4 ч, внутренний диаметр реактора 13 мм, значение Δc/c₀ получается равным примерно 0.2.

Целью настоящей работы является описание влияния неоднородности потока на химический процесс в зерне при наличии внутридиффузионного сопротивления, а именно расчет распределения концентрации реагента внутри зерна и степени использования катализатора.

УРАВНЕНИЕ ДЛЯ ЗЕРНА В НЕОДНОРОДНОМ ПОТОКЕ

Учитывая, что на размере зерна концентрация реагента меняется не сильно, зависимость концентрации вне зерна от продольной координаты можно аппроксимировать линейной зависимостью

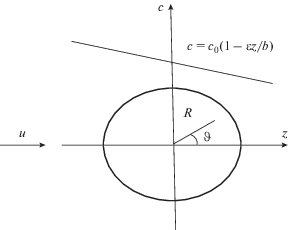
где ось z совпадает с направлением движения реакционной смеси, ε – безразмерный коэффициент неоднородности потока. Например, при ε = 0.1, концентрация реагента на размере радиуса зерна меняется на 10%.

На рис. 1 показана схема расположения зерна в неоднородном потоке с обозначениями переменных. R, ϑ – сферические координаты, ϑ ‑ угол между осью z и радиус-вектором выбранной точки, наклонная линия иллюстрирует изменение концентрации реагента во внешнем потоке. При z = 0 c = c₀.

В сферических координатах концентрация реагента вне зерна будет иметь вид

Внутри зерна, с учетом осевой симметрии, безразмерная концентрация реагента описывается функцией y(x, ϑ). На поверхности зерна безразмерная концентрация совпадает с концентрацией во внешнем потоке:

Концентрация реагента внутри зерна подчиняется уравнению [3]:

где Δ – оператор Лапласа.

В безразмерных переменных уравнение имеет вид

С учетом осевой симметрии уравнение в сферической системе координат будет

На функцию y(x, ϑ) кроме граничного условия (3) накладывается еще условие ограниченности при x → 0.

РЕШЕНИЕ УРАВНЕНИЯ И ЕГО АНАЛИЗ

Учитывая граничное условие при x = 1 (3), решение уравнения (4) будем искать в виде

где f(x) – пока неизвестная функция.

После подстановки в уравнение (4) получим уравнение для f(x):

Граничные условия для f(x) будут:

Полученное уравнение имеет аналитическое решение [5]:

где С₁ и С₂ – неопределенные константы.

Данное решение можно записать также через гиперболические функции, используя зависимости

где A₁ и A₂ – неопределенные константы.

Решение (6) можно вывести также другим способом. Продифференцируем уравнение (1) по x:

Из полученного уравнения следует, что функция $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ удовлетворяет уравнению (5), и общее решение для этого уравнения можно получить путем дифференцирования общего решения (2).

Константы A₁ и A₂ находим из граничных условий.

Из f(0) < ∞ и f(1) = 1 следует

В результате функция f(x) будет

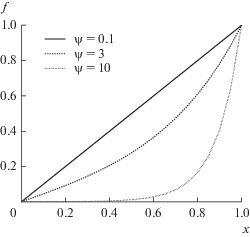
Функция f(x) обладает следующими свойствами: f(0) = 0, является монотонно возрастающей и f(1) = 1. При ψ → 0 f(x) → x, а при больших ψ функция f(x) отлична от нуля только в тонком слое у поверхности зерна с характерной толщиной 1/ψ.

График функции f(x) при различных значения параметра Тиле показан на рис. 2.

Выражение для безразмерной концентрации реагента внутри зерна будет иметь вид

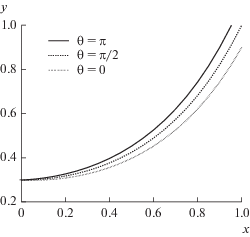
Анализ решения (7) показывает, что в области 0 ≤ ϑ < π/2 (тыльная часть зерна) концентрация уменьшается по сравнению с таковой в однородном потоке, а при π/2 < ϑ ≤ π (лобовая часть зерна) – увеличивается. Наибольшие отклонения наблюдаются при x = 1, ϑ = 0 и ϑ = π. При ϑ = π/2 профиль y(x) совпадает с профилем в однородном потоке. Значение концентрации в центре зерна такое же, как и для однородного потока, и равно ψ/sh(ψ). Однако это значение не является минимальным, т.к. точка минимума концентрации смещается по оси z в тыльную область зерна. При ψ → 0 распределение концентрации внутри зерна совпадает с распределением концентрации во внешнем потоке:

На рис. 3 показаны профили y(x) при ψ = 3, ε = 0.1 и различных значениях ϑ.

Степень использования зерна η рассчитывается через интеграл по объему зерна:

где V₀ – объем зерна.

Интеграл по объему зерна от второго члена в выражении (7) равен нулю. Это означает, что при линейной зависимости концентрации реагента от продольной координаты реактора степень использования зерна такая же, как и в однородном потоке, и увеличение скорости реакции в лобовой части зерна компенсируется уменьшением скорости реакции в тыльной части.

Можно заметить, что данная задача легко обобщается на случай, когда концентрация реагента вне зерна зависит линейно не только от координаты z, но и от других декартовых координат. Если перейти в новую систему координат, в которой ось z располагается параллельно градиенту концентрации, то более общая задача сводится к вышерассмотренной.

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрена задача о сферическом зерне, помещенном в неоднородный поток с линейной зависимостью концентрации реагента от продольной координаты реактора при наличии внутридиффузионного сопротивления. Для случая реакции первого порядка получено аналитическое решение для распределения концентрации реагента внутри зерна. Показано, что по сравнению с зерном в однородном потоке концентрация реагента увеличивается в лобовой полусфере и уменьшается в тыльной полусфере катализатора, а степень использования зерна не меняется, т.к. повышение скорости реакции в лобовой полусфере компенсируется ее снижением в тыльной полусфере.