Кинетика и катализ, 2021, T. 62, № 1, стр. 8-13

Нелинейные кинетические законы сохранения в линейных химических реакциях

Н. И. Кольцов^a, *

^a ФГБОУ ВО Чувашский государственный университет им. И.Н. Ульянова, химико-фармацевтический факультет
428015 Чебоксары, Московский просп., 15, Россия

^* E-mail: koltsovni@mail.ru

Поступила в редакцию 03.04.2020
После доработки 21.08.2020
Принята к публикации 07.09.2020

DOI: 10.31857/S0453881121010068

Полный текст (PDF)

Аннотация

Разработан не описанный ранее в литературе подход для установления новых нелинейных кинетических законов сохранения (НКЗС) в химических реакциях, протекающих по линейным многостадийным механизмам в изотермических безградиентных реакторах. Эти НКЗС представляют собой моноэкспериментную разновидность точных мультиреагентных кинетических автономных инвариантов, которые можно наблюдать на основе данных, измеренных в одном нестационарном эксперименте с определенными заданными начальными условиями. Показана применимость подхода для определения НКЗС конкретных реакций, протекающих в закрытом и открытом безградиентных реакторах.

Ключевые слова: химическая кинетика, линейные реакции, нелинейные законы сохранения

Нелинейные законы сохранения (ЗС) представляют собой не зависящие от времени (автономные) комбинации нестационарных концентраций реагентов и параметров реакции [1–14]. “Полный” набор автономных ЗС химической реакции включает линейные стехиометрические ЗС (ЛСЗС) и нелинейные кинетические ЗС (НКЗС). ЛСЗС зависят только от стехиометрии реакции и легко находятся. Установить линейные кинетические ЗС (ЛКЗС) и НКЗС сложнее, они зависят от кинетических параметров реакции и концентраций реагентов. В закрытых системах число независимых ЛСЗС определяется числом различных атомов, участвующих в реакции. В работах [2–4] было показано, что в закрытых системах точное число независимых ЛСЗС N_s = n − R_k ≥ 1, а точное число ЛКЗС N_k = R − R_k ≥ 0, где n − общее число реагентов (включая зависимые), R_k − ранг стехиометрической матрицы по комплексам реагентов (различным необратимым стадиям), R − ранг стехиометрической матрицы по всем реагентам (всем стадиям). Это означает, что в закрытых системах всегда есть хотя бы один (основной) независимый ЛСЗС, а ЛКЗС могут отсутствовать. Число НКЗС неизвестно даже для закрытых систем, но отельные их виды найдены для некоторых классов реакций [4, 5]. Недавно для закрытых и открытых систем были обнаружены новые виды НКЗС, основанные на данных нескольких экспериментов (мультиэкспериментые) [6–14]. По числу экспериментов и реагентов эти НКЗС делятся на двухэкспериментные мультиреагентные (ДМ) на основе двух взаимно-обратных граничных экспериментов и мультиэкспериментые монореагентные (ММ) на основе множества любых (необязательно граничных) экспериментов. ДМ-НКЗС (термодинамические временные инварианты, thermodynamic time invariaces) найдены для линейных и некоторых нелинейных реакций в закрытых системах [6–11]. ММ-НКЗС (автономные кинетические инварианты, autonomous kinetic invariants) найдены для линейных и некоторых нелинейных реакций в закрытых и открытых системах [12–14]. Определение новых видов автономных НКЗС, особенно в открытых системах, является актуальным, так как они могут быть использованы при решении обратных задач химической кинетики.

В данной статье описана новая разновидность автономных ММ-НКЗС для линейных многостадийных реакций, основанных на одном нестационарном эксперименте в закрытых и открытых изотермических безградиентных системах.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция протекает через s линейных элементарных стадий

(1)

$\sum\limits_i {{{a}_{{ij}}}{{{\mathbf{А}}}_{j}}} = \sum\limits_i {{{a}_{{ - ij}}}{{{\mathbf{А}}}_{j}}} ,\,\,\,\,i = 1, \ldots ,s,$

где a_ij, a_−ij − стехиометрические коэффициенты реагентов А_j, j = 1, …, n в левых и правых частях стадии i. В закрытых системах для каждой линейной стадии выполняются ЛЗСЗ атомов $\sum\limits_j {{{a}_{{ij}}}} $ = = $\sum\limits_j {{{a}_{{ - ij}}}} $ = 1. В открытых системах эти ЛСЗС могут нарушаться. Динамика таких реакций в открытом изотермическом безградиентном реакторе в рамках закона действующих масс описывается системой линейных обыкновенных дифференциальных уравнений (ОДУ)

(2)

$\begin{gathered} А_{j}^{'} = \sum\limits_i {\left( {{{a}_{{ - ij}}}_{~} - {{a}_{{ij}}}} \right)} \left( {{{r}_{i}} - {{r}_{{ - i}}}} \right) + {{q}_{0}}{{A}_{{0j}}} - q{{A}_{j}}, \\ j = 1, \ldots ,n, \\ \end{gathered} $

где А_j − концентрации реагентов А_j (мол. д.), A_0j − начальные условия (н. у.), r_i = k_i$\prod {A_{j}^{{aij}}} $ и r_−i = = k_−i$\prod {A_{j}^{{a - ij}}} $ − скорости стадий в прямом и обратном направлениях соответственно (1/с), k_i и k_−i − константы скоростей прямой и обратной стадий соответственно (1/с), q₀ и q – начальная и текущая скорости реакционного потока соответственно (1/с) (в закрытом безградиентном реакторе q = = q₀ = 0).

Общее решение системы (2) запишется как

(3)

$\begin{gathered} {{A}_{j}}(t) = {{A}_{{j\infty }}} + \sum\limits_k {{{С}_{{jk}}}} {\text{exp}}\left( {{{\lambda }_{k}}t} \right), \\ j = 1, \ldots ,n,\,\,\,\,k = 1, \ldots ,n, \\ \end{gathered} $

где A_j∞(k_i,k_−i,A_0j,q₀) – координаты единственного устойчивого стационарного состояния, С_jk(k_i,k_−i,A_0j,q₀) − константы, λ_k(k_i,k_−i,A_0j,q₀) < 0 − различные собственные числа.

В закрытом безградиентном реакторе для реакции (1) всегда выполняется как минимум один основной автономный ЛСЗС

(4)

$\sum\limits_j {{{A}_{j}}} = \sum\limits_j {{{A}_{{0j}}}} = \sum\limits_j {{{A}_{{j\infty }}}} = 1.$

В открытом безградиентном реакторе с ростом q этот ЛСЗС нарушается и формируется новый ЗС

$\sum\limits_j {A_{j}^{'}} = {{q}_{0}}\sum\limits_j {{{A}_{{0j}}}} - q\sum\limits_j {{{A}_{j}}} ,$

который после интегрирования принимает вид

(5)

$\sum\limits_j {{{A}_{j}}} ~ = \sum\limits_j {{{A}_{{0j}}}} {{\left[ {{{q}_{0}} + {\text{exp}}( - qt)\left( {q - {{q}_{0}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{q}_{0}} + {\text{exp}}( - qt)\left( {q - {{q}_{0}}} \right)} \right]} q}} \right. \kern-0em} q}.$

При q ≠ q₀ этот ЗС зависит от времени (неавтономный), но при q = q₀ он становится автономным и совпадает с выражением (4). Это означает, что при постоянной скорости потока открытый безградиентный реактор становится подобным закрытому безградиентному реактору.

В работе [12] дан критерий существования ММ-НКЗС с использованием двух и более экспериментов с разными н. у. (мультиэкспериментов). При использовании только одного эксперимента (моноэксперимента) аналогичный критерий можно переписать в виде

(6)

$\begin{gathered} {{С}_{{j0k}}} = 0\,\,{\text{при}}\,\,k \ne {{k}_{0}}, \\ {{С}_{{j0k0}}} \ne 0,\,\,\,\,{{С}_{{jk1}}} \ne 0\,\,{\text{при}}\,\,j \ne {{j}_{0}}. \\ \end{gathered} $

Если условия (6) выполнимы при физичных значениях параметров реакции, то решения (3) могут быть представлены в виде

(7)

${{A}_{{j0}}}\left( t \right) = {{A}_{{j0\infty }}} + {{С}_{{j0k0}}}{\text{exp}}\left( {{{\lambda }_{{k0}}}t} \right),$

(8)

$\begin{gathered} {{A}_{j}}\left( t \right) = {{A}_{{j\infty }}} + {{С}_{{jk1}}}{\text{exp}}\left( {{{\lambda }_{{k1}}}t} \right) + \sum\limits_k {{{С}_{{jk}}}} {\text{exp}}\left( {{{\lambda }_{k}}t} \right), \\ j \ne {{j}_{0}},\,\,\,\,k \ne {{k}_{1}}. \\ \end{gathered} $

Соотношения (7) позволяют выразить все экспоненты через одну (любую) выбранную экспоненту, концентрации реагентов и кинетические параметры реакции

$\begin{gathered} {\text{exp}}\left( {{{\lambda }_{k}}t} \right) = {{\left[ {{\text{exp}}\left( {{{\lambda }_{{k0}}}t} \right)} \right]}^{{{{\lambda k} \mathord{\left/ {\vphantom {{\lambda k} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}} = \\ = {{\left[ {{{\left( {{{A}_{j}}_{0} - {{A}_{{j0\infty }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{A}_{j}}_{0} - {{A}_{{j0\infty }}}} \right)} {{{С}_{{jk0}}}}}} \right. \kern-0em} {{{С}_{{jk0}}}}}} \right]}^{{{{\lambda k} \mathord{\left/ {\vphantom {{\lambda k} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}},\,\,\,\,k = 1, \ldots ,n. \\ \end{gathered} $

Подстановка этих равенств в выражение (8) дает до n – 1 моноэкспериментных p-реагентных НКЗС

(10)

$\begin{gathered} {{K}_{{pj}}}(t) \equiv {{A}_{j}} - {{С}_{{jk1}}}{{\left[ {{{\left( {{{A}_{{j0}}} - {{A}_{{j0\infty }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{A}_{{j0}}} - {{A}_{{j0\infty }}}} \right)} {{{С}_{{jk0}}}}}} \right. \kern-0em} {{{С}_{{jk0}}}}}} \right]}^{{{{\lambda k1} \mathord{\left/ {\vphantom {{\lambda k1} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}} - \\ - \,\,\sum\limits_k {{{С}_{{jk}}}{{{\left[ {{{\left( {{{A}_{{j0}}} - {{A}_{{j0\infty }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{A}_{{j0}}} - {{A}_{{j0\infty }}}} \right)} {{{С}_{{jk0}}}}}} \right. \kern-0em} {{{С}_{{jk0}}}}}} \right]}}^{{{{\lambda k1} \mathord{\left/ {\vphantom {{\lambda k1} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}}} = {{A}_{{j\infty }}},\,\,\,\,j \ne {{j}_{0}}. \\ \end{gathered} $

Таким образом, если реакция протекает через линейные стадии (1) в закрытой или открытой изотермических безградиентных системах при выполнении условий (6), то для нее, кроме ЛЗСЗ вида (4), реализуются p-реагентные моноэкспериментные НКЗС вида (10). Покажем это на примерах конкретных реакций.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пример 1. Пусть реакция протекает с участием только двух (n = 2) реагентов

(1.1)

$1)\,\,{\mathbf{A}} = {\mathbf{B}}.$

Для схемы (1.1) ОДУ (2) в открытом и закрытом (q₀ = q = 0) изотермических безградиентных реакторах запишутся как

(1.2)

$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B + {{q}_{0}}{{A}_{0}} - qA, \\ B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B + {{q}_{0}}{{B}_{0}} - qB. \\ \end{gathered} $

Из (1.2) видно, что, если реакция (1.1) протекает в закрытой системе, то для нее выполняется один автономный ЛСЗС вида (4)

$A + B = 1.$

В открытом безградиентном реакторе этот ЛСЗС не выполняется, а справедлив неавтономный ЗС вида (5)

$A + B = {{\left[ {{{q}_{0}} + {\text{exp}}( - qt)\left( {q - {{q}_{0}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{q}_{0}} + {\text{exp}}( - qt)\left( {q - {{q}_{0}}} \right)} \right]} q}} \right. \kern-0em} q}.$

Проанализируем возможность существования для реакции (1.1) автономных НКЗС в открытом и закрытом безградиентных реакторах. Для этого запишем решение (3) для системы (1.2):

(1.3)

$\begin{gathered} A = {{A}_{\infty }} + {{C}_{{A1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{A2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right), \\ B = {{B}_{\infty }} + {{C}_{{B1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{B2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right), \\ \end{gathered} $

где C_A1 = k₋₁(k₋₁A₀q + qk₋₁B₀ + A₀q² + q²B₀ − q₀A₀k₁ − – q₀A₀k₋₁ − k₋₁q₀B₀ − q₀B₀k₁ + A₀qk₁ + k₁qB₀–− qq₀B₀– q₀A₀q/S, ${{C}_{{A{\text{2}}}}}\,\, = \,\,q\left( { - k_{{ - {\text{1}}}}^{{\text{2}}}{{B}_{{\text{0}}}}\,\,\, + \,\,\,{{A}_{{\text{0}}}}{{k}_{{ - {\text{1}}}}}{{k}_{{\text{1}}}}\,\,\, - } \right.\,\,\,{{k}_{{ - {\text{1}}}}}{{B}_{{\text{0}}}}{{k}_{{\text{1}}}}\,\,\, + \,\,\,{{k}_{{ - {\text{1}}}}}{{q}_{{\text{0}}}}{{k}_{{ - {\text{10}}}}}\,\,\, - $ ${{\left. { - q{{k}_{{ - {\text{1}}}}}{{B}_{{\text{0}}}} - {{q}_{{\text{0}}}}{{A}_{{\text{0}}}}{{k}_{{\text{1}}}} + {{A}_{{\text{0}}}}k_{{\text{1}}}^{{\text{2}}} + {{A}_{{\text{0}}}}q{{k}_{{\text{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left. { - q{{k}_{{ - {\text{1}}}}}{{B}_{{\text{0}}}} - {{q}_{{\text{0}}}}{{A}_{{\text{0}}}}{{k}_{{\text{1}}}} + {{A}_{{\text{0}}}}k_{{\text{1}}}^{{\text{2}}} + {{A}_{{\text{0}}}}q{{k}_{{\text{1}}}}} \right)} S}} \right. \kern-0em} S}{\text{,}}$ C_B1 = k₁(k₋₁A₀q + qk₋₁B₀ + A₀q² + q²B₀ − q₀A₀k₁ − − q₀A₀k₋₁ − k₋₁q₀B₀ − q₀B₀k₁ + A₀qk₁ + k₁qB₀ − qq₀B₀ − − q₀A₀q)/S, C_B2 = −C_A2, A_∞ = q₀[k₋₁(A₀ + B₀) + A₀q]/ [q(k₁ + k₋₁ + q)], B_∞ = q₀[k₁(A₀ + B₀) + B₀q]/[q(k₁ + + k₋₁ + q)], S = (k₁ + + k₋₁)/[q(k₁ + k₋₁ + q)], λ₁ = −q, λ₂ = −(k₁ + k₋₁ + q).

Критерий (6) выполняется, если C_A1 = 0, C_B1 ≠ 0 или C_A2 = 0, C_B2 ≠ 0. Однако оба эти случая невозможны, так как пары C_A1 и C_B1 или C_A2 и C_B2 обращаются в ноль одновременно при q = q₀ или q = q₀ – – (k₁ + k₋₁) соответственно. Следовательно, в открытом и закрытом изотермических безградиентных реакторах для реакции (1.1) не существуют автономные НКЗС вида (10). Для нее выполняется только автономный ЛСЗС A + B = 1 в закрытом изотермическом безградиентном реакторе.

Пример 2. Пусть реакция протекает по параллельной схеме с тремя (n = 3) реагентами

(2.1)

$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{A}} = {\mathbf{С}}.$

Динамика этой реакции в закрытом безградиентном изотермическом реакторе описывается системой ОДУ

$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B - {{k}_{2}}A + {{k}_{{ - 2}}}C,$
$B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B,$
$C{\kern 1pt} ' = {{k}_{2}}A - {{k}_{{ - 2}}}C,$

из которой следует, что для реакции (2.1) существует один автономный ЛСЗС

$A + B + С = 1.$

Решения уравнений (2.2) имеют вид

(2.3)

$A = {{C}_{{A1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{A2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + {{A}_{\infty }},$

$B = {{C}_{{B1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{B2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + {{B}_{\infty }},$

$C = {{C}_{{C1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{C2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + {{C}_{\infty }},$

где C_A1, C_A2, C_B1, C_B2, C_C1, C_C2 − константы, λ_1,2 = −(k₁ + k₋₁ + k₂ + k₋₂)/2 ± $\left[ {\left( {k_{{\text{1}}}^{{\text{2}}} + k_{{ - {\text{1}}}}^{{\text{2}}} + k_{{ - {\text{2}}}}^{{\text{2}}} + } \right.} \right.$ $ + \,\,k_{{\text{2}}}^{{\text{2}}}\,\, + \,\,\,{\text{2}}{{k}_{{\text{1}}}}{{k}_{{\text{2}}}}\,\,\, + \,\,\,{\text{2}}{{k}_{{\text{2}}}}{{k}_{{ - {\text{2}}}}} + {\text{2}}{{k}_{{\text{1}}}}{{k}_{{ - {\text{1}}}}} - {\text{2}}{{k}_{{\text{1}}}}{{k}_{{ - {\text{2}}}}} - {\text{2}}{{k}_{{ - {\text{1}}}}}{{k}_{{ - {\text{2}}}}}\,\,\, - $${{\left. {{{{\left. { - \,\,{\text{2}}{{k}_{{\text{2}}}}{{k}_{{ - {\text{1}}}}}} \right)}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \right]} \mathord{\left/ {\vphantom {{\left. {{{{\left. { - \,\,{\text{2}}{{k}_{{\text{2}}}}{{k}_{{ - {\text{1}}}}}} \right)}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \right]} {\text{2}}}} \right. \kern-0em} {\text{2}}}{\text{,}}$ A_∞ = k₋₁k₋₂/S, B_∞ = k₂k₋₁/S, C_∞ = k₁k₂/S, S = k₋₁k₋₂ + k₁k₋₂ + k₂k₋₁. Анализ показал, что критерий (6) выполняется, например, при k₁ = k₋₁ = k₂ = k₋₂ = 1, тогда C_A1 = 0, C_B1 ≠ 0, C_C1 ≠ 0, λ₁ = −1, λ₂ = −3, A_∞ = B_∞ = C_∞ = 1/3 и решения (2.3) примут вид

(2.4)

$\,\,\,\,\,\,A = \left( {{{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$

$\begin{gathered} C = \left( {{{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{C}_{0}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right){\text{exp}}( - t) + \\ + \,\,\left( {{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6} - {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2}} \right){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $

Отсюда следует exp(−3t) = (A − 1/3)/(A₀ − 1/3), exp(−t) = exp^1/3(−3t) = [(A − 1/3)/(A₀ − 1/3)]^1/3 и НКЗС

(2.5)

$\begin{gathered} C = \left( {{{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{C}_{0}} - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right) \times \\ \times \,\,{{\left[ {{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)} {\left( {{{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {{{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - \,\,{A \mathord{\left/ {\vphantom {A 2}} \right. \kern-0em} 2} + 1, \\ \end{gathered} $

(2.6)

$\begin{gathered} B = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} - {{C}_{0}}} \right) \times \\ \times \,\,{{\left[ {{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)} {\left( {{{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {{{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - {A \mathord{\left/ {\vphantom {A 2}} \right. \kern-0em} 2} + 1. \\ \end{gathered} $

При A₀ ≥ 1/3, например, A₀ = 2/3, B₀ = 1/3, C₀ = 0 эти НКЗС принимают физичные значения

(2.7)

${{K}_{{21}}} = C - \,\,{{{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \mathord{\left/ {\vphantom {{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} {\left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \,\,{A \mathord{\left/ {\vphantom {A 2}} \right. \kern-0em} 2} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$

(2.8)

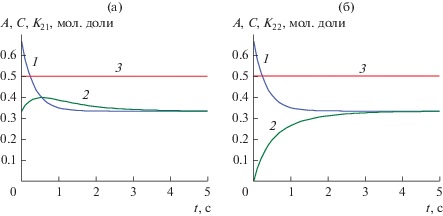
${{K}_{{22}}} = B + \,\,{{{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \mathord{\left/ {\vphantom {{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{{\left( {A - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} {\left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \,\,{A \mathord{\left/ {\vphantom {A 2}} \right. \kern-0em} 2} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$

и соответствуют горизонтальным (не зависящим от времени) прямым (см. рис. 1). Отметим, что для реакции (2.1) автономные НКЗС (2.5) и (2.6) существуют при любых н. у. и равных значениях констант скоростей стадий. В общем случае, при других значениях параметров НКЗС возможны только при определенных н. у. Например, при k₁ = 1, k₋₁ = 2, k₂ = k₋₂ = 1 они наблюдаются при н. у. С₀ = 1 + A₀(2^−1/2 − 1). Следовательно, в закрытом изотермическом безградиентном реакторе для параллельной реакции с тремя реагентами, кроме ЛСЗС, могут наблюдаться и моноэкспериментные автономные НКЗС вида (10).

Рис. 1.

Концентрационные зависимости от времени и нелинейные кинетические законы сохранения для реакции (2.1) в закрытом изотермическом безградиентном реакторе при k₁ = k₋₁ = k₂ = k₋₂ = 1: а – 1 – А(t), 2 – C(t), 3 – K₂₁(t); б – 1 – А(t), 2 – В(t), 3 – K₂₂(t).

Пример 3. Динамика той же реакции (2.1) в открытом изотермическом безградиентном реакторе описывается ОДУ

(3.1)

$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B - {{k}_{2}}A + {{k}_{{ - 2}}}C + {{q}_{0}}{{A}_{0}} - qA,$

$B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B + {{q}_{0}}{{B}_{0}} - qB,$

$C{\kern 1pt} ' = {{k}_{2}}A - {{k}_{{ - 2}}}C + {{q}_{0}}{{C}_{0}} - qC.$

Для этой системы ЛСЗС не существуют, а ее решения запишутся как

(3.2)

$\begin{gathered} A = {{C}_{{A1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{A2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + \\ + \,\,{{C}_{{A3}}}{\text{exp}}\left( {{{\lambda }_{3}}t} \right) + {{A}_{\infty }}, \\ \end{gathered} $

$B = {{C}_{{B1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{B2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + {{C}_{{B3}}}{\text{exp}}\left( {{{\lambda }_{3}}t} \right) + {{B}_{\infty }},$

$C = {{C}_{{C1}}}{\text{exp}}\left( {{{\lambda }_{1}}t} \right) + {{C}_{{C2}}}{\text{exp}}\left( {{{\lambda }_{2}}t} \right) + {{C}_{{C3}}}{\text{exp}}\left( {{{\lambda }_{3}}t} \right) + {{C}_{\infty }},$

где λ_2,3 = −q − (k₁ + k₋₁ + k₂ + k₋₂)/2 ± $\left[ {k_{{\text{1}}}^{{\text{2}}} + k_{{ - {\text{1}}}}^{{\text{2}}} + } \right.$ $ + \,\,k_{{\text{2}}}^{{\text{2}}} + k_{{ - {\text{2}}}}^{{\text{2}}}$ + 2(k₁k₂ + k₂k₋₂ + k₁k₋₁ − k₁k₋₂ − k₂k₋₁ − ${{\left. {{{{\left. { - {{k}_{{ - {\text{1}}}}}{{k}_{{ - {\text{2}}}}}} \right)}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \right]} \mathord{\left/ {\vphantom {{\left. {{{{\left. { - {{k}_{{ - {\text{1}}}}}{{k}_{{ - {\text{2}}}}}} \right)}}^{{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-0em} {\text{2}}}}}}} \right]} {\text{2}}}} \right. \kern-0em} {\text{2}}}{\text{,}}$ λ₁ = −q, A_∞ = q₀[A₀(q² + k₋₂q + k₋₁q + + k₋₁k₋₂) + +B₀(k₋₁q + k₋₁k₋₂) + C₀(k₋₂q + k₋₁k₋₂)]/S, B_∞ = q₀[A₀(k₁q + k₁k₋₂) + B₀(q² + k₋₁q + k₂q + k₋₂q + + k₁k₋₂) + C₀k₁k₋₂]/S, C_∞ = q₀[A₀(k₂q + k₂k₋₁) + + B₀k₂k₋₁ + C₀(q² + k₋₁q + + k₂q + k₁q + k₂k₋₁)]/S, S = q[q(q + k₁ + k₂ + k₋₁ + k₋₂) + k₁k₋₂ + k₋₁k₋₂ + + k₂k₋₁]; C_A1, C_A2, C_A3, C_B1, C_B2, C_B3, C_C1, C_C2, C_C3 − константы.

Анализ показал, что критерий (6) выполняется, например, при k₁ = k₋₁ = k₂ = k₋₂ = 1, q₀ = q = 1, тогда λ₁ = −1, λ₂ = −2, λ₃ = −4, A_∞ = A₀/2 + B₀/4 + C₀/4, B_∞ = A₀/4 + 5B₀/8 + C₀/8, C_∞ = A₀/4 + B₀/8 + 5C₀/8, C_A1 = C_A2 = 0, C_A3 = A₀/2 − C₀/4 − B₀/4, C_B1 = 0, C_B2 = B₀/4 − C₀/4, C_B3 = −A₀/4 + C₀/8 + B₀/8, C_C1 = 0, C_C2 = C₀/4 − B₀/4, C_C3 = −A₀/4 + C₀/8 + B₀/8 и решения (3.2) примут вид

(3.3)

$A = {{C}_{{A3}}}{\text{exp}}( - 4t) + {{A}_{\infty }},$

$B = {{C}_{{B2}}}{\text{exp}}( - 2t) + {{C}_{{B3}}}{\text{exp}}( - 4t) + {{B}_{\infty }},$

$C = {{C}_{{C2}}}{\text{exp}}( - 2t) + {{C}_{{C3}}}{\text{exp}}( - 4t) + {{C}_{\infty }}.$

Отсюда следует:

${\text{exp}}( - 4t) = {{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}},$

${\text{exp}}( - 2t) = {\text{ex}}{{{\text{p}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}( - 4t) = {{\left[ {{{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

и НКЗС

(3.4)

$\begin{gathered} B = {{C}_{{B2}}}{{\left[ {{{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,{{C}_{{B3}}}\left[ {{{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}}} \right] + {{B}_{\infty }}, \\ \end{gathered} $

(3.5)

$\begin{gathered} C = {{C}_{{C2}}}{{\left[ {{{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,{{C}_{{C3}}}\left[ {{{\left( {A - {{A}_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {{A}_{\infty }}} \right)} {{{C}_{{A3}}}}}} \right. \kern-0em} {{{C}_{{A3}}}}}} \right] + {{C}_{\infty }}. \\ \end{gathered} $

При C_A3 > 0 эти НКЗС принимают физичные значения. Например, для A₀ = 2/3, B₀ = 1/3, C₀ = 0 получим A_∞ = 5/12, B_∞ = 3/8, C_∞ = 5/24, C_A3 = 1/4, C_B2 = 1/12, C_B3 = −1/8, C_C2 = −1/12, C_C3 = −1/8 и

(3.6)

$\begin{gathered} {{K}_{{21}}} = B - {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,{{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)} 2}} \right. \kern-0em} 2} = {3 \mathord{\left/ {\vphantom {3 8}} \right. \kern-0em} 8}, \\ \end{gathered} $

(3.7)

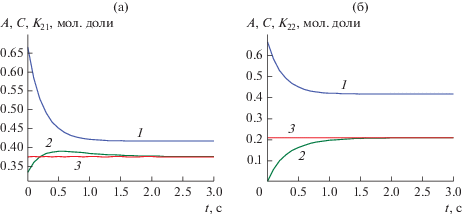
$\begin{gathered} {{K}_{{22}}} = С + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,{{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)} \mathord{\left/ {\vphantom {{\left( {A - {5 \mathord{\left/ {\vphantom {5 {12}}} \right. \kern-0em} {12}}} \right)} 2}} \right. \kern-0em} 2} = {5 \mathord{\left/ {\vphantom {5 {24}}} \right. \kern-0em} {24}}. \\ \end{gathered} $

Эти НКЗС и кривые изменения концентраций во времени приведены на рис. 2. Следовательно, и в открытом изотермическом безградиентном реакторе для параллельной реакции с тремя реагентами, несмотря на отсутствие ЛСЗС, справедливы моноэкспериментные автономные НКЗС вида (10).

Рис. 2.

Концентрационные зависимости от времени и нелинейные кинетические законы сохранения для реакции (3.1) в открытом изотермическом безградиентном реакторе при k₁ = k₋₁ = k₂ = k₋₂ = 1: а – 1 – А(t), 2 – B(t), 3 – K₂₁(t); б – 1 – А(t), 2 – C(t), 3 – K₂₂(t).

Проведенный анализ показал, что НКЗС вида (10) существуют и для более сложных многостадийных линейных реакций, протекающих в закрытых и открытых безградиентных системах.

ЗАКЛЮЧЕНИЕ

Установлены новые нелинейные моноэкспериментные кинетические законы сохранения (НКЗС) для многостадийных линейных химических реакций, протекающих в закрытых и открытых безградиентных изотермических реакторах. Такие НКЗС представляют собой не зависящие от времени (автономные) комбинации кинетических параметров реакции и концентраций реагентов, измеренных в одном нестационарном эксперименте с заданными начальными условиями. Однако следует учитывать, что на практике эти НКЗС могут выполняться только приближенно с погрешностью, определяемой точностью используемого оборудования. Для повышения точности НКЗС и надежности следующих из них выводов необходимо проведение повторных экспериментов с теми же или другими начальными условиями и усреднение полученных результатов. Описанные в статье нелинейные кинетические законы сохранения расширяют представления о релаксационных закономерностях химических реакций и могут быть использованы при решении обратных задач химической кинетики.

Список литературы

Горбань А.Н., Быков В.И., Яблонский Г.С. Очерки о химической релаксации. Новосибирск: Наука, 1986. 320 с.
Корзухин М.Д. // Журн. физ. химии. 1972. Т. 46. № 7. С. 1845.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1992. Т. 66. № 12. С. 3219.
Кольцов Н.И. Математическое моделирование каталитических реакций. Чебоксары: Изд-во Чуваш. ун-та, 2007. 294 с.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1988. Т. 62. № 11. С. 3069.
Yablonsky G.S., Gorban A.N., Constales D., Galvita V.V., Marin G.B. // Europhys. Lett. 2011. V. 93. № 2. Art. 20 004.
Constales D., Yablonsky G.S., Marin G.B. // Chem. Eng. Sci. 2012. V. 73. P. 20.
Yablonsky G.S. // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 551.
Peng B., Yablonsky G.S., Constales D., Marin G.B., Muhler M. // Chem. Eng. Sci. 2018. V. 191. P. 262.
Yablonsky G.S., Branco P.D., Marin G.B., Constales D. // Chem. Eng. Sci. 2019. V. 196. P. 384.
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. // Chem. Eng. Sci. 2020. V. 211. Art. 115 291.
Федотов В.Х., Кольцов Н.И. // Кинетика и катализ. 2019. Т. 60. № 6. С. 756.
Федотов В.Х., Кольцов Н.И., Косьянов П.М. // Хим. физика. 2020. Т. 39. № 3. С. 48.
Кольцов Н.И. // Кинетика и катализ. 2020. Т. 61. № 4. С. 482.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал