Кинетика и катализ, 2021, T. 62, № 4, стр. 410-415

Многореагентные автономные кинетические инварианты химических реакций

Н. И. Кольцов^a, *

^a ФГБОУ ВО Чувашский государственный университет им. И.Н. Ульянова, химико-фармацевтический факультет
428015 Чебоксары, Московский просп., 15, Россия

^* E-mail: koltsovni@mail.ru

Поступила в редакцию 12.11.2020
После доработки 09.02.2021
Принята к публикации 28.02.2021

DOI: 10.31857/S0453881121040067

Полный текст (PDF)

Аннотация

Установлены новые точные многореагентные автономные кинетические инварианты для химических реакций, протекающих в безградиентном изотермическом реакторе. Инварианты представляют собой независящие от времени комбинации кинетических параметров реакции и концентраций двух и более реагентов. Такие инварианты сохраняют постоянные значения в ходе реакции. Приведены примеры определения инвариантов в закрытых и открытых безградиентных реакторах.

Ключевые слова: химическая кинетика, нестационарные эксперименты, многореагентные инварианты, безградиентный изотермический реактор

ВВЕДЕНИЕ

Автономные кинетические инварианты представляют собой независящие от времени комбинации нестационарных концентраций реагентов с кинетическими параметрами химических реакций. Они являются нестехиометрическими законами сохранения (ЗС) и могут использоваться для экспериментальной проверки механизмов химических реакций. Такие инварианты делятся на одно-, двух- и многореагентные и обнаруживаются с помощью одного [1–3], двух [4–8] или любого (одного и более) числа [9, 10] нестационарных экспериментов. Первые найденные кинетические многореагентные инварианты базировались на данных одного эксперимента и концентрациях всех участвующих в реакции реагентов. Недавно были установлены многореагентные нестехиометрические инварианты на основе двух экспериментов с разными граничными взаимно-обратными (термодинамическими) начальными условиями (н. у.) [4–8]. Инварианты [1–8] применимы для любых линейных и некоторых нелинейных реакций в закрытых системах. В работах [9, 10] изложен метод построения однореагентных инвариантов на основе нескольких нестационарных экспериментов с любыми (не обязательно граничными) н. у. для линейных и нелинейных реакций не только в закрытых, но и открытых системах. Другие виды точных кинетических инвариантов в настоящее время неизвестны, и установление новых автономных инвариантов продолжает оставаться актуальной задачей химической кинетики. Ниже описаны новые автономные многореагентные кинетические инварианты, которые могут быть найдены в химических реакциях на основе одного или нескольких нестационарных экспериментов с любыми н. у. с помощью предлагаемого в представленной работе подхода.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция протекает через s элементарных стадий

(I)

$\sum\limits_j {{{a}_{{ij}}}{{{\mathbf{А}}}_{j}}} = \sum\limits_j {{{a}_{{ - ij}}}_{{}}{{{\mathbf{А}}}_{j}}} ,\,\,\,\,i = {\text{ }}1, \ldots ,s,\,\,\,j = {\text{ }}1, \ldots ,n,$

где a_ij, a_−ij − стехиометрические коэффициенты веществ А_j в стадии i; n – число реагентов. Динамика этой реакции в безградиентном изотермическом реакторе описывается системой обыкновенных дифференциальных уравнений (ОДУ)

(1)

$\begin{gathered} {{А}_{j}}(t)' = \sum {({{a}_{{ - ij}}} - {{a}_{{ij}}})({{r}_{i}} - {{r}_{{ - i}}})} + \\ + \,\,{{q}_{0}}{{A}_{{0j}}} - q{{A}_{j}},\,\,\,\,j = {\text{ }}1, \ldots ,n, \\ \end{gathered} $

где А_j(t) − концентрации реагентов А_j, мол. доли; t − время, с; A_0j = A_j(0) − н. у.; r_i = ${{k}_{i}}\prod {A_{j}^{{aij}}} $ и r_−I = = ${{k}_{{ - i}}}\prod {A_{j}^{{a - ij}}} $ − скорости стадий в прямом и обратном направлениях, 1/с; k_i и k_−i − константы скоростей стадий, 1/с; q₀ и q – начальная и текущая скорости реакционного потока, 1/с. Построим многореагентные инварианты для линейных реакций при значениях кинетических параметров, отвечающих монотонной кинетике. Для таких реакций решение системы (1) запишется [9]:

(2)

$\begin{gathered} {{A}_{j}}(t) = \sum {{{С}_{{jk}}}{\text{exp}}({{\lambda }_{k}}t)} + {{A}_{j}}_{\infty }, \\ j = 1, \ldots ,\,\,n,\,\,\,\,\,k = 1, \ldots ,\,\,n, \\ \end{gathered} $

где C_jk – константы, зависящие от н. у., q₀ и q; λ_k − различные собственные числа (с. ч.); A_j∞. − стационарные концентрации реагентов. В закрытом реакторе (q = q₀ = 0) эти решения связаны N стехиометрическими законами сохранения (СЗС)

(3)

$\begin{gathered} \sum {{{\alpha }_{{mj}}}{{A}_{j}}} ~ = \sum {{{\alpha }_{{mj}}}{{A}_{{0j}}}} = \sum {{{\alpha }_{{mj}}}{{A}_{j}}_{\infty }} , \\ m = {\text{ }}1, \ldots ,N, \\ \end{gathered} $

где α_mj – константы, зависящие от стехиометрии стадий (I). В открытом реакторе (q ≠ 0) все СЗС (3) нарушаются, но выполняются более общие неавтономные СЗС вида

(4)

$\begin{gathered} q\sum {{{a}_{{mj}}}{{A}_{j}}} = \sum {{{\alpha }_{{mj}}}{{A}_{{0j}}}} \left[ {{{q}_{0}} + (q - {{q}_{0}}){\text{exp}}( - qt)} \right], \\ m = 1, \ldots ,N. \\ \end{gathered} $

Эти соотношения зависят от потоковой экспоненты exp(−qt), соответствующей с. ч. λ₁ = −q. В зависимости от значений скорости реакционного потока, рассмотрим три вида изотермических безградиентных реакторов − открытый, квазиоткрытый (квазизакрытый) и закрытый. При q ≠ q₀ (открытый реактор) ЗС (4) позволяют выразить потоковую экспоненту через нестационарные концентрации и кинетические параметры реакции:

(5)

$\begin{gathered} {{E}_{1}} \equiv {\text{exp}}( - qt) = \\ = \,\,{{\left[ {q{{\sum {{{\alpha }_{{mj}}}{{A}_{j}}} } \mathord{\left/ {\vphantom {{\sum {{{\alpha }_{{mj}}}{{A}_{j}}} } {\sum\limits_j {{{\beta }_{{mj}}}{{A}_{{0j}}} - {{q}_{0}}} }}} \right. \kern-0em} {\sum\limits_j {{{\beta }_{{mj}}}{{A}_{{0j}}} - {{q}_{0}}} }}} \right]} \mathord{\left/ {\vphantom {{\left[ {q{{\sum {{{\alpha }_{{mj}}}{{A}_{j}}} } \mathord{\left/ {\vphantom {{\sum {{{\alpha }_{{mj}}}{{A}_{j}}} } {\sum\limits_j {{{\beta }_{{mj}}}{{A}_{{0j}}} - {{q}_{0}}} }}} \right. \kern-0em} {\sum\limits_j {{{\beta }_{{mj}}}{{A}_{{0j}}} - {{q}_{0}}} }}} \right]} {(q - {{q}_{0}})}}} \right. \kern-0em} {(q - {{q}_{0}})}}, \\ m = {\text{ }}1,{\text{ }}2,\,\,.... \\ \end{gathered} $

Все остальные экспоненты находятся через эту экспоненту с помощью соотношений

(6)

$\begin{gathered} {{E}_{k}} \equiv {\text{exp}}({{\lambda }_{k}}t) = {{[{\text{exp}}( - qt)]}^{{{{ - \lambda k} \mathord{\left/ {\vphantom {{ - \lambda k} q}} \right. \kern-0em} q}}}} = \\ = \,\,E_{1}^{{{{ - \lambda k} \mathord{\left/ {\vphantom {{ - \lambda k} q}} \right. \kern-0em} q}}},\,\,\,\,k = {\text{ }}1, \ldots ,n. \\ \end{gathered} $

Подстановка (5) в (2) позволяет исключить из них время и получить n различных p-реагентных одноэкспериментных инвариантов

(7)

${{I}_{p}}_{1}\left( t \right) \equiv {{A}_{j}} - \sum {{{С}_{{jk}}}{{E}_{k}}} = {{A}_{j}}_{\infty },j = 1, \ldots ,n.$

Особенностью инвариантов (7) является то, что они определяются не только через нестационарные концентрации нескольких реагентов, но и через стационарные концентрации любого реагента, что удобно для экспериментальной поверки предполагаемого механизма реакции.

При q = q₀ ≠ 0 (квазиоткрытый/квазизакрытый реактор) или q = q₀ = 0 (закрытый реактор) соотношения (5)−(7) неприменимы, и исключить время из выражений (2) можно с помощью дополнительных нестационарных экспериментов с другими н. у. [9, 10]. Проведем первую пару таких экспериментов и запишем для них решения (2):

(8)

${{A}_{j}}_{1} = \sum {{{С}_{{jk,1}}}{\text{exp}}({{\lambda }_{k}}t)} + {{A}_{j}}_{{1\infty }},\,\,j = 1, \ldots ,n,$

(9)

${{A}_{j}}_{2} = \sum {{{С}_{{jk,2}}}{\text{exp}}({{\lambda }_{k}}t)} + {{A}_{j}}_{{2\infty }},\,\,\,\,j = 1, \ldots ,n.$

Если первый эксперимент этой пары провести с н. у.

(10)

${{С}_{{jk}}}_{{,1}} = 0,\,\,k \ne {{k}_{1}}\,\,{\text{и}}\,\,{{С}_{{jk,1}}} \ne 0,$

а второй − с любыми н. у., то любая кинетическая экспонента выражается из (8) через концентрации, кинетические параметры реакции и н. у. n способами

(11)

${{E}_{1}} \equiv {\text{exp}}({{\lambda }_{{k1}}}t) = {{({{A}_{{j1}}} - {{A}_{j}}_{{1\infty }})} \mathord{\left/ {\vphantom {{({{A}_{{j1}}} - {{A}_{j}}_{{1\infty }})} {{{С}_{{j1,k1}}}}}} \right. \kern-0em} {{{С}_{{j1,k1}}}}},j = 1, \ldots ,n,$

(12)

$\begin{gathered} {{E}_{k}} \equiv {\text{exp}}({{\lambda }_{k}}t) = {{[{\text{exp}}({{\lambda }_{{k1}}}t)]}^{{\lambda k/\lambda k1}}} = \\ = \,\,{{[{{({{A}_{j}}_{1} - {{A}_{{j1\infty }}})} \mathord{\left/ {\vphantom {{({{A}_{j}}_{1} - {{A}_{{j1\infty }}})} {{{C}_{{j1,k1}}}}}} \right. \kern-0em} {{{C}_{{j1,k1}}}}}]}^{{\lambda k/\lambda k1}}},\,\,j = 1, \ldots ,n. \\ \end{gathered} $

Если номера реагентов в (8)−(12) изменять синхронно, то подстановка (11), (12) в (9) дает n однореагентных двухэкспериментых инвариантов

(13)

${{I}_{{12}}}\left( t \right) \equiv {{A}_{{j2}}} - \sum {{{С}_{{jk,2}}}{{E}_{k}}} = {{A}_{{j2\infty }}},\,\,j = 1, \ldots ,n.$

Если же в соотношениях (11), (12) перебирать все возможные различные сочетания номеров реагентов, то подстановка их в соответствующие соотношения (9) дает до n² новых типов автономных p-реагентных двухэкспериментых кинетических инвариантов

(14)

${{I}_{{p2}}}(t) \equiv {{A}_{j}}_{2} - \sum {{{С}_{{jk,2}}}{{E}_{k}}} ~ = {{F}_{{p2}}},\,\,\,j = 1, \ldots ,n,$

где F_p − константы, зависящие от сочетаний реагентов, кинетических параметров и н. у. Описанный процесс можно продолжить несколькими способами. Например, проведем вторую пару экспериментов, оставляя первое н. у. таким же (10), но заменяя второе н. у. на третье (произвольное). Запишем решения (2) для этой пары экспериментов

(15)

${{A}_{{j1}}} = \sum {{{С}_{{j,k1}}}{\text{exp}}({{\lambda }_{{k1}}}t)} + {{A}_{{j1\infty }}},\,\,\,j = 1, \ldots ,n,$

(16)

${{A}_{{j3}}} = \sum {{{С}_{{j,k3}}}{\text{exp}}({{\lambda }_{{k3}}}t)} {\text{ }} + {{A}_{{j3\infty }}},\,\,j = 1, \ldots ,n.$

Эти соотношения дают еще n однореагентных двухэкспериментых инвариантов

(17)

${{I}_{{13}}}\left( t \right) \equiv {{A}_{{j3}}} - \sum {{{С}_{{jk,3}}}{{E}_{k}}} = {{A}_{{j3\infty }}},\,\,\,j = 1, \ldots ,n$

и до n² других автономных p-реагентных двухэкспериментых кинетических инвариантов

(18)

${{I}_{p}}_{3}(t) \equiv {{A}_{{j3}}} - \sum {{{С}_{{jk,3}}}{{E}_{k}}} ~ = {{F}_{{p3}}},\,\,\,j = 1, \ldots ,n.$

Аналогичные инварианты получаются, если выбрать другие н. у. (10) для первого эксперимента и варьировать н. у. последующих экспериментов. В общем виде автономные p-реагентные m-экспериментные кинетические инварианты можно записать так:

(19)

${{I}_{{pm}}}(t) \equiv {{A}_{{jm}}} - \sum {{{С}_{{jk,m}}}{{E}_{k}}} = {{F}_{{pm}}},\,\,\,j = {\text{ }}1,{\text{ }} \ldots ,n.$

Многореагентные инварианты вида (19) выражают новые типы нестационарных кинетических законов сохранения (КЗС), не описанные ранее в литературе. Они раскрывают неочевидные связи между концентрациями различных реагентов, измеренными в экспериментах с разными н. у., и кинетическими параметрами реакции. На графиках зависимостей “концентрация−время” такие сложные связи наблюдаются в виде простых горизонтальных линий (с учетом погрешностей измерений). Это свойство отличает их от других нестационарных кинетических зависимостей, в первую очередь, хорошо известных СЗС, и позволяет экспериментально (визуально) проверять гипотезы о предполагаемых механизмах химических реакций. Аналогично конструируются многореагентные инварианты для любых линейных и нелинейных реакций [10], допускающих точные решения.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пример 1. Рассмотрим последовательную реакцию

(II)

$1)\,\,{\mathbf{A}} = {\mathbf{B}},~\,\,\,2)\,\,{\mathbf{B}} = {\mathbf{С}},$

динамика которой в безградиентном изотермическом реакторе описывается ОДУ вида (1)

(1.1)

$\begin{gathered} A' = - {{k}_{1}}A + {{k}_{ - }}_{1}B + {{q}_{0}}{{A}_{0}} - qA, \\ B' = {{k}_{1}}A - {{k}_{ - }}_{1}B - {{k}_{2}}B + {{k}_{ - }}_{2}C + {{q}_{0}}{{B}_{0}} - qB, \\ C' = {{k}_{2}}B - {{k}_{{ - 2}}}C + {{q}_{0}}{{C}_{0}} - qC. \\ \end{gathered} $

В закрытом (q = q₀ = 0) и квазиоткрытом/квазизакрытом (q = q₀ ≠ 0) реакторах для реакции (II) выполняется СЗС (3) A + B + C = 1. Зададим значения констант, например, k₁ = k₋₁ = k₂ = k₋₁ = 1, тогда λ₁ = −1, λ₂ = −3, A_∞ = С_∞ = 1/3 и решения (2) системы (1.1) запишутся

(1.2)

$\begin{gathered} A = {{({{A}_{0}} - {{C}_{0}}){\text{exp}}( - t)} \mathord{\left/ {\vphantom {{({{A}_{0}} - {{C}_{0}}){\text{exp}}( - t)} 2}} \right. \kern-0em} 2} + \\ + \,\,({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ \end{gathered} $

(1.3)

$\begin{gathered} C = {{({{C}_{0}} - {{A}_{0}}){\text{exp}}( - t)} \mathord{\left/ {\vphantom {{({{C}_{0}} - {{A}_{0}}){\text{exp}}( - t)} 2}} \right. \kern-0em} 2} + \\ + \,\,({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $

Для закрытого реактора соотношения (5)−(7) неприменимы, и одного эксперимента для определения мультиреагентных инвариантов недостаточно. Воспользуемся соотношениями (8)−(19) и проведем два эксперимента на их основе. Выберем н. у. для первого эксперимента согласно (10), например, A₀₁ = 0, B₀₁ = 1/3, C₀₁ = 2/3, а для второго эксперимента − произвольно, например, A₀₂ = = 2/3, B₀₂ = 0, C₀₂ = 1/3. Тогда A_1∞ = A_2∞ = С_1∞ = = С_2∞ = 1/3 и решения (1.2)−(1.3) в виде (8)−(9) примут вид

(1.4)

$\begin{gathered} {{A}_{1}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}{\text{exp}}( - t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{C}_{1}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}{\text{exp}}( - t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ \end{gathered} $

(1.5)

$\begin{gathered} {{A}_{2}} = {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{\text{exp}}( - t) + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{C}_{2}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}{\text{exp}}( - t) + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}{\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $

Из (1.4) следуют соотношения

(1.6)

$\begin{gathered} {\text{exp}}( - t) = 1 - 3{{A}_{1}} = 3{{C}_{1}} - 1,\,\, \\ {\text{exp}}( - 3t) = {\text{ex}}{{{\text{p}}}^{3}}( - t) = \\ = \,\,{{(1 - 3{{A}_{1}})}^{3}} = {{(3{{C}_{1}} - 1)}^{3}}. \\ \end{gathered} $

Подставим (1.6) в (1.5) и найдем инварианты: два однореагентных двухэкспериментных

(1.7)

$\begin{gathered} {{I}_{{12}}}(t) \equiv 6{{A}_{2}} - (1 - 3{{A}_{1}}) - {{(1 - 3{{A}_{1}})}^{3}} = \\ = \,\,6{{С}_{2}} + (3{{C}_{1}} - 1) - {{(3{{C}_{1}} - 1)}^{3}} = 2 \\ \end{gathered} $

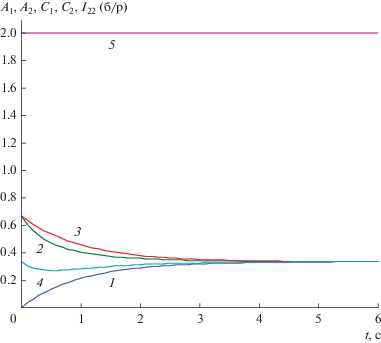
и четыре двухреагентных двухэкспериментных

(1.8)

$\begin{gathered} {{I}_{{22}}}\left( t \right) \equiv 6{{A}_{2}} - \left( {3{{C}_{1}} - 1} \right) - {{\left( {3{{C}_{1}} - 1} \right)}^{{3~}}} = \\ = \,\,6{{С}_{2}} + \left( {1 - 3{{A}_{1}}} \right) - {{\left( {1 - 3{{A}_{1}}} \right)}^{3}} = ~ \\ = 6{{A}_{2}} - (1 - 3{{A}_{1}}) - {{(3{{C}_{1}} - 1)}^{3}} = \\ = \,\,6{{С}_{2}} + {\text{ }}(3{{C}_{1}} - 1) - {{(1 - 3{{A}_{1}})}^{3}} = 2.~ \\ \end{gathered} $

Многореагентные инварианты (1.8) выражают новые локальные нестационарные КЗС, которые ранее в литературе не были описаны. Временные зависимости инвариантов (1.8) и концентраций реагентов для реакции (II) в закрытом реакторе приведены на рис. 1. Здесь горизонтальная линия соответствует сразу четырем двухреагентным инвариантам, которые выражаются любыми из соотношений (1.8). Если при исследовании реакции (II) с учетом ошибок измерений наблюдаются такие линии, то ее предполагаемый механизм согласуется со всеми гипотезами, использованными в модели (1.1). Если при тех же н. у. первого эксперимента A₀₁ = 0, B₀₁ = 1/3, C₀₁ = 2/3 выбирать другие н. у. для третьего и последующих экспериментов, например, A₀₃ = 1/3, B₀₃ = 0, C₀₃ = 2/3 или A₀₄ = 1/4, B₀₄ = 0, C₀₄ = 3/4, то для каждой пары экспериментов можно найти еще столько же описываемых соотношениями (1.7)−(1.8) новых инвариантов и т.д. Если же взять другие н. у. и для первого эксперимента, например, A₀₁ = C₀₁ = 1/2, B₀₁ = 0, то получим снова столько же новых инвариантов, сколько было найдено в предыдущих экспериментах.

Рис. 1.

Концентрации реагентов А и С реакции (II) в двух экспериментах закрытого реактора и двухреагентные инварианты (1.8): 1 − A₁(t); 2 − A₂(t); 3 − С₁(t); 4 − С₂(t); 5 − I₂₂(t).

В открытом реакторе q ≠ q₀ соотношения (4)−(7) становятся уже применимыми и позволяют найти также и одноэкспериментные многореагентные инварианты. Например, при q₀ = 1, q = 2 и k₁ = k₋₁ = k₂ = k₋₁ = 1, решения (2) системы (1.1) запишутся

(1.9)

$\begin{gathered} A = {{C}_{A}}_{1}{\text{exp}}({{\lambda }_{1}}t) + {{C}_{{A2}}}{\text{exp}}({{\lambda }_{2}}t) + \\ + \,\,{{C}_{{A3}}}{\text{exp}}({{\lambda }_{3}}t) + {{A}_{\infty }}, \\ \end{gathered} $

(1.10)

$\begin{gathered} B = {{C}_{{B1}}}{\text{exp}}({{\lambda }_{1}}t) + {{C}_{{B2}}}{\text{exp}}({{\lambda }_{2}}t) + \\ + \,\,{{C}_{{B3}}}{\text{exp}}({{\lambda }_{3}}t) + {{B}_{\infty }}, \\ \end{gathered} $

(1.11)

$\begin{gathered} C = {{C}_{C}}_{1}{\text{exp}}({{\lambda }_{1}}t) + {{C}_{{C2}}}{\text{exp}}({{\lambda }_{2}}t) + \\ + \,\,{{C}_{{C3}}}{\text{exp}}({{l}_{3}}t) + {{C}_{\infty }}, \\ \end{gathered} $

где λ₁ = −q, λ₂ = −1 − q, λ₃ = −3 − q, C_A1 = 1/6S₀, C_A2 = 1/3(A₀ − C₀), C_A3 = 2/15A₀ − 4/15B₀ + 2/15C₀, C_B1 = 1/6S₀, C_B2 = 0, C_B3 = 8/15B₀ − 4/15A₀ − 4/15C₀, C_C1 = 1/6S₀, C_C2 = 1/3(С₀ − A₀), C_C3 = 2/15A₀ − 4/15B₀ + + 2/15C₀, S₀ = A₀ + B₀ + C₀, A_∞ = 11/30A₀ + 1/10B₀ + + 1/30C₀, B_∞ = 1/10A₀ + 3/10B₀ + 1/10C₀, C_∞ = = 1/30A₀ + 1/10B₀ + 11/30C₀. Неавтономный ЗС (4) примет вид

(1.12)

$A + B + C = {\text{exp}}({{\lambda }_{1}}t)({{S}_{0}} - {{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q}) + {{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q},$

а выражения (5), (6) соответственно запишутся

(1.13)

$\begin{gathered} {{E}_{1}} \equiv {\text{exp}}( - qt) = \\ = \,\,{{[(A + B + C)--{{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q}]} \mathord{\left/ {\vphantom {{[(A + B + C)--{{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q}]} {({{S}_{0}} - {{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q})}}} \right. \kern-0em} {({{S}_{0}} - {{{{q}_{0}}{{S}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}{{S}_{0}}} q}} \right. \kern-0em} q})}}, \\ \end{gathered} $

(1.14)

${{E}_{2}} \equiv {\text{exp}}({{\lambda }_{2}}t) = E_{1}^{{ - \lambda 2/q}},\,\,\,{{E}_{3}} \equiv {\text{exp}}({{\lambda }_{3}}t) = E_{1}^{{ - \lambda 3/q}}.$

Соотношения (1.9)−(1.14) дают три трехреагентных одноэкспериментных инварианта (7):

(1.15)

${{I}_{{31,1}}}\left( t \right) \equiv A - {{C}_{A}}_{1}{{E}_{1}} - {{C}_{A}}_{2}{{E}_{2}}~ - {{C}_{A}}_{3}{{E}_{3}} = {{A}_{\infty }},$

(1.16)

${{I}_{{31,2}}}\left( t \right) \equiv B - {{C}_{B}}_{1}{{E}_{1}} - {{C}_{B}}_{2}{{E}_{2}} - {{C}_{B}}_{3}{{E}_{3}} = {{B}_{\infty }},$

(1.17)

${{I}_{{31,3}}}\left( t \right) \equiv C - {{C}_{C}}_{1}{{E}_{1}} - {{C}_{C}}_{2}{{E}_{2}}~ - {{C}_{C}}_{3}{{E}_{3}} = {{C}_{\infty }}.$

Эти инварианты не зависят от времени, т.к. определяются стационарными концентрациями реагентов и реализуются в одном нестационарном эксперименте при любых скоростях реакционного потока и н. у. (рис. 2).

Рис. 2.

Концентрации реагентов А, B и С реакции (II) в одном эксперименте открытого реактора и трехреагентные инварианты (1.15)−(1.17): 1 − A(t); 2 − B(t); 3 − С(t); 4 – I_31,1(t), 5 – I_31,2(t), 6 – I_31,3(t).

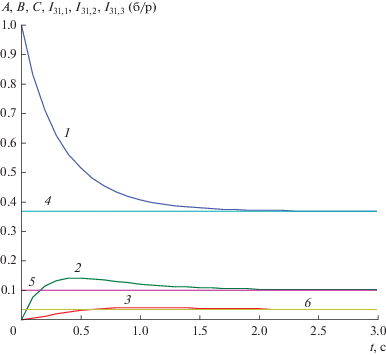
Три горизонтальных линии на рис. 2 описывают три инварианта (1.15)−(1.17), которые наблюдаются в одном эксперименте с н. у. A₀ = 1, B₀ = 0, C₀ = 0 при стационарных концентрациях A_∞ = = 11/30, B_∞ = 1/10, C_∞= 1/30 и визуально легко проверяются.

Пример 2. Рассмотрим параллельную реакцию

(III)

$1)\,\,{\mathbf{A}} = {\mathbf{B}},{\text{ }}2)\,\,{\mathbf{A}} = {\mathbf{С}}.$

Эта реакция в закрытом реакторе с учетом СЗС A + B + C = 1 описывается ОДУ

(2.1)

$\begin{gathered} A' = - {{k}_{1}}A + {{k}_{ - }}_{1}(1 - A - C) - {{k}_{2}}A{\text{ }} + {\text{ }}{{k}_{ - }}_{2}C, \\ C' = {{k}_{2}}(1 - A - C) - {{k}_{{ - 2}}}C. \\ \end{gathered} $

Решения ОДУ (2.1) при значениях констант скоростей k₁ = k₋₁ = k₂ = k₋₁ = 1 запишутся

(2.2)

$A = ({{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$

(2.3)

$C = ({{C}_{0}} - {{A}_{0}}){\text{exp}}( - 2t) + {\text{ }}({{A}_{0}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}.$

Для двух н. у. A₀₁ = 0, C₀₁ = 2/3 и A₀₂ = 2/3, C₀₂ = = 1/3 эти решения примут вид

(2.4)

$\begin{gathered} {{A}_{1}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}{\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{A}_{2}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}{\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ \end{gathered} $

(2.5)

$\begin{gathered} {{C}_{1}} = {{2{\text{exp}}( - 2t)} \mathord{\left/ {\vphantom {{2{\text{exp}}( - 2t)} 3}} \right. \kern-0em} 3} - {{{\text{exp}}( - 3t)} \mathord{\left/ {\vphantom {{{\text{exp}}( - 3t)} 3}} \right. \kern-0em} 3} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{C}_{2}} = {{ - {\text{exp}}( - 2t)} \mathord{\left/ {\vphantom {{ - {\text{exp}}( - 2t)} 3}} \right. \kern-0em} 3} + {{{\text{exp}}( - 3t)} \mathord{\left/ {\vphantom {{{\text{exp}}( - 3t)} 3}} \right. \kern-0em} 3} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $

Из (2.4) следуют соотношения

(2.6)

$\begin{gathered} {\text{exp}}( - 3t) = 1 - 3{{A}_{1}} = 3{{A}_{2}} - 1, \\ {\text{exp}}( - 2t) = {\text{ex}}{{{\text{p}}}^{{2/3}}}( - 3t) = \\ = \,\,{{(1 - 3{{A}_{1}})}^{{2/3}}} = {{(3{{A}_{2}} - 1)}^{{2/3}}}. \\ \end{gathered} $

Подставив (2.6) в (2.5), найдем инварианты: один однореагентный двухэкспериментный

(2.7)

${{I}_{{12}}}(t) \equiv 3{{A}_{1}} + {\text{ }}3{{A}_{2}} = 2,$

четыре двухреагентных двухэкспериментных

(2.8)

$\begin{gathered} {{I}_{{22}}}\left( t \right) \equiv 3{{С}_{1}} - 2{{(3{{A}_{2}} - 1)}^{{2/3}}} + 3{{A}_{2}} - 1 = \\ = \,\,3{{С}_{2}} + {{(1 - 3{{A}_{1}})}^{{2/3}}} + 3{{A}_{1}} - 1 = \\ = \,\,{{3{{C}_{1}}} \mathord{\left/ {\vphantom {{3{{C}_{1}}} 2}} \right. \kern-0em} 2} + 3{{C}_{2}} - {{3{{A}_{2}}} \mathord{\left/ {\vphantom {{3{{A}_{2}}} 2}} \right. \kern-0em} 2} = {{3{{C}_{1}}} \mathord{\left/ {\vphantom {{3{{C}_{1}}} 4}} \right. \kern-0em} 4} + \\ + \,\,{{3{{C}_{2}}} \mathord{\left/ {\vphantom {{3{{C}_{2}}} 2}} \right. \kern-0em} 2} + {{3{{A}_{1}}} \mathord{\left/ {\vphantom {{3{{A}_{1}}} 4}} \right. \kern-0em} 4} = 1, \\ \end{gathered} $

и два двухреагентных одноэкспериментных

(2.9)

$\begin{gathered} {{I}_{{21}}}(t) \equiv 3{{С}_{1}} - 2{{(1 - 3{{A}_{1}})}^{{2/3}}} + 1 - 3{{A}_{1}} = \\ = \,\,3{{С}_{2}} + {{(3{{A}_{2}} - 1)}^{{2/3}}} + 1 - 3{{A}_{2}} = 1. \\ \end{gathered} $

Для реакции (III), как и для реакции (II), в открытом безградиентном реакторе могут быть найдены и одноэкспериментные многореагентные инварианты вида (7).

ЗАКЛЮЧЕНИЕ

В настоящей работе получены новые разновидности многореагентных автономных кинетических инвариантов химических реакций, которые можно наблюдать с помощью одного или нескольких нестационарных экспериментов в изотермическом безградиентном реакторе. Эти инварианты представляют собой комбинации концентраций реагентов и кинетических параметров реакции, которые могут быть использованы для идентификации механизмов химических реакций.

Список литературы

Prelle M.J., Singer M.F. Elementary first integrals of differential equations / Proceedings of the 1981 ACM Symp. of Symbolic and Algebraic Computation. Snowbird Utah, August 5−7, 1981. P. 30.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. хим. 1988. Т. 62. № 11. С. 3069. (Alekseev B.V., Koltsov N.I., Fedotov V.Kh. // Zhurn. fiz. khim. 1988. V. 62. № 11. P. 3069.)
Патмар Э.С., Кольцов Н.И. // Известия вузов. Химия и хим. технология. 2008. Т. 51. № 1. С. 61. (Patmar E.S., Kol’tsov N.I. // Izvestiya vuzov. Khimiya i khim. tekhnologiya. 2008. V. 51. № 1. P. 61 (in Russ.)).
Яблонский Г.С. // Теор. основы хим. технол. 2014. V. 48. №. 5. P. 551. DOI: 10.7868/S0040357114050121. (Yablonsky G.S. // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 608.)
Branco-Pinto D., Yablonsky G., Marin G., Constales D. // Entropy. 2015. V. 17. P. 6783.
Branco P.D., Yablonsky G., Marin G.B., Constales D. // Chem. Eng. Sci. 2017. V. 158. P. 370. https://doi.org/10.1016/J.CES.2016.10.032
Peng B., Yablonsky G.S., Constales D., Marin G.B. // Chem. Eng. Sci. 2018. V. 191. P. 262. https://doi.org/10.1016/J.CES.2018.06.065
Yablonsky G.S., Branco P.D., Marin G.B., Constales D. // Chem. Eng. Sci. 2019. V. 196. P. 384. https://doi.org/10.1016/J.CES.2018.11.010
Федотов В.Х., Кольцов Н.И. // Кинетика и катализ. 2019. Т. 60. № 6. С. 756. https://doi.org/10.1134/S0453881119060042. (Fedotov V.Kh., Kol’tsov N.I. // Kinet. Catal. 2019. V. 60. № 6. P. 776.)10.1134/S0453881119060042
Кольцов Н.И. // Кинетика и катализ. 2020. Т. 61. № 4. С. 482. https://doi.org/10.31857/S045388112003017X. (Kol’tsov N.I. // Kinet. Catal. 2020. V. 61. № 4. P. 530.)10.31857/S045388112003017X

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал