1. На главную
  2. Электронные версии
  3. Кинетика и катализ
  4. T. 62, № 4, 2021

Кинетика и катализ, 2021, T. 62, № 4, стр. 418-425

Определение констант скорости реакций Cr + O2 + M → CrO2 + M и Cr + O2 → CrO + O

П. А. Власов a, А. Е. Плоскирев a, В. Н. Смирнов a, *

a ФГБУН Федеральный исследовательский центр химической физики им. Н.Н. Семенова РАН
119991 Москва, Россия

* E-mail: vns1951@yandex.ru

Поступила в редакцию 28.01.2021
После доработки 18.03.2021
Принята к публикации 02.04.2021

Полный текст (PDF)

Аннотация

На основе нового метода обработки экспериментальных данных определены константы скоростей взаимодействия атомов хрома с молекулярным кислородом по двум возможным каналам, рекомбинационному и обменному: Cr + O2 + M → CrO2 + M (I) и Cr + O2 → CrO + O (II). Полученные результаты в совокупности с имеющимися литературными данными приводят к следующим выражениям для констант скорости рекомбинации в пределе низких давлений и обменной реакции: ${{k}_{{1,0}}}(300 < T < 2000\,{\text{K}}) = {\text{ }}3.7{\text{ }} \times {\text{ }}{{10}^{{18}}}{{\left( {\frac{T}{{1000}}} \right)}^{{ - 1.49}}},\,\,\,{\text{с}}{{{\text{м}}}^{{\text{6}}}}{\text{ мол}}{{{\text{ь}}}^{{ - 2}}}\,{{{\text{с}}}^{{ - 1}}},$ ${{k}_{2}}(700 < T < 4000\,{\text{K}}) = $ $4.0 \times {{10}^{{14}}}{{\left( {\frac{T}{{1000}}} \right)}^{{ - 0.32}}}exp\left( { - \frac{{4480{\kern 1pt} \,{\text{K}}}}{T}} \right)$ см3 моль‒1 c‒1. На основе k2(T) и константы равновесия для реакции (II) получено выражение для константы скорости обратной реакции: ${{k}_{{ - 2}}}(700 < T < 4000\,{\text{K}}) = 3.6 \times {{10}^{{13}}}{{\left( {\frac{T}{{1000}}} \right)}^{{ - 0.64}}}$ см3 моль‒1 c‒1. Моделирование в рамках теории РРКМ показывает, что для расчета константы скорости k1,0(T) недостаточно учитывать только основное электронное состояние молекулы CrO2 ‒ требуется включить также низколежащие возбужденные электронные состояния, вплоть до порога диссоциации. Сопоставление измеренных и расчетных температурных зависимостей показывает, что наилучшее согласие между ними достигается при средней порции энергии, передаваемой в деактивирующих столкновениях возбужденной молекулы CrO2 с молекулами газа-разбавителя, равной ΔE = = 2.8 кДж/моль.

Ключевые слова: атомы Cr, молекулярный кислород, рекомбинация, обменная реакция, константы скорости, теория РРКМ

1. ВВЕДЕНИЕ

Взаимодействие атомов хрома с молекулярным кислородом в газовой фазе представляет значительный интерес как с точки зрения фундаментальных исследований реакционной способности [1, 2], так и для ряда приложений [3–8], например, для анализа образования и превращений соединений хрома при сжигании угля, промышленных и бытовых отходов [3‒5], объяснения ингибирующего действия хрома на горение газов [6, 7], а также для создания моделей эпитаксиального роста пленок диоксида хрома [8].

Как и реакция Fe + O2 [9], взаимодействие атома хрома с молекулой кислорода может происходить по двум каналам ‒ рекомбинационному и обменному:

(I)
${\text{Cr}} + {{{\text{O}}}_{{\text{2}}}} + {\text{M}} \to {\text{Cr}}{{{\text{O}}}_{{\text{2}}}} + {\text{M,}}$
(II)
${\text{Cr}} + {{{\text{O}}}_{{\text{2}}}} \to {\text{CrO}} + {\text{O}}{\text{.}}$

Насколько нам известно, константу скорости реакции (I) измеряли только в трех работах [10–12]. В работе [10] измерения проводили в статическом реакторе в диапазоне температур и давлений 298–323 K и 2–600 Торр соответственно. Заметных признаков протекания обменной реакции обнаружено не было, что вполне объяснимо, поскольку реакция (II) существенно эндотермична [13, 14].

В работе [11] эксперименты по взаимодействию атомов хрома с молекулярным кислородом осуществляли в быстропроточном реакторе в диапазоне температур и давлений 290–1510 K и 11–460 Торр соответственно. Экспериментальные данные были интерпретированы в рамках следующих предположений: 1) при температурах ниже 709 К реакция (II) не вносит существенного вклада в наблюдаемую константу скорости расходования атомов хрома; 2) реакция (I) идет в переходной по давлению области. При более высоких температурах реакция (I) протекает в режиме низких давлений, поэтому наблюдаемая константа скорости была представлена авторами как сумма константы скорости реакции (I) умноженной на полную концентрацию и константы скорости реакции (II) (формула (6) в [11]). Это представление мы применили в настоящей работе для новой интерпретации данных из [11], результат которой, наряду с результатами из [10‒12], был использован для сопоставления с предсказаниями описанной ниже модели для расчета константы скорости реакции (I) в пределе низких давлений.

В работе [12] взаимодействие атомов Cr с O2 исследовали в ударной трубе, снабженной средствами атомно-абсорбционной регистрацией атомов хрома, в интервале температур 720–3550 K при полной плотности газа 2.8 × 10–6 моль/см3 и в области 720–980 K при 1.4 × 10–5 моль/см3. Константы скорости реакций (I) и (II) были получены с применением достаточно сложной процедуры, основанной на предположении, что при ~700 K вклад обменной реакции (II) пренебрежимо мал. При этой температуре с использованием переходных кривых были вычислены температурные зависимости констант скорости реакции (I) в пределе низких и высоких давлений и с помощью теории Райса–Рамспергера–Касселя–Маркуса (РРКМ) экстраполированы в область температур вплоть до 4000 K. Далее на основе этих температурных зависимостей в области 720‒4000 K и метода переходных кривых была вычислена температурная зависимость константы скорости реакции (I) при полной плотности 2.8 × 10–6 моль/см3 и вычтена из температурной зависимости наблюдаемой (полной) константы скорости взаимодействия Cr с O2 с тем, чтобы получить константу скорости обменной реакции (II).

Одним из неожиданных результатов упомянутых исследований было то, что константа скорости рекомбинации атомов Cr с O2 в пределе низких давлений оказалась существенно выше, чем для аналогичной реакции других атомов, включая атомы металлов (рис. 3 в [12]). В работе [12] сделано предположение, что это связано с большим числом низколежащих электронных термов, которые, складываясь вместе, создают высокую плотность колебательных уровней вблизи барьера диссоциации молекулы CrO2, величина которой, согласно теории РРКМ, пропорциональна константе скорости диссоциации (рекомбинации) в пределе низких давлений [15]. Однако в то время не было ни информации об этих электронных термах, ни подходящей модели для расчета их вклада. Впоследствии такие данные появились [16, 17], а в работе [9] была развита модель для вычисления константы скорости в пределе низких давлений, учитывающая вклад электронных термов.

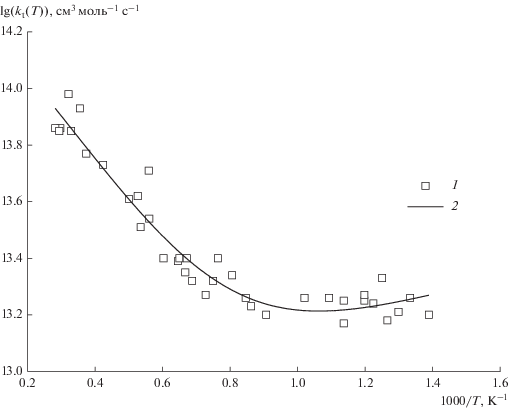
Рис. 1.

Температурная зависимость суммарной константы скорости расходования атомов Cr в реакциях (I) и (II), kt(T), построенная на основе данных из [12]: 1 ‒ экспериментальные точки, 2 ‒ аппроксимация функциональной зависимостью (10).

В настоящей работе рассчитана константа скорости реакции рекомбинации (I) в пределе низких давлений в рамках аддитивной модели, предложенной в [9], и проведено сопоставление результатов с имеющимися литературными данными. Кроме того, обработка результатов экспериментов из [12] с помощью нового метода позволила получить уточненные значения констант скорости реакций (I) и (II).

2. МОДЕЛЬ ДЛЯ ВЫЧИСЛЕНИЯ КОНСТАНТ СКОРОСТИ РЕАКЦИЙ (I) И (–I) В ПРЕДЕЛЕ НИЗКИХ ДАВЛЕНИЙ

Константу скорости реакции рекомбинации (I) находили по формуле

(1)
${{k}_{{{\text{1,0}}}}}(T) = {{k}_{ - }}_{{{\text{1,0}}}}(T){{K}_{{1,eq}}}\left( T \right),$
где k–1,0(T) – константа скорости обратной реакции и K1,eq(T) – константа равновесия. Выражение для K1,eq(T) имеет вид [13]:
(2)
$K{}_{{{\text{1,eq}}}}(T) = {{({{R}_{p}}T)}^{{ - \Delta n}}}\exp \left( {\frac{{{{\Delta }_{{{\text{r1}}}}}\Phi ^\circ (T)}}{R} - \frac{{{{\Delta }_{{{\text{r1}}}}}H^\circ (0)}}{{RT}}} \right),$
где ΔrФ(T) и ΔrH(0) – изменение приведенной энергии Гиббса при температуре T и изменение энтальпии при 0 K для реакции (I), Rp – универсальная газовая постоянная (Rp = 82.057 см3 атм моль–1 K–1), Δn – изменение числа молей (Δn = –1 для реакции (I)). ΔrФ○(T) и ΔrH○(0) для реакции (I) рассчитывали по формулам

$\begin{array}{*{20}{c}} {{{\Delta }_{{r1}}}\Phi ^\circ \left( T \right) = \Phi ^\circ \left( {{\text{Cr}}{{{\text{O}}}_{{\text{2}}}}{\text{,}}T} \right)--\Phi ^\circ \left( {{\text{Cr}},T} \right) - \Phi ^\circ \left( {{{{\text{O}}}_{2}},T} \right),} \\ {{{\Delta }_{{r1}}}H^\circ \left( T \right) = H^\circ \left( {{\text{Cr}}{{{\text{O}}}_{2}},T} \right)--H^\circ \left( {{\text{Cr}},T} \right)--H^\circ \left( {{{{\text{O}}}_{2}},T} \right).} \end{array}$

Величины Φ°(Cr, T) и Φ°(O2, T) взяты из [13, 14].

Константу скорости диссоциации CrO2 в пределе низких давлений находили по формуле [15]

(3)
${{k}_{ - }}_{{{\text{1,0}}}}(T) = {{{{\beta }}}_{{\text{с}}}}{{k}_{{ - 1{\text{,sc}}}}}(T),$
где βс ‒ коэффициент эффективности передачи энергии при столкновениях, k–1,sc ‒ константа скорости диссоциации в пределе сильных столкновений.

Расчет константы скорости диссоциации молекулы CrO2 в пределе сильных столкновений представляет достаточно сложную задачу из-за необходимости учета большого числа низколежащих возбужденных электронных уровней. Экспериментальная информация о молекулярных параметрах CrO2 весьма ограничена: измерены только некоторые колебательные частоты молекул OCrO и CrOO в криогенных матрицах [16]. С другой стороны, квантово-химические расчеты показывают, что молекула CrO2 существует в виде трех изомеров: оксо- (OCrO), пероксо- (Cr(O2), циклическая структура) и суперпероксо-формы (CrOO), каждый из которых имеет сложную систему вложенных электронных термов [16, 17].

Согласно [9] k–1,sc может быть представлена как сумма вкладов от индивидуальных электронных состояний:

(4)
${{k}_{{ - 1{\text{,sc}}}}}(T) = \sum\limits_{i = 1}^l {{{k}_{{ - 1{\text{,sc,}}i}}}(T)} ,$
(5)
$\begin{gathered} {{k}_{{ - 1,sc,i}}} = {{Z}_{{{\text{LJ}}}}}RT \times \\ \times \,\,\frac{{{{M}_{i}}{{Q}_{{{\text{r}},i}}}(T){{\rho }_{{{\text{v}},i}}}({{E}_{0}} - {{E}_{i}}){{F}_{{{\text{r}},i}}}(T){{F}_{{E,i}}}(T){{F}_{{{\text{anh}}}}}}}{{\sum\limits_{i = 1}^l {{{M}_{i}}{{Q}_{{{\text{v}},i}}}(T){{Q}_{{{\text{r}},i}}}(T)\exp ({{ - {{E}_{i}}} \mathord{\left/ {\vphantom {{ - {{E}_{i}}} {RT}}} \right. \kern-0em} {RT}})} }} \times \\ \times \,\,\exp ({{ - {{E}_{0}}} \mathord{\left/ {\vphantom {{ - {{E}_{0}}} {RT}}} \right. \kern-0em} {RT}}), \\ \end{gathered} $
где i – номер электронного состояния, l – число учитываемых электронных состояний, R – универсальная газовая постоянная, T – температура, E0 – барьер диссоциации, а Ei – энергия, ρv,i (E0 – Ei) – плотность колебательных уровней вблизи барьера диссоциации, Fr,i(T) – вращательный фактор, FE,i – энергетический фактор, Fanh – поправка на ангармонизм, Qv,i(T) – колебательная статистическая сумма, Mi – мультиплетность, Qr,i(T) – вращательная статистическая сумма i-го электронного состояния. Величины Qv,i(T) и Qr,i(T) определяли стандартным образом [13] . Фактор частоты газокинетических столкновений ZLJ рассчитывали по формуле [15]
(6)
${{Z}_{{{\text{LJ}}}}} = {{N}_{{\text{A}}}}\pi {{{{\sigma }}}^{2}}{{\left( {\frac{{8kT}}{{{\mu }}}} \right)}^{{0.5}}}{{\left[ {0.7 + 0.52\lg \left( {{{kT} \mathord{\left/ {\vphantom {{kT} {{\varepsilon }}}} \right. \kern-0em} {{\varepsilon }}}} \right)} \right]}^{{ - 1}}},$
где NA – число Авогадро, k – постоянная Больцмана, μ – приведенная молекулярная масса партнеров по столкновению, CrO2–Ar. Значения параметров потенциала Леннарда–Джонса, σ и ε, взяты из работы [10] : σ(CrO2–Ar) = 5.0 Å, ε(CrO2–Ar)/k = 400 K.

Коэффициент эффективности передачи энергии при столкновениях вычисляли по формуле, полученной из выражения, представленного в [15]:

(7)
${{{{\beta }}}_{{\text{с}}}} = {{\left\{ {{{{\left[ {{{{\left( {\frac{{\Delta E}}{{2RT{{F}_{E}}}}} \right)}}^{2}} + \frac{{\Delta E}}{{RT{{F}_{E}}}}} \right]}}^{{0.5}}} - \frac{{\Delta E}}{{2RT{{F}_{E}}}}} \right\}}^{2}},$
где 〈ΔE〉 – средняя порция энергии, передаваемая во всех столкновительных переходах (вниз и вверх); остальные обозначения смотри выше. Энергетический фактор FE в выражении (7) был представлен как сумма значений FE,i, взвешенных по удельным вкладам электронных состояний в константу скорости диссоциации в пределе сильных столкновений:

(8)
${{F}_{E}} = \frac{{\sum\limits_{i = 1}^l {{{F}_{{E,i}}}} {{k}_{{ - 1{\text{,sc,}}i}}}(T)}}{{{{k}_{{ - 1{\text{,sc}}}}}(T)}}.$

Поправку на ангармонизм в выражении (5) рассчитывали по формуле [15]:

(9)
${{F}_{{{\text{anh}}}}}{\text{ = }}{{\left( {\frac{{s - 1}}{{s - 1.5}}} \right)}^{m}},$
где s – полное число осцилляторов и m – число осцилляторов Морзе. Применительно к исследуемой системе, m = 3 для OCrO и m = 2 для Cr(O2) и CrOO.

Следует отметить, что данную модель следует рассматривать как первое приближение, поскольку остается неясным, как различные изомеры CrO2 и их электронные состояния взаимодействуют друг с другом при высоких энергиях возбуждения, в частности, вблизи барьера диссоциации, и какова результирующая структура энергетических уровней в этой области. Кроме того, большинство молекулярных параметров, а именно, все параметры электронно-возбужденных состояний, находят из расчетов, при этом результат существенно зависит как от квантово-химического метода, так и базисного набора.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Как отмечалось во введении, температурная зависимость k1,0(T), представленная в работе [12], была получена достаточно сложным путем. Кроме того, данные, приведенные в [12] для высоких давлений, демонстрируют значительный разброс. Это побудило нас попытаться найти альтернативный, более простой подход к определению констант скорости реакций (I) и (II). С этой целью, как и в работе [11], суммарная (наблюдаемая) константа скорости расходования атомов хрома в реакции с молекулярным кислородом, измеренная в [12] при низкой полной концентрации газовой смеси ([M] = 2.8 × 10‒6 моль/см3), была представлена суммой

(10)
${{k}_{{\text{t}}}}(T) = {{k}_{{1,0}}}(T)\left[ {\text{M}} \right] + {{k}_{2}}(T)$
c k1,0(T) и k2(T) в виде
(11)
${{k}_{{1,0}}}(T) = {{A}_{1}}{{\left( {\frac{T}{{1000}}} \right)}^{{{{n}_{1}}}}},$
(12)
${{k}_{2}}(T) = {{A}_{2}}{{\left( {\frac{T}{{1000}}} \right)}^{{{{n}_{2}}}}}exp\left( { - \frac{{{{\Delta }_{{{\text{r2}}}}}H^\circ (0\,K)}}{{RT}}} \right),$
где A1, A2, n1 и n2 ‒ константы; Δr2H°(0 K) ‒ изменение энтальпии в реакции (II) при 0 K (37.385 кДж/моль [13, 14]). Аппроксимация выражением (10) экспериментально измеренной температурной зависимости kt(T), показанной на рис. 1, дала следующее значения параметров для интервала 700‒4000 K: A1 = 4.3 × 1018 см6 моль‒2 c‒1, n1 = ‒1.17; A2 = 3.9 × 1014 см3 моль‒1 c‒1, n2 = ‒0.22.

На рис. 2 показана температурная зависимость константы скорости реакции рекомбинации (I) в пределе низких давлений, полученная в настоящей работе из экспериментальных данных, приведенных в [12], с помощью вышеописанного метода, и соответствующие литературные данные. Показаны также теоретические температурные зависимости этой константы скорости, рассчитанные при различных значениях средней порции энергии, передаваемой во всех столкновительных переходах. Как видно из рис. 2, экспериментальная температурная зависимость k1,0(T) (кривая 4), найденная в настоящей работе, находится в хорошем согласии с результатами измерений из работ [10] и [11] (кривые 1, 2). В тоже время температурная зависимость k1,0(T), определенная в [12] с помощью сложной процедуры (кривая 3), существенно отличается от остальных ‒ как экспериментальных, так и теоретических.

Рис. 2.

Температурные зависимости константы скорости рекомбинации атомов Cr с O2 (реакция (I)) в пределе низких давлений. Эксперимент: 1, 2, 3 ‒ данные из [10], [11] и [12] соответственно; 4 ‒ получена в настоящей работе из экспериментальных результатов, представленных в [12] (формула (11) с A1 = 4.3 × 1018 см6 моль–2 c–1 и n1 = –1.17 ); 5 ‒ обобщающая зависимость для результатов настоящей работы и данных из [10] и [11] (формула (11) с A1 = 3.7 × 1018 см6 моль–2 c–1 и n1 = –1.49). Теория: 6, 7 ‒ расчет в пределе сильных столкновений (∆E → ∞, соответственно, βс = 1) с учетом только основного (6) и всех (7) электронных состояний молекулы CrO2; 8‒10 ‒ с учетом всех электронных состояний при различных значениях средней порции передаваемой энергии ∆E в выражении для βс (формула (7)): ∆E равна 1.0 (8), 3.0 (9) и 5.0 кДж/моль (10).

Рис. 3.

Температурная зависимость константы скорости обменной реакции (II): 1 и 2 ‒ данные из [11] и [12] соответственно, 3 ‒ настоящая работа, 4 ‒ обобщающая аппроксимация выражением (13).

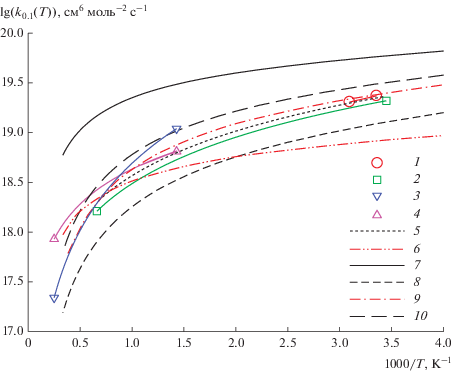
Обобщающая зависимость для результатов настоящей работы и данных из [10] и [11] (кривая 5) описывается формулой (11) с A1 = 3.7 × 1018 см6 моль‒2 c‒1, n1 = ‒1.49.

Как видно из рис. 2, даже в пределе сильных столкновений значения k1,0(T), вычисленные без учета возбужденных низколежащих электронных состояний, лежат ниже экспериментальных величин. Для расчетов с учетом всех возбужденных низколежащих электронных состояний наилучшее согласие с экспериментом достигается при средней порции передаваемой энергии ΔE = = 2.8 кДж моль‒1. Эта величина близка к значению, полученному для рекомбинации атомов железа с молекулярным кислородом: ΔE = 3.3 кДж моль‒1 [9].

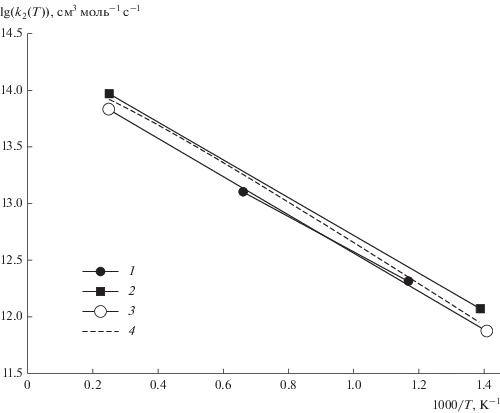
На рис. 3 показаны температурные зависимости константы скорости обменной реакции (II), найденные в настоящей работе (кривая 3) и в [11] (кривая 1) и [12] (кривая 2). В отличие от k1,0(T), все они находятся в хорошем согласии друг с другом. В температурном интервале, где эти зависимости перекрываются, наблюдается согласие в пределах 25%. Кроме того, энергия активации, полученная в настоящей работе, несколько выше, чем измеренная в [11]. Аппроксимация экспериментальных данных, представленных на рис. 3 с использованием выражения (12), дает

(13)
$\begin{gathered} {{k}_{2}}(700 < T < 4000\,{\text{K}}) = 4.0 \times {{10}^{{14}}}{{\left( {\frac{T}{{1000}}} \right)}^{{ - 0.32}}} \\ \times \,\,exp\left( { - \frac{{4480{\kern 1pt} \,{\text{K}}}}{T}} \right),\,\,{\text{с}}{{{\text{м}}}^{{\text{3}}}}\,\,{\text{мол}}{{{\text{ь}}}^{{ - 1}}}\,\,{{{\text{c}}}^{{ - 1}}}. \\ \end{gathered} $

На рис. 3 эта зависимость показана точечной линией.

Вычисленная с помощью константы равновесия константа скорости обратной реакции имеет вид

(14)
$\begin{gathered} {{k}_{{ - 2}}}(700 < T < 4000\,{\text{K}}) = \\ = 3.6 \times {{10}^{{13}}}{{\left( {\frac{T}{{1000}}} \right)}^{{ - 0.64}}},\,\,{\text{с}}{{{\text{м}}}^{3}}\,\,{\text{мол}}{{{\text{ь}}}^{{ - 1}}}\,\,{{{\text{c}}}^{{ - 1}}}. \\ \end{gathered} $

Эта реакция играет важную роль в механизме ингибирования воспламенения водорода атомами хрома [18, 19].

ЗАКЛЮЧЕНИЕ

Предложен новый способ определения констант скорости взаимодействия атомов металлов с молекулярным кислородом, протекающего по двум каналам ‒ рекомбинационному и обменному ‒ и продемонстрирована возможность его применения на примере реакции Cr + O2. Получены константы скорости реакции Cr + O2 + M = = CrO2 + M (I) в пределе низких давлений и реакции Cr + O2 = CrO + O (II) в прямом и обратном направлениях. Для вычисления константы скорости реакции (I) использована аддитивная модель, развитая в [9]. Показано, что без учета низколежащих возбужденных электронных состояний невозможно удовлетворительно описать кинетические параметры реакции (I). Вычисления в рамках предложенной модели с учетом всех электронных состояний позволили оценить среднюю порцию энергии, передаваемую возбужденной молекулой CrO2, в столкновениях с молекулами газа-разбавителя. Следует, однако, констатировать, что полученные кинетические параметры нуждаются в уточнении на основе новых расчетных и экспериментальных данных. В частности, было бы весьма желательно провести более детальные квантово-химические расчеты молекулярных параметров всех изомеров CrO2.

Таблица 1.

   Электронные состояния, их энергии Ei, произведения моментов инерции (I1I2I3)0.5 и колебательные частоты для различных изомеров CrO2

№ Состояние Ei,
кДж моль–1		 (I1I2I3)0.5,
а. е. м1.5 Å3		 ν1 ν2 ν3
см–1
OCrOа
1 13B1 0.0 235.2 973 253 1001
2 11B1 34.7 230.1 987 254 1007
3 13A1 72.4 246.2 952 339 984
4 11A1 98.4 243.8 1013 255 997
5 11A2 151.5 273.1 962 344 925
6 13B2 161.1 267.7 963 346 944
7 11A2 179.5 271.6 974 352 949
8 15A2 194.0 166.7 794 132 548
9 11B2 201.7 266.9 969 348 950
10 15A' 226.6 227.2 608 166 968
11 15B2 324.2 269.4 782 185 1391
Cr(O2)б
12 5B2 234.3 258.7 919 608 575
13 3B1 309.6 256.9 1189 428 312
14 7A2 338.9 324.0 1161 463 979
CrOOб
15 5A'' 280.3 301.5 1165 128 526
16 7A' 347.3 305.4 1141 201 540

а, б Вычислены в [17] и [16] соответственно.

Список литературы

  1. Schroden J.J., Davis H.F. // Adv. Ser. Phys. Chem. 2004. V. 14. Part 2. P. 215.

  2. Fontijn A. // Pure Appl. Chem. 1998. V. 70. P. 469.

  3. Abanades S., Flamant G., Gagnepain B., Gauthier D. // Waste Manage Res. 2002. V. 20. P. 55.

  4. Kashireninov O.E., Fontijn A. // Combust. Flame. 1998. V. 113. P. 498.

  5. Lissianski V.V., Maly P.M., Zamansky V.M., Gardiner W.C. // Ind. Eng. Chem. Res. 2001. V. 40. P. 3287.

  6. Koshiba Y., Agata S., Takahashi T., Ohtani H. // Fire Saf. J. 2015. V. 73. P. 48.

  7. Linteris G.T., Rumminger M.D., Babushok V.I. // Prog. Energy Combust. Sci. 2008. V. 34. P. 288.

  8. Wang J., Pathak M., Zhong X., LeClair P., Klein T.M., Gupta A. // Thin Solid Films. 2010. V. 518. P. 6853.

  9. Смирнов В.Н. // Хим. физика. 2013. Т. 32. С. 15.

  10. Parnis J.M., Mitchell S.A., Hackett P.A. // J. Phys. Chem. 1990. V. 94. P. 8152.

  11. Narayan A.S., Slavejkov A.G., Fontjin A. / Proc. 24th Intern. Sympos. on Combust. Pittsburgh: The Combust. Inst., 1992. P. 727.

  12. Смирнов В.Н. // Кинетика и катализ. 1993. Т. 34. С. 783. (Smirnov V.N. // Kinet. Catal. 1993. V. 34. P. 699.)

  13. Термодинамические свойства индивидуальных веществ. Справочник. Под ред. В.П. Глушко. Москва: Наука, 1978.

  14. Термодинамические свойства индивидуальных веществ: Элементы Zn, Cu, Cr, Co, Ni, Mn, Cr, V, Ti, Sc и их соединения. Электронный справочник. http:www.chem.msu.su/rus/tsiv/welcome.html.

  15. Troe J. // J. Chem. Phys. 1977. V. 66. P. 4758.

  16. Chertihin G.V., Bare D.W., Andrews L. // J. Chem. Phys. 1997. V. 107. P. 2798.

  17. Grein F. // Chem. Phys. 2008. V. 343. P. 231.

  18. Yu S., Kennedy I.M. // Combust. Sci. Tech. 2000. V. 160. P. 35.

  19. Yu S., Jones A.D., Chang D.P.Y., Kelly P.B., Kennedy I.M. / Proc. 27th Intern. Sympos. on Combust. Pittsburgh: The Combust. Inst., 1998. P. 1639.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал