Коллоидный журнал, 2019, T. 81, № 1, стр. 70-77

О вкладе дисперсионных сил в линейную и точечную энергию графена

А. И. Русанов^{1, 2, *}

¹ Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия

² Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский проспект, 31, Россия

^* E-mail: airusanov@mail.ru

Поступила в редакцию 26.06.2018

DOI: 10.1134/S0023291219010099

Полный текст (PDF)

Аннотация

Для двумерных структур линейная энергия и точечная энергия являются физическими величинами того же значения, что и, соответственно, поверхностная энергия и линейная энергия для трехмерных тел. Представленная теория рассчитывает вклад дисперсионных сил в локальную энергию когезии, локальную линейную энергию и точечную энергию графена из его микроскопических параметров: постоянной решетки, двумерной атомной плотности и парного потенциала взаимодействия. Расчет локальных величин ведется на основе тензора давления Ирвинга–Кирквуда внутри плоскопараллельной пустой двумерной щели конечной протяженности между двумя прямоугольными кусками графена, лежащими в одной плоскости. Расчет производится для абсолютного нуля температуры (когда энергия равносильна свободной энергии). Структура графена предполагается жесткой, что означает пренебрежение эффектом релаксации в ходе разъединения двух кусков графена. Результат расчета зависит от направления граничной линии графена. Для расчетов выбрана линия поперек σ-связей, соответствующая естественной границе графена. Расчет линейной и точечной энергии графена проведен для модели жестких шаров с дисперсионными силами и модели Леннард-Джонса. Установлено, что вблизи угла прямоугольного куска графена линейная энергия становится переменной величиной в пределах пяти расстояний между атомами в решетке, что позволяет оценить вклад дисперсионных сил в точечную энергию графена.

ВВЕДЕНИЕ

Для такой двумерной структуры, какой является графен, линейная энергия имеет тот же смысл, что и поверхностная энергия для трехмерных тел. В свою очередь, обычная линейная энергия при понижении размерности имеет своим аналогом точечную энергию в виде некоторой избыточной величины на краях линейной границы. В термодинамике графена [1] есть и другие энергетические характеристики. В основе их определения лежит работа разъединения двух смежных областей графенового листа

(1)

$w = \int\limits_\delta ^\infty {f(H){\kern 1pt} dH} ,$

где $f(H)$ – сила когезии на единицу длины разреза, H – расстояние между разделяемыми областями графена и δ – его минимальное значение. Если процесс разделения производится в адиабатических условиях, выражение (1) дает удвоенную линейную энергию ε графена:

(2)

$2\varepsilon = \int\limits_\delta ^\infty {f(H){\kern 1pt} dH} .$

Если же процесс изотермический, работа (1) дает удвоенную линейную свободную энергию (термодинамическое линейное натяжение по аналогии с термодинамическим поверхностным натяжением [2–4]). При абсолютном нуле энергия и свободная энергия совпадают, а потому энергию ε в (2) можно трактовать и как термодинамическое линейное натяжение графена. Однако с повышением температуры линейная энергия изменяется слабо, тогда как термодинамическое линейное натяжение – очень сильно (благодаря энтропийному эффекту). По этой причине, хотя расчет ведется при нулевой температуре [5], полученное значение ε может иметь смысл и для более высоких температур именно как линейная энергия, а не линейное натяжение.

Формулу (2) можно отнести к бесконечной двумерной плоскопараллельной щели, но ее можно понимать и как локальное соотношение в системах более сложной конфигурации. Тем самым вводится представление о локальной линейной энергии. Если теперь представить, что сила когезии зависит от координаты x вдоль линии разреза, то из формулы (2) выводится зависимость локальной линейной энергии от положения на линии

(3)

$2\varepsilon (x) = \int\limits_\delta ^\infty {f(H,x){\kern 1pt} dH} .$

Следующий шаг – введение точечного натяжения. Если линия разреза не бесконечна и у нее есть край, то при приближении к нему локальная линейная энергия изменяется по формуле (3). Тогда точечную энергию η можно определить выражением

(4)

$\eta \equiv \int {[\varepsilon (x)} - \varepsilon ]{\kern 1pt} dL,$

где ε – значение линейной энергии вдали от края (где оно не зависит от x). Интегрирование проводится по всей длине L линии разреза, и при длине внутри нанодиапазона результат зависит от L. Если же длина выходит за пределы нано-диапазона, подынтегральная функция в (4) обращается в нуль, и точечная энергия обретает статус постоянной величины, не зависящей от пределов интегрирования. Тем самым она становится одним из показателей графена.

Для графена сила когезии $f(H,x)$ содержит три компоненты: ковалентную химическую связь, дисперсионные силы и силы отталкивания. Из них лишь дисперсионные силы являются дальнодействующими, что особенно важно для расчета точечной энергии (атом должен “чувствовать” не только соседа, но и другие атомы на граничной линии). Парный потенциал дисперсионных сил (без запаздывания) дается выражением

(5)

$\emptyset (R) = - \frac{\lambda }{{{{R}^{6}}}}{\text{ }}(R \geqslant \delta ),$

где λ – константа взаимодействия и R – расстояние между взаимодействующими частицами (атомами углерода в нашем случае). В строгом смысле выражение (5) является асимптотическим соотношением, а потому в каждой задаче R отсчитывается от некоторого минимального значения δ. В приближении нулевого дальнодействия химических связей и сил отталкивания потенциала (5) достаточно для расчета локальной линейной и точечной энергии графена, но в общем случае речь может идти об оценке только вклада дисперсионных сил в эти величины.

Целью данного сообщения является исследование вклада дисперсионных сил в линейную и точечную энергию графена. Имея в виду силицен, германен и аналогичные двумерные структуры будущего, сначала построим общую теорию и лишь потом примерим к ней конкретные параметры взаимодействия графена.

ОБЩИЕ СООТНОШЕНИЯ ДЛЯ ДВУМЕРНЫХ СТРУКТУР

Функцию $f(H,x)$ нельзя получить простым суммированием всех парных взаимодействий молекул по обе стороны разреза. Такая процедура дает усредненное значение и годится лишь для бесконечно длинного разреза [1, 5]. Чтобы получить локальное значение силы когезии $f(H,x)$ в конечной системе, мы отождествим ее с локальным нормальным напряжением E_N на одной из границ разреза:

(6)

$f(H,x) = {{E}_{\operatorname{N} }}.$

Тогда дело сводится к нахождению этой величины.

Тензор напряжений Ирвинга–Кирквуда

Для расчета нормального напряжения E_N воспользуемся тензором напряжений Ирвинга–Кирквуда статистической механики, силовая часть которого в условиях равновесия имеет вид [6]

(7)

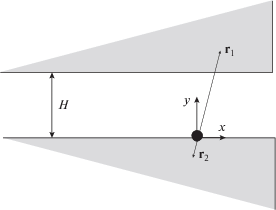
$\begin{gathered} {\mathbf{E}}({\mathbf{r}}) = \frac{1}{2}\sum\limits_{i,j} {\int {\frac{{{\mathbf{R}} \times {\mathbf{R}}}}{R} \emptyset _{{ij}}^{{\text{'}}}(R)d{\mathbf{R}} \times } } \\ \times \,\,\int\limits_0^1 {\rho _{{ij}}^{{(2)}}({\mathbf{r}} - \xi {\mathbf{R}},{\mathbf{r}} - \xi {\mathbf{R}} + {\mathbf{R}})d\xi } , \\ \end{gathered} $

где $E({\mathbf{r}})$ – значение тензора напряжений в точке r, R – вектор, соединяющий две взаимодействующие частицы на расстоянии R друг от друга и проходящий через точку r (запись ${\mathbf{R}} \times {\mathbf{R}}$ означает прямое векторное произведение, что является тензором), $\emptyset _{{ij}}^{{\text{'}}}(R)$ – производная парного потенциала ${{\emptyset }_{{ij}}}(R)$ для частиц сортов i и j (т.е. сила взаимодействия между частицами), $d{\mathbf{R}}$ – произведение декартовых составляющих $d{{R}_{k}}$, R – модуль вектора R, $\rho _{{ij}}^{{(2)}}({\mathbf{r}} - \xi \,{\mathbf{R}},\,\;{\mathbf{r}} - \xi \,{\mathbf{R}} + \,\,{\mathbf{R}})$ – двухчастичная функция распределения для частиц, одновременно расположенных в точках ${\mathbf{r}} - \xi \,{\mathbf{R}}$ и ${\mathbf{r}} - \xi \,{\mathbf{R}} + \,\,{\mathbf{R}}$ в противоположных сторонах от единичной поверхности с координатой r (это контролируется дополнительной переменной ξ). Интегрирование по R ведется по всему пространству. В расчетной схеме тензора напряжений Ирвинга–Кирквуда учитываются только те молекулярные пары, соединительная прямая линия которых проходит через элементарную единичную площадку с координатой r (она разбивает R на доли ξ и 1 – ξ).

Переходя к вычислениям, представим, что мы находимся у края макроскопического листа графена прямоугольной формы и делаем разрез листа по нормали к краю, а затем разводим две части листа на расстояние H в той же плоскости. Вся операция делается в вакууме (отчего нам и требуется только силовая часть тензора напряжений). Преобразуем сначала выражение (7) применительно к рассматриваемому случаю. Расположим расчетную точку r (в которой ищется тензор напряжений) на нижней стороне разреза на расстоянии x от его края (рис. 1). Установим начало декартовой системы координат в расчетной точке и направим ось x вдоль линии разреза к ее краю, а ось y – перпендикулярно линии разреза снизу вверх, дав верхней части листа маркировку 1, а нижней – 2. Положение двух взаимодействующих атомов, один из которых расположен в области 1, а другoй – в области 2, характеризуется векторами r₁ и r₂. Очевидно, они направлены противоположно, но лежат на одной прямой, поскольку отрезок прямой длиной R, соединяющий два взаимодействующих атома, должен проходить через расчетную точку (рис. 1). Мы тогда можем записать

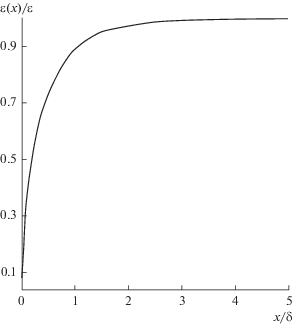
(8)

${{{\mathbf{r}}}_{1}} = (1 - \xi ){\mathbf{R}},\,\,\,\,{{{\mathbf{r}}}_{2}} = - \xi {\mathbf{R}},$

так что $R = {{r}_{1}} - {{r}_{{\text{2}}}}.$

Рис. 1.

Образование двух углов при разрезании полубесконечного листа графена: H – расстояние между двумя частями листа, векторы r₁ и r₂ показывают расположение атомов, взаимодействующих через точку, где ищется тензор (черный кружок).

Поскольку выражение (8) сформулировано в векторной форме, оно в равной степени легко применимо к трехмерным и двумерным системам. Применительно к рассматриваемому двумерному случаю интегрирование производится по трем переменным R_x, R_y и ξ. Удобно провести замену переменных на x₁, y₁ (компоненты вектора r₁) и y₂ (y-компонента вектора r₂). Якобиан такого преобразования рассчитан в приложении А (формула (А4)). Его абсолютное значение, необходимое для преобразования интегралов в (7), равно ${1 \mathord{\left/ {\vphantom {1 {{{y}_{1}}}}} \right. \kern-0em} {{{y}_{1}}}}.$. При переходе к новым переменным запишем, как это вытекает из (8),

(9)

${\mathbf{R}} = {{{\mathbf{r}}}_{1}}\frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}},\,\,\,\,R = {{r}_{1}}\frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}},$

где ${{r}_{1}}$ – модуль вектора ${{{\mathbf{r}}}_{1}}.$ Из (9) следует соотношение

(10)

$\frac{{{\mathbf{R}} \times {\mathbf{R}}}}{R} = \frac{{{{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}}}{{{{r}_{1}}}}\,\,\frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}}.$

Обратимся теперь к двухчастичной функции распределения $\rho _{{ij}}^{{(2)}}$ в (7). Для рассматриваемого твердого двумерного объекта, считая его однородным по плотности, можно представить двухчастичную функцию распределения как произведение одночастичных функций распределения в областях 1 и 2:

(11)

$\rho _{{12}}^{{(2)}} = \rho _{1}^{{(1)}}\rho _{2}^{{(1)}}.$

Последние же зададим в виде

(12)

$\begin{gathered} \rho _{1}^{{(1)}}(y) = \rho {\text{ (}}{{y}_{1}} > H),\,\,\,\,\rho _{1}^{{(1)}}(y) = 0{\text{ (}}{{y}_{1}} < 0), \\ \rho _{2}^{{(1)}}(y) = \rho {\text{ (}}{{y}_{2}} < 0),\,\,\,\,\rho _{2}^{{(1)}}(y) = 0{\text{ (}}{{y}_{2}} > H), \\ \end{gathered} $

где ρ – плотность (число атомов углерода на единицу площади) графена (величина постоянная). Внутри пустого разреза между областями 1 и 2 эта плотность, очевидно, равна нулю. К этому надо добавить, что оба условия (12) работают в пределах протяженности разреза: за его границами вещества нет вообще, и, значит, тензор давления Ирвинга–Кирквуда нулевой. Легко сообразить, что он равен нулю и на границах разреза. Действительно, если мы поместим расчетную точку на самом краю разреза (при x = 0), то проходящий через нее прямой отрезок длиной R при движении любым своим концом внутри одной из областей 1 или 2 другим концом попадает в вакуум, и взаимодействия не будет.

Наконец, упростим саму процедуру вычислений. Будем интегрировать только по положительным значениям y₁, а полученный результат умножать на два (тогда множитель 1/2 в правой части (7) исчезает). Переменная x₁ будет пробегать как положительные, так и отрицательные значения. Очевидно, верхним пределом для нее является x, а вот чтобы установить нижний предел (в области отрицательных значений x₁), необходимо учесть, что невидимая переменная x₂ в этом случае находится в области положительных значений и имеет своим пределом ту же величину x. Поскольку переменные x₁ и x₂ связаны, согласно (8), соотношением пропорциональности

(13)

$\frac{{{{x}_{1}}}}{{{{x}_{2}}}} = \frac{{{{y}_{1}}}}{{{{y}_{2}}}},$

мы должны положить нижний предел для ${{x}_{1}}$ равным ${{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}$(величине отрицательной, так как y₁ и y₂ имеют разные знаки). С учетом всего сказанного и соотношений (9)–(13) выражение (7) преобразуется к виду

(14)

$\begin{gathered} {\mathbf{E}} = - {{\rho }^{2}}\int\limits_H^\infty {d{{y}_{1}}} \int\limits_{ - \infty }^0 {d{{y}_{2}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {d{{x}_{1}}} \frac{{{{r}_{1}} \times {{{\mathbf{r}}}_{1}}}}{{{{r}_{1}}}}\,\,\frac{{{{y}_{1}} - {{y}_{2}}}}{{y_{1}^{2}}} \times \\ \times \,\,\emptyset _{{12}}^{{\text{'}}}\left[ {\frac{{{{r}_{1}}({{y}_{1}} - {{y}_{2}})}}{{{{y}_{1}}}}} \right]. \\ \end{gathered} $

Формула (14) справедлива для парного потенциала любого вида.

Когезионная функция для случая дисперсионных сил

Обращаясь теперь к дисперсионным силам, в соответствии с (5) и (9) запишем парный потенциал взаимодействия в форме

(15)

${{\emptyset }_{{12}}}\left[ {\frac{{{{r}_{1}}({{y}_{1}} - {{y}_{2}})}}{{{{y}_{1}}}}} \right] = - \frac{{\lambda y_{1}^{6}}}{{r_{1}^{6}{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}.$

Отсюда получаем

(16)

$\emptyset _{{12}}^{{\text{'}}}\left[ {\frac{{{{r}_{1}}({{y}_{1}} - {{y}_{2}})}}{{{{y}_{1}}}}} \right] = \frac{{6\lambda y_{1}^{7}}}{{r_{1}^{7}{{{({{y}_{1}} - {{y}_{2}})}}^{7}}}}.$

Подстановка (16) в (14) дает

(17)

${\mathbf{E}} = 6\lambda {{\rho }^{2}}\int\limits_H^\infty {y_{1}^{5}d{{y}_{1}}} \int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}}--{{y}_{2}})}}^{6}}}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {d{{x}_{1}}} \frac{{{{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}}}{{r_{1}^{8}}}.$

Дальнейшие вычисления нужно производить для каждой составляющей тензора давления по отдельности. В соответствии с (6) нас интересует нормальная составляющая ${{E}_{\operatorname{N} }} \equiv {{E}_{{yy}}}.$ Заменяя ${{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}$ на $y_{1}^{2}$ и попутно ${{r}_{1}}$ на ${{(x_{1}^{2} + y_{1}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ из (17) имеем

(18)

$\begin{gathered} f(H,x) = {{E}_{\operatorname{N} }} = \\ = 6\lambda {{\rho }^{2}}\int\limits_H^\infty {y_{1}^{7}d{{y}_{1}}} \int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {\frac{{d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}}} . \\ \end{gathered} $

При x → ∞ (18) принимает легко интегрируемую форму

(19)

$\begin{gathered} f(H) = {{E}_{\operatorname{N} }} = \\ = 6\lambda {{\rho }^{2}}\int\limits_H^\infty {y_{1}^{7}d{{y}_{1}}} \int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} \int\limits_{ - \infty }^\infty {\frac{{d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}}} . \\ \end{gathered} $

После взятия последнего и предпоследнего интегралов (см. приложение Б, формулы (Б.1) и (Б.2)) $f(H)$ легко вычисляется как

(20)

$f(H) = 6\lambda {{\rho }^{2}}\frac{\pi }{{16}}\int\limits_H^\infty {\frac{{d{{y}_{1}}}}{{y_{1}^{5}}}} = \frac{{3\pi \lambda {{\rho }^{2}}}}{{32{{H}^{4}}}}.$

Что касается (18), то интегралы этого выражения, конечно, тоже берутся (тем более, с помощью компьютера), но на вид весьма громоздки. Ниже мы приведем конечный результат, а пока оставим (18) как наиболее компактную запись.

Локальная линейная энергия

Из (2) и (20) находим вклад дисперсионных сил в линейную энергию бесконечно длинной линейной границы как

(21)

$\varepsilon = \frac{1}{2}\int\limits_\delta ^\infty {f(H)dH = \frac{{3\pi \lambda {{\rho }^{2}}}}{{64}}} \int\limits_\delta ^\infty {\frac{{dH}}{{{{H}^{4}}}}} = \frac{{\pi \lambda {{\rho }^{2}}}}{{64{{\delta }^{3}}}},$

что согласуется с результатом расчета другим путем [1, 5]. Для локальной же линейной энергии вблизи от вершины угла двумерной структуры из (3) и (18) находим

(22)

$\begin{gathered} \varepsilon (x) = 3\lambda {{\rho }^{2}}\int\limits_\delta ^\infty {dH} \int\limits_H^\infty {y_{1}^{7}d{{y}_{1}}} \times \\ \times \,\,\int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {\frac{{d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}}} . \\ \end{gathered} $

Выражая теперь ${{x}_{1}},{{y}_{1}},{{y}_{2}}$ и H в единицах δ и используя (21), упростим (22) к виду

(23)

$\frac{{\varepsilon (x)}}{\varepsilon } = \frac{{192}}{\pi }\int\limits_1^\infty {dH} \int\limits_H^\infty {y_{1}^{7}d{{y}_{1}}} \int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {\frac{{d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}}} .$

Детали вычислений даны в приложении В, а здесь мы сразу приведем конечный результат интегрирования в (23):

(24)

$\begin{gathered} \frac{{\varepsilon (x)}}{\varepsilon } = \left[ {9\pi - 18x + 54\pi {{x}^{2}} - 102{{x}^{3}} + 135\pi {{x}^{4}}} \right. - \\ - \,\,714{{x}^{5}} + 810\pi {{x}^{6}} + 634{{x}^{7}} - 810\pi {{x}^{8}} + \\ + \,\,1242{{x}^{9}} + 558\pi {{x}^{{10}}} + 78{{x}^{{11}}} + 243\pi {{x}^{{12}}} + \\ + \,\,130{{x}^{{13}}} + 90\pi {{x}^{{14}}} + 30{{x}^{{15}}} + 15\pi {{x}^{{16}}} + \\ + \,\,(30{{x}^{4}} + 180{{x}^{6}} + 450{{x}^{8}} + 600{{x}^{{10}}} + 450{{x}^{{12}}} + \\ + \,\,180{{x}^{{14}}} + 30{{x}^{{16}}}){\text{arctg}}x - (18 + 108{{x}^{2}} + \\ + \,\,270{{x}^{4}} + 360{{x}^{6}} + 270{{x}^{8}} + 108{{x}^{{10}}} + \\ + \,\,18{{x}^{{12}}}){\text{arctg}}({{x}^{{ - 1}}}) - (288{{x}^{5}} - 2112{{x}^{7}} + \\ {{\left. { + \,\,1440{{x}^{9}})\ln x} \right]} \mathord{\left/ {\vphantom {{\left. { + \,\,1440{{x}^{9}})\ln x} \right]} {30\pi {{x}^{4}}}}} \right. \kern-0em} {30\pi {{x}^{4}}}}(1 + 6{{x}^{2}} + 15{{x}^{4}} + \\ + \,\,20{{x}^{6}} + 15{{x}^{8}} + 6{{x}^{{10}}} + {{x}^{{12}}}),{\text{ }} \\ \end{gathered} $

где, напоминаем, x надо рассматривать как x/δ. Графическое представление функции (24) (рис. 2) выглядит намного проще и предсказуемо демонстрирует асимптотическое приближение $\varepsilon (x)$ к своему постоянному значению ε в пределах нанодиапазона $0 \leqslant {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0em} \delta } \leqslant 5.$ Поскольку ε(x) < ε на всем протяжении графика, мы можем заранее сказать, что, в соответствии с (4), вклад дисперсионных сил в точечную энергию двумерной структуры должен быть отрицательным.

Рис. 2.

Приближение линейной энергии графена ε(x) к своему постоянному значению ε при отходе от угла графенового листа (δ – минимальное межатомное расстояние поперек граничной линии).

Точечная энергия

Осталось найти выражение для вклада дисперсионных сил в точечную энергию η двумерной структуры. Преобразуем (4) к виду (где x исчисляется в единицах δ)

(25)

$\frac{\eta }{{\varepsilon \delta }} = \int\limits_0^\infty {\left[ {\frac{{\varepsilon (x)}}{\varepsilon } - 1} \right]dx} .$

Теперь, подставив сюда (24) и произведя интегрирование, получаем

(26)

$\eta = - \frac{4}{{3\pi }}\varepsilon \delta $

или, после подстановки (21),

(27)

$\eta = - \frac{{\lambda {{\rho }^{2}}{\kern 1pt} }}{{48{{\delta }^{2}}}}.{\kern 1pt} $

После того, как общие соотношения для двумерных структур установлены, можно перейти к конкретным расчетам для графена.

ХАРАКТЕРИСТИКИ ГРАФЕНА

В графене длина σ-связи b = 0.142 нм, а в двумерной гексагональной упаковке связь между ρ (число атомов углерода на единицу площади) и b находится следующим образом. При длине стороны правильного шестиугольника b его площадь равна $({3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})\sqrt 3 {{b}^{2}}$, и, значит, число шестиугольников на единицу площади составит ${2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}\sqrt 3 {{b}^{2}}$. Каждый из них включает шесть молекул углерода, но каждая молекула принадлежит сразу трем шестиугольникам, так что

(28)

$\rho = \frac{4}{{3\sqrt 3 {{b}^{2}}}} \approx \frac{{0.7698}}{{{{b}^{2}}}}.$

При указанной величине b из формулы (28) имеем $\rho \approx 38.177$ нм^–2. Подставляя (28) в (21) и (27), получаем для линейной энергии

(29)

$\varepsilon = \frac{{\pi \lambda }}{{108{{b}^{4}}{{\delta }^{3}}}}$

и для точечной энергии

(30)

$\eta = - \frac{\lambda }{{81{{b}^{4}}{{\delta }^{2}}}}.$

Чтобы делать расчеты, нам также нужно задать постоянную дисперсионного взаимодействия λ для графена. Для этого используем классическое уравнение Леннард-Джонса, хорошо исследованное применительно к парному взаимодействию углерод–углерод (CC),

(31)

$\emptyset (R) = 4{{\varepsilon }_{{\operatorname{CC} }}}\left[ {{{{\left( {\frac{{{{\sigma }_{{\operatorname{CC} }}}}}{R}} \right)}}^{{12}}} - {{{\left( {\frac{{{{\sigma }_{{\operatorname{CC} }}}}}{R}} \right)}}^{6}}} \right].$

Уточненные значения констант уравнения (31) составляют: ${{\varepsilon }_{{\operatorname{CC} }}}$ = 0.03550 × 10^–20 Дж и ${{\sigma }_{{\operatorname{CC} }}}$ = = 0.34585 нм [1]. Сопоставляя уравнения (5) и (31), находим

(32)

$\lambda = 4{{\varepsilon }_{{\operatorname{CC} }}}\sigma _{{С С }}^{6},$

что при указанных значениях дает λ = 2.43005 × × 10^–78 Дж м⁶. Остается параметр δ, но о нем разговор особый.

Выбор параметра δ

До сих пор было лишь указано, что δ – минимальное расстояние для расчетов. Теперь пришло время конкретизировать этот параметр для графена. Прежде всего, необходимо выбрать направление разреза листа графена для создания линейной границы. При этом желательно найти такое направление, для которого работа разреза была бы минимальной и, значит, соответствовала естественной линейной границе (если пытаться разорвать лист графена, то он с наибольшей вероятностью порвется по этому направлению). Этот вопрос подробно обсуждался в [1, 5], и было установлено, что такой разрез соответствует разрыву σ-связей графена по зигзагообразной границе (рис. 3). Тот факт, что именно это направление отвечает реальной линейной границе графена, был также подтвержден в работе [7]. Ниже мы будем адресоваться к этой границе. Дальнейшие рассуждения требуют некоторых модельных представлений об атомах углерода.

Рис. 3.

Граничная линия листа графена поперек σ‑связей длиной b.

Модель жестких шаров с дисперсионными силами. Обычно жесткими шарами моделируются силы отталкивания, но мы прибавим к ним и химическую связь. Иными словами, в данной модели считается, что при малейшем увеличении расстояния между атомами углерода в графене химическая связь разрывается и в дальнейшем никак себя не проявляет, как и силы отталкивания. Это значит, что дисперсионные силы сразу дают вклад в работу разъединения двух кусков графена, как только расстояние между атомами углерода превышает параметр решетки b, т.е. δ = b. Тогда формулы (29) и (30) принимают вид для линейной энергии

(33)

$\varepsilon = \frac{{\pi \lambda }}{{108{{b}^{7}}}}$

и для точечной энергии

(34)

$\eta = - \frac{{\lambda {\kern 1pt} }}{{81{{b}^{6}}}}.{\kern 1pt} $

При приведенных выше значениях λ и b это дает $\varepsilon \approx 0.607 \times {{10}^{{ - 10}}}$ Дж/м и $\eta \approx - {\kern 1pt} 0.366 \times {\text{1}}{{{\text{0}}}^{{ - 20}}}$ Дж.

Модель Леннард-Джонса. Представим теперь, что положение с химическими связями остается прежним (они сразу рвутся при увеличении межатомного расстояния в графене), а силы отталкивания обретают малое дальнодействие согласно уравнению (31). В этом случае сразу после разрыва химических связей внешними силами система попадает в область отталкивательных сил и уже спонтанно (скачком) увеличивает просвет между разъединяемыми частями листа графена до определенного расстояния δ, соответствующего равновесию между силами притяжения и отталкивания. Дальнейшее увеличение расстояния уже потребует работы внешних сил, и именно от значения δ нужно стартовать в расчетах работы. Расчет же самой равновесной величины δ легко осуществляется при помощи (31) и дает результат [1]

(35)

$\delta = {{\left( {\frac{{21}}{{80}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}{{\sigma }_{{\operatorname{CC} }}} \approx 0.277\,\,{\text{н м ,}}$

что почти вдвое превышает параметр решетки b. Теперь, используя (32) и (35), мы можем выразить линейную и точечную энергию в терминах параметров потенциала Леннард-Джонса. Из (29) находим для линейной энергии

(36)

$\varepsilon = \frac{\pi }{{27}}{{\left( {\frac{{80}}{{21}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{\varepsilon }_{{\operatorname{CC} }}}}}{b}{{\left( {\frac{{{{\sigma }_{{\operatorname{CC} }}}}}{b}} \right)}^{3}},$

а из (30) – для точечной энергии

(37)

$\eta = \frac{4}{{81}}{{\left( {\frac{{80}}{{21}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{\varepsilon }_{{\operatorname{CC} }}}{{\left( {\frac{{{{\sigma }_{{\operatorname{CC} }}}}}{b}} \right)}^{4}} \approx 0.077{{\varepsilon }_{{\operatorname{CC} }}}{{\left( {\frac{{{{\sigma }_{{\operatorname{CC} }}}}}{b}} \right)}^{4}}.$

При заданных значениях ${{\varepsilon }_{{\operatorname{CC} }}}$, ${{\sigma }_{{\operatorname{CC} }}}$ и b формулы (36) и (37) дают результаты $\varepsilon \approx 0.818 \times {{10}^{{ - 11}}}$ Дж/м и $\eta \approx 0.962 \times {{10}^{{ - 21}}}$ Дж. Для линейной энергии это в 7.4 раза, а для точечной энергии в 3.8 раза меньше, чем в расчете по модели жестких шаров. Результат понятен: в данном случае расчет начинается с гораздо большего расстояния δ, когда силы притяжения уже значительно ослаблены.

В отношении линейной энергии графена полученный в данной части результат (формула (36)) согласуется с работой [1], где на основании потенциала Леннард-Джонса был произведен расчет с учетом сил отталкивания (расчет точечной энергии там не проводился). В таком варианте (без химических связей) вклад в линейную энергию графена составляет около $0.545 \times {{10}^{{ - 11}}}$ Дж/м [1], откуда (в сравнении с приведенной выше величиной) видно, что силы отталкивания “съедают” треть расчетной величины дисперсионной составляющей линейной энергии графена.

ЗАКЛЮЧЕНИЕ

Отметим два обстоятельства. Ранее было показано, что основной вклад в линейную энергию графена вносят химические связи между атомами углерода, вклад же дисперсионных сил на порядок меньше [1]. Значит ли это, что такое соотношение должно сохраняться и для точечной энергии? Отнюдь. Дело в том, что линейная энергия находится непосредственно из работы когезии, а точечная энергия – из избытка работы когезии, связанного с близостью к углу прямоугольного куска графена. Здесь вклад конкретных сил зависит от их дальнодействия. В данной работе мы оценили вклад дисперсионных сил в точечную энергию графена в абсолютном выражении. В рассмотренных двух моделях с нулевым дальнодействием химических сил лишь дисперсионные силы вносят вклад в точечную энергию, которая, в этом случае, рассчитана полностью. Реальный же вклад химических сил в точечную энергию еще не определен, и лишь после его нахождения можно будет судить об относительном вкладе дисперсионных сил в точечную энергию графена. Расчет вклада химических связей в точечную энергию графена остается вызовом современной квантовой химии.

Второе обстоятельство, которое необходимо отметить, состоит в том, что структура листа графена считалась неизменной в процессе разъединения двух его частей. В реальности идет процесс релаксации граничных зон. Рассчитать его сложно, но компьютерное моделирование показывает, что наибольшие искажения происходят как раз вблизи углов образца [8]. С одной стороны, это подчеркивает важность расчета точечной энергии двумерной структуры, а, с другой – неполноту проведенного расчета и в этом направлении. Строгая оценка точечной энергии графена должна включать в себя учет не только химических связей, но и релаксации структуры графена (локальной плотности атомов углерода) вблизи линии разреза и ее концов.

В манипуляциях с незыблемой структурой в виде угла возникает еще один нюанс. Ведь у каждого угла две стороны, две линии. Мы оперировали с одной из них, которая может быть названа активной, ибо взаимодействует с противоположной линией двумерной щели. Вторая линия (ориентированная перпендикулярно щели, рис. 1) была неактивной. Однако обе линии должны быть одинаковыми в конечном состоянии равновесия, когда одна часть графена удалена от другой на бесконечное расстояние и ведет себя независимо. Очевидно, конечная унификация сторон угла достигается перераспределением внутренней энергии, и, поскольку удаленная часть тела находится в вакууме и не взаимодействует ни с какими другими телами, этот процесс не требует дополнительной работы. Таким образом, хотя мы имели дело лишь с одной из сторон, рассчитанная работа образования угла дает величину точечной энергии, верную для конечного энергетического состояния в отсутствие релаксации.

Автор признателен А.К. Щёкину и М.С. Кшевецкому за помощь в расчетах.

ПРИЛОЖЕНИЕ А

РАСЧЕТ ЯКОБИАНА

Из (8) имеем

(A1)

${{x}_{1}} = (1 - \xi ){{R}_{x}},\,\,\,\,{{y}_{1}} = (1 - \xi ){{R}_{y}},\,\,\,\,{{y}_{2}} = - \xi {{R}_{y}}$

или

(A2)

${{R}_{x}} = {{x}_{1}} - \frac{{{{x}_{1}}{{y}_{2}}}}{{{{y}_{1}}}},\,\,\,\,{{R}_{y}} = {{y}_{1}} - {{y}_{2}},\,\,\,\,1 - \xi = \frac{{{{y}_{1}}}}{{{{y}_{1}} - {{y}_{2}}}}.$

Отсюда находим производные

(A3)

$\begin{gathered} \frac{{\partial {{R}_{x}}}}{{\partial {{x}_{1}}}} = \frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}},\,\,\,\,\frac{{\partial {{R}_{x}}}}{{\partial {{y}_{1}}}} = \frac{{{{x}_{1}}{{y}_{2}}}}{{y_{1}^{2}}},\,\,\,\,\frac{{\partial {{R}_{x}}}}{{\partial {{y}_{2}}}} = - \frac{{{{x}_{1}}}}{{{{y}_{1}}}}, \\ \frac{{\partial {{R}_{y}}}}{{\partial {{x}_{1}}}} = 0,\,\,\,\,\frac{{\partial {{R}_{y}}}}{{\partial {{y}_{1}}}} = 1,\,\,\,\,\frac{{\partial {{R}_{y}}}}{{\partial {{y}_{2}}}} = - 1, \\ \frac{{\partial \xi }}{{\partial {{x}_{1}}}} = 0,\,\,\,\,\frac{{\partial \xi }}{{\partial {{y}_{1}}}} = \frac{{{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}},\,\,\,\,\frac{{\partial \xi }}{{\partial {{y}_{2}}}} = - \frac{{{{y}_{1}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}} \\ \end{gathered} $

и конструируем якобиан:

(A4)

$\begin{gathered} \left| {\begin{array}{*{20}{c}} {\frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}},}&{\frac{{{{x}_{1}}{{y}_{2}}}}{{y_{1}^{2}}},}&{ - \frac{{{{x}_{1}}}}{{{{y}_{1}}}}} \\ {0,}&{1,}&{ - 1} \\ {0,}&{\frac{{{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}},}&{ - \frac{{{{y}_{1}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}}} \end{array}} \right| = \\ = \frac{{{{y}_{1}} - {{y}_{2}}}}{{{{y}_{1}}}}\left[ {\frac{{{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}} - \frac{{{{y}_{1}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{2}}}}} \right] = - \frac{1}{{{{y}_{1}}}}. \\ \end{gathered} $

ПРИЛОЖЕНИЕ Б

РАСЧЕТ ИНТЕГРАЛОВ В (19)

Удобно перенести $y_{1}^{7}$ из первого интеграла в последний. Тогда вычисление последнего интеграла дает

(Б1)

$\begin{gathered} \int\limits_{ - \infty }^\infty {\frac{{y_{1}^{7}d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}}} = \frac{{{{x}_{1}}y_{1}^{5}}}{{6{{{(x_{1}^{2} + y_{1}^{2})}}^{3}}}} + \frac{{5{{x}_{1}}y_{1}^{3}}}{{24{{{(x_{1}^{2} + y_{1}^{2})}}^{2}}}} + \\ + \,\,\frac{{5{{x}_{1}}{{y}_{1}}}}{{16(x_{1}^{2} + y_{1}^{2})}} + \frac{5}{{16}}\operatorname{arctg} \left. {\frac{{{{x}_{1}}}}{{{{y}_{1}}}}} \right|_{{ - \infty }}^{\infty } = \\ = \frac{5}{{16}}[\operatorname{arctg} \infty - \operatorname{arctg} ( - \infty )] = \frac{{5\pi }}{{16}}. \\ \end{gathered} $

Соответственно предпоследний интеграл берется элементарно:

(Б2)

$\int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} = \left. {\frac{1}{{5{{{({{y}_{1}} - {{y}_{2}})}}^{5}}}}} \right|_{{ - \infty }}^{0} = \frac{1}{{5y_{1}^{5}}}.$

ПРИЛОЖЕНИЕ В

РАСЧЕТ ИНТЕГРАЛОВ В (23)

По аналогии с (Б.1) имеем

(В.1)

$\begin{gathered} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {\frac{{y_{1}^{7}d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}} = } \frac{{xy_{1}^{5}}}{{6{{{({{x}^{2}} + y_{1}^{2})}}^{3}}}} + \frac{{5xy_{1}^{3}}}{{24{{{({{x}^{2}} + y_{1}^{2})}}^{2}}}} + \\ + \,\,\frac{{5x{{y}_{1}}}}{{16({{x}^{2}} + y_{1}^{2})}} + \frac{5}{{16}}\operatorname{arctg} \frac{x}{{{{y}_{1}}}} - \\ - \frac{{xy_{2}^{5}}}{{6{{{({{x}^{2}} + y_{2}^{2})}}^{3}}}} - \frac{{5xy_{2}^{3}}}{{24{{{({{x}^{2}} + y_{2}^{2})}}^{2}}}} - \\ - \,\,\frac{{5x{{y}_{2}}}}{{16({{x}^{2}} + y_{2}^{2})}} - \frac{5}{{16}}\operatorname{arctg} \frac{x}{{{{y}_{2}}}}. \\ \end{gathered} $

Дальнейшее интегрирование по y₂ означает для первых четырех членов правой части (В.1) просто деление на $5y_{1}^{5}$, а для других нужно писать интегралы:

(В.2)

$\begin{gathered} \int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{2}} - {{y}_{2}})}}^{6}}}}} \int\limits_{{{x{{y}_{1}}} \mathord{\left/ {\vphantom {{x{{y}_{1}}} {{{y}_{2}}}}} \right. \kern-0em} {{{y}_{2}}}}}^x {\frac{{y_{1}^{7}d{{x}_{1}}}}{{{{{(x_{1}^{2} + y_{1}^{2})}}^{4}}}} = } \frac{x}{{30{{{({{x}^{2}} + y_{1}^{2})}}^{3}}}} + \\ + \,\,\frac{x}{{24y_{1}^{2}{{{({{x}^{2}} + y_{1}^{2})}}^{2}}}} + \frac{{x{{y}_{1}}}}{{16y_{1}^{4}({{x}^{2}} + y_{1}^{2})}} + \\ + \,\,\frac{1}{{16y_{1}^{5}}}\operatorname{arctg} \frac{x}{{{{y}_{1}}}} - \frac{x}{6}\int\limits_{ - \infty }^0 {\frac{{y_{2}^{5}d{{y}_{2}}}}{{{{{({{x}^{2}} + y_{2}^{2})}}^{3}}{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} - \\ - \,\,\frac{{5x}}{{24}}\int\limits_{ - \infty }^0 {\frac{{y_{2}^{3}d{{y}_{2}}}}{{{{{({{x}^{2}} + y_{2}^{2})}}^{2}}{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} - \\ - \,\,\frac{{5x}}{{16}}\int\limits_{ - \infty }^0 {\frac{{{{y}_{2}}d{{y}_{2}}}}{{({{x}^{2}} + y_{2}^{2}){{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} - \frac{5}{{16}}\int\limits_{ - \infty }^0 {\frac{{d{{y}_{2}}}}{{{{{({{y}_{1}} - {{y}_{2}})}}^{6}}}}} \operatorname{arctg} \frac{x}{{{{y}_{2}}}}.{\text{ }} \\ \end{gathered} $

После их вычисления остается только интегрирование по ${{y}_{1}}$ и H без домножения на какие-либо величины, что и приводит к формуле (24) в основном тексте.

Список литературы

Rusanov A.I. // Surf. Sci. Rep. 2014. V. 69. P. 296.
Rusanov A.I. // Surf. Sci. Rep. 1996. V. 23. P. 173.
Rusanov A.I. // Surf. Sci. Rep. 2005. V. 58. P. 111.
Русанов А.И. Лекции по термодинамике поверхностей. СПб.: Лань, 2013.
Rusanov A.I. // Nanoscale. 2014. V. 6. P. 8130.
Irving J.H., Kirkwood J.G. // J. Chem. Phys. 1950. V. 18. P. 817.
Li Z.-L., Li Z.-M., Cao H.-Y., Yang J.-H., Shu Q., Zhang Y.-Y., Xiang H.J., Gong X.G. // Nanoscale. 2014. V. 6. P. 4309.
Barnard A.S., Snook I.K. // J. Chem. Phys. 2008. V. 128. P. 094707.
Русанов А.И. // Коллоид. журн. 2010. Т. 72. С. 666.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал