Коллоидный журнал, 2019, T. 81, № 2, стр. 146-152

При рассмотрении многих систем возникает вопрос о влиянии формы частиц, их составляющих, на изучаемые свойства. В коллоидной химии этот вопрос активно изучается на протяжении многих лет. Среди первых можно назвать работу Онзагера [1], который анализировал влияние формы на электростатическое взаимодействие коллоидных частиц. Однако наряду с электростатическими силами существенный вклад во взаимодействие коллоидных частиц дают силы Ван-дер-Ваальса. Точный учет формы частиц при описании свойств дисперсных систем представляет собой трудно решаемую задачу даже в приближении Гамакера [2]. Поэтому, как отмечено в [3], часто численное решение оказывается наиболее предпочтительным. Основные проблемы, обсуждаемые в [3, 4], связаны с изучением дисперсионного взаимодействия различных тел на основе теории Лифшица, хотя в них достаточно подробно описаны наиболее важные достижения предыдущих лет, полученные методом суммирования Гамакера. Среди них можно выделить работы с расчетами энергии взаимодействий эллипсоидов и сравнением ее с взаимодействием двух шаров [5], тонких стержней [6], бесконечных цилиндров [7, 8] и прямоугольных параллелепипедов [8]. Тем не менее, для аналитических оценок часто использовались формулы, впервые полученные Гамакером для сил взаимодействия либо двух макроскопических тел с плоскими границами, либо сферической частицы с плоской поверхностью [9]. И до настоящего времени продолжаются поиски наиболее эффективных способов определения взаимодействия частиц разной формы [10–17], в том числе и с учетом более точных подходов к описанию межмолекулярных сил, включая эффекты неаддитивности [10] и запаздывания [12–14]. Вклад шероховатости в силу взаимодействия частицы с поверхностью на примере конуса в качестве модели шероховатости оценивался в [10]. Показано, что вклад шероховатости значителен при расстояниях между поверхностями порядка размера шероховатости. В [11] получено, что расчет силы в рамках подхода Гамакера может быть использован для получения эмпирических значений параметров из экспериментальных данных. Оценки эффекта запаздывания во взаимодействии двух сфер, сферы с плоской поверхностью и сферы с цилиндром проводились в [12–14] при использовании эмпирических поправок к формуле Лондона для различных соотношений размеров частиц и расстояний между ними. Авторы работы [13] пришли к заключению, что вклад сил запаздывания становится существенным при расстояниях порядка радиуса сферической частицы. В [15] предложена процедура вычисления сил притяжения плоской поверхностью частиц произвольной формы путем разбиения объема частиц на множество одинаковых элементов. Затем для каждого элемента находится распределение сил для всевозможных ориентаций, на основе которых путем суммирования проводится подсчет сил для самих частиц. Обобщению подхода Дерягина для описания взаимодействия сферических частиц с бесконечной плоской поверхностью в применении к частицам произвольной формы посвящена работа [16]. Предложенная техника применена авторами [16] и для случая запаздывания. Приближенные формулы для взаимодействия двух бесконечных цилиндров в зависимости от расстояния между ними с учетом краевых эффектов были выведены в [17]. Более точный учет краевых эффектов был выполнен в наших работах [18–24] на основе тензора давления Ирвинга–Кирквуда [25]. Однако специально вопрос о форме частиц в этих работах не изучался, хотя в случае наноразмерных частиц их форма должна оказывать существенное влияние на все свойства.

Хотя в упомянутых работах многосторонне изучался вопрос о влиянии формы частиц на их взаимодействие, прямого сравнения сил для разных частиц не предпринималось. Чтобы оценить эффект формы, следует рассчитать энергию и силу взаимодействия одинаковых по природе, массе и объему, но геометрически различных частиц. Для решения этой задачи мы ограничимся случаем взаимодействия различных частиц простой геометрической формы с бесконечной поверхностью твердого тела и продемонстрируем аналитическое решение такой задачи на примере дисперсионных сил и на основе подхода Гамакера.

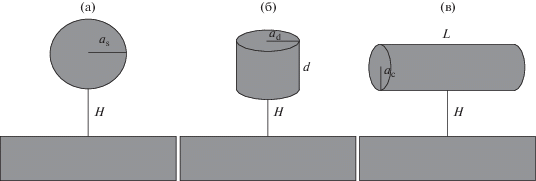
Взаимодействие с однородной плоской твердой поверхностью сравним для трех видов частиц: шара радиуса a_s, цилиндрического диска радиуса a_d и толщины d и тонкого цилиндрического стержня радиуса a_c и длины L. Обе последние частицы представляют собой цилиндры, но, имея в виду их разную ориентацию по отношению к твердой поверхности, будем называть диском цилиндр с осью, перпендикулярной поверхности, и соответственно стержнем – цилиндр с осью, параллельной поверхности (рис. 1). Диск можно рассматривать как модель пластинчатых частиц, а стержень – палочкообразных.

Обратимся к расчету энергии и силы взаимодействия наночастицы с твердой подложкой в рамках подхода Гамакера. Как и в [2], ограничимся пустой щелью и дисперсионными взаимодействиями, межмолекулярный потенциал которых имеет вид

где R – расстояние между взаимодействующими молекулами сортов i и j, ${{A}_{{ij}}}$ – постоянная взаимодействия. Проинтегрировав этот потенциал по объемам взаимодействующих тел с учетом их частичной плотности, получим выражения для энергии взаимодействия U₁₂ рассматриваемых тел, зависящие от расстояния H между телами. Поскольку одно из тел (присвоим ему номер 1) представляет собой макроскопическое твердое тело с плоской поверхностью, то в качестве исходного выражения можно использовать энергию дисперсионного поля на расстоянии z от поверхности твердого тела где c₁ обозначает частичную плотность твердого тела. Чтобы получить формулу для взаимодействия наночастицы с таким телом, остается произвести интегрирование U(z) по объему частицы.

Формулы для энергии и силы взаимодействия шара с твердым телом (рис. 1а) были получены самим Гамакером [2]. Для шара с радиусом a_s и частичной плотностью вещества c₂

где $С \equiv {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} \mathord{\left/ {\vphantom {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} 6}} \right. \kern-0em} 6}$ – постоянная Гамакера, а H – расстояние наибольшего сближения шара с твердой поверхностью (величина зазора между ними). Дифференцированием энергии U_s по H c учетом направления оси z от твердой поверхности в сторону шара получаем выражение для силы (формально z-составляющей вектора силы) притяжения шара твердым телом

Аналогичным образом находим формулы для энергии U_d и силы F_d притяжения твердой поверхностью цилиндрического диска радиуса a_d и толщиной d (рис. 1б):

и формулы того же типа для цилиндрического стержня радиуса a_c и длиной L (рис. 1в)

Все полученные выражения являются монотонными функциями расстояния H между частицами и поверхностью твердого тела. Абсолютные значения как энергии, так и силы взаимодействия с твердым телом будут уменьшаться при увеличении H и возрастать с увеличением размера частиц. Если частицы имеют одинаковый объем, но различны по форме, то возникает вопрос: каково соотношение энергий и сил их взаимодействия с твердой подложкой? Величины энергии должны определять равновесное распределение различных по форме наночастиц вблизи твердой поверхности, а силы влиять на скорость кинетических процессов вблизи поверхности. Чтобы сравниваемые наночастицы имели одинаковый объем, их геометрические параметры должны удовлетворять следующим соотношениям:

Если выбрать величину a_d в качестве единицы измерения расстояния, то при заданной толщине диска d однозначно определяется радиус шара, но один из параметров стержня может меняться независимо.

Наряду с самими величинами энергии и силы взаимодействия для более очевидного сравнения характера взаимодействия различных частиц можно ввести так называемые форм-факторы. Обычно форм-фактор (обозначим его буквой Θ) представляет собой отношение соответствующих функций для тел одинакового объема. Мы будем определять форм-факторы для рассматриваемых частиц относительно шара. Тогда для диска энергетический форм-фактор представляется выражением

Силовой же форм-фактор для диска имеет вид

Аналогично для стержня определяются энергетический форм-фактор

и силовой

Очевидно, при бесконечном увеличении расстояния частиц до поверхности все форм-факторы частиц будут стремиться к единице.

Используя полученные выше формулы, можно сравнить взаимодействие разных частиц с твердым телом. На рис. 2 показана зависимость сил и силовых форм-факторов от приведенного расстояния наибольшего сближения H/a_d для сферы, диска и двух стержней с L = 10d и L = 20d при d = 0.1a_d, d = a_d и d = 5a_d. Значения силы отнесены к величине C/a_d. В рассмотренном интервале значений H функции энергии демонстрируют аналогичное поведение. Видно, что при d ≤ a_d сила взаимодействия шара с твердым телом уступает силам для других частиц во всем интервале значений расстояния наибольшего сближения. Это значит, что в этих критериях взаимодействие шара с твердым телом энергетически менее выгодно, чем для диска и стержней. Стоит обратить внимание на изменение соотношений сил и форм-факторов для диска и стержней при изменении толщины диска. В случае тонкого диска c d = 0.1a_d его взаимодействие с твердым телом оказывается предпочтительнее, чем для стержней, и силовой форм-фактор для него превосходит форм-факторы для стержней (кривые 2 на рис. 2а и 2б). С увеличением толщины диска до d = a_d соотношения как сил, так и форм-факторов изменяются на противоположные (кривые 2 на рис. 2в и 2г). Для стержней же сохраняется очевидное соотношение: чем длиннее стержень, тем сильнее его взаимодействие с твердым телом (кривые 3 и 4 на рис. 2).

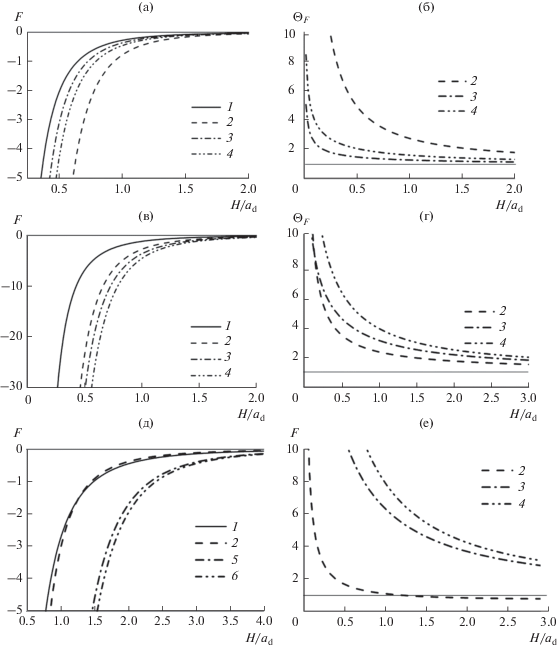
В предыдущей работе [26] было отмечено, что при толщине диска d = 5a_d значение нормального давления на его торце очень близко к давлению на торце полубесконечного цилиндра. Это означает, что его взаимодействие с твердым телом можно оценить из формулы (6) в пределе d → ∞, что дает силу ${{ - С \pi a_{\operatorname{d} }^{2}} \mathord{\left/ {\vphantom {{ - С \pi a_{\operatorname{d} }^{2}} {{{H}^{3}}}}} \right. \kern-0em} {{{H}^{3}}}}.$ Очевидно, что в пределе d → ∞ должен существовать интервал значений H, в котором взаимодействие более компактной сферической частицы будет более сильным даже по сравнению с полубесконечным цилиндром. Поэтому можно ожидать, что для достаточно толстых дисков появится область расстояний, где взаимодействие шара будет превосходить взаимодействие диска. Это мы и наблюдаем на рис. 2д. Видно, что вблизи поверхности притяжение диска толщиной 5a_d будет сильнее, чем шара, но с увеличением зазора соотношение сил для шара и диска меняется на обратное. Это происходит при H $ \approx $ 1.25a_d. При этом силовой форм-фактор диска становится меньше единицы при дальнейшем увеличении расстояния. Если вспомнить, что форм-фактор в пределе должен стремиться к единице, приходим к выводу, что форм-фактор для дисков большой толщины будет проходить через минимальное значение.

Форма тела всегда связана с распределением вещества тела в пространстве, а, значит, и с положением его центра масс. Сравнивая взаимодействие частиц с твердым телом при одной и той же величине зазора, мы не исключаем разницу в положении их центров масс, что фактически означает различное удаление частиц разной формы от поверхности твердого тела и связанный с этим тривиальный эффект (чем дальше частица, тем она слабее взаимодействует). Чтобы его исключить, нужно сравнивать интенсивность взаимодействия частиц с твердым телом при одном и том же расстоянии (обозначим его H₀) их центров масс от поверхности. Для этого следует заменить H на H₀ – a_s для сферы в формулах (3) и (4), H на H₀ – 0.5d для диска в (5), (6), (10) и (11) и H на H₀ – a_c для стержня в (7), (8), (12) и (13). В частности, это приводит к соотношениям для сил

и соответственно для силовых форм-факторов частиц

При переходе к этому способу описания общая картина несколько изменится. Во-первых, у частиц разного вида нижняя граница доступных расстояний ${{H}_{0}}$ будет различна. Поэтому сравнение функций частиц необходимо проводить в области расстояний, начиная с наибольшего значения нижней границы. В случае тонких дисков и стержней наибольшей она окажется для шара, чья энергия и сила будут превосходить по абсолютной величине соответствующие характеристики для других частиц.

На рис. 3 сравниваются силы и силовые форм-факторы, рассчитанные по формулам (14)–(18) для двух случаев: d = 0.1a_d и d = a_d. Такой же характер зависимостей демонстрирует и энергия. Очевидно, что для d = a_d все зависимости смещаются в область бóльших значений ширины щели. При этом преобладание силы взаимодействия шара относительно как диска, так и стержня становится более выраженным. Соотношения же сил для диска и стержней останутся теми же, что и при рассмотрении зависимостей от расстояния H наибольшего сближения (рис. 2). А именно, тонкие диски превосходят стержни как по энергии, так и по силе взаимодействия (рис. 3а), и наоборот, толстые диски проигрывают во взаимодействии по сравнению со стержнями (рис. 3в). Следует сказать, что при d ≥ 2.45a_d, когда расстояние от поверхности до центра масс становится больше для диска, чем для шара, соотношение взаимодействий диска и шара становится более сложным. Как отмечалось выше, при увеличении толщины диска его взаимодействие приближается к взаимодействию полубесконечного цилиндра. В этом пределе уже становится бессмысленным описывать его взаимодействие в терминах расстояния центра масс частиц до поверхности твердого тела. Тогда нужно вернуться к использованию расстояния наибольшего сближения H, как упоминалось выше при обсуждении рис. 2. В этих случаях существует такое значение H, при котором происходит изменение соотношения сил для шара и диска на противоположное.

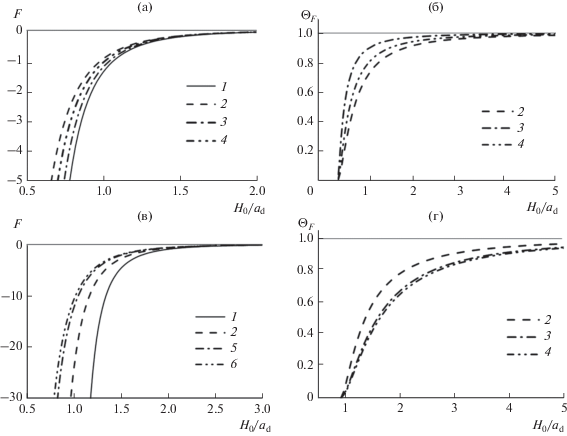
Наиболее отчетливо различие взаимодействий частиц проявляется при использовании форм-факторов, представляющих собой отношение соответствующих характеристик тел одинакового объема. На рис. 3б и 3г представлены силовые форм-факторы различных частиц по отношению к шару в зависимости от расстояния центра масс частиц H₀ до поверхности твердого тела, полученные по формулам (17) и (18). Очевидно, с увеличением расстояния функции $\Theta _{F}^{{(\operatorname{d} )}}\left( {{{H}_{0}}} \right)$ и $\Theta _{F}^{{(\operatorname{c} )}}\left( {{{H}_{0}}} \right)$ стремятся к единице так же, как и функции $\Theta _{F}^{{(\operatorname{d} )}}\left( H \right)$ и $\Theta _{F}^{{(\operatorname{c} )}}\left( H \right),$ но их зависимости совершенно различны. В последнем случае форм-факторы стремятся к единице сверху от больших значений в узких щелях, ширина которых может быть сколь угодно малой (рис. 2б, 2г, 2е). При переходе к расстояниям центра масс частиц область бесконечно узких щелей становится недоступной для шара, что ограничивает снизу область определения рассматриваемых функций. При увеличении ширины щели эти функции H₀ стремятся к единице снизу от бесконечно малых значений в узких щелях. При сравнении форм-факторов дисков и стержней видно, что с толщиной диска его силовой форм-фактор увеличивается по отношению к стрежню (рис. 3б, 3г).

Таким образом, при сравнении наночастиц различной формы, но с одинаковым объемом и одинаковым удалением их центров масс от твердой поверхности сильнее других оказывается взаимодействие шара с твердой поверхностью. Этот вывод справедлив в области значений толщины диска d ≤ 2.45a_d, пока центр масс шара ограничивает область определения доступных расстояний от поверхности твердого тела. При наличии же одного и того же зазора (H) между поверхностью и частицей шарообразные частицы утрачивают свое преимущество.