Коллоидный журнал, 2019, T. 81, № 2, стр. 185-189
Новые уравнения моментов в хроматографии
А. В. Ларин *
Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский проспект, 31, Россия
* E-mail: larin@phyche.ac.ru
Поступила в редакцию 10.10.2018
После доработки 26.10.2018
Принята к публикации 22.10.2018
Аннотация
Проведен анализ точного решения прямой задачи хроматографии, полученного в модели слоя равновесной адсорбции с использованием подынтегрального уравнения гаммa-функции Эйлера. Представлены аналитические решения первых трех обычных, двух нормированных и двух центральных моментов в виде функций, представляющих собой одночленные дроби и включающих длину слоя адсорбента, скорость подвижной фазы, эффективную кинетическую константу и константу Генри. Новые уравнения моментов существенным образом отличаются от используемых в настоящее время.
ВВЕДЕНИЕ
Метод моментов решает обратную задачу динамики адсорбции и позволяет определять константы слоя адсорбента в хроматографической колонке: адсорбционную константу Генри и эффективную кинетическую константу. Приближенные аналитические выражения для центра тяжести и некоторых центральных моментов получены в [1] для кривой элюирования, описываемой полиномами Эрмита. Вычисление константы Генри при этом проводится через выражение для центра тяжести, представляющее собой сумму двух членов, а вычисление эффективной кинетической константы возможно без каких-либо аналитических уравнений через отношение квадрата центра тяжести ко второму центральному моменту, каковые рассчитываются непосредственно из экспериментальной кривой элюирования.
В [2, 3] в рамках модели слоя равновесной адсорбции [4] были проанализированы решения для центра тяжести кривой элюирования и второго центрального момента. Кривая элюирования задавалась выражением в виде подынтегрального уравнения гамма-функции Эйлера. В полученных выражениях для центра тяжести кривой элюирования и второго центрального момента эти параметры прямо пропорциональны относительной длине слоя адсорбента. Сравнение коэффициентов этих зависимостей с экспериментальными данными элюирования хладона 13В1 в потоке воздуха через слои активированного угля разной длины подтвердило корректность полученных решений.
Наряду с получением решений для моментов [2, 3], в последнее время продолжает интенсивно развиваться предложенное в [1] к представление аналитических решений для моментов более высоких порядков, вплоть до четвертого [5–9]. По-видимому, это обусловлено необходимостью описания процесса элюирования на адсорбентах со структурой ядро–пористая оболочка (в англоязычной литературе core–shell particles). В свою очередь, это может быть связано с созданием нового вида таких адсорбентов на основе металлоорганических каркасов, характеризующихся низкими транспортными свойствами [10]. Такое же внимание к центральным моментам наблюдалось в 70-х гг. прошлого века (см., например, [11]).
В [5–9] на основе общей модели скоростей линейной хроматографии представлены аналитические выражения для обычных и центральных моментов и проведен их анализ. Решения для обычных или временны'х моментов (temporal moments в англоязычной литературе) приведены не полностью. Имеются решения для временных моментов нулевого и первого порядков [6, 8], а в [9] и для момента четвертого порядка.
Уравнения для центральных моментов вызывают сомнения. В частности, по уравнениям для центра тяжести, называемого в литературе также первым центральным моментом, и второго центрального момента, представленным в работах [5–9, 11], не рассчитывается корректно относительная длина (эффективность) слоя адсорбента. Актуальным становится аналитическое представление обычных и двух первых центральных моментов для конкретизации отклика, рассчитываемого из экспериментальной кривой элюирования.
Целью работы явился анализ функций моментов в хроматографии на основе точных аналитических решений в рамках достоверной модели слоя равновесной адсорбции.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В теории тарелок [12] для решения прямой задачи хроматографии применяется уравнение, которое в модели слоя равновесной адсорбции записывается в виде
(1)
${{{{c}_{n}}\left( t \right)} \mathord{\left/ {\vphantom {{{{c}_{n}}\left( t \right)} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}} = {{{\text{exp}}\left( { - bt} \right){{{\left( {bt} \right)}}^{{n - 1}}}} \mathord{\left/ {\vphantom {{{\text{exp}}\left( { - bt} \right){{{\left( {bt} \right)}}^{{n - 1}}}} {\left( {n - 1} \right)!}}} \right. \kern-0em} {\left( {n - 1} \right)!}},$В теории тарелок уравнение (1) используется как промежуточное для получения симметричной кривой Гаусса при допущении
$n \to \infty .$ В модели слоя равновесной адсорбции уравнение (1) обосновано на основе численных решений [13] для натуральных $n.$ Позднее уравнение (1) было распространено на область действительных 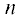 [14, 15], когда факториал действительного числа определяется через гамма-функцию Эйлера.
[14, 15], когда факториал действительного числа определяется через гамма-функцию Эйлера.
Обычные моменты вычисляются по уравнению
где $k$ – порядок обычного момента, $c\left( t \right)$ – экспериментальная или теоретическая кривая элюирования.В математике известно равенство $\int_0^\infty {{{e}^{{ - t}}}{{t}^{n}}dt = n!} ,$ полученное интегрированием по частям. Используя тот же прием интегрирования по частям, из уравнений (1) и (2) получаем аналитические решения для первых трех обычных моментов:
(3)
$\begin{gathered} {{m}_{0}} = {{\left( {n - 1} \right)!} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)!} {b\left( {n - 1} \right)!}}} \right. \kern-0em} {b\left( {n - 1} \right)!}} = {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}, \\ {{m}_{1}} = {{n!} \mathord{\left/ {\vphantom {{n!} {{{b}^{2}}\left( {n - 1} \right)!}}} \right. \kern-0em} {{{b}^{2}}\left( {n - 1} \right)!}} = {n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}, \\ {{m}_{2}} = {{\left( {n + 1} \right)!} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)!} {{{b}^{3}}\left( {n - 1} \right)!}}} \right. \kern-0em} {{{b}^{3}}\left( {n - 1} \right)!}} = {{n\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{n\left( {n + 1} \right)} {{{b}^{3}}}}} \right. \kern-0em} {{{b}^{3}}}}. \\ \end{gathered} $Отметим, что уравнение ${{m}_{0}} = {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}$ впервые было получено в [15] и описывает площадь под кривой (1).
Центр тяжести ${{t}_{{\text{c}}}}$ (первый центральный момент) был вычислен в [2] как отношение первых двух моментов задаваемых соотношениями (3):
(4)
${{t}_{{\text{c}}}} = {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} = {{\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}} \right)}} = {n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b}.$Из обычных моментов (3) легко получить выражения для нормированных моментов ${{\vartheta }_{k}} = {{{{m}_{k}}} \mathord{\left/ {\vphantom {{{{m}_{k}}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}{\text{:}}$
(5)
${{\vartheta }_{1}} = {n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b},\,\,\,\,{{\vartheta }_{2}} = {{n\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{n\left( {n + 1} \right)} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}.$Второй центральный момент был вычислен в [3] по уравнению
(6)
${{{\mu }}_{2}} = {{\vartheta }_{2}} - \vartheta _{1}^{2} = {{n\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{n\left( {n + 1} \right)} {{{b}^{2}} - {{{({n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b})}}^{2}}}}} \right. \kern-0em} {{{b}^{2}} - {{{({n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b})}}^{2}}}} = {n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}.$Выражения для центра тяжести и второго центрального момента, описываемые уравнениями (4) и (6), приведены в табл. 1.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Экспериментальные результаты [16], анализируемые в настоящей работе, получены по описанной ранее методике [17]. Исследуемое вещество – хладон 13 (CF3Cl). Характеристики структуры адсорбента представлены в [16]. Активный уголь и воздух были практически сухими.
Методика эксперимента заключалась в следующем. В поток газа-носителя (воздуха) перед адсорбентом, помещенным в стеклянную трубку, с помощью шприца вводили 8.8 мг хладона (диаметр слоя адсорбента – 2.0 см, скорость газа-носителя – 2.2 дм3/мин, температура опыта – 333 К). Далее с помощью пламенно-ионизационного детектора анализировали изменение во времени концентрации хладона за слоем адсорбента. Длину слоя адсорбента варьировали в интервале от 1 до 4 см с шагом 1 см.
Для полученных кривых элюирования были рассчитаны моменты и значения $n$. Табличные данные [16] представлены в виде зависимостей центра тяжести и второго центрального момента от $n$ на рис. 1. Результаты аппроксимации этих данных линейными функциями приведены в табл. 2.
Рис. 1.
Табличные данные об элюировании хладона 13 в потоке воздуха через активированный уголь [16] в виде зависимостей центра тяжести ${{t}_{{\text{c}}}}$ (1) и второго центрального момента ${{{\mu }}_{2}}$ (2) от относительной длины n слоя адсорбента.
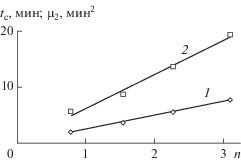
Таблица 2.
Значения коэффициентов зависимостей (4) и (6) и рассчитанная из них константа $b$ для экспериментальных данных [16]
| Анализируемый момент | Тангенс угла наклона | Свободный член | ${{R}^{2}}$ | $b,$ мин–1 |
|---|---|---|---|---|
| ${{t}_{{\text{c}}}},$ мин | 2.45 | 0.05 | 0.997 | 0.41 |
| ${{{\mu }}_{2}},$ мин2 | 5.96 | 0.29 | 0.987 | 0.41 |
ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Сравним уравнения моментов, полученные выше на основе модели слоя равновесной адсорбции, с уравнениями, представленными в литературе. Эти уравнения моментов, особенно высших порядков, содержат большое количество слагаемых [1, 5–9, 11]. Каждое слагаемое представляет собой произведение и отношение физико-химических констант и опытных величин, т.е. является рациональной алгебраической дробью. В модели слоя равновесной адсорбции моменты описываются одночленными дробями (табл. 1), которые представляют собой простое отношение $n$ к константе $b$ с изменяющейся степенью.
При анализе решений, полученных в работах [1, 5–7, 11], введем упрощения. Например, в случае решений из работы [1] предположим, что используемые в слагаемых уравнений выражения типа
(7)
$1 + {{K}_{{\text{n}}}}\,\,{\text{и л и }}\,\,1 + \epsilon {{K}_{{\text{c}}}}\left( {1 + {{K}_{{\text{n}}}}} \right),$Выражения для моментов из [11] при допущении, подобном (7), содержат по сравнению с выражениями из [1] уже несколько другое число слагаемых. В [5–7] по сравнению с [1] и [11] число слагаемых можно считать одинаковым. В [6, 8, 9] число слагаемых для ${{{\mu }}_{2}}$ изменяется от 4 до 6, что связано с выбранными начальными условиями. В целом, число слагаемых в уравнениях для моментов, приведенных в табл. 1, соответствует уровню современных работ в этой области.
Корректность уравнений (4) и (6) для ${{t}_{{\text{c}}}}$ и ${{{\mu }}_{2}}$ соответственно была доказана в [3]. Известно, что при решении обратной задачи хроматографии методом моментов для вычисления относительной длины (эффективности) слоя адсорбента используется простое отношение в виде ${{t_{{\text{c}}}^{2}} \mathord{\left/ {\vphantom {{t_{{\text{c}}}^{2}} {{{{\mu }}_{2}}}}} \right. \kern-0em} {{{{\mu }}_{2}}}}.$ Подстановкой этого отношения в функции (4) и (6) в [3] было получено точное соответствие решений (4) и (6) искомой величине эффективности слоя адсорбента,
(8)
$n = {{{{{\left( {{n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b}} \right)}}^{2}}} {\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)}}} \right. \kern-0em} {\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)}} = n.$Другим доказательством корректности уравнений (4) и (6) в [3] были результаты экспериментального элюирования хладона 13В1 (CF3Br) на активированном угле в виде линейных зависимостей ${{t}_{{\text{c}}}}$ и ${{{\mu }}_{2}}$ от 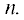 Дополним это доказательство результатами работы [16], в которой изучено элюирование хладона 13 (CF3Cl) потоком воздуха на активированном угле. Табличные данные для ${{t}_{{\text{c}}}},$ ${{{\mu }}_{2}}$ и $n$ из работы [16] представлены в виде соответствующих графических зависимостей на рис. 1. Обе зависимости, (4) и (6), были аппроксимированы линейными функциями, результаты
аппроксимации суммированы в табл. 2.
Дополним это доказательство результатами работы [16], в которой изучено элюирование хладона 13 (CF3Cl) потоком воздуха на активированном угле. Табличные данные для ${{t}_{{\text{c}}}},$ ${{{\mu }}_{2}}$ и $n$ из работы [16] представлены в виде соответствующих графических зависимостей на рис. 1. Обе зависимости, (4) и (6), были аппроксимированы линейными функциями, результаты
аппроксимации суммированы в табл. 2.
Результаты, представленные в табл. 2, свидетельствуют об удовлетворительном соответствии эксперимента теоретическим соотношениям (4) и (6). Значения константы $b,$ рассчитанные из тангенсов углов наклона этих зависимостей, совпадают и равны 0.41 мин–1.
Отличие свободных членов эмпирических зависимостей от нуля может быть обусловлено ошибкой эксперимента, недостаточным обоснованием интервала интегрирования и неучетом влияния входного сигнала на точность вычисления моментов именно в слое адсорбента. Поскольку адсорбируемость хладонов достаточно велика, то влияние входного сигнала может быть не таким заметным, как при элюировании веществ, обладающих меньшей адсорбционной способностью.
Таким образом, корректность уравнений моментов (4) и (6) может считаться вновь доказанной. Выше указывалось, что в методе моментов для вычисления константы Генри необходимо аналитическое решение для центра тяжести кривой элюирования, а эффективность слоя адсорбента рассчитывается непосредственно из моментов экспериментальных выходных кривых. Рассмотрим теперь возможности уравнений моментов, используемых сегодня в литературе.
Из данных табл. 1 следует, что даже формально решения для уравнений моментов, представленные в [1, 5–9, 11] и других многочисленных работах различных авторов, нельзя назвать удачными и удобными для анализа результатов. Эти решения не только контрастируют с более удобными решениями, полученными с использованием модели слоя равновесной адсорбции (табл. 1, 2-oй столбец), но и могут приводить к существенным ошибкам при анализе экспериментальных данных. Рассмотрим имеющиеся в литературе уравнения моментов в последовательности возрастания их порядка.
Для центра тяжести, который в литературе достаточно часто называют первым моментом, необходимо аналитическое выражение для вычисления константы Генри или удельного удерживаемого объема. Преобразуем уравнение (4), раскрыв выражения для $n$ и $b.$ Тогда
(9)
${{t}_{{\text{c}}}} = {{L\left( {1 + {\Gamma }} \right)} \mathord{\left/ {\vphantom {{L\left( {1 + {\Gamma }} \right)} u}} \right. \kern-0em} u}.$При вычислениях константы Генри или удельного удерживаемого объема используется допущение ${\Gamma } \approx \left( {1 + {\Gamma }} \right).$ В [16] константа Генри или удельный удерживаемый объем скорее интуитивно вычисляли по уравнению (9). Уравнения (4) или (9) можно использовать для анализа зависимостей центра тяжести не только от длины или массы слоя адсорбента, но и от скорости подвижной фазы.
В [18] была изучена хроматография этана, пропана и нормального бутана на силикагеле. С учетом входного сигнала, заданного прямоугольником, получены достоверные данные для зависимости центра тяжести от обратного значения скорости подвижной фазы. Все полученные зависимости линейны и исходят из точки начала координат, т.е. соответствуют уравнению (9). В [18] также отмечается, что тангенс угла наклона полученных зависимостей должен быть пропорционален константе Генри ${\Gamma }$, что и соблюдается в (9).
Таким образом, несмотря на наличие разумного решения для центра тяжести кривой элюирования в виде уравнений (4) и (9) в литературе до настоящего времени приводится и используется решение в виде двухчленного уравнения. Например, такие уравнения приводятся в [1, 5–9, 18, 19], а в [20] такой расчет проведен для вычисления константы Генри углеводородов на металлоорганических каркасах.
Переходя ко второму центральному моменту, отметим, что он представляет собой дисперсию кривой элюирования и вместе с центром тяжести позволяет вычислить относительную длину или эффективность слоя адсорбента. Выше указывалось, что для вычисления относительной длины (эффективности) слоя адсорбента используется простое соотношение в виде ${{t_{{\text{c}}}^{2}} \mathord{\left/ {\vphantom {{t_{{\text{c}}}^{2}} {{{{\mu }}_{2}}}}} \right. \kern-0em} {{{{\mu }}_{2}}}}.$. Авторы метода моментов [21], используя соотношение для высоты, эквивалентной теоретической тарелке (ВЭТТ), $H = {{{{{\mu }}_{2}}L} \mathord{\left/ {\vphantom {{{{{\mu }}_{2}}L} {t_{{\text{c}}}^{2}}}} \right. \kern-0em} {t_{{\text{c}}}^{2}}},$ и упрощенное выражение для ${{{\mu }}_{2}},$ не получили значение $n$, а обнаруженную зависимость ВЭТТ от переменных посчитали возможным применить для описания функций, подобных функции Ван Деемтера [22]. Такой прием, на наш взгляд, не является корректным. Тем не менее, он использовался [11] и используется в настоящее время (см., например, [6, 8]).
Полученное для второго центрального момента аналитическое решение (6) после раскрытия $n$ и $b$ и при допущении ${\Gamma } \approx 1 + {\Gamma }$ приводится к виду
(10)
${{{\mu }}_{2}} = {{L{{{\Gamma }}^{2}}{{L}_{{\text{e}}}}} \mathord{\left/ {\vphantom {{L{{{\Gamma }}^{2}}{{L}_{{\text{e}}}}} {{{u}^{2}}}}} \right. \kern-0em} {{{u}^{2}}}}.$Используя уравнение (10) и зависимости эффективной кинетической константы от скорости подвижной фазы, предложенные в [22], можно найти корреляции между ${{{\mu }}_{2}}$ и $u$ для различных интервалов скорости подвижной фазы. Например, в [5] получена линейная зависимость ${{{\mu }}_{2}}{{u}^{2}}$ от $u,$ что, по-видимому, согласуется с уравнением (10). Отметим, что корреляции, представленные в [5, 18, 23] и других работах, могут быть полезны для анализа получаемых в хроматографии результатов. Однако они не заменяют анализа результатов на основе достоверных решений.
Третий центральный момент и моменты более высокого порядка в данной работе не рассматриваются. Отметим, что все утверждения о том, что высшие моменты, начиная с момента третьего порядка, могут дать дополнительную информацию, до настоящего времени вразумительного объяснения не получили. Эти моменты следует рассмотреть в отдельном исследовании.
ЗАКЛЮЧЕНИЕ
Таким образом, проведенный анализ уравнений метода моментов, применяемых сегодня в хроматографии для описания центра тяжести и дисперсии (второго центрального момента) кривой элюирования, позволяет считать, что эти уравнения не являются корректными.
В литературе первый момент или центр тяжести представляется суммой двух рациональных дробей, из которой без каких-либо допущений константа Генри не может быть рассчитана. Такой же сложный вид имеет выражение для второго центрального момента.
Также вызывает сомнение процедура, когда выражение для ВЭТТ получают с использованием этих некорректных уравнений. Это приводит к возможности появления недостоверных зависимостей, внешне подобных уравнению Ван Деемтера.
Представленные в настоящей работе моменты (центр тяжести и второй центральный момент) являются более реалистичными.
Список литературы
Kucera E. // J. Chromatogr. 1965. V. 19. P. 237.
Ларин А.В. // Коллоид. журн. 2011. Т. 73. С. 858.
Ларин А.В. // Коллоид. журн. 2012. Т. 74. С. 430.
Ларин А.В. // Изв. АН СССР. Серия хим. 1983. С. 236.
Gao H., Wu X., Lin B. // J. Chromatogr. Sci. 2010. V. 48. P. 742.
Qamar S., Abbasi J. N., Mehwish A., Seidel-Morgenstern A. // Chem. Eng. Sci. 2015. V. 137. P. 352.
Miyabe K. // Trends Anal. Chem. 2016. V. 81. P. 79.
Qamar S., Seidel-Morgenstern A. // Trends Anal. Chem. 2016. V. 81. P. 87.
Qamar S., Akram N., Seidel-Morgenstern A. // Chem. Eng. Res. Design. 2016. V. 111. P. 13.
Ларин А.В., Притчард К.Е. // Коллоид. журн. 2016. Т. 78. С. 405.
Vidal-Madjar C., Guiochon G. // J. Chromatogr. 1977. V. 142. P. 61.
Martin A.J.P., Synge R.L.M. // Biochem. J. 1941. V. 35. P. 1358.
Ларин А.В. // Изв. АН СССP. Серия хим. 1984. С. 1212.
Ларин А.В. // Инж.-физ. журн. 2011. Т. 84. С. 1175.
Ларин А.В. // Изв. АН. Серия хим. 2011. С. 367.
Polyakov N.S., Larin A.V., Goubkina M. L. // Adsorp. Sci. Technol. 1993. V. 10. P. 173.
Губкина М.Л., Ларин А.В., Шеховцова Л.Г. // Изв. АН СССР. Серия хим. 1985. С. 513.
Schneider P., Smith J.M. // Am. Inst. Chem. Eng. J. 1968. V. 14. P. 762.
Asnin L., Sharma K., Park S.W. // J. Chromatogr. 2011. V. 1218. P. 5263.
Finsy V., De Bruyne S., Alaerts L., De Vos D., Jacobs P.A., Baron G.V., Denayer J.F.M. // Stud. Surf. Sci. Catal. B. 2007. V. 170. P. 2048.
Grubner O., Ralek M., Kucera E. // Coll. Czech. Chem. Comm. 1966. V. 31. P. 2629.
Van Deemter I.I., Zuiderweg F.J., Klinkenberg A. // Chem. Eng. Sci. 1956. V. 5. P. 271.
Gao H., Wu X., Lin B. // J. Chromatogr. Sci. 2010. V. 48. P. 478.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


