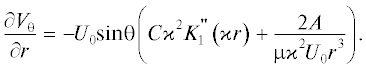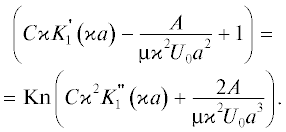Коллоидный журнал, 2019, T. 81, № 3, стр. 356-359

Гидродинамическое сопротивление и эффективность фильтрации бимодальными волокнистыми материалами

А. Л. Черняков^1, *, А. А. Кирш¹

¹ НИЦ “Курчатовский институт”
123182 Москва, пл. Курчатова, 1, Россия

Поступила в редакцию 30.10.2018
После доработки 06.11.2018
Принята к публикации 08.11.2018

DOI: 10.1134/S0023291219020034

Аннотация

Исследованы гидродинамическое сопротивление и эффективность фильтрации газов бимодальными волокнистыми материалами в зависимости от объемной доли тонких волокон. Для уравнений, описывающих гидродинамику газа в пористой среде, образованной смесью волокон двух различных диаметров, вычислена зависимость постоянной Бринкмана от содержания волокон с меньшим диаметром. Рассчитана величина проскока аэрозольных частиц в зависимости от их диаметра для различных бимодальных фильтров. Результаты вычислений сравниваются с экспериментом.

1. ВВЕДЕНИЕ

Бимодальные или двухкомпонентные фильтры изготавливают на основе фильтрующих материалов состоящих из двух сортов волокон с резко разными диаметрами. На протяжении нескольких десятилетий, начиная с 30х годов, все типы высокоэффективных фильтров изготавливались из смеси грубодисперсных целлюлозных, хлопковых или шерстяных волокон с добавками тонко диспергированных волокон асбеста [1]. В настоящее время бимодальные фильтры изготавливают из стеклянных или полимерных волокон разного диаметра. Отличительная особенность этих фильтров – высокие пористость и пылеемкость. Поэтому в современных системах тонкой очистки газов они используются в качестве предфильтров и устанавливаются перед фильтрами ULPA, характеризующимися сверхвысокой эффективностью очистки воздуха.

Теория фильтрации газов волокнистыми материалами также продолжает активно развиваться. От ранних простейших моделей [2] постепенно переходят к компьютерной генерации и исследованию трехмерных монодисперсных волокнистых сред и вычислению их свойств [3, 4]. Появились даже работы, в которых создавались трехмерные модели бимодальных фильтров и методом решеточного уравнения Больцмана [5, 6] вычислялись их свойства [7]. Эти работы приближают нас к пониманию и предсказанию эффективности фильтрации реальными промышленными фильтрами. Однако расчеты трехмерных бимодальных фильтров методом решеточного уравнения Больцмана требуют большого машинного времени, поэтому для определения влияния различных параметров на эффективность фильтрации требуются простые качественные методы расчета.

В работе [8] на основе самосогласованной теории [9] был предложен простой метод вычисления перепада давления и эффективности фильтрации для полидисперсных волокнистых материалов для случая произвольной функции распределения длин волокон по их диаметрам. Были проведены вычисления для логнормальной функции распределения. В этой работе мы применим самосогласованную модель к бимодальным фильтрам и сравним результаты вычисления с экспериментом [10].

2. ГИДРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ БИМОДАЛЬНЫХ ФИЛЬТРОВ

Волокнистые фильтры представляют собой тонкие листы материала, волокна в которых ориентированы в основном в плоскости материала. Считаем, что поток газа направлен перпендикулярно к плоскости фильтра, поэтому скорость течения газа вблизи каждого волокна в среднем направлена перпендикулярно к его оси.

В самосогласованной теории поле течения несжимаемой жидкости вблизи отдельного цилиндрического волокна в пористой среде описывается уравнением Бринкмана [11]

(1)

$\Delta V - {{\varkappa }^{2}}V = \frac{1}{{\mu }}\nabla p,\,\,\,\,{\text{div}}V = 0,$

где V – скорость потока, p – давление, μ – динамическая вязкость газа, $\varkappa $ – постоянная Бринкмана пористой среды. Из условия несжимаемости жидкости следует, что давление является гармонической функцией, т.е.

(2)

$\Delta p = 0.$

Решение уравнения (2) для давления p вблизи волокна имеет вид

(3)

$p = \left( {\frac{A}{r} - {\mu }{{\varkappa }^{2}}{{U}_{0}}r} \right)\cos {\theta }{\text{.}}$

Функция тока в цилиндрической системе координат с осью z, направленной вдоль волокна, ищется в виде $\psi = {{e}_{z}}{{U}_{0}}\sin {\theta }f(r),$ где U₀ – средняя скорость течения газа в среде.

Вектор скорости потока равен $V = {\text{rot}}\psi ,$ а его компоненты имеют вид

(4)

${{V}_{r}} = \frac{1}{r}\frac{{\partial {\psi }}}{{\partial {\theta }}},\,\,\,\,{{V}_{{\theta }}} = - \frac{{\partial {\psi }}}{{\partial r}}.$

Взяв ротор от уравнения (1), получим уравнение для функции тока

(5)

$\Delta \left( {\Delta {\psi } - {{\varkappa }^{2}}{\psi }} \right) = 0.$

Решение этого уравнения равно

(6)

${\psi } = {{U}_{0}}{sin\theta }\left( {C{{K}_{1}}\left( {\varkappa r} \right) + \frac{A}{{{\mu }{{\varkappa }^{2}}{{U}_{0}}r}} + r} \right),$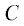

где ${{K}_{1}}\left( {\varkappa r} \right)$ – модифицированная функция Бесселя первого рода, а $A$ и

– неизвестные постоянные.

Из (6) получаем следующие выражения для компонент скорости:

(7)

$\quad{{V}_{r}} = {{U}_{0}}{cos\theta }\left( {C\frac{1}{r}{{K}_{1}}\left( {\varkappa r} \right) + \frac{A}{{{\mu }{{\varkappa }^{2}}{{U}_{0}}{{r}^{2}}}} + 1} \right),$

(8)

${{V}_{{\theta }}} = - {{U}_{0}}{\text{sin}}\theta \left( {C\varkappa K_{1}^{'}\left( {\varkappa r} \right) - \frac{A}{{{\mu }{{\varkappa }^{2}}{{U}_{0}}{{r}^{2}}}} + 1} \right),$

(9)

Постоянные 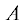и $C$ определяются из граничных условий. На поверхности волокна должна равняться нулю радиальная компонента скорости,

(10)

$C\frac{1}{a}{{K}_{1}}\left( {\varkappa a} \right) + \frac{A}{{{\mu }{{\varkappa }^{2}}{{U}_{0}}{{a}^{2}}}} + 1 = 0,$

а касательная скорость пропорциональна ее производной по радиусу,

(11)

Для тонких волокон при вычислении касательной скорости нужно учесть эффект скольжения газа, который характеризуется числом Кнудсена, пропорциональным отношению длины свободного пробега молекул газа ${\lambda }$ к радиусу волокна, ${\text{Kn}} = {{c}_{{\text{m}}}}\frac{{\lambda }}{a}.$ Постоянная ${{c}_{{\text{m}}}}$ – порядка единицы, и мы будем полагать ее просто равной 1.

Из уравнений (10) и (11) найдем постоянные $A$ и $C{\text{:}}$

(12)

$\begin{gathered} C = \frac{2}{{\varkappa {{K}_{0}}\left( {\varkappa a} \right)}}G\left( {{\text{Kn}},\varkappa a} \right),\,\,\,\,\frac{A}{{{\mu }{{U}_{0}}{{\varkappa }^{2}}{{a}^{2}}}} = - 1 - \frac{{C{{K}_{1}}\left( {\varkappa a} \right)}}{a}, \\ G\left( {{\text{Kn}},\varkappa a} \right) = \frac{{1{\;} + {\text{Kn}}}}{{1 + {\text{Kn}}\left( {1{\;} + \varkappa a\frac{{{{K}_{1}}\left( {\varkappa a} \right)}}{{{{K}_{0}}\left( {\varkappa a} \right)}}} \right)}} \approx \\ \approx \,\,1 - {\text{Kn}}\frac{{\varkappa a{{K}_{1}}\left( {\varkappa a} \right)}}{{{{K}_{0}}\left( {\varkappa a} \right)}}. \\ \end{gathered} $

Последнее равенство справедливо, так как гидродинамическое приближение для описания влияния числа ${\text{Kn}}$ на различные характеристики фильтра применимо только при ${\text{Kn}} \ll 1.$

Сила сопротивления, действующая на каждое волокно, выражается через постоянную Бринкмана $\varkappa $ и радиус этого волокна $a$ как

(13)

$\quad{{F}_{x}}\left( a \right) = 4{\pi \mu }{{U}_{0}}\left[ {\frac{1}{2}{{\varkappa }^{2}}{{a}^{2}} + \frac{{\varkappa a{{K}_{1}}\left( {\varkappa a} \right)}}{{{{K}_{0}}\left( {\varkappa a} \right)}}G} \right].$

Условие самосогласования дает следующее уравнение для определении постоянной Бринкмана $\varkappa $ для бимодальной волокнистой среды:

(14)

${{\varkappa }^{2}} = 4{\pi }\sum\limits_i {\left( {\frac{1}{2}{{\varkappa }^{2}}a_{i}^{2} + \frac{{\varkappa {{a}_{i}}{{K}_{1}}\left( {\varkappa {{a}_{i}}} \right)}}{{{{K}_{0}}\left( {\varkappa {{a}_{i}}} \right)}}G\left( {\varkappa {{a}_{i}}} \right)} \right){{l}_{i}}} .$

Длины волокон каждого диаметра в единице объема волокнистой среды $\quad{{l}_{i}}$ можно выразить через плотность упаковки ${\alpha }$ и объемные концентрации волокон ${{c}_{i}}{\text{:}}$

$\quad{{l}_{i}} = \frac{{\alpha }}{{{\pi }a_{i}^{2}}}{{c}_{i}},\,\,\,\,{{c}_{1}} + {{c}_{2}} = 1.$

Подставляя эти выражения в (14), получим уравнение для определения постоянной Бринкмана для бимодальной среды:

(15)

$\begin{gathered} \varkappa {{a}_{1}} = \frac{{4{\alpha }}}{{1 - 2{\alpha }}}\left[ {\frac{{{{K}_{1}}\left( {\varkappa {{a}_{1}}} \right)}}{{{{K}_{0}}\left( {\varkappa {{a}_{1}}} \right)}}G\left( {\varkappa {{a}_{1}}} \right){{c}_{1}} + } \right. \\ \left. { + \,\,\frac{{{{K}_{1}}\left( {\varkappa {{a}_{2}}} \right)}}{{{{K}_{0}}\left( {\varkappa {{a}_{2}}} \right)}}\frac{{{{a}_{1}}}}{{{{a}_{2}}}}G\left( {\varkappa {{a}_{2}}} \right){{c}_{2}}} \right]. \\ \end{gathered} $

Падение давления на фильтре толщиной $H$ выражается через постоянную Бринкмана $\varkappa {\text{:}}$

(16)

$\Delta p = {\mu }{{\varkappa }^{2}}{{U}_{0}}H.$

3. ЭФФЕКТИВНОСТЬ БИМОДАЛЬНЫХ ФИЛЬТРОВ

Для вычисления влияния диффузии аэрозольных частиц на эффективность фильтрации мы воспользуемся качественным рассмотрением. Толщина диффузионного размытия ${\delta }$ траектории частицы радиуса $R\quad$ при прохождении вблизи отдельного волокна радиуса $a$ определяется временем пролета, $\quad{{{\delta }}^{2}}\sim Dt,$ где коэффициент диффузии $D$ зависит от радиуса улавливаемых частиц и длины свободного пробега молекул газа [12]:

$D\left( R \right) = \frac{T}{{6{\pi \mu }R}}\left[ {1 + \frac{{\lambda }}{R}\left( {1.257 + 0.4\exp \left( { - \frac{{1.1R}}{{\lambda }}} \right)} \right)} \right].$

Время пролета частицы $t$ определяется касательной компонентой скорости ${{V}_{{\theta }}}\quad$ на расстоянии $\tilde {r} = a + R + {\delta }$ от центра волокна:

(17)

${{t\sim \tilde {r}} \mathord{\left/ {\vphantom {{t\sim \tilde {r}} {{{V}_{{\theta }}}\left( {\tilde {r}} \right)}}} \right. \kern-0em} {{{V}_{{\theta }}}\left( {\tilde {r}} \right)}}.$

Используя выражение (8) для касательной компоненты скорости, получаем уравнение для определения толщины диффузионной области

(18)

${{\left( {\frac{{\delta }}{a}} \right)}^{2}}\left[ {C\varkappa K_{1}^{'}\left( {\varkappa \tilde {r}} \right) - \frac{A}{{{\mu }{{\varkappa }^{2}}{{U}_{0}}{{{\tilde {r}}}^{2}}}} + 1} \right]\frac{a}{{\tilde {r}}} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} {\left( {{\text{Pe}} + b} \right)}}} \right. \kern-0em} {\left( {{\text{Pe}} + b} \right)}},$

где число Пекле ${\text{Pe}} = \frac{{2a{{U}_{0}}}}{D},$ а параметры ${{c}_{0}}$ и $b\quad$ должны быть выбраны исходя из экспериментальных данных. Параметр $b$ ограничивает рост диффузионного слоя при ${\text{Pe}} \to 0.\quad$ При больших числах ${\text{Pe,}}$ например для точечной частицы, и без учета скольжения газа при выборе константы ${{c}_{0}} = {{2.9}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ коэффициент захвата η = ${{{\psi }\left( {a + {\delta }} \right)} \mathord{\left/ {\vphantom {{{\psi }\left( {a + {\delta }} \right)} {\left( {a{{U}_{0}}} \right)}}} \right. \kern-0em} {\left( {a{{U}_{0}}} \right)}},$ как показано в [8], переходит в формулу Натансона [13]. Определив толщину диффузионного слоя для каждого типа волокон, можно вычислить проскок по формуле

(19)

$P = {\text{exp}}\left[ { - \left( {\frac{{{{c}_{1}}}}{{{\pi }a_{1}^{2}}}{{{\psi }}_{1}}\left( {{{{\tilde {r}}}_{1}},\frac{{\pi }}{2}} \right) + \frac{{{{c}_{2}}}}{{{\pi }a_{2}^{2}}}{{{\psi }}_{2}}\left( {{{{\tilde {r}}}_{2}},\frac{{\pi }}{2}} \right)} \right)\frac{{2{\alpha }H}}{{{{U}_{0}}}}} \right],$

где функции тока $\quad{{{\psi }}_{{1,2}}}$ определяются формулой (6).

Мы сравним результаты расчетов проскока по формулам (18), (19) с экспериментальными данными работы [10], в которой были изготовлены волокнистые материалы с различным процентным содержанием стеклянных волокон диаметром 0.78 и 3 мкм. Для различных образцов были измерены одновременно перепад давления и проскок аэрозольных частиц разного размера при скорости потока ${{U}_{0}} = 10{\;}{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}{\text{.}}$ К сожалению, для полученных материалов осталась неизвестной плотность упаковки. Для изготовленных фильтров известен вес на единицу поверхности ${{P}_{{\text{g}}}}{\;} \approx 75{\;}{{\text{г }} \mathord{\left/ {\vphantom {{\text{г }} {{{{\text{м }}}^{2}}}}} \right. \kern-0em} {{{{\text{м }}}^{2}}}},$ через который, зная толщину материала $H\quad$ и плотность стекла ${\rho \;} \approx {\;}2\quad\,{{\text{г }} \mathord{\left/ {\vphantom {{\text{г }} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с }}{{{\text{м }}}^{{\text{3}}}}}},$ можно найти плотность упаковки ${\alpha } = \frac{{{{P}_{{\text{g}}}}}}{{{\rho }H}}.$ О толщине полученных фильтров никаких упоминаний в статье [10] не содержится, кроме того, что она не сильно различается для всех образцов.

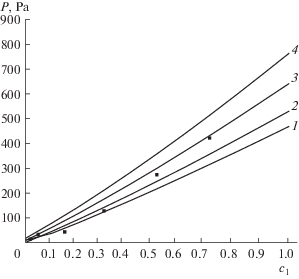
На рис. 1 приведены результаты вычислений по формулам (15), (16) зависимости перепада давления от доли ${{c}_{1}}$ частиц диаметром 0.78 мкм в бимодальном волокнистом материале при нескольких значениях плотности упаковки ${\alpha }{\text{.}}$ Квадратными значками показаны экспериментальные значения [10]. Видно, что наилучшим приближением к эксперименту является значение ${\alpha } = 0.005.$ При вычислении эффективности фильтрации мы будем использовать именно это значение плотности упаковки.

Рис. 1.

Зависимость перепада давления на фильтре от доли в нем тонких волокон при разных значениях плотности их упаковки α: 1 – 10^–3, 2 – 2 × 10^–3, 3 – 5 × 10^–3, 4 – 10^–2. Экспериментальные точки взяты из работы [10].

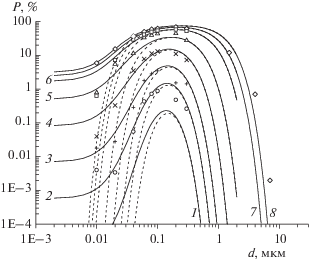
На рис. 2 приведены результаты вычислений проскока аэрозольных частиц через различные бимодальные фильтры, выполненные по формулам (18), (19). Был выбран параметр c₀ = = $0.5 \times {{2.9}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$ На рис. 2 сплошными кривыми показаны результаты вычислений при $b = 15,$ а пунктирными – при $b = 0.$ Видно удовлетворительное согласие изложенной простой самосогласованной теории с измерениями, проведенными в работе [10].

Рис. 2.

Проскок $P\quad$ аэрозольных частиц в зависимости от их диаметра d через бимодальные фильтры с различной долей тонких волокон c₁: 1 (1), 0.7 (2), 0.5 (3), 0.3 (4), 0.15 (5), 0.05 (6), 0.02 (7), 0 (8). Сплошные кривые – расчет при b = 15, пунктирные – при b = 0. Соответствующие экспериментальные данные работы [10] показаны различными значками.

4. ЗАКЛЮЧЕНИЕ

Качественная феноменологическая теория фильтрации полидисперсными фильтрами [8] была использована для расчета перепада давления и эффективности фильтрации для бимодальных волокнистых материалов. Были проведены расчеты для параметров, соответствующих экспериментам, выполненным в работе [10]. Полученные результаты для эффективности фильтрации не только качественно, но и удовлетворительно количественно согласуются с экспериментальными данными [10] при учете ограничения ширины диффузионного слоя при малых числах Пекле.

Работа выполнена при поддержке НИЦ “Курчатовский институт” (проект № 1607 от 05.07.18).

Список литературы

Высокоэффективная очистка воздуха / Под ред. Уайта П. и Смита С. М.: Атомиздат, 1967.
Kirsch A.A., Stechkina I.B. // Fundamentals of Aerosol Science. Ed. by Shaw D.T. N.Y.: Wiley, 1978. P. 165.
Clague D.S., Ronald J.P. // Phys. Fluids. 1997. V. 9. P. 1562.
Hosseini S.A., Tafreshi H.V. // Powder Technol. 2010. V. 201. P. 153.
Succi S., Foti E. Higuera F. // Europhys. Lett. 1989. V. 10. P. 433.
Succi S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford: Oxford University Press, 2001.
Rebai M., Drolet F., Vidal D., Vadeiko I., Bertrand F. // Asia-Pac. J. Chem. Eng. 2011. V. 6. P. 29.
Черняков А.Л., Кирш А.А. // Коллоид. журн. 2018. Т. 80. С. 349.
Spielman L., Goren S.L. // Environ. Sci. Technol. 1968. V. 2. P. 279.
Brown R.C., Thorpe A. // Powder Technol. 2001. V. 118. P. 3.
Brinkman H.C. // Appl. Sci. Res. A. 1947. V. l. P. 27.
Райст П. Аэрозоли. М.: Мир, 1987.
Натансон Г.Л. // ДАН СССР. 1957. Т. 112. С. 100.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал