Коллоидный журнал, 2019, T. 81, № 3, стр. 275-280
Численное описание быстрой релаксации в мицеллярных растворах на основе модели сфероцилиндров
Л. В. Аджемян 1, Ю. А. Ерошкин 2, Т. Л. Ким 2, А. К. Щёкин 2, *
1 Санкт-Петербургский государственный технологический институт (технический университет),
факультет экономики и менеджмента
190013 Санкт-Петербург, Московский проспект, 26, Россия
2 Санкт-Петербургский государственный университет, физический факультет
199034 Санкт-Петербург, Университетская наб., 7/9, Россия
* E-mail: a.shchekin@spbu.ru
Поступила в редакцию 07.12.2018
После доработки 10.12.2018
Принята к публикации 10.12.2018
Аннотация
Недавно на основе кинетических уравнений Беккера–Дёринга был разработан полуаналитический метод расчета времени быстрой релаксации в растворах поверхностно-активных веществ с цилиндрическими мицеллами, позволяющий без потери точности значительно сократить процедуру вычислений. Для кинетических коэффициентов присоединения мономеров к агрегату использовалась модель мицеллы в виде вытянутого эллипсоида, для которой задача нахождения диффузионного потока мономеров на мицеллу имеет аналитическое решение. В настоящей работе проведены численные расчеты диффузионного потока и времени быстрой релаксации для более реалистичной модели мицеллы в виде сфероцилиндра. Результаты сопоставлены с ранее известными.
ВВЕДЕНИЕ
Большую роль в кинетике агрегирующих систем играет как можно более точное задание коэффициентов соответствующего кинетического уравнения, будь это уравнение Беккера–Дёринга [1], описывающее молекулярный механизм агрегации, уравнение коагуляции Смолуховского [2] или обобщенное уравнение Смолуховского [3–5] при механизме слияния и распада агрегатов.
В кинетике мицеллообразования [6, 7] для задания коэффициентов кинетических уравнений Беккера–Дёринга используются выражения для равновесного распределение мицелл по числам агрегации и для стационарного диффузионного потока мономеров поверхностно-активных вещества (ПАВ) на мицеллу при заданном числе агрегации. Для сферических агрегатов эти выражения хорошо известны [4–8], однако для цилиндрических мицелл приходится использовать доступные аппроксимации. Так, недавно для работы агрегации в равновесном распределении цилиндрических мицелл в [9] была взята за основу линейная по числу агрегации работа агрегации сфероцилиндров, а для коэффициентов присоединения мономеров к агрегату использовались линейная по числу агрегации функция и полученное более строго аналитическое выражение для диффузионного потока на вытянутый эллипсоид.
В настоящей работе будет рассмотрена более реалистичная модель коэффициентов присоединения мономеров к мицелле в виде сфероцилиндра. Для этого будут проведены численные расчеты диффузионных потоков на сфероцилиндры с разными числами агрегации и соответствующего этим потокам наименьшего из обратных времен быстрой релаксации для мицеллярного раствора. Результаты будут сопоставлены с ранее известными.
1. КИНЕТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕЛАКСАЦИИ ЦИЛИНДРИЧЕСКИХ МИЦЕЛЛ
Кинетические уравнения Беккера–Дёринга для концентраций ${{c}_{n}}$ агрегатов ПАВ с числами агрегации $n = 2,3,...$ имеют вид
(1)
$\begin{gathered} \frac{{\partial {{c}_{n}}}}{{\partial t}} = - \left( {{{J}_{n}} - {{J}_{{n\, - \,1}}}} \right){\kern 1pt} \hfill \\ \end{gathered} .$Поток ${{J}_{n}}$ агрегатов вдоль оси чисел агрегации дается выражением
(2)
${{J}_{n}} = {{a}_{n}}\left( {{{c}_{1}}{{c}_{n}} - \frac{{{{{\tilde {c}}}_{1}}{{{\tilde {c}}}_{n}}}}{{{{{\tilde {c}}}_{{n\,\, + \,\,1}}}}}{{c}_{{n\,\, + \,\,1}}}} \right),$Для малых отклонений ${{\xi }_{n}} = {{\left( {{{c}_{n}} - {{{\tilde {c}}}_{n}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{c}_{n}} - {{{\tilde {c}}}_{n}}} \right)} {{{{\tilde {c}}}_{n}}}}} \right. \kern-0em} {{{{\tilde {c}}}_{n}}}}$ от равновесного распределения агрегатов ${{\tilde {c}}_{n}},$ т.е. при ${{\xi }_{n}} \ll 1,$ поток ${{J}_{n}}$ в (2) можно линеаризовать,
(4)
${{J}_{n}} = {{a}_{n}}{{\tilde {c}}_{1}}{{\tilde {c}}_{n}}\left( {{{\xi }_{1}} + {{\xi }_{n}} - {{\xi }_{{n + 1}}}} \right).$Линеаризованную систему уравнений Беккера–Дёринга для концентраций агрегатов удобно записать в терминах переменной ${{u}_{n}} = {{\xi }_{n}}\sqrt {{{{\tilde {c}}}_{n}}} {\text{:}}$
(5)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} = - {{{\mathbf{\hat {A}}}}_{*}}{\mathbf{u}}{\kern 1pt} .$Здесь ${{{\mathbf{\hat {A}}}}_{*}}$ – симметричная трехдиагональная матрица с ненулевыми первой строкой и столбцом. Ее собственные значения определяют спектр обратных времен релаксации мицеллярной системы.
Равновесная концентрация агрегатов ПАВ описывается флуктуационной формулой Больцмана
где ${{W}_{n}}$ – минимальная работа агрегации (выраженная в единицах $kT,$ $k$ – постоянная Больцмана, $T$ – абсолютная температура). Для идеального мицеллярного раствора зависимость работы ${{W}_{n}}$ от концентрации мономеров ${{\tilde {c}}_{1}}$ определяется выражением $ - \,(n - 1)\ln {{\tilde {c}}_{1}}$ [7], так что работа агрегации ${{\bar {W}}_{n}} \equiv {{W}_{n}} + (n - 1)\ln {{\tilde {c}}_{1}}$ не зависит в идеальном растворе от концентрации мономеров ${{\tilde {c}}_{1}}$ и является функцией лишь числа агрегации $n.$ Здесь и в дальнейшем концентрация мономеров ${{\tilde {c}}_{1}}$ предполагается измеренной в относительных единицах. Соответственно, ${{W}_{n}}$ совпадает с ${{\bar {W}}_{n}}$ при концентрации ${{\tilde {c}}_{1}} = 1.$ В терминах работы ${{\bar {W}}_{n}}$ соотношение (6) примет видСледуя работе [10], будем использовать для работы ${{\bar {W}}_{n}}$ следующее выражение:
(8)
${{\bar {W}}_{n}} = \left( {\begin{array}{*{20}{c}} \begin{gathered} {{w}_{1}}{{(n - 1)}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{w}_{2}}(n - 1) + {{w}_{3}}{{(n - 1)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},\,\,\,\,n \leqslant {{n}_{0}}, \hfill \\ \begin{gathered} {{{\bar {W}}}_{0}} + \frac{{n - {{n}_{0}}}}{{{{{\bar {n}}}_{*}} - {{n}_{0}}}},\,\,\,\,n > {{n}_{0}}. \hfill \\ \end{gathered} \hfill \\ \end{gathered} \end{array}} \right.$Для агрегатов с числом агрегации $n \leqslant {{n}_{0}}$ работа ${{\bar {W}}_{n}}$ соответствует капельной модели сферических мицелл [11, 12], а при $n > {{n}_{0}}$ – линейной модели цилиндрических мицелл [13]. Параметры ${{w}_{i}}$ и ${{n}_{0}}$ выбираются из условия непрерывности функции ${{\bar {W}}_{n}}$ и ее производной по $n$ при $n = {{n}_{0}}.$ Параметр ${{\bar {n}}_{*}}$ имеет смысл среднего значения числа агрегации цилиндрических мицелл по области $n > {{n}_{0}}$ при концентрации мономеров ${{\tilde {c}}_{1}} = 1.$
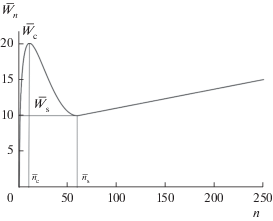
На рис. 1 показан график зависимости от числа $n$ работы ${{\bar {W}}_{n}},$ определенной по формуле (8) с параметрами ${{w}_{1}} = 1.01126,$ ${{w}_{2}} = - 8.21261,$ w3 = = $17.3055,$ ${{n}_{0}} = 62.0334,$ ${{\bar {W}}_{0}} = 10.0268,$ выбранными из условий ${{\bar {W}}_{n}} = 20,$ ${{\bar {n}}_{s}} = 60,$ ${{\bar {W}}_{s}} = 10,$ ${{\bar {n}}_{*}} = 100.$ Общей чертой этой работы с работой для системы сферических мицелл [6, 7] является наличие потенциального горба и ямы. Для сферических мицелл потенциальная яма относительно узка и имеет параболическую форму, так что равновесное распределение (6) – почти монодисперсное, тогда как равновесное распределение, соответствующее кривой для цилиндрических мицелл на рис. 1, является широким. При численном нахождении спектра обратных времен релаксации ранг матрицы ${{{\mathbf{\hat {A}}}}_{*}}$ ограничивают некоторым значением $N$ числа агрегации, которое выбирается достаточно большим, чтобы исключить его влияние на наименьшие собственные значения матричного спектра. Для цилиндрических мицелл это значение оказывается значительно большим, чем для сферических мицелл, и это существенно усложняет вычисления. Разработанный в [9] полуаналитический подход позволяет значительно сократить объем вычислений.
2. ВЫЧИСЛЕНИЕ СКОРОСТИ ПРИСОЕДИНЕНИЯ МОНОМЕРОВ В МОДЕЛИ СФЕРОЦИЛИНДРА
Как уже отмечалось, еще одной важной кинетической характеристикой мицеллярной системы является зависимость коэффициента присоединения ${{a}_{n}}$ от $n.$ Если пренебречь подвижностью агрегата по сравнению с подвижностью мономеров, то проблема нахождения этого коэффициента сводится к задаче нахождения полного диффузионного потока $P = {{a}_{n}}{{\tilde {c}}_{1}}$ мономеров на поверхность $S$ неподвижной цилиндрической мицеллы. Этот поток можно записать как
(9)
$P = D{{\int {\left. {\frac{{\partial {{c}_{1}}({\mathbf{r}})}}{{\partial {\mathbf{n}}}}} \right|} }_{S}}dS,$Локальная концентрация мономеров ${{c}_{1}}({\mathbf{r}})$ удовлетворяет стационарному уравнению диффузии
($\Delta $ – оператор Лапласа) с граничными условиями(11)
${{\left. {{{c}_{1}}({\mathbf{r}})} \right|}_{S}} = 0;\,\,\,\,{{c}_{1}}({\mathbf{r}}) \to {{\tilde {c}}_{1}},\,\,\,\,r \to \infty .$В качестве модели цилиндрической мицеллы можно принять сфероцилиндр, ограниченный цилиндрической поверхностью с длиной $L$ и радиусом $R$ и двумя полусферами радиуса $R$ на концах. Однако для такой модели аналитического решения задачи (10), (11) не существует, поэтому в работе [9] мицеллы моделировались вытянутыми эллипсоидами с малыми осями $b = c = R$ и большой осью a. Учитывая, что объем сфероида $V$ равен $V = {{4\pi a{{b}^{2}}} \mathord{\left/ {\vphantom {{4\pi a{{b}^{2}}} 3}} \right. \kern-0em} 3},$ а объем ${{\text{v}}_{0}},$ приходящийся на один мономер в мицелле, не зависит от числа агрегации $n$, справедливы соотношения
(12)
$n = \frac{{4\pi a{{R}^{2}}}}{{3{{\text{v}}_{0}}}},\,\,\,\,\frac{a}{R} = \frac{n}{{{{n}_{0}}}},$(14)
${{\left. {\varphi ({\mathbf{r}})} \right|}_{S}} = {{\varphi }_{{\text{s}}}};\,\,\,\,\varphi ({\mathbf{r}}) \to 0,\,\,\,\,r \to \infty .$Связь полного заряда сфероида $e$ и потенциала $\varphi ({\mathbf{r}})$ определяется соотношением, аналогичным (9):
(15)
$e = - \frac{1}{{4\pi }}{{\int {\left. {\frac{{\partial \varphi ({\mathbf{r}})}}{{\partial {\mathbf{n}}}}} \right|} }_{S}}dS.$Согласно решению задачи (13)–(15), приведенному в [14], потенциал ${{\varphi }_{{\text{s}}}}$ на поверхности выражается через полный заряд сфероида соотношением
(16)
${{\varphi }_{{\text{s}}}} = \frac{e}{R}\frac{1}{{f\left( {\frac{a}{R}} \right)}},\,\,\,\,f(x) = \frac{{\sqrt {{{x}^{2}} - 1} }}{{\ln (x + \sqrt {{{x}^{2}} - 1} )}}{\kern 1pt} .$Задача диффузии сводится к задаче электростатики заменами
(17)
$\varphi ({\mathbf{r}}) = {{c}_{1}}({\mathbf{r}}) - {{\tilde {c}}_{1}},\,\,\,\,e = \frac{{ - P}}{{4\pi D}},\,\,\,\,{{\varphi }_{{\text{s}}}} = {{\tilde {c}}_{1}}.$В результате получаем
В пределе $a \to R$ выражение (18) сводится к стационарному диффузионному потоку на поверхность фиксированной сферы:
Формулы (18), (19), (12) с учетом соотношения $P = {{a}_{n}}{{\tilde {c}}_{1}}$ определяют выражение для скорости присоединения мономеров ${{a}_{n}}$ для вытянутых эллипсоидов с числами агрегации $n > {{n}_{0}}{\text{:}}$
(20)
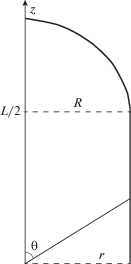
${{a}_{n}} = {{a}_{{{{n}_{0}}}}}f(x){\kern 1pt} ,\,\,\,\,f(x) = \frac{{\sqrt {{{x}^{2}} - 1} }}{{\ln (x + \sqrt {{{x}^{2}} - 1} )}},\,\,\,\,x \equiv \frac{n}{{{{n}_{0}}}}.$Задача нахождения диффузионного потока на сфероцилиндр, как и в рассмотренном случае, эквивалентна определению поля $\varphi ({\mathbf{r}})$ заряженного сфероцилиндра. Будем решать ее в сферической системе координат с полярной осью (ось $z$), направленной по оси цилиндра, и началом координат в центре симметрии сфероцилиндра. В силу симметрии задачи поле $\varphi ({\mathbf{r}})$ зависит только от полярного угла $\theta $ и расстояния $r$ от начала координат: $\varphi ({\mathbf{r}}) = \varphi (r,\theta ).$ Симметрия задачи относительно отражения $z \to - z$ означает, что $\varphi (r,\theta )$ = $ = \varphi (r,\pi - \theta ),$ и выполнения граничного условия ${{\left. {\varphi (r,\theta )} \right|}_{S}} = {{\varphi }_{{\text{s}}}}.$ достаточно потребовать на правой границе сечения сфероцилиндра, показанного на рис. 2.
Рис. 2.
Сечение сфероцилиндра. Жирной линией показана граница, на которой ставится условие ${{\left. {\varphi ({\mathbf{r}})} \right|}_{S}} = {{\varphi }_{s}}.$
Число мономеров в сфероцилиндре равно $n = {{\left( {{{4\pi {{R}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{R}^{3}}} 3}} \right. \kern-0em} 3} + \pi {{R}^{2}}L} \right)} \mathord{\left/ {\vphantom {{\left( {{{4\pi {{R}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{R}^{3}}} 3}} \right. \kern-0em} 3} + \pi {{R}^{2}}L} \right)} {{{\text{v}}_{0}}}}} \right. \kern-0em} {{{\text{v}}_{0}}}},$ отношение
зависит только от ${L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R}.$ В силу масштабной инвариантности отношение ${{{{a}_{n}}} \mathord{\left/ {\vphantom {{{{a}_{n}}} {{{a}_{{{{n}_{0}}}}}}}} \right. \kern-0em} {{{a}_{{{{n}_{0}}}}}}} = {{{{P}_{n}}} \mathord{\left/ {\vphantom {{{{P}_{n}}} {{{P}_{{{{n}_{0}}}}}}}} \right. \kern-0em} {{{P}_{{{{n}_{0}}}}}}}$ также зависит только от этого параметра, поэтому все расчеты проводились при $R = 1$ с соответствующим переходом к аргументу ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ согласно (21).Будем искать решение в виде разложения по системе гармонических функций ${{\phi }_{n}}(r,\theta )$ = = ${{r}^{{ - 1\, - \,n}}}{{P}_{n}}(\cos \theta ),$ где ${{P}_{n}}(u)$ – полиномы Лежандра, $u = \cos \theta .$ Функции ${{\phi }_{n}}(r,\theta )$ удовлетворяют уравнению $\Delta {{\phi }_{n}}(r,\theta ) = 0$ и условию ${{\phi }_{n}}(r,\theta ) \to 0$ при $r \to \infty ,$ для выполнения условия $\varphi (r,\theta )$ = $ = \varphi (r,\pi - \theta )$ надо использовать четные значения $n$. Таким образом, запишем решение в виде
Точность полученного решения оценивалась по отклонениям потенциала на поверхности ${{\left. {\varphi (r,\theta )} \right|}_{S}}$ от значения ${{\varphi }_{{\text{s}}}}.$ Для контроля проводилось сравнение аналогичного приближенного расчета для модели сфероида с точным решением (20). Погрешность расчета возрастает с увеличением отношения ${L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R}$ (с ростом ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$). Мы довели расчеты до значения ${L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R} = 4$ (${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = 4$). Максимальная относительная погрешность составила 0.1%.
Представим результаты в виде $\begin{gathered} {{a}_{n}} = {{a}_{{{{n}_{0}}}}}F(x){\kern 1pt} , \hfill \\ \end{gathered} $ $x = {n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}.$ Функция $F(x)$ в области $1 \leqslant x \leqslant {{11} \mathord{\left/ {\vphantom {{11} 8}} \right. \kern-0em} 8}$ ($0 \leqslant {L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R} \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$) достаточно хорошо аппроксимируется полиномом F(x) = $1 + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)(x - 1)$ – ‒ $0.051{{(x - 1)}^{2}}$ (соответствующее разложение функции $f(x)$ имеет вид $f(x) \approx 1 + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right)(x - 1)$ – $ - \,\,\left( {{1 \mathord{\left/ {\vphantom {1 {45}}} \right. \kern-0em} {45}}} \right){{(x - 1)}^{2}}$ с тем же начальным наклоном). В области $x > {{11} \mathord{\left/ {\vphantom {{11} 8}} \right. \kern-0em} 8}$ (${L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R} > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$) отношение ${{f(x)} \mathord{\left/ {\vphantom {{f(x)} {F(x)}}} \right. \kern-0em} {F(x)}}$ хорошо аппроксимируется линейной функцией. Нормируя эту функцию на точку $x = {7 \mathord{\left/ {\vphantom {7 4}} \right. \kern-0em} 4}$ (${L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R} = 1$), в которой рассчитанное значение отношения ${{f(x)} \mathord{\left/ {\vphantom {{f(x)} {F(x)}}} \right. \kern-0em} {F(x)}}$ равно 1.0114, получаем окончательно
(23)
$F(x) = \left\{ \begin{gathered} 1 + \frac{1}{3}(x - 1) - 0.051\,{{(x - 1)}^{2}},\,\,\,\,x \leqslant \frac{{11}}{8}\,, \hfill \\ \frac{{f(x)}}{{1.0114 + 0.021\,(x - 1.75)}},\,\,\,\,x > \frac{{11}}{8}\,. \hfill \\ \end{gathered} \right.$Такое аналитическое представление результата удобно для дальнейших расчетов и может рассматриваться как экстраполяция в область ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} > 4$ (разумеется, пока поправка в знаменателе (23) невелика).
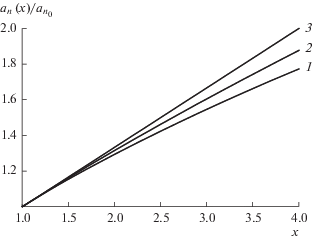
На рис. 3 показаны графики зависимости $F(x)$ и $f(x),$ рассчитанные по формулам (23), (20), а также их линейная аппроксимация.
Рис. 3.
Зависимость скорости присоединения мономеров от числа агрегации $x = {n \mathord{\left/ {\vphantom {n {{{n}_{0}}{\text{:}}}}} \right. \kern-0em} {{{n}_{0}}{\text{:}}}}$ кривая 1 – для модели сфероцилиндров, 2 – для модели вытянутых эллипсоидов, 3 – линейная аппроксимация.
Коэффициент присоединения для сфероцилиндров всюду меньше коэффициента для вытянутых эллипсоидов (максимальное отличие при $x = 4$ составляет 6%). Это можно интерпретировать как следствие того, что при одинаковых объемах площадь сфероида больше площади сфероцилиндра (при одинаковых $R$). Попробуем учесть этот факт в виде поправочного множителя к (20), предполагая, что средние диффузионные потоки на единицу поверхности сфероцилиндра и сфероида близки по величине. Запишем условие равенства объемов сфероида и сфероцилиндра: $\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right)\pi {{R}^{2}}a = \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right)\pi {{R}^{3}} + \pi {{R}^{2}}L,$ отсюда L = (4/3) × × $(a - R).$ Площадь сфероцилиндра равна ${{S}_{{{sph\_cyl}}}}$ = $ = 2\pi R(2R + L)$ = $\left( {{{2\pi R} \mathord{\left/ {\vphantom {{2\pi R} 3}} \right. \kern-0em} 3}} \right)(2R + 4a),$ а площадь сфероида для $x = {a \mathord{\left/ {\vphantom {a R}} \right. \kern-0em} R} \geqslant 1$ определяется формулой ${{S}_{{{\text{spheroid}}}}}$ = $2\pi {{R}^{2}}\left[ {1 + \left( {{{{{x}^{2}}} \mathord{\left/ {\vphantom {{{{x}^{2}}} {\sqrt {{{x}^{2}} - 1} }}} \right. \kern-0em} {\sqrt {{{x}^{2}} - 1} }}} \right)\arcsin \left( {{{\sqrt {{{x}^{2}} - 1} } \mathord{\left/ {\vphantom {{\sqrt {{{x}^{2}} - 1} } x}} \right. \kern-0em} x}} \right)} \right].$ Отсюда искомый поправочный множитель равен
(24)
$\beta \equiv \frac{{{{S}_{{{sph\_cyl}}}}}}{{{{S}_{{{\text{spheroid}}}}}}} = \frac{2}{3}\frac{{1 + 2x}}{{1 + \frac{{{{x}^{2}}}}{{\sqrt {{{x}^{2}} - 1} }}\arcsin \left( {\frac{{\sqrt {{{x}^{2}} - 1} }}{x}} \right)}}.$Будем рассматривать функцию
(25)
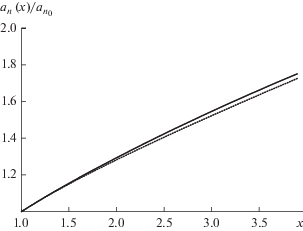
$\begin{gathered} {{F}_{1}}(x) \equiv \beta (x)f(x) = \frac{2}{3} \times \\ \times \,\,\frac{{(1 + 2x)\,({{x}^{2}} - 1)}}{{\left[ {\sqrt {{{x}^{2}} - 1} + {{x}^{2}}\arcsin \left( {\frac{{\sqrt {{{x}^{2}} - 1} }}{x}} \right)} \right]\ln (x + \sqrt {{{x}^{2}} - 1} )}}{\kern 1pt} , \\ x \equiv \frac{n}{{{{n}_{0}}}}, \\ \end{gathered} $Рис. 4.
Зависимость скорости присоединения мономеров от $x = {n \mathord{\left/ {\vphantom {n {{{n}_{0}}{\text{:}}}}} \right. \kern-0em} {{{n}_{0}}{\text{:}}}}$ сплошная кривая – расчет по формуле (23), пунктир – по формуле (25).
3. НАИБОЛЬШЕЕ ИЗ ВРЕМЕН БЫСТРОЙ РЕЛАКСАЦИИ
Рассчитанная функция $F(x)$ была использована для вычисления ${{\lambda }_{{\min }}}$ – наименьшего из обратных времен быстрой релаксации. Расчет проводился полуаналитическим методом, предложенным в работе [9], для работы агрегации использовалось выражение (8). Как и в [9], время измерялось в единицах $\begin{gathered} {{\tau }_{0}} = {{3{{n}_{0}}({{n}_{*}} - {{n}_{0}})} \mathord{\left/ {\vphantom {{3{{n}_{0}}({{n}_{*}} - {{n}_{0}})} {{{a}_{{{{n}_{0}}}}}{{{\tilde {c}}}_{1}}}}} \right. \kern-0em} {{{a}_{{{{n}_{0}}}}}{{{\tilde {c}}}_{1}}}} \hfill \\ \end{gathered} .$ Графики зависимости ${{\lambda }_{{\min }}}$ от концентрации для сфероцилиндров и вытянутых эллипсоидов показаны на рис. 5.
Рис. 5.
Зависимость наименьшего из обратных времен быстрой релаксации ${{\lambda }_{{\min }}}$ от концентрации мономеров ${{\tilde {c}}_{1}}{\text{:}}$ сплошная кривая – для модели вытянутых эллипсоидов, пунктир – для модели сфероцилиндров.
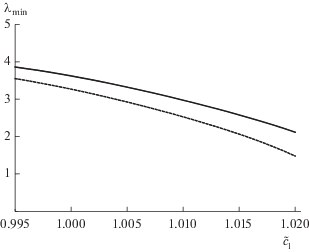
В рассмотренном диапазоне концентраций ${{\tilde {c}}_{1}}$ степень мицеллизации возрастала от $\alpha = 0.109$ при ${{\tilde {c}}_{1}} = 0.995$ до $\alpha = 0.83$ при ${{\tilde {c}}_{1}} = 1.02,$ а среднее число агрегации мицелл – от ${{\bar {n}}_{*}} = 94$ до ${{\bar {n}}_{*}} = 215.$ Ввиду меньшего значения коэффициента ${{a}_{n}}$ для сфероцилиндра, релаксация происходит медленнее, относительная разность времен увеличивается с ростом концентрации, т.к. при этом возрастает роль крупных мицелл, для которых отличие коэффициентов ${{a}_{n}}$ существеннее.
ЗАКЛЮЧЕНИЕ
Таким образом, проведенный численный расчет скорости присоединения мономеров показал, что для модели цилиндрических мицелл в виде вытянутых эллипсоидов эта величина несколько завышена по сравнению с более реалистичной моделью сфероцилиндров.
Получена аналитическая формула, описывающая с точностью порядка 1% зависимость скорости присоединения в модели сфероцилиндров от числа агрегации.
Вычислено наименьшее из обратных времен быстрой релаксации в модели сфероцилиндров при различных числах агрегации, оно оказалось в среднем на 10% меньше, чем для модели вытянутых эллипсоидов.
Работа выполнена при финансовой поддержке Российского научного фонда (грант № 14-13-00112).
Список литературы
Becker R., Döring W. // Ann. Phys. 1935. V. 24. P. 719.
Friedlander S.K. Smoke, Dust, and Hase. Fundamentals of Aerosol Dynamics. Oxford: Oxford University Press, 2000. P. 190.
Ball J.M., Carr J. // J. Stat. Phys. 1990. V. 61. P. 203.
Zakharov A.I., Adzhemyan L.Ts., Shchekin A.K. // J. Chem. Phys. 2015. V. 143. 124902.
Shchekin A.K., Babintsev I.A., Adzhemyan L.Ts. // J. Chem. Phys. 2016. V. 145. 174105.
von Smoluchowski M. // Z. Phys. Chem. 1917. V. 92. P. 129.
Русанов А.И., Щёкин А.К. Мицеллообразование в растворах поверхностно-активных веществ. 2-е изд. СПб.: Изд-во Лань, 2016.
Щёкин А.К., Аджемян Л.Ц., Бабинцев И.А., Волков Н.А. // Коллоид. журн. 2018. Т. 80. С. 115.
Adzhemyan L.Ts., Eroshkin Y.A., Babintsev I.A., Shchekin A.K. // Physica A. 2019. V. 518. P. 299.
Babintsev I.A., Adzhemyan L.T., Shchekin A.K. // Soft Matter. 2014. V. 10. P. 2619.
Русанов А.И., Гринин А.П., Куни Ф.М., Щёкин А.К. // Журн. общей химии. 2002. Т. 72. С. 651.
Русанов А.И., Куни Ф.М., Гринин А.П., Щёкин А.К. // Коллоид. журн. 2002. Т. 64. С. 670.
Kuni F.M., Shchekin A.K., Rusanov A.I., Grinin A.P. // Langmuir. 2006. V. 22. P. 1534.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 8. Электродинамика сплошных сред. 4-е изд. М.: Физматлит, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал