Коллоидный журнал, 2019, T. 81, № 5, стр. 563-570
Влияние гидростатического давления на краевой угол сидящего пузырька
Н. Е. Есипова 1, *, А. И. Русанов 1, 2, В. Д. Соболев 1, С. В. Ицков 1
1 Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва,
Ленинский проспект, 31, Россия
2 Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург,
Университетская наб., 7, Россия
* E-mail: nesipova@mail.ru
Поступила в редакцию 16.04.2019
После доработки 21.04.2019
Принята к публикации 24.04.2019
Аннотация
Хотя обычные давления типично слабо влияют на свойства конденсированных фаз и их поверхностных слоев, в физико-химии поверхностей обнаружена величина – краевой угол жидкости на линии трехфазного контакта – весьма чувствительная к гидростатическому давлению. В опытах с прилипшим к твердой поверхности пузырьком воздуха в воде увеличение гидростатического давления менее чем вдвое давало прирост краевого угла более чем на 10°, если сам угол достаточно меньше 90°. При этом линия трехфазного контакта оставалась неподвижной, и дело сводилось лишь к изменению ориентации поверхности жидкость–газ. Если же угол (неважно, острый или тупой) близок к 90°, возникает подвижность линии трехфазного контакта в качестве альтернативного пути достижения равновесия. Для объяснения этих явлений сформулирована термодинамическая теория на основе обобщенного уравнения Юнга. Показано, что при фиксированной линии трехфазного контакта повышение давления в жидкости всегда вызывает рост краевого угла.
ВВЕДЕНИЕ
Вместе с температурой давление является одним из основополагающих параметров состояния, а потому – важным параметром любой физической задачи. Естественно, давление выступает в роли одной из основных переменных и в термодинамике поверхностных явлений [1, 2]. Однако исследований, посвященных этой величине, чрезвычайно мало. Если температурная зависимость поверхностных величин представлена в литературе сотнями публикаций, то влияние давления изучалось буквально в единичных работах (в качестве примера можно привести исследование зависимости поверхностного натяжения жидкостей от давления [3–6]).
Из сказанного следует, что от применения обычных давлений в физике поверхностных явлений можно ожидать лишь незначительных, можно сказать, пренебрежимо малых эффектов. Но это не всегда так. В данной работе, посвященной изучению краевого угла воды в прилипшем пузырьке, наблюдался значительный эффект, вызываемый изменением гидростатического давления. Как обнаружилось, увеличение давления жидкости в пределах от одной до двух атмосфер смещает краевой угол на величины, далеко выходящие за пределы погрешностей. Об этом феномене предварительно сообщалось [7]. В данной публикации мы представляем работу в полном формате с обсуждением привходящих факторов.
МЕТОДИКА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА
Для проведения эксперимента с измерением краевого угла была изготовлена из оптического кварца рабочая ячейка емкостью около 2 мл, к верхней стенке которой крепилась пластина (например, полированная пластинка кремния). Одна из боковых сторон ячейки плотно закрывалась крышкой с резиновой прокладкой. Для опытов использовали трижды дистиллированную воду. После того, как ячейка заполнялась водой целиком, через резиновую прокладку с помощью микрошприца подавался воздушный пузырек размером около 1 мм, который, всплывая, садился на верхнюю стенку. Затем с помощью шприца, соединенного с манометром, повышалось гидростатическое давление в жидкости, и велось наблюдение за пузырьком. Для этого ячейка помещалась на столик перед видеокамерой, и изображение пузырька передавалось на дисплей компьютера. При этом измерялись два параметра формы прилипшего пузырька: диаметр основания d и высота пузырька h.
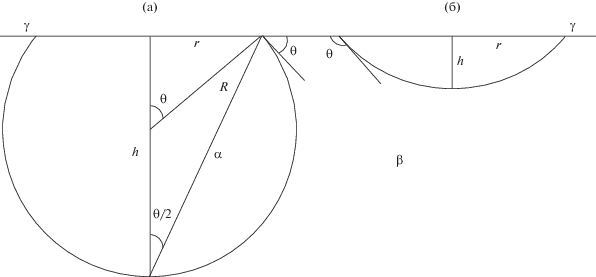
На рис. 1 изображен профиль сидящего пузырька в виде кругового сегмента с краевым углом θ и радиусом круговой линии трехфазного контакта r = d/2. Изображение подразумевает, что межфазная поверхность жидкость–газ является сферической (с радиусом R) и, значит, прилипший пузырек имеет форму сферического сегмента. Для пузырьков размером 1 мм и менее это действительно так, поскольку данный размер значительно меньше капиллярной постоянной воды (около 4 мм при температуре 20°C). При этом, если вода смачивает стенку (θ < 90°), то сегмент больше половины шара (h > R, рис. 1а), а если не смачивает (θ > 90°), то меньше половины шара (h < R, рис. 1б). На рис. 2 это иллюстрируется фотографиями наблюдаемых пузырьков. Из геометрии рис. 1а сразу следует соотношение
(1)
$\operatorname{tg} \frac{\theta }{2} = \frac{r}{h},\,\,\,\,\theta = 2\operatorname{arctg} \frac{r}{h},$Рис. 1.
Сидящий на твердой поверхности пузырь в случае смачивающей (θ < 90°) и не смачивающей (θ > 90°) поверхность жидкости (случаи (а) и (б) соответственно): h и R – высота и радиус шарового сегмента, r – радиус его основания, θ – краевой угол. Обозначение фаз: α – газ, β – жидкость, γ – твердое тело.
Естественно, обращалось внимание на то, чтобы измеряемый угол был равновесным. В нашем случае, это не представляло проблемы, так как при посадке пузыря на твердую подложку сначала формируется отступающий угол смачивания, который быстро (в течение минуты) приходит к равновесию. Попутно с краевым углом измерялись площадь посадки и радиус пузырька (величины r и R, рис. 1).
В опытах использовались поверхности с разной степенью гидрофильности. Для понижения последней полированная пластинка кремния предварительно гидрофобизовалась обработкой парами гексаметилдисилазана [(CH3)3Si]2NH. Степень гидрофильности поверхности оценивалась краевым углом сидячей капли воды. Все измерения проводились при комнатной температуре.
Перейдем теперь к обзору полученных результатов. На рис. 3 представлены графики зависимости краевого угла пузырька от гидростатического давления воды на смачиваемых кремниевых подложках при небольшой гидрофобизации их поверхностей (кривые 1 и 2). При исходных значениях 40° и 60° краевой угол увеличивается почти линейно на 15°–20° с ростом давления на 1 атм. Для этих же зависимостей на рис. 4 приведены результаты измерения площади посадки пузырька $S = \pi {{r}^{2}},$ которая (а, значит, и радиус r) практически не изменяется во всем интервале давлений.
Рис. 3.
Зависимость краевого угла θ от давления p для пузырька на полированной поверхности чистого кремния (кривая 1) и на ней же после небольшой гидрофобизации (кривая 2).
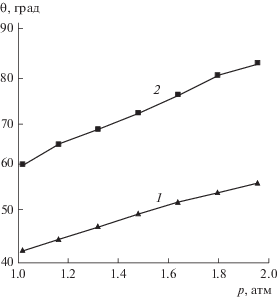
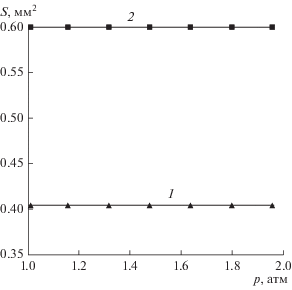
Рис. 4.
Зависимость площади посадки пузырька S от давления воды p, отвечающая кривым 1 и 2 на рис. 3.
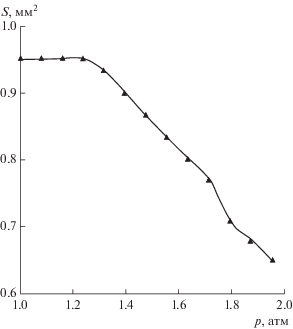
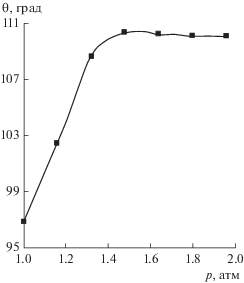
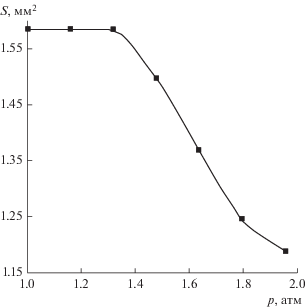
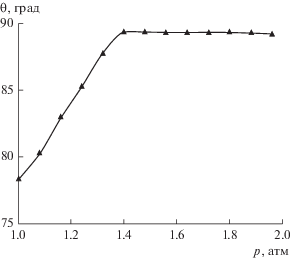
С уменьшением смачиваемости подложки и увеличением начального значения краевого угла (когда оно становится ближе к 90°), характер зависимости краевого угла от давления меняется. Так, при начальной величине 78° (рис. 5) краевой угол с увеличением давления сначала растет, но при приближении к 90° становится постоянным. В то же время, как видно на рис. 6, контактная площадь пузырька в данном эксперименте не изменяется при увеличении избыточного давления до 0.32 атм (пока краевой угол растет), а при стабилизации угла площадь посадки начинает уменьшаться. Забегая вперед, отметим, что такая особенность характерна для всех экспериментов с нагнетанием давления: если площадь посадки пузырька не изменяется, то краевой угол растет, и, наоборот, при уменьшении площади контакта краевой угол становится постоянным.
Рис. 5.
Зависимость краевого угла θ от давления p для пузырька на гидрофобизованной поверхности кремния при начальном значении угла 78°.
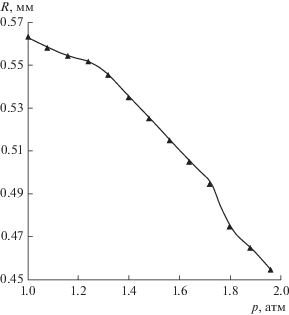
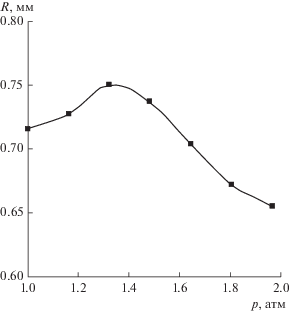
В противоположность этому радиус пузырька R на смачиваемой подложке (θ < 90°) всегда монотонно уменьшается при повышении давления. В качестве примера на рис. 7 показана такая зависимость, соответствующая рис. 5 и 6. Тем более, монотонное уменьшение R наблюдалось и в более простых случаях, отвечающих рис. 3 и 4 (соответствующие графики не приводились выше, чтобы не загромождать экспериментальный материал).
На рис. 8 представлена зависимость краевого угла от давления при использовании уже гидрофобной поверхности с начальным значением краевого угла больше 90°. Здесь краевой угол сначала возрастает и достигает максимального значения, равного 110°, а затем почти не изменяется (или даже немного уменьшается). Соответственно площадь посадки пузырька на гидрофобной подложке S остается постоянной при росте краевого угла, но далее с повышением давления уменьшается, как показано на рис. 9. Что касается радиуса пузырька, то он ведет себя иначе, чем в случае гидрофильной подложки: сначала растет с давлением, а затем падает. Таким образом, график характеризуется наличием максимума R (рис. 10).
Подводя итог обзору результатов, обратим внимание на то, что наблюдаемый эффект изменения краевого угла весьма значителен. Он намного выходит за пределы погрешностей, а постоянство радиуса r, где оно наблюдается, надежно фиксируется.
ТЕОРИЯ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Посмотрим сначала, что можно получить из геометрии сидячего пузырька. Объем шарового сегмента V дается выражением
(2)
$V = \frac{\pi }{3}(3R - h)h = \frac{\pi }{2}\left( {{{r}^{2}} + \frac{{{{h}^{2}}}}{3}} \right)h.$Поскольку в опытах измерялся и радиус пузырька R, для дальнейшего обсуждения желательно представить выражение (2) в терминах R и r. Для этого используем геометрическое соотношение
которое также универсально. Действительно, h – R пишется для случая смачивающей жидкости (рис. 1a). Для противоположного случая (рис. 1б) нужно брать R – h. Но квадраты этих двух разностей идентичны. Решая квадратное уравнение (3) относительно h, находим(4)
$h = R \pm {{({{R}^{2}} - {{r}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(5)
$\begin{gathered} V = \frac{\pi }{3}\left[ {{{R}^{2}} + {{r}^{2}} + R{{{({{R}^{2}} - {{r}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right] \times \\ \times \,\,\left[ {R + {{{({{R}^{2}} - {{r}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right] \\ \end{gathered} $(6)
$\begin{gathered} V = \frac{\pi }{3}[{{R}^{2}} + {{r}^{2}} - R{{({{R}^{2}} - {{r}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}] \times \\ \times \,\,[R - {{({{R}^{2}} - {{r}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}]. \\ \end{gathered} $В дополнение к (1) для краевого угла запишем
Запись (7) очевидна для смачивающей жидкости и непосредственно следует из рис. 1а. Для случая же несмачивающей жидкости в аналогичном построении имеем и, в силу $\cos (\pi - \theta ) = - \cos \theta ,$ вновь приходим к выражению (7), которое, таким образом, оказывается универсальным. Подставляя теперь (4) в (7), получаем где, как и в (4), верхний знак плюс относится к случаю смачивающей жидкости (рис. 1а), а нижний знак минус – к случаю несмачивающей жидкости (рис. 1б).Посмотрим, к каким выводам приводит формула (8) в отношении радиуса сидящего пузырька. Если площадь контакта пузырька с подложкой не меняется и величина r постоянна, то с увеличением краевого угла и уменьшением $\cos \theta $ радиус R уменьшается под влиянием внешнего давления в случае гидрофильной поверхности (рис. 7) и возрастает в случае гидрофобной поверхности (рис. 10). Если же, наоборот, r изменяется, а θ и $\cos \theta $ постоянны, то, согласно (8), отношение r/R должно стать неизменным. Это значит, что при уменьшении r радиус пузырька R также должен уменьшаться. Так получает свое объяснение максимум на рис. 10.
Из сказанного ясно и удивительно, что для формального объяснения эксперимента с сидячим пузырьком оказалось достаточно элементарных геометрических соотношений. Из формул (1) и (8) видно, что если r – величина постоянная, то краевой угол должен обязательно меняться с размером пузырька. Если же постоянен краевой угол, то радиус r (как и площадь контакта пузырька со стенкой) не может быть постоянным. Все это подтверждается экспериментом и иллюстрируется выше рис. 3–10. Но на этом этапе выходит из тени физика поверхностей и начинает задавать свои вопросы. Мы остановимся на двух из них – чем объясняется столь значительное изменение краевого угла с ростом давления и почему (и когда) контактная площадь пузырька оказывается постоянной?
Обратимся к физике явления. В условиях равновесия краевой угол θ удовлетворяет обобщенному уравнению Юнга [8, 9]
(9)
$\cos \theta = \frac{{{{k}_{\operatorname{s} }}}}{\gamma }({{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}) + \frac{{{{k}_{\operatorname{l} }}}}{\gamma }\left( {\frac{\kappa }{r} + \frac{{\partial \kappa }}{{\partial r}}} \right),$Присмотримся к уравнению (9) применительно к пузырьку в условиях переменного внешнего давления. Для пузырька внешней средой является жидкость, уже обладающая внутренним давлением порядка десяти тысяч атмосфер. Поэтому, если меняющееся давление остается порядка атмосферного, изменением межфазных свойств на границе жидкости с малорастворимым газом или твердым телом можно пренебречь. Из таких величин мы находим в уравнении (9) γ, ${{\sigma }^{{\beta \gamma }}}$ и κ. Последняя величина (термодинамическое линейное натяжение) входит во второе слагаемое в (9), которое мы сразу можем отбросить, поскольку рассматриваем хоть и малый, но макроскопический пузырек. Это тем более можно делать в условиях постоянства радиуса r, когда второе слагаемое дает малый вклад в величину краевого угла, но совсем не дает вклада в интересующее нас изменение краевого угла. То же можно сказать и о коэффициенте шероховатости ${{k}_{\operatorname{s} }}$ (он мог бы измениться лишь при высоких давлениях, приводящих к деформации твердого тела). Остается величина ${{\sigma }^{{\alpha \gamma }}},$ и мы можем теперь заключить на основании уравнения (9), что наблюдающееся в эксперименте уменьшение косинуса краевого угла с повышением давления может быть вызвано только снижением термодинамического поверхностного натяжения твердого тела в контакте с пузырьком. Рассмотрим эту величину поподробнее.
Когда пузырек, поднимаясь и расталкивая жидкость, упирается в верхнюю стенку сосуда, то между ним и стенкой остается жидкая прослойка, характеризуемая в литературе как тонкая смачивающая пленка [10–13]. Как любая тонкая пленка, она обладает расклинивающим давлением, в данном случае совпадающим с капиллярным давлением Лапласа:
где p – фазовое давление. Подчеркнем, что расклинивающее давление и гидростатическое давление воды (соответствующее величине ${{p}^{\beta }}$ в формуле (10)) – это разные величины.Отметим, что в термодинамике тонких пленок [14–18] смачивающие пленки занимают особое место в связи с тем, что, в отличие от свободных пленок, они являются неавтономными (зависят от свойств подложки). В случае свободной пленки можно оперировать ее натяжением как самостоятельной величиной. Натяжение же смачивающей пленки (типично отрицательное) является лишь частью общего межфазного натяжения между твердым телом и прилегающей фазой. С этим-то общим натяжением и приходится иметь дело во всех термодинамических соотношениях. Из них наиболее популярным (идущим от А.Н. Фрумкина [18]) является соотношение, которое в нашем случае записывается как [1, c. 295, формула (XIII.109)]
(11)
${{\left( {\frac{{d{{\sigma }^{{\alpha \gamma }}}}}{{d\Pi }}} \right)}_{{T,{{p}^{\beta }}}}} \approx \tau ,$Описанный умозрительный эксперимент не имеет отношения к тем опытам, которые обсуждаются в данной работе. Принципиальное отличие состоит в том, что у нас давление в жидкости переменно. При постоянстве температуры уравнение Гиббса–Дюгема для однокомпонентной жидкости гласит, что
где ρ – плотность жидкости и μ – ее химический потенциал. Ввиду малой сжимаемости жидкости вдали от критической точки величину ρ можно считать практически постоянной, а величины dp и dμ – пропорциональными друг другу согласно (12). В пренебрежении растворимостью воздуха соотношение (12) применимо к реальной воде (в наших обозначениях $dp \equiv d{{p}^{\beta }}$).При переменном давлении проще всего рассматривать смачивающую пленку как адсорбционный слой воды, находящийся в равновесии с паром воды внутри пузырька, и исходить из уравнения адсорбции Гиббса. Последнее, напомним, было выведено для жидких поверхностей Гиббсом, а для твердых – значительно позже [19–21]. В случае твердой поверхности обобщенное уравнение адсорбции может быть записано в терминах как механического (через тензор поверхностного натяжения $\hat {\gamma }$), так и термодинамического поверхностного натяжения σ. Нам, естественно, нужен второй вариант, и мы ограничимся не самой сложной формой [20]
(13)
$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT + (\hat {\gamma } - {{\sigma }^{{\alpha \gamma }}}\hat {1}):d{{\hat {e}}^{\sigma }} - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} ,$Считая температуру постоянной, стенку, куда устроился пузырек, – недеформируемой и пренебрегая малыми примесями (в частности, растворимостью воздуха в воде), получаем из (13) предельно простое соотношение
или, после подстановки (12), где τ – вновь толщина смачивающей пленки ввиду соотношения $\tau \approx {\Gamma \mathord{\left/ {\vphantom {\Gamma \rho }} \right. \kern-0em} \rho }.$ Из формулы (15) видно, что с повышением давления в жидкости термодинамическое поверхностное натяжение твердого тела снижается. Соответственно уменьшается косинус краевого угла, а сам угол увеличивается. Это и наблюдается в эксперименте, и, значит, уравнение (15) уже дает его качественное объяснение. Однако нам важна и количественная сторона: ведь наблюдаются значительные эффекты. Из (12) видно, что если давление повышается в два раза, то точно так же в два раза увеличивается химический потенциал воды. Равновесие с малым пузырьком устанавливается очень быстро, так что химический потенциал пара воды внутри пузырька тоже увеличивается в два раза. Из выражения же (14) следует, что, поскольку адсорбция также растет с химическим потенциалом, удвоение последнего означает падение термодинамического поверхностного натяжения более чем в два раза. Из сказанного следует, что увеличение давления в жидкости всего лишь в два раза уже достаточно для получения больших эффектов.Остается обсудить постоянство (или, наоборот, непостоянство) площади основания пузырька и его радиуса r при изменении давления. Здесь опять нужно вспомнить неавтономность смачивающей пленки и необходимость учета твердой части поверхностных слоев при написании условий равновесия. Твердые слои не обладают подвижностью, и единственная подвижная межфазная граница – это поверхность αβ, от положения которой зависит величина краевого угла. При анализе обобщенного уравнения Юнга в пренебрежении вторым слагаемым (куда и входит r) мы установили, что для макроскопического пузырька изменение термодинамического поверхностного натяжения компенсируется именно изменением краевого угла. Последнее не требует изменения радиуса r, и именно постоянство r является энергетически менее затратным в сравнении с движением линии трехфазного контакта по поверхности даже полированного поликристаллического образца. Однако возможность компенсировать изменение натяжения смачивающей пленки изменением краевого угла имеет свои ограничения. Если всего возможного диапазона изменения краевого угла все же не хватает для компенсации, вступает в действие другой механизм, и радиус r начинает изменяться. Это особенно заметно при краевом угле вблизи 90°, когда компенсирующая способность краевого угла становится минимальной.
Список литературы
Русанов А.И. Фазовые равновесия и поверхностные явления. Л.: Химия, 1967.
Rusanov A.I. Phasengleichgewichte und Grenzflächenerscheinungen. Akademie-Verlag: Berlin, 1978.
Русанов А.И., Кочурова Н.Н., Хабаров В.Н. // Докл. АН СССР. 1972. Т. 202. С. 304.
Хабаров В.Н., Кочурова Н.Н., Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 92.
Хабаров В.Н., Кочурова Н.Н., Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 407.
Хабаров В.Н., Кочурова Н.Н., Русанов А.И. // Коллоид. журн. 1976. Т. 38. С. 1201.
Русанов А.И., Есипова Н.Е., Соболев В.Д. // Докл. АН. 2019. Т. 202. С. 304.
Rusanov A.I. // Surf. Sci. Rep. 1996. V. 23. C. 173.
Русанов А.И. // Коллоид. журн. 1998. Т. 60. С. 815.
Дерягин Б.В., Чураев Н.В. Смачивающие пленки. М.: Наука, 1984.
Зорин З.М., Коларов Т., Есипова Н.Е., Платиканов Д., Сергеева И.П. // Коллоид. журн. 1990. Т. 52. С. 666.
Зорин З.М., Гасанов Э.К., Есипова Н.Е., Корнильев И.Н. // Коллоид. журн. 1991. Т. 53. С. 25.
Есипова Н.Е., Ицков С.В., Чураев Н.В. // Коллоид. журн. 2002. Т. 64. С. 775.
Русанов А.И. // Коллоид. журн. 1966. Т. 28. С. 718.
Русанов А.И. // Коллоид. журн. 1967. Т. 29. С. 142.
Русанов А.И. // Коллоид. журн. 1967. Т. 29. С. 149.
Русанов А.И. // Коллоид. журн. 1967. Т. 29. С. 237.
Фрумкин А.Н. // Журн. физ. химии. 1938. Т. 12. С. 337.
Eriksson J.C. // Surf. Sci. 1969. V. 14. P. 221.
Rusanov A.I. // J. Colloid Interface Sci. 1978. V. 63. P. 330.
Rusanov A.I. // Pure Appl. Chem. 1992. V. 64. P. 111.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал