Коллоидный журнал, 2019, T. 81, № 6, стр. 724-733

1. ВВЕДЕНИЕ

Изучение испарения сидячих капель является задачей более сложной по сравнению с испарением свободных капель, имеющих сферическую форму [1–3]. Форма сидячей капли, существенно влияющая на процесс ее испарения, определяется эффектами поверхностного натяжения и свойствами подложки, прежде всего, степенью ее гидрофобности. Капли малого размера, для которых незначительно влияние силы тяжести, имеют форму шарового сегмента. Обычно предполагается, что испарение происходит в режиме стационарной диффузии пара. Теория такого режима для однокомпонентной капли в форме шарового сегмента при изотермическом испарении была разработана в [4] с использованием полученного ранее аналитического решения сходной задачи электростатики [5]. В дальнейшем подход [4] использовался многими авторами, в частности, в недавних работах [6, 7] при рассмотрении испарения сидячей капли в условиях гистерезиса краевого угла. В работе [8] проведено сравнение теоретических предсказаний, полученных в рамках предположения о стационарности и изотермичности процессов, с результатами прямого эксперимента по наблюдению за изменением объема и краевого угла при испарении сидячей капли воды.

Состояние бинарной капли, в отличие от капли чистой жидкости, задается не только ее геометрическими параметрами, но и концентрацией раствора в капле, контролировать изменение которой в процессе испарения достаточно сложно. Этим обстоятельством значительно усложняется теоретическое описание, поскольку требуется тем или иным способом найти связь концентрации раствора в капле с измеряемыми ее характеристиками. В работе [9] в изотермическом приближении рассматривалась задача об испарении бинарной капли, состоящей из двух жидкостей, полностью смешивающихся друг с другом. Была сформулирована система уравнений, в общем случае описывающая рассматриваемую ситуацию, и на ее основе проанализированы экспериментальные данные по испарению капель водного раствора серной кислоты в атмосфере воздуха с заданной влажностью. В ходе анализа установлено, что с течением времени концентрация кислоты в капле во всех случаях стремится к некоторому стационарному значению, определяемому температурой и влажностью окружающего воздуха, а капля переходит в стационарный режим медленного испарения. Совершенно иное поведение продемонстрировано в работе [10], в которой представлены результаты опытов по испарению капель водных растворов 1-пропанола. Наблюдаются два сценария поведения таких капель в зависимости от начальной концентрации раствора и влажности воздуха. В одном случае краевой угол капли монотонно уменьшается со временем, в другом случае наблюдается этап его значительного роста. Аналогичная ситуация при испарении капель водных растворов этанола была описана ранее в работе [11], в которой исследовалось поведение краевого угла испаряющейся капли при различных значениях относительной влажности окружающего воздуха. Такое поведение краевого угла естественно связать, как указано в [10, 11], с различным характером изменения концентрации спирта в капле в процессе ее испарения. Наблюдаемый рост краевого угла объясняется испарением спирта из капли (стремление концентрации раствора к нулю) и соответствующим увеличением поверхностного натяжения на границе капли с воздухом вследствие роста содержания воды. Монотонное уменьшение краевого угла реализуется в ситуации, когда в процессе испарения капли концентрация спирта остается конечной. Таким образом, на качественном уровне объяснялась причина того или иного сценария в наблюдаемом поведении краевого угла капли. При этом, однако, количественные оценки для начальной концентрации спирта в капле и влажности воздуха, при которых реализуется один или другой вариант изменения краевого угла, в этих работах не рассматривались.

Основной целью данной работы является количественная оценка влияния параметров растворов и среды на характер эволюции бинарной капли в процессе испарения и сопоставление полученных оценок с экспериментальными результатами [9–11].

2. УРАВНЕНИЯ ДИНАМИКИ ИСПАРЕНИЯ СИДЯЧЕЙ БИНАРНОЙ КАПЛИ

Рассмотрим сидячую бинарную каплю на твердой подложке. Если число частиц первого компонента (растворенного вещества) в капле равно ${{N}_{1}},$ а растворителя – ${{N}_{2}},$ то мольная доля первого компонента в растворе есть

где $N = {{N}_{1}} + {{N}_{2}}$ – полное число молекул в капле. При этом мольная доля растворителя равна, очевидно, $1 - x.$ Дифференцирование (1) по времени приводит к выражению которое можно переписать в виде Потоки частиц ${{\dot {N}}_{1}}$ и ${{\dot {N}}_{2}}$ в предположении о стационарности процесса диффузии молекул пара в окружающем каплю воздухе находятся на основе решения уравнения Лапласа для концентрации пара каждого компонента с соответствующими граничными условиями на поверхности капли и на поверхности подложки [4, 6]. Получаемое при этом выражение для потока ${{\dot {N}}_{i}}$ может быть записано в виде Здесь ${{D}_{i}}$ – коэффициент диффузии пара $i$-го компонента раствора в воздухе, ${{n}_{{i\infty }}}\left( x \right)$ – объемная концентрация насыщенного пара $i$-го компонента вблизи поверхности капли, ${{n}_{{i0}}}$ – объемная концентрация пара $i$-го компонента на удалении от капли, $R$ – радиус основания капли, ${\theta }$ – краевой угол.

Подставляя выражение (4) в (3), получаем

Уравнение, описывающее изменение объема $V$ капли со временем, записывается при этом в виде

где ${{{v}}_{1}}$ и ${{{v}}_{2}}$ – парциальные объемы молекул соответствующих компонентов в растворе в капле. По измеряемым в опыте зависимостям от времени радиуса основания $R\left( t \right)$ и высоты капли $h\left( t \right)$ текущие значения объема капли и краевого угла рассчитываются с использованием выражений

Для того, чтобы приведенные уравнения позволяли полностью описать динамику процесса испарения бинарной капли, необходимо знание зависимостей ${{n}_{{1\infty }}}\left( x \right)$ и ${{n}_{{2\infty }}}\left( x \right).$ С учетом неидеальности раствора в капле эти зависимости можно представить в виде

где ${{n}_{{1\infty }}}$ и ${{n}_{{2\infty }}}$ – концентрации насыщенного пара у поверхности чистых жидкостей соответствующих компонентов, а f₁(x) и ${{f}_{2}}\left( x \right)$ – коэффициенты активности компонентов в растворе. Для зависимостей ${{f}_{1}}\left( x \right)$ и ${{f}_{2}}\left( x \right)$ в случае реального раствора можно использовать табличные данные или полуэмпирические аппроксимации [12, 13].

Будем рассматривать ситуацию, когда в окружающем воздухе изначально присутствует только водяной пар, так что ${{n}_{{10}}} = 0.$ В этом случае уравнение (7), описывающее эволюцию объема капли, можно представить в виде

     Введем обозначение ${\gamma } = {{{{n}_{{20}}}} \mathord{\left/ {\vphantom {{{{n}_{{20}}}} {{{n}_{{2\infty }}}}}} \right. \kern-0em} {{{n}_{{2\infty }}}}} < 1$ для относительной влажности воздуха и определим параметр ε выражением ${\varepsilon } = {{{{{v}}_{1}}{{D}_{1}}{{n}_{{1\infty }}}} \mathord{\left/ {\vphantom {{{{{v}}_{1}}{{D}_{1}}{{n}_{{1\infty }}}} {{{{v}}_{2}}{{D}_{2}}{{n}_{{2\infty }}}}}} \right. \kern-0em} {{{{v}}_{2}}{{D}_{2}}{{n}_{{2\infty }}}}}$ и параметр α выражением ${\alpha } = {{{{D}_{1}}{{n}_{{1\infty }}}} \mathord{\left/ {\vphantom {{{{D}_{1}}{{n}_{{1\infty }}}} {{{D}_{2}}{{n}_{{2\infty }}}}}} \right. \kern-0em} {{{D}_{2}}{{n}_{{2\infty }}}}}.$ Тогда, с учетом соотношений (9), уравнения (6) и (10) после несложных преобразований приобретают вид

3. ПРИБЛИЖЕНИЕ ИДЕАЛЬНОГО РАСТВОРА. СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ

Приближение идеального раствора отвечает условию ${{f}_{1}}\left( x \right) = {{f}_{2}}\left( x \right) = 1.$ Уравнения (11) и (12) в этом случае можно представить в виде

Эта система уравнений детально проанализирована в [9], где получена, в частности, в явном виде связь между концентрацией раствора в капле и ее объемом. Здесь мы, следуя [9], детально рассмотрим эволюцию мольной доли первого компонента в растворе в капле со временем.

Как видно из (14), скорость изменения мольной доли $x$ со временем противоположна по знаку выражению

в квадратных скобках в правой части этого уравнения. При условии ${\alpha } > 1$ имеем ${\varphi }\left( {x,{\gamma } = 0} \right) > 0,$ и из уравнения (14) в этом случае следует, что при любых значениях начальной мольной доли ${{x}_{0}}$ и влажности воздуха ${\gamma }$ мольная доля $x$ раствора в капле монотонно убывает с течением времени. Условие ${\alpha } > 1$ выполняется, в частности, для водного раствора этанола, для которого при комнатной температуре имеем ${\alpha } \approx 1.24.$

В случае ${\alpha } < 1$ возникают различные ситуации в зависимости от величины влажности. При условии ${\gamma } > 1 - {\alpha }$ имеем ${\varphi }\left( {x,{\gamma }} \right) > 0,$ так что концентрация раствора в капле, как и в случае ${\alpha } > 1,$ монотонно убывает с течением времени. Если же ${\gamma } < 1 - {\alpha ,}$ то функция ${\varphi }\left( {x,{\gamma }} \right)$ меняет знак при значении $x = \bar {x}\left( {\gamma } \right),$ определяемом выражением

Как следствие, относительная концентрация раствора при любом начальном значении ${{x}_{0}}$ будет с течением времени монотонно стремиться к значению $\bar {x}\left( {\gamma } \right),$ а капля постепенно переходит в режим стационарного испарения, при котором ее состав остается неизменным. Для скорости изменения объема капли со временем в таком режиме из выражения (13) с использованием (16) находим

Условие ${\alpha } < 1$ выполняется для рассматриваемых нами здесь водных растворов серной кислоты и 1-пропанола. Для водного раствора серной кислоты имеем ${\alpha } \approx {{10}^{{ - 6}}}.$ Аномальная малость этого параметра обусловлена крайне низким значением плотности насыщенного пара серной кислоты по сравнению с плотностью водяного пара. Таким образом, практически при любом значении влажности воздуха выполнено условие ${\gamma } < 1 - {\alpha ,}$ и относительная концентрация кислоты в капле должна монотонно стремиться к стационарному значению $\bar {x}\left( {\gamma } \right),$ определяемому выражением (16). Изменение объема капли со временем будет при этом различным в зависимости от начальной концентрации кислоты в растворе капли. Если начальная мольная доля ${{x}_{0}}$ ниже $\bar {x}\left( {\gamma } \right),$ то объем капли должен монотонно уменьшаться. При условии ${{x}_{0}} > \bar {x}\left( {\gamma } \right)$ объем капли вначале (в процессе установления стационарного режима испарения) будет увеличиваться за счет поглощения водяного пара, а затем монотонно уменьшаться. При этом, как видно из (17), это уменьшение должно быть очень медленным в силу малости величины ${{n}_{{1\infty }}}.$

В экспериментах [9] по испарению водных растворов серной кислоты с различной начальной концентрацией исследовалась, прежде всего, зависимость объема капли от времени. Наблюдаемое поведение качественно вполне соответствует выводам приближения идеального раствора, а именно, при низкой начальной концентрации кислоты в капле ее объем вначале сравнительно быстро уменьшался с течением времени, а затем очень долго (на протяжении нескольких суток) оставался практически неизменным. При высоком начальном содержании кислоты объем капли вначале интенсивно возрастал, а впоследствии, как и в случае капли с низкой начальной концентрацией, практически не изменялся. Такое поведение соответствует указанному выше установлению стационарного режима испарения капли при постоянстве ее состава. Уменьшение объема капли в этом режиме не было зафиксировано в силу крайней медленности процесса испарения. Что касается мольной доли серной кислоты в капле в режиме стационарного испарения, то ее значение, которое с высокой точностью определяется из условия практически постоянного количества кислоты в капле в процессе установления стационарного режима, отличается от предсказываемого в приближении идеального раствора. Это отличие обусловлено влиянием неидеальности раствора. Действительно, из (13) имеем для стационарного значения мольной доли $\bar {x}$ уравнение

Это уравнение, которое с учетом чрезвычайной малости величины ${\alpha }$ в рассматриваемом случае сводится к $\bar {x} \approx 1 - {{\gamma } \mathord{\left/ {\vphantom {{\gamma } {{{f}_{2}}\left( {\bar {x}} \right)}}} \right. \kern-0em} {{{f}_{2}}\left( {\bar {x}} \right)}},$ имеет, как и соответствующее уравнение в приближении идеального раствора, единственное решение. Получаемое из (18) с использованием табличных данных для зависимостей ${{f}_{1}}\left( x \right)$ и ${{f}_{2}}\left( x \right)$ стационарное значение $\bar {x}$ вполне согласуется с найденным из экспериментальных данных. Для скорости изменения объема капли в стационарном режиме испарения из уравнения (12), используя (18), находим

Таким образом, наблюдаемый характер эволюции испаряющейся капли водного раствора серной кислоты качественно соответствует описанию в приближении идеального раствора. Учет неидеальности приводит только к изменению количественных характеристик стационарного состава капли и скорости уменьшения ее объема в стационарном режиме испарения.

Для раствора 1-пропанола при комнатной температуре имеем ${\alpha } \approx 0.38.$ Таким образом, условие ${\gamma } > 1 - {\alpha ,}$ при выполнении которого концентрация спирта в капле должна монотонно уменьшаться в процессе испарения, сводится к неравенству ${\gamma } > 0.62.$ При влажности ${\gamma } < 0.62$ мольная доля спирта в процессе испарения должна стремиться к значению $\bar {x}\left( {\gamma } \right) = 1 - {{\gamma } \mathord{\left/ {\vphantom {{\gamma } {0.62}}} \right. \kern-0em} {0.62}}.$ В качестве примера рассмотрим данные из [10] по испарению капли раствора 1-пропанола с его начальной мольной долей ${{x}_{0}} = 0.14$ при двух различных значениях влажности воздуха.

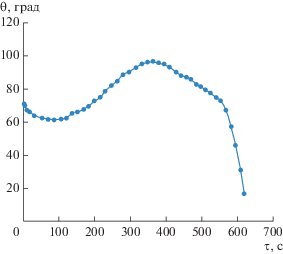
Зависимость краевого угла капли от времени при влажности ${\gamma } = 0.87$ показана на рис. 1.

Согласно рис. 1 для капли раствора 1-пропанола при указанных условиях наблюдается быстрый рост краевого угла, который достигает значения, отвечающего капле чистой воды на той же подложке (103°). Таким образом, спирт практически полностью испаряется из капли. Подобное поведение при влажности ${\gamma } = 0.87$ соответствует, по крайней мере на качественном уровне, предсказываемому в приближении идеального раствора при ${\gamma } > 0.62.$

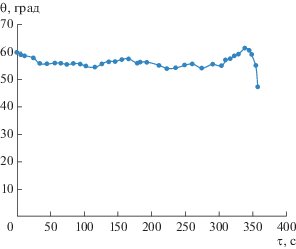
При уменьшении влажности воздуха до значения ${\gamma } = 0.26$ поведение кривой зависимости краевого угла капли от времени изменяется. Это поведение иллюстрируется рис. 2. В приближении идеального раствора в капле мольная доля 1-пропанола при влажности ${\gamma } = 0.26$ должна в процессе испарения возрастать и стремиться к стационарному значению $\bar {x}\left( {\gamma } \right) = 1 - {{\gamma } \mathord{\left/ {\vphantom {{\gamma } {0.62 \approx }}} \right. \kern-0em} {0.62 \approx }}0.42.$ Соответственно краевой угол должен был бы монотонно уменьшаться, а не демонстрировать область значительного роста, наблюдаемого в эксперименте. Таким образом, в рассматриваемом случае наблюдаемое поведение капель раствора 1-пропанола качественно отличается от предсказываемого в модели идеального раствора, и для адекватного описания необходим явный учет неидеальности.

4. ЭВОЛЮЦИЯ КОНЦЕНТРАЦИИ 1-ПРОПАНОЛА В КАПЛЕ ПРИ УЧЕТЕ НЕИДЕАЛЬНОСТИ

Исходим из общего уравнения (12), содержащего коэффициенты активности обоих компонентов раствора. Скорость изменения мольной доли $x$ со временем противоположна по знаку выражению

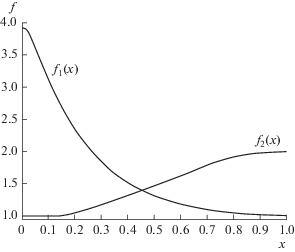
которое, в отличие от расмотренного ранее выражения ${\varphi }\left( {x,{\gamma }} \right),$ является существенно нелинейной функцией концентрации. Для входящих в (20) коэффициентов активности ${{f}_{1}}\left( x \right)$ и ${{f}_{2}}\left( x \right)$ воспользуемся в расчетах данными из [13]. Графики соответствующих зависимостей приведены на рис. 3. Стационарные значения мольной доли 1-пропанола $\bar {x}\left( {\gamma } \right)$ определяются корнями уравнения ${\psi }\left( {\bar {x}\left( {\gamma } \right),{\gamma }} \right) = 0$ и могут быть найдены путем соответствующего графического построения. Из представленного на рис. 4 графика видно, что, в отличие от приближения идеального раствора, когда функция ${\varphi }\left( {x,{\gamma } = 0} \right)$ имела один корень $\bar {x}\left( {{\gamma } = 0} \right) = 1,$ функция ${\psi }\left( {x,{\gamma } = 0} \right)$ имеет два корня. На рис. 4 это корни ${{\bar {x}}_{1}}\left( {{\gamma } = 0} \right) \approx 0.21$ и ${{\bar {x}}_{2}}\left( {{\gamma } = 0} \right) = 1.$ Функция ${\psi }\left( {x,{\gamma } = 0} \right) > 0$ в области $x < {{\bar {x}}_{1}}.$ Соответственно, при ${\gamma } = 0$ (испарение в сухом воздухе) концентрация 1-пропанола в капле будет монотонно уменьшаться в процессе испарения, если ${{x}_{0}} < 0.21,$ и монотонно возрастать, если ${{x}_{0}} > 0.21.$ Минимальное значение функции ${\psi }\left( {x,{\gamma } = 0} \right)$ достигается при мольной доле 1-пропанола $x \approx 0.58$ и составляет ${{{\psi }}_{{\min }}}\left( {x,{\gamma } = 0} \right) \approx - 0.66.$ Поскольку ${\psi }\left( {x,{\gamma }} \right) = {\psi }\left( {x,{\gamma } = 0} \right) + {\gamma ,}$ то при влажности воздуха ${\gamma } > 0.66$ имеем ${\psi }\left( {x,{\gamma }} \right) > 0$ для любой концентрации раствора в капле. При таких значениях влажности концентрация спирта в испаряющейся капле, независимо от ее начального значения, будет монотонно уменьшаться, что приводит к наблюдаемому возрастанию краевого угла капли.

В диапазоне значений влажности $0 < {\gamma } < 0.66$ уравнение ${\psi }\left( {x,{\gamma }} \right) = 0$ имеет, очевидно, два корня: ${{\bar {x}}_{1}}\left( {\gamma } \right)$ и ${{\bar {x}}_{2}}\left( {\gamma } \right),$ причем ${{\bar {x}}_{1}}\left( {{\gamma } = 0} \right) < {{\bar {x}}_{1}}\left( {\gamma } \right) < $ $ < {{\bar {x}}_{2}}\left( {\gamma } \right) < {{\bar {x}}_{2}}\left( {{\gamma } = 0} \right),$ что соответствует условию $0.21 < {{\bar {x}}_{1}}\left( {\gamma } \right) < {{\bar {x}}_{2}}\left( {\gamma } \right) < 1.$ Функция ${\psi }\left( {x,{\gamma }} \right)$ положительна в промежутках $x < {{\bar {x}}_{1}}\left( {\gamma } \right)$ и $x > {{\bar {x}}_{2}}\left( {\gamma } \right)$ (в этой области $\dot {x} < 0$) и отрицательна в промежутке ${{\bar {x}}_{1}}\left( {\gamma } \right) < x < {{\bar {x}}_{2}}\left( {\gamma } \right)$ между корнями (здесь имеет место $\dot {x} > 0$). Соответственно, при $x < {{\bar {x}}_{1}}\left( {\gamma } \right)$ мольная доля спирта в капле монотонно стремится к нулю, а при $x > {{\bar {x}}_{1}}\left( {\gamma } \right)$ она с течением времени стремится к значению ${{\bar {x}}_{2}}\left( {\gamma } \right).$ Поэтому можно говорить, что точка ${{\bar {x}}_{1}}\left( {\gamma } \right)$ отвечает неустойчивому, а ${{\bar {x}}_{2}}\left( {\gamma } \right)$ – устойчивому равновесию относительно изменения концентрации раствора. С ростом влажности величина ${{\bar {x}}_{1}}\left( {\gamma } \right)$ возрастает, а ${{\bar {x}}_{2}}\left( {\gamma } \right)$ уменьшается. При достижении значения влажности ${\gamma } = 0.66$ корни сливаются, а функция ${\psi }\left( {x,{\gamma }} \right)$ становится положительной при любом значении концентрации раствора в капле.

Проведенное рассмотрение позволяет детально проанализировать и объяснить результаты экспериментов по испарению капель водного раствора 1-пропанола из [10]. Становится понятным, в частности, поведение зависимости краевого угла капли от времени, показанной на рис. 2. Начальная мольная доля спирта в капле ${{x}_{0}} = 0.14$ в этом эксперименте удовлетворяет условию ${{x}_{0}} < {{\bar {x}}_{1}}\left( {\gamma = 0} \right)$ и, тем более, условию ${{x}_{0}} < {{\bar {x}}_{1}}\left( {{\gamma } = 0.26} \right).$ Как следует из проведенного выше анализа, концентрация раствора в такой ситуации монотонно стремится к нулю в процессе испарения, что и приводит к наблюдаемому росту краевого угла капли.

Рассмотрим теперь данные из [10] по испарению капли с начальной мольной долей 1-пропанола ${{x}_{0}} = 0.41.$ Зависимость краевого угла такой капли от времени при испарении в воздухе с влажностью ${\gamma } = 0.3$ приведена на рис. 5. Для корней функции ${\psi }\left( {x,{\gamma }} \right)$ при указанной влажности имеем ${{\bar {x}}_{1}}\left( {{\gamma } = 0.3} \right) \approx 0.29,$ ${{\bar {x}}_{2}}\left( {{\gamma } = 0.3} \right) \approx 0.9.$ Поскольку ${{x}_{0}} > {{\bar {x}}_{1}}\left( {{\gamma } = 0.3} \right),$ то мольная доля 1-пропанола с течением времени должна меняться в направлении значения ${{\bar {x}}_{2}}\left( {{\gamma } = 0.3} \right).$ Это полностью согласуется с показанным на рис. 5 видом зависимости, который как раз и отвечает ситуации, когда концентрация спирта остается в процессе испарения конечной.

Более сложная ситуация возникает при испарении капли с такой же начальной концентрацией ${{x}_{0}} = 0.41$ при влажности воздуха ${\gamma } = 0.45.$ При этой влажности нулями функции ${\psi }\left( {x,{\gamma }} \right)$ являются ${{\bar {x}}_{1}}\left( {{\gamma } = 0.45} \right) \approx 0.35,$ ${{\bar {x}}_{2}}\left( {{\gamma } = 0.45} \right) \approx 0.83.$ Поскольку ${{x}_{0}}$ превосходит, хотя и не на много, величину ${{\bar {x}}_{1}}\left( {{\gamma } = 0.45} \right),$ то, согласно приведенным выше оценкам, концентрация раствора в капле должна, как и в случае ${\gamma } = 0.3,$ возрастать со временем, а краевой угол монотонно уменьшаться. Вместе с тем, как следует из рис. 6, имеет место совершенно иное поведение краевого угла. После небольшого начального уменьшения краевой угол достаточно длительное время остается практически постоянным, а затем наблюдается стадия его значительного роста. Это означает, что концентрация раствора в капле на этой стадии заметно снижается. Объяснение указанному расхождению можно найти, если иметь в виду, что используемые оценки получены в изотермическом приближении и принять во внимание тепловые эффекты при испарении капли.

5. ВЛИЯНИЕ ТЕПЛОВЫХ ЭФФЕКТОВ

Температура испаряющейся капли $T$ отличается от температуры ${{T}_{0}}$ окружающего воздуха. Влияние неизотермичности испарения или конденсации на динамику изменения состава свободных бинарных капель было проведено в [14, 15]. Аналогичный подход может быть применен и для испаряющихся сидячих бинарных капель. Для концентрации насыщенного пара чистой жидкости $i$-го компонента из уравнения Клапейрона–Клаузиуса имеем

где ${{q}_{i}}$ – парциальная удельная теплота парообразования в расчете на одну молекулу $i$-го компонента раствора, ${{k}_{{\text{B}}}}$ – постоянная Больцмана. Используя (21) в уравнении (6), получаем обобщение уравнения эволюции мольной доли $x$ (12) с учетом тепловых эффектов в виде

Для раствора 1-пропанола в воде при комнатной температуре ${{T}_{0}}$ имеем $\frac{{{{q}_{1}}}}{{{{k}_{{\text{B}}}}{{T}_{0}}}} \approx 16$ и $\frac{{{{q}_{2}}}}{{{{k}_{{\text{B}}}}{{T}_{0}}}} \approx 17.6.$ Это позволяет переписать уравнение (22) с хорошей точностью следующим образом:

Отметим что в процессе испарения капли $\Delta T < 0,$ так что $\exp \left( {\frac{{{{q}_{2}}\Delta T}}{{{{k}_{{\text{B}}}}T_{0}^{2}}}} \right) < 1.$

Сравнение уравнений (12) и (23), показывает, что тепловые эффекты в рассматриваемой ситуации проявляются двояко. Они приводят как к торможению процесса изменения концентрации (множитель $\exp \left( {\frac{{{{q}_{2}}\Delta T}}{{{{k}_{{\text{B}}}}T_{0}^{2}}}} \right)$ в правой части (23)), так и к “перенормировке” значения влажности

в выражении в квадратных скобках. Вследствие этого величины ${{\bar {x}}_{1}}\left( {\gamma } \right)$ и ${{\bar {x}}_{2}}\left( {\gamma } \right)$ заменяются на ${{\bar {x}}_{1}}\left( {{\tilde {\gamma }}} \right)$ и ${{\bar {x}}_{2}}\left( {{\tilde {\gamma }}} \right)$ соответственно. Поскольку, очевидно, ${\tilde {\gamma }} > {\gamma }$, то ${{\bar {x}}_{1}}\left( {{\tilde {\gamma }}} \right) > {{\bar {x}}_{1}}\left( {\gamma } \right).$ Для того, чтобы капля перешла в режим монотонного уменьшения концентрации, необходимо выполнение условия ${{\bar {x}}_{1}}\left( {{\tilde {\gamma }}} \right) \geqslant {{x}_{0}}.$ Для рассматриваемой ситуации, где ${{x}_{0}} = 0.41$ и ${\gamma } = 0.45,$ это приводит к требованию ${{\bar {x}}_{1}}\left( {0.45\exp \left( { - \frac{{{{q}_{2}}\Delta T}}{{{{k}_{{\text{B}}}}T_{0}^{2}}}} \right)} \right) \geqslant 0.41.$ Отсюда с использованием численных значений функции ${\psi }\left( {x,{\gamma } = 0.45} \right)$ получаем условие $\exp \left( { - \frac{{{{q}_{2}}\Delta T}}{{{{k}_{\operatorname{B} }}T_{0}^{2}}}} \right) \geqslant 1.2,$ определяющее требуемое понижение температуры капли. В результате, используя приведенные выше численные данные, находим, что капля переходит в режим монотонного испарения спирта, если понижение ее температуры удовлетворяет условию $\left| {\Delta T} \right| \geqslant 3\operatorname{K} .$ Как следует из результатов работы [16], это условие при испарении водного раствора спирта вполне выполнимо.

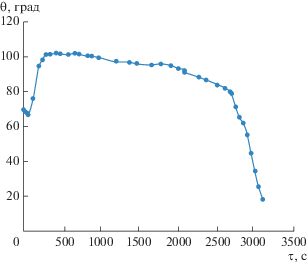
Подобная ситуация наблюдается и в другом из описанных в [10] экспериментов. В этом опыте рассматривалось испарение капли 1-пропанола при влажности воздуха ${\gamma } = 0.63.$ Зависимость краевого угла капли от времени для этого случая приведена на рис. 7. Как и при испарении капли с начальной концентрацией ${{x}_{0}} = 0.41$ при влажности ${\gamma } = 0.45,$ краевой угол в данном случае после небольшого начального уменьшения длительное время остается почти постоянным, и только на заключительной стадии наблюдается его заметный рост. Иными словами, существенное снижение концентрации спирта в капле начинается только близко к завершению процесса испарения.

Функция ${\psi }\left( {x,{\gamma } = 0.63} \right)$ принимает отрицательные значения в интервале значений концентрации $0.49 < x < 0.66,$ при этом $ - 0.03 < {\psi }$$\left( {x,{\gamma } = 0.63} \right) < 0.$ Соответственно, при начальной мольной доле 1-пропанола ${{x}_{0}} \approx 1$ мы должны, согласно уравнению изотермического приближения (12), наблюдать стремление концентрации к значению ${{\bar {x}}_{2}}\left( {{\gamma } = 0.63} \right) \approx 0.66.$ Поведение кривой на рис. 7 показывает, что так и происходит в течение первых 5 мин. Наблюдаемый после этого рост краевого угла свидетельствует, что изменение концентрации не останавливается при достижении предсказываемого изотермической теорией стационарного значения. Это, как и в предыдущем случае, можно объяснить влиянием тепловых эффектов. Поскольку в рассматриваемой ситуации ${\psi }\left( {x,{\gamma } = 0.63} \right) > - 0.03,$ достаточно обеспечить выполнение условия ${\tilde {\gamma }} - {\gamma } > 0.03,$ чтобы капля перешла в режим монотонного снижения концентрации спирта. Это условие сводится к требованию $\left( {\exp \left( { - \frac{{{{q}_{2}}\Delta T}}{{{{k}_{\operatorname{B} }}T_{0}^{2}}}} \right) - 1} \right){\gamma } > 0.03.$ Подставляя сюда численные данные, получаем необходимое условие для отклонения температуры капли от температуры окружающего воздуха в виде $\left| {\Delta T} \right| \geqslant 0.8\operatorname{K} ,$ что заведомо выполняется в рассматриваемой ситуации. Существенно, что в обоих рассмотренных случаях необходимое для заметного увеличения краевого угла снижение концентрации 1-пропанола в капле достигается ранее момента ее полного испарения.

6. РОЛЬ НЕИДЕАЛЬНОСТИ РАСТВОРА В ДИНАМИКЕ ИСПАРЕНИЯ КАПЕЛЬ ВОДНЫХ РАСТВОРОВ ЭТАНОЛА

Этанол обладает существенно более высокой летучестью, чем 1-пропанол. Как отмечалось выше при обсуждении приближения идеального раствора, параметр ${\alpha }$ для водного раствора этанола имеет значение ${\alpha } \approx 1.24,$ в то время как для раствора 1-пропанола ${\alpha } \approx 0.38.$ Соответственно, в этом приближении следует вывод о том, что концентрация этанола в капле должна монотонно убывать в процессе ее испарения при любой влажности окружающего воздуха. В реальности ситуация оказывается более сложной, что обусловлено, как и в случае 1-пропанола, сильной неидеальностью раствора.

Как и при обсуждении особенностей испарения капель раствора 1-пропанола, проанализируем возможное поведение концентрации этанола в капле в зависимости от ее начального состава и влажности окружающего воздуха. Для коэффициентов активности ${{f}_{1}}\left( x \right)$ и ${{f}_{2}}\left( x \right)$ компонентов раствора в капле воспользуемся данными из [13]. Зависимости этих величин от мольной доли этанола в капле представлены на рис. 8, а соответствующая им зависимость ${\psi }\left( {x,{\gamma } = 0} \right)$ показана на рис. 9.

Нулями функции ${\psi }\left( {x,{\gamma } = 0} \right)$ являются ${{\bar {x}}_{1}}\left( {{\gamma } = 0} \right) = 0.55$ и ${{\bar {x}}_{2}}\left( {{\gamma } = 0} \right) = 1.$ Таким образом, при ${\gamma } = 0$ (испарение в сухом воздухе) концентрация этанола в капле будет монотонно уменьшаться в процессе испарения, если ${{x}_{0}} < 0.55,$ и монотонно возрастать, если ${{x}_{0}} > 0.55.$ Минимальное значение функции ${\psi }\left( {x,{\gamma } = 0} \right)$ достигается при мольной доле этанола $x \approx 0.74$ и составляет ${{{\psi }}_{{\min }}}\left( {x,{\gamma } = 0} \right) \approx - 0.13.$ При ${\gamma } > 0.13$ имеем ${\psi }\left( {x,{\gamma }} \right) > 0,$ и концентрация раствора в капле монотонно убывает со временем. В интервале значений влажности $0 < {\gamma } < 0.13$ уравнение ${\psi }\left( {x,{\gamma }} \right) = 0$ имеет два корня, ${{\bar {x}}_{1}}\left( {\gamma } \right)$ и ${{\bar {x}}_{2}}\left( {\gamma } \right),$ причем $0.55 < $ ${{\bar {x}}_{1}}\left( {\gamma } \right) < {{\bar {x}}_{2}}\left( {\gamma } \right) < 1.$ Как следствие, концентрация этанола в капле в процессе испарения может стремиться к конечному стационарному значению только при влажности воздуха ${\gamma } < 0.13$ и начальном значении мольной доли этанола в капле ${{x}_{0}} > {{\bar {x}}_{1}}\left( {\gamma } \right) > 0.55.$ Эти ограничения являются более жесткими, чем в рассмотренном выше случае 1-пропанола. При начальном значении мольной доли этанола ${{x}_{0}} < 0.55$ концентрация спирта в капле будет монотонно уменьшаться со временем. При этом, однако, наблюдаемое поведение краевого угла испаряющейся капли будет существенным образом зависеть от влажности воздуха. Как следует из уравнения (14) с учетом определения (20), снижение концентрации спирта в капле при текущем значении его мольной доли происходит тем быстрее, чем больше величина ${\psi }\left( {x,{\gamma }} \right) = {\psi }\left( {x,{\gamma } = 0} \right) + {\gamma }{\text{.}}$

Если, например, начальная мольная доля спирта ${{x}_{0}}$ чуть меньше, чем ${{\bar {x}}_{1}}\left( {{\gamma } = 0} \right) = 0.55,$ то при достаточно низкой влажности концентрация спирта в испаряющейся капле снижается медленно, и на всем протяжении процесса испарения капли краевой угол остается практически постоянным. С повышением влажности скорость снижения концентрации спирта возрастает, а концентрация воды в капле достигает значений, достаточных для наблюдаемого увеличения краевого угла. При этом участок роста краевого угла должен появляться тем раньше, чем выше влажность воздуха. Именно такое поведение наблюдалось в экспериментах по испарению капель водного раствора этанола [11]. В этой работе исследовано, в частности, поведение краевого угла капли раствора с начальным содержанием этанола 70 об. % при различных значениях влажности. Соответствующее начальное значение ${{x}_{0}}$ мольной доли спирта в капле есть ${{x}_{0}} \approx 0.42.$ Результаты измерений иллюстрируются приведенными в [11] графиками (рис. 6б в [11]). Так, при влажности ${\gamma } = 0.1$ краевой угол капли остается практически постоянным на всем протяжении процесса испарения. При влажности ${\gamma } = 0.42$ участок роста краевого угла появляется близко к завершению процесса испарения, когда объем капли составляет около одной десятой части начального. С увеличением влажности участок роста наблюдается, как и указывалось выше, на более раннем этапе испарения, и при влажности ${\gamma } = 0.94$ краевой угол начинает резко возрастать, когда объем капли уменьшается примерно вдвое.

7. ЗАКЛЮЧЕНИЕ

Проведенное рассмотрение еще раз свидетельствует, что испарение сидячих бинарных капель является весьма сложным и многовариантным процессом. Описание динамики этого процесса требует учета многих факторов, каждый из которых может при определенных обстоятельствах играть существенную роль. В отсутствие возможности контроля текущего состава капли в процессе ее испарения важно иметь адекватные оценки реализации того или иного сценария эволюции капли, основываясь на данных о начальном состоянии капли, свойствах раствора и внешних условиях, в которых капля испаряется. Полученные в работе результаты показывают, что наблюдаемые на опыте особенности испарения сидячих капель водных растворов серной кислоты, 1-пропанола и этанола могут быть объяснены при корректном учете неидеальности раствора в капле и возможного влияния тепловых эффектов даже без специального обсуждения внутреннего установления объемной концентрации раствора. В частности, полученные численные оценки параметров, при которых реализуется тот или иной сценарий эволюции капель рассматриваемых растворов спиртов, вполне согласуются с соответствующими экспериментальными данными.