1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 82, № 1, 2020

Коллоидный журнал, 2020, T. 82, № 1, стр. 3-10

Эффективная свободная поверхностная энергия зародышей кристаллической фазы

В. Г. Байдаков 1, *, К. Р. Проценко 1

1 Институт теплофизики, Уральское отделение Российской академии наук
620016 Екатеринбург, ул. Амундсена, 107а, Россия

* E-mail: baidakov@itp.uran.ru

Поступила в редакцию 06.06.2019
После доработки 25.06.2019
Принята к публикации 28.06.2019

Полный текст (PDF)

Аннотация

Путем молекулярно-динамического моделирования методами среднего времени жизни, выборки прямого потока и внедрения исследована кинетика спонтанной кристаллизации переохлажденной леннард-джонсовской жидкости. В широких интервалах температуры и давления при изменении частоты нуклеации на 195 порядков определены предельные переохлаждения (пересжатия) жидкой фазы. По полученным данным с использованием классической теории зародышеобразования рассчитана зависимость эффективной свободной поверхностной энергии зародышей кристаллической фазы от кривизны поверхности разрыва. Расчеты проведены по трем изотермам и четырем изобарам. Определены первая (длина Толмена) и вторая поправки к эффективной свободной поверхностной энергии на кривизну межфазной границы.

1. ВВЕДЕНИЕ

Кристаллизация переохлажденной жидкости, как и распад любого метастабильного состояния, начинается с образования зародыша новой фазы. В отсутствиe готовых и легко активируемых центров кристаллизации зародыши образуются термофлуктуационным путем. Этот процесс описывается классической теорией зародышеобразования (КТЗ) [1–3].

Вероятность появления жизнеспособного зародыша определяется минимальной работой ${{W}_{{\text{*}}}},$ которую необходимо затратить на его образование. Если состояние среды не изменяется при появлении равновесного включения новой фазы, то ${{W}_{{\text{*}}}}$ численно равна приращению любого из термодинамических потенциалов системы. Ввиду малости зародышей значительная часть относящихся к ним молекул входит в состав межфазного (поверхностного) слоя, поэтому зародышеобразование является не только флуктуационным, но и поверхностным явлением. По мере увеличения кривизны поверхности разрыва возрастает разность давлений в сосуществующих фазах и, когда радиус зародыша становится сопоставимым с толщиной поверхностного слоя, начинает проявляться зависимость термодинамических свойств, и в первую очередь свободной поверхностной энергии, от размера зародыша.

Свободная поверхностная энергия (поверхностное натяжение) на плоской межфазной границе надежно измеряется в системе жидкость–пар. Прямые измерения этого параметра на границе жидкость–кристалл затруднены. При сопоставлении экспериментальных данных по кристаллизации переохлажденных жидкостей с КТЗ свободная поверхностная энергия обычно рассматривается как “свободный” параметр [4].

Зависимость поверхностного натяжения капелек жидкости и пузырьков пара от кривизны поверхности разрыва широко обсуждалась в литературе [5–9]. Для кристаллических зародышей, у которых свободная поверхностная энергия является функцией кристаллографических ориентаций граней кристалла, этот вопрос менее изучен. В случае межфазной границы жидкость–газ поверхностное натяжение на плоской и искривленной границе, а также первая поправка на кривизну поверхности разрыва (длина Толмена) ${{\delta }_{\infty }}$ могут быть вычислены суммированием тензора давления через границу фаз [10]. Такая процедура расчета ${{\delta }_{\infty }}$ не применима к границе кристалл–жидкость, так как для анизотропной системы локальный тензор давления не определен [11, 12]. Этому препятствует и упругая энергия, запасенная в кристалле.

Подход, позволяющий оценить длину Толмена для плоской границы кристалл–жидкость при молекулярно-динамическом (МД) моделировании, предложен в работе [13]. Используя метадинамику, авторы [13] рассчитали свободную поверхностную энергию на эквимолекулярной разделяющей поверхности кристалл–жидкость и, определив в рамках капиллярно-волновой модели свободную поверхностную энергию на поверхности натяжения, нашли ${{\delta }_{\infty }}.$ При температурах, близких к температуре тройной точки леннард-джонсовской (ЛД) системы, величина ${{\delta }_{\infty }}$ оказалась отрицательной и равной по модулю (0.3–0.5)$\sigma $, где $\sigma $ – параметр потенциала. Связь длины Толмена с термодинамическими характеристиками двухфазной системы кристалл–жидкость рассматривалась в работе [14].

В данной статье исследуется размерная зависимость свободной поверхностной энергии кристаллических зародышей, которая определяется по результатам изучения спонтанной кристаллизации переохлажденной жидкости при МД-моделировании. Расчеты проводятся по изобарам и изотермам в широких интервалах температуры и давления (включая его отрицательные значения).

Статья состоит из введения, четырех разделов и заключения.

2. ЗАРОДЫШЕОБРАЗОВАНИЕ И СВОЙСТВА ЗАРОДЫШЕЙ КРИСТАЛЛИЧЕСКОЙ ФАЗЫ

2.1. Элементы классической теории зародышеобразования

Свободная поверхностная энергия кристалла $\gamma $ является функцией кристаллографических ориентаций граней. Анизотропия свободной поверхностной энергии изменяет условия локального равновесия фаз с искривленной поверхностью разрыва по сравнению с изотропной поверхностью. При заданных температуре T и давлении p в переохлажденной жидкости работа образования кристаллического зародыша определяется изменением термодинамического потенциала Гиббса $\Delta G.$ Неустойчивому равновесию кристаллического зародыша с переохлажденной жидкостью, отвечающему минимальной работе его образования ${{W}_{{\text{*}}}}$, соответствует форма поверхности, определяемая правилом Гиббса–Кюри–Вульфа [15, 16]. Для работы образования кристаллического критического зародыша имеем

(1)
${{W}_{{\text{*}}}} = \Delta G\left( {{{V}_{*}},A{{{\kern 1pt} }_{*}}} \right) = \frac{1}{3}\int\limits_{{{A}_{*}}} {\gamma dA} = \frac{1}{3}\sum {{{\gamma }_{i}}{{A}_{i}}} ,$
где ${{V}_{*}},$ $A{{{\kern 1pt} }_{*}}$ – объем и поверхность кристаллика критического размера с равновесной формой, ${{\gamma }_{i}}$ и ${{A}_{i}}$ – свободная поверхностная энергия и площадь поверхности i-ой грани равновесно ограненного зародыша.

Путем введения эффективной свободной поверхностной энергии

(2)
${{\gamma }_{e}} = \frac{1}{{4\pi R_{*}^{2}}}\int\limits_{{{A}_{*}}} {\gamma dA} ,$

можно представить работу образования критического зародыша кристаллической фазы в таком же виде, как и зародыша изотропной фазы

(3)
${{W}_{*}} = \frac{{16\pi }}{3}\frac{{\gamma _{e}^{3}}}{{{{{\left( {{{p}_{*}} - p} \right)}}^{2}}}} = \frac{2}{3}\pi R_{*}^{3}\left( {{{p}_{*}} - p} \right),$
где $R{{{\kern 1pt} }_{*}}$ – радиус поверхности натяжения критического зародыша, ${{p}_{*}}$ – давление в зародыше.

Выражение (2) задает сферическую аппроксимацию кристаллического зародыша. При этом сохраняется объем зародыша, выполняются равенство химических потенциалов фаз $\mu {{{\kern 1pt} }_{l}}(T,p) = {{\mu }_{s}}(T,{{p}_{*}})$ (условие вещественного равновесия) и уравнение Лапласа ${{p}_{*}} - p = {{2{{\gamma }_{e}}} \mathord{\left/ {\vphantom {{2{{\gamma }_{e}}} {R{{{\kern 1pt} }_{*}}}}} \right. \kern-0em} {R{{{\kern 1pt} }_{*}}}}$ (условие механического равновесия).

Работа образования критического зародыша определяет частоту зародышеобразования J – число жизнеспособных (закритических) кристалликов, образующихся в единицу времени в единице объема переохлажденной жидкости. Согласно КТЗ [3]

(4)
$J = \rho {\kern 1pt} {{Z}_{*}}{\kern 1pt} {{D}_{*}}{\kern 1pt} \exp \left( {{{ - {{W}_{*}}} \mathord{\left/ {\vphantom {{ - {{W}_{*}}} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right),$
где $\rho $ – число частиц в единице объема жидкости, Z – неравновесный фактор Зельдовича, D – коэффициент диффузии зародышей в пространстве их размеров, ${{k}_{B}}$ – постоянная Больцмана. Как и выше, “звездочка” указывает на принадлежность величины к критическому зародышу.

Сферическая аппроксимация и принцип Гиббса–Кюри–Вульфа позволяют использовать однопараметрическое описание кинетики кристаллизации переохлажденной жидкости, т.е. характеризовать рост зародыша одним параметром – его радиусом. В работе [17] отмечается, что сферическая аппроксимация применима для достаточно больших активационных барьеров, когда ${{{{W}_{*}}} \mathord{\left/ {\vphantom {{{{W}_{*}}} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}} > {{10}^{2}}.$

2.2. Размерная зависимость эффективной свободной поверхностной энергии кристаллического зародыша

Гиббсом в рамках метода разделяющих поверхностей получено уравнение [18] для изотермической зависимости свободной поверхностной энергии изотропной системы от радиуса кривизны поверхности разрыва

(5)
$\frac{1}{{{{\gamma }_{e}}}}{{\left( {\frac{{\partial {{\gamma }_{e}}}}{{\partial R}}} \right)}_{T}} = {{\frac{{2\delta }}{{{{R}^{2}}}}} \mathord{\left/ {\vphantom {{\frac{{2\delta }}{{{{R}^{2}}}}} {\left( {1 + \frac{{2\delta }}{R}} \right)}}} \right. \kern-0em} {\left( {1 + \frac{{2\delta }}{R}} \right)}}.$

Параметр $\delta $ есть

(6)
$\delta = {{\delta }^{{(T)}}} = \frac{\Gamma }{{{{\rho }_{s}} - {{\rho }_{l}}}},$
где Г – абсолютная адсорбция, ${{\rho }_{l}}$ и ${{\rho }_{s}}$ – плотности жидкой и кристаллической фаз.

Уравнение (5) сохраняет свой вид и при условии постоянства давления в окружающей зародыш фазе [10]. В этом случае $\delta $ определяется выражением

(7)
$\delta = {{\delta }^{{\left( p \right)}}} = \frac{{\Gamma - {{\bar {s}} \mathord{\left/ {\vphantom {{\bar {s}} {{{s}_{l}}}}} \right. \kern-0em} {{{s}_{l}}}}}}{{{{\rho }_{s}}\left( {1 - {{{{s}_{s}}} \mathord{\left/ {\vphantom {{{{s}_{s}}} {{{s}_{l}}}}} \right. \kern-0em} {{{s}_{l}}}}} \right)}}.$

Здесь ${{s}_{l}},$ ${{s}_{s}}$ – молярные энтропии жидкой и кристаллической фаз, $\bar {s}$ – избыточная энтропия на единицу поверхности межфазного слоя.

Если радиус кривизны поверхности разрыва существенно превышает толщину межфазного слоя, то $\delta $ можно считать постоянной и равной значению ${{\delta }_{\infty }}$ на плоской границе фаз. В этом случае интегрирование (5) дает

(8)
${{\gamma }_{e}}\left( R \right) = {{\gamma }_{\infty }}\left( {1 - \frac{{2{{\delta }_{\infty }}}}{R}} \right),$
где ${{\gamma }_{\infty }}$ – эффективная свободная поверхностная энергия плоской межфазной границы.

По виду уравнение (8) совпадает с уравнением Толмена [5]. Будем называть ${{\delta }_{\infty }}$ длиной Толмена. Формулы (6) и (7) позволяют выразить ${{\delta }_{\infty }}$ через термодинамические характеристики двухфазной системы жидкость–кристалл с плоской межфазной границей [14].

Выражение (8) можно рассматривать как первые члены разложения ${{\gamma }_{e}}$ в ряд по кривизне поверхности разрыва [19, 20]. При учете квадратичного по кривизне члена зависимость ${{\gamma }_{e}}(R)$ принимает вид

(9)
${{\gamma }_{e}}(R) = {{\gamma }_{\infty }}\left( {1 - \frac{{2{{\delta }_{\infty }}}}{R} + \frac{{{{\alpha }_{\infty }}}}{{{{R}^{2}}}}} \right).$

Запись (9) предполагает следующую асимптотическую формулу: $\delta (R) = {{\delta }_{\infty }} + {{{{\alpha }_{\infty }}} \mathord{\left/ {\vphantom {{{{\alpha }_{\infty }}} {2R}}} \right. \kern-0em} {2R}},$ где параметр ${{\alpha }_{\infty }} = {{{{2d\delta } \mathord{\left/ {\vphantom {{2d\delta } {d\left. {\left( {{1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R}} \right)} \right|}}} \right. \kern-0em} {d\left. {\left( {{1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R}} \right)} \right|}}}_{{R \to \infty }}}$ [21].

Согласно (8), при больших значениях R характер зависимости эффективной свободной поверхностной энергии от радиуса кривизны поверхности разрыва определяется знаком ${{\delta }_{\infty }}{\text{:}}$ если ${{\delta }_{\infty }} < 0,$ то ${{\gamma }_{\infty }}$ с увеличением кривизны поверхности разрыва возрастает, а при ${{\delta }_{\infty }} > 0$ – убывает. Насколько длительно сохранится такое поведение ${{\gamma }_{e}}(R),$ будет зависеть от знака и величины параметра ${{\alpha }_{\infty }}.$ Если ${{\delta }_{\infty }}$ и ${{\alpha }_{\infty }}$ отрицательны, то при увеличении кривизны поверхности разрыва эффективная свободная поверхностная энергия будет проходить через максимум.

3. МЕТОДЫ ИССЛЕДОВАНИЯ СПОНТАННОЙ КРИСТАЛЛИЗАЦИИ ПЕРЕОХЛАЖДЕННОЙ ЖИДКОСТИ

Для определения зависимости эффективной свободной поверхностной энергии кристаллических зародышей от их размера исследован процесс спонтанного зарождения кристаллической фазы в переохлажденной леннард-джонсовской жидкости. При МД-моделировании использованы три подхода к расчету основных характеристик процесса зародышеобразования: метод среднего времени жизни (СВЖ) метастабильной системы [22], методы выборки прямого потока (ВПП) [23–25] и внедрения зародыша новой фазы [26, 27]. Рассчитаны частота зародышеобразования, число частиц в критическом зародыше, коэффициент диффузии зародышей в пространстве их размеров и др. Это позволило перекрыть по частоте зародышеобразования интервал от 10–160 до 1034 с–1 м–3 и определить эффективную свободную поверхностную энергию кристаллических зародышей с радиусом от 2σ до 15σ.

В методе СВЖ, при заданных значениях температуры и давления в переохлажденной жидкости, регистрировалось 100–500 времен ожидания событий кристаллизации τ, по которым определялось среднее время жизни $\bar {\tau }$ метастабильной системы. При заданном объеме системы V частота зародышеобразования J связана с $\bar {\tau }$ соотношением $J = {{\left( {\bar {\tau }V} \right)}^{{ - 1}}}$ [22]. Для систем, содержащих от нескольких тысяч до нескольких миллионов взаимодействующих частиц, метод позволяет рассчитать частоту зародышеобразования в интервале от 1031 до 1034 с–1 м–3.

Для продвижения в область более низких (до 1020 с–1 м–3) значений J использован метод ВПП [25]. В рамках данного подхода фазовое пространство исследуемой системы делится конечным числом непересекающихся поверхностей, задаваемых параметром порядка λ. В качестве такого параметра использовался размер наибольшего кристаллического зародыша, который рассчитывался по методике, описанной в работах [23–25]. Если в некотором (метастабильном) состоянии параметр $\lambda = {{\lambda }_{0}},$ а в конечном (двухфазном) $\lambda = {{\lambda }_{n}},$ то частота нуклеации

(10)
$J = {{J}_{0}}\prod\limits_{i = 0}^{n - 1} {P\left( {\left. {{{\lambda }_{{i + 1}}}} \right|{{\lambda }_{i}}} \right)} ,$
где ${{J}_{0}} = {{{{N}_{0}}} \mathord{\left/ {\vphantom {{{{N}_{0}}} {\left( {tV} \right)}}} \right. \kern-0em} {\left( {tV} \right)}}$ – частота перехода системы через поверхность ${{\lambda }_{0}},$ ${{N}_{0}}$ – число пересечений поверхности ${{\lambda }_{0}}$ в направлении возрастания параметра порядка за время t, $P\left( {\left. {{{\lambda }_{{i\, + \,1}}}} \right|{{\lambda }_{i}}} \right)$ – вероятность того, что система, вышедшая из исходного состояния и достигшая поверхности ${{\lambda }_{i}},$ далее пересечет поверхность ${{\lambda }_{{i\,\, + \,\,1}}},$ а не вернется в исходное состояние.

Наряду с частотой зародышеобразования метод ВПП позволяет определить число частиц в критическом зародыше. Для этого рассчитывалась вероятность перехода системы с поверхности ${{\lambda }_{i}}$ в конечное состояние

(11)
${{P}_{n}}\left( {{{\lambda }_{i}}} \right) = P\left( {\left. {{{\lambda }_{n}}} \right|{{\lambda }_{i}}} \right) = {{J}_{0}}\prod\limits_{j\, = \,i}^{n - 1} {P\left( {\left. {{{\lambda }_{{j\, + \,1}}}} \right|{{\lambda }_{j}}} \right)} .$

Значение параметра порядка ${{\lambda }_{i}} = {{\lambda }_{*}},$ при котором ${{P}_{n}}\left( {{{\lambda }_{*}}} \right) = 0.5,$ определяет число частиц в критическом зародыше ${{n}_{*}}.$

В методе внедрения зародыша [26] после удаления из переохлажденной жидкости части частиц на их место помещался сферический кристаллический ГЦК-кластер. Между внедренным кластером и жидкой фазой оставалась пустая прослойка толщиной σ. Частицы внедренного кластера были неподвижны (это достигалось приписыванием им нулевой скорости и существенно большей массы, чем частицам жидкости). В результате теплового движения частиц жидкой фазы происходило формирование межфазного слоя. После этого удержание частиц внедренного кластера отключалось, и микродвухфазная система приходила к состоянию начального локального равновесия. Фазовая принадлежность частиц определялась так, как это описано в работах [28, 29]. После разделения частиц на кристалло- и жидкоподобные рассчитывался размер кристаллического кластера. В методе внедрения, ввиду малости исследуемых переохлаждений (J < 1015 с–1 м–3), вероятность спонтанного возникновения еще одного зародыша, помимо внедренного, близка к нулю. Для определения состояния, при котором внедренный кластер является критическим зародышем, для нескольких значений температуры регистрировалось число частиц в кластере и рассчитывалась вероятность его роста. Если при некоторой температуре ${{T}_{*}}$ эта вероятность равнялась 0.5, то отвечающий ей кристаллический кластер, содержащий ${{n}_{*}}$ частиц, считался критическим зародышем.

Знание температуры ${{T}_{*}}$ и давления в переохлажденной жидкости, а также числа частиц в кластере позволяет из условия вещественного равновесия критический зародыш–жидкость определить плотность ${{\rho }_{*}},$ давление ${{p}_{*}}$ в зародыше и его радиус $R{{{\kern 1pt} }_{*}}.$ Из условия механического равновесия рассчитывалась эффективная свободная поверхностная энергия.

4. МОДЕЛЬ И ДЕТАЛИ РАСЧЕТА

Эффективная свободная поверхностная энергия кристаллических зародышей рассчитана для систем, содержащих от 2048 до 500 000 ЛД-частиц. Радиус обрезания потенциала Леннарда–Джонса принимался равным 6.78σ. Параметры потенциала σ и ε, масса частицы m и постоянная Больцмана ${{k}_{B}}$ использовались для приведения рассчитываемых величин к безразмерному виду. Единица температуры – ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{k}_{B}}}}} \right. \kern-0em} {{{k}_{B}}}},$ давления – ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{\sigma }^{3}}}}} \right. \kern-0em} {{{\sigma }^{3}}}},$ плотности – ${1 \mathord{\left/ {\vphantom {1 {{{\sigma }^{3}}}}} \right. \kern-0em} {{{\sigma }^{3}}}},$ времени – ${{\left( {{m \mathord{\left/ {\vphantom {m \varepsilon }} \right. \kern-0em} \varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sigma ,$ частоты нуклеации – ${{{{{\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon m}} \right. \kern-0em} m}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon m}} \right. \kern-0em} m}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{{\sigma }^{4}}}}} \right. \kern-0em} {{{\sigma }^{4}}}}.$ Далее все величины приводятся в безразмерном виде.

Частицы размещались в кубической ячейке с периодическими граничными условиями. Расчеты проводились по четырем изобарам p = 6.912, 3.6, 0.0, –0.995 и трем изотермам T = 0.865, 0.7, 0.55.

МД-моделирование выполнялось в программе LAMMPS [30]. Использовались NVE-, NVT- и NPT-ансамбли. В NVT- и NPT-ансамблях температура поддерживалась постоянной с помощью стохастического термостата Басси и др. [31]. При интегрировании уравнений движения частиц применялся скоростной алгоритм Верле [32]. Шаг интегрирования по времени составлял $\Delta t$ = = 0.002318132.

Программный код реализации метода ВПП разработан на основе пакета SSAGES 0.8.3. [33]. Моделирование этим методом выполнялось в NVT-ансамбле. Число частиц в модели N = 5324.

Метод внедрения реализован в NPT-ансамбле. Число частиц жидкой фазы составляло от 32 000 до 100 000. Внедряемые кластеры содержали от 150 до 10 000 частиц. При заданной температуре вероятность роста кластера определялась по 200 МД-запускам.

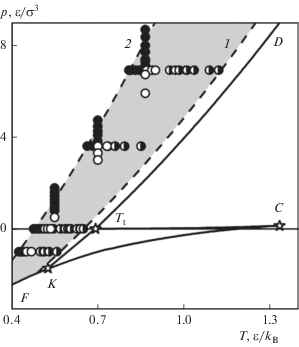
Область исследованных параметров состояния представлена на фазовой диаграмме ЛД-системы, где показаны линия плавления, спинодаль растянутой (перегретой) жидкости, а также характерные точки – тройная, критическая и конечная точка линии плавления (рис. 1).

Рис. 1.

Фазовая диаграмма ЛД-системы: DK – линия плавления, CF – спинодаль растянутой жидкости, C – критическая точка, ${{T}_{t}}$ – тройная точка, K – конечная точка линии плавления. Темные точки – метод СВЖ, светлые – ВПП, черно-белые – внедрения. Штриховые линии – линии достижимого переохлаждения, отвечающие частоте нуклеации J = 10–200 (1) и J = 10–6 (2).

Рассчитанные методами СВЖ и ВПП температурные зависимости частоты кристаллизации переохлажденной ЛД-жидкости при четырех значениях давления показаны на рис. 2. Там же приведены данные метода внедрения кластера. В этом случае частота зародышеобразования рассчитывалась по уравнению (4) с использованием значений работы образования критического зародыша, полученных в ходе моделирования.

Рис. 2.

Температурная зависимость логарифма частоты кристаллизации переохлажденной ЛД-жидкости при p = 6.912 (1), 3.6 (2), 0.0 (3), –0.995 (4). Темные точки – метод СВЖ, светлые – ВПП, черно-белые – внедрения. Сплошные линии – аппроксимирующие кривые, штриховые – КТЗ.

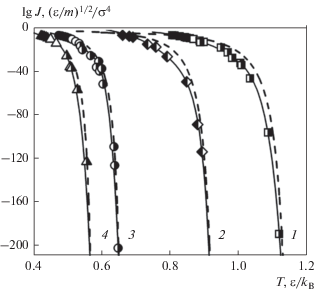
Рис. 3 иллюстрирует барическую зависимость частоты зародышеобразования при трех фиксированных значениях температуры.

Рис. 3.

Частота кристаллизации переохлажденной ЛД-жидкости как функция давления в жидкости при $T = 0.865$ (1), 0.7 (2), 0.55 (3). Темные точки – метод СВЖ [20], светлые – ВПП. Сплошные линии – аппроксимирующие кривые, штриховые – КТЗ.

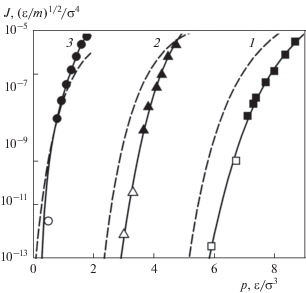
На рис. 2 и 3 данные МД-моделирования сопоставляются с расчетами по КТЗ (уравнение (4)) в макроскопическом приближении (${{\gamma }_{e}} = {{\gamma }_{\infty }}$), т.е. без учета зависимости эффективной свободной поверхностной энергии от размера зародыша. Использованы значения ${{\gamma }_{\infty }}$ из работы [34]. Методика МД-расчетов предэкспоненциального множителя (коэффициент диффузии зародышей ${{D}_{*}},$ неравновесный фактор Зельдовича ${{Z}_{*}}$) подробно описана в наших работах [35, 36]. Как следует из рис. 2 и 3, при высоких значениях температуры, давления и частоты зародышеобразования имеет место существенное рассогласование (до 5 порядков по J) между данными МД-моделирования и КТЗ.

5. ЗАВИСИМОСТЬ ЭФФЕКТИВНОЙ СВОБОДНОЙ ПОВЕРХНОСТНОЙ ЭНЕРГИИ КРИСТАЛЛИЧЕСКИХ ЗАРОДЫШЕЙ ОТ РАДИУСА КРИВИЗНЫ ПОВЕРХНОСТИ РАЗРЫВА

Результаты МД-моделирования спонтанной кристаллизации переохлажденной ЛД-жидкости позволяют оценить эффективную свободную поверхностную энергию кристаллических зародышей. В методах СВЖ и ВПП из уравнения (4) по данным о частоте зародышеобразования определялась работа образования кристаллического зародыша. Далее из условия вещественного равновесия зародыш–жидкость с использованием уравнений состояния жидкой и кристаллической фаз [37, 38] находились давление ${{p}_{*}}$ и плотность ${{\rho }_{*}}$ в критическом зародыше, из уравнения (3) – эффективная свободная поверхностная энергия ${{\gamma }_{e}}$ и радиус критического зародыша ${{R}_{*}}.$ В методе ВПП значения ${{\gamma }_{e}}$ могли быть также получены привлечением данных о числе частиц в критическом кластере ${{n}_{*}}.$

В методе внедрения зависимость ${{\gamma }_{e}}$ от кривизны поверхности разрыва определялась из условия механического равновесия по данным о числе частиц в критическом зародыше и давлении внутри него.

Эффективная свободная поверхностная энергия критических зародышей кристаллической фазы как функция кривизны поверхности разрыва при условии постоянства давления в жидкой фазе или температуры представлена, соответственно, на рис. 4 и 5. Сплошные линии – результат аппроксимации этих данных уравнением (9). Полученные при аппроксимации параметры этого уравнения приводятся на рис. 6.

Рис. 4.

Эффективная свободная поверхностная энергия кристаллических зародышей как функция кривизны поверхности разрыва при давлении в жидкости p = 6.912 (1), 3.6 (2), 0.0 (3), –0.995 (4). Темные точки – метод СВЖ, светлые – ВПП, черно-белые – внедрения. Сплошные линии – аппроксимирующие кривые, штриховые – эффективная свободная поверхностная энергия на плоской межфазной границе, отвечающая температуре, при которой кристаллический кластер данного размера является критическим зародышем [10].

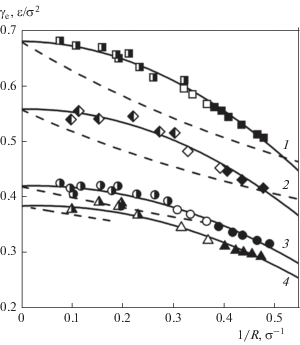
Рис. 5.

Эффективная свободная поверхностная энергия кристаллических зародышей как функция кривизны поверхности разрыва при $T = 0.865$ (1), 0.7 (2), 0.55 (3). Темные точки – метод СВЖ [20], светлые – ВПП. Сплошные линии – аппроксимирующие кривые, штриховые – эффективная свободная поверхностная энергия на плоской межфазной границе при заданных температурах [10].

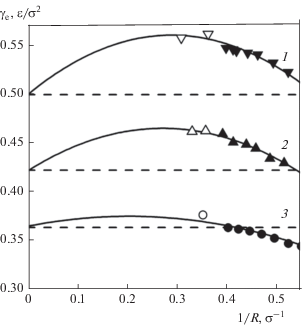
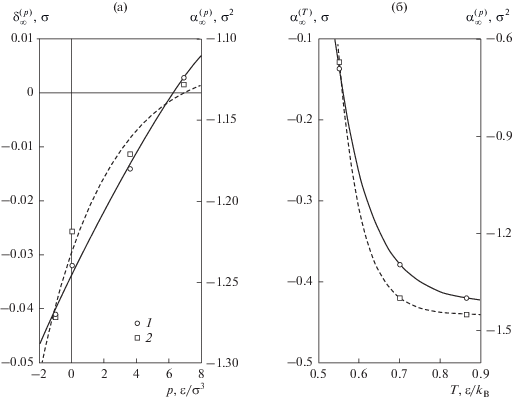
Рис. 6.

Барическая (а) и температурная (б) зависимости параметров уравнения (9) ${{\delta }_{\infty }}$ (1) и ${{\alpha }_{\infty }}$ (2).

При p < 6 искривление межфазной границы кристалл–жидкость в условиях постоянства давления в жидкой фазе сопровождается незначительным повышением ${{\gamma }_{e}},$ которое затем быстро сменяется его снижением. На рис. 4 штриховыми линиями показаны значения эффективной свободной поверхностной энергии на плоской межфазной границе, отвечающие температуре, при которой кристаллический кластер данного размера является критическим зародышем. С увеличением переохлаждения жидкости (с понижением R) рост расхождения между ${{\gamma }_{e}}(R)$ и ${{\gamma }_{\infty }}$ сменяется его снижением. В области низких давлений (p = 0.0 и –0.995) величина ${{\gamma }_{\infty }}$ определена только при значениях температуры выше температуры конечной точки линии плавления ${{T}_{K}}$ = 0.529 [39]. Однако это не исключает существования свободной поверхностной энергии на искривленной поверхности разрыва и при $T < {{T}_{K}}.$

В изотермических условиях (рис. 5) увеличение кривизны поверхности разрыва сопровождается более резким возрастанием эффективной свободной поверхностной энергии, чем в изобарических. Наличие максимума на зависимости ${{\gamma }_{e}}(R)$ характерно для всех исследованных температур. Рост температуры приводит к увеличению рассогласований в значениях ${{\gamma }_{e}}(R)$ и ${{\gamma }_{\infty }}$ в области средних радиусов кривизны зародышей. По мере понижения температуры максимум на зависимости ${{\gamma }_{e}}({1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R})$ перемещается в область больших радиусов кривизны поверхности разрыва, расхождения между ${{\gamma }_{e}}(R)$ и ${{\gamma }_{\infty }}$ уменьшаются и при R < 2.5 (T = 0.55) значения ${{\gamma }_{e}}(R)$ становятся меньше, чем на плоской межфазной границе.

6. ЗАКЛЮЧЕНИЕ

В данной работе мы представили результаты МД-моделирования спонтанной кристаллизации переохлажденной ЛД-жидкости. Методами СВЖ, ВПП и внедрения рассчитаны основные характеристики процесса зародышеобразования: частота зародышеобразования, размер критического зародыша, коэффициент диффузии зародышей в пространстве их размеров и т.д. Расчеты проведены в широких интервалах температуры и давления, включая его отрицательные значения, по нескольким изотермам и изобарам. Сопоставление полученных данных с КТЗ в макроскопическом приближении, т.е. без учета зависимости свободной поверхностной энергии кристаллических зародышей от их размера, выявило систематическое расхождение результатов теории и моделирования. В предположении, что выявленные рассогласования связаны с кривизной поверхности разрыва зародыш–жидкость, из КТЗ по данным моделирования определена эффективная свободная поверхностная энергия кристаллических зародышей критического размера. Установлено, что при постоянстве как температуры, так и давления в жидкой фазе (если p < 6) рост кривизны поверхности разрыва сопровождается ростом эффективной свободной поверхностной энергии кристаллических зародышей. В изобарическом процессе это возрастание примерно на порядок меньше, чем в изотермических условиях. При больших переохлаждениях (пересжатиях) рост эффективной свободной поверхностной энергии сменяется ее снижением, и вблизи значений температуры, близких к температуре конечной точки линии плавления (отрицательные давления), ${{\gamma }_{e}}(R) < {{\gamma }_{\infty }}.$

Список литературы

  1. Volmer M., Weber A. // Z. Phys. Chem. 1926. Bd. A119. № 1. C. 277.

  2. Зельдович Я.Б. // ЖЭТФ. 1942. Т. 12. С. 525.

  3. Turnbull D., Fisher J.C. // J. Chem. Phys. 1949. V. 17. P. 71.

  4. Скрипов В.П., Коверда В.П. Спонтанная кристаллизация переохлажденных жидкостей. М.: Наука, 1984.

  5. Tolman R.C. // J. Chem. Phys. 1948. V. 16. P. 758.

  6. Fisher M.P.A., Wortis M. // Phys. Rev. B. 1984. V. 29. P. 6252.

  7. Block B.J., Das S.K., Oettel M., Virnau P., Binder K. // J. Chem. Phys. 2010. V. 133. 154702.

  8. Байдаков В.Г., Скрипов В.П. // ЖФХ. 1982. Т. 56. С. 818.

  9. Baidakov V.G., Boltachev G.Sh. // J. Chem. Phys. 2004. V. 121. 17. P. 8594.

  10. Русанов А.И. Фазовые равновесия и поверхностные явления. Л.: Химия, 1967.

  11. Irving J.H., Kirkwood J.G. // J. Chem. Phys. 1950. V. 18. P. 817.

  12. Blokhuis E.M., Bedeaux D. // J. Chem. Phys. 1992. V. 97. P. 3576.

  13. Cheng B., Ceriotti M. // J. Chem. Phys. 2018. V. 148. 231102.

  14. Schmelzer J.W.P., Abyzov A.S., Ferreira E.B., Fokin V.M. // Int. J. Appl. Glass Sci. 2019. V. 10. № 1. P. 57.

  15. Ландау Л.Д. О равновесной форме кристаллов. Собрание трудов. Т. 2. М.: Наука, 1969. С. 119.

  16. Herring C. // Phys. Rev. 1951. V. 82. 1. P. 87.

  17. Koß P., Statt A., Virnau P., Binder K. // Phys. Rev. E. 2014. V. 96. 042609.

  18. Гиббс Дж. В. Термодинамические работы. М.-Л.: Гостехиздат, 1950.

  19. Байдаков В.Г., Болтачев Г.Ш. // Журн. физ. химии. 1995. Т. 69. С. 515.

  20. Baidakov V.G., Boltachev G.Sh. // Phys. Rev. E. 1999. V. 59. P. 469.

  21. Baidakov V.G., Boltachev G.Sh., Chernykh G.G. // Phys. Rev. E. 2004. V. 70. P. 011603.

  22. Скрипов В.П. Метастабильная жидкость. М.: Наука, 1972.

  23. Bolhuis P.G., Chandler D., Dellago C., Geissker P.L. // Ann. Rev. Phys. Chem. 2002. V. 53. P. 291.

  24. Van Erp T.S., Moroni D., Bolhuis P.G. // J. Chem. Phys. 2003. V. 118. P. 7762.

  25. Allen R.J., Valeriani C., ten Wolde P.R. // J. Phys.: Condens. Matter. 2009. V. 21. 463102.

  26. Espinosa J.R., Vega C., Valeriani C., Sanz E. // J. Chem. Phys. 2015. V. 142. 194709.

  27. Espinosa J.R., Vega C., Valeriani C., Sanz E. // J. Chem. Phys. 2016. V. 144. 034501.

  28. ten Wolde P.R., Ruiz-Montero M.J., Frenkel D. // J. Chem. Phys. 1996. V. 104. P. 9932.

  29. Lechner W., Dellago C. // J. Chem. Phys. 2008. V. 129. 114707.

  30. Plimpton S. // J. Comp. Phys. 1995. V. 117. P. 1.

  31. Bussi G., Donadio D., Parrinello M. // J. Chem. Phys. 2007. V. 126. 014101.

  32. Verlet L. // Phys. Rev. 1967. V. 159. P. 98.

  33. Sidky H., Colón Y.J., Helfferich J. et al. // J. Chem. Phys. 2018. V. 148. 044104.

  34. Baidakov V.G., Protsenko S.P., Tipeev A.O. // J. Chem. Phys. 2013. V. 139. P. 224703.

  35. Байдаков В.Г., Проценко С.П. // Докл. АН. 2004. Т. 394. С. 752.

  36. Baidakov V.G., Tipeev A.O. // J. Chem. Phys. 2012. V. 136. 074510.

  37. Байдаков В.Г., Проценко С.П. // ЖЭТФ. 2006. Т. 103. С. 1014.

  38. Болтачев Г.Ш., Байдаков В.Г. // ТВТ. 2003. Т. 41. С. 314.

  39. Baidakov V.G., Protsenko S.P. // Phys. Rev. Lett. 2005. V. 95. 015701.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал