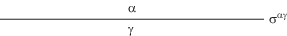Коллоидный журнал, 2020, T. 82, № 1, стр. 66-74

К термодинамике тонких пленок. J-потенциал

А. И. Русанов^*

Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия

^* E-mail: airusanov@mail.ru

Поступила в редакцию 17.06.2019
После доработки 28.06.2019
Принята к публикации 02.07.2019

DOI: 10.31857/S0023291220010139

Полный текст (PDF)

Аннотация

Работа знакомит читателя с современным аппаратом химической термодинамики в науке о поверхностях и коллоидах. Новой величиной является J-потенциал, символизирующий целую серию термодинамических потенциалов и определяемый для флюидных систем как большой термодинамический потенциал в сумме с произведением объема системы на некое давление $p{\kern 1pt} '.$ Дана классификация с выделением классического J-потенциала (когда $p{\kern 1pt} '$ – внешнее давление) и специальных J-потенциалов ( при других значениях $p{\kern 1pt} '$). Для обоих классов рассмотрены гибридные виды потенциалов, когда для одной группы компонентов в качестве переменных выбираются химические потенциалы, а для другой – число молекул или молей. Основное внимание уделено приложению всех рассмотренных видов J-потенциала к системе при наличии в ней плоской тонкой пленки. В частности, проанализирован случай, когда в качестве $p{\kern 1pt} '$ фигурирует давление в материнской фазе тонкой пленки. Результирующие фундаментальные уравнения сформулированы в терминах расклинивающего давления.

ВВЕДЕНИЕ

Из двух составляющих термодинамики – тепла и работы – последняя несравненно сложнее и разнообразнее в описании, а потому можно сказать, что тип термодинамики определяется, прежде всего, тем, как рассчитывается работа. Термодинамика Гиббса отличается от предыдущих методов тем, что работа вычисляется с помощью термодинамических потенциалов – специальных термодинамических функций с размерностью энергии, изменение которых в заданных внешних условиях и определяет работу. Еще более крупным шагом было развитие Гиббсом, помимо тепла и работы, химической составляющей термодинамики, символизируемой химическим потенциалом. Тем самым была создана химическая термодинамика, в рамках которой мы и работаем.

Вначале термодинамические потенциалы формулировались для гомогенных (однофазных) систем. Это, например, энергия

(1)

$U = TS - pV + \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$

свободная энергия

(2)

$F \equiv U - TS = - pV + \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$

большой термодинамический потенциал

(3)

$\Omega \equiv F - \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} = - pV$

и энергия Гиббса

(4)

$G \equiv F + pV = \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$

где T – температура, S – энтропия, p – внешнее давление, V – объем, ${{\mu }_{i}}$ и ${{N}_{i}}$ – химический потенциал и число молекул (или молей) компонента i. Термодинамические потенциалы (1)–(4) особенно популярны в термодинамике растворов.

Нужно также отметить гибридный термодинамический потенциал

(5)

$\tilde {\Omega } \equiv F - \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} = - pV + \sum\limits_j {{{\mu }_{j}}{{N}_{j}}} ,$

где суммирование по i распространяется не на все компоненты системы.

Впервые такой потенциал был введен в термодинамике твердого тела [1], где под i понимались подвижные, а под j – неподвижные компоненты твердого тела. Но в общем случае разбиение компонентов на группы i и j может быть совершенно произвольным, и именно так нужно понимать гибридный потенциал (5). Тогда можно сказать, что для компонентов группы i потенциал $\tilde {\Omega }$ играет роль большого термодинамического потенциала, а для компонентов группы j – роль свободной энергии.

Мы заметили, что при переходе к большому термодинамическому потенциалу от свободной энергии отнимается сумма с химическими потенциалами, а при переходе к энергии Гиббса – член –pV. А что, если отнять и то и другое? Для обычного (не гибридного) потенциала будет нуль, и все потеряет смысл. Да, но это так только для гомогенной системы. В коллоидной науке мы имеем дело со сложными гетерогенными системами при наличии ряда фаз, межфазных поверхностей и линий, а потому введение нового термодинамического потенциала может оказаться полезным. Эта идея была реализована автором [2, 3]. Новый термодинамический потенциал пока не имеет названия, но для его обозначения использовалась буква J (это логично, ибо, если вспомнить и частое обозначение энергии E и энтальпию H, термодинамические потенциалы, в основном, обозначаются буквами в начале латинского алфавита). Для краткости его можно называть “J-потенциал (джей-потенциал)”.

Самое общее определение J-потенциала с учетом того, что система может содержать твердые фазы под произвольным внешним нагружением, имеет вид [2, 3]

(6)

$J \equiv \Omega - \oint\limits_{(A)} {({\mathbf{P}} \cdot {\mathbf{u}})dA} ,$

где P – внешняя сила (напряжение) на единицу площади поверхности системы как функция положения на поверхности (A), u – локальный вектор смещения поверхности и A – площадь поверхности; интегрирование производится по всей поверхности системы. Если система окружена флюидной средой и единственным механическим воздействием является внешнее давление p, то определение J-потенциала можно упростить до [3]

(7)

$J \equiv \Omega + pV,$

где V – объем всей системы (ревнителям строгости напомним, что любой термодинамический потенциал определяется с точностью до постоянной). Согласно (3), для гомогенной системы определение (7) действительно приводит к нулю, но мы-то будем оперировать со сложными системами. Некая апробация J-потенциала уже состоялась в [3], где он весьма эффектно упростил вывод классических уравнений Неймана (для механического поверхностного натяжения) и Юнга (для термодинамического поверхностного натяжения).

В этом сообщении мы хотели бы инкорпорировать J-потенциал в термодинамику тонких пленок, но прежде чем сделать это, обобщим определение J-потенциала (7) к виду

(8)

$J \equiv \Omega + p{\kern 1pt} 'V,$

где $p{\kern 1pt} '$ – некоторое выбранное давление. Это может быть внешнее давление по отношению к гетерогенной системе в целом, давление в одной из фаз гетерогенной системы или любое другое давление. В варианте (8) термин J-потенциал уже обозначает целую серию потенциалов определенного типа. В классическом подходе, как при переходе к энергии Гиббса, $p{\kern 1pt} '$ полагается равным внешнему давлению $(p{\kern 1pt} ' = p).$ Для краткости мы будем называть этот тип J-потенциала классическим (обозначение ${{J}_{\operatorname{c} }}),$ а все другие типы, происходящие от выражения (8), – специальными J-потенциалами (обозначение ${{J}_{\operatorname{s} }}).$ Теперь мы можем сказать, что введенное в [3] определение (7) относится лишь к классическому J-потенциалу, а определение (8) включает в себя и специальные J-потенциалы.

Термодинамика тонких пленок – относительно новый раздел химической термодинамики, выходящий за рамки гиббсовской термодинамики и сформулированный ближе к середине 20 в. [4–9] (современный обзор см. в [10, 11]). Спецификой тонкой пленки является наличие расклинивающего давления [12]

(9)

$\Pi \equiv {{p}^{\alpha }} - {{p}^{\beta }},$

где ${{p}^{\alpha }}$ – внешнее давление на пленку, а ${{p}^{\beta }}$ – давление в равновесной материнской объемной фазе β тонкой пленки. Фаза β может находиться в равновесии с пленкой при контакте с ее торцом, но реальное присутствие фазы β не обязательно (${{p}^{\beta }}$ может быть расчетным значением давления для фазы β при тех же значениях температуры и химических потенциалов, какие есть в пленке). Открытие расклинивающего давления и его последующие исследования школой Дерягина подробно описаны в монографии [13].

ОБЩИЕ СООТНОШЕНИЯ ДЛЯ J-ПОТЕНЦИАЛА

Хотя в теории пленок часто фигурируют твердые подложки, в термодинамике это не так важно. Для простоты будем оперировать с термодинамическим формализмом жидких фаз и пользоваться определением (8). Запишем сначала выражение для большого термодинамического потенциала применительно к произвольной многофазной многокомпонентной системе:

(10)

$\Omega = - \sum\limits_k {{{p}^{k}}} {{V}^{k}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$

где k – номер фазы с давлением ${{p}^{k}}$ и объемом ${{V}^{k}},$ s – номер поверхности с поверхностным натяжением ${{\sigma }^{s}}$ и площадью ${{A}^{s}}$ и t – номер линии с линейным натяжением ${{\kappa }^{t}}$ и длиной ${{L}^{t}}.$ Запишем теперь дифференциальное фундаментальное уравнение для большого термодинамического потенциала. В простейшем случае гомогенной системы для большого потенциала (3) пишут

(11)

$d\Omega = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - pdV.$

Но мы рассматриваем сложную гетерогенную систему. При равновесии температура и химические потенциалы во всех частях системы одинаковы, какой бы сложной система ни была. Поэтому первые два члена в правой части (11) сохраняются в любом случае. Давления же могут быть разными в разных частях системы, но если система равновесна, то изменение любого термодинамического потенциала за счет работы возможно лишь тогда, когда речь идет о работе внешних сил. Но тогда и третье слагаемое в правой части (11) сохраняется при условии, что под p понимается внешнее давление. Внешние силы могут также вызвать изменение площадей поверхностей и длин линий (естественно тех, которые доходят до границ системы; какие-то замкнутые поверхности или линии внутри системы могут не входить в их число), так что соответствующие члены тривиально добавятся к правой части (11). В результате дифференциальное фундаментальное уравнение для большого потенциала (10) принимает вид

(12)

$\begin{gathered} d\Omega = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - pdV + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Для полноты картины приведем заодно и фундаментальное уравнение для гибридного потенциала $\tilde {\Omega }{\text{:}}$

(13)

$\begin{gathered} d\tilde {\Omega } = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} - \\ - \,\,pdV + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Найдем теперь фундаментальные уравнения для J-потенциала. Используя определение (8) с учетом очевидного условия

(14)

$V = \sum\limits_k {{{V}^{k}}} ,$

из (10) и (12) получаем

(15)

$J = - \sum\limits_k {({{p}^{k}} - p{\kern 1pt} '){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$

(16)

$\begin{gathered} dJ = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - (p - p{\kern 1pt} ')dV + Vdp{\kern 1pt} '\,\, + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Напомним, что величина р в уравнении (16) – это внешнее давление. Если $p{\kern 1pt} '$ – тоже внешнее давление (случай классического J-потенциала), то уравнения (15) и (16) преобразуются к виду

(17)

${{J}_{\operatorname{c} }} = - \sum\limits_k {({{p}^{k}} - p){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$

(18)

$\begin{gathered} d{{J}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + Vdp + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Уравнение (18) можно упростить. Для этого в правой части (18), используя вновь (14), прибавим и отнимем выражение $\sum\nolimits_k {{{V}^{k}}d{{p}^{k}}} $ и вспомним, что для каждой объемной фазы работает уравнение Гиббса–Дюгема

(19)

$ - {{S}^{k}}dT - \sum\limits_i {N_{i}^{k}d{{\mu }_{i}}} + {{V}^{k}}d{{p}^{k}} = 0,$

которое уничтожает составляющие первых двух слагаемых в правой части (18), относящиеся к объемным фазам. Тогда уравнение (18) принимает вид

(20)

$\begin{gathered} d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + \sum\limits_k {{{V}^{k}}d(p - {{p}^{k}})} + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

где чертой отмечены избыточные величины, относящиеся к поверхностям и линиям. Можно сказать, что уравнение (20) для классического J-потенциала просто напрашивается к использованию в термодинамике поверхностей.

По аналогии с (8) можем определить гибридный J-потенциал через гибридный большой термодинамический потенциал $\tilde {\Omega }$ как

(21)

$\tilde {J} \equiv \tilde {\Omega } + p{\kern 1pt} 'V$

и записать фундаментальные уравнения

(22)

$\begin{gathered} \tilde {J} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - p{\kern 1pt} '){{V}^{k}}} + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $

(23)

$\begin{gathered} d\tilde {J} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} - \\ - \,\,(p - p{\kern 1pt} ')dV + Vdp{\kern 1pt} '\, + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Здесь также можно различать классический гибридный J-потенциал (при $p{\kern 1pt} ' = p$) и специальные гибридные J-потенциалы. Для классического гибридного J-потенциала фундаментальные уравнения (22) и (23) упрощаются к виду

(24)

$\begin{gathered} {{{\tilde {J}}}_{\operatorname{c} }} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - p){{V}^{k}}} + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $

(25)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d{{N}_{j}}} + \\ + \,\,Vdp + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Что касается специальных гибридных J-потенциалов, то для каждого из них уравнения (22) и (23) видоизменяются в соответствии с выбором давления $p{\kern 1pt} '.$

КЛАССИЧЕСКИЙ J-ПОТЕНЦИАЛ СИСТЕМЫ С ТОНКОЙ ПЛЕНКОЙ

Будем считать, что тонкая пленка располагается между фазами α и γ (обозначение β сбережем для материнской фазы пленки). Как межфазную границу αγ, так и находящуюся на ней тонкую пленку будем предполагать плоскими. Посмотрим, как классический J-потенциал такого объекта выглядит в различных подходах.

Стандартный подход Гиббса

Гиббсовская термодинамика не выделяет тонкую пленку как отдельный объект и учитывает ее как любую другую часть межфазной поверхности. Для двухфазной системы α–γ, содержащей тонкую пленку (рис. 1), J-потенциал формируется на основе уравнения (17) следующим образом. Индекс k принимает значения α и γ, причем ${{p}^{\alpha }} = {{p}^{\gamma }},$ так как единственная присутствующая в системе поверхность плоская. Очевидно, в этом случае ${{p}^{\alpha }}$ играет роль внешнего давления и, значит, равно р, но тогда весь первый член в правой части (17) исчезает. Линий в нашей системе нет, а поверхность одна, и согласно (17), можем теперь записать

(26)

${{J}_{\operatorname{c} }} = {{\sigma }^{{\alpha \gamma }}}{{A}^{{\alpha \gamma }}},$

или (поскольку площади параллельных разделяющих поверхностей одинаковы, индекс площади можно опустить)

(27)

${{j}_{\operatorname{c} }} \equiv {{{{J}_{\operatorname{c} }}} \mathord{\left/ {\vphantom {{{{J}_{\operatorname{c} }}} A}} \right. \kern-0em} A} = {{\sigma }^{{\alpha \gamma }}},$

где ${{j}_{\operatorname{c} }}$ – поверхностная плотность классического J-потенциала.

Рис. 1.

Фазы, разделяющая поверхность и поверхностное натяжение в методе Гиббса.

С другой стороны, согласно (20),

(28)

$d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + {{\sigma }^{{\alpha \gamma }}}dA.$

Из (26) и (28) сразу следует уравнение адсорбции Гиббса

(29)

$Ad{{\sigma }^{{\alpha \gamma }}} = - {{\bar {S}}^{{\alpha \gamma }}}dT - \sum\limits_i {\bar {N}_{i}^{{\alpha \gamma }}d{{\mu }_{i}}} $

или

(30)

$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {s}}^{{\alpha \gamma }}}dT - \sum\limits_i {\Gamma _{i}^{{\alpha \gamma }}d{{\mu }_{i}}} ,$

где $\bar {s} \equiv {{\bar {S}} \mathord{\left/ {\vphantom {{\bar {S}} A}} \right. \kern-0em} A}$ – избыток энтропии на единицу поверхности и ${{\Gamma }_{i}} \equiv {{{{{\bar {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\bar {N}}}_{i}}} A}} \right. \kern-0em} A}$ – абсолютная адсорбция компонента i. Поскольку избыточные величины зависят от выбора положения разделяющей поверхности, уравнение (29) рассматривается совместно с уравнениями Гиббса–Дюгема (19) для примыкающих к поверхности фаз. Путем исключения одного из химических потенциалов ${{\mu }_{j}}$ коэффициенты при dT и $d{{\mu }_{i}}$ переходят в некоторую комбинацию величин, инвариантную к перемещению разделяющей поверхности и обозначаемую как ${{s}_{{(j)}}}$ и ${{\Gamma }_{{i(j)}}}$ соответственно. Величина ${{\Gamma }_{{i(j)}}}$ называется относительной адсорбцией компонента i (относительно компонента j) и не зависит от положения разделяющей поверхности. Численно же ${{\Gamma }_{{i(j)}}}$ равна абсолютной адсорбции ${{\Gamma }_{i}}$ для такого положения разделяющей поверхности, где выполняется условие ${{\Gamma }_{j}} = 0.$ Переход от абсолютных к относительным адсорбциям – азы гиббсовской термодинамики поверхностей, это путь превращения уравнения адсорбции Гиббса (30) в реальное физическое соотношение

(31)

$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}_{{(j)}}^{{\alpha \gamma }}dT - \sum\limits_i {\Gamma _{{i(j)}}^{{\alpha \gamma }}d{{\mu }_{i}}} ,$

которое также именуется уравнением адсорбции Гиббса. В выражениях (26) и (28) не просматривается связь с тонкой пленкой, вся она скрыта в величине ${{\sigma }^{{\alpha \gamma }}}.$ Например, какие-то слагаемые уравнения адсорбции Гиббса для ${{\sigma }^{{\alpha \gamma }}}$ могут относиться к компонентам тонкой пленки.

Метод Гиббса с двумя разделяющими поверхностями

Чтобы сделать тонкую пленку явным объектом межфазной поверхности, необходимо введение двух разделяющих поверхностей [8–10]. Такой подход идет от представления о существовании некоей третьей объемной фазы (материнской фазы пленки β), утончением которой и образована тонкая пленка. Реальная или воображаемая фаза β должна быть обязательно в равновесии с тонкой пленкой (т.е. иметь одни и те же значения температуры и химических потенциалов), и отсюда ясно, что определение расклинивающего давления (9) носит термодинамический характер, хоть и включает только механические величины. Гиббсовские избытки берутся теперь следующим образом. Пространство между двумя параллельными разделяющими поверхностями мысленно заполняем фазой β, переходя таким путем к трехфазной системе с разделяющими поверхностями αβ и βγ (рис. 2). Избытки для разделяющей поверхности αβ берутся со стороны фаз α и β, а для поверхности βγ – со стороны фаз β и γ. Существенно, что в случае тонкой пленки избытки (например, адсорбции) по обеим сторонам фазы β не являются независимыми и должны рассматриваться совместно. Это, в частности, касается и поверхностных натяжений ${{\sigma }^{\alpha }}$ (между фазами α и β) и ${{\sigma }^{\gamma }}$ (между фазами γ и β), показанных на рис. 2.

Рис. 2.

Расположение фаз и поверхностные натяжения в методе двух разделяющих поверхностей, отстоящих на расстоянии H друг от друга.

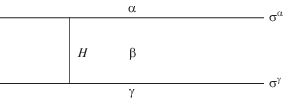
Теперь, в соответствии с (17), составим выражение для J-потенциала. Очевидно, не имеет значения, какую из фаз, α или γ, считать внешней, ибо обе они имеют одно и то же давление ${{p}^{\alpha }},$ которое и является внешним давлением p. Тогда объемные члены для фаз α и γ из выражения (17) исчезают, и остается только один член, относящийся к фазе β. Поверхностных же членов будет, наоборот, два, ибо теперь у нас две разделяющих поверхности. В результате из выражения (17) имеем

(32)

${{J}_{{\text{c}}}} = - ({{p}^{\beta }} - {{p}^{\alpha }}){{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A$

или, после использования определения расклинивающего давления (9),

(33)

${{J}_{{\text{c}}}} = \Pi {{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A.$

Из (33) находим выражение для поверхностной плотности J-потенциала:

(34)

${{j}_{\operatorname{c} }} = \Pi H + {{\sigma }^{\alpha }} + {{\sigma }^{\gamma }},$

где $H \equiv {{{{V}^{\beta }}} \mathord{\left/ {\vphantom {{{{V}^{\beta }}} A}} \right. \kern-0em} A}$ – расстояние между разделяющими поверхностями, которое после уточнений можно понимать как толщину тонкой пленки.

Сравнивая (26) и (34), приходим к соотношению

(35)

${{\sigma }^{{\alpha \gamma }}} = {{\sigma }^{\alpha }} + {{\sigma }^{\gamma }} + \Pi H,$

известному в термодинамике тонких пленок со времен работ [4–8] и полученному там другим путем. При $H \to \infty $ расклинивающее давление быстрее стремится к нулю, обращая в нуль и произведение $\Pi H,$ так что правая часть (34) и (35) переходит в сумму уже независимых поверхностных натяжений ${{\sigma }^{{\alpha \beta }}}$ и ${{\sigma }^{{\beta \gamma }}},$ а тонкая пленка превращается в толстую. Этот важный результат запишем как

(36)

${{\left. {{{j}_{\operatorname{c} }}} \right|}_{{H \to \infty }}} = {{\left. {{{\sigma }^{{\alpha \gamma }}}} \right|}_{{H \to \infty }}} = {{\sigma }^{{\alpha \beta }}} + {{\sigma }^{{\beta \gamma }}}.$

Обратимся теперь к дифференциальному фундаментальному уравнению для классического J-потенциала. Снова полагая $p \equiv {{p}^{\alpha }}$ и учитывая наличие двух поверхностей и отсутствие линий, из уравнения (20) находим

(37)

$\begin{gathered} d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + \\ + \,\,{{V}^{\beta }}d({{p}^{\alpha }} - {{p}^{\beta }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA \\ \end{gathered} $

или, с учетом определения расклинивающего давления (9),

(38)

$d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + {{V}^{\beta }}d\Pi + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA.$

Сравнивая теперь (33) и (38), получаем уравнение адсорбции Гиббса в виде

(39)

$Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }},$

где $\bar {S} \equiv {{\bar {S}}^{\alpha }} + {{\bar {S}}^{\gamma }}$ и ${{\bar {N}}_{i}} \equiv \bar {N}_{i}^{\alpha } + \bar {N}_{i}^{\gamma }.$ После деления на А уравнение (39) принимает форму [10]

(40)

$d({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {s}dT - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} - \Pi dH$

или, если использовать (35) [11],

(41)

$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} + Hd\Pi .$

После стандартной операции перехода от абсолютных к относительным адсорбциям уравнения (40) и (41) принимают вид [10, 11]

(42)

$d({{\sigma }^{\beta }} + {{\sigma }^{\gamma }}) = - {{\bar {s}}_{{(j)}}}dT - \Pi d{{H}_{{(j)}}} - \sum\limits_{i \ne j} {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} ,$

(43)

$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {s}}_{{(j)}}}dT - \sum\limits_i {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} + {{H}_{{(j)}}}d\Pi .$

Смысл величин, стоящих в уравнениях (42) и (43), подробно обсуждался в [10], включая и ${{H}_{{(j)}}}$ как термодинамическое определение толщины тонкой пленки, связанное с переходом к относительной адсорбции и образом поверхности с нулевой адсорбцией.

ГИБРИДНЫЙ КЛАССИЧЕСКИЙ J-ПОТЕНЦИАЛ

Рассмотрим теперь использование классического J-потенциала в гибридной форме. Общая запись, которую мы использовали выше, не исключает возможность проникновения всех компонентов системы во все фазы, и это самый сложный случай для идентификации тонкой пленки. Но по существу пленки в этом случае и нет, есть лишь поверхностный слой, т.е. неоднородная переходная межфазная зона. Понятие пленки подразумевает какую-то обособленность вещества. Простейший случай – фазы α и γ ни в чем не растворимы и сами не способны что-либо растворять, т.е. полностью инертны в отношении остального вещества системы. Такие подложки неспособны к проникновению и имеют четко выраженные граничные поверхности, расстояние между которыми задает толщину тонкой пленки. Такие подложки формально можно считать однокомпонентными. Пусть компонент фазы α имеет номер m, а компонент фазы γ – номер n. Как и в предыдущем разделе, посмотрим, как выглядят фундаментальные уравнения для гибридного классического потенциала при использовании одной и двух разделяющих поверхностей.

Одна разделяющая поверхность

В этом случае из (24) и (25) имеем

(44)

${{\tilde {J}}_{\operatorname{c} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } + {{\sigma }^{{\alpha \gamma }}}A,$

(45)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + \\ + \,\,{{\mu }_{n}}dN_{n}^{\gamma } + Vd{{p}^{\alpha }} + {{\sigma }^{{\alpha \gamma }}}dA, \\ \end{gathered} $

где единственный оставшийся член со знаком суммы, очевидно, относится к компонентам тонкой пленки. Дифференцируя (44) и сравнивая с (45), приходим к уравнению

(46)

$\begin{gathered} Ad{{\sigma }^{{\alpha \gamma }}} = - SdT + Vd{{p}^{\alpha }} - N_{m}^{\alpha }d{{\mu }_{m}} - \\ - \,\,N_{n}^{\gamma }d{{\mu }_{n}} - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} , \\ \end{gathered} $

которое является аналогом уравнения адсорбции Гиббса для поверхностного слоя конечной толщины [8] (должно быть ${{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }},$ но, поскольку ${{p}^{\alpha }} = {{p}^{\gamma }}$ и, при одной разделяющей поверхности, $V = {{V}^{\alpha }} + {{V}^{\gamma }},$ это и есть $Vd{{p}^{\alpha }}$).

Для фаз α и γ действуют уравнения Гиббса–Дюгема

(47)

$\begin{gathered} {{V}^{\alpha }}d{{p}^{\alpha }} = {{S}^{\alpha }}dT + N_{m}^{\alpha }d{{\mu }_{m}}, \\ {{V}^{\gamma }}d{{p}^{\gamma }} = {{S}^{\gamma }}dT + N_{n}^{\gamma }d{{\mu }_{n}}, \\ \end{gathered} $

с учетом которых все члены для обеих объемных фаз в уравнении (46) взаимно уничтожаются. Это переводит уравнение (46) в уравнение адсорбции Гиббса

(48)

$Ad{{\sigma }^{{\alpha \gamma }}} = - \bar {S}dT - \bar {N}_{m}^{\alpha }d{{\mu }_{m}} - \bar {N}_{n}^{\gamma }d{{\mu }_{n}} - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} ,$

где черта означает избыток на данной разделяющей поверхности по отношению к фазам α и γ. Последний член остался без изменений, но это не означает, что здесь мы не перешли к избыткам. Дело в том, что компоненты тонкой пленки, отмеченные индексом i, отсутствуют в обеих фазах α и γ, а потому их реальные количества ${{N}_{i}}$ одновременно являются избытками по отношению к этим фазам.

Две разделяющие поверхности

Для этого случая (см. рис. 2) из тех же самых уравнений (24) и (25) получаем

(49)

${{\tilde {J}}_{\operatorname{c} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } + \Pi {{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$

(50)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + \\ + \,\,{{\mu }_{n}}dN_{n}^{\gamma } + Vd{{p}^{\alpha }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $

Используя определение (9), условие (14) и равенство ${{p}^{\alpha }} = {{p}^{\gamma }},$ представим

(51)

$Vd{{p}^{\alpha }} = {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + {{V}^{\beta }}d{{p}^{\beta }} + {{V}^{\beta }}d\Pi ,$

после чего уравнение (50) примет вид

(52)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } + \\ + \,\,{{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + {{V}^{\beta }}d{{p}^{\beta }} + \\ + \,\,{{V}^{\beta }}d\Pi + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $

Если теперь продифференцировать (49) и сравнить с (52), придем к уравнению

(53)

$\begin{gathered} Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \\ - \,\,N_{m}^{\alpha }d{{\mu }_{m}} - N_{n}^{\gamma }d{{\mu }_{n}} - \Pi d{{V}^{\beta }}, \\ \end{gathered} $

что представляет собой аналог уравнения адсорбции Гиббса для поверхностного слоя конечной толщины при использовании двух разделяющих поверхностей. При упрощении уравнения (53) с помощью уравнений Гиббса–Дюгема нужно принять во внимание, что к уравнениям (48) добавляется их аналог для фазы β:

(54)

${{V}^{\beta }}d{{p}^{\beta }} = {{S}^{\beta }}dT + \sum\limits_i {N_{i}^{\beta }d{{\mu }_{i}}} .$

С учетом (48) и (54) уравнение (53) преобразуется к виду

(55)

$\begin{gathered} Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - \\ - \,\,\bar {N}_{m}^{\alpha }d{{\mu }_{m}} - \bar {N}_{n}^{\gamma }d{{\mu }_{n}} - \Pi d{{V}^{\beta }}. \\ \end{gathered} $

Напомним, что в методе двух разделяющих поверхностей избытки берутся не только со стороны фаз α и γ, как в предыдущем примере, но и со стороны фазы β. Как следствие, в уравнении (55) вместо ${{N}_{i}}$ появились избыточные величины ${{\bar {N}}_{i}}.$ Само же уравнение (55) фактически совпадает с уравнением (39), где индекс i относился ко всем фазам. Поэтому все, что относилось к уравнению (39), применимо и к уравнению (55). В аналогичном положении находится уравнение (48), и, чтобы избежать повторений, обсуждение уравнений (48) и (55) в данном контексте можно закончить.

СПЕЦИАЛЬНЫЙ J-ПОТЕНЦИАЛ ТОНКОЙ ПЛЕНКИ

Вернемся к фундаментальным уравнениям (15) и (16) и положим $p{\kern 1pt} ' = {{p}^{\beta }}.$ Поскольку ${{p}^{\beta }}$ – давление в материнской фазе тонкой пленки, специфика данного выбора состоит в том, что он может относиться только к случаю существования тонкой пленки. Адресуясь к рис. 1 и 2 , по-прежнему будем считать ${{p}^{\alpha }}$ внешним давлением (p = = ${{p}^{\alpha }} = {{p}^{\gamma }}).$ Соответственно перепишем (15) и (16) как

(56)

${{J}_{\operatorname{s} }} = - \sum\limits_k {({{p}^{k}} - {{p}^{\beta }}){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$

(57)

$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - ({{p}^{\alpha }} - {{p}^{\beta }})dV + \\ + \,\,Vd{{p}^{\beta }} + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Посмотрим, как уравнения (56) и (57) выглядят в подходах с различными разделяющими поверхностями.

Одна разделяющая поверхность

На рис. 1 видно, что в данном случае имеются только две фазы (α и γ), и использование давления третьей фазы может показаться странным. Но мы уже отмечали, что фаза β может быть и воображаемой. Посмотрим все-таки, что получается. С учетом определения (9) и отсутствия линий, уравнения (56) и (57) принимают вид

(58)

${{J}_{\operatorname{s} }} = - \Pi V + {{\sigma }^{{\alpha \gamma }}}A,$

(59)

$d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi dV + Vd{{p}^{\beta }} + {{\sigma }^{{\alpha \gamma }}}dA$

(напомним, что в данном подходе $V = {{V}^{\alpha }} + {{V}^{\gamma }}$). Прибавив и отняв $Vd{{p}^{\alpha }}$ в правой части (59) и использовав уравнения Гиббса–Дюгема (47), можем упростить уравнение (59) к форме

(60)

$d{{J}_{\operatorname{s} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - d(\Pi V) + {{\sigma }^{{\alpha \gamma }}}dA.$

Теперь, дифференцируя (58) и сравнивая с (60), приходим, как и положено, к уравнению адсорбции Гиббса (29). Это говорит о правильности физического построения в данном подходе.

Две разделяющие поверхности

Теперь у нас две поверхности и три объемные фазы (рис. 2), в соответствии с чем уравнения (56) и (57) записываются в форме

(61)

${{J}_{\operatorname{s} }} = - \Pi ({{V}^{\alpha }} + {{V}^{\gamma }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$

(62)

$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi dV + \\ + \,\,Vd{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA, \\ \end{gathered} $

где $V = {{V}^{\alpha }} + {{V}^{\gamma }} + {{V}^{\beta }}.$ С учетом этого соотношения и определения (9) можно представить (62) в виде

(63)

$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }} - \\ - \,\,d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + \\ + \,\,{{V}^{\beta }}d{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $

Включая теперь уравнения Гиббса–Дюгема (47) и (54), сократим (63) до

(64)

$\begin{gathered} d{{J}_{\operatorname{s} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }} - \\ - \,\,d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $

Наконец, дифференцируя (61) и сравнивая с (64), получаем уже рассмотренный выше вариант уравнения адсорбции Гиббса (39), что освобождает нас от продолжения изложения в данном подходе.

ГИБРИДНЫЙ СПЕЦИАЛЬНЫЙ J-ПОТЕНЦИАЛ ТОНКОЙ ПЛЕНКИ

Вернемся к общим фундаментальным уравнениям для гибридного J-потенциала (22) и (23) и применим их к гибридному специальному J-потенциалу при $p = {{p}^{\alpha }} = {{p}^{\gamma }}$ и $p{\kern 1pt} ' = {{p}^{\beta }}{\text{:}}$

(65)

$\begin{gathered} {{{\tilde {J}}}_{\operatorname{s} }} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - {{p}^{\beta }}){{V}^{k}}} + \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $

(66)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} - \\ - \,\,\Pi dV + Vd{{p}^{\beta }} + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $

Как и в случае гибридного классического J-потенциала, используем иллюстративный пример

(67)

$\sum\limits_j {{{\mu }_{j}}{{N}_{j}}} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma },$

когда фазы α и γ нерастворимы, непроницаемы и формально считаются однокомпонентными. Посмотрим теперь, как преображаются уравнения (65) и (66) в подходах с одной и двумя разделяющими поверхностями.

Одна разделяющая поверхность

Учитывая определение (9), условие (67) и наличие только двух фаз ($V = {{V}^{\alpha }} + {{V}^{\gamma }}),$ имеем

(68)

${{\tilde {J}}_{\operatorname{s} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } - \Pi V + {{\sigma }^{{\alpha \gamma }}}A,$

(69)

Уравнение (69) удобно преобразовать, прибавив и отняв в правой части $Vd{{p}^{\alpha }}$ и применив определение расклинивающего давления (9):

(70)

Дифференцируя теперь (68) и сравнивая с (70), приходим к аналогу уравнения адсорбции Гиббса для поверхностного слоя конечной толщины [8], записанному выше в форме (46). Дальнейшие манипуляции с привлечением уравнений Гиббса–Дюгема приводят уравнение (46) к традиционному уравнению адсорбции Гиббса.

Две разделяющие поверхности

В этом случае ($V = {{V}^{\alpha }} + {{V}^{\gamma }} + {{V}^{\beta }}$) уравнения (65) и (66) принимают вид

(71)

${{\tilde {J}}_{\operatorname{s} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } - \Pi ({{V}^{\alpha }} + {{V}^{\gamma }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$

(72)

Подобно переходу от (62) к (63), уравнение (72) можно записать как

(73)

$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } - \\ - \,\,\Pi d{{V}^{\beta }} - d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + \\ + \,\,{{V}^{\beta }}d{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $

Теперь, дифференцируя (71) и сравнивая с (73), снова приходим к уравнению (53) как аналогу уравнения адсорбции Гиббса для межфазной области, содержащей тонкую пленку. Все дальнейшие операции те же, что с уравнением (53), и здесь мы их опускаем.

ЗАКЛЮЧЕНИЕ

Данная работа знакомит читателя с современным аппаратом химической термодинамики, куда теперь вошел J-потенциал, символизирующий целую серию термодинамических потенциалов. Известно, что физический результат не должен зависеть от выбора термодинамического потенциала. В данной работе мы это многократно продемонстрировали на примере уравнения адсорбции Гиббса, но в нашем случае это имело значение еще и со стороны проверки правильности конструирования нового термодинамического потенциала. Ценность последнего определяется удобством его использования и внешними условиями, в которых оно проявляется. J-потенциал удобен для коллоидной науки, ибо, не будучи сам избыточной величиной, он уже включает в себя гиббсовские избытки термодинамических параметров по отношению к поверхностям и линиям.

Естественно, представленная совокупность J-потенциалов не является исчерпывающей. Мы сосредоточились на гетерогенных системах, содержащих тонкие пленки, но ограничились случаем плоских пленок. Но и в этих рамках можно спросить, почему не рассматривался вариант построения J-потенциала при величине ${{p}^{\beta }}$ в качестве внешнего давления. Ведь реально существуют системы, где внешней фазой является материнская фаза тонкой пленки (например, вокруг прилипшего к стенке пузырька со смачивающей тонкой пленкой [14]). Ответ следующий. Поскольку при определении J-потенциала мы стартуем от большого термодинамического потенциала, пространственная область (от нее зависит и объем) системы может быть очерчена из соображений удобства. Например, границы системы могут быть выбраны так, чтобы всегда внешней фазой была фаза α (или γ), как показано на рис. 1 и 2 . Тогда ${{p}^{\alpha }}$ будет неизменно внешним давлением.