Коллоидный журнал, 2020, T. 82, № 1, стр. 75-81

ВВЕДЕНИЕ

В недавней публикации [1] мы уже касались старинных работ [2–5] ([3, 5] – немецкий перевод [2, 4]) в связи с уравнением Фрумкина – одного из центральных соотношений термодинамики тонких пленок. Теперь мы обратимся к другому, не менее важному соотношению, также идущему от работ [2–5]. Используя современную терминологию, можно сказать, что речь идет о соотношении, которое связывает все поверхностные натяжения, имеющие отношение к смачивающей пленке, с ее расклинивающим давлением и краевым углом.

Обратимся сначала к работе Фрумкина [2], в которой он анализировал устойчивость смачивающей пленки прилипшего пузырька. Используя представления Поляни об адсорбционном потенциале W, Фрумкин пришел к результату

где v – молярный объем жидкости пленки, ${{\sigma }_{0}}$ – сумма поверхностных натяжений на сторонах пленки, когда она становится толстой, и h – толщина пленки. Надо полагать, что σ – поверхностное натяжение при наличии тонкой пленки. В начале статьи Р определено как избыточное давление в пузырьке, а первое равенство в (1) обосновано следующим образом: “… при соприкосновении с парами B (вещество пленки – А.Р.), термодинамический (читайте “химический” – А.Р.) потенциал которых равен μ, А (подложка – А.Р.) покрывается слоем жидкости такой толщины h, что на расстоянии h ${{\mu }_{0}} - \mu = W...$”. Надо считать, что ${{\mu }_{0}}$, как и ${{\sigma }_{0}},$ относится к толстой пленке, когда уже имеется объемная фаза, а логика рассуждений такая: деление разности химических потенциалов на молярный объем дает разность давлений. Но ведь это опять (что уже было при выводе уравнения Фрумкина [1, 2]) применение уравнения Гиббса–Дюгема к тонкой пленке, хотя оно выведено только для объемных фаз. Отметим, что Фрумкин трактует смачивающую пленку как адсорбционную, и в этом нет ничего плохого. Совсем недавно было еще раз продемонстрировано, что подобный подход может оказаться чрезвычайно полезным при анализе тонкой пленки прилипшего пузырька [6].

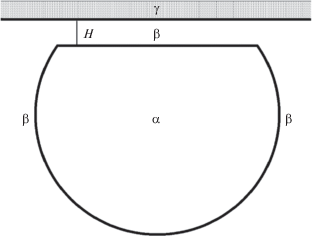
Попробуем перевести результат Фрумкина (1) на язык современной термодинамики тонких пленок [7–11]. Пусть α – фаза внутри пузырька, β – материнская фаза тонкой пленки и γ – объемная фаза подложки (рис. 1); двойные индексы будем приписывать поверхностям. В наших обозначениях

Избыточное давление внутри пузырька P есть лапласова разность давлений ${{p}^{\alpha }} - {{p}^{\beta }},$ но она же и расклинивающее давление Π [7]: Для мало сжимаемых жидкостей молярный объем v – почти постоянная величина. Пренебрегая его изменением, можем ввести v в формуле (1) под знак интеграла и дифференциала. Подставляя затем (2) и (3) во вторую формулу (1), представим ее (с заменой h на H в наших обозначениях) в окончательном виде Напомним, что ${{\sigma }^{{\alpha \gamma }}}$ – это поверхностное натяжение границы α–γ при наличии на ней тонкой пленки фазы β.

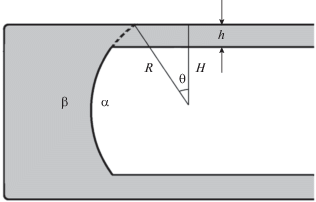
Перейдем теперь к работе Дерягина по капиллярной конденсации [4], где H – расстояние между стенками капилляра (на рис. 2 это 2H), h – толщина смачивающей пленки на стенке капилляра. Рассуждения ведутся в терминах свободной энергии. Поверхностное натяжение σ дается как свободная поверхностная энергия смачивающей жидкости и вводится поправочная (тоже на единицу поверхности) свободная энергия f для тонкой пленки. По ходу вывода уравнения Кельвина встречается выражение (под номером 6, пусть у нас будет 6Д) для “напряжения смачивания” (θ – краевой угол)

а в сноске говорится: “Для вывода соотношения (6), очевидно (в силу уравнения Юнга – А.Р.), достаточно доказать, что поверхностное натяжение ${{\sigma }_{f}}$ пленки толщиной h отличается от суммы $\sigma + {{\sigma }_{1}}$ поверхностных натяжений обеих поверхностей раздела, ее ограничивающих, на величину $f(h) - hf{\kern 1pt} '(h)$”. Тут же приводится доказательство, основанное на вычислении работы растяжения пленки при ее фиксированных массе и объеме. Сразу отметим, что выполнение этого условия возможно лишь в объемной фазе. Тонкая пленка неоднородна, а потому, если она растягивается при сохранении массы, то ее объем обязательно изменяется. С другой стороны, свободная энергия является термодинамическим потенциалом лишь при постоянстве того и другого, а это значит, что она не годится для данного расчета (термодинамический потенциал для данного расчета выбран не совсем правильно). Остается пренебречь сжимаемостью пленки. Результирующее в ходе вывода выражение не воспринимается из-за типографских ошибок, но, имея вышеприведенную цитату, можно заключить, что оно должно иметь вид И, наконец, еще одна цитата из [4]: “Заметим, что $ - f{\kern 1pt} '(h)$ есть не что иное, как величина $P(h),$ названная нами расклинивающим действием …”. Если так, то $f(h)$ должно быть интегралом от расклинивающего давления, и тогда (5) можно сравнивать с выражением (1) Фрумкина.

Нужно отметить, что уравнение Фрумкина–Дерягина было в работах [2–5] лишь попутным эпизодом. Больше внимания оно привлекло в монографии [12], где были представлены еще два варианта его доказательства. Один из них, связанный с уравнением адсорбции Гиббса, мы рассмотрим ниже, в соответствующем разделе. Другой опирается на “известное уравнение, выражающее постоянство химического потенциала молекул жидкости в слое переменной толщины $h(x,y,z)$” [12, с. 76]

где σ – поверхностное натяжение жидкости, $K(x,y,z)$ – локальная кривизна поверхности слоя и ${{P}_{0}}$ – капиллярное давление равновесного мениска или капли. Уравнение (6) (также идущее от Дерягина) весьма привлекательно, но его обоснование вызывает вопросы. Относящаяся к нему в [12] цитируемая литература заканчивается 1977 г., когда понятие расклинивающего давления относилось только к плоскопараллельным пленкам (переход к клиновидным и более сложным пленкам произошел уже в 21-ом в. [12–16]). Использование расклинивающего давления в этом виде в (6) – уже приближение, а потому такой подход с самого начала нельзя считать строгим. Конечная формула дается в виде (см. рис. 2) или, с учетом ${{P}_{0}} = {{\sigma \cos \theta } \mathord{\left/ {\vphantom {{\sigma \cos \theta } H}} \right. \kern-0em} H}$ (здесь ${H \mathord{\left/ {\vphantom {H {\cos \theta }}} \right. \kern-0em} {\cos \theta }}$ – радиус R на рис. 2) что сопоставимо с (6Д). Дальнейший переход производится с помощью уравнения Юнга (S – твердое тело, L – жидкость, V – пар; двойные индексы отвечают межфазным поверхностям) Заметим, что в логике этих рассуждений, как и в [4], первичной оказывается формула с косинусом краевого угла, хотя последующая формула (9) является более общей, чем (8). Было бы неплохо в этом разобраться. Другой интригой веет от второго слагаемого в правой части (8) и (9). Как следует из рис. 2, в данном случае, как и в случае прилипшего пузырька, капиллярное давление и расклинивающее давление совпадают, т.е. выполняется условие (3). Почему ${{P}_{0}}$ в (8) и (9) не заменено на Π?

Подводя итог анализу предшествующих выводов уравнения Фрумкина–Дерягина, отметим, что ни один из них не обошелся без замечаний (в основном, термодинамического характера). Видимо, не хватает еще одного, более строгого вывода, который снял бы все вопросы. Ниже мы попытаемся это сделать, причем двумя путями. Первый – это выбор подходящего термодинамического потенциала.

ВЫВОД НА ОСНОВЕ J-ПОТЕНЦИАЛА

Термодинамический потенциал – инструмент для решения термодинамических задач. Чем шире инструментарий, тем больше возможностей, и, значит, исследователям нужно стремиться к увеличению числа термодинамических потенциалов. Недавно их совокупность пополнилась целой серией под общим названием “J-потенциал”. Он определяется как [17, 18]

где P – внешняя сила (напряжение) на единицу площади поверхности системы как функция положения на поверхности (A), u – локальный вектор смещения поверхности и A – площадь поверхности; интегрирование производится по всей поверхности системы. Если система окружена флюидной средой с давлением p, то определение J-потенциала можно упростить до [18] где Ω – большой термодинамический потенциал и V – объем всей системы. В работе [19] было дано более общее определение где $p{\kern 1pt} '$ – некоторое выбранное давление. При совпадении $p{\kern 1pt} '$ с внешним давлением (12) переходит в (11). Это случай классического J-потенциала $({{J}_{\operatorname{c} }}).$ Если же $p{\kern 1pt} ' \ne p,$ речь идет о специальном J-потенциале $({{J}_{\operatorname{s} }}).$

Существует и гибридный J-потенциал, происходящий, в соответствии с определениями (11) и (12), от гибридного большого термодинамического потенциала [20]

где F – свободная энергия. Термодинамическая функция $\tilde {\Omega }$ обладает дуализмом: по отношению к компонентам с индексом i она играет роль большого термодинамического потенциала, а по отношению к компонентам с индексом j – роль свободной энергии. Соответственно гибридный J-потенциал определяется как В случае классического J-потенциала выражение (14) можно переписать в виде где G – энергия Гиббса. Здесь дуализм заключается в том, что для компонентов с индексом i гибридный классический J-потенциал играет роль большого термодинамического потенциала, а для компонентов с индексом j – роль энергии Гиббса.

В предыдущей публикации [19] было рассмотрено приложение J-потенциала всех видов к термодинамике тонких пленок. Среди них был и специальный J-потенциал, в котором в качестве $p{\kern 1pt} '$ в определении (11) было взято давление в материнской фазе тонкой пленки (фазе β на рис. 1 и 2): $p{\kern 1pt} ' = {{p}^{\beta }}.$ Такой J-потенциал кажется весьма подходящим для вывода уравнения Фрумкина–Дерягина. Вид соответствующих фундаментальных уравнений зависит от числа (1 или 2) используемых разделяющих поверхностей. Традиционный метод Гиббса оперирует с единственной разделяющей поверхностью независимо от присутствия тонкой пленки на межфазной поверхности. При таком подходе фундаментальные уравнения для специального J-потенциала при $p{\kern 1pt} ' = {{p}^{\beta }}$ имеют вид [19]

В уравнении (17) чертой отмечены избыточные (по Гиббсу) величины (относящиеся к единственной разделяющей поверхности αγ), хотя в левой части стоит полный (а не избыточный) J-потенциал. Последний, таким образом, просто проникнут термодинамикой поверхностей. Заметим, что в случае одной разделяющей поверхности система состоит только из двух фаз ($V = {{V}^{\alpha }} + {{V}^{\gamma }}$). Фазы β нет, но мы искусственно ввели давление ${{p}^{\beta }}$ и, тем самым, расклинивающее давление в приведенные уравнения, которые, естественно, имеют смысл лишь при наличии тонкой пленки.

При использовании двух разделяющих поверхностей $(V = {{V}^{\alpha }} + {{V}^{\gamma }} + {{V}^{\beta }})$ фундаментальные уравнения для специального J-потенциала при $p{\kern 1pt} ' = {{p}^{\beta }}$ приобретают форму [19]

где ${{\sigma }^{\alpha }}$ и ${{\sigma }^{\gamma }}$ – поверхностные натяжения пленки на границах с фазами α и γ. В случае тонкой пленки натяжения ${{\sigma }^{\alpha }}$ и ${{\sigma }^{\gamma }}$ не являются независимыми и всегда рассматриваются совместно [8, 9]. Что касается расположения разделяющих поверхностей, то они определяются либо физическими условиями (характерно для твердых тел), либо эквимолекулярными поверхностями (при непрерывном распределении компонентов между фазами) [10].

Сравнивая (16) и (18), находим

или где ${{V}^{\beta }}$ – объем тонкой пленки (пространство, мысленно заполняемоe фазой β при введении натяжений ${{\sigma }^{\alpha }}$ и ${{\sigma }^{\gamma }}$ по Гиббсу) и $H = {{{{V}^{\beta }}} \mathord{\left/ {\vphantom {{{{V}^{\beta }}} A}} \right. \kern-0em} A}$ – ее толщина. Соотношение (21) хорошо известно в термодинамике тонких пленок [8, 9]. Известно, что при неограниченном возрастании H расклинивающее давление стремится к нулю так, что произведение $\Pi H$ обращается в нуль. Тогда ${{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}$ переходит в сумму уже независимых поверхностных натяжений ${{\sigma }^{{\alpha \beta }}}$ и ${{\sigma }^{{\beta \gamma }}},$ а тонкая пленка превращается в толстую. При этом из (20) следует Теперь возвратимся к уравнению (18) и посмотрим, как J-потенциал выполняет свою основную задачу – вычисление работы. Согласно исходному дифференциальному фундаментальному уравнению для ${{J}_{\operatorname{s} }}$ при $p{\kern 1pt} ' = {{p}^{\beta }}$ [19] функция ${{J}_{\operatorname{s} }}$ обретает свойства термодинамического потенциала при постоянстве температуры, химических потенциалов, объема системы, давления в материнской фазе пленки и площади межфазной поверхности. При выполнении этих условий разность ${{J}_{\operatorname{s} }}$ для двух разных состояний дает работу перехода из одного состояния в другое. Но, если мы закрепим температуру и все химические потенциалы, то, согласно уравнению Гиббса–Дюгема, станут постоянными и давления во всех фазах, а вся система перейдет в нонвариантное состояние. При этом, казалось бы, уже все закреплено, ан нет! Мы еще не определили положение разделяющих поверхностей пленки, и именно это спасет положение.

Хотя мы рассматриваем случай свободного распределения компонентов системы, само наличие пленки предопределяет некоторую обособленность вещества. Можно представить, что в фазе α найдется компонент, в наибольшей степени присущий именно этой фазе и в меньшей – другим фазам (или, еще лучше, в них отсутствующий). Присвоим ему номер j и зададим положение разделяющей поверхности со стороны фазы α условием ${{\bar {N}}_{j}} = 0$ (эквимолекулярная поверхность в отношении компонента j). Аналогично расположение второй разделяющей поверхности пленки (со стороны фазы γ) определим условием ${{\bar {N}}_{k}} = 0,$ где k – преимущественный компонент фазы γ. Тогда химические потенциалы ${{\mu }_{j}}$ и ${{\mu }_{k}}$ исчезнут из уравнения (18), и необходимость их закрепления отпадает. При этом восстанавливается вариабельность давлений ${{p}^{\alpha }} = {{p}^{\gamma }},$ играющих роль внешнего давления для пленки. Что касается фазы β (материнской фазы пленки), то там закреплены температура и все химические потенциалы, а, значит, требование постоянства ${{p}^{\beta }}$ выполняется автоматически (тогда $d{{p}^{\alpha }} = d\Pi $).

Теперь ничто не мешает нам рассчитать работу утончения пленки с помощью J-потенциала. Для этого проинтегрируем обе части уравнения (19) от $H = \infty $ до H при постоянстве $T,$ ${{\mu }_{{i \ne j,k}}},$ $A,$ $V{\text{:}}$

Интеграл в левой части (24) сразу находим при помощи (18): Правая же часть, с учетом $d{{V}^{\beta }} = AdH$ при постоянстве A и тривиальности второго интеграла, принимает вид Подставив (25) и (26) в (24) и поделив обе части равенства на A, придем к окончательному результату в рамках подхода с двумя разделяющими поверхностями (при указании закрепленных величин A и V можно теперь опустить, оставив только параметры состояния) Сумму натяжений в этом подходе можно выразить через межфазное натяжение ${{\sigma }^{{\alpha \gamma }}}$ в подходе с одной разделяющей поверхностью согласно (21). Тогда приходим к соотношению которое и является уравнением Фрумкина–Дерягина в строгом исполнении. Оно соответствует формулам (5) и (6Д) Дерягина, причем мы видим, что именно формула (5), а не (6Д), является первичной. Сравнивая же (9) и (28), убеждаемся, что ${{P}_{0}}$ в формуле (9) действительно должно быть заменено на Π, как указывалось выше. Используя интегрирование по частям, уравнение (28) также можно представить в виде что соответствует уравнению Фрумкина (4). Однако, в отличиe от (4), уравнение (29) – точное соотношение.

ВЫВОД НА ОСНОВЕ УРАВНЕНИЯ АДСОРБЦИИ ГИББСА

Как мы обещали, ознакомимся сначала с выводом, приведенным в [12, с. 86]. Тонкая пленка на поверхности твердого тела рассматривается как результат адсорбции пара, а уравнение адсорбции Гиббса задается в форме

где Γ – адсорбция пара и ${{\sigma }_{{\operatorname{SV} }}}$ – межфазное натяжение на границе твердого тела с паром при наличии адсорбционной пленки. Интегрирование (30) дает где обозначения те же, что и в (9). Осталось перейти от (31) к (9), и здесь проблема. Если приближение $h \approx {{{v}}_{m}}\Gamma $ (${{{v}}_{m}}$ – молярный объем жидкости) приемлемо для достаточно толстой пленки, то условие $\mu (h) = - {{{v}}_{m}}\Pi (h)$ вызывает вопросы (достаточно сказать, что химический потенциал определяется с точностью до постоянной, тогда как Π – разностная величина). Таким образом, данный вывод не только ограничен единственным компонентом, но и недостаточно строг. Посмотрим, как его можно улучшить.

Вернемся к предыдущему разделу и как бы продолжим наши рассуждения с J-потенциалом при подходе с двумя разделяющими поверхностями. Дифференцируя (18) и сравнивая с (19), находим

или, относя все к единичной поверхности, где при суммировании по всем компонентам учтен наш выбор положения обеих разделяющих поверхностей. Уравнение (33) и есть уравнение адсорбции Гиббса в данном подходе. Используя (21), можем выразить левую часть (33) в терминах межфазного натяжения ${{\sigma }^{{\alpha \gamma }}}{\text{:}}$Это не значит, что мы перешли к единой разделяющей поверхности. Все избытки в (34), как и в (33), относятся одновременно к двум разделяющим поверхностям.

Мы не раз отмечали, что термодинамический потенциал – лишь инструмент для решения задач, и его выбор связан с соображениями удобства. В этой работе мы впервые вывели уравнения адсорбции Гиббса с помощью потенциала ${{J}_{\operatorname{s} }},$ но это известные соотношения, и раньше они были получены другими путями [1, 10, 19]. Внимательный читатель уже заметил, что интегрированием (33) сразу получается уравнение (28), а интегрированием (34) с учетом (22) – уравнение (29). Интересно, что в последнем случае, как только мы закрепляем температуру и химические потенциалы, уравнение адсорбции Гиббса (34) превращается в соотношение типа уравнения Фрумкина [21]

т.е. при определенной схеме уравнение Фрумкина может стать этапом вывода уравнения Фрумкина–Дерягина.

Отметим, что вывод уравнения Фрумкина–Дерягина через уравнение адсорбции Гиббса не только прост, но хорош еще и тем, что допускает присутствие твердой фазы. Хотя Гиббс вывел свое знаменитое уравнение только для жидких фаз, позже было доказано [20–22], что уравнение адсорбции Гиббса сохраняет свой вид и при наличии твердого тела, если его можно считать недеформируемым. Это условие вполне приемлемо для многих твердых фаз в явлениях смачивания.

ПЕРЕХОД К КРАЕВОМУ УГЛУ

После того как мы установили общие соотношения (28), (29), можно рассмотреть их частный случай при наличии краевого угла θ. Существование последнего значительно ограничивает возможные значения поверхностных натяжений благодаря уравнению Юнга

и тому факту, что все значения косинуса лежат в интервале от нуля до единицы. В наших обозначениях α – газ, β – жидкость и γ – твердое тело (рис. 1), а потому величины ${{\sigma }^{{\alpha \gamma }}}$ и ${{\sigma }^{{\beta \gamma }}}$ требуют особых пояснений. Напомним, что еще Гиббс открыл дуализм поверхностного натяжения твердого тела, который состоит в том, что, в отличие от жидкости, механическое (через тензор напряжений) и термодинамическое (через работу образования поверхности) определения поверхностного натяжения не совпадают. У нас ${{\sigma }^{{\alpha \gamma }}}$ – это термодинамическое поверхностное натяжение твердой фазы γ на границе с газовой фазой α при наличии тонкой пленки (рис. 1), а ${{\sigma }^{{\beta \gamma }}}$ – термодинамическое поверхностное натяжение твердой фазы γ на границе с жидкой фазой β. Заметим, что (36) – это классическая формулировка уравнения Юнга. В современной формулировке пишутся поправки на термодинамическое линейное натяжение, но они исчезают, если линии прямые или их кривизной можно пренебречь.

Посмотрим сначала, что следует из самого уравнения Юнга. Если температура и химические потенциалы компонентов фазы β закреплены, то и давление ${{p}^{\beta }}$ и все другие параметры состояния фазы β постоянны. Постоянными будут и оба поверхностных натяжения фазы β: ${{\sigma }^{{\alpha \beta }}}$ и ${{\sigma }^{{\beta \gamma }}}$ (это следует из уравнения адсорбции Гиббса). Тогда в уравнении (36) остаются всего две переменные – ${{\sigma }^{{\alpha \gamma }}}$ и $\cos \theta ,$ которые изменяются в одном направлении. Соответственно сам угол θ и ${{\sigma }^{{\alpha \gamma }}}$ изменяются в разных направлениях (если натяжение растет, то угол падает). При помощи уравнения Фрумкина можно связать краевой угол и с расклинивающим давлением. Согласно (35) ${{\sigma }^{{\alpha \gamma }}}$ и Π изменяются симбатно, а это значит, что с ростом расклинивающего давления краевой угол должен уменьшаться.

Подстановка (36) в (28) приводит к соотношению

которое наводит на мысль о возможном расчете краевого угла по экспериментальным или теоретическим изотермам расклинивающего давления $\Pi (H).$ Однако путь этот не прост. Во-первых, существуют разные виды расклинивающего давления [11], и мы даже не знаем, все ли виды открыты и изучены. Во-вторых, изотермы должны удовлетворять условиям постоянства температуры и химических потенциалов, указанным в (37) (с точки зрения термодинамики это условие не усложняет, а упрощает картину, поскольку подразумевается неизменность состояния материнской фазы тонкой пленки). Даже если пленка однокомпонентна, ее химический потенциал должен быть закреплен.

О попытке такого расчета уже сообщалось [23, 24], но он проводился по усеченной формуле

В связи с этим нам придется вернуться к формуле (6Д) и вспомнить, что последний член в ней Дерягин объявлял пренебрежимо малым и доказывал это с помощью большой ширины капилляра, в котором идет капиллярная конденсация (издержки переплетения разных задач) [4, 5]. При этом имелась в виду малость ΠH по отношению не к интегралу, а ко всей правой части (6Д). Если же сравнивать ΠH с интегралом, то, например, в случае дисперсионных сил без запаздывания, имеем (A – константа взаимодействия) т.е. по абсолютной величине ΠH оказывается в два раза больше, чем интеграл. В [12] вопрос о малости члена ${{P}_{0}}h$ в формуле (9) никак не затрагивался, хотя при переходе к (38) он исчезает. Таким образом, можно констатировать, что этот вопрос остается открытым. Но, в любом случае, начало вычислениям положено.