Коллоидный журнал, 2020, T. 82, № 2, стр. 204-222

1. ВВЕДЕНИЕ

Наночастицы ферромагнетиков и ферритов успешно используются в различных инженерных и биомедицинских приложениях как сами по себе, например, в виде добавок, повышающих контраст изображений в МРТ [1, 2], или биосенсоров [3], так и в качестве активных элементов сложных физико-химических систем: магнитных полимеросом [4, 5], микроферрогелей [6, 7]. Фронт исследования этих систем непрерывно расширяется, нацеливаясь на множество потенциальных приложений. В их числе: направленный транспорт лекарств [8], термическое воздействие на злокачественные клетки (локальная магнитоиндукционная абляция и гипертермия [9, 10]), управляемое деформирование клеточной мембраны [11] или силовое проникновение частицы-наноинструмента через нее [12], формирование опорного каркаса заданной конфигурации для наращивания костной ткани [13, 14] и т.д.

Любая из этих прикладных идей предполагает или манипулирование магнитным микро- или наноэлементом, или возбуждение/анализ его магнитного отклика посредством приложенного поля. Тем самым очевидно, что залогом продвижения магнитной тераностики и наномедицины является прогресс в решении большого ряда комплексных физических задач. С одной стороны, при описании частиц столь малого размера прикладная физика магнитных явлений должна обязательно сочетаться с теорией броуновского движения (как оказывается, отдельно частиц и их магнитных моментов). С другой стороны, сложное строение сред, в которых находятся частицы, требует обращения к физике конкретного мягкого вещества, например вязкоупругой жидкости (движение частиц в цитозоле), физике макромолекулярных мембран (проникновение частицы через клеточную оболочку), физике полимеров (поведение частиц в феррогелях) и т.д.

Использование магнитных наночастиц в качестве сенсоров положения и/или индикаторов присутствия определенных биомолекул – одно из наиболее простых, но и универсальных приложений. In vivo (или на имитационных моделях) оно позволяет контролировать распределение наночастиц-векторов в организме и их локализацию в очагах-мишенях. Но шире всего магнитные наносенсоры используются in vitro для лабораторного анализа малых проб на содержание определенных веществ (аналитов).

Наночастицы, функционализированные к искомому аналиту, вводятся в пробу в определенной дозе. Затем образец помещается в слабое переменное магнитное поле и проводится мониторинг магнитного отклика. При наличии аналита в пробе, его молекулы адсорбируются на частицах-зондах, и это вызывает изменение амплитудно-частотной характеристики магнитного отклика образца. Следует отметить, что наиболее распространенный режим такого мониторинга – это не гармоническое зондирование, а магнитная релаксометрия: регистрация сигнала, которым система откликается на резкое изменение приложенного поля [15–17].

В настоящей работе выполнено решение именно такой задачи применительно к сферической броуновской частице, несущей “вмороженный” магнитный момент и находящейся в вязкоупругой среде, механика которой описывается схемой Джефриса – очень распространенной феноменологической моделью, способной эффективно моделировать широкий спектр реологических свойств: от почти неньютоновской жидкости до геля. Предположение о “вмороженности” магнитного момента означает, что частица обладает внутренней магнитной анизотропией, поле которой существенно превосходит напряженности полей, применяемых для релаксометрии; такому случаю отвечает, например, использование наночастиц феррита кобальта.

Раздел 2 содержит общее описание модели. В разделе 3 представлены уравнения вращательного движения частицы – система уравнений Ланжевена и соответствующее ей уравнение Фоккера–Планка (УФП), а в разделе 4 рассмотрено исходное равновесное состояние частицы. Разделы 5–7 посвящены выводу в трехмерной постановке системы моментных уравнений, описывающей ориентационное движение частицы (и ее магнитного момента), и построению метода точного решения этой системы применительно к задаче о магнитной релаксометрии. Для сопоставления в разделе 8 приведено приближенное решение той же системы уравнений методом эффективного поля, т.е. с учетом только первых двух статистических моментов. В разделе 9 дано полное решение задачи и показано, что метод эффективного поля, в действительности, можно применять для интерпретации релаксометрических экспериментов только в очень ограниченной области материальных параметров вязкоупругой среды.

2. МОДЕЛЬ

Поскольку наночастица, взвешенная в любой жидкой среде, подвержена интенсивному броуновскому движению, в отсутствие внешнего магнитного поля направления магнитных моментов в разбавленном ансамбле таких частиц распределены по случайному закону. Техника магнитной релаксометрии предполагает, что в начале теста этот ансамбль помещается в постоянное и однородное поле и пребывает в нем до достижения равновесия. Приложенное поле намагничивает систему – создает в ней определенную степень ориентационного упорядочения магнитных моментов. Затем поле резко (ступенчато) изменяется, и регистрируется сигнал, генерируемый магнитными частицами при переходе ансамбля к новому ориентационному равновесию. Таким образом, возбуждаемый релаксационный процесс содержит информацию о свойствах среды, в которой происходит поворот частицы.

В том случае, когда поле выключается полностью, возврат системы к изотропному состоянию определяется только свободным броуновским движением (диффузией), т.е. определяется размером частицы и температурой. Если же поле изменяется между двумя конечными значениями напряженности: H и H ± ΔH (ΔH $ \ll $ H), то релаксационный процесс оказывается еще и функцией величины “поля смещения” H.

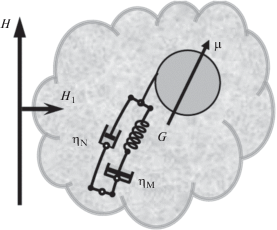
Частица погружена в вязкоупругую среду Джефриса, выбор этой модели (подробное описание см., например, в [18, 19]) обусловлен, в том числе, тем обстоятельством, что она позволяет корректным образом осуществлять переход к броуновской динамике, не порождая артефактов [20–22]. Реология жидкости Джефриса описывается посредством трех феноменологических параметров, см. рис. 1. Коэффициент вязкости ${{{\eta }}_{{\text{N}}}}$ принято относить к низкомолекулярной (квази-ньютоновской) компоненте среды, а коэффициент η_M – к высокомолекулярной (квази-максвелловской) компоненте. Предполагая, что η_N$ \ll $ η_M, видим, что реакция жидкости Джефриса на внешнее воздействие имеет быструю и медленную составляющие. Модуль упругости G характеризует упругость полимерной сетки, за необратимую деформацию которой отвечает коэффициент вязкости η_M.

3. УРАВНЕНИЯ ЛАНЖЕВЕНА И ФОККЕРА–ПЛАНКА

Система уравнений, описывающих ориентационное движение броуновской частицы в жидкости Джефриса без учета инерции, имеет вид [21, 22]

Здесь ${\mathbf{e}}$ – единичный вектор ориентации частицы, ${\mathbf{\Omega }}$ – угловая скорость, $E$ – энергия взаимодействия частицы с полем, а ${\mathbf{\hat {L}}}$ – оператор бесконечно малого поворота, и использовано стандартное обозначение для векторного произведения. Коэффициенты реакции среды задаются стандартными для микрореологии соотношениями [23] где $G$ – динамический модуль упругости, а ${{\eta }_{\alpha }}$ – ньютонова ($\alpha = {\text{N}}$) и максвеллова ($\alpha = {\text{M}}$) вязкости, $V$ – гидродинамический объем частицы. Случайные силы, моделирующие тепловой шум в системе, в соответствии с флуктуационно-диссипативной теоремой определяются следующими корреляционными соотношениями [21, 22]: В этой формуле и далее температура $T$ измеряется в энергетических единицах (${{k}_{{\text{B}}}} = 1$). В системе уравнений (1) величина ${\mathbf{Q}}$ имеет смысл момента сил, действующих на частицу со стороны динамической квазисетки с временем жизни узлов ${{\tau }_{{\text{M}}}}.$ Эта фазовая переменная моделирует запаздывающую реакцию среды. В рассматриваемой модели, как видно из (1), механизмы запаздывающего и обычного вязкого трения, обусловленного диссипативным взаимодействием частицы с низкомолекулярной компонентой среды, работают параллельно. Равновесную сетку в хорошем растворителе (гель) можно рассматривать как предельный случай, когда ${{\tau }_{{\text{M}}}} \to \infty .$ При указанном предельном переходе уравнение для запаздывающего момента сил трения сводится [24, 25] к простому соотношению ${\mathbf{\dot {Q}}} = - K{\mathbf{\Omega }},$ означающему чисто упругую реакцию среды. Для такой системы в случае плоского вращения частицы уравнения (1) приводят к одномерной модели Кельвина, эта ситуация рассмотрена в работе [25].

Системе стохастических уравнений (1) соответствует кинетическое УФП для функции распределения $W({\mathbf{e}},{\mathbf{Q}},t),$ получаемое стандартным способом (см., например, [22, 26]):

Здесь и далее используется безразмерная фазовая переменная ${\mathbf{Q}},$ т.е. в исходной системе уравнений (1) произведена замена ${\mathbf{Q}} \to K{\mathbf{Q}}.$ Из структуры УФП следует, что его стационарным (равновесным) решением является обобщенное распределение Больцмана Эта функция показывает, что равновесное состояние системы в отсутствие поля $(E = 0)$ изотропно и даже в постоянном внешнем поле фазовые переменные $({\mathbf{e}}{\text{,}}{\mathbf{Q}})$ остаются статистически независимыми. Это важное свойство существенно используется при построении приводимых ниже решений.

В рассматриваемой задаче магнитный дипольный момент ${\mathbf{\mu }}$ закреплен (вморожен) в теле частицы, так что энергия его взаимодействия с полем имеет стандартный вид ориентационного потенциала Зеемана:

При записи магнитного поля здесь учтено, что оно имеет две составляющие: постоянную ${\mathbf{H}} = H{\mathbf{k}}$ (поле смещения), направленную по оси $oz{\text{:}}\,\,{\mathbf{k}} = (0,0,1),$ и переменную плоско поляризованную ${{{\mathbf{H}}}_{1}} = \varepsilon (t)H{\mathbf{p}},$ $(\varepsilon (t) \ll 1).$ Наличие поля смещения придает статистическому ансамблю таких частиц стационарную ориентационную анизотропию, и поэтому для характеристики магнитного отклика ферроколлоида на слабое зондирующее поле следует использовать тензор восприимчивости где $n$ – числовая концентрация частиц; по предположению, размеры и магнитные моменты всех частиц ансамбля одинаковы, т.е. рассматривается монодисперсный ферроколлоид.

Для расчета восприимчивости (3) будем использовать метод усреднения стохастических уравнений (1), хорошо зарекомендовавший себя при решении широкого круга задач физической кинетики [26]. После подстановки явного вида потенциала взаимодействия частиц с полем, система (1) принимает форму

Здесь для удобства обозначения введены операторы $\hat {H},$ $\hat {Q}$ и $\hat {U},$ описывающие, соответственно, действие магнитного поля, запаздывающего трения и случайных сил на фазовые переменные в среде Джефриса. Корреляционные функции случайных сил, входящих в эту систему, определяются соотношением (2).

4. РАВНОВЕСНОЕ СОСТОЯНИЕ

Равновесная функция распределения, куда подставлен явный вид потенциала Зеемана, принимает вид

Здесь введены обозначения для безразмерной величины поля $\xi = {{\mu H} \mathord{\left/ {\vphantom {{\mu H} T}} \right. \kern-0em} T}$ и безразмерной температуры $\tilde {T} = {T \mathord{\left/ {\vphantom {T {K.}}} \right. \kern-0em} {K.}}$ Равновесные статистические моменты ориентационной функции распределения задаются рекуррентным соотношением которое получается интегрированием по частям.

Таким образом, в равновесном состоянии ансамбль магнитных частиц имеет одноосную анизотропию, задаваемую направлением постоянного поля. В этой ситуации любой тензор второго ранга можно представить через разложение по набору проекционных тензоров

обладающих простой структурой, причем этот набор является полным и ортогональным. Удобство такого разложения очевидно: в этом представлении все матричные операции сводятся к простым скалярным действиям с соответствующими компонентами: Согласно (5) распределение фазовой переменной ${\mathbf{Q}}$ остается изотропным даже при наличии постоянного поля, в силу чего все нечетные равновесные статистические моменты этой величины обращаются в нуль, а четные моменты задаются выражениями

5. ФУНКЦИОНАЛЬНЫЙ БАЗИС НЕРАВНОВЕСНОГО РАСПРЕДЕЛЕНИЯ

Зондирующее поле выводит систему из равновесного состояния. Найдем линейные по этому возмущению неравновесные компоненты функции распределения. Для изотропного состояния (в отсутствие поля смещения) такая задача была решена в работе [22]. Ниже мы покажем, что построенный в этой работе базис можно использовать и при наличии поля смещения. В самом деле, из системы уравнений (4) следует, что в линейном по зондирующему полю – “дипольном” – приближении зацепление моментных уравнений обусловлено только запаздывающим трением, т.е. моментом сил ${\mathbf{Q}}$. Так, например, в уравнении для первой базисной функции ${\mathbf{e}}$, имеющей нулевой порядок по ${\mathbf{Q}}$, присутствует функция первого порядка – $({\mathbf{Q}} \times {\mathbf{e}}).$ В свою очередь, в уравнении для этой величины появится функция второго порядка и так далее. Запишем эти соотношения в общем виде, используя введенный при записи (4) оператор ${\mathbf{\hat {Q}}}{\text{:}}$

Из этих выражений видно, что в силу изотропии равновесного состояния по переменной ${\mathbf{Q}}$ искомые базисные функции следует разделить на взаимно ортогональные подбазисы – нечетный и четный. В свою очередь, четный подбазис можно рассматривать как суперпозицию двух ортогональных между собой наборов функций. Это утверждение основано на следующем очевидном равенстве, справедливом для любой функции ${\Phi }$, зависящей от модуля переменной ${\mathbf{Q}}{\text{:}}$Если использовать указанные обстоятельства, то в дипольном приближении все базисные функции можно разделить на три взаимно ортогональных набора (подбазиса): где $\Psi _{n}^{{{\text{(}}k{\text{)}}}}$ – скалярные функции, позволяющие провести ортогонализацию внутри каждого из этих наборов последовательно шаг за шагом по процедуре Грама–Шмидта [27].

Из условия сохранения нормировки неравновесного решения $W({\mathbf{e}}{\text{,}}{\mathbf{Q}},t)$ УФП для первой базисной функции находим

Скалярные функции $\Psi _{n}^{{{\text{(}}k{\text{)}}}}$ в подбазисах (7) являются полиномами, степень которых обозначает нижний индекс. Верхний индекс указывает на степень дополнительного множителя (вес), с которым эти многочлены ортогональны: Это соотношение является прямым следствием определения ортогональных базисных функций (7). Способ построения и техника работы с полным “дипольным” базисом изложены в Приложении.

С учетом сделанного выбора функционального базиса представим неравновесное решение УФП в виде

и найдем связь между амплитудами этого разложения и усредненными значениями базисных функций – неравновесными статистическими моментами. Выполняя усреднение первой базисной функции с распределением (8), получаем откуда, используя определение проекционных матриц (6), находим явное выражение для первой амплитуды неравновесного распределения Аналогичным способом получаются и соотношения, выражающие связь амплитуд разложения (8) с моментами более высокого порядка:

6. ЦЕПОЧКА МОМЕНТНЫХ УРАВНЕНИЙ

В рассматриваемой задаче наибольший интерес представляет наблюдаемый (средний по ансамблю) вектор ориентации частицы. Формальное усреднение первого уравнения системы (4) дает

Последнее слагаемое в правой части, определяющее вклад вращательной диффузии, вычисляется следующим способом [22, 26, 28]. Так как в искомое выражение входит случайная δ-коррелированная функция, то для его расчета достаточно найти только сингулярную, т.е. пропорциональную случайной силе, часть решения уравнения (4) для фазовой переменной ${\mathbf{e}}(t)$: Эта формула учитывает в явном виде принцип причинности, согласно которому состояние физической системы в данный момент времени может зависеть только от предшествующих воздействий. Усреднение слагаемого со случайной силой с помощью определения (11) и корреляционных соотношений (2) приводит к уравнению движения вектора ориентации в форме Здесь – известное дебаевское время броуновской вращательной диффузии сферической частицы в ньютоновой жидкости с вязкостью ${{\eta }_{{\text{N}}}}.$

В термодинамическом равновесии, когда нет переменного зондирующего поля, отсюда следует связь между первым и вторым моментами вектора ${\mathbf{e}}{\text{:}}$ ${{\gamma }_{{\text{D}}}}{{\left\langle {\mathbf{e}} \right\rangle }_{0}}$ = ${{\gamma }_{{\text{H}}}}{{\left\langle {({\mathbf{e}} \times {\mathbf{k}} \times {\mathbf{e}})} \right\rangle }_{0}}.$ Использование этой подстановки позволяет записать уравнение для неравновесной составляющей ориентации в виде

Здесь второе слагаемое в правой части должно быть усреднено по неравновесному распределению (8). Пользуясь изложенной выше техникой проецирования, имеем Учитывая связь (9) между первой амплитудой неравновесного распределения и статистическим моментом $\left\langle {\delta e} \right\rangle $ и разделяя затем зондирующее поле на продольную и поперечную составляющие, приходим к окончательной форме уравнения для неравновесной ориентации:

В случае ньютоновой среды-носителя, когда упругость отсутствует (G = 0) и параметр γ_N обращается в нуль, уравнение (14) совпадает с уравнением для намагниченности, полученным в работе [29]. Таким образом, именно последнее слагаемое в правой части уравнения (14) описывает влияние вязкоупругости на степень ориентации ансамбля феррочастиц, т.е., в конечном счете, на намагниченность системы.

Используя аналогичную технику преобразования (детали расчета даны в Приложении), получаем уравнение для момента сил запаздывающего трения

В случае изотропной системы, когда постоянное поле отсутствует и ${{c}_{2}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$ это уравнение совпадает с уравнением для момента $\left\langle {\mathbf{M}} \right\rangle ,$ полученным в работе [22]. Анизотропию ориентационного и, тем самым, магнитного отклика вносит тензор A_ij, компоненты которого отличны от нуля в присутствии поля.

Если ограничить рассмотрение только этой парой уравнений, то придем к приближенному описанию магнитной релаксации вязкоупругого ферроколлоида методом эффективного поля, для чего достаточно в уравнении (15) положить ${\mathbf{L}}(2) = {\mathbf{K}}(2) = 0.$ Указанное рассмотрение было проведено в работе [24], и, как детально продемонстрировано ниже, пренебрежение высшими моментами функции распределения приводит к заметному отличию результатов от точного решения.

Способ вывода полной цепочки зацепляющихся моментных уравнений представлен в Приложении. Такая система содержит бесконечное число уравнений, и, строго говоря, для получения точного решения нужно решить все из них. На деле, требование оказывается не таким строгим. Для того чтобы обеспечить высокую точность решения в физически интересном для рассматриваемой задачи диапазоне параметров, достаточно ограничить количество решаемых уравнений вполне умеренными значениями: 10–20.

7. ОРИЕНТАЦИОННАЯ МАГНИТОДИНАМИКА ВЯЗКОУПРУГОГО ФЕРРОКОЛЛОИДА

Расчет отклика намагниченности на слабое поле $\left( {{{H}_{{\text{1}}}} \sim \exp ( - i\omega t)} \right)$ начнем, однако, с построения полной формальной схемы решения. Сохраним обозначения для моментов отклика на зондирующий сигнал, опуская для краткости индекс частоты $\omega {\kern 1pt} .$ В безразмерном виде матричные уравнения для каждой из двух (параллельной и перпендикулярной полю смещения) проекций имеют вид

где векторы искомых компонент отклика и вынуждающей силы задаются соотношениями Верхний индекс T указывает на транспонирование. Приведем явный вид начального фрагмента матрицы ${\mathbf{R}}$ с опущенным для краткости индексом проекции: Диагональные элементы матрицы ${\mathbf{R}}$ имеют вид Здесь $\beta = {K \mathord{\left/ {\vphantom {K T}} \right. \kern-0em} T}$ – параметр упругости среды-носителя, а параметр B идентифицирует подбазис, к которому относится функция γ^(α). Из расчета (см. Приложение) получаем

Элементы, стоящие ниже главной диагонали матрицы (поддиагональные), тоже зависят от величины поля смещения и согласно Приложению задаются формулами

Сопоставление с решением задачи для случая нулевого поля смещения [22] показывает, что матричное уравнение (16) имеет ту же структуру – это ленточная пятидиагональная матрица. Отличие заключается в появлении полевой зависимости матричных элементов, которая полностью определяется набором из восьми функций; при нулевом поле смещения эти функции принимают единичные значения.

Запишем уравнение (16) в виде пятичленного рекуррентного соотношения

Из явного вида (17) фрагмента матрицы хорошо видно, что коэффициенты этой формулы и ее правую часть можно представить как соответствующие компоненты следующих векторов:

Уравнение (18) удобно решать методом прогонки (см., например, [22, 30]). Для этого связь компонент отклика разных индексов представляется в виде суммы, содержащей два коэффициента прогонки и свободный член: ${{X}_{n}} = {{S}_{n}}{{X}_{{n\,\, - \,\,{\text{1}}}}} + {{P}_{n}}{{X}_{{n\,\, - \,\,{\text{2}}}}} + {{a}_{n}}.$ Такая подстановка позволяет выразить в уравнении (18) два слагаемых со старшими индексами через компоненты с индексами $ \leqslant {\kern 1pt} \,\,n$ и тем самым привести (18) к трехчленному рекуррентному соотношению; сравнение последнего с выбранным видом решения дает систему уравнений прогонки Использование коэффициентов прогонки позволяет вывести аналитическую формулу для динамической восприимчивости вязкоупругого ферроколлоида. Рассмотрим совместно первое из уравнений моментной цепочки (16) и соотношение прогонки для второй компоненты отклика: ${{g}_{{\text{0}}}}{{X}_{{\text{1}}}} - {{\beta {{X}_{{\text{2}}}}} \mathord{\left/ {\vphantom {{\beta {{X}_{{\text{2}}}}} {\text{2}}}} \right. \kern-0em} {\text{2}}} = {{Y}_{{\text{1}}}}{\text{,}}$ ${{X}_{{\text{2}}}} = {{S}_{{\text{2}}}}{{X}_{{\text{1}}}} + {{a}_{{\text{2}}}}{\text{.}}$ Используя формулы прогонки и явный вид коэффициентов, входящих в них, получаем: ${{S}_{{\text{2}}}} = {{\gamma {\text{(}}{\mathbf{e}}{\text{)}}} \mathord{\left/ {\vphantom {{\gamma {\text{(}}{\mathbf{e}}{\text{)}}} {{{Z}_{{\text{2}}}}}}} \right. \kern-0em} {{{Z}_{{\text{2}}}}}}{\text{,}}$ ${{a}_{{\text{2}}}} = {{ - {{Y}_{{\text{1}}}}} \mathord{\left/ {\vphantom {{ - {{Y}_{{\text{1}}}}} {{{Z}_{{\text{2}}}}}}} \right. \kern-0em} {{{Z}_{{\text{2}}}}}}{\text{.}}$ В результате находим выражение для неравновесного дипольного момента ${{X}_{1}} = \left\langle {\delta {\mathbf{e}}} \right\rangle .$ Учитывая определение восприимчивости (6) и восстанавливая все опущенные обозначения, получаем С формальной точки зрения это выражение является точным, поскольку до сих пор мы рассматривали безразмерную функцию ${{S}_{2}}(\omega ,\beta ,\xi )$ как одну из компонент бесконечной последовательности {S_n}, определенной из решения всей бесконечной цепочки рекуррентных уравнений (19).

Для реального вычисления восприимчивости систему рекуррентных соотношений приходится обрывать на некотором номере N, накладывая на систему (19) “начальные” условия

которые отражают естественное предположение о том, что амплитуды статистических моментов неравновесного распределения убывают с ростом их номера. Таким образом, N – это порядок наивысшего учитываемого момента, и с помощью этого числа легко контролировать точность вычислений. Как оказалось, для рассматриваемой задачи во всем физически интересном диапазоне изменения материальных параметров системы достаточно использовать значение $N = 10.$

В работе [31] представлено обсуждение результатов расчета динамической восприимчивости по полученным выше формулам. Основной результат этого анализа состоит в том, что в системе с развитой упругостью $(\beta \gg 1)$ и в относительно слабом поле смещения $(\beta > 2{{\gamma }^{{(\alpha )}}}{\text{(}}{\mathbf{e}}{\text{)}})$ наряду с высокочастотной областью дисперсии (ωτ_D ~ β) имеется и низкочастотная (ωτ_D ~ 1/β). По мере роста параметра упругости амплитуда этой низкочастотной компоненты растет, а высокочастотной уменьшается.

Построенный ниже формализм применяется для того, чтобы выяснить влияние магнитного поля смещения и реологических параметров среды-носителя на кинетику релаксации намагниченности. В самом деле, зондирование ферроколлоидов ступенчатыми импульсами поля – это, по-видимому, наиболее распространенный способ экспериментального изучения микрореологии и магнитодинамики сложных ферроколлоидов, см., например, [15–17].

8. ВРЕМЕНА РЕЛАКСАЦИИ: ПРИБЛИЖЕНИЕ ЭФФЕКТИВНОГО ПОЛЯ

Рассмотрим схему стандартного релаксометрического эксперимента, заключающегося в регистрации сигнала, возникающего при быстром выключении слабого магнитного поля, величина которого на протяжении длительного времени поддерживалась неизменной:

при этом воздействии магнитное поле смещения ${\mathbf{H}}$ всегда остается постоянным и по величине, и по направлению.

Простые формулы, пригодные для качественного анализа переходного процесса, вызванного воздействием (21), можно получить в приближении эффективного поля. В этом подходе для того, чтобы описать затухание неравновесной компоненты намагниченности системы $K{\text{(}}t{\text{)}} = {{\left\langle {\delta {\mathbf{e}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\delta {\mathbf{e}}} \right\rangle } {{{{\left\langle {\delta {\mathbf{e}}} \right\rangle }}_{0}}}}} \right. \kern-0em} {{{{\left\langle {\delta {\mathbf{e}}} \right\rangle }}_{0}}}},$ полученная выше система моментных уравнений (16) сокращена до первых двух. Указанную пару уравнений первого порядка по времени удобно преобразовать в единственное уравнение второго порядка, которому удовлетворяет K(t):

Индекс проекции намагниченности $\left\langle {\delta e} \right\rangle $ на поле смещения здесь для краткости опущен. В соответствии со схемой обсуждаемого эксперимента уравнение (22) следует решать с начальными условиями

Решение сформулированной задачи находится стандартным способом и имеет вид

Входящие в эту формулу декременты затухания ${{\lambda }_{{{\text{s,f}}}}}$ являются корнями характеристического уравнения, соответствующего (22). Начальный наклон этой релаксационной кривой задается величиной $\gamma {\text{(}}{\mathbf{e}}{\text{),}}$ которая, в свою очередь, определяется только временем ${{\tau }_{{\text{D}}}}$ и безразмерной величиной постоянного поля. Важно отметить, что $\gamma {\text{(}}{\mathbf{e}}{\text{)}}$ не зависит от вязкоупругости (η_M и G) среды. Так происходит потому, что на начальном этапе релаксации успевает включиться только быстрый релаксационный механизм изучаемой модели – обычное вязкое трение c коэффициентом η_N.

Полное время релаксационного процесса удобно характеризовать так называемым интегральным временем, которое учитывает все моды релаксации [26]. Для функции (24) оно легко вычисляется и в размерной форме имеет вид

Заметим, что в это выражение входят все реологические постоянные модели.

Простая формула (25) качественно верно описывает зависимость процесса релаксации намагниченности от материальных параметров системы. Начнем с изотропного случая (поле смещения равно нулю), когда согласно данным выше определениям $\gamma {\text{(}}{\mathbf{e}}{\text{)}} = \gamma {\text{(}}{\mathbf{M}}{\text{)}} = {\text{1}}{\text{.}}$ Из (25) имеем

Как видно, описание с помощью интегрального времени предсказывает три существенно различающихся режима ориентационной релаксации наночастицы в жидкости Джефриса. Из формулы (26) следует, с одной стороны, что релаксация всегда имеет диффузионный характер: затравочным масштабом времени является обратно пропорциональное температуре дебаевское время τ_D (13). С другой стороны, реальная скорость релаксации может изменяться на несколько порядков, уменьшаясь от $\tau _{{\text{D}}}^{{ - 1}}$ до ${{\left( {q{{\tau }_{{\text{D}}}}} \right)}^{{ - 1}}};$ напомним, что отношение $q = {{{{\eta }_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\eta }_{{\text{M}}}}} {{{\eta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\eta }_{{\text{N}}}}}}$ в типичных случаях составляет 10³–10⁵. Согласно (26), переход между режимами определяет безразмерный параметр $\beta = {K \mathord{\left/ {\vphantom {K T}} \right. \kern-0em} T}{\text{,}}$ выражающий соотношение между упругой и флуктуационной силами, действующими на частицу ферроколлоида.

При сильном тепловом движении и/или слабой упругости ($\beta = {K \mathord{\left/ {\vphantom {K T}} \right. \kern-0em} T} < 1$) релаксационный процесс протекает быстро: он фактически определяется дебаевским временем ${{\tau }_{{\text{D}}}}.$ Иными словами, в этом режиме воздействие среды Джефриса на наночастицу очень похоже на то, что оказывала бы на нее простая ньютонова жидкость с коэффициентом вязкости ${{\eta }_{{\text{N}}}}.$

При очень высокой упругости ($\beta \gg 2q$) интегральное время ориентационной релаксации (26) приобретает вид

Как видно, оно сохраняет свой дебаевский характер (${{\tau }_{{{\text{int}}}}} \propto {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}$), но теперь эффективная вязкость жидкой среды, в которой происходит ориентационная диффузия частицы, задается не ньютоновым (${{\eta }_{{\text{N}}}}$), а максвелловым (${{\eta }_{{\text{M}}}}$) коэффициентом модели Джефриса. Таким образом, в пределе $\beta \gg 2q$ процесс релаксации замедляется в q раз по сравнению с предельным случаем среды со слабой упругостью. Примечательно, что ни в той, ни в другой ситуации скорость релаксации не зависит явно от параметра упругости.

Наибольший физический интерес имеет представленная в формуле (26) промежуточная асимптотика: $\beta > 1$ при $\beta \ll 2q.$ В самом деле, случай $\beta < 1,$ как указано выше, тривиален, а предел $\beta \gg 2q,$ которому можно придать вид ${{\tau }_{{\text{D}}}} \gg {{\tau }_{{\text{M}}}},$ в реальных коллоидах не может быть достигнут ввиду малости размеров частиц.

Таким образом, типичный для вязкоупругого ферроколлоида процесс ориентационной релаксации характеризуется интегральным временем

которое возрастает пропорционально параметру упругости; при переходе к соотношению (28) мы положили, что $\beta $ заметно превосходит единицу. Важной особенностью времени (28) является его “недебаевский” вид – квадратичная зависимость от обратной температуры.

Проделанный выше анализ легко распространить на случай релаксометрии ферроколлоида, находящегося под действием постоянного поля смещения (21). Используя полученные выше формулы для величин $\gamma {\text{(}}{\mathbf{e}}{\text{)}}$ и $\gamma {\text{(}}{\mathbf{M}}{\text{),}}$ находим выражения, позволяющие оценить влияние поля смещения на интегральную релаксацию поперечной (${\mathbf{k}} \bot {\mathbf{p}}$) и продольной (${\mathbf{k}}\parallel {\mathbf{p}}$) компонент намагниченности:

Для изотропной системы эти формулы совпадают и описываются промежуточной асимптотикой (средняя строчка) из (26).

В случае сильного поля смещения $(\xi \gg 1),$ т.e. при $H \gg {T \mathord{\left/ {\vphantom {T \mu }} \right. \kern-0em} \mu }$ указанные выражения в первом порядке по малому параметру ${1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0em} \xi }$ принимают вид

Такое поле обеспечивает высокую степень ориентации частиц, и при его изменении на малую величину главным механизмом релаксации является не тепловая диффузия, а вынуждаемый полем поворот магнитного момента. Как видно, в пределе сильного поля смещения интегральные времена релаксации убывают как ${1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0em} \xi } \propto {1 \mathord{\left/ {\vphantom {1 H}} \right. \kern-0em} H},$ при этом тот факт, что среда-носитель обладает упругостью, заметно сказывается только на поперечном времени. Хотя время ${{\tau }_{{\text{H}}}},$ задающее темп релаксации, не зависит от температуры (см. (30)), асимптотическая формула для времени $\tau _{{{\text{int}}}}^{ \bot }$ содержит такую зависимость: она входит в нее через параметр $\beta = {K \mathord{\left/ {\vphantom {K {T.}}} \right. \kern-0em} {T.}}$ За счет этого в средах с заметной упругостью релаксометрический эксперимент может показывать существенную перенормировку величины $\tau _{{{\text{int}}}}^{ \bot }$ даже в сильном поле смещения.

Представленные выше результаты свидетельствуют о том, что присутствие поля смещения всегда ускоряет ориентационную релаксацию в вязкоупругом ферроколлоиде. Хотя этот вывод получен в рамках довольно грубой модели (приближение эффективного поля), но, как показано ниже, он сохраняет свою силу и при решении релаксационной задачи в полной постановке.

9. МАГНИТНАЯ РЕЛАКСОМЕТРИЯ ВЯЗКОУПРУГОГО ФЕРРОКОЛЛОИДА

Используем построенное в разделе 6 решение для расчета динамики спада намагниченности вязкоупругого ферроколлоида. Согласно теории линейного отклика (см., например, [26]), если известна динамическая восприимчивость системы, то ее реакция на мгновенное выключение зондирующего поля выражается соотношением

Для интегрального времени релаксации, подставляя в (31) найденное точное решение (20), получаем Величина ${{S}_{2}}$ находилась численно решением системы рекуррентных уравнений (19). Число использованных уравнений N достигало 20, однако уже при N = 10 относительная погрешность результатов становилась очень малой: не превышала 0.1%; с учетом этого обстоятельства большинство вычислений было выполнено при N = 10.

Расчет по формуле (31) показал, что начальные условия (23) для функции релаксации выполняются для приближения любого порядка. Независимость стартовых условий релаксации от порядка приближения прямо следует из рассматриваемой схемы эксперимента. Действительно, в момент времени, непосредственно следующий за скачком величины зондирующего поля, в системе существует лишь один неравновесный статистический момент $\left\langle {\delta {\mathbf{e}}} \right\rangle ;$ все остальные моменты тождественно равны нулю. Поэтому начальная стадия релаксации определяется быстрым ньютоновым трением и не зависит от вязкоупругих параметров среды-носителя.

На рис. 2 представлены релаксационные кривые изотропного (нулевое поле смещения) ферроколлоида при различной упругости дисперсионной среды. Сплошными линиями обозначены точные результаты, рассчитанные по формуле (31), а штриховыми – полученные в приближении эффективного поля (24). Как следствие условий (23), начальные (при t = 0) наклоны всех линий совпадают. На малых временах кривые K(t) с одинаковыми значениями β близки друг к другу, и интервал их близости тем протяженнее, чем меньше величина этого параметра.

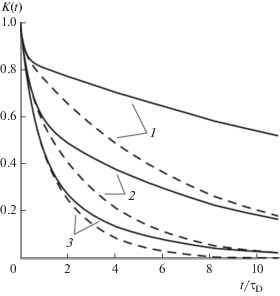
При малой упругости системы среда−носитель по своим свойствам мало отличается от ньютоновой жидкости, так что рассматриваемый ферроколлоид очень похож на феррожидкость. Поэтому релаксация намагниченности фактически происходит по простому экспоненциальному закону с единственным временем ${{\tau }_{{\text{D}}}}$ и различия между кривыми K(t) приближенного и точного решений не велики.

Как хорошо видно на графиках рис. 2, с увеличением упругости среды процесс магнитной релаксации замедляется. Точные решения все сильнее отличаются от приближенных, причем расхождение кривых $K\left( t \right)$ становится значительным на все более коротких временах. Очевидно, что такое поведение указывает на возрастающее влияние динамики высших (по величине $Q$) моментов функции распределения на долговременную часть намагниченности. Действительно, например, при $\beta = 10$ на временах, в 3–5 раз превышающих ${{\tau }_{{\text{D}}}},$ ошибка приближенного решения оказывается порядка самой измеряемой величины, а при $t > 6{{\tau }_{{\text{D}}}}$ уже существенно превосходит ее.

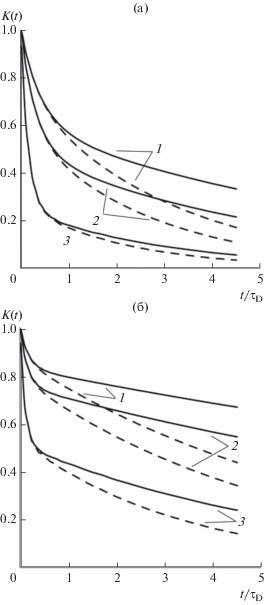
Присутствие постоянного магнитного поля ускоряет релаксационные процессы. На рис. 3 показаны кривые релаксации поперечной намагниченности для ферроколлоидов с фиксированной упругостью при различных значениях постоянного поля. Здесь так же, как и выше, сплошные линии отвечают точному расчету, а штриховые – приближенному, выражаемому формулой (24). Видно, что приближение эффективного поля хорошо справляется с описанием процесса релаксации на малых временах, однако оно приводит к значительной (и нарастающей со временем) ошибке, величина которой тем больше, чем выше упругость системы. Тем самым оказывается, что главный недостаток приближенного расчета – его непригодность для описания релаксации на промежуточных и больших временах, реальный процесс установления равновесия протекает гораздо медленнее.

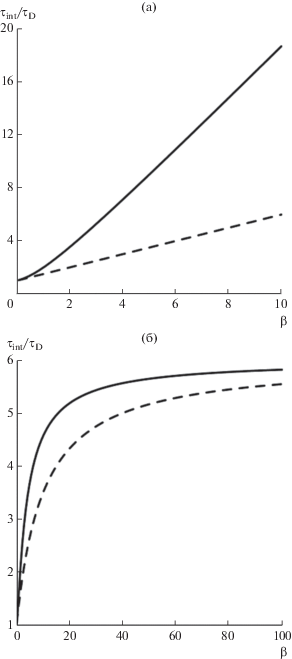
Эффект замедления релаксации с увеличением упругости среды иллюстрирует рис. 4, где показано, как зависит от параметра упругости интегральное время релаксации поперечной намагниченности при $\xi = 0,$ рассчитанное по формуле (32). Сплошная кривая – точный многомоментный расчет $(N = 10)$, а штриховая – приближение эффективного поля, формула (25). На рис. 4а представлен случай $q \gg 1,$ и поэтому форма штриховой линии описывается простым линейным соотношением ${{{{\tau }_{{{\text{int}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{int}}}}}} {{{\tau }_{{\text{D}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{D}}}}}} = 1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0em} 2}.$ Точный расчет (сплошная кривая на рис. 4a) показывает, что при малых значениях параметра упругости функция ${{\tau }_{{{\text{int}}}}}\left( \beta \right)$ нелинейна. При больших значениях этого параметра линейность зависимости восстанавливается, однако наклон кривой существенно увеличивается (примерно в 3.6 раза) по сравнению с результатом приближения эффективного поля. На рис. 4б показано, как интегральное время выходит на асимптотику медленной диффузии – превращается в $q{{\tau }_{{\text{D}}}},$ см. формулу (27), – при увеличении упругости в системе, вязкоупругость которой невелика $(q = 5).$

Влияние постоянного поля на темп релаксации поперечной компоненты намагниченности ферроколлоида демонстрирует рис. 5. Видно, что сильнее всего поле ускоряет релаксацию в системах с большой упругостью.

ВЫВОДЫ

Предложен основанный на кинетическом подходе метод расчета линейного отклика намагниченности вязкоупругого ферроколлоида при наличии постоянного поля (магнитного смещения). Вязкоупругость описывается моделью Джефриса, так что броуновская феррочастица при своем вращении, индуцированном приложенным полем, рассеивает энергию через два “канала” трения. Во-первых, это обычная (ньютонова) вязкость, доминирующая на малых временах. Во-вторых, это запаздывающее (максвеллово) диссипативное взаимодействие, которое характеризуется динамической упругостью и высокой вязкостью; этот механизм проявляет себя на больших временах. В нашей предыдущей работе [24] указанная задача была решена приближенно: кинетика системы описывалась с помощью только первой пары неравновесных моментов функции распределения, а наличие постоянного поля (магнитное смещение) не учитывалось. Построенный в настоящей работе полный функциональный базис для неравновесной функции распределения позволил снять эти ограничения, найти новые эффекты и оценить область применимости приближения [24].

Прежде всего, отметим, что наличием вязкоупругости – запаздывающим трением о среду-носитель – обусловлено появление медленной моды релаксации намагниченности ферроколлоида. Эта мода наиболее сильно выражена в системах со значительной упругостью; она существует и в присутствие относительно небольшого постоянного поля. Однако в сильном поле, когда магнитным моментам броуновских феррочастиц доступна лишь узкая зона углов в направлении поля, решающую роль в релаксации намагниченности играет быстрое, вязкое трение, отвечающее за их мелкомасштабные ориентационные флуктуации. Наличие медленной моды предсказывает уже приближение эффективного поля [24], но точный расчет радикально изменяет значение характерного времени релаксации этой моды. Указанное различие между точным и приближенным результатами иллюстрирует рис. 4а.

Экспериментальным подтверждением существования медленной моды релаксации в ферроколлоидах с линейной вязкоупругостью служат результаты работы [32]. Там при исследовании слабых желатиновых феррогелей было обнаружено, что характерное время релаксации намагниченности образца быстро растет с увеличением концентрации желатина, то есть упругости среды-носителя. При содержании желатина до 5 об. % этот рост квазилинеен, что в качественном отношении полностью согласуется с нашим расчетом – см. сплошную кривую на рис. 4а. При дальнейшем увеличении плотности системы рост времени магнитной релаксации убыстряется по сравнению с линейным, что, видимо, объясняется сильной нелинейной зависимостью упругости гидрогеля от концентрации желатина, однако этот случай выходит за рамки использованной модели.