Коллоидный журнал, 2020, T. 82, № 3, стр. 386-390

Несмотря на давнее существование теории межфазных явлений, некоторые ее важные вопросы до сих пор остаются в поле дискуссий. В частности, это касается зависимости поверхностного натяжения ${\sigma }$ от кривизны межфазной поверхности. Данную зависимость принято называть размерной зависимостью поверхностного натяжения. В настоящее время отсутствует единое мнение о характере этой зависимости даже для тривиального случая малой сферической капли. Так, например, в фундаментальных работах [1, 2] и хорошо известных монографиях [3–5] указывается на то, что с уменьшением радиуса капли поверхностное натяжение должно уменьшаться. В работах автора [6–10], как и во многих других работах, поддерживается такая же точка зрения. Существует и прямо противоположное мнение [11–20], причем приведенный здесь список работ далеко не полон. Рассмотрим вопрос более подробно.

i. Обратимое увеличение площади межфазной поверхности на величину dω требует затраты работы dA против межатомных или межмолекулярных сил взаимодействия. Это обуславливает поверхностное натяжение, которое является мерой избытка свободной энергии или энергии Гиббса в поверхностном слое по сравнению с объемами сосуществующих фаз:

где F и G – избыточная свободная энергия и избыточный потенциал Гиббса.

Зависимость поверхностного натяжения малой сферической капли от ее размера является решением уравнения Гиббса–Толмена–Кенига–Баффа (ГТКБ) [1, 3–5]

где r – радиус капли, δ – длина Толмена, равная по модулю расстоянию между поверхностью натяжения и эквимолекулярной поверхностью. Для не слишком малых капель можно считать, что δ = = const [1–5]. Если δ > 0, то с уменьшением радиуса капли поверхностное натяжение уменьшается; если δ < 0, то поверхностное натяжение возрастает; при δ = 0 размерная зависимость поверхностного натяжения отсутствует. Интегрирование уравнения ГТКБ различными способами проводилось в ряде работ [6–10, 20–24]. Если для капли принять условие δ > 0, то (1) интегрируется методом замены переменной и решение представляется в наиболее компактном виде: где ${{\sigma }^{{(\infty )}}}$ – поверхностное натяжение плоской поверхности, $x = r{\text{/}}\delta .$ Случай $\delta < 0$ с помощью уравнения (1) рассматривался в [20]. Следует отметить, что полученная в этой работе формула (3) не воспроизводит расчеты, выполненные по (2) при $\delta > 0$ и путем численного интегрирования (1) для произвольных значений δ. Можно предположить, что в [20] имеется издательская опечатка, но в одноименной работе этих же авторов, размещенной на сайте arXiv, приведена аналогичная формула.

ii. В [5, с. 190] проанализирован случай малого радиуса капли. Было отмечено, что при $r \to 0$ независимо от специфики системы поверхностное натяжение всегда понижается с уменьшением радиуса кривизны, т.е. должно выполняться условие $\delta > 0.$ При этом получена формула

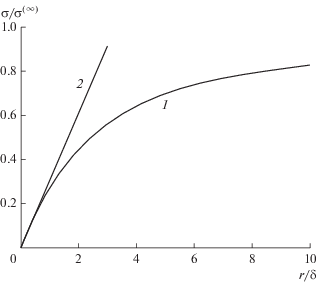
где K – положительный коэффициент, зависящий от температуры и состава конденсированной фазы. Вычисляя производную функции (2) в точке $x = 0,$ находим: $K = 0.304{{\sigma }^{{(\infty )}}}{\text{/}}\delta .$ В (3) должно быть $K \geqslant 0,$ поэтому приходим к условию $\delta > 0.$ На рис. 1 показаны графики решений (2) и (3).

Отрицательный знак длины Толмена для малой капли может являться особенностью той или иной теоретической модели [11], т.е. может и не иметь отношения к реальным жидкостям. При моделировании малой капли методом молекулярной динамики неизбежно возникают неопределенности в расчетах положений поверхности натяжения и эквимолекулярной поверхности [25]. Причем эти неопределенности зависят не только от числа частиц и потенциала их взаимодействия в ансамбле, но и от деталей реализации численных алгоритмов моделирования (граничные условия, термостат, вычисление давления и температуры, накопление ошибок и т.п.). В целом, если в какой-либо теоретической модели получается, что длина Толмена по абсолютной величине меньше межатомных расстояний в конденсированной фазе, то, учитывая флуктуации термодинамических параметров и возможные экспериментальные погрешности их определения, следует, по-видимому, принять, что поверхность натяжения и эквимолекулярная поверхность совпадают. Так, в [17, 18] приводится значение для длины Толмена $\delta = - 0.56\,\,{\text{{\AA}}},$ что по абсолютной величине сопоставимо, например, с таким квантовым параметром, как боровский радиус. В классической термодинамике, в рамках которой выведено уравнение (1), такие величины вообще не могут рассматриваться, поскольку не превышают равновесные (и тем более неравновесные) флуктуации радиуса капли. Как и любому термодинамическому параметру, поверхностному натяжению свойственны флуктуации, которые зависят от температуры. В [7] найдено общее выражение для равновесной флуктуации поверхностного натяжения

где ${{k}_{{\text{B}}}}$ – постоянная Больцмана, T – температура. В силу положительности (4) можно заключить, что функция $\sigma (r)$ в (1) для капли не должна быть убывающей. Из (3), (4) находим Для малых капель ($r \leqslant 1$ нм) при T = 300 К из (5) получатся оценка $\left\langle {{{{\left( {\Delta \sigma } \right)}}^{2}}} \right\rangle {\text{/}}\sigma \sim {{10}^{{ - 4}}}$ Н/м.

iii. Длина Толмена при $T > 0$ характеризует неоднородность межфазной области. Если $\delta < 0,$ то при уменьшении размера капли первым обращается в нуль радиус эквимолекулярной поверхности, что представляется малоправдоподобным [21]. Помимо этого, отрицательный знак длины Толмена для капли противоречит простым физическим соображениям. На выпуклой поверхности атомы “оголяются” и их потенциальная энергия меньше, чем на плоской и, тем более, на вогнутой поверхности. Следовательно, поверхностное натяжение выпуклой поверхности должно быть меньше, чем плоской или вогнутой поверхности, т.е. для капли должно быть $\delta > 0.$ В этом несложно убедиться, если вычислить поверхностное натяжение капли, используя парный межатомный потенциал. Из (1) имеем $\sigma = \Delta A{\text{/}}{{\omega }_{0}},$ где ΔΑ – работа, требующаяся для отрыва поверхностного атома, ${{{\omega }}_{{\text{0}}}}$ – площадь, занимаемая поверхностным атомом. В континуальном приближении

где n – объемная плотность атомов жидкости, V – объем капли, φ(ρ) – парный межатомный потенциал, ρ – расстояние от поверхностного атома до некоторой точки в объеме капли. В сферической системе координат интеграл (6) преобразуется к виду При записи (7) предполагалось, что поверхностный атом занимает лунку радиусом z. Равновесное значение z находится из условия минимума $(\Delta A)_{z}^{'} = 0,$ что эквивалентно уравнению $\varphi (z) = 0.$ Потенциал выберем в форме Ми–Ленарда-Джонса: где $D$ и ${{r}_{0}}$ – глубина потенциальной ямы и равновесное расстояние для взаимодействия между двумя атомами, a и b – параметры, отвечающие за силы притяжения и отталкивания. Выбор потенциала (8) обусловлен тем, что с его помощью были успешно рассмотрены зависимости поверхностной энергии от размеров и формы нанокристаллов [26].

Из (8) определяем равновесный радиус атомной лунки: $z = {{r}_{0}}{{({a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b})}^{{{1 \mathord{\left/ {\vphantom {1 {(b - a)}}} \right. \kern-0em} {(b - a)}}}}}.$ Подставляя (8) в (7) и выполняя интегрирование, при естественном условии $r \gg {{r}_{0}},z$ находим

где учтена площадь атомной лунки в виде полусферы ${{\omega }_{0}} \approx 2\pi {{z}^{2}}.$ Заметим, что формула вида (9) получается также из разложения (2) в ряд по степеням $\delta {\text{/}}r{\text{.}}$ При выводе (9) предполагалось, что капля является однородной. В связи с этим, значение параметра δ в (9) следует считать минимально возможным. При a = 6 и b = 12 имеем $\delta = 0.376{{r}_{0}}{\text{,}}$ что хорошо согласуется с результатом, полученным с помощью статистической механики [2] и тензора давления Ирвинга–Кирквуда: $\delta \approx {{r}_{0}}{\text{/}}3$ при $T \to 0$ [3, с. 115]. С увеличением температуры происходит рост толщины межфазного слоя и, соответственно, длины Толмена. Межфазный слой утолщается за счет превращения обеих граничащих фаз в неоднородную промежуточную фазу. В критической точке промежуточная фаза распространяется на весь объем, и поверхностное натяжение, согласно (2) и (3), обращается в нуль ($\delta \to \infty {\text{,}}$ $\sigma \to 0$). Экспериментально это проявляется, например, в виде критической опалесценции.

Формула (9) получена при достаточно грубых предположениях, но она вполне удовлетворительно воспроизводит экспериментальные данные по поверхностному натяжению. В табл. 1 в качестве примера представлены результаты расчетов поверхностного натяжения жидких инертных газов по формуле ${{\sigma }^{{(\infty )}}} \approx 0.792nD{{r}_{0}}{\text{,}}$ которая получается из (9) при a = 6 и b = 12. Все необходимые для расчетов численные данные были взяты из работ [27, 28] и соответствуют тройной точке. Среднее отклонение расчетных данных от экспериментальных составляет 5%.

iv. В данной статье рассмотрен самый простой случай, когда δ можно считать постоянной величиной. Однако вследствие сжимаемости жидкости при высоких капиллярных давлениях могут иметь место изменения величины и даже знака длины Толмена в зависимости от радиуса поверхности натяжения капли [29–33]. Как следствие, у искомой функции σ(r) появляется характерный максимум [5, 31–33]. Подобные изменения можно ожидать для определенных жидкостей при малых значениях радиуса капли, например при $r < 10$ нм. В рамках принятого здесь подхода этот вопрос требует специального рассмотрения, поэтому мы ограничимся только общими замечаниями. Во-первых, функция δ(r) должна быть такой, чтобы в целом обеспечивалась положительность решения уравнения (1). Во-вторых, это решение должно быть ассоциировано с конечными положительными флуктуациями поверхностного натяжения. Длина Толмена, к сожалению, не может быть экспериментально измерена прямыми методами, что не позволяет осуществить надежную поверку всех имеющихся теоретических моделей. В качестве максимального абсолютного значения δ можно приближенно принять толщину межфазного слоя [3, с. 44], измеренную, например, с помощью просвечивающей электронной микроскопии или эллипсометрии. Из косвенных методов изучения размерного эффекта поверхностного натяжения заслуживают внимания новые методы измерения параметров испарения и смачивания [34–36] для малых капель в зависимости от их размеров в различных PT-условиях.

Таким образом, на ряде примеров нами показано, что для малой сферической капли неполярной жидкости длина Толмена при условии ее постоянства является положительной величиной и поверхностное натяжение представляет собой неубывающую функцию радиуса капли.