Коллоидный журнал, 2020, T. 82, № 3, стр. 354-362
Термодинамика краевого угла сидячего пузырька
А. И. Русанов *
Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия
* E-mail: rusanov32@list.ru
Поступила в редакцию 26.11.2019
После доработки 02.12.2019
Принята к публикации 04.12.2019
Аннотация
Экспериментальный материал по краевым углам велик, но в большинстве своем относится к сидячим каплям, хотя пузырьки более интересны с точки зрения коллоидной науки, поскольку сидячий пузырек отличается наличием равновесной тонкой пленки жидкости на границе газа и твердого тела. В данной работе приводится вся совокупность современных термодинамических уравнений, необходимых для описания краевого угла пузырька любого размера. Однако, ввиду их сложности, выводятся и анализируются конкретные соотношения для малых, но макроскопических пузырьков. Рассматривается зависимость краевого угла пузырька от температуры, давления в жидкости, состава жидкой фазы и шероховатости твердой поверхности. В случае чистой жидкости, когда газовая фаза состоит из ее пара, полученные соотношения имеют значения для теории кавитации. Работа в целом имеет рамочный характер, так как представлены лишь общие основные результаты. Их детализация возможна в сочетании с экспериментальными данными.
ВВЕДЕНИЕ
Среди поверхностных явлений краевой угол относится к наиболее визуальным величинам и просто напрашивается для измерений. Экспериментальный материал по этой теме огромен. В то же время, являясь сложным и многофакторным параметром теории, краевой угол малопривлекателен для общих термодинамических построений. Исторически, больше всего времени и внимания ушло на вывод, интерпретацию и обобщение уравнения Юнга – основного термодинамического соотношения для краевого угла, связывающего его с поверхностными натяжениями прилегающих поверхностей (см. обзоры [1, 2], последнее упрощение достигнуто с использованием J-потенциала как нового термодинамического потенциала в теории поверхностей [3]) и линейным натяжением [4–6]. Однако краевой угол связан и с другими параметрами состояния. Недавно новые данные были получены для зависимости краевого угла сидячего пузырька от давления [7, 8]. Как известно, на границе пузырька с твердым телом образуется тонкая смачивающая пленка, обладающая расклинивающим давлением. Поэтому не удивительно, что интерес к сидячему пузырьку, проявившийся еще на заре исследования тонких пленок [9, 10], не увядает и в новые времена [11–14].
В данной работе, исходя из общих термодинамических соотношений, мы попытаемся рассмотреть зависимость краевого угла сидячего пузырька от основных параметров состояния. Чтобы избежать громоздкости результатов и облегчить их восприятие, ограничимся случаем малого, но макроскопического пузырька. Постараемся также избежать осложнений, связанных с термодинамикой твердого тела, которое неизменно присутствует в задачах о смачивании. В свое время Гиббсом был открыт дуализм поверхностного натяжения твердого тела. Он состоит в том, что обычное механическое определение поверхностного натяжения γ (для твердого тела оно становится тензорной величиной) не совпадает с термодинамическим определением поверхностного натяжения σ (обозначение Гиббса) как работы разрезания тела (для жидкостей γ = σ). Термодинамика твердых поверхностей может быть сформулирована в терминах как γ, так и σ. Поскольку именно последняя величина входит в уравнение Юнга, мы будем пользоваться вариантом с σ. Заметим, что и в описании объемной фазы твердого тела встречаются трудности понимания, связанные, прежде всего, с тем, что химический потенциал вещества твердого тела становится тензорной величиной [1, 2]. Чтобы уменьшить подобные трудности, будем считать твердое тело механически недеформируемым и застывшим в своей структуре при данной температуре. Тогда, что бы ни происходило в системе, над твердым телом не совершается никакой работы, а, значит, в изотермических условиях оно не дает вклада в изменение энергии системы.
ОБЩИЕ ТЕРМОДИНАМИЧЕСКИЕ СООТНОШЕНИЯ
Имея в виду, что упрощения, о которых говорилось выше, в будущем могут быть сняты, будем исходить из современных наиболее точных (пусть и сложных) соотношений, а уж потом вводить упрощения. На рис. 1 показан объект нашего рассмотрения – сидячий пузырек. Обозначим газовую фазу символом α, жидкую – символом β и твердую – символом γ (совпадает с обозначением поверхностного натяжения, но будет встречаться только в индексах). Межфазные поверхности будем обозначать двойными фазовыми символами. Краевой же угол θ относится к линии соприкосновения всех трех фаз. Этой линии приписывается линейное натяжение, которое, в полной аналогии с поверхностным натяжением, также обладает дуализмом (различием механического и термодинамического определений), если линия проходит по твердому телу. Мы будем адресоваться к термодинамическому линейному натяжению κ.
Рис. 1.
Сидячий пузырек на твердой поверхности: h и R – высота и радиус пузырька, r – радиус его основания, θ – краевой угол. Обозначение фаз: α – газ, β – жидкость, γ – твердое тело.

На сегодняшний день обобщенное уравнение Юнга для равновесного краевого угла имеет вид [1, 15]
(1)
$\cos {\kern 1pt} \theta = \frac{{{{k}_{{\text{s}}}}}}{\gamma }({{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}) + \frac{{{{k}_{{\text{l}}}}}}{\gamma }\left( {\frac{\kappa }{r} + \frac{{\partial \kappa }}{{\partial r}}} \right),$В правой части уравнения (1) имеются два слагаемых. Первое представляет собой уравнение Юнга с поправкой на шероховатость твердой поверхности. Второе связано с учетом линейного натяжения и вносит вклад тем весомее, чем меньше радиус кривизны линии трехфазного контакта. Для макроскопического пузырька этим вкладом можно пренебречь, и тогда уравнение (1) принимает вид
(2)
$\cos {\kern 1pt} \theta = \frac{{{{k}_{{\text{s}}}}}}{\gamma }({{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}})$(3)
$\begin{gathered} d{\kern 1pt} \cos {\kern 1pt} \theta = \frac{{{{k}_{\operatorname{s} }}}}{\gamma }(d{{\sigma }^{{\alpha \gamma }}} - d{{\sigma }^{{\beta \gamma }}}) - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{{{{\gamma }^{2}}}}({{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}})d\gamma + \frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{\gamma }d{{k}_{\operatorname{s} }}. \\ \end{gathered} $Дифференциалы поверхностных натяжений можно выразить через параметры состояния при помощи обобщенного уравнения адсорбции Гиббса [16]
(4)
$\begin{gathered} d{{\sigma }^{{lm}}} = - {{{\bar {s}}}^{{lm}}}dT + ({{{\hat {\gamma }}}^{{lm}}} - {{\sigma }^{{lm}}}\hat {1}):d{{{\hat {e}}}^{{lm}}} - \sum\limits_i {\Gamma _{i}^{{lm}}d{{\mu }_{i}}} , \\ (l \ne m;\,\,\,\,l,m = \alpha ,\beta ,\gamma ), \\ \end{gathered} $(5)
$d{{\sigma }^{{\alpha \beta }}} = d\gamma = - {{\bar {s}}^{{\alpha \beta }}}dT - \sum\limits_i {\Gamma _{i}^{{\alpha \beta }}d{{\mu }_{i}}} .$(6)
$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {s}}^{{\alpha \gamma }}}dT - \sum\limits_i {\Gamma _{i}^{{\alpha \gamma }}d{{\mu }_{i}}} ,$(7)
$d{{\sigma }^{{\beta \gamma }}} = - {{\bar {s}}^{{\beta \gamma }}}dT - \sum\limits_i {\Gamma _{i}^{{\beta \gamma }}d{{\mu }_{i}}} .$При формулировке уравнения адсорбции Гиббса всегда встает вопрос о выборе положения разделяющей поверхности. Для твердой поверхности это эквимолекулярная поверхность по отношению к веществу твердого тела, что для недеформируемого тела совпадает с его реальной физической поверхностью, т.е. граничной поверхностью твердого тела. В случае же жидкой поверхности, в подходе Гиббса разделяющая поверхность берется либо как эквимолекулярная поверхность в отношении основного компонента жидкости, например, растворителя (если поверхность плоская), либо как поверхность натяжения (если поверхность искривленная). Для последней действует уравнение Лапласа, но для произвольной разделяющей поверхности условие механического равновесия между двумя флюидными фазами записывается в виде
(8)
${{p}^{\alpha }} - {{p}^{\beta }} = \frac{{2\gamma }}{R} + \frac{{\partial \gamma }}{{\partial R}},$Подстановка (5)–(7) в (3) приводит к фундаментальному уравнению
(9)
$\begin{gathered} d{\kern 1pt} \cos {\kern 1pt} \theta = \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\left( { - {{{\bar {s}}}^{{\alpha \gamma }}} + {{{\bar {s}}}^{{\beta \gamma }}} + \frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{\gamma }{{{\bar {s}}}^{{\alpha \beta }}}} \right)dT - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{\gamma }\Gamma _{i}^{{\alpha \beta }}} \right)d{{\mu }_{i}}} + \\ + \,\,\frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{\gamma }d{{k}_{\operatorname{s} }}. \\ \end{gathered} $(10)
$\begin{gathered} d{\kern 1pt} \cos {\kern 1pt} \theta = \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\left( { - {{{\bar {s}}}^{{\alpha \gamma }}} + {{{\bar {s}}}^{{\beta \gamma }}} + \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}{{{\bar {s}}}^{{\alpha \beta }}}} \right)dT - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right)d{{\mu }_{i}}} + \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}d{{k}_{\operatorname{s} }}, \\ \end{gathered} $(11)
$d{{\mu }_{i}} = - s_{i}^{l}dT + \nu _{i}^{l}d{{p}^{l}} + \sum\limits_{k = 1}^{n - 1} {\frac{{\partial {{\mu }_{i}}}}{{\partial x_{k}^{l}}}} dx_{k}^{l}{\text{ }}\,\,\,\,(l = \alpha ,\beta ),$(12)
${{V}^{l}}d{{p}^{l}} = - {{S}^{l}}dT + \sum\limits_i {N_{i}^{l}d{{\mu }_{i}}} \,\,\,\,(l = \alpha ,\beta ),$Из уравнений (8)–(12) следует целая совокупность частных соотношений, которая и образует термодинамику краевого угла. Примеры таких соотношений приводятся ниже.
ВЛИЯНИЕ ШЕРОХОВАТОСТИ
Если температура и химические потенциалы всех компонентов закреплены, то состояние обеих флюидных фаз меняться уже не может, и остается только влияние шероховатости. Уравнение (10) в этом случае приводит к соотношению
(13)
${{\left( {\frac{{d{\kern 1pt} \ln \left| {\cos {\kern 1pt} \theta } \right|}}{{d\ln {{k}_{{\text{s}}}}}}} \right)}_{{T,{{\mu }_{i}}}}} = 1,$ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ КРАЕВОГО УГЛА
Этот вид зависимости наиболее сложен, поскольку в его формировании участвует не только флюидная, но и твердотельная часть системы. Ведь даже бездефектная решетка твердого тела с как угодно большим модулем упругости способна проводить тепло. Согласно уравнению (10), вид температурной зависимости краевого угла связан с внешними условиями, в которых находится исследуемая система. Предположим сначала, что давление и состав фазы β закреплены. Тогда из уравнения (11) имеем
Подставив (14) в (10) и принимая, что в качестве разделяющей поверхности на границе αβ используется эквимолекулярная поверхность в отношении компонента j (тогда $\Gamma _{j}^{{\alpha \beta }} = 0),$ находим Последнее слагаемое в (15) отражает влияние температуры на шероховатость подложки. Когда температура невелика и речь идет лишь о тепловом расширении тела, то величина производной коэффициента шероховатости зависит от структуры тензора теплового расширения. Если тензор шаровой (т.е. коэффициент линейного теплового расширения не зависит от направления) и геометрия шероховатости остается подобной себе при изменении температуры, то производная обращается в нуль и последнее слагаемое в (15) исчезает. При достаточно высокой температуре, приводящей дефекты кристалла в движение, начинается сглаживание шероховатости, и производная $d{\kern 1pt} \ln {\kern 1pt} {{k}_{{\text{s}}}}{\text{/}}dT$ становится отрицательной. Тогда в случае смачивания (θ < π/2, $\cos {\kern 1pt} \theta $ > 0) последнее слагаемое в (15) ослабляет, а в случае несмачивания (θ > π/2, $\cos {\kern 1pt} \theta $ < 0) – усиливает температурную зависимость краевого угла.Предположим теперь, что твердая поверхность гладкая $({{k}_{{\text{s}}}} = 1),$ а флюидная часть системы состоит из одного компонента (пусть это будет компонент j), т.е. фаза β – чистая жидкость (без примесей), а фаза α – ее пар. При этом уравнение (15) упрощается к виду
(16)
$\begin{gathered} ~\gamma {{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{dT}}} \right)}_{{{{p}^{\beta }}}}} = - {{{\bar {s}}}^{{\alpha \gamma }}} + {{{\bar {s}}}^{{\beta \gamma }}} + {{{\bar {s}}}^{{\alpha \beta }}}{\kern 1pt} \cos {\kern 1pt} \theta + \\ + \,\,\left( {\Gamma _{j}^{{\alpha \gamma }} - \Gamma _{j}^{{\beta \gamma }}} \right)s_{j}^{\beta }. \\ \end{gathered} $Хотя соотношение (16) значительно проще, чем (15), оно остается весьма сложным. Ведь пять избыточных величин в правой части (16) являются составными характеристиками. Особенно это касается энтропии. Например, полная избыточная энтропия ${{\bar {s}}^{{\alpha \gamma }}}$ разбивается на избыток ${{\bar {s}}^{{\alpha \gamma (\alpha )}}}$ со стороны фазы α и избыток ${{\bar {s}}^{{\alpha \gamma (\gamma )}}}$ со стороны фазы γ:
(17)
${{\bar {s}}^{{\alpha \gamma }}} = {{\bar {s}}^{{\alpha \gamma (\alpha )}}} + {{\bar {s}}^{{\alpha \gamma (\gamma )}}},$(18)
${{\bar {s}}^{{\alpha \gamma (\alpha )}}} \equiv \int\limits_{ - \infty }^{{{z}_{0}}} {({{s}_{\nu }} - s_{\nu }^{\alpha })dz} ,$(19)
${{\bar {s}}^{{\alpha \gamma (\gamma )}}} \equiv \int\limits_{{{z}_{0}}}^\infty {({{s}_{\nu }} - s_{\nu }^{\gamma })dz} ,$(20)
${{\bar {s}}^{{\beta \gamma }}} = {{\bar {s}}^{{\beta \gamma (\beta )}}} + {{\bar {s}}^{{\beta \gamma (\gamma )}}},$(21)
${{\bar {s}}^{{\beta \gamma (\beta )}}} \equiv \int\limits_{ - \infty }^{{{z}_{0}}} {({{s}_{\nu }} - s_{\nu }^{\beta })dz} ,$(22)
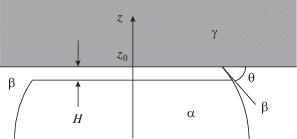
${{\bar {s}}^{{\beta \gamma (\gamma )}}} \equiv \int\limits_{{{z}_{0}}}^\infty {({{s}_{\nu }} - s_{\nu }^{\gamma })dz} .$Рис. 2.
Смачивающая пленка толщиной H на границе пузырька с твердым телом: z – декартова координата по нормали к твердой поверхности, ${{z}_{0}}$ – координата разделяющей поверхности.
Локальная плотность энтропии ${{s}_{\nu }}$ связана с молекулярной энтропией ${{s}_{j}}$ и концентрацией ${{c}_{j}} \equiv {{N}_{j}}{\text{/}}V$ компонента j соотношением
Известно, что для пара молекулярная энтропия в разы больше, чем для жидкости. Однако вдали от критической точки концентрация (плотность) вещества в паре на порядки меньше, чем в жидкости. А потому из двух величин под знаком интеграла в (18) малой оказывается все-таки $s_{\nu }^{\alpha }.$ Прежде, чем пренебречь ею, мы должны отметить, что интегрирование фактически проводится по области смачивающей пленки. Учитывая также (24), получим(25)
$\begin{gathered} \int\limits_{ - \infty }^{{{z}_{0}}} {({{s}_{\nu }} - s_{\nu }^{\alpha })dz} \approx \int\limits_{{{z}_{0}} - H}^{{{z}_{0}}} {{{s}_{j}}{{c}_{j}}dz} = \\ = \,\,\left\langle {{{s}_{j}}} \right\rangle \int\limits_{{{z}_{0}} - H}^{{{z}_{0}}} {{{c}_{j}}dz} \approx \left\langle {{{s}_{j}}} \right\rangle \Gamma _{j}^{{\alpha \gamma }}, \\ \end{gathered} $(26)
$ - \int\limits_{ - \infty }^{{{z}_{0}}} {({{s}_{\nu }} - s_{\nu }^{\alpha })dz + \Gamma _{j}^{{\alpha \gamma }}s_{j}^{\beta }} \approx \Gamma _{j}^{{\alpha \gamma }}\left( {s_{j}^{\beta } - \left\langle {{{s}_{j}}} \right\rangle } \right)$С учетом всего сказанного после подстановки (17) и (20) в (16) находим
(27)
$~\gamma {{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{dT}}} \right)}_{{{{p}^{\beta }}}}} \approx {{\bar {s}}^{{\beta \gamma \left( \beta \right)}}} + {{\bar {s}}^{{\alpha \beta }}}{\kern 1pt} \cos {\kern 1pt} \theta ,$Лучше всего была бы экспериментальная проверка. Большой материал по температурной зависимости “равновесного” краевого угла был набран в 20-ом веке (см., например, обзор [27]); ныне больше внимания уделяется динамическим краевым углам и компьютерному моделированию. Однако проведенные измерения относились, в основном, к наступающему краевому углу, что соответствует капле, а не пузырьку. В опытах с открытыми каплями полное равновесие между паром и смачивающей пленкой обычно не достигается, тогда как в случае пузырька оно гарантируется. Очевидно, создание базы данных для краевых углов пузырьков ждет своей реализации.
Выше мы рассмотрели случай однокомпонентной системы, когда пузырек состоит из пара жидкости. Очевидно, однако, что проведенный анализ приложим и к случаю пузырька нерастворимого газа. Это может быть, например, пузырек гелия в воде или, в пренебрежении растворимостью компонентов воздуха в жидкости, пузырек воздуха.
ЗАВИСИМОСТЬ КРАЕВОГО УГЛА ПУЗЫРЬКА ОТ ДАВЛЕНИЯ В ЖИДКОЙ ФАЗЕ
Далее мы будем анализировать только изотермические зависимости. При этом постулируется недеформируемость твердого тела, а потому не только первое, но и последнее слагаемое в правой части (10) исчезает. В результате уравнение (10) принимает вид
(28)
$d{\kern 1pt} \cos {\kern 1pt} \theta = - \frac{{{{k}_{s}}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{s}}}}\Gamma _{i}^{{\alpha \beta }}} \right)d{{\mu }_{i}}} .$(29)
$d{{\mu }_{i}} = \nu _{i}^{\beta }d{{p}^{\beta }} + \sum\limits_{k = 1}^{n - 1} {\frac{{\partial {{\mu }_{i}}}}{{\partial x_{k}^{\beta }}}} dx_{k}^{\beta }.$(30)
$\begin{gathered} d{\kern 1pt} \cos {\kern 1pt} \theta = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right){{\nu }_{i}}d{{p}^{\beta }}} - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_{i,k} {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right)} \frac{{\partial {{\mu }_{i}}}}{{\partial x_{k}^{\beta }}}dx_{k}^{\beta }, \\ \end{gathered} $(31)
${{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{d{{p}^{\beta }}}}} \right)}_{{T,x_{i}^{\beta }}}} = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right){{\nu }_{i}}} .$Заметим, что, ввиду малой концентрации любого компонента в паре, его адсорбция $\Gamma _{i}^{{\alpha \gamma }}$ на поверхности твердого тела фактически равна его реальному количеству в смачивающей (адсорбционной) пленке. Будем считать, что к пленке применимо соотношение термодинамики растворов
Поскольку адсорбция относится к единице площади поверхности, то и объем после суммирования будет относиться к единице площади, а это не что иное, как толщина пленки H (рис. 2): Подстановка (33) в (31) дает(34)
${{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{d{{p}^{\beta }}}}} \right)}_{{T,x_{i}^{\beta }}}} = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }H + \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_i {\left( {\Gamma _{i}^{{\beta \gamma }} + \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right){{\nu }_{i}}} .$(35)
$\begin{gathered} {{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{d{{p}^{\beta }}}}} \right)}_{{T,x_{i}^{\beta }}}} = - \frac{{{{k}_{{\text{s}}}}}}{\gamma }(H - \Gamma _{j}^{{\beta \gamma }}{{\nu }_{j}}) + \\ + \,\,\frac{{{{k}_{{\text{s}}}}}}{\gamma }\sum\limits_{i \ne j} {\left( {\Gamma _{i}^{{\beta \gamma }} + \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{{\text{s}}}}}}\Gamma _{i}^{{\alpha \beta }}} \right){{\nu }_{i}}} . \\ \end{gathered} $Если при растворителе j в число растворенных веществ в фазе β входят лишь малые примеси поверхностно-инактивных (или слабо поверхностно-активных) компонентов, то второе слагаемое в правой части (35) можно опустить, и мы приходим к соотношению
(36)
${{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{d{{p}^{\beta }}}}} \right)}_{{T,x_{i}^{\beta }}}} = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }(H - \Gamma _{j}^{{\beta \gamma }}{{\nu }_{j}}).$При наличии только одного компонента во флюидной части системы (когда пузырек состоит из пара компонента j) адсорбция $\Gamma _{j}^{{\beta \gamma }}$ становится автоадсорбцией жидкости, обусловленной ее сжимаемостью. Вдали от критической точки сжимаемость мала, и величиной $\Gamma _{j}^{{\beta \gamma }}$ в (36) можно пренебречь, что приводит к выражению
Его можно также рассматривать как приближенную форму соотношения (36). Все величины, стоящие в выражении (37), доступны экспериментальному определению. Но и само выражение (37) можно использовать для нахождения одной из стоящих в нем величин по значениям других.ЗАВИСИМОСТЬ КРАЕВОГО УГЛА ПУЗЫРЬКА ОТ СОСТАВА ЖИДКОСТИ
При закреплении температуры и давления в фазе β уравнение (30) упрощается к виду
(38)
$d{\kern 1pt} \cos {\kern 1pt} \theta = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_{i,k} {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right)} \frac{{\partial {{\mu }_{i}}}}{{\partial x_{k}^{\beta }}}dx_{k}^{\beta },$(39)
$\begin{gathered} d{\kern 1pt} \cos {\kern 1pt} \theta = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }(\Gamma _{j}^{{\alpha \gamma }} - \Gamma _{j}^{{\beta \gamma }})\sum\limits_k {\frac{{\partial {{\mu }_{j}}}}{{\partial x_{k}^{\beta }}}} dx_{k}^{\beta } - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{\gamma }\sum\limits_{i,k} {\left( {\Gamma _{i}^{{\alpha \gamma }} - \Gamma _{i}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{i}^{{\alpha \beta }}} \right)} \frac{{\partial {{\mu }_{i}}}}{{\partial x_{k}^{\beta }}}dx_{k}^{\beta }, \\ \end{gathered} $В простейшем случае, когда имеется только одно растворенное вещество, соотношение (39) принимает форму
(40)
$\begin{gathered} {{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{dx_{1}^{\beta }}}} \right)}_{{T,{{p}^{\beta }}}}} = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }(\Gamma _{2}^{{\alpha \gamma }} - \Gamma _{2}^{{\beta \gamma }})\frac{{d{{\mu }_{2}}}}{{dx_{1}^{\beta }}} - \\ - \,\,\frac{{{{k}_{\operatorname{s} }}}}{\gamma }\left( {\Gamma _{1}^{{\alpha \gamma }} - \Gamma _{1}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{1}^{{\alpha \beta }}} \right)\frac{{d{{\mu }_{1}}}}{{dx_{1}^{\beta }}}, \\ \end{gathered} $(42)
$\begin{gathered} {{\left( {\frac{{d{\kern 1pt} \cos {\kern 1pt} \theta }}{{dx_{1}^{\beta }}}} \right)}_{{T,{{p}^{\beta }}}}} = - \frac{{{{k}_{\operatorname{s} }}}}{\gamma }\left[ {\Gamma _{1}^{{\alpha \gamma }} - \Gamma _{1}^{{\beta \gamma }} - \frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{1}^{{\alpha \beta }} - } \right. \\ - \,\,\left. {\frac{{x_{1}^{\beta }}}{{1 - x_{1}^{\beta }}}(\Gamma _{2}^{{\alpha \gamma }} - \Gamma _{2}^{{\beta \gamma }})} \right]\frac{{d{{\mu }_{1}}}}{{dx_{1}^{\beta }}}. \\ \end{gathered} $(43)
$\begin{gathered} {{\left( {\frac{{d\theta }}{{dx_{1}^{\beta }}}} \right)}_{{T,{{p}^{\beta }}}}} > 0{\text{,}}\,\,\,\,{\text{если }}\Gamma _{1}^{{\alpha \gamma }} - \Gamma _{1}^{{\beta \gamma }} - \\ - \,\,\frac{{\cos {\kern 1pt} \theta }}{{{{k}_{\operatorname{s} }}}}\Gamma _{1}^{{\alpha \beta }} - \frac{{x_{1}^{\beta }}}{{1 - x_{1}^{\beta }}}(\Gamma _{2}^{{\alpha \gamma }} - \Gamma _{2}^{{\beta \gamma }}) > 0. \\ \end{gathered} $Знак выражения в правом неравенстве (43) зависит от соотношения величин пяти адсорбций, которые определяются природой вещества всех трех фаз, включая твердое тело. С этим же связаны содержание растворенного вещества в объемных фазах и величина краевого угла. Вариантов и комбинаций здесь множество. Например, если речь идет о настоящих поверхностно-активных веществах (ПАВ), то для них характерны большая адсорбция и малая концентрация в объеме раствора. Тогда $x_{1}^{\beta } \ll 1{\text{ }}--x_{1}^{\beta }{\text{,}}$ и, поскольку в последнем слагаемом (43) фигурируют адсорбции не ПАВ, а растворителя, это слагаемое можно отбросить. Крупные молекулы ПАВ малолетучи и практически отсутствуют в газовой фазе пузырька, а потому и адсорбцией $\Gamma _{1}^{{\alpha \gamma }}$ можно пренебречь. Если твердое тело (фаза γ) неполярно (скажем, это тефлон или парафин), а жидкость полярна (как, например, вода), то адсорбционные монослои ПАВ на поверхностях αβ и βγ одинаковы по ориентации молекул, и адсорбции $\Gamma _{1}^{{\alpha \beta }}$ и $\Gamma _{1}^{{\beta \gamma }}$ близки друг другу. Однако первая имеет при себе множитель $\cos {\kern 1pt} \theta {\text{/}}{{k}_{\operatorname{s} }},$ где всегда $\left| {\cos {\kern 1pt} \theta } \right| < 1$ и ${{k}_{\operatorname{s} }} > 1,$ так что типично адсорбция $\Gamma _{1}^{{\beta \gamma }}$ становится доминирующей величиной в (43). Сама она положительна, но стоит со знаком минус, и, следовательно, все правое выражение в (43) становится отрицательным. Тогда по правилу (43) становится отрицательной и производная $d\theta {\text{/}}dx_{1}^{\beta }{\text{:}}$ с увеличением содержания ПАВ в растворе краевой угол уменьшается. Можно сказать, что в данном случае под влиянием ПАВ происходит процесс лиофилизации лиофобной поверхности.
ЗАКЛЮЧЕНИЕ
Приведенное изложение термодинамики краевого угла можно назвать рамочным, ибо установлены только общие и главные соотношения, многое остается за кадром. Некоторые конкретные результаты были приведены лишь в качестве примеров. Во избежание подобия схоластики, более подробное рассмотрение и анализ частных случаев лучше проводить в связи с экспериментальными данными, и мы оставляем это на будущее. Нужно отметить, что здесь мы касались только равновесной термодинамики, тогда как теория таких важных явлений с участием пузырьков как кавитация или флотация требует более широкого подхода. При использовании неравновесной термодинамики систем при наличии потоков (прежде всего, теплового потока от твердой поверхности, на которой сидит пузырек) требуется знание динамического краевого угла. Наука успешно развивается в этом направлении [18–26], но и равновесная термодинамика сохраняет свое значение. Во-первых, это краеугольный камень, на который опирается дальнейшее развитие теории. Во-вторых, даже в динамических условиях некоторые вопросы разрешаются с помощью равновесной термодинамики [20].
Список литературы
Rusanov A.I. // Surf. Sci. Rep. 1996. V. 23. P. 173.
Rusanov A.I. // Surf. Sci. Rep. 2005. V. 58. P. 111.
Rusanov A.I. // Colloids Surf. 2014. V. 443. P. 363.
Rusanov A.I., Shchekin A.K., Tatyanenko D.V. // Colloids Surf. 2004. V. 250. P. 263.
Tatyanenko D.V., Shchekin A.K. // Interfacial Phenomena Heat Transfer. 2017. V. 5. P. 113.
Татьяненко Д.В., Щёкин А.К. // Коллоид. журн. 2019. Т. 81. С. 517.
Русанов А.И., Есипова Н.Е., Соболев В.Д. // Докл. АН СССР. 2019. Т. 202. С. 304.
Есипова Н.Е., Русанов А.И., Соболев В.Д., Ицков С.В. // Коллоид. журн. 2019. Т. 81. С. 507.
Frumkin A.N. // Acta Physicochim. URSS. 1938. V. 9. P. 313.
Derjaguin B.V. // Acta Physicochim. URSS. 1940. V. 12. P. 181.
Чураев Н.В., Соболев В.Д. // Коллоид. журн. 1995. Т. 57. С. 888.
Churaev N.V., Sobolev V.D. // Adv. Colloid Interface Science. 1995. V. 61. P. 1.
Русанов А.И. // Коллоид. журн. 2019. Т. 81. С. 767.
Русанов А.И. // Коллоид. журн. 2020. Т. 82. С. 75.
Русанов А.И. // Коллоид. журн. 1998. Т. 60. С. 815.
Rusanov A.I. // J. Colloid Interface Sci. 1978. V. 63. P. 330.
Kuni F.M., Shchekin A.K., Rusanov A.I., Widom B. // Adv. Colloid Interface Sci. 1996. V. 65. P. 71.
Eddington R.I., Kenning D.B.R. // Int. J. Heat Mass Transfer. 1979. V. 22. P. 1231.
Chigarev N.B., Chigareva T.S. // J. Eng. Phys. 1986. V. 50. P. 398.
Lubetkin S.D., Akhtar M. // J. Colloid Interface Sci. 1996. V. 180. P. 43.
Abarajith H.S., Dhir V.K. // Amer. Soc. Mech. Eng., Heat Transfer Div. 2002. V. 372. P. 467.
Mukherjee A., Kandlikar S.G. // Amer. Soc. Mech. Eng., Heat Transfer Div. 2004. V. 375. P. 555.
Phan H.T., Caney N., Marty P., Colasson S., Gavillet J. // Int. Commun. Heat Mass Transfer. 2010. V. 37. P. 964.
Nikolayev V.S., Janeček V. // Int. J. Heat Mass Transfer. 2012. V. 55. P. 7352.
Ardron K.H., Giustini G., Walker S.P. // Int. J. Heat Mass Transfer. 2017. V. 114. P. 1274.
Gheitaghy A.M., Saffari H., Arshadi S.S., Tabatabaei S.S. // Heat Transfer Res. 2018. V. 49. P. 423.
Neumann A.W. // Adv. Colloid Interface Sci. 1974. V. 4. P. 105.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал



