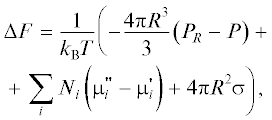Коллоидный журнал, 2020, T. 82, № 3, стр. 263-291

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ……………………………………….. ..263

1. СТАДИЯ НУКЛЕАЦИИ И ДРУГИЕ СТАДИИ В ФАЗОВОМ ПЕРЕХОДЕ ПЕРВОГО РОДА..……………………………………………………………264

2. СОСТАВ И РАЗМЕР КРИТИЧЕСКОГО ЗАРОДЫША НОВОЙ ФАЗЫ .…......................266

3. РАБОТА ОБРАЗОВАНИЯ КРИТИЧЕСКОГО ЗАРОДЫША И СКОРОСТЬ НУКЛЕАЦИИ ………………………………………………………………....269

4. ДИНАМИКА СТАЦИОНАРНОГО ДИФФУЗИОННОГО РОСТА МНОГОКОМПОНЕНТНОЙ ЗАКРИТИЧЕСКОЙ ЧАСТИЦЫ НОВОЙ ФАЗЫ.…………………………………………….............271

5. КИНЕТИКА СТАДИИ НУКЛЕАЦИИ В ПОДХОДЕ СРЕДНЕГО ПОЛЯ ПЕРЕСЫЩЕНИЯ. ОСОБЕННОСТИ РОСТА ПУЗЫРЬКОВ И КАПЕЛЬ........................................................275

6. ДИНАМИКА АВТОМОДЕЛЬНОГО РОСТА МНОГОКОМПОНЕНТНОЙ ЗАКРИТИЧЕСКОЙ ЧАСТИЦЫ НОВОЙ ФАЗЫ ………….....278

7. КИНЕТИКА СТАДИИ НУКЛЕАЦИИ В ПОДХОДЕ С ИСКЛЮЧЕННЫМ ОБЪЕМОМ. РАСПУХАНИЕ РАСТВОРОВ ПРИ ДЕГАЗАЦИИ .………........................................................283

8. О ПРИМЕНИМОСТИ ТЕОРИИ КРИСТАЛЛИЗАЦИИ КОЛМОГОРОВА В ТЕОРИИ СТАДИИ НУКЛЕАЦИИ.....………………………. 287

ЗАКЛЮЧЕНИЕ..………………………………….  288

СПИСОК ЛИТЕРАТУРЫ ………………………289

ВВЕДЕНИЕ

Построение теоретического описания фазовых переходов первого рода в метастабильных системах различной природы представляет первостепенный интерес для фундаментальной науки о коллоидных системах и межфазных поверхностях и опирающихся на нее новых технологий. Распад метастабильной фазы при фазовом переходе первого рода сопровождается зарождением (нуклеацией) частиц новой фазы. Возникающие на различных стадиях нуклеации дисперсные системы характеризуются распределениями частиц по размерам и составу, знание которых позволяет контролировать их эволюцию и применять при создании новых материалов, в методах быстрой очистки и разделения смесей, для формирования нанодисперсий с заданными свойствами в промышленных и медицинских целях [1–5]. Решение возникающих здесь задач связано с развитием термодинамики малых систем и кинетики нуклеации [6–11]. Работа в этой области требует объединения усилий специалистов по коллоидной химии, статистической физике и физико-химической механике.

Ключевыми термодинамическими характеристиками гомогенной нуклеации являются химические потенциалы компонентов в частицах новой фазы и работа образования критического зародыша новой фазы (т.е., частицы новой фазы, находящейся в неустойчивом равновесии с исходной метастабильной фазой), определенные как функции размера частиц и состава метастабильной фазы. Важнейшими кинетическими характеристиками оказываются скорости нуклеации (т.е., число критических зародышей новой фазы, формирующихся за единицу времени в единице объема системы) и скорости индивидуального роста закритических (т.е., превышающих критический размер) частиц новой фазы. Статистические характеристики дисперсных систем и их эволюция в любой момент времени задаются текущей функцией распределения закритических частиц новой фазы по их размерам и составу. Новым результатам для этих ключевых характеристик при нуклеации в замкнутых многокомпонентных системах, полученным за последние десять лет, и посвящен данный обзор. Причем, наряду с уже известными результатами, в обзор включены новые соотношения и обсуждения, являющиеся дальнейшим развитием работ авторов обзора. Ниже будут рассмотрены исходно гомогенные системы с произвольным числом компонентов и любыми значениями быстро создаваемых пересыщений в метастабильной фазе. Общий подход будет проиллюстрирован на примерах нуклеации газовых пузырьков в жидких растворах и нуклеации капель в пересыщенных парах. Будет представлен анализ эффектов нестационарной диффузии метастабильного вещества в закритические частицы новой фазы и показано, что эти эффекты могут быть очень значительными при нуклеации многокомпонентных газовых пузырьков в растворах при высоких пересыщениях и при большой растворимости газовых компонентов. В частности, будет продемонстрировано, что только учет нестационарности диффузии при росте пузырьков позволяет описать сильное увеличение объема и вспенивание жидкого раствора. Для капель влияние нестационарной диффузии оказывается существенным только при учете стефановского течения при неизотермичности конденсации.

1. СТАДИЯ НУКЛЕАЦИИ И ДРУГИЕ СТАДИИ В ФАЗОВОМ ПЕРЕХОДЕ ПЕРВОГО РОДА

В условиях быстрого установления метастабильности в замкнутой системе фазовые переходы, независимо от того, образуются ли капельки, поры, кристаллики или пузырьки газа как частицы новой фазы и соблюдаются или нет условия изотермичности, проходят через одни и те же стадии с определенной иерархией временн${\text{ы}}'$х масштабов [9, 12–17]. Начальной и самой быстрой является инкубационная стадия, на которой первые закритические частицы новой фазы появляются с преодолением активационного барьера нуклеации [15–18]. На следующей стадии, называемой стадией нуклеации, квазистационарное зарождение закритических частиц новой фазы продолжается вместе с ростом уже сформированных ранее частиц, причем увеличение числа и размера растущих частиц в условиях замкнутой системы останавливает в конечном итоге образование новых закритических частиц [9, 12–14, 18]. Гораздо более длительной стадией является стадия интенсивного роста крупных закритических частиц новой стабильной фазы без образования новых до почти полного истощения пересыщения исходной фазы [15, 18]. Конечной и самой долгой стадией является стадия созревания Оствальда (стадия Лифшица–Слёзова или стадия переконденсации), когда большие закритические частицы новой фазы растут за счет исчезновения малых частиц [19–22].

Традиционный подход к кинетическому описанию нуклеации основан на предположениях о том, что гомогенное зарождение закритических частиц новой фазы в закрытой системе происходит синхронно и равномерно по объему системы с уменьшением пересыщения метастабильной фазы. Это называется подходом среднего поля пересыщения к теории нуклеации. В рамках этого подхода скорость образования новых закритических зародышей снижается по всей системе одновременно с пересыщением. Приближение среднего поля пересыщения также подразумевает, что перенос молекул метастабильной фазы в растущие частицы новой фазы является стационарным.

Кинетическая теория нуклеации в однокомпонентных системах в приближении среднего поля пересыщения в настоящее время хорошо разработана. Влияние неизотермичности на разных стадиях нуклеации было описано Куни в рамках квазиодномерного подхода в [23–27] и в рамках двухмерного подхода Грининым и Куни в [27–32]. Было сделано очень важное развитие теории нуклеации в динамических условиях, когда пересыщения в системе устанавливаются достаточно медленно и подстраиваются под начинающийся фазовый переход [33]. Пределы применимости однокомпонентной кинетической теории зародышеобразования для стадии нуклеации, стадии роста и начала стадии переконденсации были проанализированы Дубровским и Назаренко в работах [34, 35] с уделением особого внимания эффектам, связанным с учетом флуктуаций в скорости роста частиц (при сохранении второй производной по размерам частиц новой фазы в кинетическом уравнении нуклеации). Было продемонстрировано, что эффектами, вызываемыми флуктуациями, можно пренебречь на стадии нуклеации, где расширение спектра размеров частиц новой фазы из-за нелинейного граничного условия для кинетического уравнения намного больше, чем флуктуационное. Другой предел применимости кинетической теории зародышеобразования связан с влиянием конечности количества молекул, доступных для нуклеации в малой замкнутой системе, на химический потенциал молекул в метастабильной фазе. Существуют различные физические ситуации [36–50], имеющие практическое значение, где такой эффект ограниченности объема приводит к затруднению фазового превращения и поэтому может быть важным как в однокомпонентных, так и в многокомпонентных системах. Нуклеация капель в порах, нуклеация пузырьков в микрокапельках, кристаллизация нелетучего компонента в каплях раствора и молекулярно-динамическое моделирование нуклеации и мицеллообразования в ячейках с периодическими граничными условиями требуют учета этого эффекта.

Отметим, что предположение о равномерном (по всему объему системы) уменьшении концентрации метастабильного вещества, безусловно, не выполняется в начале стадии нуклеации, когда из-за небольшого числа зарождающихся частиц новой фазы возникающие вокруг них области неоднородности концентраций еще не перекрываются [51–53]. Кроме того, использование допущений о стационарной диффузии метастабильного вещества в закритические частицы новой фазы существенно сужает область применимости теории, поскольку рост таких частиц зависит от степени пересыщения, и диффузия может быть нестационарной при сильном пересыщении. Особенно это относится к газовым пузырькам в пересыщенном газом растворе [54]. Чтобы учесть влияние неоднородности растворенного газа и нестационарной диффузии на зарождение и рост пузырьков, мы ранее сформулировали подход [55, 56], основанный на идее исключенного объема в процессе зародышеобразования. Подход с исключенным объемом учитывает, что в неоднородной диффузионной оболочке, окружающей растущий пузырек, рождение новых пузырьков сильно подавляется из-за снижения концентрации растворенного газа. Другими словами, сферическая оболочка жидкого раствора некоторой толщины вокруг каждого пузырька может быть исключена из области зародышеобразования, тогда как в остальной части раствора интенсивность зарождения закритических пузырьков остается на начальном уровне. Аналогичная ситуация существует и при нуклеации капель в пересыщенном паре, когда зарождение новых закритических капель подавляется вблизи уже растущей капли [57].

При использовании подхода с исключенным объемом зарождение закритических пузырьков в сильно перенасыщенном растворе ранее обсуждалось с использованием предположения, что в случае сильного пересыщения газа исключенные объемы отдельных пузырьков в растворе представляют собой тонкие сферические оболочки [54], которые не перекрываются. В работах [58, 59] были исследованы пределы подхода среднего поля пересыщений, а подход с исключенным объемом был расширен для описания изотермического и неизотермического зарождения закритических капель в пересыщенном паре с возможностью перекрытия диффузионных оболочек вокруг отдельных капель, которое может происходить на заключительном этапе стадии нуклеации. В [60] соответствующее расширение было сделано для стадии нуклеации закритических пузырьков газа. Следует отметить, что в случае конденсации пара в каплях диффузия пара в капли близка к стационарному процессу из-за сильной разницы в значениях плотности пара и жидкости в капле. С другой стороны, в случае нуклеации в пересыщенном газом растворе большая плотность жидкого раствора и соответствующая высокая теплопроводность раствора ослабляют тепловые эффекты зарождения газовых пузырьков и позволяют их не учитывать. Избыточное давление Лапласа в однокомпонентных закритических газовых пузырьках в случае умеренного пересыщения газа в растворе было недавно учтено в теории стадии нуклеации [61].

Если система имеет более одного компонента, по которому фаза метастабильна, картина нуклеации значительно усложняется [9, 62]. Со времен пионерских работ Рисса [63], Хиршфельдера [64], Мирабела и Каца [65], Штауфера [66] и Тринкауса [67] большой вклад в теорию бинарной и многокомпонентной нуклеации был сделан с точки зрения определения состава критического зародыша, скорости нуклеации и пути перехода в закритическую область размеров и составов на поверхности работы образования как функции нескольких независимых переменных [62, 68–81]. Развитие этой теории и ее экспериментальная проверка были выполнены в работах [82–87]. Общий кинетический подход к инкубационной стадии многокомпонентной нуклеации был построен с помощью метода полного разделения стабильных и неустойчивых переменных описания зародыша, предложенного Куни с соавторами [88, 89], развитого в работах [90–93] и распространенного на гетерогенное зародышеобразование на растворимых ядрах нуклеации в работах [94, 46 ]. Было показано, что переменные описания зародыша в дифференциальном уравнении Беккера–Деринга для многокомпонентной нуклеации могут быть разделены в окрестностях минимумов и седловых точек работы образования капель. Построены аналитические решения полученных одномерных дифференциальных уравнений, и найдены соответствующие времена релаксации к квазиравновесному и квазистационарному распределениям многокомпонентных зародышей к концу стадии инкубации [46]. Обсуждались также размерные зависимости поверхностного натяжения для критического многокомпонентного зародыша новой фазы [95–99]. Слезов и Шмельцер разработали подход к кинетической теории стадий нуклеации и роста многокомпонентной новой фазы в твердых растворах с заданным стехиометрическим составом [99]. Как было показано, основные кинетические уравнения, описывающие стадии нуклеации и роста в многокомпонентной системе, могут быть формально сведены к уравнениям, полученным для однокомпонентных систем, где эффективные коэффициенты диффузии и эффективное пересыщение выражаются в виде комбинаций термодинамических и кинетических параметров компонентов системы. Были получены результаты для квазистационарной скорости нуклеации, количества зародышей новой фазы, образовавшихся в результате нуклеации, и эволюции распределения зародышей по размеру во времени.

В данном обзоре проблемы, касающиеся инкубационной стадии и связи с классической теорией нуклеации, вообще не рассматриваются. Подробно обсуждаются результаты в кинетической теории стадии нуклеации закритических многокомпонентных пузырьков и капель, полученные за последние десять лет.

2. СОСТАВ И РАЗМЕР КРИТИЧЕСКОГО ЗАРОДЫША НОВОЙ ФАЗЫ

Нашей целью в этом разделе будет формулировка общих уравнений и приближений для описания термодинамического состояния одного сферического многокомпонентного зародыша новой фазы в неограниченной среде. Более конкретно, нас будет интересовать применение общих термодинамических соотношений к равновесному критическому газовому пузырьку в пересыщенном жидком растворе с несколькими растворенными газами и к равновесной критической капельке в атмосфере с несколькими конденсирующимися парами в неконденсирующемся газе-носителе. Полученные соотношения будут также применяться в разделах 3–7 для рассмотрения динамики роста отдельных закритических газовых пузырьков и закритических капель и эволюции их ансамблей на стадии нуклеации.

При равновесии жидкой и газовой фазы при давлении $P$ и абсолютной температуре $T$ химические потенциалы ${{\mu }_{i}}$ ($i = 1,2,...,k$) молекул компонентов, присутствующих в обеих фазах, равны:

Здесь и далее зависимость величин от температуры T в аргументах явно не указываем, так как температура в дальнейшем считается фиксированной, нижний индекс ${\text{l}}$ относится к жидкому раствору, а индекс g – к газовой фазе, {n₁} = (n₁₁, n₂₁, ...., ${{n}_{{k{\text{l}}}}})$ и $\left\{ {{{n}_{{\text{g}}}}} \right\} = ({{n}_{{1{\text{g}}}}},{{n}_{{2{\text{g}}}}},...,{{n}_{{k{\text{g}}}}}){\text{,}}$ где ${{n}_{{i{\text{l}}}}}$ и ${{n}_{{i{\text{g}}}}}$ – объемные концентрации i-го компонента в жидкой и газовой фазах.

Пусть номер k относится к растворителю. Химический потенциал молекул i-го компонента ($i = 1,2,...,k - 1$) в несжимаемой жидкой фазе может быть записан как

Здесь ${{P}_{0}}$ – выбранное опорное значение давления, ${{v}_{{i{\text{l}}}}}$ – парциальный молекулярный объем i-го компонента в растворе, ${{\mu }_{{i{\text{l}}}}}\left( {{{P}_{0}},\left\{ {{{n}_{{{\text{l}}0}}}} \right\}} \right)$ – химический потенциал i-го компонента при давлении P₀ и концентрациях $\left\{ {{{n}_{{{\text{l}}0}}}} \right\},$ ${{\gamma }_{i}} = {{\gamma }_{i}}\left( {{{P}_{0}},\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ – коэффициент активности i-го компонента в растворе при давлении P₀ с мольными долями $\left\{ {{{x}_{{\text{l}}}}} \right\}{\text{,}}$ ${{k}_{{\text{B}}}}$ – постоянная Больцмана.

Химический потенциал ${{\mu }_{{i{\text{g}}}}}\left( {P,\left\{ {{{n}_{{\text{g}}}}} \right\}} \right)$ молекул i-го ($i = 1,2,...,k$) компонента в газовой фазе можно записать в приближении идеального газа как функцию объемной концентрации n_ig этого компонента в виде

где ${{\mu }_{{i{\text{g}}}}}\left( {{{n}_{{i{\text{g}}0}}}} \right)$ – химический потенциал i-го компонента в газовой смеси при заданной температуре T и концентрации n_ig0. Если в (2.2) взять давление P₀ и концентрации $\left\{ {{{n}_{{{\text{g}}0}}}} \right\},$ при которых μ_il(P₀, {n₁₀}) = $ = {{\mu }_{{i{\text{g}}}}}\left( {{{n}_{{i{\text{g}}0}}}} \right)$, то из равенства (2.1) следует Соотношение (2.6) представляет собой обобщенную форму закона Рауля (см. также [96]) с коэффициентом пропорциональности между концентрацией n_ig молекул i-го компонента в газовой фазе и мольной долей x_il этого же компонента в жидкой фазе при давлении P. Видим, что этот коэффициент зависит от состава, давления и температуры жидкого раствора.

Перейдем теперь к рассмотрению равновесия газового пузырька в многокомпонентном растворе. Пусть давление в жидком растворе равно P₁ и полное давление газов в пузырьке с радиусом поверхности натяжения R между раствором и пузырьком равно ${{P}_{R}}{\text{.}}$ Обозначим поверхностное натяжение пузырька для поверхности натяжения как σ. Условие механического равновесия такого пузырька может быть записано в виде формулы Лапласа [100]

Будем прененебрегать присутствием пара растворителя (k-го компонента) в пузырьке и считать, что все десорбировавшиеся в пузырек газы равномерно распределены по пузырьку. Вместе с объемными концентрациями газов в пузырьке определим мольную долю i-го газового компонента в пузырьке радиуса R как

В предположении идеальности газов в пузырьке мы имеем связь между полной концентрацией газа в пузырьке ${{n}_{{{\text{g}},R}}} = \sum\nolimits_{i\, = \,1}^{k\, - \,1} {{n}_{{i{\text{g}}}}}\left( R \right)$ и внутренним давлением P_R в форме С учетом (2.7) удобно переписать (2.9) как где

Обозначим объемную концентрацию растворенного i-го газового компонента в жидком растворе на границе пузырька радиуса R как ${{\left. {{{n}_{{i{\text{l}}}}}} \right|}_{R}}$ ($i = 1,2,...,k - 1$). Соответствующая мольная доля равна ${{\left. {{{x}_{{i{\text{l}}}}}} \right|}_{R}} = {{{{{\left. {{{n}_{{i{\text{l}}}}}} \right|}}_{R}}} \mathord{\left/ {\vphantom {{{{{\left. {{{n}_{{i{\text{l}}}}}} \right|}}_{R}}} {{{n}_{{\text{l}}}}}}} \right. \kern-0em} {{{n}_{{\text{l}}}}}}.$ Выберем в случае пузырька в качестве концентрации ${{n}_{{i{\text{g}}0}}}$ ($i = 1,2,...,k - 1$) для каждого из растворенных газов их концентрацию ${{\tilde {n}}_{{i{\text{g}}}}}$ при равновесии этого газа с плоской поверхностью его раствора в жидком растворителе при заданной температуре и давлении ${{P}_{{\text{l}}}}{\text{.}}$ Применяя обобщенный закон Рауля (2.6) к идеальной газовой смеси, находящейся под давлением ${{P}_{R}}$ в химическом равновесии с реальным раствором при давлении $P = {{P}_{{\text{l}}}},$ с учетом (2.4) и ${{P}_{0}} = {{P}_{{\text{l}}}}$ получаем

Соотношение (2.12) определяет связи между ${{n}_{{i{\text{g}}}}}\left( R \right)$ и равновесным составом $\left\{ {{{{\left. {{{n}_{{i{\text{l}}}}}} \right|}}_{R}}} \right\}$ или мольным составом $\left\{ {{{{\left. {{{x}_{{i{\text{l}}}}}} \right|}}_{R}}} \right\}$ раствора на поверхности пузырька радиуса R. Используя (2.8) и (2.10), перепишем (2.12) в виде

В приближении разбавленного раствора, т.е. при ${{{{{\left. {{{{\left. {{{x}_{{i{\text{l}}}}}} \right|}}_{R}} = {{n}_{{i{\text{l}}}}}} \right|}}_{R}}} \mathord{\left/ {\vphantom {{{{{\left. {{{{\left. {{{x}_{{i{\text{l}}}}}} \right|}}_{R}} = {{n}_{{i{\text{l}}}}}} \right|}}_{R}}} {{{n}_{{\text{l}}}}}}} \right. \kern-0em} {{{n}_{{\text{l}}}}}} \ll 1$ ($i = 1,2,...,k - 1$), и в предположении ${{\gamma }_{i}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right) \approx {{\tilde {\gamma }}_{i}}\left( {\left\{ {{{{\tilde {x}}}_{{\text{l}}}}} \right\}} \right)$ из (2.13) и (2.4), (2.8) и (2.10) следует линейное соотношение между ${{\left. {{{n}_{{i{\text{l}}}}}} \right|}_{R}}$ и ${{n}_{{i{\text{g}}}}}\left( R \right)$ в виде закона Генри:

где – растворимость i-го газового компонента в объемном жидком растворителе. В приближении разбавленного раствора растворимость ${{s}_{i}}$ не зависит от давления и состава в жидком растворе. В отсутствие других газов, кроме i-го газового компонента, давление ${{P}_{{\text{l}}}}$ в газовой фазе равно ${{P}_{{\text{l}}}} = {{\tilde {n}}_{{i{\text{g}}}}}{{k}_{{\text{B}}}}T$ и

Определим пересыщение ${{\zeta }_{i}}$ i-го газового компонента в многокомпонентном жидком растворе при давлении ${{P}_{{\text{l}}}}$ через отклонение объемной концентрации ${{n}_{{i{\text{l}}}}}$ от концентрации ${{\tilde {n}}_{{i{\text{l}}}}}{\text{:}}$

Пузырек радиуса ${{R}_{{\text{c}}}}$ называется критическим, если он находится в химическом равновесии с раствором для каждого газового компонента. Объемные концентрации растворенных газовых компонентов в случае критического пузырька однородны и равны ${{n}_{{i{\text{l}}}}} = {{\left. {{{n}_{{i{\text{l}}}}}} \right|}_{{{{R}_{{\text{c}}}}}}}$ ($i = 1,2,...,k - 1$), в то время как состав газов в критическом пузырьке можно обозначить как $\left\{ {{{x}_{{{\text{gc}}}}}} \right\}.$

Как следует из (2.14), (2.16) и (2.17), при заданных пересыщениях газов

С учетом равенства $\sum\nolimits_{i\, = \,1}^{k\, - \,1} {{{x}_{{i{\text{gс}}}}}} = 1$ из (2.18) вытекают следующие выражения для критического радиуса ${{R}_{{\text{c}}}}$ пузырька и концентрации газа ${{x}_{{i{\text{gc}}}}}$ [101]: где мы ввели полное пересыщение $\bar {\zeta }$ газа для многокомпонентного раствора соотношением Заметим, что в правой части (2.20) стоит не относительная доля i-го газового компонента в растворе, а более сложная, ввиду определения (2.17), величина ${{\left( {{{{{n}_{{i{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{i{\text{l}}}}}} {{{{\tilde {n}}}_{{i{\text{l}}}}}}}} \right. \kern-0em} {{{{\tilde {n}}}_{{i{\text{l}}}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{n}_{{i{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{i{\text{l}}}}}} {{{{\tilde {n}}}_{{i{\text{l}}}}}}}} \right. \kern-0em} {{{{\tilde {n}}}_{{i{\text{l}}}}}}}} \right)} {\left[ {\sum\nolimits_{m\, = \,1}^{k\, - \,1} {{{{{n}_{{m{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{m{\text{l}}}}}} {{{{\tilde {n}}}_{{m{\text{l}}}}}}}} \right. \kern-0em} {{{{\tilde {n}}}_{{m{\text{l}}}}}}}} } \right]}}} \right. \kern-0em} {\left[ {\sum\nolimits_{m\, = \,1}^{k\, - \,1} {{{{{n}_{{m{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{m{\text{l}}}}}} {{{{\tilde {n}}}_{{m{\text{l}}}}}}}} \right. \kern-0em} {{{{\tilde {n}}}_{{m{\text{l}}}}}}}} } \right]}},$ которую с учетом (2.16) можно выразить через растворимости компонентов как ${{\left( {{{{{n}_{{i{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{i{\text{l}}}}}} {{{s}_{i}}}}} \right. \kern-0em} {{{s}_{i}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{n}_{{i{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{i{\text{l}}}}}} {{{s}_{i}}}}} \right. \kern-0em} {{{s}_{i}}}}} \right)} {\left[ {\sum\nolimits_{m\, = \,1}^{k\, - \,1} {{{{{n}_{{m{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{m{\text{l}}}}}} {{{s}_{m}}}}} \right. \kern-0em} {{{s}_{m}}}}} } \right]}}} \right. \kern-0em} {\left[ {\sum\nolimits_{m\, = \,1}^{k\, - \,1} {{{{{n}_{{m{\text{l}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{m{\text{l}}}}}} {{{s}_{m}}}}} \right. \kern-0em} {{{s}_{m}}}}} } \right]}}.$

Полное пересыщение $\bar {\zeta }$ является удобным количественным параметром, характеризующим метастабильность многокомпонентной жидкогазовой смеси. Как правило, поверхностное натяжение пузырька σ (и с учетом уравнения (2.11) радиус ${{R}_{ * }}$) является функцией всех концентраций $\left\{ {{{n}_{{\text{l}}}}} \right\}$ компонентов раствора. Кроме того, возможен учет неидеальности раствора на основе уравнения (2.13). Все это дает дополнительные вклады в зависимость критического радиуса пузырька от состава жидкого раствора, приводя к более сложной зависимости от пересыщений растворенных газов.

В случае сферической капли радиуса R в атмосфере с несколькими конденсирующимися парами в неконденсирующемся газе-носителе давление ${{P}_{{\text{g}}}}$ есть полное давление в газовой фазе, а ${{P}_{R}}$ – давление в капле. При механическом равновесии капли с газовой атмосферой формула Лапласа (2.7) может быть записана как

где σ имеет смысл поверхностного натяжения для поверхности натяжения капли радиуса R. В общем случае будем считать поверхностное натяжение σ функцией мольных долей всех k компонентов раствора в капле и радиуса капли.

Обозначим объемную концентрацию i-го компонента в газовой фазе на границе капли радиуса R как ${{\left. {{{n}_{{i{\text{g}}}}}} \right|}_{R}}$ ($i = 1,2,...,k$). Выберем в случае капельки в качестве концентрации ${{n}_{{i{\text{g}}0}}}$ ($i = 1,2,...,k$) для каждого из паров их концентрацию ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}$ при равновесии этого пара с плоской поверхностью его чистой жидкости при заданной температуре и давлении ${{P}_{{\text{l}}}}$ (в присутствии неконденсирующегося пассивного газа). Применяя обобщенный закон Рауля (2.6) к жидкому раствору, находящемуся под давлением $P = {{P}_{R}}$ в химическом равновесии с идеальной газовой смесью при давлении ${{P}_{{\text{g}}}}{\text{,}}$ учитывая равенства ${{P}_{0}} = {{P}_{{\text{g}}}}$ и ${{\gamma }_{{i0}}}{{x}_{{i{\text{l}}0}}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\gamma } }_{i}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }_{{i{\text{l}}}}} = 1$ (при ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }_{{i{\text{l}}}}} = 1$), (2.22) и определение (2.4), получаем

Это соотношение при заданных $\left\{ {{{x}_{{\text{l}}}}} \right\}{\text{,}}$ ${{P}_{{\text{g}}}}$ и R определяет равновесные концентрации паров на границе капли. Для равновесной газовой фазы ${{\left. {{{n}_{{i{\text{g}}}}}} \right|}_{{{{R}_{{\text{с}}}}}}} = {{n}_{{i{\text{g}}}}}$ ($i = 1,2,...,k$).

Определим пересыщение ${{\zeta }_{i}}$ i-го парового компонента в атмосфере вокруг капли при давлении ${{P}_{{\text{g}}}}$ через отклонение объемной концентрации ${{n}_{{i{\text{g}}}}}$ от концентрации ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}$ как

Если заданы все пересыщения $\left\{ \zeta \right\}$ в газовой фазе и газовая фаза равновесна, то с помощью (2.23) можем найти радиус ${{R}_{{\text{c}}}}$ критической капли и ее состав $\left\{ {{{x}_{{{\text{lc}}}}}} \right\}$. Полагая в (2.23) $R = {{R}_{{\text{c}}}},$ учитывая равенства ${{\left. {{{n}_{{i{\text{g}}}}}} \right|}_{{{{R}_{{\text{с}}}}}}} = {{n}_{{i{\text{g}}}}}$ ($i = 1,2,...,k$) и определение (2.24), получаем, что критический радиус ${{R}_{{\text{c}}}}$ капли равен

Удобно определить новую величину V:

Тогда выражение (2.25) для радиуса критической капли записывается как Как видно из (2.26), величина V является параметром, который не зависит от номера компонента и связан с молекулярными объемами и составом $\left\{ {{{x}_{{{\text{lc}}}}}} \right\}$ критической многокомпонентной капли.

В случае идеального раствора в капле имеем

В этом случае выражение (2.26) преобразуется к виду Это позволяет выразить мольную долю ${{x}_{{i{\text{lc}}}}}$ i-го компонента ($i = 1,2,...,k$) в критической капле через параметр V как откуда с учетом равенства $\sum\nolimits_{i\, = \,1}^k {{{x}_{{i{\text{lс}}}}}} = 1$ получаем

Трансцендентное уравнение (2.31) неявно определяет неизвестный параметр $v = v\left( {\left\{ \zeta \right\}} \right)$ как функцию пересыщений всех паров $\left\{ \zeta \right\}$ при идеальности раствора в критической капле. Подстановка найденной функции в соотношение (2.30) позволяет явно выразить все мольные доли ${{x}_{{i{\text{lc}}}}}$ (i = 1, 2, $...,k$) в критической капле также как функции пересыщений всех паров $\left\{ \zeta \right\}{\text{.}}$

Определим полное пересыщение паров в газовой атмосфере как

Как следует из (2.27), образование критической капли возможно при $v > 0$ (требуется положительное значение радиуса ${{R}_{{\text{c}}}}$). Это условие, как следует из уравнения (2.31) и определения (2.32), приводит к условию $\bar {\zeta } > 0$ на полное пересыщение системы. Для однокомпонентного случая это условие превращается в обычное условие положительности пересыщения конденсирующегося пара. В этом смысле полное пересыщение $\bar {\zeta }$ играет ту же роль в многокомпонентной системе, что и пересыщение пара в однокомпонентном случае. В случае, когда все парциальные пересыщения ${{\zeta }_{i}}$ ($i = 1,2,...,k$) равны нулю для многокомпонентной системы с $k > 1$, из (2.32) находим $\bar {\zeta } \equiv $ $ \equiv k - 1.$ Согласно определению (2.27) в этом случае ${{R}_{{\text{c}}}} > 0$, т.е. это случай пересыщенной смеси паров.

В случае неидеального раствора нам необходимо точно знать все активности ${{\gamma }_{i}} = {{\gamma }_{i}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ и парциальные объемы ${{v}_{{i{\text{l}}}}} = {{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ ($i = 1,2,...,k$) в жидком растворе как функции состава капли $\left\{ {{{x}_{{\text{l}}}}} \right\}{\text{.}}$ Перепишем (2.26) в виде

Подстановка (2.33) в равенство $\sum\nolimits_{i\, = \,1}^k {{{x}_{{i{\text{lс}}}}}} = 1$ дает Уравнения (2.33) и (2.34) образуют систему нелинейных уравнений, которые определяют неизвестный параметр v и мольные доли ${{x}_{{i{\text{lc}}}}}$ (i = 1, 2, $...,k$) в критической капле как функции пересыщений $\left\{ \zeta \right\} = \left( {{{\zeta }_{1}},...,{{\zeta }_{k}}} \right)$ всех компонентов пара в случае неидеального раствора в капле [102].

3. РАБОТА ОБРАЗОВАНИЯ КРИТИЧЕСКОГО ЗАРОДЫША И СКОРОСТЬ НУКЛЕАЦИИ

Определим выраженную в единицах ${{k}_{{\text{B}}}}T$ минимальную работу ΔF образования многокомпонентной частицы новой фазы с радиусом поверхности натяжения R и давлением P_R как [40, 100]

где $P$ – давление в метастабильной фазе, ${\mu }_{i}^{'}$ и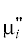 – химические потенциалы компонентов соответственно в метастабильной и новой фазах (индекс i нумерует компоненты, присутствующие в этих фазах), ${{N}_{i}}$ – полное количество молекул i-го компонента в частице (включая адсорбционный избыток Гиббса этого компонента). Для критического зародыша новой фазы 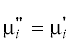для всех $i{\text{.}}$ Использование в (3.1) формул Лапласа (2.7) или (2.22) для поверхности натяжения дает известное выражение Гиббса для работы $\Delta {{F}_{{\text{c}}}}$ образования критического зародыша в виде

С учетом определений (2.19) и (2.11) в случае критического пузырька в пересыщенном газами растворе при полном пересыщении $\bar {\zeta }$ формула (3.2) сводится к

В случае критической капли в атмосфере пересыщенных паров из (3.2) с учетом соотношения (2.27) имеем

Следует отметить, что соотношения (3.3) и (3.4) учитывают зависимость поверхностного натяжения в критическом пузырьке и критической капельке и парциальных объемов компонентов в критической капельке от их состава, который, как показано в разделе 2, определяется пересыщениями $\left\{ \zeta \right\}$ компонентов в метастабильной фазе. Как видно из (3.3), в пренебрежении зависимостью поверхностного натяжения σ от состава критического пузырька зависимость работы образования критического пузырька определяется полным пересыщением $\bar {\zeta }$ растворенных газов в жидком растворе. В случае идеального раствора в капельке при равенстве всех парциальных объемов компонентов ${{v}_{{i{\text{l}}}}} = {{v}_{{\text{l}}}}$ можно связать параметр V в соотношении (2.31) с полным пересыщением паров $\bar {\zeta }$ вокруг критической капельки в виде

что позволяет нам представить (3.4) как Тогда в пренебрежении зависимостью поверхностного натяжения σ от состава критической капли работа образования критической капли также определяется полным пересыщением $\bar {\zeta }$ (в данном случае паров в атмосфере вокруг критической капли). Во всех других случаях зависимость $\Delta {{F}_{{\text{c}}}}$ от пересыщений в формулах (3.3) и (3.4) является более сложной. При идеальности раствора вокруг пузырька или в капле требуется использование уравнений (2.20), (2.30), (2.31) с учетом явного задания поверхностного натяжения $\sigma \left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ как функции состава раствора. При неидеальности жидкого раствора потребуется и явное задание коэффициентов активности ${{\gamma }_{i}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ как функций состава раствора.

Выражение для скорости нуклеации $J$ частиц новой фазы в любой точке метастабильной фазы можно записать [6–8] как

где C – предэкспоненциальный множитель. Величины $\Delta {{F}_{{\text{c}}}}$ и C являются функциями всех пересыщений $\left\{ \zeta \right\}$ в метастабильной фазе и могут изменяться во времени вместе с этими пересыщениями на стадии нуклеации. Однако можно ожидать, что множитель C является медленно меняющейся функцией $\left\{ \zeta \right\}$ по сравнению с ${{e}^{{ - \Delta {{F}_{{\text{c}}}}}}}{\text{.}}$ Поэтому зависимость работы $\Delta {{F}_{{\text{c}}}}$ от пересыщений $\left\{ \zeta \right\}$ является более важной и играет решающую роль для стадии нуклеации.

Введем новую величину ${{\varphi }_{i}}(t)$ соотношением

Поскольку, в силу (2.32), $\sum\nolimits_i {{{\varphi }_{i}}\left( t \right)} = \left( {{{{\bar {\zeta }}}_{0}} - } \right.$ $ - {{\left. {\bar {\zeta }\left( t \right)} \right)} \mathord{\left/ {\vphantom {{\left. {\bar {\zeta }\left( t \right)} \right)} {{{{\bar {\zeta }}}_{0}}}}} \right. \kern-0em} {{{{\bar {\zeta }}}_{0}}}}{\text{,}}$ то ${{\varphi }_{i}}(t)$ представляет собой вклад i-го компонента в относительное уменьшение полного пересыщения $\bar {\zeta }$ к моменту времени t. Как будет показано в разделах 4 и 6, на стадии нуклеации отклонения ${{\zeta }_{{i,0}}} - {{\zeta }_{i}}\left( t \right)$ должны быть относительно небольшими. Учитывая только линейные по ${{\varphi }_{i}}(t)$ отклонения, можно переписать выражения (3.2) для $\Delta {{F}_{{\text{c}}}}(t)$ и (3.7) для $J(t)$ в виде где Поскольку на стадии нуклеации максимальное значение выражения $\sum\nolimits_i {{{\Gamma }_{i}}{{\varphi }_{i}}} $ в показателе экспоненты в (3.10) порядка единицы, то линейное по ${{\varphi }_{i}}(t)$ приближение в разложении (3.9) оправдано, если хотя бы одна из величин ${{\Gamma }_{i}}$ будет намного больше единицы. Такая ситуация имеет место вдали от спинодали при не слишком большой скорости нуклеации, когда $\Delta {{F}_{{{\text{c}},0}}} \gg 1.$ Убедимся в этом в случаях многокомпонентных критических пузырьков и капелек. Из (3.13) с учетом (3.3) и (2.21) для пузырьков находим а из (3.4) с учетом (3.13) для капелек следует

С помощью (2.17) можно исключить производные ${{\partial {\kern 1pt} \ln {\kern 1pt} {{x}_{{j{\text{l}}}}}} \mathord{\left/ {\vphantom {{\partial {\kern 1pt} \ln {\kern 1pt} {{x}_{{j{\text{l}}}}}} {\partial {{\zeta }_{i}}}}} \right. \kern-0em} {\partial {{\zeta }_{i}}}}$ в (3.14) и свести параметры ${{\Gamma }_{i}}$ для критических пузырьков в случае разбавленного раствора газов к виду

Используя соотношение (2.26), перепишем (3.15) для критических капель как где ${{v}_{0}} = v\left( {\left\{ {{{\zeta }_{0}}} \right\}} \right){\text{,}}$ ${{v}_{{i{\text{l}},0}}} = {{v}_{{i{\text{l}}}}}\left( {\left\{ {{{\zeta }_{0}}} \right\}} \right){\text{.}}$ Соотношения для производных ${{\partial {\kern 1pt} \ln {\kern 1pt} {{x}_{{m{\text{l}}}}}} \mathord{\left/ {\vphantom {{\partial {\kern 1pt} \ln {\kern 1pt} {{x}_{{m{\text{l}}}}}} {\partial {\kern 1pt} \ln {\kern 1pt} {{\zeta }_{i}}}}} \right. \kern-0em} {\partial {\kern 1pt} \ln {\kern 1pt} {{\zeta }_{i}}}}$ в правой части (3.17) обеспечиваются уравнениями (2.33) и (2.34) при заданных для реального раствора зависимостях ${{\gamma }_{i}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)$ и ${{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right){\text{.}}$ Главную роль в правых частях выражений (3.16) и (3.17) играют первые слагаемые, так что величины ${{\Gamma }_{i}}$ оказываются одного порядка с $\Delta {{F}_{{{\text{c}},0}}}{\text{.}}$ Соответственно как для пузырьков, так и для капелек необходимое условие ${{\Gamma }_{i}} \gg 1$ выполняется одновременно с условием $\Delta {{F}_{{{\text{c}},0}}} \gg 1.$

4. ДИНАМИКА СТАЦИОНАРНОГО ДИФФУЗИОННОГО РОСТА МНОГОКОМПОНЕНТНОЙ ЗАКРИТИЧЕСКОЙ ЧАСТИЦЫ НОВОЙ ФАЗЫ

В отличие от частиц новой фазы критического размера, при рассмотрении закритического пузырька или капельки с радиусом $R \gg {{R}_{{\text{с}}}}$ можно пренебречь адсорбцией компонентов на их поверхности. Тогда для мольных долей ${{x}_{i}}$ компонентов в частице можно взять определение

где ${{N}_{i}}$ и ${{N}_{R}} = \sum\nolimits_{i\, = \,1}^k {{{N}_{i}}} $ – соответственно полные количества молекул i-го компонента и всех компонентов в частице с радиусом R (как и ранее, в случае пузырька пренебрегаем паром растворителя и полагаем ${{x}_{{k{\text{g}}}}} = 0$).

Если мольная доля ${{x}_{i}}$ i-го компонента в частице новой фазы изменяется во времени со скоростью ${{\dot {x}}_{i}}{\text{,}}$ то из (4.1) следует

где ${{\dot {N}}_{i}}$ – поток на частицу молекул i-го компонента и ${{\dot {N}}_{R}}$ – полный поток всех компонентов. Из соотношения (4.2) видно, что для растущих закритических частиц новой фазы при ${{\dot {N}}_{R}} > 0$ и при не зависящем от радиуса R частицы отношении потоков ${{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}}$ ($i = 1,2,...,k$) существует возможность установления режима роста частицы со стационарным составом $\left\{ {{{x}_{{\text{s}}}}} \right\} = \left( {{{x}_{{{\text{1s}}}}},...,{{x}_{{k{\text{s}}}}}} \right){\text{,}}$ отвечающим корням уравнений Если, например, ${{\dot {N}}_{R}} > 0$ и ${{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}} > {{x}_{i}}$ (i = 1, 2, $...,k$) для закритических частиц в какой-либо момент времени, то ${{\dot {x}}_{i}} > 0{\text{,}}$ и мольная доля x_i i-го компонента в частице возрастает со временем. Однако это увеличение приводит, в свою очередь, к уменьшению относительного вклада этого компонента в общий поток из-за возрастания испускательной способности частиц по данному компоненту. Как следствие, по мере роста частицы ее состав и потоки ${{\dot {N}}_{i}}$ изменяются таким образом, что модуль разности $\left| {{{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}} - {{x}_{i}}} \right|$ монотонно уменьшается со временем. Если при этом соотношение ${{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}}$ перестает зависеть от радиуса частицы, то разность $\left| {{{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}} - {{x}_{i}}} \right|$ стремится к нулю, а состав частицы становится стационарным и соответствует $\left\{ {{{x}_{{\text{s}}}}} \right\} = \left( {{{x}_{{1{\text{s}}}}},...,{{x}_{{k{\text{s}}}}}} \right){\text{.}}$ Это общее утверждение об устойчивости стационарного состава растущих закритических частиц новой фазы и детальный анализ динамики нестационарного и стационарного роста закритической капель в атмосфере нескольких паров и газа-носителя в изотермических и неизотермических условиях и стационарного диффузионного роста пузырьков газа в пересыщенных газами растворах были представлены в работах [103–113].

Если время установления стационарного состава в закритических частицах мало по сравнению с общей продолжительностью стадии нуклеации (это будет так, если максимальный размер частиц новой фазы к концу стадии нуклеации достаточно велик), то можно утверждать, что состав закритических частиц новой фазы является стационарным для большей части стадии нуклеации.

Для неравновесных закритических пузырьков давление P_R внутри пузырька связано с радиусом пузырька и скоростью его роста уравнением Рэлея–Плессе [114–117]

где ρ₁ и η, – соответственно, плотность и вязкость жидкого раствора, точка над величиной означает производную по времени. Учет вязких вкладов в (4.4) может быть важен для растущих газовых пузырьков в вязких магмах и расплавах стекол [118–120]. Как показано в [101], мы можем пренебречь в большинстве случаев вкладом от инерционных эффектов (заданных левой частью уравнения (4.4)) и вязкостью (заданной последним слагаемым в правой части уравнения (4.4)), а также неизотермическими эффектами, связанными с теплотами испарения в пузырек. Тогда уравнение (4.4) переходит в уравнение Лапласа (2.7). В этом случае рост закритических пузырьков в пересыщенных газами растворах описывается только уравнениями для изменения чисел ${{N}_{{i{\text{g}}}}}$ молекул газов в пузырьке вследствие диффузии ($i = 1,2,...,k - 1$). При стационарной диффузии в закритический пузырек радиуса $R \gg {{R}_{ * }}$ с составом газов $\left\{ {{{x}_{{\text{g}}}}} \right\}$ эти уравнения с учетом граничного условия (2.14) и выражения (2.15) для растворимости s_i имеют вид где ${{D}_{{i{\text{l}}}}}$ – коэффициент диффузии молекул i-го растворенного газа в растворителе (компоненте k). При выполнении сильного неравенства ${{n}_{{k{\text{l}}}}} \gg $ $ \gg \sum\nolimits_{i\, = \,\,1}^{k\, - \,1} {{{n}_{{i{\text{l}}}}}} $ можем считать все коэффициенты диффузии не зависящими от состава раствора. Из уравнения (4.5) следует, что с ростом мольной доли ${{x}_{{i{\text{g}}}}}$ поток ${{\dot {N}}_{{i{\text{g}}}}}$ уменьшается, и отношение ${{{{{\dot {N}}}_{{i{\text{g}}}}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{{i{\text{g}}}}}} {\sum\nolimits_{j\, = \,1}^{k\, - \,1} {{{{\dot {N}}}_{{j{\text{g}}}}}} }}} \right. \kern-0em} {\sum\nolimits_{j\, = \,1}^{k\, - \,1} {{{{\dot {N}}}_{{j{\text{g}}}}}} }}$ не зависит от радиуса R. Тогда, принимая во внимание сказанное выше о выходе на стационарный состав закритической частицы, мы можем на стадии нуклеации газовых пузырьков приближенно заменить в правой части уравнения (4.5) мольные доли ${{x}_{{i{\text{g}}}}}$ на ${{x}_{{i{\text{gs}}}}}{\text{.}}$ Изменения концентраций газов в растворе вокруг пузырька на стадии нуклеации мы ожидаем малыми и соответственно можем заменить ${{n}_{{i{\text{l}}}}}\left( t \right)$ в правой части (4.5) их начальными значениями ${{n}_{{i{\text{l}},0}}} \equiv {{n}_{{i{\text{l}}}}}\left( 0 \right){\text{.}}$ Также, с учетом равенств ${{N}_{{i{\text{g}}}}} = {{n}_{{i{\text{g}}}}}{{4\pi {{R}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{R}^{3}}} 3}} \right. \kern-0em} 3}{\text{,}}$ (2.8) и (2.10) при $R \gg {{R}_{ * }}{\text{,}}$ заменим в левой части уравнения (4.5) поток ${{\dot {N}}_{{i{\text{g}}}}}$ на $4\pi \left( {{{{{P}_{{\text{l}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{l}}}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}} \right){{x}_{{i{\text{gs}}}}}{{R}^{2}}\dot {R}{\text{.}}$ В итоге получаем

С учетом определения (2.17) начальная объемная концентрация ${{n}_{{i{\text{l}},0}}}$ i-го газа связана с начальным значением ${{\zeta }_{{i,0}}} \equiv {{\zeta }_{i}}\left( 0 \right)$ пересыщения этого газа в растворе соотношением

Принимая во внимание равенство (2.16), окончательно перепишем уравнение (4.6) как уравнение для скорости изменения радиуса пузырька в виде где

Предположение о стационарности диффузионных потоков растворенных газов накладывает очень жесткие ограничения на параметры a_i (i = $ = 1,2,...,k - 1$). Действительно, характерное время изменения радиуса пузырька можно оценить как ${{t}_{R}} = {R \mathord{\left/ {\vphantom {R {\dot {R}}}} \right. \kern-0em} {\dot {R}}}{\text{.}}$ Условием стационарности для поля концентрации i-го компонента газа в растворе является требование, чтобы радиус R пузырька был мал по сравнению с соответствующим диффузионным масштабом ${{\left( {{{D}_{{i{\text{l}}}}}{{t}_{R}}} \right)}^{{1/2}}}{\text{,}}$ т.е. $R \ll {{\left( {{{D}_{{i{\text{l}}}}}{{t}_{R}}} \right)}^{{1/2}}}$ при любом $i = 1,2,...,k - 1.$ Это условие эквивалентно

Как следует из уравнения (4.8), неравенство (4.10) выполняется при

Используя определение (4.9), это неравенство можно переписать в виде В итоге, именно выполнение этого условия необходимо для стационарности диффузионных потоков в пузырек всех компонентов газа.

Интегрирование уравнения (4.8) при пренебрежении радиусом пузырьков околокритических размеров определяет линейную зависимость квадрата радиуса пузырька от времени:

где – скорость роста квадрата радиуса пузырька при стационарной диффузии.

Применяя уравнение (4.8) к разным компонентам, находим

Уравнение (4.8) также позволяет выразить стационарную мольную долю ${{x}_{{i{\text{gs}}}}}$ i-го компонента газа в пузырьке через скорость A^(b): Используя равенство $\sum\nolimits_{i\, = \,1}^{k\, - \,1} {{{x}_{{i{\text{gs}}}}}} = 1$, из (4.16) получаем Соотношения (4.16) и (4.17) дают полный набор алгебраических уравнений для стационарных мольных долей ${{x}_{{i{\text{s}}}}}$ ($i = 2,...,k - 1$) и скорости A^(b) роста квадрата радиуса закритического пузырька.

В [101, 113] были рассмотрены три частных случая, когда стационарные мольные доли в закритическом пузырьке можно найти аналитически. В первом случае это можно сделать для бинарного пузырька, для которого из (4.15) и равенства ${{x}_{{2{\text{gs}}}}} = 1 - {{x}_{{1{\text{gs}}}}}$ получаем квадратное уравнение для ${{x}_{{1{\text{gs}}}}}{\text{:}}$

где

Физически значимый корень уравнения (4.18) при $\varepsilon > 1$ имеет вид

Второй случай реализуется, есликоэффициенты диффузии всех компонентов равны друг другу, т.е. ${{D}_{{i{\text{l}}}}} \equiv {{D}_{{\text{l}}}}{\text{.}}$ Из уравнения (4.14) следует, что в этом случае ${{a}_{i}} \equiv a{\text{,}}$ и тогда согласно (4.16) стационарные мольные доли равны

(4.21)

${{x}_{{i{\text{gs}}}}} = \frac{{{{s}_{i}}({{\zeta }_{{i,0}}} + 1)}}{{a + {{s}_{i}}}}\,\,\,\,\left( {i = 1,2,...,k - 1} \right),$

где в согласии с (4.17) соответствующее значение параметра a находится как корень уравнения

(4.22)

$\sum\limits_{i\, = \,1}^k \frac{{{{s}_{i}}({{\zeta }_{{i,0}}} + 1)}}{{a + {{s}_{i}}}} = 1.$

Сравнение соотношений (4.20), (4.21) и (2.20) показывает, что стационарный состав газа в растущем закритическом пузырьке в первых двух рассмотренных случаях отличается от состава критического пузырька. Если же для каждого газового компонента равны произведения коэффициента диффузии ${{D}_{{i{\text{l}}}}}$ и растворимости ${{s}_{i}}{\text{,}}$ т.е. ${{D}_{{i{\text{l}}}}}{{s}_{i}} \equiv {{d}_{{\text{l}}}}{\text{,}}$ то в этом случае из (4.17) следует

(4.23)

$\frac{{2{{d}_{{\text{l}}}}}}{{2{{d}_{{\text{l}}}} + {{A}^{{\left( {\text{b}} \right)}}}}} = \frac{1}{{\sum\limits_{i\, = \,1}^k {\left( {{{\zeta }_{{i,0}}} + 1} \right)} }}.$

Используя (4.23) и определение ${{\bar {\zeta }}_{0}} + 1 \equiv $ $ \equiv \sum\nolimits_{i\, = \,1}^k \left( {{{\zeta }_{{i,0}}} + 1} \right){\text{,}}$ находим из (4.16)

(4.24)

${{x}_{{i{\text{gs}}}}} = \frac{{{{\zeta }_{{i,0}}} + 1}}{{{{{\bar {\zeta }}}_{0}} + 1}}\,\,\,\,\left( {i = 1,2,...,k - 1} \right).$

Этот результат показывает, что стационарный состав закритического пузырька совпадает в данном случае с составом критического пузырька в начальный момент времени (соотношение (2.20)).

Аналитические результаты, выраженные соотношениями (4.20), (4.21) и (4.24), могут быть полезны в качестве контрольных соотношений, позволяющих проверить результаты численного моделирования растворов с растворенными газами.

Перейдем теперь к рассмотрению стационарного диффузионного роста многокомпонентных закритических капель в атмосфере k паров и пассивного неконденсирующегося газа. При изотермической стационарной диффузии молекул i-го пара в закритическую каплю радиуса $R \gg {{R}_{{\text{c}}}}$ с составом $\left\{ {{{x}_{{\text{l}}}}\left( t \right)} \right\}$ уравнение для скорости ${{\dot {N}}_{{i{\text{l}}}}}\left( t \right)$ изменения числа молекул i-го компонента в капле с учетом граничного условия (2.23) при $R \gg $ $ \gg {{2{{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)\sigma } \mathord{\left/ {\vphantom {{2{{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{\text{l}}}}} \right\}} \right)\sigma } {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ и в пренебрежении стефановским течением [103, 121–123] имеет вид

(4.25)

${{\dot {N}}_{{i{\text{l}}}}} = 4\pi {{R}^{2}}{{D}_{{i{\text{g}}}}}\frac{{{{n}_{{i{\text{g}}}}}\left( t \right) - {{\gamma }_{i}}{{x}_{{i{\text{l}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}}}{R}\,\,\,\,\left( {i = 1,2,...,k} \right),$

где ${{D}_{{i{\text{g}}}}}$ – коэффициент диффузии молекул i-го пара в пассивном газе вокруг капли. Если концентрация n_p пассивного газа удовлетворяет сильному неравенству ${{n}_{{\text{p}}}} \gg \sum\nolimits_{i\, = \,1}^k {{{n}_{{i{\text{g}}}}}} {\text{,}}$ то можно считать все коэффициенты диффузии паров не зависящими от состава парогазовой атмосферы вокруг капли. Уравнение (4.25) аналогично уравнению (4.5), поэтому для растущей закритической капли также установливается стационарный состав, и мы можем на стадии нуклеации приближенно заменить в правой части уравнения (4.25) мольные доли ${{x}_{{i{\text{l}}}}}$ ($i = 1,2,...,k$) на ${{x}_{{i{\text{ls}}}}}$ и концентрации паров ${{n}_{{i{\text{g}}}}}\left( t \right)$ в атмосфере вокруг капли их начальными значениями ${{n}_{{i{\text{g}},0}}} \equiv {{n}_{{i{\text{g}}}}}\left( 0 \right){\text{.}}$ Также с помощью (4.3) заменим в левой части уравнения (4.25) поток ${{\dot {N}}_{{i{\text{l}}}}}$ на ${{x}_{{i{\text{ls}}}}}{{\dot {N}}_{R}}\left( {\left\{ {{{x}_{{{\text{ls}}}}}} \right\}} \right){\text{,}}$ определим средний молекулярный объем при стационарной концентрации соотношением ${{v}_{{{\text{ls}}}}} \equiv \sum\nolimits_{i\, = \,1}^k {{{x}_{{i{\text{ls}}}}}{{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{{\text{ls}}}}}} \right\}} \right)} {\text{,}}$ учтем равенство ${{v}_{{{\text{ls}}}}}{{N}_{R}} = \frac{{4\pi {{R}^{3}}}}{3}$ и связь ${{n}_{{i{\text{g}},0}}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}\left( {1 + {{\zeta }_{{i,0}}}} \right)$ с начальным значением ${{\zeta }_{{i,0}}} \equiv {{\zeta }_{i}}\left( 0 \right)$ пересыщения i-го пара. В итоге получаем

(4.26)

$R\dot {R} = {{D}_{{i{\text{g}}}}}{{v}_{{{\text{ls}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}\left( {\frac{{{{\zeta }_{{i,0}}} + 1}}{{{{x}_{{i{\text{ls}}}}}}} - {{\gamma }_{{i{\text{s}}}}}} \right).$

Из (4.26) следует, что условие (4.10) стационарности для поля концентрации i-го парового компонента в атмосфере вокруг капли выполняется при

(4.27)

$\sqrt {{{v}_{{{\text{ls}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {\frac{{{{\zeta }_{{i,0}}} + 1}}{{{{x}_{{i{\text{ls}}}}}}} - {{\gamma }_{{i{\text{s}}}}}} \right)} \ll 1\,\,\,\,\left( {i = 1,2,...,k} \right).$

Выполнение неравенства (4.27) обеспечивается сильным неравенством ${{v}_{{{\text{ls}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}} \ll 1$ при любом i = 1, $2,...,k{\text{.}}$

С учетом равенствa ${{\dot {N}}_{R}} = \sum\nolimits_{i\, = \,1}^k {{{{\dot {N}}}_{{i{\text{l}}}}}} $ из (4.25) и (4.26) также находим

(4.28)

$\begin{gathered} {{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {{{\zeta }_{{i,0}}} + 1 - {{x}_{{i{\text{ls}}}}}{{\gamma }_{{i{\text{s}}}}}} \right) - \\ - \,\,{{x}_{{i{\text{ls}}}}}\sum\limits_{m\, = \,1}^k {{{D}_{{m{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{m{\text{g}}}}}\left( {{{\zeta }_{{m,0}}} + 1 - {{x}_{{m{\text{ls}}}}}{{\gamma }_{{m{\text{s}}}}}} \right)} = 0 \\ \left( {i = 1,2,...,k} \right), \\ \end{gathered} $

а с учетом равенства $\frac{{4\pi {{R}^{3}}}}{3} = \sum\nolimits_{i\, = \,1}^k {{{N}_{{i{\text{l}}}}}{{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{{\text{ls}}}}}} \right\}} \right)} $ имеем

(4.29)

$R\dot {R} = \sum\limits_{i\, = \,1}^k {{{D}_{{i{\text{g}}}}}{{v}_{{i{\text{l}}}}}\left( {\left\{ {{{x}_{{{\text{ls}}}}}} \right\}} \right){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {{{\zeta }_{{i,0}}} + 1 - {{x}_{{i{\text{ls}}}}}{{\gamma }_{{i{\text{s}}}}}} \right)} .$

Введем новую величину ${{A}^{{\left( {\text{d}} \right)}}}$ как

(4.30)

$\begin{gathered} {{A}^{{\left( {\text{d}} \right)}}} \equiv 2{{v}_{{{\text{ls}}}}}\sum\limits_{m = 1}^k {{{D}_{{m{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{m{\text{g}}}}}\left( {{{\zeta }_{{m,0}}} + 1 - {{x}_{{m{\text{ls}}}}}{{\gamma }_{{m{\text{s}}}}}} \right)} = \\ = 2{{v}_{{{\text{ls}}}}}{{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {\frac{{{{\zeta }_{{i,0}}} + 1}}{{{{x}_{{i{\text{ls}}}}}}} - {{\gamma }_{{i{\text{s}}}}}} \right). \\ \end{gathered} $

Соответственно уравнение (4.28) можно переписать в виде

(4.31)

${{x}_{{i{\text{ls}}}}} = \frac{{2{{v}_{{ls}}}{{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {{{\zeta }_{{i,0}}} + 1} \right)}}{{2{{v}_{{{\text{l}}s}}}{{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}{{\gamma }_{{i{\text{s}}}}} + {{A}^{{\left( {\text{d}} \right)}}}}}\,\,\,\,\left( {i = 1,2,...,k} \right).$

Подстановка соотношения (4.31) в равенство $\sum\nolimits_{i\, = \,1}^k {{{x}_{{i{\text{ls}}}}}} = 1$ дает

(4.32)

$\sum\limits_{i\, = \,1}^k {\frac{{2{{v}_{{{\text{ls}}}}}{{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {{{\zeta }_{{i,0}}} + 1} \right)}}{{2{{v}_{{{\text{ls}}}}}{{D}_{{i{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}{{\gamma }_{{i{\text{s}}}}} + {{A}^{{\left( {\text{d}} \right)}}}}}} = 1.$

Уравнения (4.31) и (4.32) образуют систему нелинейных уравнений, которая определяет неизвестную величину ${{A}^{{\left( {\text{d}} \right)}}}$ и стационарные мольные концентрации ${{x}_{{i{\text{ls}}}}}$ ($i = 1,2,...,k$) в закритической капле как функции начальных пересыщений $\left\{ {{{\zeta }_{0}}} \right\} = \left( {{{\zeta }_{{1,0}}},...,{{\zeta }_{{k,0}}}} \right)$ всех паровых компонентов в случае неидеального раствора в капле.

Очевидно, что уравнения (4.31) и (4.32) аналогичны уравнениям (4.16) и (4.17), а величина ${{A}^{{\left( {\text{d}} \right)}}}$ представляет скорость роста квадрата радиуса закритической капельки. Действительно, из (4.26), (4.28)–(4.30) и определения среднего молекулярного объема ${{v}_{{{\text{ls}}}}} \equiv \sum\nolimits_{i\, = \,1}^k {{{x}_{{i{\text{ls}}}}}{{v}_{{{\text{il}}}}}\left( {\left\{ {{{x}_{{{\text{ls}}}}}} \right\}} \right)} $ при стационарном составе закритической капельки следует

(4.33)

$R\dot {R} = {{{{A}^{{\left( {\text{d}} \right)}}}} \mathord{\left/ {\vphantom {{{{A}^{{\left( {\text{d}} \right)}}}} 2}} \right. \kern-0em} 2},\,\,\,\,{{R}^{2}}\left( t \right) = {{A}^{{\left( {\text{d}} \right)}}}t.$

Рассмотренные выше три частных случая, когда стационарные мольные доли в закритическом пузырьке можно найти аналитически, реализуются и для закритических капель с идеальным раствором. Для бинарной капельки в этом случае получаем из (4.28) и равенства ${{x}_{{2{\text{ls}}}}} = 1 - {{x}_{{1{\text{ls}}}}}$ при ${{\gamma }_{{1{\text{s}}}}} = {{\gamma }_{{2{\text{s}}}}} = 1$ следующее квадратное уравнение для ${{x}_{{1{\text{s}}}}}$ [103]:

(4.34)

$\left( {\omega - 1} \right)x_{{1{\text{ls}}}}^{2} + \left( {{{\zeta }_{{1,0}}} + \omega {{\zeta }_{{2,0}}} + 2} \right){{x}_{{1{\text{ls}}}}} - {{\zeta }_{{1,0}}} - 1 = 0,$

где

(4.35)

$\omega \equiv \frac{{{{D}_{{2{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{2{\text{g}}}}}}}{{{{D}_{{1{\text{g}}}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{1{\text{g}}}}}}}.$

Физически значимый корень уравнения (4.34) при $\omega > 1$ совпадает по виду с (4.20) при замене ε на ω. Если коэффициенты диффузии всех паров в парогазовой среде равны друг другу, т.е. ${{D}_{{i{\text{g}}}}} \equiv {{D}_{{\text{g}}}}{\text{,}}$ и раствор в капле идеальнен, то из уравнения (4.31) следует, что стационарные мольные доли компонентов в капле равны

(4.36)

${{x}_{{i{\text{ls}}}}} = \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}\left( {{{\zeta }_{{i,0}}} + 1} \right)}}{{{{{{A}^{{\left( d \right)}}}} \mathord{\left/ {\vphantom {{{{A}^{{\left( d \right)}}}} {2{{v}_{{{\text{ls}}}}}{{D}_{{\text{g}}}}}}} \right. \kern-0em} {2{{v}_{{{\text{ls}}}}}{{D}_{{\text{g}}}}}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}}}\,\,\,\,\left( {i = 1,2,...,k} \right),$

где в согласии с (4.32) соответствующее значение параметра ${{{{{{A}^{{\left( {\text{d}} \right)}}}} \mathord{\left/ {\vphantom {{{{A}^{{\left( {\text{d}} \right)}}}} {2{{v}_{{{\text{ls}}}}}D}}} \right. \kern-0em} {2{{v}_{{{\text{ls}}}}}D}}}_{{\text{g}}}}$ находится как корень уравнения

(4.37)

$\sum\limits_{i\, = \,1}^k {\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{{\text{ig}}}}}\left( {{{\zeta }_{{i,0}}} + 1} \right)}}{{{{{{A}^{{\left( d \right)}}}} \mathord{\left/ {\vphantom {{{{A}^{{\left( d \right)}}}} {2{{v}_{{{\text{ls}}}}}{{D}_{{\text{g}}}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{{\text{ig}}}}}}}} \right. \kern-0em} {2{{v}_{{{\text{ls}}}}}{{D}_{{\text{g}}}} + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{{\text{ig}}}}}}}}}} = 1.$

Если же для каждого пара равны произведения коэффициента диффузии ${{D}_{{i{\text{l}}}}}$ и концентрации ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}{\text{,}}$ т.е. ${{D}_{{i{\text{g}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{{\text{ig}}}}} \equiv {{d}_{{\text{g}}}}{\text{,}}$ то в случае идеального раствора в капле из (4.32) и (4.31) следует

(4.38)

$\frac{{{{d}_{{\text{g}}}}}}{{{{{{A}^{{\left( {\text{d}} \right)}}}} \mathord{\left/ {\vphantom {{{{A}^{{\left( {\text{d}} \right)}}}} {2{{v}_{{{\text{ls}}}}}}}} \right. \kern-0em} {2{{v}_{{{\text{ls}}}}}}} + {{d}_{{\text{g}}}}}} = \frac{1}{{\sum\limits_{i\, = \,1}^k {\left( {{{\zeta }_{{i,0}}} + 1} \right)} }},$

(4.39)

${{x}_{{i{\text{ls}}}}} = \frac{{{{\zeta }_{{i,0}}} + 1}}{{{{{\bar {\zeta }}}_{0}} + 1}}\,\,\,\,\left( {i = 1,2,...,k} \right).$

Интересно отметить, что выражение (4.39) совпадает по виду с выражением (4.24), описывающим стационарный состав закритического пузырька, растущего в жидком растворе. Дело в том, что величины ${{D}_{{i{\text{l}}}}}{{s}_{i}}$ в случае растущего пузырька играют такую же роль, как величины ${{v}_{{{\text{ls}}}}}{{D}_{{i{\text{g}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}}$ в случае капли идеального раствора. В сказанном легко убедиться, сравнивая уравнение (4.17) для ${{A}^{{\left( {\text{b}} \right)}}}$ с уравнением (4.32) для ${{A}^{{\left( {\text{d}} \right)}}}$ при ${{\gamma }_{{i{\text{s}}}}} = 1.$ Соответственно условие ${{D}_{{i{\text{l}}}}}{{s}_{i}} \equiv {{d}_{{\text{l}}}}$ для пузырька эквивалентно условию ${{D}_{{i{\text{g}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}} \equiv {{d}_{{\text{g}}}}$ для капли. Вместе с тем, стационарный состав многокомпонентной закритической капли, в отличие от многокомпонетного пузырька, не совпадает даже в приближении идеального раствора с составом критической капли в начальный момент времени.

5. КИНЕТИКА СТАДИИ НУКЛЕАЦИИ В ПОДХОДЕ СРЕДНЕГО ПОЛЯ ПЕРЕСЫЩЕНИЯ. ОСОБЕННОСТИ РОСТА ПУЗЫРЬКОВ И КАПЕЛЬ

В данном разделе проведем детальное рассмотрение кинетики стадии нуклеации в подходе среднего поля пересыщений в закрытой системе при мгновенном создании метастабильного состояния системы в начальный момент времени. В этом подходе, который можно назвать классическим, предполагается, что в процессе зарождения закритических частиц новой фазы и их дальнейшего роста в замкнутой системе пересыщение ${{\zeta }_{i}}$ i-го компонента относительно медленно уменьшается со временем t равномерно по объему метастабильной фазы, т.е. остается, как и начальное пересыщение ${{\zeta }_{{i,0}}}{\text{,}}$ однородным в пространстве.

Если мольные концентрации в растущих закритических частицах новой фазы являются стационарными и равными ${{x}_{{i{\text{s}}}}}$ и все частицы растут благодаря стационарной диффузии компонентов метастабильной фазы по законам (4.13) или (4.33), то единственной переменной, определяющей распределение закритических сферических частиц новой фазы, является квадрат ее радиуса ${{R}^{2}}{\text{.}}$ Пренебрегая флуктуациями в скорости роста частиц, мы можем связать функцию распределения $f({{R}^{2}},t)$ закритических частиц в единице объема исходной фазы в данный момент времени $t$ и скорость нуклеации $J\left( \tau \right)$ критических частиц в предыдущие моменты времени ${\tau }$ интегральным соотношением

где δ есть дельта-функция Дирака и ${{R}^{2}}(t,\tau )$ – квадрат радиуса в момент времени t частицы, зародившейся в момент времени τ. Как следует из уравнения (4.13) для закритических пузырьков и уравнения (4.33) для закритических капелек, при стационарности диффузии зависимость ${{R}^{2}}(t,{\tau })$ линейна по времени роста t – τ закритической частицы новой фазы. Подставляя по очереди (4.13) и (4.33) в уравнение (5.1), используя соотношение (3.10) и свойства дельта-функции, для пузырьков и капелек находим соответственно

Пренебрегая общим количеством новой фазы в докритических частицах и адсорбцией в закритических частицах, используя соотношение (4.1) и формулу для полного числа ${{N}_{R}}$ молекул в частице новой фазы, можно связать потерю i-го компонента метастабильной фазы из-за перехода этого компонента в частицы новой фазы с функцией распределения частиц $f({{R}^{2}},t)$ интегральным уравнением баланса вещества в единице объема исходной фазы. С учетом вытекающего из (2.9) равенства ${{N}_{R}} = \frac{{4\pi {{R}^{3}}}}{3}\frac{{{{P}_{l}}}}{{{{k}_{{\text{B}}}}T}}$ и определения (2.4) имеем для локального баланса каждого газового компонента в закритических пузырьках и растворе:

Аналогично, для локального баланса i-го компонента в газовой фазе и в каплях с учетом равенства ${{v}_{{{\text{ls}}}}}{{N}_{R}} = \frac{{4\pi {{R}^{3}}}}{3}$ находим

Определение (3.8) и соотношения (5.2) и (5.3) позволяют преобразовать уравнения (5.4) и (5.5) в систему интегральных уравнений для изменений $\left\{ {{{{\varphi }}^{{\left( {\text{b}} \right)}}}\left( t \right)} \right\}$ пересыщений газовых компонентов системы. Соответственно в случае нуклеации пузырьков находим

где мы учли соотношение (2.16) для растворимости ${{s}_{i}}{\text{.}}$ Аналогично в случае нуклеации капелек имеем

Умножая обе части уравнений (5.6) и (5.7) на множители ${\Gamma }_{i}^{{\left( {\text{b}} \right)}}$ и, соответственно, ${\Gamma }_{i}^{{\left( {\text{d}} \right)}}$ и суммируя по всем газовым компонентам, получим

Замена в правой части уравнения (5.8) переменной интегрирования ${{R}^{2}}$ на произведение ${{A}^{{\left( {\text{b}} \right)}}}(t - \tau )$ и аналогичная замена в (5.9) R² на ${{A}^{{\left( {\text{d}} \right)}}}(t - \tau )$ дают

Полученные интегральные уравнения (5.10) и (5.11) являются аналогами уравнения для относительного уменьшения пересыщения на стадии нуклеации в однокомпонентной системе [15, 60] и в многокомпонентной системе, управляемой полным пересыщением [101]. Эти интегральные уравнения могут быть решены аналитически с помощью итерационной процедуры. В частности, подставив $\sum\nolimits_i {{{\Gamma }_{i}}{{\varphi }_{i}}\left( \tau \right)} = 0$ в подынтегральное выражение в правой части уравнений (5.10) и (5.11), получим в качестве первой итерации

Подставляя (5.12) в (5.2) и (5.13) в (5.3), получаем явные выражения для распределений закритических пузырьков и соответственно капель в виде

Подстановка (5.12) в подынтегральное выражение в уравнении (5.6) и (5.13) в подынтегральное выражение в уравнении (5.7) определяет понижение ${{\varphi }_{i}}\left( t \right)$ пересыщения каждого газа и соответственно каждого пара в системе на стадии нуклеации как функции времени:

Характерное время ${{t}_{1}}$ длительности стадии нуклеации определяется моментом времени, когда начальная скорость нуклеации уменьшается в е раз. Как следует из (3.10), это время удовлетворяет уравнению

Поочередно используя (5.12) и (5.13) в левой части (5.18), находим, что время ${{t}_{1}}$ для стадии нуклеации многокомпонентных пузырьков равно а для стадии нуклеации многокомпонентных капель

Рассмотрим подробнее вопрос об увеличении объема раствора при дегазации в режиме стационарной диффузии. Общий объем ${{V}_{{{\text{tot}}}}}(t)$ жидкого раствора с закритическими газовыми пузырьками газа в текущий момент времени $t$ можно определить как

Здесь ${{V}_{{\text{l}}}}$ – начальный объем жидкого раствора и ${{V}_{{\text{g}}}}(t)$ – общий объем пузырьков газа в момент времени t. Отношение ${{{{V}_{{\text{g}}}}(t)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}(t)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ характеризует распухание жидкого раствора при дегазации за счет образования пузырьков газа и может быть названо коэффициентом распухания. На стадии нуклеации при стационарном составе закритических пузырьков с учетом (5.4) и (2.16) имеем следующее уравнение баланса для i-го газового компонента во всем растворе и в пузырьках: Принимая во внимание определения (2.8) и (3.8), из уравнения (5.22) находим прямую связь между отношением ${{{{V}_{{\text{g}}}}(t)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}(t)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ и вкладом $\varphi _{i}^{{\left( {\text{b}} \right)}}\left( t \right)$ i-го компонента в относительное уменьшение полного пересыщения раствора в виде Заметим, что отношение ${{{{V}_{{\text{g}}}}(t)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}(t)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ не зависит от номера газового компонента, и, следовательно, правая часть (5.23) одинакова для всех газовых компонентов.

Подставляя в правую часть (5.23) выражение (5.16), находим

В первом приближении (полагая показатель экспоненты в подынтегральном выражении в правой части (5.24) равным нулю) получаем Правая часть (5.25) достигает своего наибольшего значения к концу стадии нуклеации. Согласно (5.19) и (5.25) это значение равно

Из соотношения (5.26) может показаться, что чем больше начальные пересыщения $\left\{ {{{\zeta }_{0}}} \right\}$ и чем выше растворимости $\left\{ s \right\}$ газов, тем больше отношение ${{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}{\text{.}}$ Однако с учетом вытекающего из требования стационарности диффузионных потоков на пузырек условия (4.12) и соотношения (3.16) имеем

Пренебрегая для оценки производными от поверхностного натяжения в правой части (5.27) и учитывая равенство ${{\bar {\zeta }}_{0}} \equiv \sum\nolimits_{i = 1}^{k - 1} \left( {{{\zeta }_{{i,0}}} + 1} \right) - 1,$ получаем $\sum\nolimits_{i = 1}^{k - 1} {\frac{{{{x}_{{i{\text{gs}}}}}\Gamma _{i}^{{\left( {\text{b}} \right)}}}}{{{{s}_{i}}{{{\bar {\zeta }}}_{0}}}}} \gg 2\Delta F_{{{\text{c}},0}}^{{\left( {\text{b}} \right)}} \gg 1.$ Тогда из (5.26) следует, что заметного распухания жидкого раствора к концу стадии нуклеации в условиях стационарности диффузионных потоков растворенных газов к пузырькам не может быть.

Подведем итоги рассмотрения кинетической теории стадии нуклеации в подходе среднего поля пересыщений в закрытой системе при мгновенном создании метастабильного состояния системы. Как уже отмечалось в начале раздела 4, время установления стационарного состава в закритических частицах должно быть мало по сравнению со временем стадии нуклеации ${{t}_{1}}{\text{.}}$ Тогда использование уравнений (4.13) и (4.33) для квадрата радиуса закритических частиц на стадии нуклеации оправдано. Соответственно параметры систем должны быть такими, чтобы обеспечить неравенство ${{R}^{2}}\left( {t_{1}^{{\left( {\text{d}} \right)}}} \right) \gg R_{{{\text{c}},0}}^{2}$ для закритических капель и неравенство ${{R}^{2}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right) \gg R_{ * }^{2}$ для закритических пузырьков. С учетом (4.13), (5.19) и (4.33), (5.20) эти условия для стадии нуклеации пузырьков и капелек можно записать в виде

При выполнении условий (5.28) и (5.29) нам нужно знать для описания стадии нуклеации только состав $\left\{ {{{x}_{{\text{c}}}}} \right\}$ критической частицы и стационарный состав $\left\{ {{{x}_{{\text{s}}}}} \right\}$ закритических частиц как функции начальных пересыщений компонентов. Подчеркнем, что радиус R закритической частицы оказывается единственной переменной, существенной на стадии нуклеации при фиксированном составе закритических частиц, и найденные функции (5.14) и (5.15) описывают эволюцию во времени распределения закритических частиц по R².

6. ДИНАМИКА АВТОМОДЕЛЬНОГО РОСТА МНОГОКОМПОНЕНТНОЙ ЗАКРИТИЧЕСКОЙ ЧАСТИЦЫ НОВОЙ ФАЗЫ

Как следует из анализа, представленного в разделах 4 и 5, область применимости подхода среднего поля пересыщений к теории стадии нуклеации строго ограничена условиями (4.12) и (4.27) применимости стационарного описания диффузии. Эти условия подразумевают квазиоднородность в системе вследствие диффузионного перемешивания. В случае дегазации раствора условия (4.12) требуют, чтобы раствор был лишь слегка пересыщенным и растворимости газов были невелики, при этом общий объем образовавшихся газовых пузырьков будет небольшим по сравнению с объемом жидкого раствора. Ограничения, которые следуют из условий (4.27) для стационарной диффузии паров в закритические капельки, на первый взгляд, не существенны в случае стадии нуклеации капелек в пересыщенных парах из-за выполнения сильного неравенства ${{v}_{{{\text{ls}}}}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }_{{i{\text{g}}}}} \ll 1$ при любом $i = 1,2,...,k$ вдали от критической точки. Однако предположение о равномерном по объему системы уменьшении концентрации паров не выполняется в начале стадии нуклеации закритических капель, когда из-за небольшого числа зародившихся капель возникающие вокруг них области неоднородности концентраций еще не перекрываются, и в ситуации, когда зарождение новых закритических капель подавляется вблизи уже растущей капли [57–59]. В присутствии тепловых эффектов [111, 124] влияние неоднодности может быть существенным и на стадии нуклеации капелек [59, 125].

Чтобы снять указанные выше ограничения, рассмотрим сначала уравнения для нестационарной диффузии растворенных газов в растущий в жидком растворителе закритический пузырек. На расстоянии r от центра пузырька в момент времени t концентрация ${{n}_{{i{\text{l}}}}}(r,t)$ молекул растворенного i-го газового компонента описывается в пренебрежении стефановским течением следующим нестационарным уравнением диффузии:

Первый член в правой части уравнения (6.1) учитывает диффузию молекул i-го газа, а второй член описывает вклад, обусловленный движением жидкого растворителя, вызываемым смещением границы растущего пузырька. При $t = 0$ концентрация i-го газа при всех $r \geqslant 0$ считается однородной: Соответственно она будет однородной на большом удалении от пузырька и в произвольный момент времени t:

На поверхности растущего пузырька при $R \gg {{R}_{ * }}$ имеем два граничных условия. Имея в виду, что в этой области размеров давление в пузырьке сравнивается с давлением в жидком растворителе, в качестве первого из условий мы можем переписать (2.14) в виде

Второе граничное условие учитывает материальный баланс для каждой газовой компоненты. Поскольку поверхность растущего пузырька с радиусом R движется в каждой точке со скоростью несжимаемого жидкого растворителя, для i-oй газовой компоненты мы имеем следующее уравнение материального баланса:

Согласно (6.4) при увеличении мольной доли ${{x}_{{i{\text{g}}}}}$ i-го газового компонента в пузырьке градиент ${{\left. {{{\partial {{n}_{{i{\text{l}}}}}(r,t)} \mathord{\left/ {\vphantom {{\partial {{n}_{{i{\text{l}}}}}(r,t)} {\partial r}}} \right. \kern-0em} {\partial r}}} \right|}_{{r = R\left( t \right)}}}$ уменьшается, а вместе с ним, согласно (6.5), уменьшается и поток ${{\dot {N}}_{i}}{\text{.}}$ При этом отношение потоков ${{{{{\dot {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\dot {N}}}_{i}}} {{{{\dot {N}}}_{R}}}}} \right. \kern-0em} {{{{\dot {N}}}_{R}}}}{\text{,}}$ в силу независимости условия (6.4) от R, также не зависит от R. Это означает, что и в случае режима нестационарной диффузии, описываемой уравнением (6.1), для растущего многокомпонентного закритического пузырька существует сравнительно короткое время релаксации, после которого относительные концентрации $\left\{ {{{x}_{{\text{g}}}}} \right\}$ газов в пузырьке достигают своих стационарных значений $\left\{ {{{x}_{{{\text{ga}}}}}} \right\}{\text{,}}$ определяемых согласно (4.3) и не зависящих от радиуса пузырька. Значения $\left\{ {{{x}_{{{\text{ga}}}}}} \right\}$ для растущего пузырька при нестационарности диффузии отличаются от значений $\left\{ {{{x}_{{g{\text{s}}}}}} \right\}$ в условиях стационарности диффузионных потоков, что мы характеризуем нижним индексом “a”.

С учетом сказанного, а также равенства N_i = $ = {{n}_{{i{\text{g}}}}}{{4\pi {{R}^{3}}} \mathord{\left/ {\vphantom {{4\pi {{R}^{3}}} 3}} \right. \kern-0em} 3}$ и соотношений (2.8) и (2.10) при $R \gg {{R}_{ * }}{\text{,}}$ граничные условия (6.4) и (6.5) на поверхности пузырька могут быть представлены в виде

Удобно перейти к автомодельной переменной [101, 115, 116, 126, 127]

Тогда граничные условия (6.2), (6.3) и (6.6) записываются как а уравнение нестационарной диффузии (6.1) сводится к обыкновенному дифференциальному уравнению для концентрации ${{n}_{{i{\text{l}}}}}(r,t) = {{n}_{{i{\text{l}}}}}(\rho {\text{):}}$

Интегрирование уравнения (6.10) с граничными условиями (6.8) дает [101]

Перепишем определение (4.9) для параметра a_i при концентрации x_iga как Тогда имеем вместо соотношения (6.12)

Как следует из (6.9), в пренебрежении вкладом околокритических размеров (т.е. при ${{R}^{2}}(0) = 0$) квадрат радиуса закритического пузырька при автомодельном режиме роста является линейной функцией времени t:

Соотношение (6.15) связывает величину b_il = $ = {{{{B}^{{\left( {\text{b}} \right)}}}} \mathord{\left/ {\vphantom {{{{B}^{{\left( {\text{b}} \right)}}}} {2{{D}_{{i{\text{l}}}}}}}} \right. \kern-0em} {2{{D}_{{i{\text{l}}}}}}}$ $\left( {i = 1,2,...,k - 1} \right)$ с параметром ${{a}_{{i{\text{a}}}}}{\text{,}}$ который зависит согласно (6.13) от растворимости ${{s}_{i}}$ и начального пересыщения ${{\zeta }_{{i,0}}}$ i-го газового компонента в исходном растворе, давления и температуры раствора, стационарной мольной доли ${{x}_{{i{\text{la}}}}}$ этого компонента в закритическом пузырьке.

Перепишем (6.14) с учетом (6.13) и (6.15) как уравнение для стационарных мольных долей ${{x}_{{i{\text{ga}}}}}$ при известной скорости ${{B}^{{\left( {\text{b}} \right)}}}$ роста квадрата радиуса пузырька:

Подставляя (6.16) в равенство $\sum\nolimits_{i = 1}^{k - 1} {{x}_{{i{\text{ga}}}}} = 1{\text{,}}$ получаем для скорости ${{B}^{{\left( {\text{b}} \right)}}}$ роста квадрата радиуса закритического пузырька следующее уравнение:

Есть два предельных случая, когда уравнения (6.16) и (6.17) существенно упрощаются. Если параметр ${{a}_{{i{\text{a}}}}} \ll 1$ для всех $i = 1,2,...,k - 1$ газовых компонентов, то (6.14) сводится к приближенному равенству

Соответственно уравнения (6.16) и (6.17) трансформируются в уравнения (4.16) и (4.17), и, как следствие, ${{B}^{{\left( {\text{b}} \right)}}} = {{A}^{{\left( {\text{b}} \right)}}}$ и ${{x}_{{i{\text{ga}}}}} = {{x}_{{i{\text{gs}}}}}{\text{.}}$ Таким образом, мы переходим к результатам для закритических пузырьков, растущих в режиме стационарной диффузии. В противоположном случае существенно нестационарного диффузионного роста пузырьков, когда ${{a}_{{i{\text{a}}}}} \gg 1$ для всех $i = 1,2,...,k - 1{\text{,}}$ из (6.14) находим В этом случае ${{B}^{{\left( {\text{b}} \right)}}}\int_1^\infty \left( {{{dz} \mathord{\left/ {\vphantom {{dz} {{{z}^{2}}}}} \right. \kern-0em} {{{z}^{2}}}}} \right){{e}^{{ - \frac{{{{B}^{{\left( {\text{b}} \right)}}}}}{{4{{D}_{{i{\text{l}}}}}}}\left( {{{z}^{2}} + \frac{2}{z} - 3} \right)}}} \approx $ $ \approx \sqrt {{{\pi {{B}^{{\left( {\text{b}} \right)}}}{{D}_{{i{\text{l}}}}}} \mathord{\left/ {\vphantom {{\pi {{B}^{{\left( {\text{b}} \right)}}}{{D}_{{i{\text{l}}}}}} 3}} \right. \kern-0em} 3}} {\text{,}}$ и уравнения (6.16) и (6.17), соответственно, преобразуются в В частности, если все произведения $\sqrt {{{D}_{{i{\text{l}}}}}} {{s}_{i}}$ равны друг другу, то из уравнения (6.21) и определения ${{{\bar {\zeta }}}_{0}} \equiv \sum\nolimits_{i = 1}^{k - 1} \left( {{{{\zeta }}_{{i,0}}} + 1} \right) - 1$ следует, что $\sqrt {{{\pi {{B}^{{\left( {\text{b}} \right)}}}} \mathord{\left/ {\vphantom {{\pi {{B}^{{\left( {\text{b}} \right)}}}} {\left( {12{{D}_{{i{\text{l}}}}}} \right)}}} \right. \kern-0em} {\left( {12{{D}_{{i{\text{l}}}}}} \right)}}} = $ $ = {{s}_{i}}{{\bar {\zeta }}_{0}}$ $\left( {i = 1,2,...,k - 1} \right){\text{.}}$ Подстановка этого результата в уравнение (6.20) и сравнение с (2.20) показывает, что стационарный состав газов в растущем закритическом пузырьке в последнем случае совпадает с составом исходного критического пузырька.

Заметим, что, в отличие от режима стационарной диффузии, условия для реализации которого требовали, чтобы начальное пересыщение было не слишком большим для всех газовых компонентов, в автомодельном режиме такие ограничения отсутствуют. Пересыщение одних компонентов может быть большим, а других – относительно небольшим. Согласно (4.10) и (6.15) степень нестационарности потоков задается параметром ${{\left( {{{R\dot {R}} \mathord{\left/ {\vphantom {{R\dot {R}} {{{D}_{{i{\text{l}}}}}}}} \right. \kern-0em} {{{D}_{{i{\text{l}}}}}}}} \right)}^{{1/2}}} = b_{{i{\text{l}}}}^{{1/2}}$ $\left( {i = 1,2,...,k - 1} \right){\text{.}}$ Как видно из (6.11), величина ${{b}_{{i{\text{l}}}}}$ характеризует толщину диффузионного слоя $i$-го газового компонента в растворе вокруг пузырька. Поскольку коэффициенты диффузии ${{D}_{{i{\text{l}}}}}$ имеют одинаковый порядок величины для всех газовых компонентов, то, несмотря на возможные сильные различия в начальных пересыщениях и растворимостях отдельных компонентов газа, степень нестационарности потоков будет приблизительно одного и того же порядка для всех компонентов. Это, в свою очередь, означает, что в многокомпонентном закритическом пузырьке в автомодельном режиме роста устанавливается такой состав, при котором толщины диффузионных слоев отдельных растворенных газов вокруг пузырька оказываются примерно одного порядка, большие или малые по сравнению с размером пузырька.

Как и в случае стационарной диффузии, задача о росте закритической капельки при нестационарной диффузии k паров в присутствии пассивного газа может быть решена аналогично задаче о закритическом пузырьке. Рассмотрим ее с учетом стефановского течения. Как известно, стефановское течение компенсирует диффузионный приток молекул пассивного газа к поверхности растущей капли и обусловлено постоянством полного давления парогазовой среды (механическое равновесие) и непроницаемостью границы капли для молекул пассивного газа. Соответственно при учете стефановского течения [122, 123] требуется определить скорость гидродинамического течения парогазовой среды вокруг растущей капли.

Как и в случае критического пузырька, будем считать, что мольные доли $\left\{ {{{x}_{{\text{l}}}}} \right\}$ компонентов в закритической капле за относительно малое время достигают своих стационарных значений $\left\{ {{{x}_{{{\text{la}}}}}} \right\} \ne $ $ \ne \left\{ {{{x}_{{{\text{ls}}}}}} \right\}{\text{,}}$ определяемых (4.3) и не зависящих от радиуса капли. Рассмотрим концентрическую с каплей подвижную сферу некоторого радиуса ${{R}_{1}}(t) > R(t){\text{.}}$ Если скорость изменения ${{R}_{1}}(t)$ со временем совпадает с радиальной скоростью $u(r,t)$ гидродинамического течения парогазовой смеси при $r = {{R}_{1}}(t){\text{,}}$ т.е.

то суммарное число молекул всех конденсирующихся компонентов и пассивного газа, заключенных внутри сферы радиуса ${{R}_{1}}(t){\text{,}}$ не изменяется с течением времени. Соответственно имеет место соотношение где ${{n}_{{{\text{la}}}}} \equiv \sum\nolimits_{i = 1}^k {{{n}_{{i{\text{la}}}}}} = {1 \mathord{\left/ {\vphantom {1 {{{v}_{{{\text{la}}}}}}}} \right. \kern-0em} {{{v}_{{{\text{la}}}}}}}$ – число молекул всех конденсирующихся компонентов в единице объема капли, ${{\bar {n}}_{{\text{g}}}} \equiv {{n}_{{\text{p}}}}(r,t) + \sum\nolimits_{i = 1}^k {{{n}_{{i{\text{g}}}}}(r,t)} $ – полная концентрация молекул парогазовой среды (включая молекулы пассивного газа), которая при постоянстве давления в газовой фазе не зависит от точки r и времени t. Дифференцируя соотношение (6.23) по времени и учитывая (6.22), находим

Поскольку найденное поле гидродинамической скорости $u(r,t)$ отвечает движению несжимаемой среды ($\nabla \vec {u} = 0$), то концентрация ${{n}_{{i{\text{g}}}}}(r,t)$ молекул i-го пара с учетом (6.24) определяется следующим уравнением диффузии:

При $t = 0$ при всех $r \geqslant 0$ и на большом удалении от капельки в произвольный момент времени t концентрация i-го пара считается однородной:

На поверхности растущей капли при $R \gg {{R}_{{{\text{c}},0}}}$ имеем два граничных условия. В качестве первого из них мы можем переписать (2.23) в виде Второе граничное условие учитывает материальный баланс для каждого пара. Сохранение числа молекул i-го компонента при его конденсации в каплю приводит к уравнению Учитывая в (6.28) равенство ${{v}_{{{\text{la}}}}}{{\dot {N}}_{{i{\text{l}}}}} = {{x}_{{i{\text{la}}}}}4\pi {{R}^{2}}\dot {R}$ и соотношение (6.24), находим откуда следует выражение для скорости роста радиуса капли $\dot {R}(t){\text{,}}$С переходом по (6.7) к автомодельной переменной ρ выражение (6.30) переписывается в виде

Как следует из (6.31), $R\dot {R}$ не зависит от размера капли. Соответственно, (6.25) может быть сведено в автомодельной переменной ${\rho }$ к обыкновенному дифференциальному уравнению

где введен новый безразмерный параметр ν:

Уравнение (6.32) совпадает с уравнением (6.10) при замене ${{b}_{{i{\text{l}}}}}\left( {\rho - {1 \mathord{\left/ {\vphantom {1 {{{\rho }^{2}}}}} \right. \kern-0em} {{{\rho }^{2}}}}} \right)$ на ${{b}_{{i{\text{g}}}}}\left( {{\rho } - {\nu \mathord{\left/ {\vphantom {\nu {{{\rho }^{2}}}}} \right. \kern-0em} {{{\rho }^{2}}}}} \right){\text{.}}$ Решение этого уравнения с граничными условиями (6.26) и (6.31) аналогично (6.11):

Граничное условие (6.27) позволяет связать скорости роста капель ${{B}^{{\left( {\text{d}} \right)}}} \equiv 2{{D}_{{i{\text{g}}}}}{{b}_{{i{\text{g}}}}}$ и стационарный состав $\left\{ {{{x}_{{{\text{la}}}}}} \right\}$ капель с начальными пересыщениями паров ${{\zeta }_{{i,0}}} = {{\left( {{{n}_{{i{\text{g}},0}}} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{n}_{{i{\text{g}},0}}} - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}} \right)} {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}}}} \right. \kern-0em} {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n} }}_{{i{\text{g}}}}}}}{\text{:}}$Подставляя (6.35) в равенство $\sum\nolimits_{i = 1}^k {{x}_{{i{\text{la}}}}} = 1{\text{,}}$ по-лучаем для скорости ${{B}^{{\left( {\text{d}} \right)}}}$ роста квадрата радиуса $\,$ закритической капли следующее уравнение: $\,$

Уравнения (6.35) и (6.36) образуют систему нелинейных уравнений, которая определяет неизвестную величину ${{B}^{{\left( {\text{d}} \right)}}}$ и стационарные мольные концентрации ${{x}_{{i{\text{la}}}}}$ ($i = 1,2,...,k$) в закритической капле как функции начальных пересыщений $\left\{ {{{\zeta }_{0}}} \right\} = \left( {{{\zeta }_{{1,0}}},...,{{\zeta }_{{k,0}}}} \right)$ всех паров в случае неидеального раствора в капле с учетом движения границы капли и нестационарного стефановского течения. В общем случае решение такой системы при заданных зависимостях ${{\gamma }_{i}}$ и ${{v}_{{\text{l}}}}$ от состава капли можно найти только численно. Как будет видно из следующего раздела, величины ${{B}^{{\left( {\text{d}} \right)}}}$ и ${{x}_{{i{\text{la}}}}}$ играют роль параметров, которые могут быть определены и экспериментально.

Хотя эффекты нестационарной диффузии при описании конденсации в многокомпонентных парах, как правило, носят поправочный характер, исключением является ситуация со стефановским течением при нестационарной диффузии паров в капли и нестационарной передачей тепла в окружающую среду при учете выделения тепла при конденсации. Анализ скорости стефановского течения, вызванного свободно растущей каплей в парогазовой атмосфере с несколькими конденсирующимися компонентами, проведенный в [125], демонстрирует появление стефановского потока вблизи растущей капли и стефановского оттока на больших расстояниях от капли вследствие нестационарности неизотермической конденсации и теплопередачи в газовую среду. Для ансамбля капель в атмосферном облаке этот отток обеспечивает увеличение общего объема облака, которое можно рассматривать как тепловое расширение облака, приводящее к его всплыванию в целом.

7. КИНЕТИКА СТАДИИ НУКЛЕАЦИИ В ПОДХОДЕ С ИСКЛЮЧЕННЫМ ОБЪЕМОМ. РАСПУХАНИЕ РАСТВОРОВ ПРИ ДЕГАЗАЦИИ

Рассмотрим развитие теории стадии нуклеации для систем, в которых условия стационарности диффузии и однородности пересыщений компонентов в метастабильной фазе не выполняются. Такое развитие при учете, что рост закритических частиц новой фазы происходит в диффузионном автомодельном режиме, описанном в предыдущем разделе, было построено для фазового превращения одного компонента в случае пузырьков газа при высоких пересыщении и растворимости газа в растворе в [55, 56] и в случае закритических капелек в [57] и названо подходом с исключенным объемом. В работах [58, 59] подход с исключенным объемом был расширен для описания неизотермического зарождения закритических капель в пересыщенном паре с возможностью перекрытия диффузионных слоев вокруг отдельных капель, которое может происходить на заключительном этапе стадии нуклеации. В [60] эффект перекрытия был учтен для пузырьков при произвольных пересыщении и растворимости газа в растворе. Дальнейшее обобщение подхода с исключенным объемом на многокомпонентные пузырьки при пренебрежении адсорбцией газов на поверхности критического пузырька было сделано в [101]. В этом разделе нашей задачей будет формулировка теории стадии нуклеации с исключенным объемом на примере дегазации пересыщенного газом раствора при произвольном количестве газовых компонентов, любой степени начального их пересыщения и любых значениях растворимости в исходном растворителе и при учете адсорбции газов на поверхности критического пузырька.

С помощью соотношений (6.11) и (2.17) локальное пересыщение ${{\zeta }_{i}}(r,t)$ i-го компонента растворенного газа в жидком растворе вокруг пузырька определяется как

Как следует из (3.10), локальная скорость нуклеации новых закритических пузырьков может быть записана в виде где с учетом (3.8) и (7.1) вклад $\varphi _{i}^{{\left( {\text{b}} \right)}}(\rho )$ i-го газового компонента в локальное относительное уменьшение полного пересыщения раствора равен

Формула (7.2) показывает, что скорость зарождения новых закритических пузырьков подавляется внутри некоторого сферического слоя вокруг растущего закритического пузырька, в котором величина $\sum\nolimits_{i = 1}^{k - 1} {{\Gamma }_{i}^{{\left( {\text{b}} \right)}}{\varphi }_{i}^{{\left( {\text{b}} \right)}}({\rho })} $ оказывется достаточно велика. В то же время скорость нуклеации остается на начальном уровне в остальном объеме раствора вокруг пузырька. Удобно ввести понятие об исключенном для нуклеации объеме ${{V}_{{{\text{ex}}}}}(t)$ вокруг одного растущего закритического пузырька радиуса $R(t)$ с помощью интегрального соотношения

Это соотношение означает, что общее количество пузырьков, образовавшихся за единицу времени вокруг выбранного пузырька при текущих профилях $\left\{ {\zeta \left( \rho \right)} \right\}$ пересыщений газов (и соответствующем по (7.2) профиле $J(\rho )$ скорости нуклеации), равно числу пузырьков, зародившихся вне исключенного объема, где сохраняется начальная скорость нуклеации ${{J}_{0}}$. Верхний предел интеграла в (7.4) носит формальный характер, поскольку, как следует из (7.2), (7.3) и (6.11), подынтегральное выражение стремится экспоненциально к нулю.

Введем отношение q исключенного объема ${{V}_{{{\text{ex}}}}}(t)$ и объема ${{V}_{R}}(t) = \left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right){{R}^{3}}(t)$ пузырька радиусом $R\left( t \right){\text{:}}$

Используя (7.5) и (7.2) в (7.4), находим

Как видно из (7.6), отношение q не зависит ни от размера пузырька, ни от времени и является одинаковым для закритического пузырька с любым радиусом. Это очень важное свойство, поскольку оно позволяет нам связать полный объем ${{V}_{{\text{g}}}}$ всех пузырьков, образовавшихся в растворе за время t, с полным исключенным объемом $V_{{{\text{ex}}}}^{{{\text{tot}}}}$ в растворе. Без учета перекрытия исключенных объемов для разных пузырьков мы имели бы $V_{{{\text{ex}}}}^{{{\text{tot}}}} = q{{V}_{{\text{g}}}}{\text{.}}$ Поскольку исключенный объем для пузырька определен соотношением (7.4) как средняя характеристика, то следует учесть случайное перекрытие диффузионных оболочек вокруг пузырьков в любом месте жидкого раствора. Для этого будем считать, что скорость изменения полного исключенного объема ${{dV_{{{\text{ex}}}}^{{{\text{tot}}}}\left( t \right)} \mathord{\left/ {\vphantom {{dV_{{{\text{ex}}}}^{{{\text{tot}}}}\left( t \right)} {dt}}} \right. \kern-0em} {dt}}$ во времени пропорциональна с множителем q скорости роста общего объема существующих пузырьков ${{d{{V}_{{\text{g}}}}\left( t \right)} \mathord{\left/ {\vphantom {{d{{V}_{{\text{g}}}}\left( t \right)} {dt}}} \right. \kern-0em} {dt}}$ и доле $1 - {{V_{{{\text{ex}}}}^{{{\text{tot}}}}\left( t \right)} \mathord{\left/ {\vphantom {{V_{{{\text{ex}}}}^{{{\text{tot}}}}\left( t \right)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ исходного объема жидкого раствора ${{V}_{{\text{l}}}}{\text{,}}$ доступной для зарождения новых пузырьков. Соответственно имеем

Интегрирование уравнения (7.7) с начальными условиями $V_{{{\text{ex}}}}^{{{\text{tot}}}}\left( 0 \right) = 0$ и ${{V}_{{\text{g}}}}\left( 0 \right) = 0$ дает соотношение между объемами $V_{{{\text{ex}}}}^{{{\text{tot}}}}\left( t \right)$ и ${{V}_{{\text{g}}}}\left( t \right)$ в виде

Полный объем системы, в котором начальная скорость нуклеации J₀ сохраняется к моменту времени t, есть

Количество $dN(\tau )$ пузырьков, зародившихся между моментами времени ${\tau }$ и $\tau + d\tau {\text{,}}$ равно Положив радиус закритического пузырька в момент его рождения равным нулю, видим, что приращение полного объема $d{{V}_{{\text{g}}}}\left( t \right),$ достигнутого всеми пузырьками газа, зародившимися между моментами времени τ и τ + dτ, к времени t, равно $d{{V}_{{\text{g}}}}\left( t \right) = {{V}_{R}}\left( {t - \tau } \right)dN\left( \tau \right){\text{.}}$ С помощью (7.10) выражаем полный объем ${{V}_{{\text{g}}}}\left( t \right)$ пузырьков как Используя (7.9) и (7.11), преобразуем уравнение (7.8) в следующее интегральное уравнение для полного объема раствора $\tilde {V}{\text{,}}$ в котором скорость нуклеации остается на начальном уровне:

Уравнение (7.12) представляет собой искомое кинетическое уравнение дегазации пересыщенного жидкого раствора с любым количеством пересыщенных растворенных газов в теории с исключенным объемом при учете возможности перекрывания диффузионных слоев закритических пузырьков. Покажем, что решение этого уравнения позволяет определить все наиболее интересные характеристики стадии нуклеации.

Для приближенного аналитического представления решения уравнения (7.12) можно воспользоваться методом итераций. Подставляя ${{\tilde {V}(\tau )} \mathord{\left/ {\vphantom {{\tilde {V}(\tau )} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}} = 1$ в подынтегральное выражение в правой части уравнения (7.12) и учитывая вытекающее из (6.15) равенство V_R(t) = (4π/3)R³(t) $ = \left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right){{\left( {{{B}^{{\left( {\text{b}} \right)}}}t} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{\text{,}}$ получаем в качестве первой итерации закон изменения объема $\tilde {V}\left( t \right)$ на стадии нуклеации в виде

где время $t_{1}^{{\left( {\text{b}} \right)}}$ определяет продожительность стадии нуклеации и равно

От соотношения для объема $\tilde {V}(t){\text{,}}$ который сам по себе не является наблюдаемой величиной, легко перейти к наблюдаемому полному числу $N(t)$ закритических пузырьков в растворе и фукции распределения пузырьков по размерам в текущий момент времени стадии нуклеации. С учетом (7.10) и (7.13), для полного числа $N(t)$ закритических пузырьков находим

Принимая во внимание (7.10), определим фукцию ${{f}^{{\left( {\text{b}} \right)}}}({{R}^{2}},t)$ распределения закритических пузырьков по квадрату их радиуса как

Используя свойства дельта-функции и (7.13), (7.14), получаем

Сравнивая (7.17) и (7.14) с соотношениями (5.14) и (5.19) в теории среднего поля пересыщений, видим, что различия обусловлены заменами ${{A}^{{\left( {\text{b}} \right)}}} \to {{B}^{{\left( {\text{b}} \right)}}}$ и $\frac{{{{{\left( {{{A}^{{\left( {\text{b}} \right)}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{{{\bar {\zeta }}}_{0}}}}\sum\nolimits_{i = 1}^{k - 1} {\frac{{{{x}_{{i{\text{gs}}}}}\Gamma _{i}^{{\left( {\text{b}} \right)}}}}{{{{s}_{i}}}}} \to q{{\left( {{{B}^{{\left( {\text{b}} \right)}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{\text{.}}$ С учетом определений (7.6), (7.3), решения (6.11), соотношений (6.12) и (6.13) параметр q в общем случае может быть представлен как

Таким образом, этот параметр вполне определен при известных начальных пересыщениях и растворимостях газов в растворе.

Можно показать, следуя [101], что соотношение (7.18) преобразуется к виду

который удобен как для исследования асимптотик, так и для численного расчета ввиду более быстрой сходимости интеграла по переменной ρ по сравнению с интегралом в (7.18). В случае чрезвычайно малых значений величин ${{b}_{{i{\text{l}}}}}$ мы можем, согласно (6.13), (6.14) и (4.9), положить ${{b}_{{i{\text{l}}}}} = {{a}_{i}}{\text{,}}$ $\left\{ {{{x}_{{{\text{ga}}}}}} \right\} = \left\{ {{{x}_{{{\text{gs}}}}}} \right\}$ и $\exp \left( { - {{b}_{{i{\text{l}}}}}\left( {{{\rho }^{2}} + \frac{2}{\rho } - 3} \right)} \right) \approx 1$ в подынтегральном выражении в (7.19). В итоге имеем Проводя интегрирование в (7.20), ожидаемо получаем С учетом (7.21) и того, что в рассматриваемом предельном случае ${{B}^{{\left( {\text{b}} \right)}}} \approx {{A}^{{\left( {\text{b}} \right)}}}{\text{,}}$ соотношения (7.17) и (7.14) переходят в (5.14) и (5.19) для теории среднего поля пересыщений.

Отметим, что выражение (7.21) для параметра q в этом случае можно получить и непосредственно из исходного выражения (7.18), если учесть, что при предельно малых значениях параметров ${{b}_{{i{\text{l}}}}}$ основной вклад в интеграл дает область больших ρ. В этой области показатель экспоненты мал, и можно положить

в результате чего выражение (7.18) приобретает вид Учитывая также, что в этом пределе $\left\{ {{{x}_{{{\text{ga}}}}}} \right\} = \left\{ {{{x}_{{{\text{gs}}}}}} \right\}{\text{,}}$ и имея в виду тождество приходим снова к выражению (7.21).

Если диффузионные потоки всех компонентов в растворе существенно нестационарны, так что условие ${{b}_{{i{\text{l}}}}} \gg 1$ выполняется для всех компонентов с $i = 1,2,...,k - 1{\text{,}}$ то общее выражение (7.19) для параметра q также можно несколько упростить. При ${{b}_{{i{\text{l}}}}} \gg 1$ можно использовать приближение ${1 \mathord{\left/ {\vphantom {1 {{{\rho }^{2}}}}} \right. \kern-0em} {{{\rho }^{2}}}}\exp ( - ({{b}_{{i{\text{l}}}}}{\text{/}}2)({{\rho }^{2}} + 2{\text{/}}\rho - 3)) \approx $ $ \approx \exp ( - (3{{b}_{{i{\text{l}}}}}{\text{/}}2){{(\rho - 1)}^{2}})$ в подынтегральных выражениях в (7.19). В результате, опуская экспоненциально малое первое слагаемое в (7.19) и используя асимптотику (6.19), получим

Особенно простой вид выражение (7.25) для параметра q приобретает в частном случае, когда все коэффициенты диффузии ${{D}_{{i{\text{l}}}}}$ ($i = 1,2,...,k - 1$) совпадают, а зависимостью поверхностного натяжения критического пузырька от состава раствора можно пренебречь. В этом случае из (6.9) и (6.14) следует

а из (3.14) имеем С использованием (7.26) и (7.27) и следующего из (6.13) равенства $\sum\nolimits_{i = 1}^{k - 1} {{{{{x}_{{i{\text{ga}}}}}{{a}_{{i{\text{a}}}}}} \mathord{\left/ {\vphantom {{{{x}_{{i{\text{ga}}}}}{{a}_{{i{\text{a}}}}}} {{{s}_{i}}}}} \right. \kern-0em} {{{s}_{i}}}} = {{{\bar {\zeta }}}_{0}}} $ соотношение (7.25) сводится к где

Выражение (7.28) совпадает с выражением, полученным ранее [60] для параметра q при сильной нестационарности диффузии в случае однокомпонентных пузырьков. Как следует из (3.14) и (3.3), величина ${{\Gamma }^{{\left( {\text{b}} \right)}}}$ обратно пропорциональна $\bar {\zeta }_{0}^{2}{\text{.}}$ Численное интегрирование правой части (7.29) показывает, что величина $\lambda \left( {{{\Gamma }^{{\left( {\text{b}} \right)}}}} \right)$ изменяется от 3.15 до 3.61 при изменении ${{\Gamma }^{{\left( {\text{b}} \right)}}}$ в широком интервале, от 50 до 150. Соответственно, величина $\lambda \left( {{{\Gamma }^{{\left( {\text{b}} \right)}}}} \right)$ слабо убывает с ростом ${{\bar {\zeta }}_{0}}{\text{.}}$ Из (7.26) и равенства $\sum\nolimits_{i = 1}^{k - 1} {{{{{x}_{{i{\text{ga}}}}}{{a}_{{i{\text{a}}}}}} \mathord{\left/ {\vphantom {{{{x}_{{i{\text{ga}}}}}{{a}_{{i{\text{a}}}}}} {{{s}_{i}}}}} \right. \kern-0em} {{{s}_{i}}}} = {{{\bar {\zeta }}}_{0}}} $ имеем

Таким образом, из (7.28) и (7.30) следует, что чем больше начальные пересыщения газов и их растворимость, тем меньше параметр q.

К числу наблюдаемых характеристик фазового превращения на стадии нуклеации относится и полный объем газовой фазы ${{V}_{{\text{g}}}}(t){\text{.}}$ Как следует из уравнений (7.8) и (7.9), отношение объемов ${{{{V}_{{\text{g}}}}(t)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}(t)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}{\text{,}}$ характеризующее распухание жидкого раствора при дегазации, составляет

Ввиду (7.13) имеем и отношение ${{{{V}_{{\text{g}}}}(t)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}(t)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ достигает своего наибольшего значения ${{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}} = {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0em} q}$ в конце стадии нуклеации при $t = t_{1}^{{\left( {\text{b}} \right)}}{\text{.}}$ Чем меньше параметр q, тем больше распухание к концу стадии нуклеации.

Представляет интерес оценить максимально возможное значение ${{\left( {{{{{V}_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}} \right)}_{{\text{m}}}}$ коэффициента распухания ${{{{V}_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}$ для многокомпонентного жидкого раствора при полной его дегазации при давлении P₁, когда весь начальный избыток растворенных газов перешел в большие закритические пузырьки и объемная концентрация i-го газа (i = 1, 2, $...,k - 1$) в растворе упала от его начального значения ${{n}_{{i{\text{l}},0}}} = \left( {{{\zeta }_{{i,0}}} + 1} \right){{s}_{i}}{{{{P}_{{\text{l}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{l}}}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ до равновесного значения ${{n}_{{i{\text{l}},\infty }}} = {{s}_{i}}{{n}_{{i{\text{g}},\infty }}}$ (для многокомпонентного раствора). Баланс количества молекул i-го газа в конечном равновесии соотносит конечную концентрацию i-го газа с максимальным значением ${{\left( {{{{{V}_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}} \right)}_{{\text{m}}}}$ коэффициента распухания как

С учетом соотношения (7.33) относительная концентрация ${{x}_{{i{\text{g}},\infty }}} = {{{{{{n}_{{i{\text{g}},\infty }}}{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{n}_{{i{\text{g}},\infty }}}{{k}_{{\text{B}}}}T} P}} \right. \kern-0em} P}}_{{\text{l}}}}$ равна Используя равенство $\sum\nolimits_{i = 1}^{k - 1} {{x}_{{i{\text{g}},\infty }}} = 1$, находим из (7.34) Уравнения (7.34) и (7.35) идентичны уравнениям (4.21) и (4.22), которые определяли стационарные концентрации газов в растущем пузырьке и параметр a при стационарности диффузии и совпадающих коэффициентах диффузии газов в растворе. В частном случае одинаковой растворимости газовых компонентов, когда ${{s}_{i}} = s$ (i = 1,2,…, $k - 1$), из (7.35) следует равенство совпадающее по виду с полученным ранее [55] для случая одного растворенного газа. Оценка (7.36) иллюстрирует возможность многократного распухания многокомпонентного жидкого раствора при дегазации в случае сильного пересыщения раствора, когда $s{{\bar {\zeta }}_{0}} \gg 1.$ При этом условии, очевидно, существенную роль в кинетике стадии нуклеации и последующего роста пузырьков играет нестационарность диффузии растворенных газов. Из равенства ${{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}\left( {t_{1}^{{\left( {\text{b}} \right)}}} \right)} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}} = {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0em} q}$ в конце стадии нуклеации и вытекающего из (7.28) и (7.30) при ${{s}_{i}} = s$ соотношения $q = {{\lambda \left( {{{\Gamma }^{{\left( {\text{b}} \right)}}}\left( {{{{\bar {\zeta }}}_{0}}} \right)} \right)} \mathord{\left/ {\vphantom {{\lambda \left( {{{\Gamma }^{{\left( {\text{b}} \right)}}}\left( {{{{\bar {\zeta }}}_{0}}} \right)} \right)} {s{{{\bar {\zeta }}}_{0}}}}} \right. \kern-0em} {s{{{\bar {\zeta }}}_{0}}}}$ заключаем, что значительное распухание раствора (до трети ${{\left( {{{{{V}_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\text{g}}}}} {{{V}_{{\text{l}}}}}}} \right. \kern-0em} {{{V}_{{\text{l}}}}}}} \right)}_{{\text{m}}}}$) происходит уже на стадии нуклеации.

8. О ПРИМЕНИМОСТИ ТЕОРИИ КРИСТАЛЛИЗАЦИИ КОЛМОГОРОВА В ТЕОРИИ СТАДИИ НУКЛЕАЦИИ

Как следует из результатов предыдущего раздела, наиболее общее описание стадии нуклеации закритических частиц новой фазы при мгновенно созданных пересыщениях исходной многокомпонентной метастабильной фазы может быть проведено в рамках подхода с исключенным объемом с учетом стохастического перекрывания нестационарных диффузионных слоев вокруг растущих частиц. Следует отметить, что подход с исключенным объемом охватывает случаи с любой степенью метастабильности начальной фазы и отклонением от стационарной диффузии вещества метастабильной фазы и может быть применен к системам с произвольным числом компонентов, участвующих в фазовом переходе. Результаты теории с самосогласованным полем пересыщений при стационарной диффузии следуют из подхода с исключенным объемом как частный случай.

В литературе за последние 10 лет можно встретить работы [128–131], посвященные анализу и применению статистической теории кристаллизации Колмогорова [132] и ее последующих расширений в работах Джонсона и Мёля [133] и Аврами [134–136] для анализа роста и поглощения вещества метастабильной фазы закритическими частицами новой фазы. Соответственно возникает вопрос о возможности применения теории Колмогорова–Джонсона–Мёля–Аврами (далее – теории КДМА) для анализа стадии нуклеации и связи этой теории с подходом с исключенным объемом, рассмотренным в разделе 7. Заметим, что некоторые соотношения подхода с исключенным объемом похожи на соотношения теории КДМА. Как и в подходе с исключенным объемом, ключевым объектом описания в теории КДМА является доля объема новой фазы и ее связь со скоростью нуклеации и скоростью роста закритических частиц новой фазы. Поэтому имеет смысл вспомнить основные положения этой теории.

Как известно [132–136], постулаты теории КДМА состоят в следующем. Предполагается, что закритические частицы новой фазы при гомогенной нуклеации появляются случайно в произвольном месте начального объема ${{V}_{0}}$ метастабильной системы. Для любой незанятой части объема ${{V}_{1}}$ метастабильной системы вероятность зарождения одной закритической частицы в этом объеме за промежуток времени $\Delta t$ равна $\alpha (t){{V}_{1}}\Delta t{\text{.}}$ Вокруг новых и ранее зародившихся частиц происходит увеличение количества вещества новой фазы с некоторой линейной скоростью $c\left( t \right){\text{,}}$ которая зависит от времени t и направления роста.

Основным результатом теории КДМА для изотропных систем является формула для вероятности $p(t)$ того, что выбранная точка объема, заполненного метастабильным веществом, оказывается в текущий момент времени t в образовавшихся частицах новой фазы:

Эта вероятность связывается с объемной долей перешедшего в новую фазу вещества простым соотношением где $\tilde {V}\left( t \right)$ – объем системы, доступный для образования новых частиц в момент времени t.

Обычно в качестве коэффициента $\alpha \left( t \right)$ берут скорость нуклеации J критических частиц новой фазы, определяемую соотношением (3.7). Однако Филипович [137, 138] обратил внимание, что коэффициент $\alpha \left( t \right)$ правильнее определить как

Множитель ${{\tilde {V}\left( t \right)} \mathord{\left/ {\vphantom {{\tilde {V}\left( t \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ в (8.3) учитывает, что нуклеация происходит в свободном от частиц объеме. С учетом (8.3) и (8.2) соотношение (8.1) может быть переписано как интегральное уравнение на объем $\tilde {V}\left( t \right){\text{:}}$

Сравнивая уравнение (8.4) с уравнением (7.12) подхода с исключенным объемом, видим, что эти уравнения совпадают, если положить ${{V}_{0}} = {{V}_{{\text{l}}}}{\text{,}}$ J(τ) = $ = {{J}_{0}}$ и $\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right){{\left( {\int_\tau ^t {c(} t{\kern 1pt} ')dt{\kern 1pt} '} \right)}^{3}} = q{{V}_{R}}(t - \tau ){\text{,}}$ где параметр q определен соотношением (7.6), а скорости роста объема ${{V}_{R}}(t - \tau )$ определены как решения уравнений (6.16) и (6.17) для закритических пузырьков или уравнений (6.36) и (6.37) для закритических капелек с учетом стефановского течения. Другими словами, на стадии нуклеации при автомодельном описании диффузионного роста закритических частиц новой фазы действительно существует прямая связь между теорией КДМА и подходом с исключенным объемом. При данном в разделе 7 определении исключенного для нуклеации объема ${{V}_{{{\text{ex}}}}}(t)$ вокруг одной растущей закритической частицы радиуса $R(t)$ этот исключенный объем может рассматриваться как эффективный объем закритической частицы в теории КДМА. Конечно, важны “микроскопические” определения параметра q и скорости ${{V}_{R}}(t)$ на основе автомодельных профилей концентраций компонентов в метастабильной фазе, которые были рассмотрены в разделе 6 и которые отличаются от обычно используемых в теории КДМА. Автомодельные профили автоматически учитывают баланс вещества компонентов.

Заметим теперь, что при применении теории КДМА к описанию нуклеации в системах с конечным объемом и диффузионным ростом закритических частиц новой фазы существует внутреннее противоречие. Оно заключается в предположении о взаимной независимости процессов зарождения и роста в любых точках системы вследствие неизбежного возникновения пространственных корреляций в поведении системы из-за эффектов исключенного объема и обратного влияния зарождения новой фазы на текущее состояние метастабильной фазы. Влияние этих эффектов на стадии нуклеации мало, но должно усиливаться к концу этой стадии и нарастать на следующей стадии фазового превращения. Как подход с исключенным объемом, так и теория КДМА в ситуации существенного перекрытия диффузионных слоев вокруг частиц новой фазы становятся неприменимыми.

ЗАКЛЮЧЕНИЕ

Мы представили обзор современных результатов кинетической теории стадии нуклеации для газовых пузырьков в жидких растворах и капелек в пересыщенных парах с произвольным числом и любыми значениями пересыщения компонентов в метастабильном состоянии.

Показано, что зависимость поверхностного натяжения критического зародыша новой фазы от состава и размера не влияет на особенности развития стадии нуклеации, но влияет на скорость нуклеации при начальных пересыщениях метастабильной фазы. Важную роль при построении замкнутого аналитического описания стадии нуклеации в многокомпонентных системах играет достаточно быстрое установление стационарного состава растущих закритических частиц новой фазы. Этот состав определяется физико-химическими характеристиками системы и начальными пересыщениями компонентов, участвующих в фазовом переходе. Современная теория позволяет прогнозировать эволюцию всего ансамбля закритических частиц новой фазы с различными размерами при самосогласованном изменении состояния исходной метастабильной фазы. Этот прогноз осуществляется через знание функции распределения закритических частиц по размерам в любой момент стадии нуклеации, позволяющей вычислять полное число закритических частиц в системе, их средний размер и дисперсию, находить текущее пересыщение каждого компонента в системе. В обзоре рассмотрены метастабильные системы со стационарной и нестационарной диффузией вещества к растущим частицам новой фазы. Показано, что эффекты нестационарности диффузии могут быть очень значительными при росте многокомпонентных пузырьков в автомодельном режиме и, в частности, ответственны за значительное распухание жидкого раствора при сбросе внешнего давления. В отличие от режима стационарной диффузии, условия реализации которого требуют, чтобы начальное пересыщение было не слишком большим для всех газовых компонентов, в автомодельном режиме такие ограничения отсутствуют, так что пересыщения некоторых газовых компонентов могут быть большими, а другие могут быть малыми. Существенно, что степень нестационарности потоков будет примерно одинаковой для всех компонентов, несмотря на возможные сильные различия в значениях начального пересыщения отдельных компонентов газа и их растворимости. Показана связь подхода с исключенным объемом и теории КДМА.

Общая картина стадии нуклеации, распределение закритических частиц как функция времени и размера частиц, уравнения для состава критических и закритических частиц могут пригодиться для планирования прямого или численного эксперимента с системами на стадии нуклеации. Знание явного вида функции распределения частиц и их состава к концу стадии нуклеации позволяет определить, в частности, начальные условия для последующей стадии фазового перехода, на которой происходит переход основной части метастабильного вещества. В настоящее время не существует адекватного теоретического описания этой стадии для многокомпонентных систем. Отметим также, что точное аналитическое решение задачи о нестационарном диффузионном росте пузырьков газа, соответствующее автомодельному режиму роста, может быть получено только без учета влияния сил Лапласа и вязкости. Поэтому важно установить, насколько быстро происходит достижение автомодельного или стационарного роста пузырьков газа в области значительного влияния сил Лапласа и вязкости как в однокомпонентном, так и в многокомпонентном случаях. Решение этой задачи также остается актуальным.