Коллоидный журнал, 2020, T. 82, № 4, стр. 463-469
Модификация закона действия масс для обратных мицелл
А. И. Русанов *
Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия
* E-mail: rusanov32@list.ru
Поступила в редакцию 21.01.2020
После доработки 27.01.2020
Принята к публикации 30.01.2020
Аннотация
Рассматриваются две модификации закона действия масс при определении критической концентрации мицеллообразования (ККМ) через константу K закона. Первая, традиционная задает ККМ как ${{K}^{{1/(1 - n)}}},$ где n – число агрегации, а вторая – как ${{(Kn)}^{{1/(1 - n)}}}.$ В обоих случаях формулировка закона действия масс чрезвычайно упрощается благодаря исключению константы, а все концентрации выражаются в единицах ККМ (которая несколько меньше во втором случае). Вторая модификация закона работает точнее в случае средних и малых чисел агрегации, характерных для обратных мицелл, а потому указанные две модификации условно причислены к прямым и обратным мицеллам. Для обеих модификаций проанализированы зависимости концентраций мицелл и мономеров от брутто-концентрации ПАВ в мицеллярном растворе, а для обратных зависимостей выведены явные аналитические выражения. Установлена и явная связь указанных концентраций со степенью мицеллизации раствора. Определена зависимость критической степени мицеллизации (соответствующей ККМ) от числа агрегации.
ВВЕДЕНИЕ
Своеобразие обратных мицелл проявляется во многих аспектах (см., например, обзор [1]). Если пользоваться термодинамическим языком, можно сказать, что для прямых мицелл главную роль играет энтропийная, а для обратных – энергетическая составляющая процесса мицеллообразования. Да и силовой механизм их образования совершенно разный. В воде молекулы ПАВ объединяются в прямые мицеллы не потому, что притягиваются друг к другу, а потому, что вода выталкивает из себя их неполярные части. Отсюда и название – “гидрофобный эффект” (“лиофобный эффект” в случае других полярных растворителей). При образовании же обратных мицелл их полярные части действительно притягиваются друг к другу, образуя полярное ядро. Размер (число агрегации) мицеллы зависит от соотношения размеров полярных и неполярных групп. Чаще полярные группы меньше неполярных (скажем, углеводородных хвостов), а потому и обратные мицеллы типично меньше прямых.
Что касается термодинамических формул в теории мицеллообразования, то они не зависят от типа сил и в равной мере применимы к мицеллам обоих типов. В первую очередь это относится к закону действия масс. Поскольку образование обратных мицелл, как и прямых, происходит типично в области малых концентраций ПАВ, в ходу форма закона действия масс в терминах концентраций
где ${{c}_{\operatorname{M} }}$ – концентрация мицелл в растворе ПАВ, $K$ – константа закона действия масс, ${{c}_{1}}$ – концентрация мономеров ПАВ и $n$ – число агрегации. Важной величиной теории также является степень мицеллизации ПАВ(2)
$\alpha \equiv \frac{{n{{c}_{\operatorname{M} }}}}{c}{\kern 1pt} ,\,\,\,\,1 - \alpha = \frac{{{{c}_{1}}}}{c},$Если учесть, что образование мицеллы происходит путем последовательного присоединения молекул, то при числе агрегации n будет всего n – 1 таких актов присоединения. Применяя к каждому из них закон действия масс с константой ${{K}_{i}}$ для i-того акта, получим [1, 2]
где $\bar {K}$ определяется как приближение, в котором все константы ${{K}_{i}}$ одинаковы и равны $\bar {K}$ [1], или, строго, как среднее геометрическое величин ${{K}_{i}}$ [3]. Подстановка (4) в (3) приводит к выражениюПоскольку рост концентрации ПАВ начинается с нуля, при малых концентрациях произведение $\bar {K}c$ намного меньше единицы, а будучи возведенной в большую степень n – 1, становится исчезающе малой. Поэтому, пока позволяет множитель n в правой части (5), будет малой и степень мицеллизации ПАВ: концентрация мицелл слишком мала для их обнаружения. Если же с ростом концентрации ПАВ произведение $\bar {K}c$ становится больше единицы, правая часть (5) возрастает как лавина, знаменуя мицеллообразование. Естественно поэтому определить критическую концентрацию мицеллообразования (ККМ) ${{c}_{\operatorname{m} }}$ из условия $\bar {K}{{c}_{\operatorname{m} }} = 1$ или [1, 2]
(6)
$K = c_{\operatorname{m} }^{{1 - n}},\,\,\,\,{{c}_{\operatorname{m} }} = {{K}^{{\frac{1}{{1 - n}}}}}.$Подстановка (6) в (3) приводит к соотношению
(7)
$\frac{{{{\alpha }_{\operatorname{m} }}}}{{{{{(1 - {{\alpha }_{\operatorname{m} }})}}^{n}}}} = n,$Распространение такого подхода на многокомпонентный случай и развитие теории мицеллообразования на этой основе было дано в [3–5]. Естественно, возможны и другие подходы к определению ККМ. Так, монотонно возрастающая функция $\alpha (c)$ имеет единственную точку перегиба, и соответствующее ей значение концентрации можно принять за ККМ [6–8]. Сравнительный анализ такого подхода и подхода, основанного на (6) и (7), обнаружил расхождение в величинах ККМ порядка одного процента, что составляет меньше экспериментальной погрешности в нахождении этой величины [4]. Добрую дюжину других возможных определений ККМ читатель найдет в [6–8].
Приведенные выше рассуждения с введением определения ККМ (6) подразумевали большие числа агрегации и, значит, относились, в основном, к прямым мицеллам. Для них была уже осуществлена модификация закона действия масс [3–6]. Однако, как известно, обратные мицеллы могут обладать малыми числами агрегации, и для них модификация закона действия масс должна быть изменена. В данном сообщении мы покажем, как это сделать, но предварительно вернемся к случаю прямых мицелл для важных добавлений.
СЛУЧАЙ ПРЯМЫХ МИЦЕЛЛ
Как известно, в теории закон действия масс выводится из установленного Гиббсом условия термодинамического равновесия для химических реакций. Он формулируется гениально просто: нужно записать химическую реакцию и заменить символы веществ их химическими потенциалами, оставив стехиометрические коэффициенты без изменений. Прилагая это к нашему случаю мицеллообразования, получаем
где μ – химический потенциал, а индекс M относится к мицеллам. Применимость условия Гиббса к агрегативным процессам, как и применимость самого понятия химического потенциала к агрегативным частицам (не обязательно мицеллам) были обоснованы в работе [9]. Можно также показать, что условие агрегативного равновесия типа (8) непосредственно вытекает из принципа равновесия Гиббса [6–8]. Остается подставить в (8) подходящее выражение для химического потенциала. Но какое?Статистическая термодинамика дает следующее выражение:
где ${{g}^{0}} = {{\mu }^{0}} + w$ – парциальная энергия Гиббса для находящейся в чистом растворителе молекулы с покоящимся центром масс (${{\mu }^{0}}$ – химический потенциал молекулы с покоящимся центром масс в вакууме, w – работа переноса молекулы из фиксированного положения в вакууме в фиксированное положение в растворителе), k – постоянная Больцмана, T – температура, a = сf – активность (f – коэффициент активности) и Λ – средняя длина волны де Бройля молекулы. По аналогии с (9) для мицеллыОтметим, что принятое в физической химии выражение для химического потенциала через мольную долю более популярно. Читатель может его встретить почти в любой статье о мицеллах. Но оно содержит “стандартную часть”, которая остается “вещью в себе”, а потому и при подстановке в (8) делает константу закона действия масс “вещью в себе”. Подстановка же (9) и (10) в (8) приводит к закону действия масс с константой [6–8]
(11)
$K = \frac{{{{\Lambda }^{{3n}}}}}{{\Lambda _{М}^{3}}}\exp \frac{{n{{g}^{0}} - G_{М}^{0}}}{{kT}},$Подстановка (6) в (1) с дополнительным делением обеих частей (1) на ${{с}_{\operatorname{m} }}$ упрощает закон действия масс к виду
где тильда указывает, что концентрация измеряется в единицах ${{с}_{\operatorname{m} }}$. Это и есть модификация закона действия масс для прямых мицелл. Ее большая привлекательность обусловлена исключительной простотой и отсутствием такой сложной величины, как константа (11). В рамках данного формализма был получен ряд детальных соотношений [4]. Среди них взаимосвязь относительной брутто-концентрации ПАВ $\tilde {с}$ и степени мицеллизации α(13)
$\tilde {c} = {{\left[ {\frac{\alpha }{{{{{(1 - \alpha )}}^{n}}n}}} \right]}^{{\frac{1}{{n - 1}}}}},$(14)
${{\tilde {c}}_{\operatorname{M} }} = {{\left( {\frac{\alpha }{{(1 - \alpha )n}}} \right)}^{{\frac{n}{{n - 1}}}}}.$(15)
${{\tilde {c}}_{1}} = {{\left( {\frac{\alpha }{{(1 - \alpha )n}}} \right)}^{{\frac{1}{{n - 1}}}}}.$Совместно выражения (13) и (14) задают параметрически (через α) зависимость ${{\tilde {c}}_{\operatorname{M} }}$ от $\tilde {c}$, а выражения (13) и (15) – зависимость ${{\tilde {c}}_{1}}$ от $\tilde {c}$ при заданном n. Именно так, через параметр α, эти зависимости были построены графически и изучены в [4]. Однако в данной задаче была упущена возможность продвинуться и чисто аналитическим путем. Сделаем это.
Исключая α из (13) и (14), находим
(16)
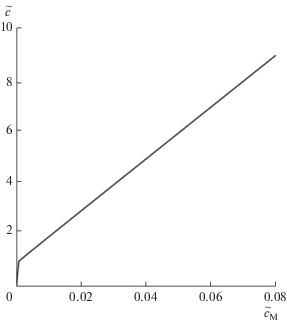
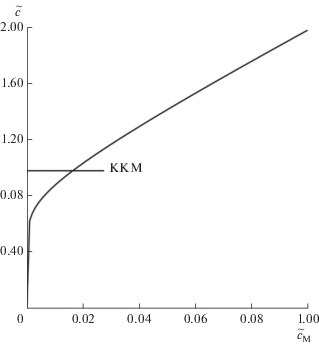
$\tilde {с} = n{{\tilde {c}}_{\operatorname{M} }} + \tilde {c}_{\operatorname{M} }^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}.$Здесь брутто-концентрация ПАВ в растворе дана как явная функция концентрации мицелл. Ее график при n = 100, представленный на рис. 1, тождественен графику на рис. 3б в [4] с перевернутыми осями. Подстановка (12) в (16) приводит к выражению
Рис. 3.
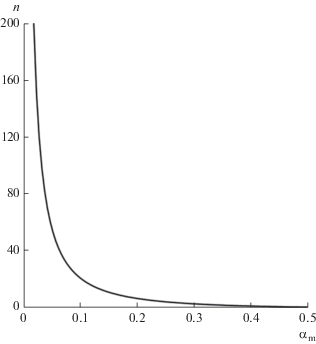
Взаимозависимость КСМ ${{\alpha }_{\operatorname{m} }}$ и числа агрегации n согласно уравнению (21). Нижняя точка графика n = 1 и ${{\alpha }_{\operatorname{m} }}$ = 0.5, верхняя точка n = 200 и ${{\alpha }_{\operatorname{m} }}\,\, \approx $ 0.0195.
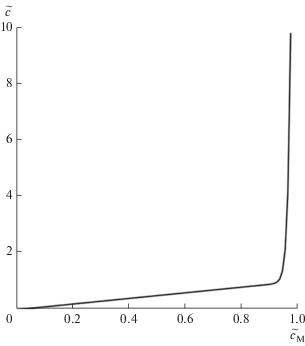
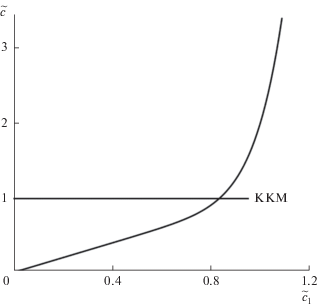
где брутто-концентрация ПАВ представлена уже как явная функция концентрации мономеров. График этой функции изображен на рис. 2, и это то же самое, что график на рис. 3а в работе [4], но с перевернутыми осями. Нужно отметить, что аналитические решения в виде явных функций типа (16) и (17) – большая редкость в теории мицеллообразования на основе закона действия масс. В этом и важность дополнения к работе [4], которое мы сейчас вносим.
Необходимо пояснить еще одно обстоятельство. В чисто практических целях простые на вид графические решения в [4] были аппроксимированы такими же простыми явными аналитическими выражениями. Было бы ошибкой думать, что с появлением соотношений (16) и (17) необходимость в этом отпадает. Дело в том, что речь шла о функциях ${{\tilde {c}}_{\operatorname{M} }}(\tilde {c})$ и ${{\tilde {c}}_{1}}(\tilde {c})$, а для них соотношения (16) и (17) остаются сложными уравнениями, для которых мы располагаем лишь графическими решениями. Именно такими являются графики на рис. 1 и 2, а потому полезность аналитических аппроксимаций сохраняется.
СЛУЧАЙ ОБРАТНЫХ МИЦЕЛЛ
Обратимся вновь к выражению (5). Чтобы более четко зафиксировать резкое возрастание его левой части с учетом числа агрегации n, нужно переписать (5) как
(18)
${\kern 1pt} \frac{\alpha }{{{{{(1 - \alpha )}}^{n}}}} = {{(\bar {K}c{{n}^{{\frac{1}{{n - 1}}}}})}^{{n - 1}}}.$Для прямых мицелл этого не делают, ибо при больших n величина ${{n}^{{\frac{1}{{n - 1}}}}}$ практически равна единице (например, приблизительно 1.05 при n = 100), и переход к (18) ничего не меняет. Но ситуация становится другой при достаточно малых числах агрегации (вплоть до n = 2), часто встречающихся для обратных мицелл. Это значит, что приведенное выше определение ККМ необходимо перенормировать для случая обратных мицелл. Теперь ${{c}_{\operatorname{m} }}$ определяется из условия
(19)
$\bar {K}{{c}_{\operatorname{m} }}{{n}^{{\frac{1}{{n - 1}}}}} = 1,\,\,\,\,Kn = c_{\operatorname{m} }^{{1 - n}},\,\,\,\,{{c}_{\operatorname{m} }} = {{(Kn)}^{{\frac{1}{{1 - n}}}}}.$Из сравнения (6) и (19) находим, что ККМ для прямых (пометим индексом d) и обратных (индекс r) мицелл соотносятся как
(20)
$\frac{{с_{\operatorname{m} }^{{(\operatorname{d} )}}}}{{с_{\operatorname{m} }^{{(\operatorname{r} )}}}} = {{n}^{{\frac{1}{{n - 1}}}}}.$Правая часть выражения (20) – монотонно убывающая функция от значения 2 при n = 2 до асимптотического предельного значения 1 при $n \to \infty .$ Таким образом, ККМ согласно (6) оказывается выше (но не более, чем в два раза), чем ККМ по (19).
С учетом (19) выражение (18) создает уравнение для КСМ в виде
(21)
$\frac{{{{\alpha }_{\operatorname{m} }}}}{{{{{(1 - {{\alpha }_{\operatorname{m} }})}}^{n}}}} = 1.$Сравнивая (7) и (21), замечаем, что для обратных мицелл теория выглядит в этом плане гораздо проще. Если (7) – трудно решаемое уравнение для функции ${{\alpha }_{\operatorname{m} }}(n)$ (ее анализ см. в [4]), то (21) дает явное выражение
(22)
$n = \frac{{\ln {{\alpha }_{\operatorname{m} }}}}{{\ln (1 - {{\alpha }_{\operatorname{m} }})}}.$График взаимной зависимости $n{\text{ и }}{{\alpha }_{\operatorname{m} }}$ показан на рис. 3. Из него видно, что при небольших числах агрегации (особенно меньше 10) зависимость ${{\alpha }_{\operatorname{m} }}$ от n резко выражена, а при значительных числах агрегации (особенно больше 100) она слаба.
Подстановка (19) в (1) придает закону действия масс форму
где константа закона действия масс исчезает, а для концентраций, помеченных тильдой, единицей измерения является ККМ, определяемая согласно (19). Уравнение (23) и есть модификация закона действия масс для обратных мицелл. По простоте она почти не уступает модификации (12) для прямых мицелл. Нужно также отметить, что, согласно (20), в (23) используется более мелкая единица измерения концентрации, чем в (12).Соединение (19) и (5) дает результат
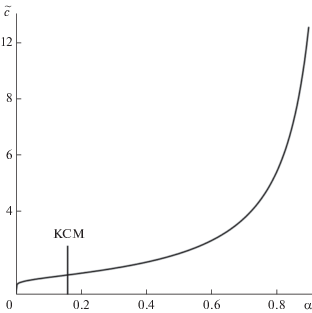
Эта формула связывает степень мицеллизации ПАВ с его брутто-концентрацией в растворе, причем функция $\tilde {с}(\alpha )$ задается в явном виде. График этой функции (рис. 4) показывает, что в районе ККМ и выше (примерно до $\tilde {с} \approx 3)$ степень мицеллизации является более чувствительной характеристикой процесса мицеллообразования, чем концентрация. При больших же значениях $\tilde {с},$ наоборот, более чувствительной характеристикой становится концентрация.
Рис. 4.
Кривая взаимозависимости брутто-концентрации ПАВ в растворе и степени мицеллизации согласно выражению (24) при $n = 10.$ Положение точки с координатами ККМ (с = 1) и КСМ $(\alpha \approx 1.65)$ соответствует точке перегиба на кривой.
В сочетании с выражениями (2) (очевидно, они не зависят от выбора единицы концентрации) формула (24) также приводит к соотношениям
(25)
${{\tilde {с}}_{\operatorname{M} }} = \frac{1}{n}{{\left( {\frac{\alpha }{{1 - \alpha }}} \right)}^{{\frac{n}{{n - 1}}}}},$(26)
${{\tilde {c}}_{1}} = {{\left( {\frac{\alpha }{{1 - \alpha }}} \right)}^{{\frac{1}{{n - 1}}}}},$(27)
$\tilde {с} = {{\tilde {с}}_{\operatorname{M} }}n + {{({{\tilde {с}}_{\operatorname{M} }}n)}^{{1/n}}},$Рис. 5.
Взаимозависимость концентрации мицелл и брутто-концентрации ПАВ согласно соотношению (25) при n = 10.
Аналогично, исключая α из (24) и (26), находим уравнение для концентрации мономеров ПАВ ${{\tilde {c}}_{1}}$
которое представлено как явная функция $\tilde {с}({{\tilde {с}}_{1}}).$ График этой функции при n = 10 изображен на рис. 6. Тем самым изображен и график обратной функции ${{\tilde {с}}_{1}}(\tilde {с}),$ являющейся решением уравнения (28). Здесь, как и на рис. 5 и в отличие от рис. 2, хорошо проявляется мицеллообразование ниже ККМ. Примерно до $\tilde {с} = $ 0.7 соблюдается равенство величин $\tilde {с}$ и ${{\tilde {c}}_{1}}$ (указывающее на практическое отсутствие мицелл), и зависимость между ними прямолинейна. Но при более высокой концентрации становится явным отклонение от прямолинейности, свидетельствующее о влиянии мицеллообразования. По достижении же ККМ концентрация мономеров уже составляет лишь 0.835 от ККМ (рис. 6), а после превышения ККМ уже слабо зависит от брутто-концентрации ПАВ (хотя вместе с последней, конечно, продолжает возрастать, как этого требуют условия устойчивости [6–8]).Рис. 6.
Взаимозависимость концентрации мономеров и брутто-концентрации ПАВ согласно соотношению (26) при n = 10.
Сравнивая рис. 5 и 6, замечаем следующее. При повышении концентрации ПАВ в мицеллярном растворе концентрация мицелл выходит на линейный рост, тогда как концентрация мономеров почти перестает изменяться. Это значит, что кривая концентрации мицелл рано или поздно пересечет кривую концентрации мономеров. Для точки пересечения (пометим ее звездочкой) из выражения (23) получаем
(29)
$\tilde {c}_{\operatorname{M} }^{ * } = \tilde {c}_{1}^{ * } = {{n}^{{\frac{1}{{n - 1}}}}}{\text{. }}$При n = 10 это дает значение относительной концентрации около 1.29. Из (25) или (26) тогда следует, что точке пересечения отвечает степень мицеллизации
что составляет около 0.91 при n = 10. Наконец, из (24) находим, что пересечение указанных кривых происходит при брутто-концентрации ПАВ $(\tilde {c} \approx 12.9$ при n = 10). Естественно, приведенные рассуждения имеют силу только при условии, что закон действия масс сохраняет свою справедливость в идеальной форме (1) даже при концентрации, соответствующей пересечению указанных кривых.ЗАКЛЮЧЕНИЕ
Отметим, прежде всего, что трактовка двух модификаций закона действия масс как относящихся к прямым и обратным мицеллам весьма условна. Строго говоря, в первом случае речь идет о возможности не включать число агрегации в определение ККМ через константу закона действия масс. Такая возможность допускается, если число агрегации достаточно велико для мицелл любого типа. Однако большие числа агрегации все же более характерны для прямых мицелл. В этом случае вступает в силу модификация закона действия масс (12), чарующая своей простотой. Вторая же модификация, которую мы рассмотрели в этом сообщении, хоть и не так проста, не имеет ограничений на число агрегации. Она лучше работает в случае любых мицелл с малыми числами агрегации, но такими оказываются типично обратные мицеллы. Более того, она точнее и для прямых мицелл со средними числами агрегации и будет полезна, если высокая точность потребуется в расчетах.
Как уже отмечалось, полученные в [4] графические решения уравнений (13)–(15) или (16) и (17) (рис. 1 и 2) были дополнены аналитическими аппроксимациями. В данном сообщении мы этого не делали, а почему – ясно из сравнения рис. 1 и 2 (при n = 100) с одной стороны и рис. 5 и 6 (при n = 10) с другой. При больших числах агрегации на графиках имеются практически прямолинейные участки, которые и напрашиваются на простые аналитические аппроксимации. При малых числах агрегации графики усложняются, линии искривляются, и вопрос об аналитической аппроксимации снимается.
Наконец, нужно отметить, что приведенная в этом сообщении теория формулировалась в рамках квазихимического приближения, т.е. при постоянном числе агрегации. Теории с переменными числами агрегации уже фигурируют в литературе (и сам автор к ним причастен [12, 13]), но все-таки более известны для прямых мицелл. Исследование обратных мицелл (а экспериментальных данных здесь явно не хватает) всегда немного отстает, и пройдет еще время, пока оно возьмет свое.
Список литературы
Eicke H.-F. Surfactants in Nonpolar Solvents // In Micelles, Topics in Current Chemistry. V. 87. Berlin: Springer, 1980. P. 85.
Lindman B., Wennerström H. Micelles. Amphiphile Aggregation in Aqueous Solution // In Micelles, Topics in Current Chemistry. V. 87. Berlin: Springer, 1980. P. 1.
Rusanov A.I. // Langmuir. 2014. V. 30. P. 14 443.
Русанов А.И. // Коллоид. журн. 2016. Т. 78. С. 358.
Русанов А.И. // Коллоид. журн. 2016. Т. 78. С. 613.
Русанов А.И. Мицеллообразование в растворах поверхностно-активных веществ. СПб.: Химия, 1992.
Rusanov A.I. Micellization in Surfactant Solutions. Chemistry Reviews. / Ed. by Vol’pin M.E. V. 22, Part 1. Reading: Harwood Academic Publishers, 1996. ISBN 90-5702-297-4.
Русанов А.И., Щёкин А.К. Мицеллообразование в растворах поверхностно-активных веществ. 2-е изд. СПб.: Лань, 2016.
Куни Ф.М., Русанов А.И. // Теор. мат. физ. 1970. Т. 2. С. 265.
Smith G.N., Brown P., Rogers S.E., Eastoe J. // Langmuir. 2013. V. 29. P. 3252.
Smith G.N., Brown P., James C., Rogers S.E., Eastoe J. // Colloids Surf. A. 2016. V. 494. P. 194.
Русанов А.И. // Коллоид. журн. 2018. Т. 80. С. 86.
Rusanov A.I. // Colloids Surf. A. 2018. V. 551. P. 158.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал