Коллоидный журнал, 2020, T. 82, № 5, стр. 611-617
Температурная зависимость краевого угла жидкости на деформируемой твердой поверхности
А. И. Русанов *
Менделеевский центр, Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия
* E-mail: airusanov@mail.ru
Поступила в редакцию 15.04.2020
После доработки 20.04.2020
Принята к публикации 24.04.2020
Аннотация
К настоящему времени прямыми методами достоверно установлено, что лежащая на поверхности твердого тела капля жидкости приводит к деформации подложки. Для тел с достаточно низкими значениями модуля упругости и, в частности, для эластомеров это явление становится доступным наблюдению, а работа деформации – достаточно большой величиной, чтобы по необходимости учитывать ее в теории. В рамках существующей теории капиллярности и обобщенного уравнения Юнга проще всего включить работу деформации (производимую вдоль и внутри линии трехфазного контакта) в линейное натяжение. Результирующее эффективное линейное натяжение на несколько порядков больше обычного (для недеформируемых твердых тел), а потому проявляет себя даже в макроскопических (но малых) каплях. Если обычное линейное натяжение является лишь малой поправкой к классическому уравнению Юнга, то при использовании эластомеров в качестве подложки эффективное линейное натяжение может стать главным членом и определять наблюдаемые поверхностные явления. Именно с этих позиций в данной публикации обсуждаются результаты работы [Budziak C.J., Varcha-Butler E.I., Neumann A.W. // J. Appl. Polym. 1991. V. 42. P. 1959] по исследованию температурной зависимости краевого угла жидкостей на эластомерах. Нашли себе объяснение следующие факты: чем выше поверхностное натяжение жидкости, тем больше краевой угол на одной и той же подложке; наиболее вероятно увеличение краевого угла с температурой; температурная зависимость краевого угла не может быть сильной из-за взаимного компенсационного действия температурных зависимостей поверхностного натяжения смачивающей жидкости и модуля упругости эластомерной подложки.
ВВЕДЕНИЕ
В явлениях смачивания твердая подложка – непременный участник, от свойств которого многое зависит. Важной спецификой является наличие упругости, что и отличает твердые тела от жидкостей. Подавляющее большинство твердых тел в исследованиях смачивания, будь то кристаллические или аморфные (стекловидные) тела, обладают высоким модулем упругости. Для них как в теории, так и в толковании эксперимента общепринятым подходом является использование модели абсолютно твердого тела. Но существуют и твердые тела с низким модулем упругости, такие как каучук, резина и гели, способные к деформации в процессе смачивания. Число таких тел неуклонно растет благодаря развитию химии эластомеров и гелей.
Существенное развитие теории смачивания деформируемых твердых тел (см. обзор [1]) пришлось на последнюю четверть 20 века и было связано с открытием анизотропии смачивания деформированных эластомеров. Первое наблюдение этого явления было сделано Бартеневым и Акопяном [2], и состояло оно в следующем. Если на одноосно растянутую пластинку эластомера посадить каплю жидкости, то она растекается сильнее в направлении растяжения и равновесный краевой угол капли меньше в продольном направлении, чем в поперечном. Авторы попытались объяснить это явление на основе силовой интерпретации уравнения Юнга
(1)
$\cos \theta = \frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{{{{\sigma }^{{\alpha \beta }}}}},$Естественно, механическое поверхностное натяжение твердой поверхности также всегда существует. Но если мы составим комбинацию, подобную (1),
(2)
$\gamma \cos \theta - {{\gamma }^{{\alpha \gamma }}} + {{\gamma }^{{\beta \gamma }}} \equiv {{f}_{\operatorname{T} }},$(3)
$\begin{gathered} \cos \theta = \frac{{{{\sigma }^{{\alpha \gamma }}} - {{\sigma }^{{\beta \gamma }}}}}{\gamma } - \frac{1}{\gamma }\left( {\frac{\kappa }{r} + \frac{{\partial \kappa }}{{\partial r}}} \right)\cos \varphi \equiv \\ \equiv \cos {{\theta }_{0}} - \frac{1}{\gamma }\left( {\frac{\kappa }{r} + \frac{{\partial \kappa }}{{\partial r}}} \right)\cos \varphi , \\ \end{gathered} $Включение работы деформации в линейное натяжение образовало подход, дающий объяснение анизотропии смачивания следующим образом [10]. Одноосное растяжение пластинки эластомера приводит к молекулярной ориентации полимера в выбранном направлении и, следовательно, к анизотропии полимера. В частности, появляется зависимость модуля упругости от направления на поверхности. Если на такую поверхность поместить каплю с конечным краевым углом, вызывающую деформацию поверхности вдоль линии трехфазного контакта, то два положения на линии обладают наибольшим различием. Первое – когда линия трехфазного контакта параллельна молекулярной ориентации и в ходе деформации конфигурация полимерных молекул не изменяется. Второе – когда линия трехфазного контакта перпендикулярна направлению ориентации, так что выпучивание поверхности сопровождается изгибом полимерных цепей. Очевидно, во втором положении как сама деформация, так и работа деформации, линейное натяжение и краевой угол будут меньше, чем в первом. Отсюда и анизотропия краевого угла, вызванная чисто энергетическими причинами. Последующее детальное исследование данного явления [11–14] показало правильность его интерпретации.
Температурная зависимость краевого угла капли на эластомерах тогда не изучалась, но вскоре такое исследование появилось [15] с иной, нежели выше, интерпретацией. В то же время, в недавних работах с участием автора [16–20], хоть и анализировалось влияние параметров состояния (давления и температуры) на краевой угол, рассматривались лишь недеформируемые твердые тела. Если же говорить о деформируемых подложках, то остается явным упущением, что благодатный материал работы [15] (выполненной в экспериментальном отношении безупречно) до сих пор не охвачен теорией автора. Пришло время закрыть этот пробел.
ТЕОРИЯ
В рассуждениях этого раздела будем опираться на результаты, достигнутые в [5–10]. Как уже указывалось, лежащая капля производит деформацию подложки благодаря действию двух сил: поверхностного натяжения γ вдоль линии трехфазного контакта и капиллярного давления Лапласа (также связанного с поверхностным натяжением) $p = {{2\gamma } \mathord{\left/ {\vphantom {{2\gamma } R}} \right. \kern-0em} R}$ (R – средний радиус кривизны поверхности αβ) по всему основанию капли. Для изотропной подложки с модулем Юнга E и коэффициентом Пуассона ν стандартная теория упругости дает следующее выражение для работы деформации:
(4)
$\begin{gathered} ~W = \frac{{2(1 - {{\nu }^{2}})r}}{E}\left[ {\frac{{4{{p}^{2}}{{r}^{2}}}}{3} - 4pr\gamma \sin \theta + } \right. \\ + \,\,{{\gamma }^{2}}{{\sin }^{2}}\theta \left( {\frac{3}{2} + 3\ln 2 - \ln \frac{t}{r}} \right) + \\ \left. { + \,\,f_{\operatorname{T} }^{2}\left( {3\ln 2 - \frac{1}{2} - \ln \frac{t}{r}} \right)} \right], \\ \end{gathered} $(5)
$\begin{gathered} W{\text{ }} = \frac{{2(1 - {{\nu }^{2}})r{{\gamma }^{2}}}}{E}\left[ {{{{\sin }}^{2}}\theta \left( {3\ln 2 - \frac{7}{6} - \ln \frac{t}{r}} \right)} \right. + \\ \left. { + \,\,{\text{ }}f_{\operatorname{T} }^{2}\left( {3\ln 2 - \frac{1}{2} - \ln \frac{t}{r}} \right)} \right]. \\ \end{gathered} $Работа (5) относится к объемной фазе твердого тела, но, очевидно, с изменением конфигурации системы изменяются и ее поверхности, что создает дополнительную работу
(6)
$~{{W}_{\sigma }} = {{\sigma }^{{\alpha \beta }}}d{{A}^{{\alpha \beta }}} + {{\sigma }^{{\alpha \gamma }}}d{{A}^{{\alpha \gamma }}} + {{\sigma }^{{\beta \gamma }}}d{{A}^{{\beta \gamma }}}.$Известно, что термодинамическое поверхностное натяжение положительно по условиям устойчивости. Термодинамическое же линейное натяжение $\kappa {\kern 1pt} '$ может иметь любой знак. Но в случае эластомеров полное термодинамическое линейное натяжение (8) положительно благодаря влиянию величины (7). В то же время из-за своей относительно большой абсолютной величины линейное натяжение на эластомерной подложке может себя проявлять уже для макроскопических капель (0.1–1 мм). При таком размере можно пренебречь производной в формуле (3) и записать ее как
Теперь поговорим об угле φ, отражающем рельеф твердой поверхности. Мы можем представить, что формула (9) настолько точна, что воспроизводит рельеф, возникший в результате деформации (правая половина рис. 1). Можно ли попытаться найти “реальный” краевой угол θ в таких условиях? Сразу ответим, что это дело бессмысленное и безнадежное. Во-первых, в ходе деформации сохраняется цилиндрическая симметрия системы, а, значит, и ориентация плоскости линии трехфазного контакта (горизонтальная линия на рис. 1). Нахождение угла φ тогда связано только с выбором точки на поверхности ранта, образовавшегося в результате деформации. Масштаб расстояний здесь микроскопический и не соответствует самой методике расчета в рамках теории сплошных сред. Во-вторых, само понятие краевого угла – макроскопическое и основано на экстраполяции видимой формы поверхности капли до ее пересечения с твердой поверхностью.Рис. 1.
Деформация подложки под влиянием лежащей капли с краевым углом θ. Обозначение фаз: α – жидкость, β – газ, γ – твердое тело.
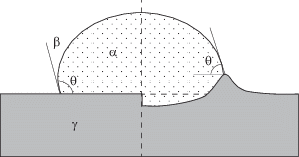
Стандартный и весьма точный метод нахождения краевого угла малой, но макроскопической капли в виде сферического сегмента дается формулой
где h – высота капли. Реальное состояние вещества в области трехфазного контакта весьма сложное, а у нас оно осложняется еще и деформацией подложки. Но суть подхода от этого не меняется. Определяя θ по формуле (10), мы наблюдаем, как энергетика всех процессов и состояний сказывается на величине краевого угла. Таким образом, угол φ в (9) указывает только начальную конфигурацию системы. Если капля покоится на плоской поверхности, то φ = 0, и из (9) получаем Соотношение (11) и будет нашей рабочей формулой для дальнейшего обсуждения смачивания эластомеров.ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ РАБОТЫ [15]
В качестве подложки в [15] использовались два эластомера: бутиловый каучук PB 101-3 фирмы Polysar Ltd. (обозначим его как I) и силиконовый каучук в виде дисперсии Dow Corning 236 (II). Особое внимание уделялось исключению шероховатости поверхности образцов. Как известно, самая гладкая поверхность у жидкости. Поэтому оба полимера растворяли в гексане или толуоле и наносили на предметные стекла для микроскопа погружением в раствор, после чего растворители испарялись. Эта техника дает возможность получать гладкие полимерные пленки в обиходе “тонкие”, но достаточно толстые для опытов по смачиванию. Чтобы иметь дело с конечными краевыми углами, в качестве смачивающих выбирались жидкости с поверхностным натяжением выше, чем у подложек I и II: глицерин, этиленгликоль, диэтиленгликоль и вода (частично, поскольку для работы в температурном интервале до 120°C нужны высококипящие жидкости). О размерах капель не сообщается, но, судя по дозатору и использованию метода сидячей капли [21] для измерения краевого угла (по профилю капли, с использованием, в частности, формулы (10)), речь идет о малых, но макроскопических каплях.
Идейная часть работы [15] ограничивалась классическим уравнением Юнга с его трактовкой, увы! как условия механического равновесия. Задачей ставилось отыскание поверхностного натяжения твердой поверхности βγ и ее производной по температуре в качестве поверхностной энтропии. Мы же, как обещали, проведем обсуждение данных [15] на основе формулы (11). В работе [18] мы уже проанализировали зависимость $\cos {{\theta }_{0}}$ от температуры. Следуя той же схеме рассуждений, мы могли бы в (11) продифференцировать по температуре и член с линейным натяжением, переходя формально к избыточной линейной энтропии согласно линейному аналогу уравнения адсорбции Гиббса [22]. Но, во-первых, избыточная линейная энтропия – еще мало освоенное понятие, о котором трудно что-либо сказать. Во-вторых, мы отнесли всю работу деформации подложки каплей к линии трехфазного контакта достаточно условно [10], чтобы выходить при этом на линейную энтропию. И уж, конечно, руководствоваться в такой ситуации физическим смыслом, как это мы часто делали в [18], затруднительно. По этой причине мы будем пользоваться формулой (11), какая она есть, вместе с выражениями (4)–(8). Главными факторами будут температурные зависимости поверхностного натяжения смачивающей жидкости и модуля упругости подложки.
Прежде чем перейти к температурной зависимости, посмотрим, какой краевой угол предсказывает сама формула (11), если считать ее часть с линейным натяжением существенной. Согласно (5), (7) и (8) термодинамическое линейное натяжение κ содержит в главном члене ${{{{\gamma }^{2}}} \mathord{\left/ {\vphantom {{{{\gamma }^{2}}} E}} \right. \kern-0em} E},$ а в (11) κ делится на γ. Таким образом, реально во втором слагаемом правой части (11) содержится отношение ${\gamma \mathord{\left/ {\vphantom {\gamma E}} \right. \kern-0em} E}.$ Если капли разных жидкостей помещаются на одну и ту же эластомерную подложку, то величина E для них одинакова, и определяющим становится поверхностное натяжение. Чем выше γ, тем больше работа деформации, больше эффективное линейное натяжение, меньше косинус краевого угла и больше сам угол. Таким образом, предсказание формулы (11) следующее: чем выше поверхностное натяжение смачивающей жидкости, тем больше и ее краевой угол на поверхности эластомера. Приведенные в первых строках табл. 1 данные [15] для эластомера I полностью этому соответствуют.
Таблица 1.
Краевой угол смачивающих жидкостей на эластомере I при 23°C и характеристики их поверхностного натяжения по данным [15]
| Жидкость | Диэтиленгликоль | Этиленгликоль | Глицерин | Вода |
|---|---|---|---|---|
| $\theta ,{\text{ град}}$ | 81.7 | 84.4 | 99.7 | 110.8 |
| $\gamma ,\,\,\,{{{\text{мН}}} \mathord{\left/ {\vphantom {{{\text{мН}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | 45.08 | 48.35 | 63.90 | 72.40 |
| $ - \frac{{d\gamma }}{{dT}} \times 100$, мН/(м град) | 0.0880 | 0.0890 | 0.0879 | 0.1477 |
| $ - \frac{1}{\gamma }\frac{{d\gamma }}{{dT}} \times 100$, град–1 | 0.1952 | 0.1841 | 0.1376 | 0.2040 |
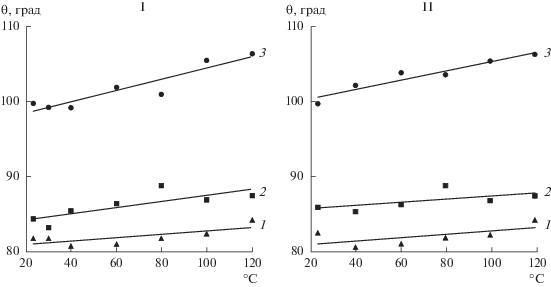
Обратимся теперь к температурной зависимости краевого угла. По табличным данным [15] мы построили графики, приведенные на рис. 2. Отметим, что линейная интерполяция вполне соответствует погрешностям, указанным в таблицах. С ее учетом виден только один результат: во всех случаях краевой угол растет с температурой. Отвечает ли это второй части формулы (11)? Напомним, что первая часть формулы (11), не связанная с линейным натяжением, подробно анализировалась в [18]. Было показано, что наиболее вероятны разные температурные зависимости для углов меньше и больше 90°: малые растут, а большие – наоборот, уменьшаются с ростом температуры. Реальность таких случаев была подтверждена экспериментально [19, 20]. В работе [15] мы как раз имеем такой случай, когда две жидкости (диэтиленгликоль и этиленгликоль) имеют краевые углы меньше, а третья (глицерин) – больше 90° (см. табл. 1). Однако для всех трех жидкостей наблюдается рост краевого угла с температурой. Это наводит на мысль, что в данном случае в формуле (11) “командует” вторая часть, связанная с линейным натяжением и ставящая однозначные требования, никак не соотносящиеся с величиной краевого угла. Но требует ли она, чтобы краевой угол именно возрастал с температурой? Ответить на этот вопрос не просто.
Рис. 2.
Температурная зависимость краевого угла диэтиленгликоля (1), этиленгликоля (2) и глицерина (3) на эластомерах I и II [15].
Как мы уже отмечали, правая часть формулы (11) содержит отношение ${\gamma \mathord{\left/ {\vphantom {\gamma E}} \right. \kern-0em} E}.$ Обе эти величины, и поверхностное натяжение жидкости и модуль упругости твердого тела, уменьшаются с ростом температуры, что создает определенный эффект компенсации. Про поверхностное натяжение мы знаем, что его температурная зависимость почти линейна вдали от критической точки. Значения производных поверхностного натяжения смачивающих жидкостей по данным [15] приведены в табл. 1, где T – температура. В последней графе этой таблицы оценивается, на какую долю процента уменьшается поверхностное натяжение жидкости при повышении температуры на один градус. Такие же сведения желательно получить для модуля упругости исследованных эластомеров или их аналогов.
Поведение модуля упругости, надо думать, сильно зависит от природы твердого тела. Если говорить о полимерах, то еще в работе [23] на примере эпоксидных смол было показано, что температурная зависимость модуля упругости может иметь экспоненциальный характер. Казалось бы, экспонента намного сильнее линейной зависимости, и это все решает. Но важны значения коэффициентов, а не только вид зависимости. К тому же нас интересуют эластомеры, а не сильно сшитые полимеры, и поведение γ и E необходимо сравнивать в одном и том же температурном интервале.
Наиболее подходящими оказались данные работы [24] по температурной зависимости модуля упругости пяти видов бутадиен-нитрильных резин (HNBR) в интервале от –70 до 100°С. В уплотнительной технике эти резины известны под номерами 56, 101, 205, 207 и 985. Для всех резин при низких температурах изменение модуля упругости очень резкое (действительно напоминает экспоненту), но при переходе к положительным температурам затухает. Из вороха табличных значений мы выбрали относящиеся к интересующему нас интервалу от 20 до 100°C и изобразили их графически на рис. 3. Эти линии можно воспринимать как хвосты экспонент, но, ввиду их пологости, возможна и линейная интерполяция, которая по точности мало уступает экспоненциальной (а в одном случае даже превосходит ее). В нашем случае линейная аппроксимация, показанная на рис. 3, более удобна для сравнения с аналогичными кривыми поверхностного натяжения. Данные линейной аппроксимации приведены в табл. 2. Четвертая графа содержит квадрат смешанной корреляции R2 как критерий качества интерполяции (максимальное значение 1 означает идеальное соответствие). Видно, что, за исключением резины 56 (для которой и экспонента дает примерно то же низкое значение R2), линейная зависимость хорошо отражает экспериментальный материал в данном температурном интервале. Последняя графа показывает, на какую долю процента понижается значение модуля упругости при повышении температуры на один градус.
Рис. 3.
Температурная зависимость модуля упругости уплотнительных резин 56 (квадраты), 205 (треугольники), 985 (перевернутые треугольники), 101 (кружки) и 207 (ромбы).
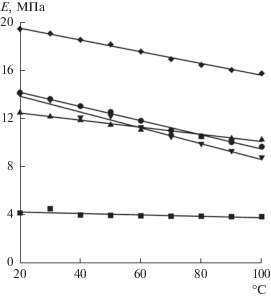
Таблица 2.
Данные линейной аппроксимации политерм модуля упругости уплотнительных резин
| Тип резины | 56 | 101 | 205 | 207 | 985 |
| E20°, МПа [24] | 4.14 | 14.1 | 12.5 | 19.4 | 13.9 |
| $ - \frac{{dE}}{{dT}},{\text{ }}{{{\text{МПа}}} \mathord{\left/ {\vphantom {{{\text{МПа}}} {{\text{град}}}}} \right. \kern-0em} {{\text{град}}}}$ | 0.00585 | 0.0587 | 0.0295 | 0.0486666 | 0.06565 |
| R2 | 0.553 | 0.9948 | 0.9738 | 0.9951 | 0.9839 |
| $\frac{1}{{{{E}_{{{{{20}}^{ \circ }}}}}}}\left( { - \frac{{dE}}{{dT}}} \right) \times 100$, град–1 | 0.1413 | 0.4163 | 0.2360 | 0.2509 | 0.4723 |
Нам осталось сравнить нижние графы табл. 1 и 2. Здесь уже есть малая статистика, позволяющая прийти к определенному заключению. Мы можем сказать теперь: да, случай, когда поверхностное натяжение смачивающей жидкости снижается с повышением температуры сильнее, чем модуль упругости некоего эластомера, возможен в каком-то температурном интервале. Но это скорее исключение. Обратная картина более вероятна и, можно сказать, типична даже при обычных и повышенных температурах, не говоря уже о пониженных температурах, где модуль упругости определяет ситуацию безраздельно. Поэтому типична ситуация, когда отношение ${\gamma \mathord{\left/ {\vphantom {\gamma E}} \right. \kern-0em} E}$ возрастает с температурой и формула (11) предсказывает увеличение краевого угла. Именно этот типичный случай иллюстрируется экспериментальными данными работы [15].
ЗАКЛЮЧЕНИЕ
В данной работе мы попытались объяснить экспериментальные данные по температурной зависимости краевого угла смачивающих жидкостей на эластомерах, исходя из основной роли эффективного линейного натяжения (включающего в себя работу деформации эластомера лежащей каплей) и пренебрегая ролью классического уравнения Юнга в ситуации с эластомерами. Мы обосновали, почему чем выше поверхностное натяжение смачивающей жидкости, тем больше краевой угол на одном и том же эластомере. Мы определили, что наиболее вероятным предсказанием такой теории является увеличение краевого угла с температурой, что и наблюдается в эксперименте. Наконец, из нашего рассмотрения также следует, что температурная зависимость краевого угла не может быть сильной из-за взаимного компенсационного действия температурных зависимостей поверхностного натяжения смачивающей жидкости и модуля упругости эластомера как подложки.
Список литературы
Rusanov A.I. // Surf. Sci. Rep. 1996. V. 23. P. 173.
Бартенев Г.М., Акопян Л.А. // Plaste u. Kautschuk. 1969. V. 16. P. 655.
Lester G.R. // J. Colloid Sci. 1961. V. 16. P. 315.
Lester G.R. // Nature. 1966. V. 209. P. 1126.
Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 678.
Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 688.
Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 695.
Русанов А.И. // Коллоид. журн. 1975. Т. 37. С. 704.
Русанов А.И. // Коллоид. журн. 1977. Т. 39. С. 704.
Русанов А.И. // Коллоид. журн. 1977. Т. 39. С. 711.
Русанов А.И., Овруцкая Н.А., Акопян Л.А. // Коллоид. журн. 1981. Т. 43. С. 685.
Беренштейн Г.В., Дьяченко А.М., Русанов А.И. // Коллоид. журн. 1985. Т. 47. С. 9.
Бартенев Г.М., Акопян Л.А., Русанов А.И. // Высокомолек. соед. А. 1986. Т. 28. С. 207.
Русанов А.И., Акопян Л.А., Овруцкая Н.А. // Коллоид. журн. 1987. Т. 49. С. 61.
Budziak C.J., Varcha-Butler E.I., Neumann A.W. // J. Appl. Polym. Sci. 1991. V. 42. P. 1959.
Русанов А.И., Есипова Н.Е., Соболев В.Д. // Докл. АН СССР. 2019. Т. 202. С. 304.
Есипова Н.Е., Русанов А.И., Соболев В.Д., Ицков С.В. // Коллоид. журн. 2019. Т. 81. С. 507.
Русанов А.И. // Коллоид. журн. 2020. Т. 82. С. 354.
Русанов А.И., Есипова Н.Е., Соболев В.Д. // Докл. АН СССР. 2020. Т. Т. 491. С. 69.
Есипова Н.Е., Русанов А.И., Соболев В.Д. // Коллоид. журн. 2020. Т. 82. (в печати).
Neumann A.W., Good R.J. // In Surface and Colloid Science. V. 11. Good R.J. and Stromberg R.R., Eds. New York: Plenum, 1979. P. 31.
Rowlinson J.S., Widom B. Molecular Theory of Capillarity. Oxford: Clarendon, 1982.
Егоров Н.Г., Малинский Ю.М., Сакварелидзе Ж.Д., Трифель Б.Ю. // Механика полимеров. 1966. Т. 2. С. 823.
Ашейчик А.А., Полонский В.Л. // Вестник СибГАУ. 2016. Т. 17. С. 656.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


