1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 82, № 6, 2020

Коллоидный журнал, 2020, T. 82, № 6, стр. 677-688

Эффективные параметры заряженных сферических частиц в растворах 1 : 1-электролита

А. И. Долинный *

Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп., 31, Россия

* E-mail: dolinnyi@mail.ru

Поступила в редакцию 22.06.2020
После доработки 01.07.2020
Принята к публикации 06.07.2020

Полный текст (PDF)

Аннотация

В рамках теории Пуассона–Больцмана проведены точные расчеты профилей электростатического потенциала вблизи погруженных в растворы 1 : 1-электролита сферических частиц. Из поведения профилей на дальних расстояниях от поверхности частиц для широкого диапазона параметров модели (плотность поверхностного заряда, радиус частицы, концентрация раствора электролита) определены значения эффективного поверхностного потенциала ${{\psi }_{{{\text{eff}}}}},$ а также предел $\psi _{{{\text{eff}}}}^{{{\text{sat}}}},$ к которому он стремится при неограниченном росте плотности поверхностного заряда. Построена универсальная кривая, которая представляет зависимость $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ от приведенного радиуса частицы κa (a – радиус, κ – величина, обратная дебаевскому радиусу экранирования) и наглядно иллюстрирует существование двух известных предельных законов изменения эффективного потенциала, отвечающего условиям насыщения. С привлечением энергетического критерия и анализа его чувствительности к порогу отсечения получены оценки толщины формирующихся вокруг сферических частиц оболочек из иммобилизованных противоионов. Проанализированы зависимости толщины оболочек от плотности поверхностного заряда, радиуса частиц и концентрации раствора 1 : 1-электролита. Установлено существование предельной толщины $l_{{{\text{eff}}}}^{{{\text{sat}}}},$ достигаемой при неограниченном росте плотности поверхностного заряда. Приведена универсальная кривая κ$l_{{{\text{eff}}}}^{{{\text{sat}}}}$(κa), и проведено ее сопоставление с кривой $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$(κa).

ВВЕДЕНИЕ

Ранее [1] с привлечением модифицированной теории Пуассона–Больцмана (ПБ), в которую введены ограничения на максимально допустимую концентрацию ионов в растворе, Cmax, определяемую их эффективными размерами, были исследованы (в условиях постоянной плотности поверхностного заряда) распределения электростатического потенциала и концентрации ионов вблизи сферической 15-нм частицы, погруженной в 0.1 М раствор 1 : 1-электролита. Можно выделить три важных результата этой работы для понимания структуры двойного электрического слоя (ДЭС), формирующегося вокруг заряженной сферической частицы.

1. Когда абсолютная величина электростатического потенциала $\left| {\varphi \left( r \right)} \right|$ становится меньше его термического значения ${{\varphi }_{{\text{T}}}} = \frac{{{{k}_{{\text{B}}}}T}}{e}$ (где kB – постоянная Больцмана, T – температура и e – элементарный заряд), что наблюдается по мере удаления от поверхности частицы, то независимо от размера ионов падение потенциала описывается характерным для линеаризованной теории ПБ уравнением [2–8]:

(1)
$\psi \left( r \right) = \frac{{\varphi \left( r \right)}}{{{{\varphi }_{{\text{T}}}}}} = {{\psi }_{{{\text{eff}}}}}\frac{a}{r}\exp \left( { - \kappa \left( {r - a} \right)} \right).$
Здесь r – расстояние от центра частицы, a – ее радиус, κ – величина, обратная дебаевскому радиусу экранирования, ${{\psi }_{{{\text{eff}}}}} = \mathop {\lim }\limits_{r \to a} \psi \left( r \right)$ – эффективный поверхностный потенциал. Для слабо заряженных частиц эффективный потенциал совпадает со структурным: ${{\psi }_{{{\text{eff}}}}} = {{\psi }_{{\text{s}}}}.$

2. В классической теории ПБ рост плотности поверхностного заряда приводит к насыщению эффективного потенциала $\left( {{{\psi }_{{{\text{eff}}}}} \to \psi _{{{\text{eff}}}}^{{{\text{sat}}}}} \right),$ причем полученный при решении нелинейного уравнения ПБ потенциал $\left| {{{\psi }_{{\text{s}}}}} \right|$ оказывается выше $\left| {{{\psi }_{{{\text{eff}}}}}} \right|$ [9–12]. В модифицированной теории, учитывающей в простейшем виде размер ионов электролита, подобный эффект насыщения отсутствует [1, 13]. Теперь величина ${{\psi }_{{{\text{eff}}}}}$ зависит и от плотности поверхностного заряда и от размера противоионов.

3. В случае противоионов большого размера $\left| {{{\psi }_{{{\text{eff}}}}}} \right|$ может значительно превосходить $\left| {{{\psi }_{{\text{s}}}}} \right|$ [1, 14, 15].

Наблюдаемые различия являются прямым следствием того, что модифицированная теория (в отличие от классической) предсказывает, что у поверхности частицы возникает конденсированный слой из противоионов концентрации Cmax, протяженность которого растет с увеличением плотности поверхностного заряда (при постоянном размере ионов) или размера ионов (при постоянной плотности заряда).

Хорошо известно, что структурная организация ДЭС является очень сложной и определяется многими факторами. В результате диссоциации поверхностных групп (или адсорбции ионов) на поверхности объекта располагаются заряды, которые создают его структурный (истинный) заряд. В дисперсионной среде вблизи заряженного объекта образуется облако, состоящее из различных носителей заряда и обеспечивающее общую электронейтральность системы. По литературным данным [3, 7, 14, 15], существенный вклад в структуру ионного облака (ДЭС) вносят исключенные объемы ионов, их взаимодействия между собой и с поверхностными группами, форма и размер объекта, ионная сила окружающей среды и т.д. Находящиеся в облаке ионы принадлежат к одной из двух популяций. Если поверхностный заряд велик, некоторое количество противоионов сильно притягиваeтся частицей и оказывается “замороженным” вблизи ее поверхности. Такие противоионы, с одной стороны, частично нейтрализуют структурный заряд частицы (нормируют его), в результате чего частица ведет себя как имеющая меньший (а порой, и гораздо меньший) заряд при взаимодействии с другими заряженными объектами, а с другой, выключаются из физических процессов, в которых участвуют свободно блуждающие ионы (например, из проводимости раствора).

Представления об эффективном (нормированном) заряде Zeff широко используются в литературе для иллюстрации значительного концентрирования противоионов в окрестности заряженных объектов и описания равновесных и динамических свойств коллоидных растворов. Многочисленные экспериментальные [16–28] и теоретические [9–15, 29–43] исследования подтвердили тот факт, что эффективный заряд является важной физической характеристикой. Его можно определить из данных по вольтамперометрии, электрофорезу, малоугловому рассеянию света и нейтронов, из измерений объемного модуля коллоидных кристаллов, из самодиффузии и осмотического давления системы и др. Сопоставление значений эффективного и структурного зарядов позволяет оценить количество связанных с частицей противоионов. Однако величина эффективного заряда зависит от того, какое свойство коллоидной системы изучается. На практике величину Zeff часто используют в качестве (подгоночного, регулируемого) параметра, с помощью которого та или иная теоретическая модель подстраивается для точной аппроксимации результатов эксперимента, например, по взаимодействию сближающихся частиц в различных средах.

Простой и интуитивно понятный сценарий существования двух семейств ионов (конденсированных и свободных) активно привлекается к исследованию структуры ДЭС. Пространственное разграничение этих семейств дает возможность оценить эффективный размер частицы (частицы, “обернутой” противоионами). Информацию о величине ${{a}_{{{\text{eff}}}}},$ как правило, получают из данных по динамическому рассеянию света. Определяемый на основании электрофоретической подвижности частиц ξ-потенциал теперь относят к поверхностному потенциалу частицы размером ${{a}_{{{\text{eff}}}}}$: $\xi = \psi \left( {{{a}_{{{\text{eff}}}}}} \right).$ Для поиска границы между этими семействами противоионов был выработан ряд правил (критериев) [30, 32–34, 36, 38]. Концентрационный критерий применяют, в основном, для (“бессолевых”) систем, в которых противоионы возникают только в процессе диссоциации поверхностных групп (дополнительно электролит в систему не вводится). Расстояние, на котором локальная концентрация противоионов равна их средней концентрации, принимается за положение границы между популяциями. В ряде случаев точка перегиба на зависимости концентрации противоионов от обратного расстояния рассматривается в качестве такой границы. Определяют положение границы и по точкам перегиба на графиках зависимости аккумулированного заряда от обратного радиального расстояния.

Наиболее широко и в различных вариантах применяется энергетический критерий, в котором энергию электростатического притяжения противоиона к частице, ${{U}_{{{\text{pi}}}}},$ сопоставляют с энергией его теплового движения:

(2)
$\frac{{{{U}_{{{\text{pi}}}}}}}{{{{k}_{{\text{B}}}}T}} = \frac{{{{Z}_{s}}{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{{\text{r}}}}a{{k}_{{\text{B}}}}T}} = \frac{{{{Z}_{s}}{{l}_{{\text{B}}}}}}{a},$
где ${{l}_{{\text{B}}}} = \frac{{{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{{\text{r}}}}{{k}_{{\text{B}}}}T}}$ – длина Бьеррума (расстояние между ионами, на котором электрическая энергия их взаимодействия равна энергии теплового движения иона), εr – диэлектрическая постоянная раствора, ε0 – диэлектрическая проницаемость вакуума. К прочно связанным относят противоионы, для которых выполняется неравенство $\frac{{{{Z}_{s}}{{l}_{{\text{B}}}}}}{a} \gg 1$ (вместе с частицей они перемещаются в пространстве как единое целое).

В то время как поведение эффективного потенциала и заряда интенсивно изучается на протяжении длительного времени, имеется мало данных о толщине слоя [27, 31, 35, 40, 41], образованного прочно связанными с частицей противоионами, даже для ситуации, в которой ионы рассматриваются как точечные объекты. В настоящей работе в рамках нелинейной теории Пуассона–Больцмана мы исследуем эффективные свойства заряженных частиц (потенциал и размер) для широкого диапазона параметров модели, характеризующих плотность поверхностного структурного заряда, размер частиц и концентрацию раствора электролита. Рассматриваем одиночную сферическую частицу в растворе 1 : 1-электролита с точечными ионами.

МОДЕЛЬ И МЕТОД РАСЧЕТА

Поместим сферическую частицу радиуса a в водный раствор электролита. Положим, что в процессе диссоциации поверхностных групп частица приобретает положительный заряд, который равномерно распределяется по ее поверхности. Появление заряда на частице приводит к возникновению неоднородного распределения ионов в растворе вследствие конкуренции между электростатическими взаимодействиями, с одной стороны, и потерями трансляционной энтропии ионов, с другой. Пренебрегая размерами последних, примем, что в условиях равновесия концентрация ионов i-ого типа на расстоянии r от центра сферической частицы подчиняется распределению Больцмана:

(3)
${{C}_{i}}\left( {\mathbf{r}} \right) = {{C}_{{0i}}}{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{{{k}_{{\text{B}}}}T}}} \right],$
где Ci и C0i – локальные концентрации i-ого иона (моль/м3) в точке с электрическим потенциалом φ(r) и в объеме раствора (φ(∞) = 0), соответственно, zi (= ±1) – валентность i-ого иона.

С распределением (3) уравнение Пуассона принимает вид:

(4)
${{\nabla }^{2}}\varphi = - \frac{{e{{N}_{{\text{A}}}}}}{{{{\varepsilon }_{{\text{r}}}}{{\varepsilon }_{0}}}}\mathop \sum \limits_{i = 1}^{2~} {{z}_{i}}{{C}_{{0i}}}{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{{{k}_{{\text{B}}}}T}}} \right].$
Здесь ∇2 – оператор Лапласа, NA – число Авогадро. Считаем, что диэлектрическая постоянная среды не зависит от концентрации раствора и остается постоянной вплоть до поверхности частиц. Для сферической частицы, погруженной в раствор 1 : 1-электролита, перепишем уравнение (4) в компактном виде:
(5)
$\frac{{{{d}^{2}}\psi }}{{d{{r}^{2}}}} + \frac{2}{r}\frac{{d\psi }}{{dr}} = 2{\text{sh}}\left( \psi \right),$
где электростатический потенциал измеряется в единицах термического потенциала φT, а расстояние − в единицах дебаевского радиуса 1/κ:

(6)
$\psi \left( {\mathbf{r}} \right) = \frac{{e\varphi \left( {\mathbf{r}} \right)}}{{{{k}_{{\text{B}}}}T}} = \frac{{\varphi \left( {\mathbf{r}} \right)}}{{{{\varphi }_{{\text{T}}}}}},$
(7)
$\kappa = \sqrt {\frac{{2{{e}^{2}}{{N}_{{\text{A}}}}{{C}_{0}}}}{{{{k}_{{\text{B}}}}T{{\varepsilon }_{{\text{r}}}}{{\varepsilon }_{0}}}}} .$

Будем считать, что плотность заряда, σ, на поверхности частицы поддерживается постоянной, а на большом расстоянии от частицы электрический потенциал обращается в нуль, т.е. накладываем следующие граничные условия:

(8)
$ - {{\left. {\frac{{d\psi }}{{dr}}} \right|}_{{r = \kappa a}}} = \frac{{e\sigma }}{{{{\varepsilon }_{{\text{r}}}}{{\varepsilon }_{0}}{{k}_{{\text{B}}}}T\kappa }} = {{\sigma }_{{\text{s}}}},\,\,\,\,\mathop {\lim }\limits_{r \to \infty } \psi \left( r \right) = 0.$

Нелинейное дифференциальное уравнение (5) с граничными условиями (8) решали численно методом итераций, предварительно проведя его дискретизацию с помощью конечных разностей второго порядка. Узлы располагали на равном расстоянии друга от друга. Когда в последовательных приближениях отклонение рассчитанного значения потенциала не отличалось от предыдущего более чем на 10–9 во всех узлах, итерации останавливали. Шаг между узлами варьировали. Анализируя получаемые результаты, выбирали такой шаг, при котором значения потенциала перестают (в пределах заданной погрешности) зависеть от величины шага.

Варьировали три параметра модели: 1) радиус частиц (a = 1–100 нм), 2) величину приведенной плотности поверхностного заряда (σs = 1–400), 3) концентрацию раствора электролита (C0 = 10–4– 10–1 М).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Эффективные потенциалы и их насыщение

Типичные профили электростатического потенциала для сферических частиц радиусом 1 и 40 нм в растворах с сильно различающейся концентрацией электролита представлены на рис. 1 в полулогарифмических координатах y(r – a) = = ln(ψ(r – a)r/a). Обнаруживаем, что зависимость $y\left( {r - a} \right)$ достаточно быстро приобретает линейный характер по мере удаления от поверхности 40-нм частиц, помещенных в растворы 1 : 1-электролита концентраций 10–4–10–1 М, при величине приведенной плотности поверхностного заряда σs = 100 (рис. 1б). В то же время для 1-нм частиц линейность наблюдается, начиная с очень малых расстояний x = r – a (кривые 1 и 2 на рис. 1а). Мы использовали экспоненциальное затухание функции y(x) на больших расстояниях (уравнение (1)), чтобы строго определить эффективный поверхностный электростатический потенциал ${{\psi }_{{{\text{eff}}}}}.$ Для этого выбирали диапазон значений x, в котором $0 > y\left( x \right) > - 7,$ и сглаживали данные при помощи прямых (коэффициент корреляции не ниже 0.999). Пересечение этих прямых с осью ординат (x = 0) дает значения эффективного потенциала $\ln \left( {{{\psi }_{{{\text{eff}}}}}} \right) = \ln \left( {\psi \left( 0 \right)} \right).$

Рис. 1.

Профили приведенного электростатического потенциала вблизи поверхности частиц радиусом 1 (а) и 40 нм (б) в растворах 1 : 1-электролита концентрации 10–4 (1), 10–3 (2), 10–2 (3) и 10–1 М (4). σs = 100.

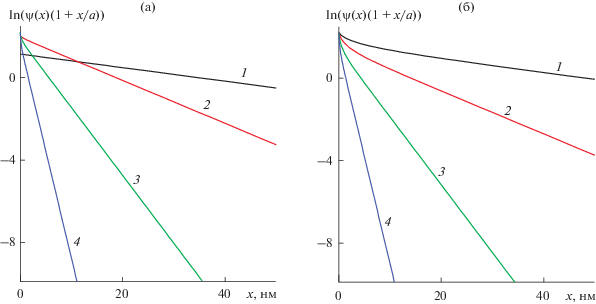
Анализ полученных результатов свидетельствует о том, что для слабо заряженных частиц значения ${{\psi }_{{{\text{eff}}}}}$ не отличается от значений ${{\psi }_{{\text{s}}}},$ а для сильно заряженных затухание потенциала вдали от частицы (в диффузной части ДЭС) может быть представлено линеаризованным уравнением ПБ (1), но теперь величина ${{\psi }_{{{\text{eff}}}}}$ оказывается (значительно) меньше ${{\psi }_{{\text{s}}}}.$ Возникающую разницу в потенциалах, как отмечалось выше, относят к формированию вблизи поверхности частицы (за счет сильного электростатического притяжения) оболочки из прочно связанных противоионов (появление такой оболочки частично нейтрализует заряд частицы).

Наклон прямых, как следует из приведенных на рис. 1 графиков, уменьшается при понижении концентрации электролита и практически совпадает с величиной, обратной радиусу экранирования Дебая в объеме раствора. Величина κ–1 характеризует протяженность ДЭС, формирующегося вблизи заряженных частиц.

Рисунок 2 иллюстрирует, как величина эффективного электростатического потенциала для наночастиц различного размера в растворах с разным содержанием электролита зависит от плотности поверхностного заряда. Выделим следующие моменты.

Рис. 2.

Зависимость приведенного эффективного потенциала от плотности поверхностного заряда для частиц размером a = 1 (1), 2 (2), 5 (3), 15 (4), 40 (5) и 100 нм (6), погруженных в растворы электролита концентрации 10–4 (а) и 10–1 М (б).

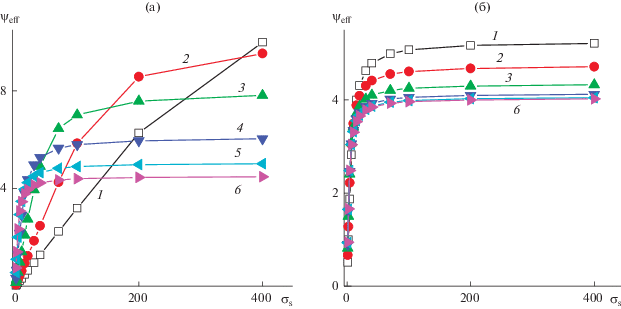
Во-первых, по мере роста плотности поверхностного заряда для рассматриваемых параметров модели (размер частиц, концентрация соли) значение эффективного потенциала увеличивается и стремится к насыщению. Отклонение эффективного потенциала от структурного служит индикатором того, что плотность поверхностного заряда достигла порогового (критического) значения, выше которого появляются прочно связанные с частицей противоионы. Критическая плотность заряда зависит от размера частиц и концентрации раствора электролита. По рис. 2 можно проследить, что в 10–4 М растворах 1 : 1-электролитов при σs = 200 эффективный потенциал насыщается, когда радиус частиц превышает 5 нм (рис. 2а), в то время как в 10–1 М растворах насыщение наблюдается и для более мелких частиц (рис. 2б).

Гиллеспи и др. [26] проверяли предсказания относительно существования критического размера сферических частиц, после достижения которого происходит аккумулирование противоионов на частицах. Были приготовлены неполярные дисперсии сферических частиц размером от 38 до 775 нм, содержащих различное количество ковалентно связанной ионной жидкости. Диссоциация поверхностно-активных групп поставляет в окружающую частицы среду с низкой диэлектрической проницаемостью противоионы. Определяя электрофоретическую подвижность частиц в этих системах в зависимости от их радиуса, объемной доли и плотности структурного заряда, авторы нашли, что она (подвижность) перестает (или почти перестает) зависеть от плотности заряда после достижения некоторого критического уровня. На графиках зависимости электрофоретической подвижности от поверхностной плотности заряда они наблюдали появление плато. Было подтверждено, что для начала конденсации радиус частиц должен превышать некоторое значение, которое, в свою очередь, растет по мере уменьшения объемной доли частиц.

Во-вторых, скорость приближения эффективного поверхностного потенциала ${{\psi }_{{{\text{eff}}}}}$ к насыщению при увеличении плотности заряда на частице растет при переходе к более крупным частицам. Наиболее ярко это проявляется при низких концентрациях растворов электролита (рис. 2а).

В-третьих, несмотря на пониженную скорость роста ${{\psi }_{{{\text{eff}}}}}$ для малых частиц, его значения оказываются выше при больших значениях плотности поверхностного заряда. Это может быть обусловлено искажениями структуры оболочки из прочно связанных противоионов, формирующейся вокруг сферических частиц, по сравнению с плоской поверхностью. Чтобы преодолеть возрастающие потери электростатической энергии, вызванные нарастанием таких искажений по мере роста кривизны поверхности частиц (уменьшения их размера), и требуется более высокая плотность поверхностного заряда. В то же время графики зависимости ${{\psi }_{{{\text{eff}}}}}\left( {{{\sigma }_{{\text{s}}}}} \right)$ весьма слабо различаются для частиц с радиусом больше 15 нм при высокой концентрации раствора электролита (рис. 2б, кривые 4–6).

Ход кривых на рис. 2 указывает на то, что соответствующий условиям насыщения эффективный электростатический потенциал $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ можно надежно определить, представляя данные ${{\psi }_{{{\text{eff}}}}}$(σs) в виде линейной формы уравнения Ленгмюра:

(9)
$\frac{{{{\sigma }_{{\text{s}}}}}}{{{{\psi }_{{{\text{eff}}}}}}} = A + B{{\sigma }_{{\text{s}}}},$
где $A = \frac{1}{{K\psi _{{{\text{eff}}}}^{{{\text{sat}}}}}},~B = \frac{1}{{\psi _{{{\text{eff}}}}^{{{\text{sat}}}}}}$, K – постоянная. Действительно, в условиях, когда заряд частицы превышает несколько единиц элементарного заряда, для различных значений параметров модели (a и C0) линейность выполняется с высокой точностью (коэффициент корреляции превышает 0.999), что позволяет по наклону прямой (по коэффициенту B в уравнении (9)) рассчитать величину $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}.$

Результаты расчетов (рис. 3) демонстрируют, что зависимость потенциала насыщения от приведенного размера частиц представляется в виде универсальной кривой, согласно которой одинаковые значения $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ можно получить, если варьировать размер частиц и концентрацию раствора, но поддерживать постоянной величину $\kappa a.$ Рисунок 3 четко указывает на существование двух предельных режимов зависимости $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}\left( {\kappa a} \right)$, между которыми располагается широкая переходная область.

Рис. 3.

Зависимость насыщенного эффективного потенциала от приведенного размера частиц. a = 1 (1), 2 (2), 5 (3), 15 (4), 40 (5) и 100 нм (6).

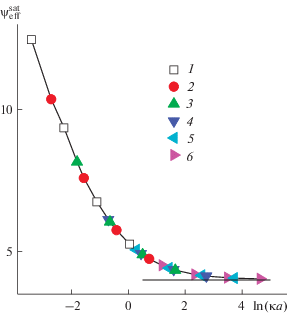
Приведенные на рис. 1–3 данные в точности совпадают с опубликованными в литературе. Так, для крупных частиц (κa $ \gg $ 1) $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}~ \to 4,$ а для мелких частиц (κa $ \ll $ 1), как показано в [31],

(10)
$\begin{gathered} \psi _{{{\text{eff}}}}^{{{\text{sat}}}} \approx \psi _{{{\text{eff}}}}^{{{\text{sat}}}}\left( {1 + \kappa a} \right) = \\ = - 2\ln \left( {\kappa a} \right) + 2\ln \left( { - \ln \left( {\kappa a} \right)} \right) + 4\ln 2. \\ \end{gathered} $
Представив результаты расчетов потенциала насыщения для малых значений приведенного размера частиц в виде функции от переменной $\ln \left( {\frac{1}{{\kappa a}}} \right) + \ln \left( {\ln \left( {\frac{1}{{\kappa a}}} \right)} \right),$ получаем прямую, наклон которой составляет –1.837 ± 0.088. Аналитическое выражение для всего диапазона значений $\kappa a$ было получено из этих предельных законов с помощью аппроксимации Паде в работе [37].

Проведенная по точкам на рис. 3 кривая разделяет рассматриваемую область на две части. В системах, которые оказываются справа от кривой, эффективный поверхностный потенциал достигает насыщения и не изменяется, когда заряд частиц повышается (рис. 2). Переход в состояние с насыщенным эффективным потенциалом можно наблюдать, увеличивая либо размер частиц при неизменной концентрации раствора электролита (κ постоянно), либо концентрацию (ионную силу) раствора при фиксированном размере частиц. Такой переход имеет место при подходящей, достаточно высокой плотности поверхностного заряда, что соответствует пересечению кривой на рис. 3. Место пересечения указывает на величину эффективного потенциала насыщения для исследуемой системы.

Рисунок 3 также иллюстрирует, что чем меньше приведенный размер частиц, тем при более высоких значениях эффективного поверхностного потенциала (заряда частиц) достигается насыщение. Когда κ → 0, величина $\psi _{{{\text{eff\;}}}}^{{{\text{sat}}}}$ → ∞, что согласуется с выводом работы Цимма и Ле Брета [29] о том, что в отсутствие добавленной соли насыщение эффективного потенциала ${{\psi }_{{{\text{eff}}}}}$ не происходит. В условиях, в которых изолированная сферическая частица подвергается воздействию растворителя и точного нейтрализующего числа противоионов, все связанные с ней противоионы “испаряются” в объем раствора независимо от величины структурного заряда.

В литературе, как правило, анализируют особенности поведения не эффективного потенциала, а эффективного поверхностного заряда (который создает на поверхности частицы данный потенциал), так как заряд является характеристикой, которая на интуитивном уровне коррелирует с накоплением противоионов у поверхности частиц. Простое соотношение связывает между собой эти величины [6, 8, 10, 32]:

(11)
$\frac{{Z_{{{\text{eff}}}}^{{{\text{sat}}}}{{l}_{{\text{B}}}}}}{a} = \psi _{{{\text{eff}}}}^{{{\text{sat}}}}\left( {1 + \kappa a} \right).$
Пересчитав с помощью соотношения (11) потенциалы в заряды, получаем зависимость насыщенного эффективного заряда от приведенного размера частиц (рис. 4). Для κ$a$ > 10 точки на рис. 4 укладываются на прямую $y = C + D\left( {\kappa a} \right)$ с параметрами C = 5.9914 ± 0.0111 и D = 4.0194 ± 0.0002, которые прекрасно согласуются с параметрами уравнения Обуи и др. [11, 43]:

(12)
$Z_{{{\text{eff}}}}^{{{\text{sat}}}}\frac{{{{l}_{{\text{B}}}}}}{a} = 6 + 4\kappa a + {\text{O}}\left( {\frac{1}{{\kappa a}}} \right).$
Рис. 4.

Зависимость насыщенного эффективного заряда от приведенного размера частиц. a = 1 (1), 2 (2), 5 (3), 15 (4), 40 (5) и 100 нм (6). На вставке показан фрагмент этой зависимости для значений κa < 2.5.

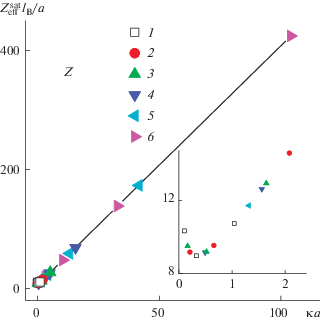
В литературе представлены экспериментальные данные, полученные с привлечением современных физико-химических методов, о свойствах ДЭС в разнообразных системах, различающихся природой заряженных сферических объектов (латексы, фиколлы, дендримеры, мицеллы и др.), размеры которых покрывают диапазон в несколько порядков (от примерно 1 нм до десятков микрон), а также природой растворителя. Из результатов этих исследований следует вывод о том, что эффективный заряд является важным физическим параметром, который контролирует поведение дисперсных систем с заряженными частицами.

Представленные в этом разделе результаты основываются на рассмотрении изменений свойств электростатического потенциала вдали от заряженной поверхности и возможности их описания с помощью линеаризованной теории ПБ. Такой подход дает эффективный поверхностный потенциал (заряд) для сильно заряженных частиц, но не позволяет получить какие-либо количественные оценки структуры ДЭС. Далее дополним примененный подход энергетическим критерием и с его помощью попытаемся оценить положение границы между свободными и прочно связанными с частицей противоионами.

Толщина оболочки из ассоциированных с частицами противоионов

Согласно результатам проведенных расчетов, для выбранных нами модельных параметров энергия электростатического взаимодействия между сильно заряженной частицей и близко расположенными противоионами может значительно превосходить энергию их теплового движения (поверхностный потенциал превышает термический φT). Вследствие этого формирующие ДЭС ионы (противоионы и ионы добавленного электролита) можно разделить на два семейства: прочно связанные (иммобилизованные) противоионы формируют так называемый слой Штерна, а обладающие достаточной кинетической энергией, чтобы свободно перемещаться, – диффузный слой Гуи–Чепмена. Отличительным признаком существования двух популяций является насыщение эффективного потенциала (заряда) (рис. 2), о чем свидетельствует наблюдаемая в экспериментах независимость электрофоретической подвижности частиц от плотности структурного заряда. Высказывается идея [41] о том, что возникновение менее подвижного состояния для противоионов, находящихся в непосредственной близости от заряженной поверхности, осуществляется как фазовый переход.

Точные профили потенциала ${{\psi }_{{{\text{PB}}}}}\left( x \right)$, полученные при численном решении нелинейного уравнения ПБ для всех значений использованных параметров, полностью совпадают с представленными уравнением (1) профилями ΨLPB(x) на дальних расстояниях от поверхности частицы (x → ∞), т.е.

(13)
$\mathop {\lim }\limits_{x~ \to ~\infty } \frac{{{{\psi }_{{{\text{LPB}}}}}\left( x \right)}}{{{{\psi }_{{{\text{PB}}}}}\left( x \right)}} = 1.$
Поведение профиля становится неэкспоненциальным (${{\psi }_{{{\text{PB}}}}}\left( x \right) > {{\psi }_{{{\text{LPB}}}}}\left( x \right)),$ когда x → 0 (рис. 1). С анализа расстояний, на которых вступают в игру нелинейные эффекты, мы начали поиски положения границы между двумя популяциями ионов в ДЭС. Нас интересовал момент отрыва касательной от кривой $y\left( x \right) = {\text{ln}}\left[ {\psi \left( x \right)\left( {1 + {x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a}} \right)} \right].$ Чтобы определить эффективный поверхностный потенциал и эффективный радиус частицы, авторы работы [27] применяли аналогичный подход. Рассчитав свойства ДЭС для растворов различных генераций дендримеров и сравнив их с измеренными с помощью прибора Zetasizer Nano ZS, они установили, что рассчитанные значения эффективного диаметра частиц удовлетворительно согласуется с измеренными в экспериментах, а полученные при моделировании значения эффективного поверхностного потенциала ($\psi _{{{\text{eff}}}}^{{{\text{sat}}}} \approx 2$) очень хорошо воспроизводят экспериментальные ζ-потенциалы для всех исследованных дендримеров.

Однако проведенные нами расчеты показали, что отклонение кривой y(x) от своей касательной происходит настолько плавно, что невозможно точно определить расстояние, на котором отрыв возникает, в то же время оценки потенциала “отрыва” приводят к величине, близкой к 1. Поэтому далее мы использовали энергетический критерий (уравнение (2)), чтобы найти положение границы между свободными и связанными противоионами. Искали расстояние (и соответственно, эффективный размер частицы), на котором электростатическая энергия притяжения противоиона к макроиону сравнима со средней тепловой энергией иона. В используемых нами единицах измерения электрического потенциала это соответствует соотношению

(14)
$\left| {\psi \left( {a{\text{\;}} + {\text{\;}}l} \right)} \right| = {{\psi }_{{{\text{lev}}}}},$
где ${{\psi }_{{{\text{lev}}}}}$ – параметр отсечения (порядка единицы), l – толщина оболочки, в которой находятся прочно связанные с частицей противоионы.

Строили графики зависимости ${{y}_{{{\text{lev}}}}}\left( x \right)$ = = ${\text{ln}}\left[ {{{\psi }_{{{\text{lev}}}}}\left( {1 + {x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a}} \right)} \right]$ для нескольких значений ${{\psi }_{{{\text{lev}}}}}$ (= 1–2) (рис. 5 и 6) и находили значения абсциссы, при которых графики ylev(x) пересекаются с y(x) и ее касательной (касательная к y(x) является продолжением из области значений x, где график y(x) становится линейным). Последние пересечения показаны на рис. 5 и 6 в виде кружочков. (Обратим внимание на то, что для 1-нм частиц в разбавленных растворах электролитов профили электростатического потенциала практически во всем диапазоне расстояний от поверхности частицы описываются линеаризованным уравнением ПБ вплоть до значений приведенной плотности поверхностного заряда σs = 100 (см. рис. 5а).)

Рис. 5.

Поиск значений потенциала, при которых происходит отрыв кривой ln(ψ(x)(1 + x/a)) от касательной, проведенной к ней на дальних расстояниях от поверхности 1-нм частиц. Кривые 1–8 на рис. 5а представляют функцию ln(ψ(x)(1 + x/a)) при значениях σs = 10 (1), 15 (2), 20 (3), 30 (4), 40 (5), 70 (6), 100 (7) и 400 (8), а кривые (1–6) на рис. 5б – при σs = 2 (1), 4 (2), 7 (3), 15 (4), 30 (5) и 400 (6). Кривые 1'–3' соответствуют функции ln(ψlev(1 + x/a)) при ψlev = 1 (1 '), 1.5 (2 ') и 2 (3 '). Точками обозначены пересечения кривых 1 '–3 ' с касательными (не показаны). Концентрация раствора электролита 10–3 (а) и 10–1 М (б).

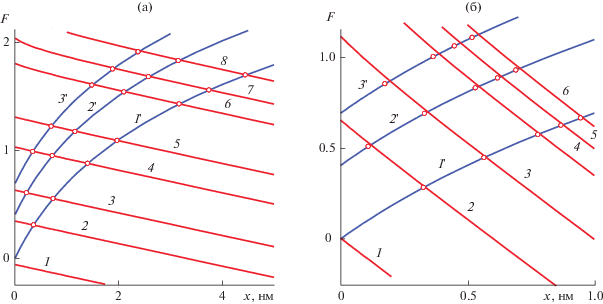
Рис. 6.

Поиск значений потенциала, при которых происходит отрыв кривой ln(ψ(x)(1 + x/a)) от касательной, проведенной к ней на дальних расстояниях от поверхности 40-нм частиц. Кривые 1–7 на рис. 6а представляют функцию ln(ψ(x)(1 + x/a)) при значениях σs = 2 (1), 4 (2), 7 (3), 10 (4), 15 (5), 30 (6) и 400 (7), а кривые 1–6 на рис. 6б – при σs = 2 (1), 4 (2), 7 (3), 15 (4), 30 (5) и 400 (6). Кривые 1 '–3 ' соответствуют функции ln(ψlev(1 + x/a)) при ψlev = 1 (1 '), 1.5 (2 ') и 2 (3 '). Точками обозначены пересечения кривых 1 '–3 ' с касательными (не показаны). Концентрация раствора электролита 10–4 (а) и 10–1 М (б).

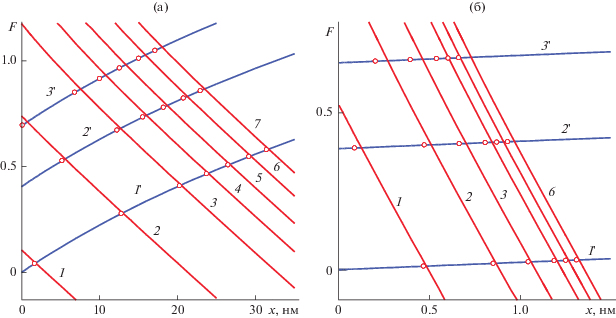
Отслеживая и сравнивая пересечения для различных значений параметра ${{\psi }_{{{\text{lev}}}}}$, обнаруживаем, что по мере отклонения величины ${{\psi }_{{{\text{lev}}}}}$ от 1 точки пересечения кривой ylev(x) с касательной удаляются от точек ее пересечения с самими кривыми y(x). Поскольку при ${{\psi }_{{{\text{lev}}}}}$ = 1 эти точки располагаются наиболее близко друг к другу, эту величину выбирали в качестве пороговой в энергетическом критерии и с ее помощью устанавливали положение границы между ассоциированными с частицей и свободными ионами для всех рассмотренных в работе модельных параметров. Итак, с помощью энергетического критерия (с величиной ψlev = 1) оценивали толщину оболочки из прочно связанных противоионов ${{l}_{{{\text{eff}}}}}$ как расстояние от поверхности частицы, на котором выполняется условие (14). Теперь находим и эффективный размер частицы: ${{a}_{{{\text{eff}}}}} = a + {{l}_{{{\text{eff}}}}}.$

Обратим внимание на результаты работы [25], авторы которой разработали и применили оптический метод, позволяющий в одном измерении получать данные как о размере стабилизированных полимерным ПАВ частиц пигментов, так и их подвижности в неполярном растворителе. Пересчитав подвижность в ξ-потенциал, они установили, что для частиц размером 200–10 000 нм выполняется соотношение: $\frac{{Z_{{{\text{eff}}}}^{{{\text{sat}}}}{{l}_{{\text{B}}}}}}{{{{a}_{{{\text{eff}}}}}}} = A\left( {1 + \kappa {{a}_{{{\text{eff}}}}}} \right),$ где A = –1.08 (отрицательный эффективный заряд). Пожалуй, это единственная работа, экспериментальные результаты которой поддерживают выбор значения ${{\psi }_{{{\text{lev}}}}}$ = 1.

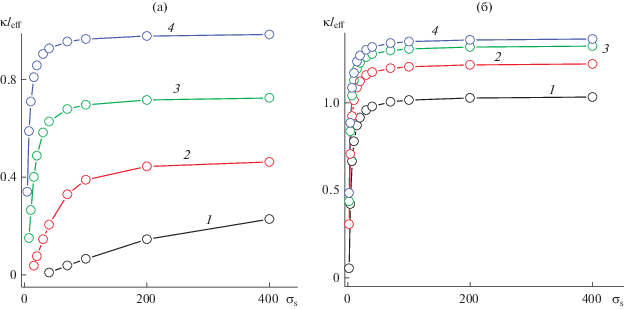
Приведенные на рис. 7 типичные результаты показывают, что по мере увеличения плотности поверхностного заряда толщина оболочки ${{l}_{{{\text{eff}}}}}$ непрерывно растет и достигает насыщения $l_{{{\text{eff}}}}^{{{\text{sat}}}},$ в точности повторяя ход кривых ${{\psi }_{{{\text{eff}}}}}$(σs) (рис. 2). После некоторого значения σs толщина формирующейся вокруг частицы оболочки, внутри которой энергия притяжения ионов к частице превышает kBT, не реагирует на увеличение плотности поверхностного заряда. Отметим, что графики зависимости κ${{l}_{{{\text{eff}}}}}$(σs) совпадают для частиц размером больше 15 нм в 0.1 М растворах электролита (рис. 7б), а расположение графиков (рис. 7) для частиц разного размера оказывается обратным по сравнению с расположением графиков ${{\psi }_{{{\text{eff}}}}}$(σs) (рис. 2).

Рис. 7.

Зависимость приведенной толщины оболочки, формирующейся вблизи частиц радиусом 1 (1), 5 (2), 40 (3) и 100 нм (4), от плотности поверхностного заряда. Концентрация раствора электролита 10–4 (а) и 10–1 M (б). ψlev = 1.

Расчеты “предельных” толщин оболочек, отвечающих условиям насыщения, проводили с применением формулы, аналогичной (9). Данные аппроксимируются прямыми с высокой точностью. Представленные на рис. 8 результаты расчетов наглядно показывают, что при всех значениях параметров модели (размер сферических частиц, концентрация раствора электролита, в который частицы погружены) рассчитанные значения $l_{{{\text{eff}}}}^{{{\text{sat}}}}$ укладываются на единую универсальную кривую $\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}}\left( {\kappa a} \right).$

Рис. 8.

Зависимость приведенной толщины оболочки, отвечающей условиям насыщения, от приведенного размера частиц для ψlev = 1. a = 1 (1), 2 (2), 5 (3), 15 (4), 40 (5) и 100 нм (6).

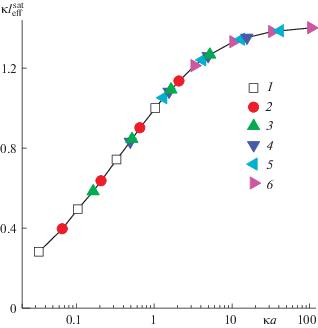
Выделим следующие моменты в этой зависимости. Во-первых, по мере роста приведенного размера частиц приведенная толщина оболочки из иммобилизованных противоионов (толщина слоя Штерна) постепенно растет и для больших частиц достигает величины примерно 1.4. Во-вторых, для малых частиц (κa < 1) протяженность оболочки меньше радиуса экранирования Дебая, но заметно превосходит размер частицы. В-третьих, толщина оболочки становится равной радиусу частицы, когда a = κ–1. В-четвертых, зависимость $\kappa l\,_{{{\text{eff}}}}^{{{\text{sat}}}}$ от приведенного размера частиц в условиях насыщения оказывается антибатной по сравнению с аналогичной зависимостью насыщенного эффективного поверхностного потенциала (рис. 3).

Перепишем теперь уравнение (1) с учетом условия (14) для ситуации с возникновением вблизи частицы иммобилизованного слоя противоионов:

(15)
$\frac{{\psi _{{{\text{eff}}}}^{{{\text{sat}}}}}}{{{{\psi }_{{{\text{lev}}}}}}} = \left( {1 + \frac{{l_{{{\text{eff}}}}^{{{\text{sat}}}}}}{a}} \right)\exp \left( {\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}}} \right).$
Имеем, что и ионная сила раствора электролита, и радиус частиц влияют на толщину оболочки. При фиксированных значениях ${{\psi }_{{{\text{lev}}}}}$ и $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ оболочка утончается при увеличении концентрации раствора. Для крупных частиц сохраняется зависимость только от первого фактора, поскольку выполняется равенство
(16)
$\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}} = {\text{ln}}\frac{{\psi _{{{\text{eff}}}}^{{{\text{sat}}}}}}{{{{\psi }_{{{\text{lev}}}}}}},$
что дает при ${{\psi }_{{{\text{lev}}}}}$ = 1 и $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ = 4
(17)
$\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}} = {\text{ln}}4 = 1.386.$
К полученному в (17) значению стремится зависимость $\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}}\left( {\kappa a} \right)$ с увеличением приведенного размера частиц (рис. 8). В литературе для больших значений приведенного размера частиц (в пределе малой кривизны, когда решение уравнения ПБ может быть аппроксимировано решением для плоскости и эффектом кривизны можно пренебречь) протяженность области, в которой доминируют нелинейные эффекты, оценивают [10] как $\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}} = 1.$ Такое значение получается из формулы (16), если принять ${{\psi }_{{{\text{lev}}}}}$ = $\frac{4}{{\exp \left( 1 \right)}} = 1.472,$ что близко к средней кинетической энергии иона (1.5kBT). Увеличение значения параметра отсечения ${{\psi }_{{{\text{lev}}}}}$ вызывает смещение графика на рис. 8 к меньшим значениям $\kappa l_{{{\text{eff}}}}^{{{\text{sat}}}}$ (которые соответствуют более тонким слоям Штерна).

Используемый нами энергетический критерий не нов. Исследователи часто его применяют, но не могут прийти к согласию относительно того, какое пороговое значение для определения положения границы между ассоциированными с частицей и свободными ионами следует выбрать. Для определения эффективного размера частиц Люкацки и Сафран [35] выбирали значение подобного ${{\psi }_{{{\text{lev}}}}}$ параметра, равное 1kBT. Затем, рассматривая энергию электростатического взаимодействия двух частиц, они оценили толщину слоя Штерна как

(18)
$2\kappa {{l}_{{{\text{eff}}}}} = {\text{ln}}\left( {\frac{{{{Z}^{2}}{{l}_{{\text{B}}}}}}{{2\left( {a + {{l}_{{{\text{eff}}}}}} \right){{{\left( {1 + \kappa a} \right)}}^{2}}}}} \right).$
В свою очередь Дентон [40] принимал (в наших обозначениях) ${{\psi }_{{{\text{lev}}}}}$ = 3 и рассчитывал величину ${{l}_{{{\text{eff}}}}}$ по уравнению
(19)
$\frac{{Z{{l}_{B}}}}{{\left[ {1 + \kappa \left( {a + {{l}_{{{\text{eff}}}}}} \right)} \right]\left( {a + {{l}_{{{\text{eff}}}}}} \right)}} = {{\psi }_{{{\text{lev}}}}}.$

ЗАКЛЮЧЕНИЕ

В рамках теории Пуассона–Больцмана рассчитаны профили электростатического потенциала вблизи погруженных в растворы 1 : 1-электролита заряженных сферических частиц. Для широкого диапазона значений параметров модели (плотности поверхностного заряда, радиуса частиц, концентрации раствора электролита) из поведения профиля на дальних от поверхности частиц расстояниях определены эффективный поверхностный потенциал ${{\psi }_{{{\text{eff}}}}},$ а также предел $\psi _{{{\text{eff}}}}^{{{\text{sat}}}},$ к которому он стремится при неограниченном росте плотности поверхностного заряда. Построена универсальная кривая, которая представляет зависимость $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$ от приведенного радиуса частицы κa и наглядно иллюстрирует существование двух известных предельных законов изменения эффективного потенциала, отвечающего условиям насыщения.

С привлечением энергетического критерия и анализа его чувствительности к порогу отсечения получены оценки толщины формирующихся вокруг сферических частиц оболочек из прочно связанных с поверхностью противоионов. Проанализированы зависимости толщины оболочек от плотности поверхностного заряда, радиуса частиц и концентрации раствора 1 : 1-электролита. Установлено существование предельной толщины $l_{{{\text{eff}}}}^{{{\text{sat}}}}$, достигаемой при неограниченном росте плотности поверхностного заряда. Приведена универсальная кривая κ$l_{{{\text{eff}}}}^{{{\text{sat}}}}$(κa), и проведено ее сопоставление с кривой $\psi _{{{\text{eff}}}}^{{{\text{sat}}}}$(κa).

Список литературы

  1. Долинный А.И. // Коллоид. журн. 2019. Т. 81. С. 690.

  2. Verwey E.J.W., Overbeek J.Th.G. Theory of the Stability of Lyophobic Colloids. New York: Elsevier, 1948.

  3. Делахей П. Двойной слой и кинетика электродных процессов. М.: Мир, 1967.

  4. Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. М.: Наука, 1985.

  5. Andelman D. Handbook of Biological Physics. Ed. by Lipowsky R., Sackmann E. Elsevier Science B.V. 1995. V. 1. Chapter 12.

  6. Levin Y. // Rep. Prog. Phys. 2002. V. 65. P. 1577.

  7. Lyklema J. Fundamentals of Interface and Colloid Science, Amsterdam: Elsevier Academic Press, 2005. V. 4. Chapter 3.

  8. Ohshima H. Nanolayer Research: Methodology and Technology for Green Chemistry. Elsevier, 2017. Chapter 2.

  9. Attard P. // J. Phys. Chem. 1995. V. 99. P. 14174.

  10. Bocquet L., Trizac E., Aubouy M. // J. Chem. Phys. 2002. V. 117. P. 8138.

  11. Aubouy M., Trizac E., Bocquet L. // J. Phys. A. 2003. V. 36. P. 5835.

  12. Manning G.S. // J. Phys. Chem. B. 2007. V. 111. P. 8554.

  13. Tellez G., Trizac E. // Phys. Rev. E. 2003. V. 68. Article 061401.

  14. González-Mozuelos P., Guerrero-García G.I., Olvera de la Cruz M. // J. Chem. Phys. 2013. V. 139. Article 064709.

  15. Guerrero-Garcıa G.I., Gonzalez-Mozuelos P., Olvera de la Cruz M. // ACS Nano. 2013. V. 7. P. 9714.

  16. Fagotti B.C., Degiorgio V., Piazza R. // Langmuir. 1991. V. 7. P. 824.

  17. Roberts J.M., O’Dea J.J., Osteryoung J.G. // Anal. Chem. 1998. V. 70. P. 3667.

  18. Huang Q.R., Dubin P.L., Moorefield C.N., Newkome G.R. // J. Phys. Chem. B. 2000. V. 104. P. 898.

  19. Quesada-Perez M., Callejas-Fernandez J., Hidalgo-Alvarez R. // J. Colloid Interface Sci. 2001. V. 233. P. 280.

  20. Wette P., Schöpe H.J., Palberg T. // J. Chem. Phys. 2002. V. 116. P. 10981.

  21. Aswal V.K., Goyal P.S. // Phys. Rev. E. 2003. V. 67. Article 051401.

  22. Garbow N., Evers M., Palberg T. Okubo T. // J. Phys.: Condens. Matter. 2004. V. 16. P. 3835.

  23. Hsiao C.C., Wang T.-Y., Tsao H.-K. // J. Chem. Phys. 2005. V. 122. Article 144702.

  24. Guo X., Kirton G.F., Dubin P.L. // J. Phys. Chem. B. 2006. V. 110. P. 20815.

  25. Strubbe F., Beunis F., Neyts K. // J. Colloid Interface Sci. 2006. V. 301. P. 302.

  26. Gillespie D.A.J., Hallett J.E., Elujoba O., Hamzah A.F.C., Richardson R.M. Bartlett P. // Soft Matter. 2014. V. 10. P. 566.

  27. Xu X., Ran Q., Haag R., Ballauff M., Dzubiella J. // Macromolecules. 2017. V. 50. P. 4759.

  28. Trefalt G., Palberg T., Borkovec M. // Curr. Opin. Colloid Interface Sci. 2017. V. 27. P. 9.

  29. Zimm B.H., Le Bret M. // J. Biomol. Struct. Dyn. 1983. V. 1. P. 461.

  30. Alexander S., Chaikin P.M., Grant P., Morales G.J., Pincus P., Hone D. // J. Chem. Phys. 1984. V. 80. P. 5776.

  31. Ramanathan G.V. // J. Chem. Phys. 1988. V. 88. P. 3887.

  32. Belloni L. // Colloids Surf. A. 1998. V. 140. P. 227.

  33. Schmitz K.S. // Langmuir. 2000. V. 16. P. 2115.

  34. Sanghiran V., Schmitz K.S. // Langmuir. 2000. V. 16. P. 7566.

  35. Lukatsky D.B., Safran S.A. // Phys. Rev. E. 2000. V. 63. Article 011405.

  36. Mukherjee A.K., Schmitz K.S., Bhuiyan L.B. // Langmuir. 2002. V. 18. P. 4210.

  37. Dufrêche J.-F., White T.O., Hansen J.-P. // Mol. Phys. 2003. V.101. P. 1741.

  38. Trizac E., Bocquet L., Aubouy M., von Grünberg H.H. // Langmuir. 2003. V. 19. P. 4027.

  39. Diehl A., Levin Y. // J. Chem. Phys. 2004. V. 121. P. 12 100.

  40. Denton A.R. // J. Phys.: Condens. Matter. 2008. V. 20. Article 494230.

  41. Lamm G., Pack G.R. // Biopolymers. 2010. V. 93. P. 619.

  42. Carnal F., Stoll S. // J. Phys. Chem. A. 2012. V. 116. P. 6600.

  43. Šamaj L., Trizac E. // J. Phys. A. 2015. V. 48. Article 265 003.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал