Коллоидный журнал, 2020, T. 82, № 6, стр. 698-706
Диффузионное осаждение наночастиц в слое гранул
В. А. Кирш 1, 2, *, А. А. Кирш 2, П. Ю. Макавеев 2
1 Институт физической химии и электрохимии им. А.Н. Фрумкина
119071 Москва, Ленинский проспект, 31, Россия
2 Национальный исследовательский центр “Курчатовский институт”
123182 Москва, пл. Академика Курчатова, 1, Россия
* E-mail: va_kirsch@mail.ru
Поступила в редакцию 17.06.2020
После доработки 23.06.2020
Принята к публикации 26.06.2020
Аннотация
Рассмотрено осаждение аэрозольных наночастиц в модельном гранульном фильтре, состоящем из параллельных монослоев контактирующих сферических гранул с квадратной укладкой, где каждый четный монослой смещен в своей плоскости относительно нечетного на радиус гранулы в двух перпендикулярных направлениях. Монослои гранул расположены перпендикулярно набегающему потоку газа. Рассчитаны диффузионные коэффициенты захвата точечных частиц гранулами в зависимости от расстояния между слоями в режиме трехмерного течения газа при малых числах Рейнольдса $\operatorname{Re} $ $ \ll $ 1 в диапазоне чисел Пекле ${\text{Pe}}$ = 102−104. Результаты расчетов согласуются с опубликованными данными и с результатами измерений осаждения монодисперсных наночастиц из азота и гелия при фильтрации через слои металлических монодисперсных сфер. Обсуждается возможность применения слоя гранул в качестве диффузионной батареи для измерения размера аэрозольных частиц.
ВВЕДЕНИЕ
Теория осаждения точечных частиц из ползущего (стоксова) потока в гранульных фильтрах находит применение при расчете и оптимизации процессов фильтрации, сушки, электрохимии, катализа в зернистых средах [1, 2]. Осаждение частиц на гранулы происходит в трехмерном потоке. В этом случае аналитические подходы не вполне применимы, и для расчета полей течения и концентрации частиц в системе гранул с заданной геометрией используются численные методы [3, 4]. Наиболее подробно изучено стоксово течение в пористых средах, которое не зависит от числа Рейнольдса. Перепад давления в слое гранул $\Delta p$ подчиняется закону Дарси, согласно которому $\Delta p$ линейно растет с ростом скорости потока. В результате многолетних экспериментальных исследований полученные данные для стоксова режима течения были обобщены в виде эмпирической формулы Козени–Кармана
(1)
${{\Delta {\kern 1pt} p} \mathord{\left/ {\vphantom {{\Delta {\kern 1pt} p} {U\mu = {{9K{{\alpha }^{2}}H} \mathord{\left/ {\vphantom {{9K{{\alpha }^{2}}H} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}}}} \right. \kern-0em} {U\mu = {{9K{{\alpha }^{2}}H} \mathord{\left/ {\vphantom {{9K{{\alpha }^{2}}H} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}}}{{\left( {1 - \alpha } \right)}^{3}},$Успешной моделью гранульного фильтра явилась так называемая ячеечная модель, в которой рассматривался слой взвешенных несоприкасающихся шаров с одинаковым расстоянием между ними в объеме слоя, и расчет осаждения выполнялся для одного шара в ячейке при условии, что осаждение наночастиц по толщине слоя описывается экспоненциальной зависимостью [1]. Плотность упаковки в такой модели равна $\alpha = {{\left( {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}} \right)}^{3}}$, где $b$ – радиус ячейки. Перепад давления в зернистом слое толщиной Н определяется по формуле
где $N = {{3\alpha H} \mathord{\left/ {\vphantom {{3\alpha H} {4\pi {{a}^{3}}}}} \right. \kern-0em} {4\pi {{a}^{3}}}}$ – число гранул на единице площади фильтра, $F$ – безразмерная сила сопротивления гранулы, учитывающая влияние соседних гранул, равная где в качестве линейного размера выбран радиус гранулы $a$, $k$ – гидродинамический фактор. Хаппелем [8] и Кувабарой [9] в рамках ячеечной модели были найдены функции тока, компоненты скоростей и силы сопротивления гранул в зависимости от $\alpha .$ Авторы приняли разные гипотетические граничные условия на поверхности ячейки. Гидродинамический фактор $k = {{6\pi } \mathord{\left/ {\vphantom {{6\pi } F}} \right. \kern-0em} F}$ по Хаппелю и Кувабаре соответственно равен(4)
${{k}_{{\text{H}}}} = \left( {1 - \frac{3}{2}{{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \frac{3}{2}{{\alpha }^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}} - {{\alpha }^{2}}} \right){{\left( {1 - \frac{2}{3}{{\alpha }^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}} \right)}^{{ - 1}}},$(5)
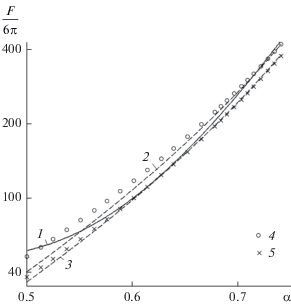
${{k}_{{\text{K}}}} = 1 - \frac{9}{5}{{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \alpha - \frac{1}{5}{{\alpha }^{2}}.$Рис. 1.
Силы сопротивления гранул поперечному потоку, рассчитанные для разных моделей: 1 – по формуле (12) для монослоя гранул с квадратной укладкой, 2, 3 – по формуле Козени–Кармана (13) с $K$ = 5 (2) и $K$ = 4.5 (3), 4 – по формуле Кувабары (5), 5 – по формуле Хаппеля (4).
При выполнении экспоненциальной зависимости осаждения частиц в слое одинаковых гранул применима формула, связывающая проскок частиц с коэффициентом захвата и параметрами фильтра:
(6)
${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = \exp \left( { - \pi {{a}^{2}}NH\eta } \right),$(7)
$\eta = A{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}},$(8)
$\eta = 3.5{{\left[ {{{\left( {1 - \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \alpha } \right)} {{{k}_{{\text{K}}}}}}} \right. \kern-0em} {{{k}_{{\text{K}}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}},$(9)
$\eta = 3.5{\kern 1pt} {{[{{(1 - {{\alpha }^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}})} \mathord{\left/ {\vphantom {{(1 - {{\alpha }^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}})} {{{k}_{{\text{H}}}}}}} \right. \kern-0em} {{{k}_{{\text{H}}}}}}]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}.$Модель Кувабары используется чаще в задачах о фильтрации волокнистыми слоями, поскольку расчеты сопротивления упорядоченного слоя волокон вплоть до $\alpha $ = 0.3 в рамках этой модели оказались в согласии с экспериментами [18]. Аналогичная экспериментальная проверка для высокопористого слоя гранул чрезвычайно трудна, поскольку для незакрепленных гранул сразу начинают сказываться боковые силы, вызывающие нарушение упорядоченности их расположения и ассиметричное обтекание гранул. Отметим, что во многих работах, в том числе в [16, 17], в формуле (6) показатель экспоненты увеличивают в ${{\left( {1 - \alpha } \right)}^{{ - 1}}}$ раз, так как в число Пекле и в гидродинамический фактор подставляют среднюю скорость внутри фильтра, которую авторы называют скоростью “невозмущенного” потока перед ячейкой, тогда как расчет по формуле (6) должен проводиться для среднерасходной скорости однородного потока перед фильтром (поскольку определяющим параметром является расход газа через заданную площадь фильтра).
Далее следует подчеркнуть, что многие экспериментальные работы по исследованию диффузионного осаждения частиц были проведены не с наноаэрозолями и для режима течения, переходящего из стоксова в инерционное. Например, в [19] авторы обосновали выбор модели Кувабары для шаров, сославшись на лучшее согласие перепада давления по Кувабаре с опытами работы [15], выполненными для $\operatorname{Re} $ = 0.1−20, не учитывая, что для слоя с $\alpha $ = 0.6 уже при $\operatorname{Re} $ > 5 начинается рост перепада давления за счет инерционности потока. Так, по оценкам по формуле Эргуна [20] при $\operatorname{Re} $ = 20 перепад давления возрастет в 1.4 раза по сравнению с перепадом давления в стоксовом течении. Поэтому при сравнении экспериментов с теоретическими оценками необходимо учитывать ограничения, связанные с предельным значением числа Рейнольдса, ниже которого течение в слое гранул не зависит от $\operatorname{Re} $. По данным разных работ при $\operatorname{Re} $ < 1 значения коэффициента $A$ лежат в пределах $A$ = 8.4−11.6, где $A$ = 8.4 при $\alpha $ = 0.62 [11], $A$ = 10.9 при $\alpha $ = 0.6 [12], $A$ = 9.64 при $\alpha $ = = 0.58−0.59 [13], $A$ = 9.54 при $\alpha $ = 0.6 [14]. В работе [15] коэффициент $A$ = 11.6 (α = 0.615), но он был получен при $\operatorname{Re} $ = 0.1−20, и, кроме того, эти эксперименты были выполнены с субмикронными частицами, а выводы о диффузионном механизме осаждения сделаны в предположении малости вклада других механизмов осаждения, связанных с конечным размером частиц.
Здесь следует отметить, что данных, полученных с точечными частицами, очень мало. Но и в опубликованных работах режим течения не был стоксовым. Так, в работе [21] приводятся данные для эффективности осаждения наночастиц диаметром 0.008−0.02 мкм в слое стеклянных сфер диаметром 2 мм (высота слоя равна 9 см, площадь 11.3 см2, пористость 0.4) при скорости $U$ = = 3−25 см/с, что соответствовало $\operatorname{Re} $ = 4−25, в результате чего коэффициент захвата оказался сильно завышенным и была получена другая функциональная зависимость $\eta \left( {{\text{Pe}}} \right)$ − коэффициент захвата оказался пропорциональным ${\text{P}}{{{\text{e}}}^{{ - 0.63}}}$ (и при этом авторы заявили, что они хотели бы создать гранульную диффузионную батарею (ДБ)).
Заметим, что хотя численные методы позволяют точно рассчитать $\eta \left( {{\text{Pe}}} \right)$ с ростом $\operatorname{Re} $, но для экспресс-анализа дисперсности частиц с помощью ДБ число $\operatorname{Re} $ − лишний параметр, и поэтому использовать ДБ из гранул имеет смысл только при $\operatorname{Re} $ < 1. Кроме того, для численного моделирования большое число гранул в расчетной ячейке нежелательно. Таким образом, чтобы сократить их число и, следовательно, время расчета, следует выбрать модель с известной упорядоченной структурой, которая позволит рассматривать осаждение частиц в слое конечной толщины на небольшом числе гранул. В то же время структура и свойства модели должны соответствовать структуре и свойствам реального слоя. Для этого необходимо учесть контакты между гранулами. Ранее [22–24] рассматривались гидродинамика и диффузия точечных частиц в изолированных монослоях контактирующих сфер с различной укладкой, и было показано, что функциональная зависимость коэффициента захвата от числа ${\text{Pe}}$ отличается от формулы (7), а совпадение наблюдается только в области очень больших Ре. Поэтому представляет интерес рассмотреть, как влияет расстояние между несколькими расположенными друг за другом монослоями на осаждение частиц и насколько результаты расчетов соответствуют опытным данным.
ДИФФУЗИОННОЕ ОСАЖДЕНИЕ НАНОЧАСТИЦ В МОДЕЛЬНОМ ГРАНУЛЬНОМ ФИЛЬТРЕ
Метод расчета гидродинамического поля течения и диффузионного осаждения частиц в упорядоченных структурах с квадратной и гексагональной укладкой гранул в условиях 3D-течения при $\operatorname{Re} $ < 1 на основе численного решения стационарных уравнений Стокса и конвективной диффузии дан в [22–24]. Рассчитанная сила сопротивления одной гранулы в изолированном монослое с квадратной укладкой гранул, равная ${{F}_{0}} = 43.9{{F}_{{{\text{St}}}}},$ где ${{F}_{{{\text{St}}}}} = 6\pi aU\mu $ − стоксова сила сопротивления изолированной сферы, почти не отличается от силы сопротивления гранулы в сомкнутых слоях, образующих кубическую упаковку с $\alpha $ = π/6, в которой ${{F}_{0}} \approx 43{{F}_{{{\text{St}}}}}$ [4, 25, 26]. Для монослоя гранул с гексагональной укладкой сила сопротивления равна ${{F}_{{{\text{hex}}}}} = 348\,{{F}_{{{\text{St}}}}}$ [22]. При 10 ≤ ${\text{Pe}}$ < 2 × 105 результаты вычислений диффузионного коэффициента захвата точечных частиц в изолированных монослоях гранул с квадратной и гексагональной упаковкой были аппроксимированы формулами [24]
(10)
${{\eta }_{{{\text{sq}}}}} = 8.71{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}} - 7{\text{P}}{{{\text{e}}}^{{ - 1}}} - 5{\text{P}}{{{\text{e}}}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0em} 3}}}},$(11)
${{\eta }_{{{\text{hex}}}}} = 13.9{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}} - 19.3{\text{P}}{{{\text{e}}}^{{ - 1}}}.$Интересно отметить, что в кубической модели каждый шар в монослое находится в гидродинамической тени от шара в предыдущем слое, но это не влияет ни на сопротивление фильтра, ни на эффективность осаждения частиц. Однако взаимное влияние соседних монослоев проявляется при смещении в кубической модели четных монослоев относительно нечетных в своей плоскости по двум перпендикулярным направлениям, которое достигает максимума, когда смещение происходит на радиус гранулы (рис. 2). Сила сопротивления одной гранулы в этом случае увеличивается от $F = 44{{F}_{{{\text{St}}}}}$ до $F = 54.1{{F}_{{{\text{St}}}}}$ и далее монотонно возрастает при сближении монослоев, т.е. с ростом плотности упаковки модели от $\alpha $ = π/6 до предельного значения $\alpha $ = 0.74, при котором монослои с квадратной укладкой гранул соприкасаются ($h = 1.414\,a$), следуя аппроксимационной формуле [24]
(12)
${F \mathord{\left/ {\vphantom {F {6\pi }}} \right. \kern-0em} {6\pi }} = 7 + 241\alpha - 514{{\alpha }^{2}} + 12.7\alpha {{\left( {1 - \alpha } \right)}^{{ - 3}}}.$(13)
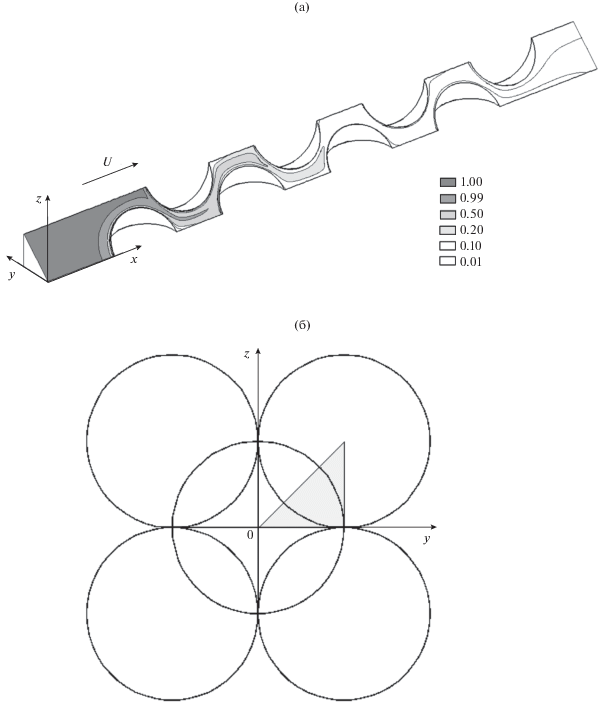
${F \mathord{\left/ {\vphantom {F {6\pi = {{2K\alpha } \mathord{\left/ {\vphantom {{2K\alpha } {{{{\left( {1 - \alpha } \right)}}^{3}}}}} \right. \kern-0em} {{{{\left( {1 - \alpha } \right)}}^{3}}}}}}} \right. \kern-0em} {6\pi = {{2K\alpha } \mathord{\left/ {\vphantom {{2K\alpha } {{{{\left( {1 - \alpha } \right)}}^{3}}}}} \right. \kern-0em} {{{{\left( {1 - \alpha } \right)}}^{3}}}}}}.$Рис. 2.
Модель фильтра из восьми монослоев гранул с $\alpha $ = 0.6. (а) Расчетная ячейка, стрелкой указано направление потока, и показаны области, ограниченные изолиниями безразмерной концентрации $С$ = 1, 0.99, 0.5, 0.2, 0.1, 0.01 при ${\text{Pe}}$ = 100; (б) поперечное сечение фильтра в плоскости yz.
В предыдущем сообщении [24] было рассмотрено осаждение наночастиц в двухслойных мембранах, состоящих из двух смещенных на радиус гранулы и сомкнутых монослоев с квадратной укладкой, где средний коэффициент захвата был аппроксимирован формулой
(14)
$\eta = 12{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}.$На рис. 3 представлены средние значения коэффициента захвата для модельного зернистого слоя из восьми ($m$ = 8) монослоев гранул для ряда значений $\alpha $, рассчитанные в предположении экспоненциального уменьшения концентрации частиц после каждого монослоя по формуле
(15)
${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = {{\left( {1 - {{4\eta } \mathord{\left/ {\vphantom {{4\eta } \pi }} \right. \kern-0em} \pi }} \right)}^{m}}.$(16)
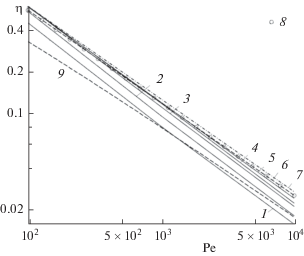
$\eta = (70{{\alpha }^{2}} - 43\alpha + 17.07){\kern 1pt} {\text{P}}{{{\text{e}}}^{{ - 0.74}}}.$Рис. 3.
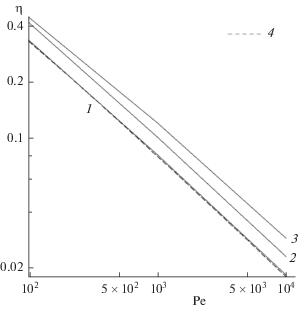
Зависимости среднего коэффициента диффузионного захвата от ${\text{Pe}}$, рассчитанные для модельных гранульных фильтров с $m$ = 8 и $\alpha $ = 0.5236 (1), 0.6 (2), 0.65 (3), 0.68 (4), 0.7 (5); 6 – расчет по формуле Кувабары (8), 7 – по формуле Хаппеля (9), 8 – по (15); 9 – изолированный монослой гранул, $m$ = 1.
На рис. 4 показано, как уменьшаются локальные коэффициенты захвата гранул по глубине фильтра при нескольких значениях числа Пекле. Видно, насколько существенен входной эффект, из-за которого при уплотнении модельного фильтра осаждение на первый монослой гранул все более отличается от осаждения на изолированный монослой (рис. 5). В то же время, как следует из рис. 5, в случае малой плотности упаковки фильтра на его первый слой осаждается столько же наночастиц, сколько и на изолированный монослой.
Рис. 4.
Изменение локального коэффициента диффузионного захвата точечных частиц гранулами по глубине модельного фильтра в зависимости от номера монослоя гранул $N$ для чисел Пекле ${\text{Pe}}$ = 100 (1), 1000 (2), 10000 (3); $\alpha $ = 0.6, $m = 8$.
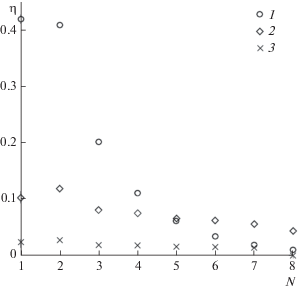
Рис. 5.
Зависимость коэффициента диффузионного захвата наночастиц в первом монослое гранул от числа Пекле при $\alpha $ = 0.345 (1), 0.6 (2), 0.74 (3) и $m$ = 8; 4 – изолированный монослой гранул.
Далее, используя развитый метод получения монодисперсных незаряженных наночастиц [27], мы провели измерения их осаждения в колонках, заполненных монодисперсными металлическими шариками, строго в режиме стоксова течения.
ИЗМЕРЕНИЕ ОСАЖДЕНИЯ ЧАСТИЦ
Для измерения диффузионного осаждения частиц в гранульном фильтре использовались одинаковые стальные шарики диаметром $2{{a}_{1}}$ = 4.0 мм (803 шт.) и $2{{a}_{2}}$ = 4.5 мм (672 шт.), которые помещались в колонки диаметром 30.0 мм между сетками, расстояние между которыми было равно ${{H}_{1}}$ = 64.5 мм и ${{H}_{2}}$ = 75.4 мм. Соответствующая плотность упаковки была равна ${{\alpha }_{1}}$ = 0.59 и ${{\alpha }_{2}}$ = 0.60. Максимальный расход наноаэрозолей через шихту составлял 12 см3/с. В этом случае сохранялся автомодельный режим, в котором течение не зависит от $\operatorname{Re} $. Для данных значений плотности упаковки предельное число Рейнольдса должно быть $\operatorname{Re} $ < 6, а минимальное число Пекле для гранул ${\text{Pe}}$ ~ 100. Размер наночастиц определяли поточным диффузионным методом с помощью сеточных ДБ [28], установленных параллельно колонкам, т.е. использовался метод сравнения проскоков одинаковых наночастиц при одинаковом расходе через сеточные ДБ и через колонки с гранулами.
Измерение проскока наночастиц проводили при одинаковом расходе наноаэрозолей через колонки и через сеточные ДБ в области значений проскока ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} \approx $ 0.35, что позволило исключить погрешности, связанные с возможной немонодисперсностью частиц. (Проскок полидисперсных наночастиц с логнормальным распределением по размерам в области, близкой к ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} \approx $ 0.35, не зависит от степени полидисперсности [29].) Проскок монодисперсных наночастиц через сеточные ДБ при скорости $U$ связан с параметрами сеток и коэффициентом диффузии частиц $D$ простой эмпирической формулой, которая подтверждена численными расчетами в диапазоне чисел Пекле ${\text{Pe}}$ > 100 [28]:
(16)
${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = \exp \left( { - 2{{a}_{{\text{s}}}}{{N}_{{\text{s}}}}{\eta \mathord{\left/ {\vphantom {\eta {{{h}_{{\text{s}}}}}}} \right. \kern-0em} {{{h}_{{\text{s}}}}}}} \right),$(17)
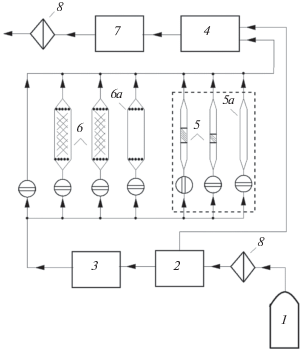
$\eta = 2.7{{\left( {1 - {{\alpha }_{{\text{s}}}}} \right)}^{{ - 1}}}{\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}.$Схема установки показана на рис. 6. Газ – азот особой чистоты или гелий из баллона 1 через расходомер 2 поступает в генератор наночастиц 3 и в укрупнитель 4. Из генератора 3 поток наночастиц по очереди направляется для измерения размеров в сеточные ДБ 5 и в параллельно расположенные колонки с шариками 6 для измерения концентрации наночастиц за колонками $n$. Параллельно ДБ и колонкам установлены пустые колонки с сетками без шариков 5а и ДБ без сеток 6а для определения входной концентрации наночастиц, ${{n}_{0}}$. После выхода из колонок 5 и из ДБ 6 поток наночастиц поступает в укрупнитель 4, где смешивается с потоком, насыщенным парами дибутилфталата, который при $t$ = 100°C проходит через шихту силикагеля, пропитанного дибутилфталатом. В результате смешивания потоков происходит укрупнение наночастиц. Поток полученных крупных частиц с диаметром порядка 1 мкм поступает в счетчик частиц 7.
Рис. 6.
Схема установки: 1 – баллон с газом, 2 – расходомеры, 3 – генератор наночастиц, 4 – укрупнитель, 5 и 5а – диффузионные батареи, 6 и 6а – колонки с гранулами, 7 – счетчик частиц, 8 – фильтры.
Величины проскока частиц из потока азота через две колонки с шариками подбирались так, чтобы они были практически одинаковыми. Проскок молибденовых наночастиц, равный ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ = = 0.38, через обе колонки достигался при $Q$ = = 11.6 см3/с для наночастиц с коэффициентом диффузии $D$ = 3.4 × 10−4 см2/с (радиус $r$ ≅ 6.1 нм).
Оцененные из экспериментальных данных по формуле (6) коэффициенты захвата, равные ${{\eta }_{1}}$ = = 0.068 и ${{\eta }_{2}}$ = 0.064, оказались в согласии со значениями ${{\eta }_{1}}$ = 0.0670, ${{\eta }_{2}}$ = 0.0632, рассчитанными прямым численным моделированием при соответствующих числах Пекле, ${\text{P}}{{{\text{e}}}_{1}}$ = 1650 и ${\text{P}}{{{\text{e}}}_{2}}$ = = 1850.
Близкие к расчетным значения $\eta $ были получены и при осаждении молибденовых наночастиц из потока гелия при $Q$ = 9.1 см3/с. Для наночастиц с $D$ = 9.6 × 10−4 см2/с ($r$ ≅ 5.7 нм) полученные коэффициенты захвата ${{\eta }_{1}}$ = 0.18 и ${{\eta }_{2}}$ = 0.17 удовлетворительно согласуются с расчетными значениями ${{\eta }_{1}}$ = 0.1507 (${\text{P}}{{{\text{e}}}_{1}}$ = 536) и ${{\eta }_{2}}$ = 0.1448 (${\text{P}}{{{\text{e}}}_{2}}$ = = 603). Из полученных значений коэффициентов захвата можно оценить коэффициент $A$ в формуле (7) при подстановке ${\text{P}}{{{\text{e}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}$, который в случае воздуха оказался равен $A$ = 9.5, а в случае гелия $A \cong $ 10. Таким образом, расчетные коэффициенты захвата точечных частиц за счет диффузии в предложенной модели гранульного фильтра удовлетворительно согласуются с литературными и полученными в данной работе экспериментальными данными и с расчетами по другим моделям.
ЗАКЛЮЧЕНИЕ
Предложен модельный гранульный фильтр, состоящий из параллельных монослоев контактирующих сферических гранул с квадратной упаковкой, в которой каждый четный монослой смещен в своей плоскости относительно нечетного на радиус гранулы в двух перпендикулярных направлениях. Эта модель отражает свойства реального фильтра, учитывает контакты между гранулами и позволяет изучать осаждение частиц по разным механизмам с учетом неоднородного трехмерного обтекания гранул.
Применимость модели показана на примере диффузионного осаждения точечных частиц. Полученные результаты расчета осаждения наночастиц согласуются с опубликованными данными и с результатами проведенных нами измерений осаждения монодисперсных наночастиц из азота и гелия в слоях одинаковых металлических шариков. Получено также согласие коэффициентов диффузионного захвата точечных частиц, рассчитанных для этой модели, с расчетами по формулам ячеечной модели в области ${\text{Pe}}$ < 104 при типичных для реальных фильтров значениях $\alpha $.
Добавим также, что полученные результаты могут быть использованы для анализа частиц с помощью гранульных диффузионных батарей. Такие батареи были бы полезны для определения дисперсности более крупных частиц, осаждение которых, тем не менее, происходит по единственному диффузионному механизму. Мы имеем в виду, например, неразбавленные аэрозоли с субмикронными частицами с неизвестными формой, плотностью и коэффициентом преломления. Также такие батареи могут быть использованы в условиях, когда другие средства измерений не применимы – в атмосфере агрессивного газа или при высокой температуре. ДС с миллиметровыми сферическими гранулами обеспечат возможность измерения среднего размера умеренно полидисперсных частиц вплоть до $2r$ = 0.1 мкм. При этом дополнительный учет зацепления для небольшой части частиц размером в несколько десятых долей микрона не отразится заметно на результате. В этом случае придется выбирать такую скорость течения, чтобы не превысить предельное число Рейнольдса, т.е. не нарушить автомодельный режим, не выйти в режим инерционного потока и в то же время исключить влияние гравитации. Также отметим, что предложенная нами модель даст возможность изучать осаждение инерционных частиц в слое гранул. Напомним, что гранульные фильтры предназначены в основном для предварительной очистки, где инерция частиц является основным механизмом осаждения, для расчета которого придется моделировать трехмерные траектории частиц в струях между соприкасающимися гранулами. Этот вопрос будет рассмотрен в следующем сообщении.
Список литературы
Pich J. // Filtration: Principles and Practices. Ed. by Matteson M. and Orr C. N.Y.: Marcel Dekker, 1987. P. 1.
Ужов В.Н., Мягков Б.И. Очистка промышленных газов фильтрами. М.: Химия, 1970.
Tien C., Ramarao B.V. Granular Filtration of Aerosols and Hydrosols. 2nd Ed. Amsterdam: Elsevier, 2007.
Zick A.A., Homsy G.M. // J. Fluid Mech. 1982. V. 115. P. 13.
Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976.
Zaman E., Jalali P. // Physica. Ser. A. 2010. V. 389. P. 205.
Kirsch A.A., Stechkina I.B. // Fundamentals of Aerosol Science / Ed. by Shaw D.T., N.Y.: Wiley-Interscience, 1978, P. 165.
Happel J. // J. Amer. Inst. Chem. Eng. 1958. V. 4. P. 197.
Kuwabara S. // J. Phys. Soc. Jpn. 1959. V. 14. P. 527.
Brinkman H.C. // Appl. Sci. Res., Ser. A. 1947. V. 1. P. 27.
Mann L.A., Goren S.L. // Aerosol Sci. Technol. 1984. V. 3. P. 915.
Wilson E.J., Geancoplis C.J. // Ind. Eng. Chem. 1966. V. 5. P. 9.
Kennard M.L., Meisen A. // Proc. Second Word Filtration Congress, 1979, London. P. 229.
Tardos G.I., Gutfinger C., Abuaf N. // AIChE. J. 1976. V. 22. P. 1147.
Gebhard J., Roth C., Stanhofen W. // J. Aerosol Sci. 1973. V. 4. P. 371.
Lee K.W., Gieseke J.A. // Environ. Sci. Technol. 1979. V. 13. P. 466.
Lee K.W. // J. Aerosol Sci. 1981. V. 12. P. 79.
Kirsch A.A., Fuchs N.A. // J. Phys. Soc. Jpn. 1967. V. 22. P. 1251.
Lee K.W., Read L.D., Gieseke J.A. // J. Aerosol Sci. 1978. V. 9. P. 483.
Ergun S. // Chem. Eng. Prog. 1952. V. 48. P. 89.
Diouri M., Boulaud D., Madelaine G. // Aerosols: Proc. 2nd Int. Aerosol Conf., Berlin. Oxford: Pergamon, 1986. P. 842.
Кирш В.А. // Коллоид. журн. 2013. Т. 75. С. 656.
Кирш В.А., Кирш А.А. // Коллоид. журн. 2016. Т. 78. С. 431.
Кирш В.А., Кирш А.А. // Коллоид. журн. 2017. Т. 79. С. 474.
Martin J.J., McCabe W.L., Monrad C.C. // Chem. Eng. Prog. 1951. V. 47. P. 91.
Sorensen J.P., Stewart W.E. // Chem. Eng. Sci. 1974. V. 29. P. 819.
Кирш А.А., Макавеев П.Ю., Кирш В.А. // Коллоид. журн. 2020. Т. 82. С. 122.
Кирш В.А., Кирш А.А. // Коллоид. журн. 2020. Т. 82. С. 432.
Fuchs N.A. Stechkina I.B., Starosselskii V.I. // Brit. J. Appl. Phys. 1962. V. 13. P. 280.
Кэй Дж., Лэби Т. Таблицы физических и химических постоянных. 2-е изд. М.: Физматгиз, 1962.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


