Коллоидный журнал, 2021, T. 83, № 4, стр. 375-381

Локальные напряжения в сферической щели с дисперсионными взаимодействиями

Е. Н. Бродская^1, *, А. И. Русанов¹

¹ Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия

Поступила в редакцию 02.04.2021
После доработки 08.04.2021
Принята к публикации 09.04.2021

DOI: 10.31857/S0023291221040029

Аннотация

Произведен расчет тензора напряжений Ирвинга–Кирквуда в сферической щели внутри аморфного твердого тела, моделирующей сферическую пору адсорбента с находящимся в ней адсорбатом. Рассчитаны как нормальная, так и тангенциальная компоненты тензора напряжений. Хотя локальное их изменение аналогично, нормальная компонента примерно в два раза больше. При заданной ширине щели компоненты тензора напряжений принимают разные значения на ограничивающих щель поверхностях, и абсолютные значения компонент на поверхности наночастицы больше, чем на поверхности макрофазы. Оценен вклад пустой полости в напряжения сферической пленки, и показано, что он незначителен. Произведен расчет расклинивающего давления сферической щели, и проведено сопоставление со случаем плоскопараллельной щели. Средняя разница двух функций составляет примерно 20%. Видно, что кривизна щели приводит к увеличению абсолютной величины расклинивающего давления на всем ее протяжении.

ВВЕДЕНИЕ

Теоретическое исследование поверхностных сил началось с суммирования парного потенциала дисперсионных взаимодействий между молекулами сортов p и q

(1)

${{\Phi }_{{pq}}}(R) = - {{A}_{{pq}}}{{R}^{{ - 6}}},$

где R – расстояние между молекулами и A – постоянная. Таким путем Гамакер [1] рассчитал силу F взаимодействия между двумя шарами, между шаром и полубесконечным твердым телом с плоской поверхностью и между двумя плоскопараллельными поверхностями (на единицу поверхности S). Последняя, пожалуй, является наиболее известным результатом классической коллоидной науки

(2)

$\Pi = \frac{F}{S} = - \frac{{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}}}{{6{{H}^{3}}}} \equiv - \frac{C}{{{{H}^{3}}}},$

и постоянная $C \equiv {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} \mathord{\left/ {\vphantom {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} 6}} \right. \kern-0em} 6}$ теперь носит имя Гамакера (c – молекулярная плотность взаимодействующих тел 1 и 2, H – расстояние между поверхностями). Дерягин [2] назвал величину Π расклинивающим давлением с общим определением

(3)

$\Pi = p - {{p}^{\alpha }},$

где p – давление на поверхностях взаимодействующих тел, а ${{p}^{\alpha }}$ – давление в материнской фазе пленки, находящейся с ней в равновесии (в случае вакуума ${{p}^{\alpha }} = 0$ и Π = p < 0). Наличие расклинивающего давления отличает тонкие пленки от толстых, и его изучение является одним из центральных направлений коллоидной науки [3].

Во многих задачах с участием поверхностных сил важным является не только сила взаимодействия наночастиц как целых, но и распределение сил в самих частицах. Это распределение задается полем тензора напряжений $\hat {E}$ (шляпка – символ тензора), вычисление которого также стало задачей коллоидной науки. Вычисления такого рода можно осуществлять методом статистической механики с помощью тензора напряжений Ирвинга–Кирквуда [4]

(4)

$\begin{gathered} \hat {Е}({\mathbf{r}}) = - kT\sum\limits_p {{{\rho }_{p}}({\mathbf{r}})\hat {1}} + \frac{1}{2}\sum\limits_{p{\kern 1pt} > {\kern 1pt} q} {\int {d{\mathbf{R}}} \frac{{{\mathbf{R}} \times {\mathbf{R}}}}{R}\Phi _{{pq}}^{'}(R)} \times \\ \times \,\,\int\limits_0^1 {d\eta \rho _{{pq}}^{{(2)}}({\mathbf{r}} - \eta {\mathbf{R}},{\mathbf{r}} - \eta {\mathbf{R}} + {\mathbf{R}})} , \\ \end{gathered} $

где $\hat {E}({\mathbf{r}})$ – значение тензора напряжений в точке r; k – постоянная Больцмана; T – температура; ${{\rho }_{p}}({\mathbf{r}})$ – одночастичная функция распределения (локальная плотность) частиц сорта p; $\hat {1}$ – единичный тензор; R – вектор, соединяющий две взаимодействующие частицы с расстоянием R между ними и проходящий через точку r (запись ${\mathbf{R}} \times {\mathbf{R}}$ символизирует прямое векторное произведение, являющееся тензором); $\Phi _{{pq}}^{'}(R)$ – производная от потенциала парного взаимодействия (1) частиц сортов p и q (т.е. сила взаимодействия этих частиц); $\rho _{{pq}}^{{(2)}}({\mathbf{r}} - \eta {\mathbf{R}},{\mathbf{r}} - \eta {\mathbf{R}} + {\mathbf{R}})$ – двухчастичная функция распределения для частиц, находящихся одновременно в точках ${{{\mathbf{r}}}_{1}} = {\mathbf{r}} - \eta {\mathbf{R}}$ и ${{{\mathbf{r}}}_{2}} = {\mathbf{r}} - \eta {\mathbf{R}} + {\mathbf{R}}$ по разные стороны от единичной площадки с координатой r (что регулируется вспомогательной переменной η). При работе с жидкостями обычно используют не тензор напряжений, а тензор давления $\hat {p}({\mathbf{r}}),$ который отличается от тензора напряжений только знаком:

(5)

$\hat {p}\left( {\mathbf{r}} \right) \equiv - \hat {E}({\mathbf{r}}).$

Первым применением тензора напряжений Ирвинга–Кирквуда в коллоидной науке был расчет тензора давления и расклинивающего давления в плоской тонкой жидкой пленке [5]. Разработанный там алгоритм расчета многократно использовался в дальнейшем для описания поверхностных сил в телах различной конфигурации (см. обзор [6]). Важным был переход (уже в 21 веке) к телам ограниченных размеров и, в частности, к клиновидным пленкам, позволивший сформулировать термодинамику трещин [7] в дополнение к усовершенствованию теории разрушения твердых тел вообще [8]. Нужно отметить, что оперировать с тензором напряжений Ирвинга–Кирквуда непросто, и подобных работ в мировой литературе чрезвычайно мало. Можно сказать, что это направление стало брендом петербургской термодинамической школы.

Одним из примеров твердых тел, для которых исследование распределения механических напряжений особенно важно, являются пористые адсорбенты. Первые расчеты с применением тензора напряжений Ирвинга–Кирквуда были проведены в работах [9, 10] для плоских (щелевидных), цилиндрических и сферических пор. Полученные там результаты вновь использовались при создании теории сорбострикции [11] – механохимического явления деформации пористого тела в процессе адсорбции. Поскольку вещество всегда адсорбируется на стенках поры, сама пора все время остается пустой в своей средней части. Но интересно рассмотреть и случай, когда пора не пустая. Например, в случае сферической полости считать, что в ее середине находится шарик какого-то вещества. Здесь сразу возникает образ сферической пустой пленки, для которой расчетов с применением тензора напряжений Ирвинга–Кирквуда еще не было, хотя интерес к расклинивающему давлению определенно имеется [12, 13]. В данном сообщении мы на основе формулы (4) проведем расчет напряжений именно для такого объекта. Чтобы можно было использовать в расчетах интегрирование, мы должны принять, что объект не является монокристаллом (иначе замена суммирования по кристаллическим плоскостям интегрированием давало бы существенную ошибку [14]). Но число компонентов ограничивать не будем.

РАСЧЕТНАЯ ПРОЦЕДУРА

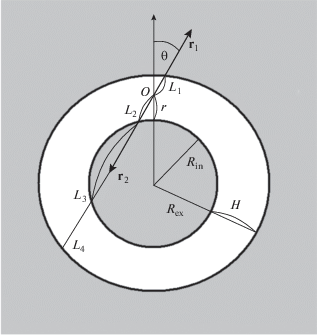
Рассматриваемая система изображена схематически на рис. 1. Сферическая щель заключена между радиусами ${{R}_{{\operatorname{ex} }}}$ и ${{R}_{{\operatorname{in} }}}$ и имеет ширину $H$ = = ${{R}_{{\operatorname{ex} }}}$ – ${{R}_{{\operatorname{in} }}}.$ Расчетная точка O лежит внутри щели. Из пары взаимодействующих молекул одна находится в наружной фазе и указана вектором ${{{\mathbf{r}}}_{1}},$ а другая – во внутренней фазе (вектор ${{{\mathbf{r}}}_{2}}$). Оба вектора исходят из точки O и лежат на одной прямой. Поскольку точка O лежит в пустоте, первое слагаемое в правой части (4) исчезает. Кроме того, если рассматривать точку r₁ только во внешней части пространства по отношению к элементарной площадке в расчетной точке, а точку r₂ – во внутренней, то множитель 1/2 перед интегралом следует опустить. В результате тензор напряжений Ирвинга–Кирквуда принимает вид

(6)

$\begin{gathered} \hat {Е}({\mathbf{r}}) = \sum\limits_{p{\kern 1pt} > {\kern 1pt} q} {\int {d{\mathbf{R}}} \frac{{{\mathbf{R}} \times {\mathbf{R}}}}{R}\Phi _{{pq}}^{'}(R)} \times \\ \times \,\,\int\limits_0^1 {d\eta \rho _{{pq}}^{{(2)}}({\mathbf{r}} - \eta {\mathbf{R}},{\mathbf{r}} - \eta {\mathbf{R}} + {\mathbf{R}})} . \\ \end{gathered} $

Рис. 1.

Схема сферической щели.

Тензор сферически симметричной системы проще всего отображается в сферической системе координат r, ϑ, φ с началом в центре системы. Тогда из шести компонент тензора ненулевыми оказываются только диагональные компоненты, из которых радиальная компонента становится нормальной ${{E}_{{rr}}} \equiv {{E}_{\operatorname{N} }},$ а две равные угловые – тангенциальными, ${{E}_{{\vartheta \vartheta }}} = {{E}_{{\varphi \varphi }}} \equiv {{E}_{\operatorname{T} }}.$ Условие механического равновесия

(7)

$\nabla \hat {E} = 0$

в случае сферической симметрии сводится к равенству

(8)

$\frac{{d({{r}^{2}}{{E}_{\operatorname{N} }})}}{{d{{r}^{2}}}} = {{E}_{\operatorname{T} }}.$

Обе эти составляющие тензора напряжений нам предстоит вычислить, а соотношение (8) послужит для контроля правильности результатов.

Приступим непосредственно к расчету. Поместим начало сферической системы координат в расчетную точку O и для удобства вычислений перейдем от переменных R и η (одна векторная и одна скалярная переменная, всего 4 переменных) к r₁ и r₂ (также 4 скалярных переменных)

(9)

${\mathbf{R}} = \frac{{{{r}_{1}} + {{r}_{2}}}}{{{{r}_{1}}}}{{{\mathbf{r}}}_{1}},\,\,\,\,R = {{r}_{1}} + {{r}_{2}},\,\,\,\,\eta = \frac{{{{r}_{2}}}}{{{{r}_{1}} + {{r}_{2}}}}{\kern 1pt} ,\,\,D = \frac{{{{r}_{1}} + {{r}_{2}}}}{{r_{1}^{2}}}{\kern 1pt} ,$

где D – якобиан данного преобразования. Условие, чтобы прямая, соединяющая молекулы 1 и 2, проходила через расчетную точку, накладывает ограничения на пределы интегрирования ${{L}_{k}}$ выбранных переменных, а именно (рис. 1):

(10a)

$\begin{gathered} {{L}_{1}} = - \,({{R}_{{{\text{in}}}}} + r)\cos \vartheta + \\ + \,\,{{\left[ {{{{({{R}_{{{\text{in}}}}} + r)}}^{2}}{{{\cos }}^{2}}\vartheta + (H - r)(2{{R}_{{{\text{in}}}}} + H + r)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{L}_{4}} = ({{R}_{{{\text{in}}}}} + r)\cos \vartheta + \\ + \,\,{{\left[ {{{{({{R}_{{{\text{in}}}}} + r)}}^{2}}{{{\cos }}^{2}}\vartheta + (H - r)(2{{R}_{{{\text{in}}}}} + H + r)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

(10b)

$\begin{gathered} {{L}_{{2,3}}} = ({{R}_{{{\text{in}}}}} + r)\cos \vartheta \mp \\ \mp \,\,{{\left[ {{{{({{R}_{{{\text{in}}}}} + r)}}^{2}}{{{\cos }}^{2}}\vartheta - r(2{{R}_{{{\text{in}}}}} + r)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

(10c)

$\begin{gathered} 0 < \varphi < 2\pi ,\,\,\,\,0 < \vartheta < {{\vartheta }_{{\lim }}} = \arcsin \frac{{{{R}_{{{\text{in}}}}}}}{{{{R}_{{{\text{in}}}}} + r}}, \\ \cos {{\vartheta }_{{{\text{lim}}}}} = \frac{{{{{\left[ {2r{{R}_{{{\text{in}}}}} + {{r}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{R}_{{{\text{in}}}}} + r}},\,\,\,\,{{R}_{{{\text{in}}}}} < r < {{R}_{{{\text{ex}}}}}. \\ \end{gathered} $

Величины L_k (k = 1, 4) определяют расстояния от точки r (начала координат) до пересечения линии, проходящей через точки 1 и 2, с ограничивающими щель поверхностями. Учитывая симметрию относительно угла φ, тензор напряжений в этих переменных запишем в следующем виде:

(11)

$\begin{gathered} \hat {E}(r) = 12\sum\limits_{p,q} {{{A}_{{pq}}}} \int\limits_0^\pi {d\varphi } \int\limits_0^{{{\vartheta }_{{\lim }}}} {\sin \vartheta d\vartheta } \times \\ \times \,\,\left[ {\int\limits_{{{L}_{2}}}^{{{L}_{3}}} {d{{r}_{2}}} \int\limits_{{{L}_{1}}}^\infty {d{{r}_{1}}\frac{{\hat {\kappa }(\varphi ,\vartheta )}}{{{{{({{r}_{1}} + {{r}_{2}})}}^{5}}}}\rho _{{pq}}^{{(2)}}} + \int\limits_{{{L}_{4}}}^\infty {d{{r}_{2}}} \int\limits_{{{L}_{1}}}^\infty {d{{r}_{1}}\frac{{\hat {\kappa }(\varphi ,\vartheta )}}{{{{{({{r}_{1}} + {{r}_{2}})}}^{5}}}}\rho _{{pq}}^{{(2)}}} } \right], \\ \end{gathered} $

где новый тензор $\hat {\kappa }(\varphi ,\vartheta )$ имеет диагональные компоненты

(12)

$\begin{gathered} {{\kappa }_{{rr}}} = {{\cos }^{2}}\vartheta ,\,\,\,\,{{\kappa }_{{\vartheta \vartheta }}} = {{\sin }^{2}}\vartheta {{\cos }^{2}}\varphi , \\ {{\kappa }_{{\varphi \varphi }}} = {{\sin }^{2}}\vartheta {{\sin }^{2}}\varphi {\kern 1pt} . \\ \end{gathered} $

Первое слагаемое в квадратных скобках выражения (11) соответствует взаимодействию молекул фазы β (наночастица внутри сферической полости) с молекулами фазы γ, а второе слагаемое учитывает взаимодействие молекул фазы γ друг с другом. В соответствии с этим разделим тензор напряжений $\hat {E}(r)$ на две части, обозначив их как ${{\hat {E}}_{1}}(r)$ и ${{\hat {E}}_{2}}(r){\text{:}}$

(13)

$\hat {E}(r) = {{\hat {E}}_{1}}(r) + {{\hat {E}}_{2}}(r).$

Второй член в правой части (13) представляет собой тензор напряжений в пустой сферической полости, и его появление в данной системе является характерной особенностью искривленной щели.

Начнем рассмотрение с первого слагаемого. Поскольку взаимодействующие молекулы находятся на расстояниях, превышающих ширину щели H, заменим двухчастичную функцию произведением соответствующих плотностей компонентов фаз β и γ. Теперь несложно провести интегрирование по φ, r₁ и r₂. Для тензора $\hat {\kappa }(\varphi ,\vartheta )$ нужно учитывать (12).

Поскольку от угла φ зависят только компоненты тензора $\hat {\kappa }(\varphi ,\vartheta ),$ то, проведя интегрирование по этому углу, получим множитель π и еще один тензор ${{\hat {\kappa }}_{1}}(\vartheta )$ с компонентами

(14)

${{\kappa }_{{1rr}}} = {{\cos }^{2}}\vartheta ,\,\,\,\,{{\kappa }_{{1\vartheta \vartheta }}} = {{\kappa }_{{1\varphi \varphi }}} = {{{{{\sin }}^{2}}\vartheta } \mathord{\left/ {\vphantom {{{{{\sin }}^{2}}\vartheta } 2}} \right. \kern-0em} 2}.$

Далее, легко выполнить интегрирование по r₁ и r₂, в результате которого получим следующее выражение для тензора напряжений:

(15)

$\begin{gathered} {{{\hat {E}}}_{1}}(r) = \pi \sum\limits_{p,q} {{{A}_{{pq}}}\rho _{p}^{\beta }\rho _{q}^{\gamma }} \int\limits_{\cos {{\vartheta }_{{\lim }}}}^1 {{{{\hat {\kappa }}}_{1}}(\vartheta ){\kern 1pt} d\cos \vartheta } \times \\ \times \,\,\left[ {\frac{1}{{{{{({{L}_{1}} + {{L}_{2}})}}^{3}}}} - \frac{1}{{{{{({{L}_{1}} + {{L}_{3}})}}^{3}}}}} \right]. \\ \end{gathered} $

Очевидно, что помимо переменной r, определяющей положение точки в щели, интеграл, а, следовательно, и тензор напряжений будут зависеть также от величин H и R_in, характеризующих щель. Для дальнейшего анализа будем использовать переменные

(16)

$x \equiv {H \mathord{\left/ {\vphantom {H {{{R}_{{{\text{in}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{in}}}}}}},\,\,\,\,y \equiv {r \mathord{\left/ {\vphantom {r {{{R}_{{{\text{in}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{in}}}}}}},\,\,\,\,z \equiv \cos \vartheta ,$

из которых переменная x характеризует относительную ширину щели, а переменная y – относительное расстояние до твердой наносферы (фазы β). В этих переменных величины L_k принимают следующий вид:

(17)

$\begin{gathered} {{L}_{1}} = - {{R}_{{{\text{in}}}}}(1 + y)z + \\ + \,\,{{R}_{{{\text{in}}}}}{{\left[ {{{{(1 + y)}}^{2}}{{z}^{2}} + (x - y)(2 + x + y)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{L}_{{2,3}}} = {{R}_{{{\text{in}}}}}(1 + y)z \mp {{R}_{{{\text{in}}}}}{{\left[ {{{{(1 + y)}}^{2}}{{z}^{2}} - y(2 + y)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $

Наконец, тензор напряжений можно записать как

(18)

${{\hat {E}}_{1}}(r,H,{{R}_{{{\text{in}}}}}) = \frac{{C{}_{1}}}{{R_{{{\text{in}}}}^{3}}}\hat {F}(x,y),$

где введены постоянный множитель

(19)

${{C}_{1}} \equiv \pi \sum\limits_{p,q} {{{A}_{{pq}}}\rho _{p}^{\beta }\rho _{q}^{\gamma }} $

и тензорный интеграл

(20)

$\begin{gathered} \hat {F}(x,y) = \frac{1}{{R_{i}^{3}{{{\left( {2 + x} \right)}}^{3}}{{x}^{3}}}}\int\limits_{\frac{{{{{(2y + {{y}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{1 + y}}}^1 {dz} {{{\hat {\kappa }}}_{1}}(z) \times \\ \times \,\,\left[ {{{{\left( {{{L}_{1}} + {{L}_{2}}} \right)}}^{3}} - {{{\left( {{{L}_{1}} + {{L}_{3}}} \right)}}^{3}}} \right]. \\ \end{gathered} $

С учетом новых переменных выражение в квадратных скобках преобразуется к виду

(21)

$\begin{gathered} {{\left( {{{L}_{1}} + {{L}_{2}}} \right)}^{3}} - {{\left( {{{L}_{1}} + {{L}_{3}}} \right)}^{3}} = 8R_{{{\text{in}}}}^{3}{{(1 + y)}^{3}} \times \\ \times \,\,{{\left[ {{{z}^{2}} - \frac{{y(2 + y)}}{{{{{(1 + y)}}^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {{{z}^{2}} - 1 + \frac{{3{{{(1 + x)}}^{2}} + 1}}{{4{{{(1 + y)}}^{2}}}}} \right). \\ \end{gathered} $

Соответственно составляющие тензорного интеграла $\hat {F}(x,y)$ будут задаваться следующими функциями:

(22)

$\begin{gathered} {{F}_{\operatorname{N} }}(x,y) = \frac{{8{{{(1 + y)}}^{3}}}}{{{{{\left( {2 + x} \right)}}^{3}}{{x}^{3}}}}\int\limits_{\frac{{\sqrt {2y + {{y}^{2}}} }}{{1 + y}}}^1 {{{z}^{2}}} {{\left[ {{{z}^{2}} - \frac{{2y + {{y}^{2}}}}{{{{{(1 + y)}}^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left( {{{z}^{2}} - 1 + \frac{{3{{{(1 + x)}}^{2}} + 1}}{{4{{{(1 + y)}}^{2}}}}} \right)dz, \\ \end{gathered} $

(23)

$\begin{gathered} {{F}_{{\text{T}}}}(x,y) = \frac{{4{{{(1 + y)}}^{3}}}}{{{{{\left( {2 + x} \right)}}^{3}}{{x}^{3}}}}\int\limits_{\frac{{\sqrt {2y + {{y}^{2}}} }}{{1 + y}}}^1 {dz} (1 - {{z}^{2}}) \times \\ \times \,\,{{\left[ {{{z}^{2}} - \frac{{2y + {{y}^{2}}}}{{{{{(1 + y)}}^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {{{z}^{2}} - 1 + \frac{{3{{{(1 + x)}}^{2}} + 1}}{{4{{{(1 + y)}}^{2}}}}} \right). \\ \end{gathered} $

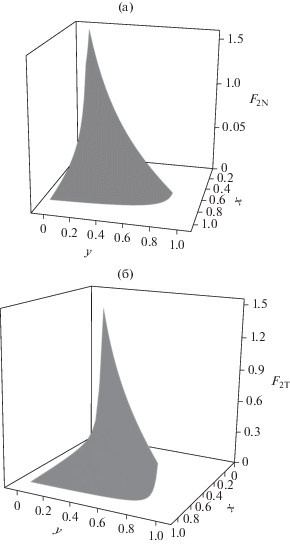
Функция $\hat {F}(x,y)$ определяет локальное поведение тензора давления. Чтобы получить значения для компонент тензора напряжения, компоненты этого интеграла следует домножить на коэффициент $\frac{{{{C}_{1}}}}{{R_{{{\text{in}}}}^{3}}}.$ Интегралы в (22) и (23) можно вычислить в явном виде, но окончательные формулы чрезвычайно громоздки, и мы их приводить не будем. При заданных x и y данный тензорный интеграл можно рассчитать численно. На рис. 2 и 3 приведены нормальная и тангенциальная компоненты этого интеграла для двух интервалов переменных x и y, то есть для H и r.

Рис. 2.

Компоненты тензора $\hat {F}(x,y)$ в сферической щели: (а) нормальная, (б) тангенциальная. Для 0.1 < < x = H/R_in < 1, 0 < y = r/R_in < x.

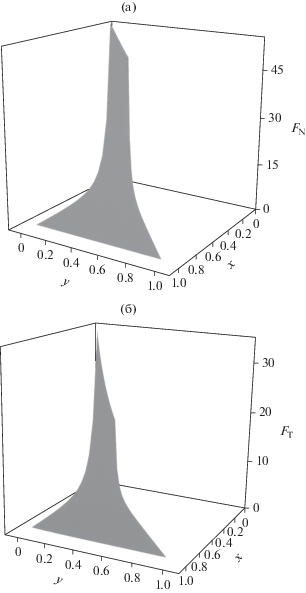
Рис. 3.

Компоненты тензора $\hat {F}(x,y)$ в сферической щели: (а) нормальная, (б) тангенциальная. Для 0.5 < < x = H/R_in < 1, 0 < y = r/R_in < x.

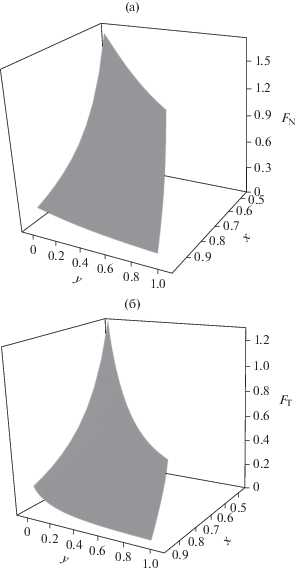
Хотя локальное поведение обеих компонент тензора напряжений аналогично, абсолютные значения нормальной компоненты почти в два раза превосходят соответствующие значения тангенциальной. Очевидно, что зависимость обеих компонент от ширины щели по сравнению с зависимостью от расстояния до твердой поверхности является более сильной, особенно в области малых значений относительной ширины. Следует отметить, что при заданной ширине щели компоненты тензора напряжений принимают разные значения на ограничивающих щель поверхностях (y = 0 и y = x), и абсолютные значения компонент на поверхности наночастицы (y = 0) больше, чем на другой поверхности (y = x). Эта особенность характеризует влияние кривизны щели на локальное давление, что особенно ярко проявляется в непостоянстве нормальной компоненты в такой щели по сравнению с плоскопараллельной щелью.

В области больших значений радиуса наночастицы R_in для тензора $\hat {F}(x,y)$ можно получить следующие предельные зависимости:

(24)

$\begin{gathered} {{F}_{\operatorname{N} }}(x,y)\xrightarrow[{{{R}_{{{\text{in}}}}} \to \infty }]{}\frac{1}{{6{{x}^{3}}}} + \frac{{{x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2} - y}}{{4{{x}^{3}}}}, \\ {{F}_{T}}(x,y)\xrightarrow[{{{R}_{{{\text{in}}}}} \to \infty }]{}\frac{1}{{24{{x}^{3}}}} + \frac{{{x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2} - y}}{{4{{x}^{3}}}}. \\ \end{gathered} $

Отсюда легко записать предельные зависимости для компонент тензора напряжений

(25)

$\begin{gathered} {{E}_{{1\operatorname{N} }}}(r,H,{{R}_{{{\text{in}}}}}) = \frac{C}{{6{{H}^{3}}}}\left( {1 + 3\frac{{H - 2r}}{{4{{R}_{{{\text{in}}}}}}}} \right), \\ {{E}_{{1\operatorname{T} }}}(r,H,{{R}_{{{\text{in}}}}}) = \frac{C}{{24{{H}^{3}}}}\left( {1 + 3\frac{{H - 2r}}{{{{R}_{{{\text{in}}}}}}}} \right). \\ \end{gathered} $

Как и должно быть, главные члены этой зависимости совпадают с известными формулами для плоскопараллельной щели (формула Гамакера (2)). А с учетом линейного вклада от кривизны щели выражения (25) удовлетворяют условию равновесия (8) для сферической симметричной системы. Относительная величина поправки одинакова для обеих компонент. Следует отметить, что вблизи наночастицы линейная поправка на кривизну поверхности положительна, но меняет знак во второй половине щели при приближении к внешней границы щели. Это согласуется с отмеченным выше общим поведением компонент тензора, когда их абсолютные значения выше вблизи внутренней границы щели (около нуля). Более отчетливо это видно на рис. 3, где отдельно приведены функции для более широких щелей (H > 0.5R_in).

ТЕНЗОР НАПРЯЖЕНИЙ В ПУСТОЙ СФЕРИЧЕСКОЙ ПОЛОСТИ

Займемся теперь вторым тензором в выражении (13), то есть ${{\hat {E}}_{2}}(r).$ Процедура рассмотрения во многом аналогична проделанной для ${{\hat {E}}_{1}}(r).$ Однако возникает проблема при замене двухчастичной функции на произведение частичных плотностей, так как уже нет ограничения на минимальное расстояние между рассматриваемыми молекулами в виде ширины щели. Тем не менее, далее мы будем использовать произведение частичных плотностей вместо двухчастичной функции, подразумевая, что следует накладывать какое-то ограничение на расстояние рассматриваемой точки до поверхности. С учетом этого условия можно сразу записать следующую формулу для тензора напряжений в сферической полости:

(26)

${{\hat {E}}_{2}}(r) = \pi \sum\limits_{p,q} {{{A}_{{pq}}}\rho _{p}^{\gamma }\rho _{q}^{\gamma }} \int\limits_0^1 {\frac{{{{{\hat {\kappa }}}_{1}}(\vartheta )d\cos \vartheta }}{{{{{({{L}_{2}} + {{L}_{4}})}}^{3}}}}} .$

Вводя по аналогии с (19) постоянный множитель C₂,

(27)

${{C}_{2}} \equiv \pi \sum\limits_{p,q} {{{A}_{{pq}}}\rho _{p}^{\gamma }\rho _{q}^{\gamma }} ,$

и подставив в интеграл выражения (10a) для L₂ и L₄, запишем для ${{\hat {E}}_{2}}(r)$ следующее выражение:

${{\hat {E}}_{2}}(r) = {{С}_{2}}\int\limits_0^1 {\frac{{{{{\hat {\kappa }}}_{1}}(\vartheta )d\cos \vartheta }}{{{{{\left( {2{{{\left[ {{{{({{R}_{{{\text{in}}}}} + r)}}^{2}}{{{\cos }}^{2}}\vartheta + (H - r)(2{{R}_{{{\text{in}}}}} + H + r)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)}}^{3}}}}} .$

Учитывая определения новых переменных (16), перепишем (28) в виде

(29)

$\begin{gathered} {{{\hat {E}}}_{2}}(r) = \\ = \frac{{{{С}_{2}}}}{{8R_{{{\text{in}}}}^{3}}}\int\limits_0^1 {\frac{{{{{\hat {\kappa }}}_{1}}(z)dz}}{{{{{\left( {{{{\left[ {{{{(1 + y)}}^{2}}{{z}^{2}} + (x - y)(2 + x + y} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)}}^{3}}}}} . \\ \end{gathered} $

Интегралы в выражении (29) вычисляются аналитически. В результате получим окончательные формулы для тензора давления в сферической полости

(30)

${{\hat {E}}_{2}}(r) = \frac{{{{С}_{2}}}}{{R_{{{\text{in}}}}^{3}}}{{\hat {F}}_{2}}(x,y),$

где нормальная и тангенциальная составляющие тензора ${{\hat {F}}_{2}}(x,y)$ даются выражениями

(31)

$\begin{gathered} {{F}_{{2\operatorname{N} }}}(x,y) = - \frac{1}{{8(1 + x){{{(1 + y)}}^{2}}}} + \\ + \,\,\frac{1}{{16{{{(1 + y)}}^{3}}}}\ln \frac{{2 + x + y}}{{x - y}}, \\ \end{gathered} $

(32)

$\begin{gathered} {{F}_{{2\operatorname{T} }}}(x,y) = \frac{{(1 + x)}}{{16(x - y)(2 + x + y){{{(1 + y)}}^{2}}}} - \\ - \,\,\frac{1}{{32{{{(1 + y)}}^{3}}}}\ln \frac{{2 + x + y}}{{x - y}}. \\ \end{gathered} $

Функции (31) и (32) расходятся при y → x, когда расчетная точка приближается к поверхности. Одной из причин, как обсуждалось выше, является пренебрежение корреляциями в двухчастичной функции. На рис. 4 показаны эти функции. Следует подчеркнуть, что эти функции описывают поведение тензора только в той части сферической полости, которая окружает сферическую наночастицу, то есть расстояние расчетной точки от ее центра меняется в пределах от R_in до R_ex. Вклады растут при уменьшении ширины щели (x → 0) и при приближении к внешней границы щели (y → x). По сравнению с вкладами от взаимодействия твердой наночастицы с фазой γ, приведенными на рис. 2 и 3 , данные вклады более чем на порядок ниже. Поэтому при качественных оценках поведения давления в сферической щели их можно не учитывать.

Рис. 4.

Компоненты тензора ${{\hat {F}}_{2}}(x,y)$ в сферической щели: (а) нормальная, (б) тангенциальная. Для 0.1 < < x = H/R_in < 1, 0 < y = r/R_in < x.

РАСКЛИНИВАЮЩЕЕ ДАВЛЕНИЕ

Появляющаяся локальная зависимость нормальной компоненты в сферической щели ставит вопрос об определении расклинивающего давления Π в ней, которое для плоскопараллельной щели определяется формулой (3), а для случая пустой щели просто равно нормальному давлению:

(33)

$\Pi = {{p}_{\operatorname{N} }} = - {{E}_{\operatorname{N} }}.$

Чтобы оценивать расклинивающее давление в сферической щели, необходимо выбрать поверхность, для которой рассчитывать нормальное давления. Следуя работам [15, 16], в качестве такой поверхности выберем поверхность твердой наночастицы, то есть внутреннюю поверхность сферической щели (r = 0, y = 0), в формулах (22) для F_N и (31) для F_2N, которые примут простой вид:

(34)

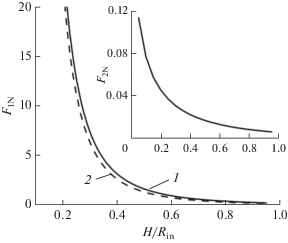
${{F}_{{\text{N}}}} = \frac{1}{{{{x}^{3}}{{{\left( {1 + {x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2}} \right)}}^{3}}}}\left( {\frac{1}{6} + \frac{{6x + 3{{x}^{2}}}}{{16}}} \right),$

(35)

${{F}_{{2{\text{N}}}}} = - \frac{1}{{8(1 + x)}} + \frac{1}{{16}}\ln \frac{{2 + x}}{x}.$

Для сравнения на рис. 5 приведены абсолютные значения расклинивающего давления в сферической и плоскопараллельной щелях по Гамакеру [1] (формула (2)). Средняя разница двух функций составляет примерно 20%. Очевидно, что функция F_2N практически на два порядка меньше F_N. Таким образом, влияние кривизны внешней поверхности на расклинивающее давление оказывается несущественным, что является следствием его определения как давления на внутренней поверхности сферической щели. Таким образом, можно прийти к выводу, что кривизна щели приводит к увеличению абсолютной величины расклинивающего давления на всем ее протяжении, как и следует из приведенных выше оценок линейного вклада кривизны.

Рис. 5.

Вклады в расклинивающее давление F_N = |Π|/C: 1 – для сферической щели, 2 – для плоской. На вставке приведен вклад от сферической полости.

ЗАКЛЮЧЕНИЕ

Проведенные расчеты на примере дисперсионных сил показывают, что наличие пустой сферической полости в твердом теле создает сравнительно небольшие напряжения. Помещение шарика внутрь полости и появление таким образом сферической щели резко меняет картину и приводит к существенным напряжениям. Такие напряжения могут деформировать пористые адсорбенты в ходе адсорбции, что и объясняет известное явление сорбострикции. Параллельно сделанные оценки вносят лепту в теорию пленок. Удивительно, что сферическая пустая пленка отличается от плоскопараллельной по расклинивающему давлению лишь на 20%, причем имеет больший эффект, чем плоская.

Список литературы

Hamaker H.C. // Physica. 1937. V. 4. P. 1058.
Derjaguin B.V. // Коллоид. журн. 1955. Т. 17. С. 207.
Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. М.: Наука, 1985.
Irving J.H., Kirkwood J.G. // J. Chem. Phys. 1950. V. 18. P. 817.
Русанов А.И., Куни Ф.М. // Исследования в области поверхностных сил. Ред. Дерягин Б.В. М.: Наука, 1967. С. 129.
Rusanov A.I., Brodskaya E.N. // Russ. Chem. Rev. 2019. V. 88. P. 837.
Rusanov A.I. // Surf. Sci. Rep. 2012. V. 67. P. 117.
Rusanov A.I. // Int. J. Fract. 2010. V. 161. P.53.
Куни Ф.M., Русанов A.И. // Коллоид. журн. 1971. Т. 33. С. 238.
Куни Ф.М., Русанов А.И. // Физическая адсорбция из многокомпонентных фаз. Ред. Дубинин М.М., Серпинский В.В. М.: Наука, 1972. С. 182.
Русанов А.И., Куни Ф.М. // Журн. общей химии. 2007. Т. 77. С. 404.
Shchekin A.K., Gosteva L.A., Lebedeva T.S. // Physica A. 2020. V. 560. P. 125105.
Shchekin A.K., Gosteva L.A., Tatyanenko D.V. // Colloids Surf. A. 2021. V. 615. P. 126277.
Rusanov A.I. // Surf. Sci. Rep. 2014. V. 69. P. 296.
Rusanov A.I., Shchekin A.K. // Mol. Phys. 2005. V. 103. P. 2911.
Rusanov A.I., Shchekin A.K. // Mol. Phys. 2007. V. 105. P. 3185.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал