Координационная химия, 2019, T. 45, № 6, стр. 359-365
Компьютерное моделирование деструкции органических комплексов лантанидов под действием ионизирующего излучения
С. В. Оболенский 1, *, А. В. Кукинов 1, 2, Т. В. Балашова 2, А. Н. Труфанов 3, М. Н. Ивин 3, О. В. Кузнецова 2, М. Н. Бочкарев 1, 2, **
1 Нижегородский государственный университет им. Н.И. Лобачевского
Нижний Новгород, Россия
2 Институт металлоорганической химии им. Г.А. Разуваева РАН
Нижний Новгород, Россия
3 НИИ измерительных систем им. Ю.Е. Седакова
Нижний Новгород, Россия
* E-mail: obolensk@rf.unn.ru
** E-mail: mboch@iomc.ras.ru
Поступила в редакцию 06.07.2018
После доработки 21.11.2018
Принята к публикации 03.12.2018
Аннотация
Расчет дефектов в структуре комплексов Sc, La, Nd, Sm, Tb и Yb с замещенными фенолятными и нафтолятными лигандами, образующихся при воздействии нейтронов со средней энергией 2 МэВ, показал, что смещение атомов-мишеней зависит от их массы и может достигать 1 мкм для O, N, S. Аналогичный результат получен при расчете деструкции комплекса Eu(TTA)3(DME)2 (HTTA = теноилтрифторацетон). Однако обработка образцов n,γ-излучением не привело к их разрушению. Обсуждаются возможные причины обнаруженного расхождения расчетных и экспериментальных данных.
Полупроводники находят широкое применение в науке и технике, в том числе в устройствах и приборах, которые могут быть подвержены действию радиационных излучений, будучи использованы в космических аппаратах, ядерных энергетических установках различной конструкции и/или в военной технике. Общим для этих материалов является их состав – все они относятся к классу неорганических веществ. Органические соединения, в частности органические комплексы редкоземельных металлов, по сравнению с неорганическими аналогами обладают рядом преимуществ, что делает их перспективными для применения во многих специальных областях [1]. В связи с этим возникает задача определения уровня радиационной стойкости органических полупроводников к воздействию гамма-квантов и нейтронов.
С целью восполнения отмеченного пробела мы выполнили расчет сечений и моделирование процессов взаимодействия нейтронов спектра деления ядер урана со всеми типами атомов, содержащихся в фенолятных, нафтолятных и подобных комплексах лантанидов, с использованием программы SRIM-2003. Использованные для моделирования соединения, синтезированные и охарактеризованные ранее [1–3], различаются по типу металлов, элементному составу и размеру лигандов. Для сравнения проведено моделирование органического соединения N,N'-дифенил-N,N'-бис(3-метилфенил)-1,1'-бифенил-4,4'-диамина (TPD), применяющегося в качестве дырочно-транспортного материала в органических светодиодах. Для определения качественного изменения соединений после обработки проводилось сопоставление их ИК и фотолюминесцентных (ФЛ) спектров.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В работе использовали диметоксиэтан (ДМЭ), который сушили натрий-бензофенонкетилом по стандартной методике и отбирали в вакууме непосредственно перед использованием. Силил-амидный комплекс европия Eu[N(SiMe3)2]3 получали по известной методике [4]. Коммерческий (Aldrich) теноилтрифторацетон (HTTA) использовали без дополнительной очистки. Выбранные для моделирования соединения [Ln(OON)3]2 (OON = 2-(2-бензоксазол-2-ил)фенолят), [Ln(SON)3]2 (SON = 2-(2-бензотиазол-2-ил)фенолят) [2], [Ln(NpOON)3]2 (NpOON = 3-(2-бензоксазол-2-ил)-2-нафтолят), [Ln(NpSON)3]2 (NpSON = 3-(2-бензотиазол-2-ил)-2-нафтолят [3] синтезировали по ранее разработанным методикам.
Синтез Eu(TTA)3(DME)2 проводили в условиях, исключающих контакт с кислородом и влагой воздуха, с использованием стандартной техники Шленка. Раствор HTTA (70 мг, 0.315 ммоль) в ДМЭ (10 мл) добавляли к раствору Eu[N(SiMe3)2]3 (67 мг, 0.106 ммоль) в ДМЭ (5 мл). Реакционную смесь перемешивали 30 мин при комнатной температуре. Цвет раствора изменился с красного на светло-желтый. ДМЭ и другие летучие продукты реакции удаляли конденсацией в вакууме. Твердый остаток промывали гексаном и высушивали в вакууме. Выход 81 мг (77%).
| Найдено, %: | C 38.54; | H 3.61; | S 9.68; | Eu 15.07. |
| Для C32H35F9O10S3Eu | ||||
| вычислено, %: | C 38.48; | H 3.53; | S 9.63; | Eu 15.22. |
ИК (ν, см–1): 3104 сл, 1627 ср, 1601 ср, 1580 ср, 1537 ср, 1509 ср, 1413 ср, 1352 ср, 1307 ср, 1252 ср, 1232 ср, 1182 ср, 1139 ср, 1054 ср, 933 ср, 862 ср, 792 ср, 769 сл, 750 сл, 736 сл, 711 ср, 684 с, 641 с, 606 сл, 581 с, 561 сл, 519 сл, 498 ср.
ИК-спектры образцов в виде суспензии в вазелиновом масле регистрировали между окнами KBr на ИК-Фурье-спектрометре ФСМ 1201 (ООО Мониторинг, Россия) в диапазоне 4000–400 см–1. Для снятия спектров эмиссии в диапазоне 200–800 нм использовали люминесцентный спектрометр LS 55 (Perkin Elmer, США). Использовали твердые образцы и растворы соединений в ацетонитриле с концентрацией 0.3 ммол/л. В качестве источника n,γ-излучения использовали ядерный реактор, образцы помещали в стеклянные запаянные ампулы.
Математическая модель. Расчет сечений взаимодействия нейтронов с атомами комплексов выполняли для средней энергии нейтронов 2 МэВ, дополнительные расчеты – для энергии 100 кэВ и 10 МэВ. В ходе расчетов варьировали энергию нейтронного излучения, а также проводили пробный расчет воздействия гамма-квантов. Анализ результатов расчетов делали на основании данных статистического усреднения распределения радиационных дефектов, ионизации и нагрева (фононов). Проводили сопоставление процессов дефектообразования в исследуемых материалах для легких и тяжелых атомов из состава материалов. Полученные результаты сравнивали с классическими полупроводниковыми материалами (кремний и арсенид галлия).
Расчет проводили методом Монте-Карло с помощью пакета программ SRIM-2003 [5]. Траектория каждого атома отдачи, получившего энергию при ударе нейтрона, начиналась с ввода его положения, направления движения и энергии. На длине свободного пробега атомов отдачи их энергия уменьшалась на величину электронных потерь на ионизацию материала, а затем, после столкновения, – на так называемые ядерные, или упругие, потери энергии, т.е. на энергию, переданную атому мишени при столкновении. Траекторию атома отдачи считали оборванной, если его энергия спадала ниже предварительно заданного значения.
Энергию, передаваемую нейтронами атомам отдачи и ответственную за радиационные нарушения, рассчитывали по формуле [5]:
(1)
${{T}_{A}} = \frac{{4{{M}_{n}}{{M}_{A}}}}{{{{{\left( {{{M}_{n}} + {{M}_{A}}} \right)}}^{2}}}}{{T}_{n}}{{\sin }^{2}}\left( {{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. \kern-0em} 2}} \right) = \frac{{4A}}{{{{{\left( {1 + A} \right)}}^{2}}}}{{T}_{n}},$Угол рассеяния в системе центра масс определялся как [5]:
Выбор атомов мишени производили с помощью случайных чисел; при этом предполагалось, что вероятность столкновения с атомом каждого вида пропорциональна его стехиометрическому коэффициенту, определяемому брутто-формулой. Различие между легкими и тяжелыми атомами в мишени заключалось в величине потенциала взаимодействия.
В модели нелокальных потерь энергии электронные потери определяли как произведение тормозной функции на длину свободного пробега атома отдачи [6]. Использовали правило Брэгга, устанавливающее, что вклад в тормозную способность каждого типа атомов мишени пропорционален их атомной доле.
Методику расчетов сводили к определению концентрации радиационных дефектов для всех типов атомов отдачи исследуемых материалов в пропорции, соответствующей брутто-формуле веществ. Также проводили анализ распределения дефектов в пространстве, сравнивали ионизацию и локальный разогрев исследуемых материалов.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Использованные в расчетах соединения, их брутто-формула и плотность приведены в табл. 1.
Таблица 1.
Соединения, использованные для моделирования
| Соединение | Брутто-формула | Плотность вещества, г/см3 |
|---|---|---|
| Sc(NON)3 | C47H43N6O5Sc | 1.391 |
| Sc(OON)3 | C39H24N3O6Sc | 1.473 |
| Sc(NpOONMe)3 | C54H46N3O7.50Sc | 1.283 |
| [La(OON)3]2 | C78H48La2N6O12 | 1.681 |
| [Nd(OON)3]2 | C78H48N6Nd2O12 | 1.683 |
| [Nd(NpOON)3]2 | C102H60N6Nd2O12 | 1.622 |
| [Sm(OON)3]2 | C78H48N6O12Sm2 | 1.658 |
| [Ce(OON)3]2 | C78H48Ce2N6O12 | 1.656 |
| [Yb(OON)3]2 | C78H48N6O12Yb2 | 1.660 |
| [Sm(SON)3]2 | C78H48N6O6S6Sm2 | 1.752 |
| [Sm(NpOON)3]2 | C102H60N6O12Sm2 | 1.622 |
| Eu(TTA)3(DME)2 | C32H25EuO10S3 | 1.72 |
| TPD | C38H32N2 | 1.16 |
Для большинства комплексов ранее было установлено молекулярное строение методом РСА [2, 3]. Схемы молекул соединений, использованных в моделировании радиационной деструкции, различаются по общему строению, металлу, элементному составу и объему лигандов:
Суммарная энергия химических связей отдельного атома с соседними атомами в исследованных молекулах не превышала 40 эВ, что на три порядка ниже энергии быстрых нейтронов и, следовательно, не может отразиться на радиационной стойкости соединений. Напротив, энергия медленных нейтронов и вторичных атомов отдачи сопоставима с энергиями химических связей, что может способствовать повышению устойчивости материала.
Сечение упругого рассеяния нейтронов на атомах, согласно теории Брейта–Вигнера, представляет сумму трех слагаемых: сечение упругого рассеяния – 4πа2, где а – радиус ядра атома, резонансного рассеяния и слагаемого, описывающего их интерференцию. В силу сложного характера резонансного взаимодействия на зависимости сечения от энергии нейтронов имеется ряд узких пиков. Из-за того, что ширина этих пиков мала по сравнению со спектром нейтронного излучения ядерного реактора, а отклонения от усредненной зависимости могут быть как в меньшую, так и в большую сторону, то, рассматривая интегральное взаимодействие, при котором узкие пики будут компенсировать друг друга, можно пользоваться усредненными спектрами. Полный результат можно представить в виде суммы упругого и неупругого рассеяния и эффекта поглощения нейтронов, связанного с ядерными реакциями. Отличительной особенностью реакций с энергиями нейтрона от 10 кэВ до 2–3 МэВ является наиболее вероятное протекание процессов с упругим рассеянием, а другие процессы либо маловероятны, либо запрещены энергетически. Использованные в работе средние сечения рассеяния нейтронов на ядрах атомов приведены в табл. 2.
Таблица 2.
Сечения рассеяния нейтронов и переданная атомам отдачи средняя энергия (для нейтронов с энергией 2 МэВ)
| Элемент | Атомная масса | Сечение рассеяния, барн | Переданная атому отдачи энергия, кэВ |
|---|---|---|---|
| H | 1 | 13 | 2000 |
| C | 12 | 2 | 568 |
| N | 14 | 2 | 500 |
| O | 16 | 2 | 443 |
| Sc | 45 | 4 | 170 |
| La | 139 | 5 | 57 |
| Се | 140 | 5 | 56 |
| Nd | 142 | 5 | 54 |
| Sm | 150 | 5.1 | 53 |
| Eu | 152 | 5.1 | 52 |
| Yb | 173 | 5.3 | 46 |
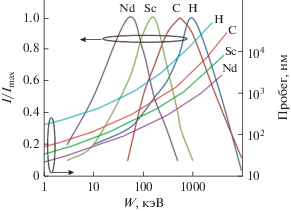
На рис. 1 представлены спектры атомов Nd, Sc, C, H, получивших энергию в результате взаимодействия с нейтронами спектра деления. Также показаны пробеги атомов отдачи Sc, C, H, получивших энергию в результате взаимодействия с нейтронами в Sc(NON)3 и Nd в [Nd(OON)3]2. Сравнение длин пробега других атомов в других исследуемых материалах показывает, что их отличие составляет не более 10–20%. Это объясняется близким химическим составом и сопоставимой плотностью материалов.
Рис. 1.
Энергетический спектр и пробеги первичных атомов Nd, Sc, C, H, получивших энергию в результате взаимодействия с нейтронами спектра деления (пробеги приведены для Sc(NON)3, для других исследуемых материалов пробеги отличаются на 15–30%).
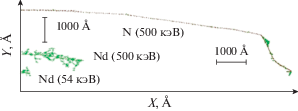
На рис. 2 представлен внешний вид каскадов смещений в [Nd(OON)3]2. Каждая точка изображения соответствует смещенному атому. Предполагалось, что нейтрон передал энергию атомам в советующей точке старта на вертикальной оси, а их первичный импульс направлен вправо. Первичный атом отдачи при движении “слева направо” образует вдоль своей траектории цепочку из смещенных атомов. Вторичные атомы отдачи, получившие значительные энергии от первичных, образуют субкаскады смещенных атомов. Каскады смещений существенно отличаются для первичных атомов различной массы: тяжелые атомы создают плотные скопления (кластеры) дефектов, а легкие – сильно вытянутые с повышением концентрации дефектов в конце пробега первичного атома отдачи. Исходная энергия атомов отдачи существенно влияет на характерные размеры кластеров дефектов (см. длины пробегов на рис. 1). Сечения взаимодействия первичных атомов с вторичными также существенно зависят от соотношения масс налетающего атома и атома-мишени, а количество первичных атомов с различной энергией определяется их энергетическими спектрами (рис. 1). В связи с этим расчет концентрации дефектов при нейтронном облучении исследуемых материалов является нетривиальной задачей, которая решалась методом Монте-Карло, описанным выше.
Рис. 2.
Сравнение каскадов атомов отдачи, образованных первичными Nd (54 и 500 кэВ) и N (500 кэВ) в [Nd(OON)3]2.
В табл. 3 приведено соотношение количества радиационных дефектов, приходящихся на 1000 смещенных нейтронами первичных атомов. Сравнение данных показывает, что в материалах со Sc основные дефекты будут созданы первичными атомами углерода, в то время как в Nd2(OON)6 основным атомом, формирующим радиационные дефекты, является неодим. Учитывая то, что сечение взаимодействия неодима с нейтронами выше, чем у скандия, можно заключить, что материалы со скандием более радиационно-стойкие. В ряду материалов Sc(OON)3, Sc(NON)3, Sc(NpOONMe)3 радиационная стойкость повышается на ~25%. Стойкость материалов [La(OON)3]2, [Nd(OON)3]2, [Yb(OON)3]2 отличается незначительно.
Таблица 3.
Соотношение количества радиационных дефектов, приходящихся на 1000 смещенных нейтронами первичных атомов (для энергии атома отдачи, указанной в табл. 2)
| Первичный атом-мишень |
Комплекс | |||||
|---|---|---|---|---|---|---|
| Sc(OON)3 | Sc(NON)3 | Sc(NpOONMe)3 | [La(OON)3]2 | [Nd(OON)3]2 | [Yb(OON)3]2 | |
| Н | 63 | 76 | 66 | 71 | 72 | 74 |
| С | 251 | 205 | 193 | 281 | 287 | 283 |
| N | 18 | 25 | 9 | 21 | 21 | 21 |
| O | 34 | 19 | 22 | 38 | 39 | 38 |
| Sc | 105 | 70 | 51 | |||
| La | 816 | |||||
| Nd | 828 | |||||
| Yb | 892 | |||||
Согласно расчетам (табл. 2, 3, рис. 2, 3), все исследованные соединения при воздействии нейтронов деления претерпевают глубокие превращения, что должно кардинально менять их физико-химические свойства, так же как это наблюдается в неорганических полупроводниках [7–9].
Рис. 3.
Спектр ФЛ комплекса Eu(TTA)3(DME)2: а – в растворе ТГФ при λвозб = 395 нм; б – твердого комплекса [La(NpSON)3]2 при λвозб = 390 нм; в – спектральная фоточувствительность кремния; г – ИК-спектры комплекса [La(NpSON)3]2 до (1) и после облучения (2). Сопоставляются спектры до и после гамма-нейтронного облучения с флюенсом 1014 см–2 для органических полупроводников (а, б) и 1013 см–2 для кремниевого р–n-перехода.
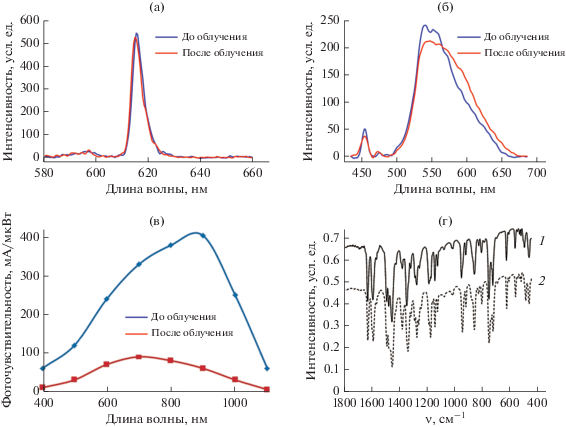
Для оценки адекватности моделирования реальным процессам, протекающим в металлоорганических материалах при ионизирующем облучении высокой энергии, выбранные комплексы Eu(TTA)3(DME)2 и [La(NpSON)3]2 подвергли импульсной обработке нейтронами деления и γ-фотонами (3 мс, поглощенная доза 130 крад, флюенс 3.6 × 1013 н/см2). Облучение не привело к изменению внешнего вида, цвета, ИК и ФЛ спектров образцов (рис. 3). Следует отметить, что в комплексе европия центром эмиссии является ион Eu3+ (f–f-переход 5D0–7F2), тогда как в комплексе лантана регистрируется полоса свечения лигандов. Интересно, что облучение рентгеновским излучением неорганического материала CaAlO4:Eu вызывает восстановление Eu3+ до Eu2+, отчетливо проявляющееся в спектре фотоэмиссии [10].
Обнаруженное расхождение расчетных и экспериментальных данных, по-видимому, объясняется невысокой плотностью органических полупроводников по сравнению с неорганическими аналогами и иным механизмом люминесценции.
Анализ неоднородности энерговыделения и радиационных дефектов в объеме дифенил-N,N'-бис(3-метилфенил)-1,1'-бифенил-4,4'-диамина и органических комплексах неодима, самария, лантана, европия, итербия и скандия при внедрении водорода, углерода, азота и атомов металлов в условиях нейтронного, электронного и гамма-облучения показал, что по сравнению с неорганическими полупроводниковыми материалами органические полупроводники имеют значительно более разреженные кластеры радиационных дефектов, что позволяет рекомендовать их как перспективные материалы для радиационно-стойкой электроники.
При моделировании рассеяния быстрых электронов в металлокомплексах неодима, самария, скандия и TPD найдено, что концентрация дефектов, возникающих в исследуемых материалах на 3–4 порядка ниже, чем при нейтронном облучении. Кроме того, в материалах не возникают кластеры дефектов, а формируются только точечные дефекты и их комплексы. Эти данные, результаты расчетов деструкции комплексов под действием нейтронов, а также результаты обработки образцов n,γ-излучением свидетельствуют о том, что исследуемые материалы имеют высокую радиационную стойкость и, следовательно, их можно рекомендовать в качестве основы для создания радиационно-стойких преобразователей энергии, прежде всего, автономных источников тока пролонгированного действия на основе бета-излучающих изотопов (бета-батареи [11–13]).
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-03-00066). Синтез соединений проводился при поддержке Российского фонда фундаментальных исследований (грант № 18-03-00241).
Список литературы
Lanthanide Luminescence: Photophysical, Analytical and Biological Aspects / Eds. Pekka H., Harri H. Springer Ser. Fluoresc., 2011. V. 7. 386 p.
Balashova T.V., Pushkarev A.P., Ilichev V.A. et al. // Polyhedron. 2013. V. 50. P. 112.
Burin M.E., Kuzyaev D.M., Lopatin M.A. et al. // Synth. Met. 2013. V. 164. P. 55.
Bradley D.C., Ghotra J.S., Hart F.A. // Dalton Trans. 1973. № 10. P. 1021.
Biersak J.P. // Nucl. Instruments Methods Phys. Res. 1987. № 1. P. 2136.
Григорьев И.С., Мейлихов Е.З. Физические величины. М.: Энергоатомиздат, 1991. 1232 с.
Lei Y., Yang Y., Liu Y. et al. // Appl. Radiation Isotopes. 2014. V. 90. P. 165.
Okuno Y., Okuda S., Akiyoshi M. et al. // J. Appl. Phys. 2017. V. 122. P. 114901.
Kawakita S., Imaizumi1 M., Ishizuka S. et al. // Phys. Status Solidi. C. 2017. P. 1600168.
Gomes M.A., Carvalho J.C., Andrade A.B. et al. // Opt. Mater. 2018. V. 75. P. 122.
Sychov M., Kavetsky A., Yakubova G. et al. // Appl. Radiat. Isot. 2008. V. 66. P. 173.
Russoa J., Litza M., Ray II W. et al. // Appl. Radiation Isotopes. 2017. V. 130. P. 66.
Zhanga Z.-R., Liu Y.-P., Tanga X.-B. et al. // Nucl. Instruments Methods Phys. Res. B. 2018. V. 415. P. 9.
Дополнительные материалы отсутствуют.
Инструменты
Координационная химия