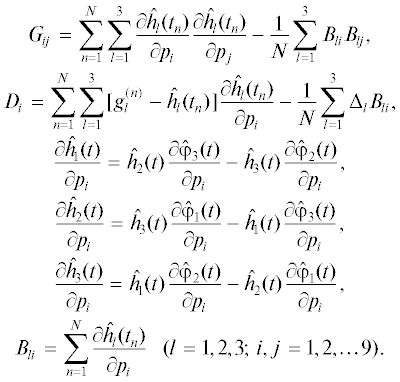Космические исследования, 2019, T. 57, № 1, стр. 61-73
Определение вращательного движения малого космического аппарата Аист-2Д по данным магнитных измерений
В. И. Абрашкин 1, К. Е. Воронов 2, А. С. Дорофеев 2, А. В. Пияков 2, Ю. Я. Пузин 1, В. В. Сазонов 3, *, Н. Д. Сёмкин 2, А. С. Филиппов 1, С. Ю. Чебуков 3
1 Ракетно-космический центр “Прогресс”
г. Самара, Россия
2 Институт космического приборостроения Самарского университета им. С.П. Королёва
г. Самара, Россия
3 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
* E-mail: sazonov@keldysh.ru
Поступила в редакцию 21.12.2017
После доработки 21.12.2017
Принята к публикации 20.04.2018
Аннотация
Приведены результаты реконструкции вращательного движения малого спутника Аист-2Д по данным бортовых измерений векторов угловой скорости и напряженности магнитного поля Земли (МПЗ), полученным летом 2016 г. Методика реконструкции основана на кинематических уравнениях вращательного движения твердого тела. В рамках этой методики данные измерений обоих типов, собранные на некотором отрезке времени, обрабатываются совместно. Измерения угловой скорости интерполируются кусочно-линейными функциями, которые подставляются в кинематические дифференциальные уравнения для кватерниона, задающего переход от приборной системы координат спутника к инерциальной системе координат. Полученные таким образом уравнения представляют собой кинематическую модель вращательного движения спутника. Решение этих уравнений, аппроксимирующее фактическое движение, находится из условия наилучшего (в смысле метода наименьших квадратов) согласования данных измерений вектора напряженности МПЗ с его расчетными значениями. При этом уточняются начальные условия аппроксимирующего решения, постоянные смещения в измерениях угловой скорости и углы, задающие матрицы перехода от собственных систем координат магнитометров к приборной системе координат спутника (в ней заданы измерения угловой скорости). Описанная методика позволяет реконструировать фактическое вращательное движение спутника одним решением кинематических уравнений на интервалах времени продолжительностью более 10 ч.
1. МАЛЫЙ КОСМИЧЕСКИЙ АППАРАТ АИСТ-2Д
Малый космический аппарат (МКА) Аист-2Д был разработан АО РКЦ “Прогресс” и выведен на орбиту 28.IV.2016 г. в 05:01:21 декретного московского времени (ДМВ) с космодрома “Восточный” ракетой-носителем “Союз-2” этапа 1а с использованием блока выведения “Волга”. Блоком выведения была сформирована целевая орбита МКА с параметрами: драконический период 5653.55 с, наклонение 97.27°, средняя высота 491.55 км, эксцентриситет 0.0004, угол между плоскостью орбиты и направлением на среднее Солнце 348.75°.
На борту МКА установлены: целевая оптико-электронная аппаратура дистанционного зондирования Земли “Аврора” среднего разрешения и комплекс научной аппаратуры (НА), включающий аппаратуру КМУ-1 (Компенсатор Микро Ускорений). Аппаратура КМУ-1 является результатом совместной разработки Института космического приборостроения Самарского университета им. С.П. Королёва и РКЦ “Прогресс”.
Функционирование НА в орбитальном полете поддерживается бортовыми обеспечивающими системами: системой контроля и управления, системой энергопитания, системой обеспечения теплового режима, системой управления движением, бортовой кабельной сетью. Передача данных от НА осуществляется по высокоскоростной радиолинии на наземные средства управления, получения и обработки информации (НСУ ПОИ) РКЦ “Прогресс”.
Аппаратура КМУ-1 позволяет измерять магнитное поле на борту, определять остаточные низкочастотные микроускорения, отрабатывать способы управления ориентацией МКА. В состав аппаратуры входят блок электроники, три электромагнита, солнечный датчик, пять датчиков засветки и два трехкомпонентных магнитометра. Измерения магнитометров вместе со штатными измерениями угловой скорости и знанием орбитального движения позволяют реконструировать вращательное движение спутника и найти микроускорения. Аппаратура КМУ-1 получает измерения угловой скорости МКА и фазового вектора его центра масс, формирует пакеты программно-телеметрической информации, которая два раза в сутки передается в НСУ ПОИ.
Включение основного комплекта НА КМУ-1 было осуществлено в 09:40 ДМВ 9.VI.2016 г. Основной комплект был выключен в 13:30 12.VIII.2016 г. Резервный комплект был включен в 14:30 ДМВ 12.VIII.2016 г. и работает до настоящего времени. Поступающая от НА информация ежесуточно обрабатывается программными средствами автоматизированного рабочего места КМУ-1 для контроля оперативных параметров, характеризующих работоспособность НА и ее отдельных структурных элементов.
Состав данных, переданных НА, позволяет решать задачу реконструкции вращательного движения МКА с использованием методического и программного обеспечения, разработанного в ИПМ им. М.В. Келдыша РАН. Ранее подобное программное обеспечение применялось для реконструкции вращательного движения спутников Бион М-1 и Фотон М-4 [1–3]. Его применение в случае МКА Аист-2Д потребовало доработки для определения матриц перехода от собственных систем координат магнитометров к приборной системе координат спутника, в которой задаются измерения угловой скорости. Ниже приводятся первые результаты реконструкция вращательного движения МКА (для удобства называемого спутником), полученные по данным НА КМУ-1.
2. ТЕСТИРОВАНИЕ МАГНИТНЫХ ИЗМЕРЕНИЙ
Магнитометры, установленные на спутнике, будем называть магнитометр 1 и магнитометр 2. Магнитные измерения проводились на отрезках полета длиной около 10 ч. Оцифровка показаний магнитометров выполнялась в единые моменты времени с шагом 21–22 с. Компоненты измеряемых векторов напряженности магнитного поля выдавались в собственных системах координат магнитометров. Собственные системы координат магнитометров 1 и 2 обозначим соответственно ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ и ${{z}_{1}}{{z}_{2}}{{z}_{3}}.$ Система ${{z}_{1}}{{z}_{2}}{{z}_{3}}$ – это штатная система координат магнитометра 2, система ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ переводится в штатную систему координат магнитометра 1 преобразованием ${{y}_{1}} \leftrightarrow {{y}_{2}},$ ${{y}_{3}} \to - {{y}_{3}}.$ Оси системы ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ составляют углы менее 5° с одноименными осями приборной системы координат спутника ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ и острые углы с одноименными осями собственной системы координат магнитометра 2.
Результаты измерений обоих магнитометров, полученные на некотором интервале времени, обозначим
(1)
${{t}_{n}},g_{1}^{{(n)}},g_{2}^{{(n)}},g_{3}^{{(n)}},h_{1}^{{(n)}},h_{2}^{{(n)}},h_{3}^{{(n)}}\,\,\,\,(n = 1,2, \ldots ,N).$Первый способ основан на предположении, что магнитометры измеряли в основном МПЗ. С учетом большого числа электрических цепей на борту спутника это предположение выглядит несколько наивным, однако, опыт магнитных измерений на двух предыдущих Аистах и ряде других спутников [1–6] позволял надеяться, что оно окажется адекватным. Этот способ состоял в сравнении модуля напряженности измеренного поля с модулем напряженности МПЗ, рассчитанной по аналитической модели IGRF. Сравнение модулей не требует знания ориентации магнитометра, надо знать только орбитальное движение спутника. Такой подход позволяет проверить данные измерений каждого магнитометра, используя минимальную дополнительную информацию.
Рассмотрим магнитометр 1. Будем считать, что его измерения (1) содержат две систематические ошибки. Одна ошибка вызвана неточным заданием масштабирующего коэффициента при оцифровке, другая – наличием постоянных смещений в измерениях. Правильные показания магнитометра в момент ${{t}_{n}}$ должны были бы быть $\bar {g}_{i}^{{(n)}} = {{\kappa }_{1}}g_{i}^{{(n)}} - {{a}_{i}}$ $(i = 1,2,3).$ Значения величин ${{\kappa }_{1}}$ и ${{a}_{i}}$ находились методом наименьших квадратов из условия минимума выражения
Аналогичным образом находились скорректированные измерения второго магнитометра $\bar {h}_{i}^{{(n)}} = {{\kappa }_{2}}h_{i}^{{(n)}} - {{b}_{i}}$ $(i = 1,2,3),$ где корректирующие параметры ${{\kappa }_{2}}$ и ${{b}_{i}}$ находились из условия минимума выражения
Найденное решение характеризовалось стандартным отклонением ${{\sigma }_{H}}$ ошибок согласования величин ${{H}_{n}}$ и
Приведем результаты коррекции измерений на трех отрезках данных, перечисленных в табл. 1. Здесь указаны начальные точки ${{t}_{1}}$ этих отрезков, числа N точек с измерениями и длины отрезков ${{t}_{N}} - {{t}_{1}}.$ Корректирующие параметры ${{\kappa }_{1}},$ ${{\kappa }_{2}},$ ${{a}_{i}},$ ${{b}_{i}}$ для этих отрезков и оценки точности их определения приведены в табл. 2, 3. Стандартные отклонения параметров указаны в скобках рядом с их значениями. Результаты сравнения модулей скорректированных измерений магнитного поля и расчетных значений модуля МПЗ иллюстрируются графиками на рис. 1. Рис. 1а построен для магнитометра 1. Верхние графики на этом рисунке представляют собой ломаные. Здесь в каждой системе координат изображены две ломаные. Звенья одной из них соединяют соседние по времени точки $({{t}_{n}},{{g}^{{(n)}}}),$ звенья другой ломаной аналогичным образом соединяют точки $({{t}_{n}},{{H}^{{(n)}}}),$ $n = 1,2, \ldots ,N.$ Эти ломаные практически совпадают, поэтому для наглядности на нижних графиках изображены ломаные, проходящие через точки $({{t}_{n}},{{g}^{{(n)}}} - {{H}^{{(n)}}}).$ Рис. 1б аналогичным образом характеризует согласие величин ${{h}^{{(n)}}}$ и ${{H}^{{(n)}}}.$
Таблица 1.
Интервалы обработки магнитных измерений
| № инт. | Дата, 2016 г. |
${{t}_{1}},$ UTC ч:мин:с |
N | ${{t}_{N}} - {{t}_{1}},$ мин |
|---|---|---|---|---|
| 1 | 17 июня | 19:03:04.0 | 1375 | 591.5 |
| 2 | 19 июня | 05:12:54.0 | 1640 | 766.5 |
| 3 | 12 июля | 18:53:31.0 | 1346 | 631.4 |
Таблица 2.
Корректирующие параметры магнитометра 1
| № инт. | ${{\sigma }_{H}},$ γ | ${{\kappa }_{1}}({{\sigma }_{{\kappa 1}}})$ | ${{a}_{1}}({{\sigma }_{{a1}}}),$ γ | ${{a}_{2}}({{\sigma }_{{a2}}}),$ γ | ${{a}_{3}}({{\sigma }_{{a3}}}),$ γ |
|---|---|---|---|---|---|
| 1 | 923 | 1.0026 (0.0011) | 294 (46) | 4057 (147) | 1205 (46) |
| 2 | 971 | 1.0090 (0.0007) | 172 (44) | 3586 (157) | 1699 (39) |
| 3 | 959 | 1.0108 (0.0010) | 347 (45) | 3693 (147) | 1324 (44) |
Таблица 3.
Корректирующие параметры магнитометра 2
| № инт. | ${{\sigma }_{H}},$ γ | ${{\kappa }_{2}}({{\sigma }_{{\kappa 2}}})$ | ${{b}_{1}}({{\sigma }_{{b1}}}),$ γ | ${{b}_{2}}({{\sigma }_{{b2}}}),$ γ | ${{b}_{3}}({{\sigma }_{{b3}}}),$ γ |
|---|---|---|---|---|---|
| 1 | 1437 | 0.9585 (0.0015) | 2276 (118) | 2350 (219) | 3282 (65) |
| 2 | 1384 | 0.9592 (0.0010) | 1654 (116) | 4285 (183) | 3642 (68) |
| 3 | 1410 | 0.9723 (0.0011) | 1043 (134) | 4541 (197) | 3781 (74) |
Рис. 1.
Сравнение модуля измерений магнитометров с модулем напряженности МПЗ на интервале 2: (а) – магнитометр 1; (б) – магнитометр 2.
Данные в табл. 2, 3 и графики на рис. 1 показывают, что измерения обоих магнитометров достаточно точно согласуются со значениями МПЗ из модели IGRF. При этом согласно значениям ${{\sigma }_{H}}$ в табл. 2, 3 магнитометр 1 оказался примерно в полтора раза точнее магнитометра 2. Однако исключение измерений магнитометра 2 из обработки было бы неосмотрительным. Как будет показано ниже, линейная комбинация измерений обоих магнитометров с правильно подобранными весами позволит точнее реконструировать движение спутника, чем использование показаний одного только магнитометра 1.
Из найденных корректирующих параметров ниже используются только параметры ${{\kappa }_{1}},$ ${{\kappa }_{2}}.$ Во-первых, они определены с малой относительной ошибкой. Во-вторых, на последующих этапах обработки магнитных измерений используются более адекватные этим этапам способы оценки смещений. После того как параметры ${{\kappa }_{1}},$ ${{\kappa }_{2}}$ найдены, величины $g_{i}^{{(n)}}$ и $h_{i}^{{(n)}}$ в (1) заменялись величинами $\kappa {}_{1}g_{i}^{{(n)}}$ и ${{\kappa }_{2}}h_{i}^{{(n)}}.$ Чтобы не вводить новых обозначений, последние величины будем обозначать $g_{i}^{{(n)}},$ $h_{i}^{{(n)}}$ и именно их считать измерениями магнитного поля.
Второй способ тестирования магнитных измерений используется в случае, когда оба магнитометра прошли первый тест. Это способ основан на следующих предположениях: 1) магнитометры измеряют одно и то же переменное поле, 2) постоянные составляющие поля в точках расположения магнитометров различны (или измерения магнитометров содержат постоянные смещения). В случае точной реализации этих предположений измерения магнитометра 2, пересчитанные в систему координат магнитометра 1, отличались бы от измерений последнего на постоянный вектор смещения. Из-за разного рода ошибок точного постоянства вектора смещения достичь невозможно, однако его вариации во времени должны быть малыми. Согласующие параметры – матрица перехода между системами координат магнитометров и постоянный вектор смещения – определялись методом наименьших квадратов. Методика определения этих параметров описана в [9] и состоит в следующем.
С высокой точностью должны выполняться соотношения
(2)
$g_{i}^{{(n)}} = {{d}_{i}} + \sum\limits_{j = 1}^3 {{{c}_{{ij}}}h_{j}^{{(n)}}} \,\,\,\,(i = 1,2,3;\,\,n = 1,2, \ldots ,N),$Следуя методу наименьших квадратов, ищем минимум выражения
Величины ${{\theta }_{i}}$ представляют собой компоненты вектора бесконечно малого поворота, характеризующего отличие матрицы C от ее оценки $C^\circ .$ Эти компоненты относятся к системе координат ${{y}_{1}}{{y}_{2}}{{y}_{3}}.$ Согласно методу наименьших квадратов параметры ${{\xi }_{i}},\,\,{{\theta }_{i}}$ образуют случайный вектор $\eta \in {{R}^{6}}$ с нулевым математическим ожиданием. Ковариационная матрица ${{K}_{\eta }}$ этого вектора выражается через матрицу P системы нормальных уравнений, получающейся линеаризацией исходной задачи по η в точке минимума выражения Z, и значение ${{Z}_{{\min }}}{\text{:}}$
Сопоставление данных измерений магнитометров описанным методом было выполнено на трех интервалах времени, указанных в табл. 1. Ниже приводится решение описанной задачи для интервала 2
Оценки точности этого решения и аналогичных решений для интервалов 1 и 3 приведены в табл. 4.
Таблица 4.
Стандартные отклонения параметров согласования показаний магнитометров
| № инт. |
${{\sigma }_{0}}$ | ${{\sigma }_{{d1}}}$ | ${{\sigma }_{{d2}}}$ | ${{\sigma }_{{d3}}}$ | ${{\sigma }_{{\theta 1}}}$ | ${{\sigma }_{{\theta 2}}}$ | ${{\sigma }_{{\theta 3}}}$ |
|---|---|---|---|---|---|---|---|
| γ | град. | ||||||
| 1 | 1702 | 49 | 49 | 48 | 0.077 | 0.101 | 0.109 |
| 2 | 1633 | 43 | 42 | 40 | 0.065 | 0.086 | 0.090 |
| 3 | 1624 | 47 | 47 | 46 | 0.072 | 0.097 | 0.099 |
Наглядное представление о результатах сопоставления дает рис. 2. На рис. 2а в каждой системе координат изображены две ломаные. Звенья одной из них последовательно соединяют точки $\left( {{{t}_{n}},g_{i}^{{(n)}}} \right),$ другая проходит через точки $\left( {{{t}_{n}},\hat {g}_{i}^{{(n)}}} \right),$ $n = 1,2, \ldots N.$ На вид эти ломаные очень близки. Чтобы наглядно показать их различие, на рис. 2б изображены разности этих ломаных, т.е. ломаные с вершинами в точках $\left( {{{t}_{n}},\Delta g_{i}^{{(n)}}} \right),$ где $\Delta g_{i}^{{(n)}} = g_{i}^{{(n)}} - \hat {g}_{i}^{{(n)}}.$ Рисунок показывает, что различие между показаниями магнитометров достаточно велико.
Рис. 2.
Согласованные данные измерений магнитометров 1, 2 на интервале 2 в системе координат магнитометра 1: (а) – данные измерений; (б) – разности компонент измерений.
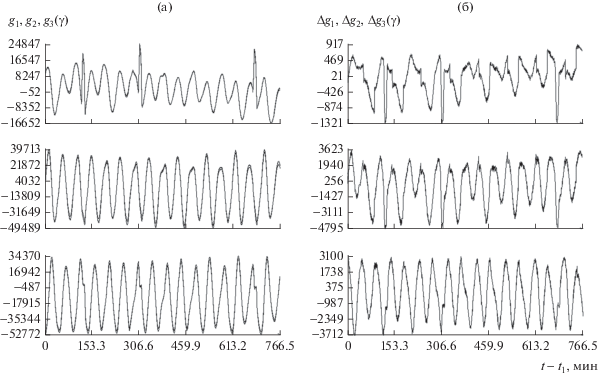
Если из данных (1) сформировать взвешенную напряженность поля в системе ${{y}_{1}}{{y}_{2}}{{y}_{3}}\,:$
(3)
$\begin{gathered} \tilde {g}_{i}^{{(n)}} = \frac{1}{{1 + \rho }}\left( {\rho g_{i}^{{(n)}} + \sum\limits_{j = 1}^3 {c{}_{{ij}}h_{j}^{{(n)}}} } \right) \\ (i = 1,2,3;\,\,n = 1,2, \ldots ,N), \\ \end{gathered} $Для интервала 1 из табл. 1 при $\rho = 2$ получим $\sigma _{H}^{'} = 671\gamma ,$ для интервала 2 при $\rho = 1.7$ получим $\sigma _{H}^{'} = 673\gamma ,$ в случае интервала 3 при $\rho = 1.8$ будем иметь $\sigma _{H}^{'} = 654\gamma .$ Эти значения заметно лучше значений ${{\sigma }_{H}}$ в табл. 2, 3.
Для решения задачи реконструкции движения спутника матрицу $C$ параметризируем углами γ, α и β, которые введем посредством следующего условия. Система координат ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ может быть переведена в систему ${{z}_{1}}{{z}_{2}}{{z}_{3}}$ тремя последовательными поворотами: 1) на угол α вокруг оси ${{y}_{2}};$ 2) на угол β вокруг оси ${{y}_{3}},$ получившейся после первого поворота; 3) на угол γ вокруг оси ${{y}_{1}},$ получившейся после первых двух поворотов и совпадающей с осью ${{z}_{1}}.$ Элементы матрицы $C$ выражаются через введенные углы с помощью формул
Углы, параметризирующие указанные выше матрицы $C^\circ ,$ приведены в табл. 5. Здесь стандартные отклонения ${{\sigma }_{\gamma }},$ ${{\sigma }_{\alpha }}$ и ${{\sigma }_{\beta }}$ (указаны в скобках рядом с оценками углов γ, α и β) вычислены по стандартным отклонениям ${{\sigma }_{{\theta {\kern 1pt} i}}}$ на основании формул θ1 = c11dγ + $ + \sin \alpha d\beta ,$ ${{\theta }_{2}} = {{c}_{{21}}}d\gamma + d\alpha ,$ ${{\theta }_{3}} = {{c}_{{31}}}d\gamma + \cos \alpha d\beta .$
Таблица 5.
Оценки углов, задающих матрицу C°
| № инт. | $\gamma ({{\sigma }_{\gamma }}),$ градус | $\alpha ({{\sigma }_{\alpha }}),$ градус | $\beta ({{\sigma }_{\beta }}),$ градус |
|---|---|---|---|
| 1 | –58.981 (0.107) | 41.574 (0.115) | 33.785 (0.092) |
| 2 | –59.364 (0.089) | 41.787 (0.101) | 34.063 (0.077) |
| 3 | –58.693 (0.098) | 41.459 (0.114) | 34.279 (0.087) |
Графики, иллюстрирующие тестирование магнитометров на интервалах 1 и 3, приведены в [10].
3. МЕТОДИКА РЕКОНСТРУКЦИИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ СПУТНИКА
Реконструкция вращательного движения спутника выполнялась по измерениям его угловой скорости и напряженности МПЗ. Методика реконструкции основана на кинематических уравнениях вращательного движения твердого тела. Опишем математические модели и приведем основные соотношения, используемые в этой методике.
Для описания вращательного движения спутника используются две правые декартовы системы координат: приборная система ${{x}_{1}}{{x}_{2}}{{x}_{3}},$ в которой интерпретируются измерения угловой скорости, и система ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$, в которой задаются двухстрочные элементы. Последняя переводится в гринвичскую систему координат поворотом по часовой стрелке вокруг оси ${{Y}_{3}}$ на угол, равный среднему звездному времени. Таким образом, система ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ весьма близка ко второй геоэкваториальной системе координат эпохи даты. В частности, плоскость ${{Y}_{1}}{{Y}_{2}}$ совпадает с плоскостью экватора, ось ${{Y}_{3}}$ – ось вращения Земли. Систему ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ считаем инерциальной.
Положение приборной системы ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно системы ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ зададим нормированным кватернионом $Q = ({{q}_{0}},{{q}_{1}},{{q}_{2}},{{q}_{3}}),$ $q_{0}^{2}\, + \,q_{1}^{2}\, + \,q_{2}^{2}\, + \,q_{3}^{2}\, = \,1.$ Кватернионная формула перехода между этими системами координат имеет вид
Матрицу перехода от приборной системы к системе ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ обозначим $A = \left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ где ${{a}_{{ij}}}$ – косинус угла между осями ${{Y}_{i}}$ и ${{x}_{j}}.$ Элементы этой матрицы выражаются через компоненты Q с помощью формул
Орбитальное движение спутника на представляющем интерес временном интервале описывается с помощью модели SGP4. Параметры модели определяются по данным двухстрочных элементов. Математическая модель вращательного движения спутника построена на основе кинематических уравнений, которым удовлетворяет кватернион Q. Эти уравнения имеют вид
(4)
$\begin{gathered} 2{{{\dot {q}}}_{0}} = - {{q}_{1}}{{\omega }_{1}} - {{q}_{2}}{{\omega }_{2}} - {{q}_{3}}{{\omega }_{3}}, \\ 2{{{\dot {q}}}_{1}} = {{q}_{0}}{{\omega }_{1}} + {{q}_{2}}{{\omega }_{3}} - {{q}_{3}}{{\omega }_{2}}, \\ 2{{{\dot {q}}}_{2}} = {{q}_{0}}{{\omega }_{2}} + {{q}_{3}}{{\omega }_{1}} - {{q}_{1}}{{\omega }_{3}}, \\ 2{{{\dot {q}}}_{3}} = {{q}_{0}}{{\omega }_{3}} + {{q}_{1}}{{\omega }_{2}} - {{q}_{2}}{{\omega }_{1}}. \\ \end{gathered} $Здесь точка над символом означает дифференцирование по времени, ${{\omega }_{1}},$ ${{\omega }_{2}}$ и ${{\omega }_{3}}$ – компоненты абсолютной угловой скорости спутника в приборной системе координат.
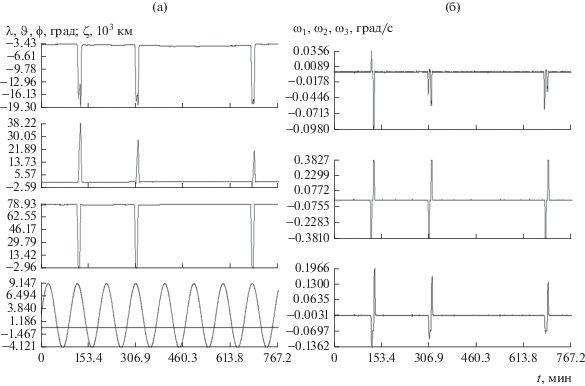
Измерения величин ${{\omega }_{i}}$ выполнялись непрерывно в течение практически всего полета. Данные этих измерений представлены в цифровом виде на единой временной сетке с постоянным шагом 12 с. По этим данным построены непрерывные кусочно-линейные функции ${{\Omega }_{i}}(t)$ $(i = 1,\;2,\;3)$, которые в узлах сетки совпадают с данными измерений величин ${{\omega }_{i}},$ а в промежутках между узлами линейны. Примеры графиков функций ${{\Omega }_{i}}(t)$ приведены на рис. 3. Однако в уравнения (1) подставлялись не эти функции, а выражения
где ${{\chi }_{i}}$ – постоянные смещения в измерениях. Уравнения (4), (5) использовались на интервалах времени не более 12 ч, причем смещения ${{\chi }_{i}}$ служили уточняемыми параметрами. В такой ситуации предположение о постоянстве этих величин оказалось вполне адекватным.Рис. 3.
Примеры функций ${{\Omega }_{i}}(t)$ $(i = 1,2,3),$ интерполирующих измерения угловой скорости. Момент $t = 0$ соответствует 18:53:28.7 UTC 12.VII.2016 г.
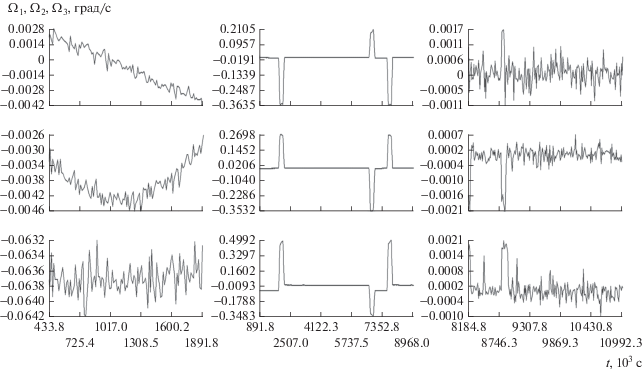
Опишем применение уравнений (4), (5) для обработки магнитных измерений, выполненных внутри отрезка $I = \{ t\,:{{t}_{a}} \leqslant t \leqslant {{t}_{b}}\} ,$ на котором построены функции ${{\Omega }_{i}}(t).$ Узлы временной сетки с магнитными измерениями, как правило, не совпадают с узлами сетки, на которой заданы функции ${{\Omega }_{i}}(t).$ Пусть для определенности обрабатываются измерения магнитометра 1 из (1), причем $[{{t}_{1}},{{t}_{N}}] \subset ({{t}_{a}},{{t}_{b}}).$ Матрицу перехода от системы ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим $\left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ где ${{b}_{{ij}}}$ – косинус угла между осями ${{y}_{i}}$ и ${{x}_{j}}.$ Эту матрицу параметризируем углами ${{\gamma }_{1}},$ ${{\alpha }_{1}}$ и ${{\beta }_{1}}$, по смыслу и формулам, принятым в п. 2 при параметризации матрицы C углами γ, α и $\beta $.
Следуя методу наименьших квадратов, реконструкцией фактического движения спутника на отрезке I будем считать решение уравнений (4), (5), доставляющее минимум функционалу
(6)
$\begin{gathered} \Phi = \sum\limits_{i = 1}^3 {\left\{ {\sum\limits_{n = 1}^N {{{{[g_{i}^{{(n)}} - {{{\hat {h}}}_{i}}({{t}_{n}})]}}^{2}}} - N\Delta _{i}^{2}} \right\}} , \\ {{\Delta }_{i}} = \frac{1}{N}\sum\limits_{n = 1}^N {[g_{i}^{{(n)}} - {{{\hat {h}}}_{i}}({{t}_{n}})]} , \\ {{{\hat {h}}}_{i}}(t) = \sum\limits_{k,j = 1}^3 {{{H}_{j}}(t)} {\kern 1pt} {\kern 1pt} {{a}_{{jk}}}(t){{b}_{{ik}}}. \\ \end{gathered} $Для простоты письма все уточняемые величины объединим в один вектор $z \in {{R}^{{10}}}.$ В принятых обозначениях $\Phi = \Phi (z),$ $z* = \arg \min \Phi (z)$ – искомая оценка вектора z. Минимизация $\Phi (z)$ выполнялась в несколько этапов разными методами. Начальные этапы, на которых ${{\gamma }_{1}} = {{\alpha }_{1}} = {{\beta }_{1}} = 0,$ описаны в [1, 2]. Здесь ограничимся описанием заключительного этапа, когда эти углы уточняются.
Описание минимизации функции Φ по z начнем с заключительного этапа, на котором применялся метод Гаусса–Ньютона [8]. На каждой итерации этого метода поправки $\Delta {{q}_{j}}({{t}_{a}})$ к имеющимся значениям ${{q}_{j}}({{t}_{a}})$ ищутся в виде (ср. уравнения (4))
(8)
$\begin{gathered} \Delta {{q}_{0}}({{t}_{a}}) = - \frac{1}{2}[{{\theta }_{1}}{{q}_{1}}({{t}_{a}}) + {{\theta }_{2}}{{q}_{2}}({{t}_{a}}) + {{\theta }_{3}}{{q}_{3}}({{t}_{a}})], \\ \Delta {{q}_{1}}({{t}_{a}}) = \frac{1}{2}[{{\theta }_{1}}{{q}_{0}}({{t}_{a}}) + {{\theta }_{3}}{{q}_{2}}({{t}_{a}}) - {{\theta }_{2}}{{q}_{3}}({{t}_{a}})], \\ \Delta {{q}_{2}}({{t}_{a}}) = \frac{1}{2}[{{\theta }_{2}}{{q}_{0}}({{t}_{a}}) + {{\theta }_{1}}{{q}_{3}}({{t}_{a}}) - {{\theta }_{3}}{{q}_{1}}({{t}_{a}})], \\ \Delta {{q}_{3}}({{t}_{a}}) = \frac{1}{2}[{{\theta }_{3}}{{q}_{0}}({{t}_{a}}) + {{\theta }_{2}}{{q}_{1}}({{t}_{a}}) - {{\theta }_{1}}{{q}_{2}}({{t}_{a}})]. \\ \end{gathered} $Параметры ${{\theta }_{i}}$ суть компоненты вектора бесконечно малого поворота, задающего изменение ориентации спутника в окрестности положения $Q({{t}_{a}}).$ Эти параметры и поправки $\Delta {{\chi }_{i}}$ находятся из системы нормальных уравнений с матрицей $\left\| {{{G}_{{ij}}}} \right\|_{{i,j = 1}}^{9}$ и правой частью $\left\| {{{D}_{i}}} \right\|_{{i = 1}}^{9}\,:$
Здесь ${{p}_{1}},{{p}_{2}}, \ldots {{p}_{9}}$ – обозначения величин θ1, θ2, θ3, ${{\chi }_{1}},$ ${{\chi }_{2}},{{\chi }_{3}},{{\gamma }_{1}},{{\alpha }_{1}},{{\beta }_{1}}$ в указанном порядке, $\partial {{\hat {\varphi }}_{l}}{{(t)} \mathord{\left/ {\vphantom {{(t)} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}$ – псевдопроизводные, служащие для представления истинных производных. Псевдопроизводная – это не частная производная некоторой функции по какому-то параметру. Запись ее в виде частной производной используется лишь для удобства. Такую запись следует воспринимать как единый символ с двумя индексами. Псевдопроизводная – это вектор, являющийся аналогом угловой скорости. В кинематике твердого тела угловая скорость служит для расчета производных по времени, а псевдопроизводная используется для расчета производных по параметру. В обозначении $\partial {{\hat {\varphi }}_{l}}{{(t)} \mathord{\left/ {\vphantom {{(t)} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}$ индекс l указывает векторную компоненту, индекс i – номер параметра, по которому выполняется дифференцирование. Приведем формулы для расчета псевдопроизводных в системе нормальных уравнений и расчета некоторых настоящих производныхЗначения псевдопроизводных ${{\partial {{\varphi }_{l}}} \mathord{\left/ {\vphantom {{\partial {{\varphi }_{l}}} {\partial {{p}_{j}}}}} \right. \kern-0em} {\partial {{p}_{j}}}}$ $(j = 1,2, \ldots 6)$ определяются в процессе интегрирования уравнений
Прибавление найденных поправок $\Delta {{q}_{j}}({{t}_{a}})$ к имеющимся значениям ${{q}_{j}}({{t}_{a}})$ нарушает условие (7), поэтому новый кватернион ориентации нормируется. Внесенные нормировкой изменения уточненных компонент кватерниона являются величинами второго порядка относительно $\Delta {{q}_{j}}({{t}_{a}}).$
Точность аппроксимации измерений и оценки ${{z}_{ * }}$ будем характеризовать, следуя методу наименьших квадратов, соответствующими стандартными отклонениями. Последние вычисляются в предположении, что ошибки в измерениях некоррелированы и имеют одинаковые дисперсии, средние значения ошибок в измерениях одной и той же векторной компоненты напряженности МПЗ равны. Такой подход выбран из соображений удобства и вида функционала (6). При сделанных допущениях $z{\text{*}}$ – случайный вектор, который имеет приблизительно нормальное распределение со средним значением, равным истинному значению z. Вследствие условия (7) это распределение – несобственное, т.е. имеет вырожденную ковариационную матрицу. Чтобы избежать вырождения и сделать характеризацию ошибок более наглядной, ошибки $\Delta {{q}_{j}}({{t}_{a}})$ в задании компонент ${{q}_{j}}({{t}_{a}})$ вектора $z{\text{*}}$ представим в виде (8), где теперь ${{\theta }_{i}}$ образуют случайный вектор бесконечно малого поворота. Величины ${{\theta }_{i}}$ имеют нулевые математические ожидания и вместе с ошибками остальных компонент $z{\text{*}}$ описываются ковариационной матрицей
Описанный подход практически без изменения применим в случае, когда вместо данных магнитометра 1 обрабатываются взвешенные данные (3) или данные магнитометра 2, пересчитанные в систему ${{y}_{1}}{{y}_{2}}{{y}_{3}}$ по формулам (2). Реализован также вариант обработки данных магнитометра 2 без пересчета их в систему ${{y}_{1}}{{y}_{2}}{{y}_{3}}.$ В этом варианте использовалась матрица перехода от системы ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе ${{z}_{1}}{{z}_{2}}{{z}_{3}}$ и уточнялись параметризирующие ее углы. Однако вариант обработки взвешенных данных дает наименьшее значение σ, и ниже приводятся результаты только этого варианта.
Вернемся к описанию методики. Чтобы обеспечить надежную сходимость описанного процесса, надо предусмотреть возможность его регуляризации. В данном случае регуляризация сводилась к предварительному использованию метода Левенберга–Марквардта [8] перед переходом к методу Гаусса–Ньютона. Почти всегда метод Левенберга–Марквардта плавно трансформировался в метод Гаусса–Ньютона, но иногда по окончании его работы метод Гаусса–Ньютона расходился. В таком случае в качестве $z{\text{*}}$ принимался результат, полученный методом Левенберга–Марквардта; он вполне обеспечивал требуемую точность реконструкции.
Пример реконструкции вращательного движения спутника на интервале времени 2 приведены на рис. 4–7. На рис. 4а изображены графики углов, характеризующих ориентацию спутника. Здесь λ и $\vartheta $ – углы отклонения оси ${{x}_{2}}$ от орта ${\mathbf{s}}$ направления “Земля–Солнце”, ${\mathbf{s}} = ({{S}_{1}},{{S}_{2}},{{S}_{3}})$ в системе ${{Y}_{1}}{{Y}_{2}}{{Y}_{3}}.$ Углы вычисляются по формулам
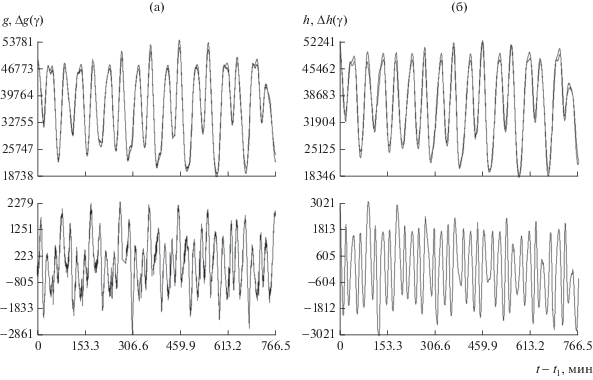
Рис. 5.
Движение КА. Момент $t = 0$ на графиках отвечает 05:12:22.2 UTC 19.VI.2016 г. $\sigma = 574\gamma ,$ смещения магнитных измерений: ${{\Delta }_{1}}$ = 1310γ, ${{\Delta }_{2}}$ = 2094γ, ${{\Delta }_{3}}$ = –1165γ.
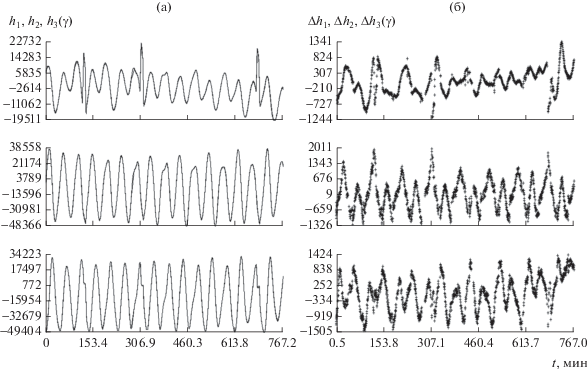
Рис. 7.
Движение КА в солнечной ориентации. Момент $t = 0$ на графиках отвечает 05:12:22.2 UTC 19.VI.2016 г.
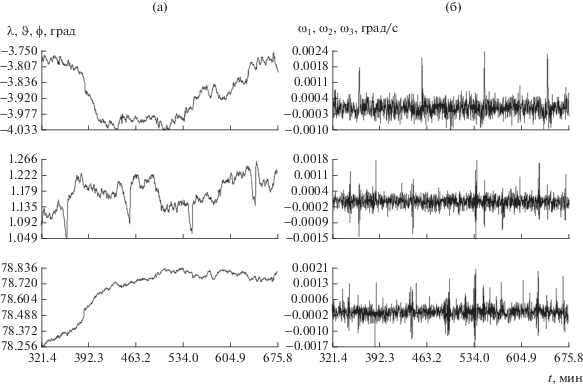
Плоскость отсчета угла $\vartheta $ содержит ось ${{Y}_{3}}$ и прямую “Земля–Солнце”. Направление отсчета этого угла – на север. Плоскость отсчета угла λ параллельна плоскости ${{Y}_{1}}{{Y}_{2}},$ направление отсчета угла λ – на восток. Угол φ – это угол между осью ${{x}_{1}}$ приборной системы и плоскостью орбиты; при $0 < \varphi < \pi $ эта ось лежит в полупространстве, в которое направлен кинетический момент орбитального движения спутника. Функция $\zeta (t)$ (нижний график) характеризует тень Земли: в тени $\zeta < 0,$ на свету $\zeta > 0.$ Эта функция рассчитывается по формуле
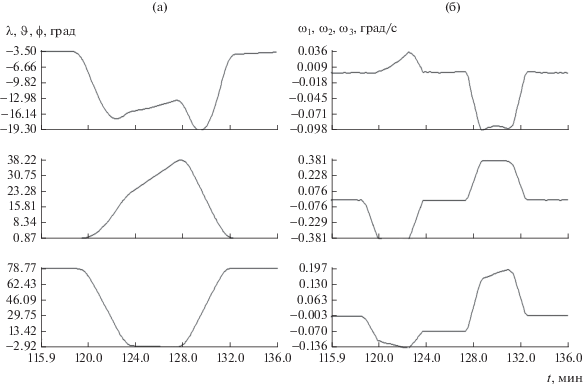
Рис. 4б содержат графики функций (5). Рис. 5а и 5б характеризуют построенную аппроксимацию магнитных измерений. На рис. 5а в каждой системе координат изображены две линии, которые практически сливаются. Одна из них – график функции ${{\hat {h}}_{i}}(t)$ (см. (6)), а другая – ломаная, звенья которой соединяют соседние по времени точки $({{t}_{n}},\tilde {g}_{i}^{{(n)}} - {{\Delta }_{i}}),$ $n = 1,2, \ldots N.$ Здесь $\tilde {g}_{i}^{{(n)}}$ – включенные в обработку измерения (3) при значениях ρ, ук-азанных в п. 2. На рис. 5б изображены аналогичные ломаные, соединяющие точки $({{t}_{n}},\Delta h_{l}^{{(n)}}),$ $\Delta h_{i}^{{(n)}} = \tilde {g}_{i}^{{(n)}} - {{\hat {h}}_{i}}({{t}_{n}}) - {{\Delta }_{i}}.$ Рис. 6 и 7 в увеличенном масштабе воспроизводят фрагменты графиков на рис. 4. Рис. 6 иллюстрирует развороты спутника, рис. 7 – режим солнечной ориентации. Судя по графикам углов λ и $\vartheta $, ориентация на Солнце оси ${{x}_{2}}$ спутника поддерживалась с требуемой точностью. Графики, иллюстрирующие реконструкции движения спутника на интервалах 1 и 3 приведены в [10].
Некоторые числовые характеристики результатов реконструкции на интервалах 1–3 в табл. 6. В табл. 7, 8 приведены оценки смещений в измерениях угловой скорости и оценки углов, задающих матрицу B (в скобках рядом с оценками указаны их стандартные отклонения).
Таблица 6.
Результаты обработки магнитных измерений и точность определения начальной ориентации спутника
| № инт. |
$\sigma $ | ${{\Delta }_{1}}$ | ${{\Delta }_{2}}$ | ${{\Delta }_{3}}$ | ${{\sigma }_{{\theta 1}}}$ | ${{\sigma }_{{\theta 2}}}$ | ${{\sigma }_{{\theta 3}}}$ |
|---|---|---|---|---|---|---|---|
| γ | рад. | ||||||
| 1 | 579 | 1851 | 1825 | –782 | 0.0024 | 0.0043 | 0.0033 |
| 2 | 574 | 1310 | 2094 | –1165 | 0.0025 | 0.015 | 0.0055 |
| 3 | 531 | 1658 | 1959 | –792 | 0.0012 | 0.0031 | 0.0033 |
Таблица 7.
Оценки смещений в измерениях угловой скорости
| № инт. | ${{\chi }_{1}}({{\sigma }_{{\chi 1}}}),\,\,{{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 1}}}$ | ${{\chi }_{2}}({{\sigma }_{{\chi 2}}}),\,\,{{10}^{{ - 6}}}\,{{{\text{c}}}^{{ - 1}}}$ | ${{\chi }_{3}}({{\sigma }_{{\chi 3}}}),\,\,{{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 1}}}$ |
|---|---|---|---|
| 1 | –2.628 (0.046) | –0.423 (0.059) | 0.494 (0.062) |
| 2 | –2.328 (0.023) | 0.915 (0.037) | 0.106 (0.039) |
| 3 | –2.524 (0.044) | 0.275 (0.056) | 0.596 (0.054) |
Таблица 8.
Оценки углов, задающих матрицу B
| № инт. | ${{\gamma }_{1}}({{\sigma }_{{\gamma 1}}}),$ рад. | ${{\alpha }_{1}}({{\sigma }_{{\alpha 1}}}),$ рад. | ${{\beta }_{1}}({{\sigma }_{{\beta 1}}}),$ рад. |
|---|---|---|---|
| 1 | 0.019 (0.0022) | –0.047 (0.0044) | –0.037 (0.0031) |
| 2 | 0.006 (0.0021) | –0.083 (0.015) | –0.051 (0.0054) |
| 3 | 0.018 (0.0018) | –0.046 (0.0038) | –0.035 (0.0028) |
Совместный анализ стандартных отклонений и собственных векторов матрицы G (см. п. 3), отвечающих ее нескольким минимальным собственным числам, позволяет понять характер неопределенности, которая возникает при реконструкции движения. Анализ основан на формуле
Таблица 9.
Минимальные собственные числа и отвечающие им собственные векторы матрицы G
| № инт. | 1 | 2 | 3 |
|---|---|---|---|
| ${{\mu }_{1}}$ | 2.2487 | 0.2693 | 2.7409 |
| ${{\mu }_{2}}$ | 22.501 | 16.577 | 39.487 |
| ${{\theta }_{1}}$ | –0.2623950 | –0.0644294 | 0.0612275 |
| ${{\theta }_{2}}$ | 0.5344448 | 0.6646836 | 0.4550442 |
| ${{\theta }_{3}}$ | 0.3806833 | 0.2350053 | 0.4972072 |
| ${{\chi }_{1}}$ | –0.0008006 | –0.0000295 | 0.0001163 |
| ${{\chi }_{2}}$ | 0.0005695 | –0.0000721 | 0.0018059 |
| ${{\chi }_{3}}$ | –0.0019524 | –0.0001282 | 0.0019804 |
| ${{\gamma }_{1}}$ | –0.2516316 | –0.0304608 | –0.2397089 |
| ${{\alpha }_{1}}$ | 0.5449980 | 0.6660038 | 0.5707202 |
| ${{\beta }_{1}}$ | 0.3745020 | 0.2330840 | 0.3984744 |
Обработка сокращенных интервалов измерений показала, что для надежного определения углов ${{\gamma }_{1}},$ ${{\alpha }_{1}},$ ${{\beta }_{1}}$ необходимо рассматривать интервалы, содержащие некоторое число интенсивных разворотов спутника.
Данная работа выполнена при поддержке РФФИ (проект 17-01-00143).
Список литературы
Абрашкин В.И., Воронов К.Е., Пияков И.В. и др. Определение вращательного движения спутника Бион М-1 средствами аппаратуры ГРАВИТОН // Космич. исслед. 2015. Т. 53. № 4. С. 306–319. (Cosmic Research. P. 286.)
Абрашкин В.И., Воронов К.Е., Пияков И.В. и др. Вращательное движение спутника Фотон М-4 // Космич. исслед. 2016. Т. 54. № 4. С. 315–322. (Cosmic Research. P. 296.)
Абрашкин В.И., Воронов К.Е., Пияков И.В. и др. Упрощенная методика определения вращательного движения спутника по бортовым измерениям угловой скорости и магнитного поля Земли // Космич. исслед. 2016. Т. 54. № 5. С. 402–414. (Cosmic Research. P. 375.)
Абрашкин В.И., Богоявленский Н.Л., Воронов К.Е. и др. Неуправляемое вращательное движение спутника Фотон М-2 и квазистатические микроускорения на его борту // Космич. исслед. 2007. Т. 45. № 5. С. 450–470. (Cosmic Research. P. 424.)
Абрашкин В.И., Воронов К.Е., Пияков А.В. и др. Неуправляемое вращательное движение малого спутника Аист // Космич. исслед. 2015. Т. 53. № 5. С. 395–408. (Cosmic Research. P. 360.)
Абрашкин В.И., Воронов К.Е., Пияков А.В. и др. Неуправляемое вращательное движение опытного образца малого космического аппарата Аист // Космич. исслед. 2017. Т. 55. № 2. С. 135–149. (Cosmic Research. P. 128.)
Hoots F.R., Roehrich R.L. Models for propagation of NORAD element sets. Spacetrack report No. 3. 1988.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М., Мир, 1985.
Панкратов В.А., Сазонов В.В. Проверка согласованности данных измерений магнитометров, установленных на борту ИСЗ. Препринты ИПМ им. М.В. Келдыша. 2010. № 42.
Абрашкин В.И., Воронов К.Е., Дорофеев А.С. и др. Определение вращательного движения малого космического аппарата Аист-2Д по данным научной аппаратуры КМУ-1. Препринты ИПМ им. М.В. Келдыша. 2017. № 57.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования