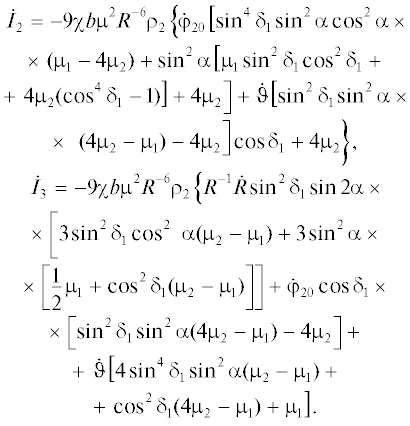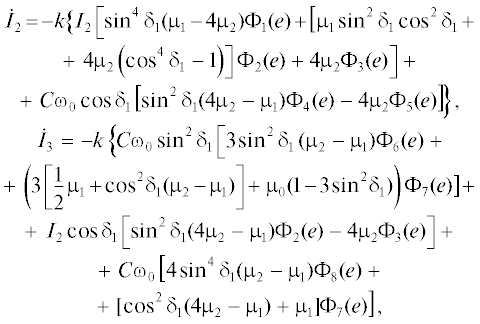Космические исследования, 2019, T. 57, № 2, стр. 147-156

О вращениях КА, несущего деформируемую антенну в гравитационном поле сил

Ю. Г. Марков¹, И. В. Скоробогатых^1, *

¹ Московский авиационный институт (национальный исследовательский университет)
г. Москва, Россия

Поступила в редакцию 17.05.2017
После доработки 27.04.2018
Принята к публикации 15.05.2018

DOI: 10.1134/S0023420619020055

Аннотация

Изучается задача о движении относительно центра масс спутника, обращающегося вокруг притягивающего центра по эллиптической орбите. Спутник состоит из осесимметричных твердой и вязкоупругой частей, причем вязкоупругая часть – это полусферическая антенна. Показано, что эволюцию вращений спутника можно разбить на два этапа – быстрый, вследствие деформаций, вызванных силами инерции, и медленный – диссипативный. Показано, что этап быстрой эволюции заключается в том, что вектор кинетического момента расположится вдоль оси симметрии спутника (в случае, если осевой момент инерции больше экваториального), и в экваториальной плоскости эллипсоида инерции (в случае, если экваториальный момент инерции больше осевого). Этап медленной эволюции был рассмотрен для случая, когда осевой момент инерции больше экваториального. Установлено, что медленная эволюция заключается в замедлении осевого вращения, и наклонении вектора кинетического момента к плоскости орбиты.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается задача об эволюции вращательного движении спутника, несущего полусферическую антенну и движущегося по эллиптической орбите вокруг притягивающего центра. Спутник состоит из твердой части, соединенной с вязкоупругой полусферической антенной в ее полюсе. Предполагается, что твердая часть спутника осесимметрична, причем ее ось симметрии совпадает с осью симметрии полусферической антенны (при отсутствии деформаций). Антенна предполагается однородной и изотропной, представляющей собой достаточно жесткое тело, деформации которого малы.

Пусть твердая часть спутника занимает область ${{\Omega }_{1}} \in {{E}^{3}},$ а вязкоупругая антенна занимает область ${{\Omega }_{2}} \in {{E}^{3}},$ при этом области ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ имеют общую границу ненулевой площади, на которой перемещения точек упругой части равны нулю. Весь спутник занимает область $\Omega = {{\Omega }_{1}} \cup {{\Omega }_{2}},$ его плотность обозначим через $\rho ,$ при этом $\rho = {{\rho }_{1}},$ когда точка принадлежит твердой части и $\rho = {{\rho }_{2}}$, когда принадлежит упругой.

В инерциальной системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ с началом в притягивающем центре O орбита центра масс спутника лежит в плоскости $O{{\xi }_{1}}{{\xi }_{2}}.$ Движение центра масс С спутника задается его радиус-вектором

(1)

$\begin{gathered} R = {{R}^{0}}R,\,\,\,\,{{R}^{0}} = \cos \vartheta \xi _{1}^{0} + \sin \vartheta \xi _{2}^{0}, \\ \dot {\vartheta } = \frac{{{{\omega }_{0}}{{{(1 + e\cos \vartheta )}}^{2}}}}{{{{{(1 - {{e}^{2}})}}^{{3/2}}}}},\,\,\,\,R = \frac{{a(1 - {{e}^{2}})}}{{1 + e\cos \vartheta }}. \\ \end{gathered} $

Здесь обозначено: ${{\omega }_{0}}$ – среднее движение центра масс спутника, e, a – эксцентриситет и большая полуось орбиты, $\vartheta $ – истинная аномалия, $\xi _{i}^{0}$ – орт по оси $O{{\xi }_{i}},\,\,i = 1,2,3.$

Пусть точка $C{\text{'}}$ – центр масс недеформированного спутника, а оси системы координат $C{\kern 1pt} {\text{'}}x_{1}^{'}x_{2}^{'}x_{3}^{'}$ направлены по его главным центральным осям инерции (в недеформированном состоянии) и жестко связаны с твердой частью. При этом ось $C{\kern 1pt} {\text{'}}x_{3}^{'}$ является осью динамической симметрии и совпадает с осью симметрии антенны. Пусть ${{{\mathbf{u}}}_{C}}$ – радиус-вектор центра масс С относительно $C{\text{'}},$ а оси $C{{x}_{i}}$ параллельны осям $C{\text{'}}x_{i}^{'}$ (i = 1, 2, 3). Радиус-вектор произвольной точки спутника относительно точки $C{\kern 1pt} {\text{'}}$ будет равен ${\mathbf{r}} + {\mathbf{u}}{\text{'}},$ а относительно центра масс С будет равен

${\mathbf{r}} + {\mathbf{u}},\,\,\,\,{\mathbf{u}} = {\mathbf{u}}{\text{'}} - {{{\mathbf{u}}}_{C}},\,\,\,\,{{{\mathbf{u}}}_{C}} = {{M}^{{ - 1}}}\int\limits_{{{\Omega }_{2}}} {{{\rho }_{2}}} {\mathbf{u}}{\text{'}}dx.$

Здесь $M = \int_\Omega {{\kern 1pt} \rho dx} $ – масса спутника; ${\mathbf{u}}$ и ${\mathbf{u}}{\text{'}}$ – соответственно вектор перемещений частицы упругой части спутника относительно систем координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и $C{\text{'}}x_{1}^{'}x_{2}^{'}x_{3}^{'},$ занимавшей в недеформированном состоянии положение ${\mathbf{r}} = {{({{x}_{1}},{{x}_{2}},{{x}_{3}})}^{T}}.$ Обозначим координаты вектора u в системе координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ через ${{u}_{1}},{{u}_{2}},{{u}_{3}}.$

Будем использовать модель линейной теории вязкоупругости малых деформаций. Функционал потенциальной энергии упругих деформаций обозначим через $E[{\mathbf{u}}],$ тогда [1]:

$E[{\mathbf{u}}] = \int\limits_{{{\Omega }_{2}}} {\sum\limits_{m.n,i,j} {\tfrac{1}{4}{{a}_{{mnij}}}\left( {\frac{{\partial {{u}_{m}}}}{{\partial {{x}_{n}}}} + \frac{{\partial {{u}_{n}}}}{{\partial {{x}_{m}}}}} \right)\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)} } dx,$

а диссипативный функционал представится как

${\text{D}}[{\mathbf{\dot {u}}}] = \chi bE[{\mathbf{\dot {u}}}].$

Здесь χ – постоянная, характеризующая рассеяние энергии в полусферической антенне при деформациях; b – размерная константа.

Заметим, что, вообще говоря, функционал энергии упругих деформаций должен зависеть от перемещений ${\mathbf{u}}{\text{'}}$ относительно системы координат $C{\kern 1pt} {\text{'}}x_{1}^{'}x_{2}^{'}x_{3}^{'},$ связанной с центром масс недеформированного спутника, и неподвижной относительно твердой части, то есть $E = E[{\mathbf{u}}{\text{'}}].$ Но, поскольку вектор ${{{\mathbf{u}}}_{C}}$ не зависит от координат ${{x}_{i}},$ то следовательно

$\frac{{\partial {\mathbf{u}}{\text{'}}}}{{\partial {{x}_{i}}}} = \frac{{\partial ({\mathbf{u}} + {{{\mathbf{u}}}_{C}})}}{{\partial {{x}_{i}}}} = \frac{{\partial {\mathbf{u}}}}{{\partial {{x}_{i}}}},$

и можно записать

$\begin{gathered} E[{\mathbf{u}}{\text{'}}] = \int\limits_{{{\Omega }_{2}}} {\sum\limits_{m.n,i,j} {\tfrac{1}{4}{{a}_{{mnij}}}\left( {\frac{{\partial u_{m}^{'}}}{{\partial {{x}_{n}}}} + \frac{{\partial u_{n}^{'}}}{{\partial {{x}_{m}}}}} \right)\left( {\frac{{\partial u_{i}^{'}}}{{\partial {{x}_{j}}}} + \frac{{\partial u_{j}^{'}}}{{\partial {{x}_{i}}}}} \right)} } dx = \\ = \int\limits_{{{\Omega }_{2}}} {\sum\limits_{m.n,i,j} {\tfrac{1}{4}{{a}_{{mnij}}}\left( {\frac{{\partial {{u}_{m}}}}{{\partial {{x}_{n}}}} + \frac{{\partial {{u}_{n}}}}{{\partial {{x}_{m}}}}} \right)\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)} } dx = E[{\mathbf{u}}], \\ \end{gathered} $

то есть, совершенно корректно можно писать $E = E[{\mathbf{u}}].$ То же самое, конечно, справедливо и для диссипативного функционала.

Потенциальная энергия гравитационного поля запишется в виде

(2)

$U = - \int\limits_\Omega {\frac{{\mu {\kern 1pt} \rho }}{{{{{\left[ {{{{({\mathbf{R}} + O({\mathbf{r}} + {\mathbf{u}}))}}^{2}}} \right]}}^{{1{\text{/}}2}}}}}dx} ,$

где $\mu $ – гравитационная постоянная притягивающего центра, О = О(t) – матрица перехода от осей $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к осям Кенига $C\xi _{1}^{'}\xi _{2}^{'}\xi _{3}^{'}.$

Функционал потенциальной энергии гравитационного поля. Преобразуем выражение (2) для функционала потенциальной энергии гравитационного поля, разложив его в ряд по степеням малого параметра $\varepsilon \sim \left| {\mathbf{u}} \right|{\text{/}}\left| {\mathbf{r}} \right|.$ Кроме того, поскольку можно считать $\left| {\mathbf{u}} \right| \ll \left| {\mathbf{r}} \right| \ll \left| {\mathbf{R}} \right|$ будем считать справедливыми следующие соотношения эквивалентности

$\frac{{\left| {\mathbf{r}} \right|}}{{\left| {\mathbf{R}} \right|}}\sim \varepsilon ,\,\,\,\,\frac{{\left| {\mathbf{u}} \right|}}{{\left| {\mathbf{R}} \right|}}\sim {{\varepsilon }^{2}}.$

Отсюда, отбрасывая члены порядка ${{\varepsilon }^{4}}$ и выше выводим

$\begin{gathered} U \approx - \frac{{\mu {\kern 1pt} M}}{R} + \frac{1}{2}\frac{{\mu {\kern 1pt} }}{{{{R}^{3}}}}\int\limits_\Omega {{{r}^{2}}\rho dx} + \frac{{\mu {\kern 1pt} }}{{{{R}^{3}}}}\int\limits_{{{\Omega }_{2}}} {{\mathbf{ru}}\rho dx} + \\ + \,\,\frac{{\mu {\kern 1pt} }}{{{{R}^{2}}}}\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},\int\limits_\Omega {{\mathbf{r}}\rho dx} } \right) + \frac{{\mu {\kern 1pt} }}{{{{R}^{2}}}}\int\limits_{{{\Omega }_{2}}} {\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}} \right)\rho dx} - \\ - \,\,\frac{3}{8}\frac{{\mu {\kern 1pt} }}{R}\int\limits_\Omega {\left( {\frac{{4{{{\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)}}^{2}}}}{{{{R}^{2}}}} + \frac{{4{{r}^{2}}\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)}}{{{{R}^{3}}}}} \right.} + \\ \left. { + \,\,8\frac{{\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}} \right)}}{{{{R}^{2}}}}} \right)\rho dx. \\ \end{gathered} $

Упростим полученное выражение для гравитационного потенциала. Для этого заметим, что первое слагаемое не зависит от параметров вращения спутника, и может быть опущено. Второе слагаемое дает

$\begin{gathered} \frac{1}{2}\frac{\mu }{{{{R}^{3}}}}\int\limits_\Omega {{{r}^{2}}\rho dx} = \frac{1}{2}\frac{{\mu {\kern 1pt} }}{{{{R}^{3}}}}\int\limits_\Omega {\left( {x_{1}^{2} + x_{2}^{2} + x_{3}^{2}} \right)\rho dx} = \\ = \frac{1}{2}\frac{{\mu {\kern 1pt} }}{{{{R}^{3}}}}\left( {\frac{1}{2}C + \frac{1}{2}B + \frac{1}{2}A} \right) = \frac{1}{2}\frac{{\mu {\kern 1pt} }}{{{{R}^{3}}}}\left( {\frac{C}{2} + A} \right). \\ \end{gathered} $

Здесь введены обозначения для моментов инерции недеформированного спутника: С – момент инерции относительно оси симметрии $C{\text{'}}x_{3}^{'}$ и А = B – моменты инерции относительно осей $C{\kern 1pt} {\text{'}}x_{1}^{'}$ и $C{\kern 1pt} {\text{'}}x_{2}^{'}.$ Это слагаемое может быть отброшено по тем же соображениям, что и первое. Четвертое слагаемое равняется нулю, поскольку $\int_\Omega {{\mathbf{r}}\rho dx} = 0.$ Пятое слагаемое также обращается в нуль, так как

$\begin{gathered} \int\limits_\Omega {{\mathbf{u}}\rho dx = \int\limits_\Omega {({\mathbf{u}}{\text{'}} - {{{\mathbf{u}}}_{C}})} } \rho dx = \\ = \int\limits_\Omega {{\mathbf{u}}{\text{'}}\rho dx - \int\limits_\Omega {{{{\mathbf{u}}}_{C}}\rho dx} = M{{{\mathbf{u}}}_{C}} - {{{\mathbf{u}}}_{C}}M = 0} . \\ \end{gathered} $

Вычислим предпоследний член

$\begin{gathered} - \frac{3}{2}\frac{\mu }{{{{R}^{4}}}}\int\limits_\Omega {{{r}^{2}}\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)\rho dx} = \\ = - \frac{3}{2}\frac{\mu }{{{{R}^{4}}}}\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},\int\limits_\Omega {{{r}^{2}}{\mathbf{r}}\rho dx} } \right). \\ \end{gathered} $

$\begin{gathered} \int\limits_\Omega {{{r}^{2}}{\mathbf{r}}\rho dx} = \int\limits_\Omega {\left( {x_{1}^{2} + x_{2}^{2} + x_{3}^{2}} \right)\left( {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right)\rho dx} = \\ = \int\limits_\Omega {\left( {\begin{array}{*{20}{c}} {x_{1}^{3} + {{x}_{1}}x_{2}^{2} + {{x}_{1}}x_{3}^{2}} \\ {x_{1}^{2}{{x}_{2}} + x_{2}^{3} + {{x}_{2}}x_{3}^{2}} \\ {x_{1}^{2}{{x}_{3}} + x_{2}^{2}{{x}_{3}} + x_{3}^{3}} \end{array}} \right){\kern 1pt} } \rho dx = 0. \\ \end{gathered} $

При вычислении интеграла использован факт, что нечетная функция дает нуль при интегрировании по симметричной области. Отсюда следует, что предпоследний член также равен нулю. В итоге получаем для гравитационного потенциала выражение:

$\begin{gathered} U \approx - \mu {{R}^{{ - 3}}}\int\limits_{{{\Omega }_{2}}} {\left[ {3\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}} \right) - ({\mathbf{r}},{\mathbf{u}})} \right]{{\rho }_{2}}dx} - \\ - \,\,\frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}\int\limits_\Omega {{{{\left( {{{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}}} \right)}}^{2}}\rho dx} . \\ \end{gathered} $

2. УРАВНЕНИЯ ДЛЯ МОДАЛЬНЫХ ПЕРЕМЕННЫХ

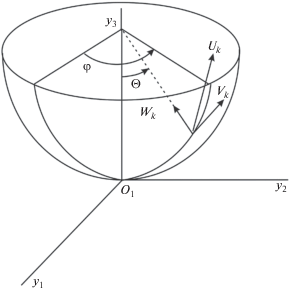
Уравнения для определения упругих перемещений получим из принципа Даламбера–Лагранжа аналогично [1]. Далее, введем некоторые физические предположения, позволяющие перейти к квазистатической постановке задачи вычисления упругих перемещений. Используем метод разделения движений, предложенный Вильке [1]. Будем предполагать, что наинизшая частота свободных упругих колебаний намного превосходит как угловую скорость орбитального движения спутника, так и угловую скорость его вращения относительно центра масс. Кроме того, будем считать, что вследствие вязкого трения свободные колебания затухли. Эти предположения позволяют отбросить члены с ${\mathbf{\ddot {R}}},{\mathbf{\ddot {u}}},{\mathbf{\dot {u}}}$ в уравнениях и перейти к квазистатической постановке. Вектор перемещений будем искать в виде ряда по собственным формам свободных упругих колебаний. Рэлей в [2] указал вид собственных форм для тонкой полусферической оболочки, закрепленной в полюсе:

(3)

$\begin{gathered} {{{\mathbf{V}}}_{k}} = {{w}_{k}}{{{\mathbf{e}}}_{r}} + {{\text{v}}_{k}}{{{\mathbf{e}}}_{\varphi }} + {{u}_{k}}{{{\mathbf{e}}}_{\theta }} = \\ = \,{{A}_{k}}{\text{t}}{{{\text{g}}}^{k}}\tfrac{\theta }{2}{\kern 1pt} ((k\, + \,\cos \theta ){\kern 1pt} \cos k\varphi ,\sin \theta \sin k\varphi ,\sin \theta \cos k\varphi ), \\ {{{\mathbf{W}}}_{k}} = {{A}_{k}} \times \\ \times \,\,{\text{t}}{{{\text{g}}}^{k}}\tfrac{\theta }{2}((k + \cos \theta )\sin k\varphi , - \sin \theta \cos k\varphi ,\sin \theta \sin k\varphi ), \\ k = 0,1,2,... \\ \end{gathered} $

Формы (3) заданы в сферических координатах r, φ, θ (рис. 1). Заметим, что если формы переобозначить и взять

${{{\mathbf{\tilde {V}}}}_{k}} = - {{{\mathbf{W}}}_{k}},\,\,\,\,{{{\mathbf{\tilde {W}}}}_{k}} = - {{{\mathbf{V}}}_{k}},$

то новые формы ${{{\mathbf{\tilde {V}}}}_{k}},{{{\mathbf{\tilde {W}}}}_{k}}$ будут иметь вид, аналогичный собственным формам осесимметричного упругого тела [1]. Опуская знак волны над формами, перепишем их в цилиндрических координатах r, φ, z в более компактной форме

(4)

$\begin{gathered} {{{\mathbf{V}}}_{k}} = \left( {{{U}_{k}}\sin k\varphi ,\,\,{{V}_{k}}\cos k\varphi ,\,\,{{W}_{k}}\sin k\varphi } \right), \\ {{{\mathbf{W}}}_{k}} = \left( {{{U}_{k}}\cos k\varphi ,\,\, - {{V}_{k}}\sin k\varphi ,\,\,{{W}_{k}}\cos k\varphi } \right). \\ \end{gathered} $

Рис. 1.

Компоненты собственных форм полусферической антенны.

Форма ${{{\mathbf{V}}}_{0}}$ будет при этом описывать крутильные деформации полусферы, а форма ${{{\mathbf{W}}}_{0}}$ – перемещения полусферы как целого вдоль ее оси симметрии. По этой причине форму ${{{\mathbf{W}}}_{0}}$ следует исключить из разложения вектора перемещений.

Используя выражения для форм (4) из принципа Даламбера–Лагранжа выведем систему уравнений для модальных переменных ${{p}_{k}}(t),{{q}_{k}}(t){\text{:}}$

(5)

Здесь использованы обозначения

$\begin{gathered} {{b}_{{kij}}} = \int\limits_{{{\Omega }_{2}}} {{{V}_{{ki}}}{{x}_{j}}dx} ,\,\,\,\,{{c}_{{kij}}} = \int\limits_{{{\Omega }_{2}}} {{{W}_{{ki}}}{{x}_{j}}dx} , \\ {{b}_{{021}}} = \pi \int\limits_{\Omega {\text{*}}} {{{V}_{0}}{{r}^{2}}drdz} ,\,\,\,\,{{b}_{{123}}} = \pi \int\limits_{\Omega {\text{*}}} {({{U}_{1}} + {{V}_{1}})zrdrdz} , \\ {{b}_{{132}}} = \pi \int\limits_{\Omega {\text{*}}} {{{W}_{1}}{{r}^{2}}drdz} ,\,\,\,\,{{b}_{{212}}} = \frac{\pi }{2}\int\limits_{\Omega {\text{*}}} {({{U}_{2}} + {{V}_{2}}){{r}^{2}}drdz} , \\ \end{gathered} $

$\Omega {\text{*}}$ – область, полученная пересечением ${{\Omega }_{2}}$ полуплоскостью, проходящей через ось симметрии твердой части спутника.

Из системы уравнений (5) видно, что деформации появляются только по формам с номерами k = 0, 1, 2, остальные модальные переменные остаются равными нулю.

Известно, что решение дифференциального уравнения

${{\nu }^{2}}q + \chi b{{\nu }^{2}}\dot {q} = A$

может быть найдено в виде ряда, приведенного в книге Вильке [1]:

$q = \sum\limits_{k = 0}^\infty {{{{( - \chi b)}}^{n}}\frac{{{{\partial }^{n}}\tilde {q}}}{{\partial {{t}^{n}}}}} ,$

где функция $\tilde {q}$ определяется из уравнения

${{\nu }^{2}}\tilde {q} = A.$

Будем решать данным способом систему (5), ограничившись первыми двумя членами ряда. В результате получим

(6)

3. ПЕРЕМЕННЫЕ АНДУАЙЕ И УРАВНЕНИЯ РАУСА

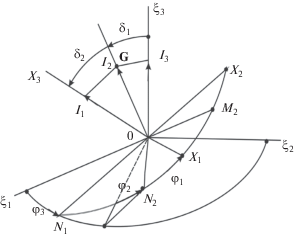
Для изучения эволюции вращательного движения КА как целого воспользуемся уравнениями Рауса. Уравнения Рауса для части переменных (в нашем случае – перемещений) имеют форму уравнений Лагранжа, а для другой части (канонических переменных) – уравнений Гамильтона. Уравнения для перемещений нами уже были получены ранее, поэтому нужно получить только уравнения для канонических переменных. В качестве канонических переменных используем переменные Андуайе [1] ${{I}_{1}},{{I}_{2}},{{I}_{3}},$ ${{\varphi }_{1}},{{\varphi }_{2}},{{\varphi }_{3}}$ (рис. 2), где ${{I}_{2}}$ – модуль кинетического момента G спутника относительно центра масс, ${{I}_{1}}$ – его проекция на ось симметрии спутника и ${{I}_{3}}$ – его проекция на нормаль к плоскости орбиты.

Рис. 2.

Переменные Андуайе.

Запишем уравнения движения для канонических переменных в форме уравнений Рауса:

(7)

${{\dot {I}}_{i}} = - {{\nabla }_{{{{\varphi }_{i}}}}}\tilde {R},\,\,\,\,{{\dot {\varphi }}_{i}} = {{\nabla }_{{{{I}_{i}}}}}\tilde {R},\,\,\,\,i = 1,2,3.$

Выпишем в явном виде выражение для функционала Рауса $\tilde {R} = \tilde {R}[{{I}_{i}},{{\varphi }_{i}},{\mathbf{u}},{\mathbf{\dot {u}}}].$ Обозначим через L функционал Лагранжа, тогда по определению функционала Рауса

$\begin{gathered} \tilde {R} = \sum\limits_{i = 1}^3 {{{I}_{i}}{{{\dot {\varphi }}}_{i}} - L} = \sum\limits_{i = 1}^3 {\frac{{\partial L}}{{\partial {{{\dot {\varphi }}}_{i}}}}{{{\dot {\varphi }}}_{i}} - L} , \\ L = T - U - E[{\mathbf{u}}], \\ \end{gathered} $

где T – кинетическая энергия, имеющая вид

$\begin{gathered} T = \frac{1}{2}\int\limits_\Omega {{{{(\omega \times (r + u) + {\mathbf{\dot {u}}})}}^{2}}\rho dx} = \\ = \frac{1}{2}\int\limits_\Omega {{{{(\omega \times (r + u))}}^{2}}\rho dx} + \\ + \,\,\int\limits_{{{\Omega }_{2}}} {(\omega \times (r + u))\dot {u}\rho dx} + \frac{1}{2}\int\limits_{{{\Omega }_{2}}} {{{{\dot {u}}}^{2}}\rho dx} . \\ \end{gathered} $

Так как

$\begin{gathered} \frac{{\partial L}}{{\partial {{{\dot {\varphi }}}_{i}}}} = \frac{\partial }{{\partial {{{\dot {\varphi }}}_{i}}}}\left( {T - U - E} \right) = \frac{{\partial T}}{{\partial {{{\dot {\varphi }}}_{i}}}} = \\ = \frac{\partial }{{\partial {{{\dot {\varphi }}}_{i}}}}\left( {\frac{1}{2}\int\limits_\Omega {{{{(\omega \times (r + u))}}^{2}}\rho dx} + \int\limits_{{{\Omega }_{2}}} {(\omega \times (r + u))\dot {u}\rho dx} } \right), \\ \end{gathered} $

то по теореме Эйлера об однородных функциях (первое слагаемое в скобках – функция второй степени, а второе – первой) получим:

$\begin{gathered} \tilde {R} = \sum\limits_{i = 1}^3 {\frac{{\partial L}}{{\partial {{{\dot {\varphi }}}_{i}}}}{{{\dot {\varphi }}}_{i}} - L} = 2\frac{1}{2}\int\limits_\Omega {{{{(\omega \times (r + u))}}^{2}}\rho dx} + \\ + \,\,\int\limits_{{{\Omega }_{2}}} {(\omega \times (r + u))\dot {u}\rho dx} - T + U + E[{\mathbf{u}}] = \\ = \frac{1}{2}\int\limits_\Omega {{{{(\omega \times (r + u))}}^{2}}\rho dx} - \frac{1}{2}\int\limits_{{{\Omega }_{2}}} {{{{\dot {u}}}^{2}}\rho dx + U + E[{\mathbf{u}}].} \\ \end{gathered} $

Кинетический момент спутника относительно центра масс записывается как:

(8)

$\begin{gathered} G = {{\nabla }_{{\mathbf{\omega }}}}T = \int\limits_\Omega {(r + u) \times [\omega \times (r + u) + \dot {u}]{\kern 1pt} \rho dx} = \\ = J\omega + {{G}_{{\mathbf{u}}}}, \\ \end{gathered} $

где

(9)

${{G}_{{\mathbf{u}}}} = \int\limits_\Omega {(r + u) \times \dot {u}\rho dx} ,$

а $J = J[{\mathbf{u}}]$ – тензор инерции. Используя формулы (8), (9) выражение для функционала Рауса преобразуем к виду:

(10)

$\begin{gathered} \tilde {R} = \\ = \frac{1}{2}(({\mathbf{G}} - {{{\mathbf{G}}}_{{\mathbf{u}}}}),{{J}^{{ - 1}}}({\mathbf{G}} - {{{\mathbf{G}}}_{{\mathbf{u}}}})) - \frac{1}{2}\int\limits_{{{\Omega }_{2}}} {{{{\dot {u}}}^{2}}\rho dx} + U + E[{\mathbf{u}}]. \\ \end{gathered} $

Вектор кинетического момента в переменных Андуайе записывается как

(11)

$G = {{\left( {\sqrt {I_{2}^{2} - I_{1}^{2}} \sin {{\varphi }_{1}},\sqrt {I_{2}^{2} - I_{1}^{2}} \cos {{\varphi }_{1}},{{I}_{1}}} \right)}^{T}},$

а матрица O(t) из формулы (2) запишется в виде

(12)

$O(t) = {{\Gamma }_{3}}({{\varphi }_{3}}){{\Gamma }_{1}}({{\delta }_{1}}){{\Gamma }_{3}}({{\varphi }_{2}}){\kern 1pt} {{\Gamma }_{1}}({{\delta }_{2}}){{\Gamma }_{3}}({\kern 1pt} {{\varphi }_{1}}),$

где

$\begin{gathered} {{\Gamma }_{3}}(\alpha ) = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }&0 \\ {\sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]; \\ {{\Gamma }_{1}}(\alpha ) = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \alpha }&{ - \sin \alpha } \\ 0&{\sin \alpha }&{\cos \alpha } \end{array}} \right]. \\ \end{gathered} $

Кроме того, справедливо равенство

$\begin{gathered} (G - {{G}_{{\mathbf{u}}}},{{J}^{{ - 1}}}(G - {{G}_{{\mathbf{u}}}})) = \\ = (\omega ,J[u]{\kern 1pt} \omega ) \approx ({{J}_{0}}\omega ,\omega ) + ({{J}_{1}}[u]{\kern 1pt} \omega ,\omega ) + ..., \\ \end{gathered} $

где ${{J}_{0}}$ – тензор инерции недеформированного спутника, ${{J}_{1}}[{\mathbf{u}}]$ – линейная по u компонента тензора инерции. Заметим, что вообще компоненты тензоров инерции спутника относительно центра масс С и центра масс в недеформированном состоянии $C{\kern 1pt} {\text{'}}$ отличаются друг от друга на члены второго порядка малости по u. Поскольку

$J[u] \approx {{J}_{0}} + {{J}_{1}}[u] + ...,$

то следовательно

${{J}^{{ - 1}}}[u] \approx {{({{J}_{0}} + {{J}_{1}}[u] + ...)}^{{ - 1}}}\, = \,{{({{J}_{0}}(E + J_{0}^{{ - 1}}{{J}_{1}}[u] + ...))}^{{ - 1}}}.$

Для любых квадратных невырожденных матриц S и P справедливо

${{(SP)}^{{ - 1}}} = {{P}^{{ - 1}}}{{S}^{{ - 1}}},$

а потому

$\begin{gathered} {{J}^{{ - 1}}}[u] \approx {{({{J}_{0}}(E + J_{0}^{{ - 1}}{{J}_{1}}[u] + ...))}^{{ - 1}}} = \\ = {{(E + J_{0}^{{ - 1}}{{J}_{1}}[u] + ...)}^{{ - 1}}}J_{0}^{{ - 1}} = \\ = (E - J_{0}^{{ - 1}}{{J}_{1}}[u] + ...)J_{0}^{{ - 1}} \approx J_{0}^{{ - 1}} - J_{0}^{{ - 1}}{{J}_{1}}[u]J_{0}^{{ - 1}}, \\ J_{0}^{{ - 1}} = {\text{diag}}\left( {{{A}^{{ - 1}}},{{A}^{{ - 1}}},{{C}^{{ - 1}}}} \right). \\ \end{gathered} $

Здесь A и C – экваториальный и осевой моменты инерции спутника в недеформированном состоянии. Найдем компоненты ${{J}_{1}}[u] = \left\| {J_{{ij}}^{1}} \right\|,$ раскладывая в ряд выражение для $J[u]$ и оставляя слагаемые пропорциональные первой степени координат вектора u:

$\begin{gathered} J_{{ii}}^{1} = 2\int\limits_{{{\Omega }_{2}}} {({\mathbf{ru}} - {{x}_{i}}{{u}_{i}}){{\rho }_{2}}dx} , \\ J_{{ij}}^{1} = - \int\limits_{{{\Omega }_{2}}} {({{x}_{i}}{{u}_{j}} + {{x}_{j}}{{u}_{i}}){\kern 1pt} } {{\rho }_{2}}dx,\,\,\,\,i \ne j. \\ \end{gathered} $

Мы считаем, что упругая часть спутника обладает достаточно большой жесткостью. Если жесткость устремить к бесконечности, то спутник становится абсолютно твердым телом, упругие перемещения u = 0, а следовательно, и ${\mathbf{\dot {u}}} = 0.$ Уравнения Рауса (7) в этом случае описывают вращение абсолютно твердого спутника. Получим уравнения (7) для этого случая.

Функция Рауса приобретает вид:

$\tilde {R} = \frac{1}{2}\left( {{\mathbf{G}},J_{0}^{{ - 1}}{\mathbf{G}}} \right) + U,$

где гравитационный потенциал

$U \approx - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}\int\limits_\Omega {{{{({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})}}^{2}}\rho dx} .$

Преобразуем выражение гравитационного потенциала:

$\begin{gathered} U = - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}\int\limits_\Omega {{{{({{\gamma }_{1}}{{x}_{1}} + {{\gamma }_{2}}{{x}_{2}} + {{\gamma }_{3}}{{x}_{3}})}}^{2}}\rho dx} = \\ = - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}\int\limits_\Omega {\left( {\gamma _{1}^{2}x_{1}^{2} + \gamma _{2}^{2}x_{2}^{2} + \gamma _{3}^{2}x_{3}^{2}} \right)\rho dx} . \\ \end{gathered} $

Но вследствие осевой симметрии

$\int\limits_\Omega {x_{1}^{2}\rho dx} = \int\limits_\Omega {x_{2}^{2}\rho dx} = \frac{1}{2}\int\limits_\Omega {\left( {x_{1}^{2} + x_{2}^{2}} \right)} \rho dx = \frac{1}{2}C.$

Кроме того

$\int\limits_\Omega {x_{3}^{2}\rho dx} = \int\limits_\Omega {\left( {x_{3}^{2} + x_{2}^{2}} \right)} \rho dx - \int\limits_\Omega {x_{2}^{2}\rho dx} = A - \frac{1}{2}C.$

Используя полученные формулы, выведем

$U \approx - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}\left[ {\frac{C}{2} + \gamma _{3}^{2}(A - C)} \right],$

при этом мы можем опустить константу С/2 в квадратных скобках, так как она не повлияет на вид уравнений Рауса, после чего выражение для U еще упростится:

$U \approx - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}(A - C)\gamma _{3}^{2}.$

Далее, первый член функционала Рауса запишется в виде

$\frac{1}{2}\left( {{\mathbf{G}},J_{0}^{{ - 1}}{\mathbf{G}}} \right) = \frac{1}{2}\left( {{{A}^{{ - 1}}}\left( {I_{2}^{2} - I_{1}^{2}} \right) + {{C}^{{ - 1}}}I_{1}^{2}} \right),$

и, таким образом, функционал Рауса станет

(13)

$\tilde {R} = \frac{1}{2}\left( {{{A}^{{ - 1}}}\left( {I_{2}^{2} - I_{1}^{2}} \right) + {{C}^{{ - 1}}}I_{1}^{2}} \right) - \frac{{3{\kern 1pt} }}{2}\mu {{R}^{{ - 3}}}(A - C)\gamma _{3}^{2},$

а уравнения Рауса приобретут вид

(14)

$\begin{gathered} {{{\dot {I}}}_{i}} = - \frac{{\partial{ \tilde {R}}{\kern 1pt} }}{{\partial {{\varphi }_{i}}}} = 3\mu {{R}^{{ - 3}}}(A - C){{\gamma }_{3}}\frac{{\partial {{\gamma }_{3}}}}{{\partial {{\varphi }_{i}}}},\,\,\,\,i = 1,2,3, \\ {{{\dot {\varphi }}}_{1}} = \frac{{\partial{ \tilde {R}}{\kern 1pt} }}{{\partial {{I}_{1}}}} = {{{\dot {\varphi }}}_{{10}}} - 3\mu {{R}^{{ - 3}}}(A - C){{\gamma }_{3}}\frac{{\partial {{\gamma }_{3}}}}{{\partial {{I}_{1}}}}, \\ {{{\dot {\varphi }}}_{{10}}} = {{I}_{1}}{{A}^{{ - 1}}}{{C}^{{ - 1}}}(A - C), \\ {{{\dot {\varphi }}}_{2}} = \frac{{\partial{ \tilde {R}}{\kern 1pt} }}{{\partial {{I}_{2}}}} = {{{\dot {\varphi }}}_{{20}}} - 3\mu {{R}^{{ - 3}}}(A - C){{\gamma }_{3}}\frac{{\partial {{\gamma }_{3}}}}{{\partial {{I}_{2}}}},\,\,\,\,{{{\dot {\varphi }}}_{{20}}} = {{A}^{{ - 1}}}{{I}_{2}}, \\ {{{\dot {\varphi }}}_{3}} = \frac{{\partial{ \tilde {R}}{\kern 1pt} }}{{\partial {{I}_{3}}}} = - 3\mu {{R}^{{ - 3}}}(A - C){{\gamma }_{3}}\frac{{\partial {{\gamma }_{3}}}}{{\partial {{I}_{3}}}}. \\ \end{gathered} $

Уравнения (14) описывают движение твердого спутника относительно центра масс как прецессию оси симметрии вокруг вектора кинетического момента G, в свою очередь прецессирующего вокруг нормали к плоскости орбиты [3]. Такое движение выберем в качестве невозмущенного.

Возмущающая часть потенциальной энергии гравитации будет иметь вид:

(15)

$U \approx - \mu {{R}^{{ - 3}}}\int\limits_{{{\Omega }_{2}}} {[3({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}) - ({\mathbf{r}},{\mathbf{u}})]{{\rho }_{2}}dx} .$

Вычислим теперь возмущающую часть кинетической энергии вращения. Для этого вначале преобразуем выражение $\frac{1}{2}(G - {{G}_{{\mathbf{u}}}},{{J}^{{ - 1}}}(G - {{G}_{{\mathbf{u}}}}))$ к виду:

$\frac{1}{2}\{ (G,J_{0}^{{ - 1}}G) - (G,J_{0}^{{ - 1}}{{J}_{1}}J_{0}^{{ - 1}}G) - 2(G,J_{0}^{{ - 1}}{{G}_{{\mathbf{u}}}})\} .$

Здесь были опущены члены более высокого чем первый порядка малости по u. Первый член в правой части равенства соответствует невозмущенному движению и не должен входить в возмущающую часть кинетической энергии. Таким образом, возмущающая функции Рауса будет иметь вид:

(16)

$\begin{gathered} \tilde {R} \approx \frac{1}{2}(G,J_{0}^{{ - 1}}G) - \frac{1}{2}(G,J_{0}^{{ - 1}}{{J}_{1}}J_{0}^{{ - 1}}G) - \\ - \,\,(G,J_{0}^{{ - 1}}{{G}_{{\mathbf{u}}}}) - \frac{1}{2}\int\limits_{{{\Omega }_{2}}} {{{{\dot {u}}}^{2}}\rho dx} - \\ - \mu {{R}^{{ - 3}}}\int\limits_{{{\Omega }_{2}}} {[3({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}) - ({\mathbf{r}},{\mathbf{u}})]{{\rho }_{2}}dx} + E[{\mathbf{u}}]. \\ \end{gathered} $

Мы будем писать уравнения Рауса только для канонических переменных, поэтому члены выражения (16), не зависящие от них, также можно опустить. Функция Рауса примет вид

(17)

$\begin{gathered} \tilde {R} \approx \tilde {R}{\text{*}} - \mu {{R}^{{ - 3}}}\int\limits_{{{\Omega }_{2}}} {3({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}){{\rho }_{2}}dx} , \\ \tilde {R}* = \frac{1}{2}\left( {G,J_{0}^{{ - 1}}G} \right) - \frac{1}{2}\left( {G,J_{0}^{{ - 1}}{{J}_{1}}J_{0}^{{ - 1}}G} \right) - \left( {G,J_{0}^{{ - 1}}{{G}_{{\mathbf{u}}}}} \right). \\ \end{gathered} $

Очевидно, что $\tilde {R}{\text{*}}$ не зависит от углов ${{\varphi }_{2}},{{\varphi }_{3}}$ и потому $\frac{{\partial{ \tilde {R}}{\text{*}}}}{{\partial {{\varphi }_{2}}}} = \frac{{\partial{ \tilde {R}}{\text{*}}}}{{\partial {{\varphi }_{3}}}} = 0.$ Уравнения Рауса для ${{I}_{i}}$ примут вид

(18)

$\begin{gathered} {{{\dot {I}}}_{i}} = - {{\nabla }_{{{{\varphi }_{i}}}}}\tilde {R}{\text{*}} + \mu {{R}^{{ - 3}}} \times \\ \times \,\,\left\{ {\int\limits_{{{\Omega }_{2}}} {3({{\nabla }_{{{{\varphi }_{i}}}}}({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}}),{\mathbf{r}})({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}){{\rho }_{2}}dx} } \right. + \\ + \left. {\,\,\int\limits_{{{\Omega }_{2}}} {3({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})({{\nabla }_{{{{\varphi }_{i}}}}}({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}}),{\mathbf{u}}){{\rho }_{2}}dx} } \right\}. \\ \end{gathered} $

Заметим, что деформации упругой части, описываемые формулами (6), вызываются двумя основными причинами – силами инерции вращения и диссипативными силами. Силы инерции при быстром вращении КА будут вызывать быструю эволюцию вращательного движения, в отличие от медленной диссипативной эволюции. Поэтому разобьем эволюцию на два этапа: быструю под действием сил инерции вращения и медленную под действием диссипативных сил, обусловленных рассеянием энергии при деформациях антенны, вызванных гравитационными силами.

4. БЫСТРАЯ ЭВОЛЮЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Из формул (17), (18) следует, что уравнения для ${{I}_{2}},{{I}_{3}}$ будут

${{\dot {I}}_{2}} = 0,\,\,\,\,{{\dot {I}}_{3}} = 0,$

т.е. переменные ${{I}_{2}},{{I}_{3}}$ не эволюционируют.

Получим уравнение для ${{I}_{1}}.$ Будем искать решения уравнений для модальных переменных, опустив члены с гравитацией и приняв $\omega \approx J_{0}^{{ - 1}}G.$ Найдем

(19)

$\begin{gathered} \omega \approx {{({{A}^{{ - 1}}}\sqrt {I_{2}^{2} - I_{1}^{2}} \sin {{\varphi }_{1}},{{A}^{{ - 1}}}\sqrt {I_{2}^{2} - I_{1}^{2}} \cos {{\varphi }_{1}},{{C}^{{ - 1}}}{{I}_{1}})}^{T}}, \\ \dot {\omega } \approx ({{A}^{{ - 1}}}\sqrt {I_{2}^{2}\, - \,I_{1}^{2}} {\kern 1pt} \cos {{\varphi }_{1}}\, \cdot \,{{{\dot {\varphi }}}_{{10}}}, \\ - {{A}^{{ - 1}}}\sqrt {I_{2}^{2}\, - \,I_{1}^{2}} {\kern 1pt} \sin {\kern 1pt} {{\varphi }_{1}}\, \cdot \,{{{\dot {\varphi }}}_{{10}}},0{{)}^{T}}. \\ \end{gathered} $

Из формул (6) и (19) определим значения модальных переменных

(20)

${{q}_{0}} = 0,\,\,\,\,{{p}_{0}} = 0,$

$\begin{gathered} {{q}_{1}} = - \nu _{1}^{{ - 2}}{{A}^{{ - 2}}}{{C}^{{ - 1}}}{{I}_{1}}\sqrt {I_{2}^{2} - I_{1}^{2}} \times \\ \times \,\,[C{{b}_{{123}}} + (2A - C){{b}_{{132}}}]\cos ({{\varphi }_{1}} - {{\alpha }_{1}}), \\ {{p}_{1}} = - \nu _{1}^{{ - 2}}{{A}^{{ - 2}}}{{C}^{{ - 1}}}{{I}_{1}}\sqrt {I_{2}^{2} - I_{1}^{2}} \times \\ \times \,\,[C{{b}_{{123}}} + (2A - C){{b}_{{132}}}]\sin ({{\varphi }_{1}} - {{\alpha }_{1}}), \\ {{q}_{2}} = - \nu _{2}^{{ - 2}}{{b}_{{212}}}{{A}^{{ - 2}}}(I_{2}^{2} - I_{1}^{2})\sin 2({{\varphi }_{1}} - {{\alpha }_{1}}), \\ {{p}_{2}} = \nu _{2}^{{ - 2}}{{b}_{{212}}}{{A}^{{ - 2}}}(I_{2}^{2} - I_{1}^{2})\cos 2({{\varphi }_{1}} - {{\alpha }_{1}}). \\ \end{gathered} $

В равенствах (20) использованы соотношения

$\begin{gathered} {{\alpha }_{1}} \approx \chi b{{{\dot {\varphi }}}_{{10}}},\,\,\,\,\cos {{\alpha }_{1}} \approx 1,\,\,\,\,\sin {{\alpha }_{1}} \approx \chi b{{{\dot {\varphi }}}_{{10}}}, \\ \cos {{\varphi }_{1}} + \chi b\sin {{\varphi }_{1}} \approx \cos {{\varphi }_{1}}\cos {{\alpha }_{1}} + \sin {{\varphi }_{1}}\sin {{\alpha }_{1}} = \\ = \cos ({{\varphi }_{1}} - {{\alpha }_{1}}). \\ \end{gathered} $

Далее находим

(21)

$J_{0}^{{ - 1}}{{J}_{1}}J_{0}^{{ - 1}} = \left\| {\begin{array}{*{20}{c}} {J_{{11}}^{1}{{A}^{{ - 2}}}}&{J_{{12}}^{1}{{A}^{{ - 2}}}}&{{{J}_{{13}}}{{A}^{{ - 1}}}{{C}^{{ - 1}}}} \\ {J_{{21}}^{1}{{A}^{{ - 2}}}}&{J_{{22}}^{1}{{A}^{{ - 2}}}}&{J_{{23}}^{1}{{A}^{{ - 1}}}{{C}^{{ - 1}}}} \\ {J_{{31}}^{1}{{A}^{{ - 1}}}{{C}^{{ - 1}}}}&{J_{{32}}^{1}{{A}^{{ - 1}}}{{C}^{{ - 1}}}}&{J_{{33}}^{1}{{C}^{{ - 2}}}} \end{array}} \right\|,$

$\begin{gathered} (G,J_{0}^{{ - 1}}{{G}_{{\mathbf{u}}}}) = (J_{0}^{{ - 1}}G,{{G}_{{\mathbf{u}}}}) = \\ = \int\limits_{{{\Omega }_{2}}} {\left[ {{{A}^{{ - 1}}}\sqrt {I_{2}^{2} - I_{1}^{2}} } \right.} \left( {({{x}_{2}}{{{\dot {u}}}_{3}} - {{x}_{3}}{{{\dot {u}}}_{2}})\sin {{\varphi }_{1}} + } \right. \\ \left. { + \,\,({{x}_{3}}{{{\dot {u}}}_{1}} - {{x}_{1}}{{{\dot {u}}}_{3}})\cos {{\varphi }_{1}}} \right) + \left. {{{C}^{{ - 1}}}{{I}_{1}}({{x}_{1}}{{{\dot {u}}}_{2}} - {{x}_{2}}{{{\dot {u}}}_{1}})} \right]{{\rho }_{2}}dx. \\ \end{gathered} $

После громоздких вычислений, используя формулы (18), (19), (20), (21), получим уравнение для ${{I}_{1}}{\text{:}}$

(22)

$\begin{gathered} {{{\dot {I}}}_{1}} = {{A}^{{ - 1}}}\sqrt {I_{2}^{2} - I_{1}^{2}} {{\rho }_{2}}\int\limits_{{{\Omega }_{2}}} {\{ ({{x}_{2}}{{{\dot {u}}}_{3}} - {{x}_{3}}{{{\dot {u}}}_{2}})\cos {{\varphi }_{1}}} - \\ - \,\,({{x}_{3}}{{{\dot {u}}}_{1}} - {{x}_{1}}{{{\dot {u}}}_{3}})\cos {{\varphi }_{1}} + {{A}^{{ - 1}}}\sqrt {I_{2}^{2} - I_{1}^{2}} \times \\ \times \,\,\left[ {({{x}_{2}}{{u}_{2}} - {{x}_{1}}{{u}_{1}})\sin 2{{\varphi }_{1}} - ({{x}_{1}}{{u}_{2}} + {{x}_{2}}{{u}_{1}})\cos 2{{\varphi }_{1}}} \right] + \\ + \,\,2{{C}^{{ - 1}}}{{I}_{1}}[{{x}_{2}}{{u}_{3}} + {{x}_{3}}{{u}_{2}})\sin {{\varphi }_{1}}\, - \,(({{x}_{1}}{{u}_{3}}\, + \,{{x}_{3}}{{u}_{1}})\cos {{\varphi }_{1}}]\} dx. \\ \end{gathered} $

Введем переменную ${{\varphi }_{{10}}} = {{\dot {\varphi }}_{{10}}}t$ (угол ${{\varphi }_{1}}$ описывает вращение вокруг оси симметрии спутника). Согласно уравнениям (14) она является быстрой переменной. Поэтому усредним уравнение (22) по переменной ${{\varphi }_{{10}}}.$ Отметим, что при усреднении все коэффициенты с номером k = 0 пропадают, что означает, что деформации по формам с индексом 0 не влияют на эволюцию вращательного движения спутника. Уравнение (22) заменится на усредненное:

(23)

$\begin{gathered} {{{\dot {I}}}_{1}} = \chi b{{A}^{{ - 5}}}{{C}^{{ - 1}}}{{\rho }_{2}}(C - A){{I}_{1}}(I_{2}^{2} - I_{1}^{2}) \times \\ \times \,\,[4(I_{2}^{2} - I_{1}^{2}){{\lambda }_{2}} + I_{1}^{2}{{\lambda }_{1}}], \\ \end{gathered} $

где

${{\lambda }_{1}}\, = \,\nu _{1}^{{ - 2}}{{[{{b}_{{123}}}\, + \,(2A{{C}^{{ - 1}}}\, - \,1){{b}_{{132}}}]}^{2}} > 0,\,\,\,{{\lambda }_{2}} = \nu _{2}^{{ - 2}}b_{{212}}^{2} > 0.$

Знак правой части уравнения (23) определяется знаком С – A. Если С > A, то производная ${{\dot {I}}_{1}} > 0$ и переменная ${{I}_{1}}$ монотонно возрастает, в случае С < A производная ${{\dot {I}}_{1}} < 0$ и переменная ${{I}_{1}}$ монотонно убывает. Стационарными движениями уравнения (23) будут ${{I}_{1}} = {{I}_{2}}$ и ${{I}_{1}} = 0.$

Уравнение в вариациях для стационарного движения ${{I}_{1}} = 0$ будет иметь вид

$\delta {{\dot {I}}_{1}} = k{{\lambda }_{2}}I_{2}^{4}\delta {{I}_{1}},\,\,\,\,k = \chi b{{A}^{{ - 5}}}{{C}^{{ - 1}}}{{\rho }_{2}}(C - A).$

Следовательно, стационарное движение ${{I}_{1}} = 0$ будет асимптотически устойчиво при С < A и неустойчиво при С > A.

Уравнение в вариациях для стационарного движения ${{I}_{1}} = {{I}_{2}}$ будет

$\delta {{\dot {I}}_{1}} = - 2k{{\lambda }_{1}}I_{1}^{4}\delta {{I}_{1}}.$

Следовательно, стационарное движение ${{I}_{1}} = {{I}_{2}}$ будет асимптотически устойчиво при С > A и неустойчиво при С < A.

Таким образом, в результате быстрой эволюции вектор кинетического момента спутника G будет либо при С > A стремиться занять положение вдоль оси симметрии $C{{x}_{3}}$ (при ${{I}_{1}} \to {{I}_{2}}$ углы ${{\delta }_{2}} \to 0,$ ${{\delta }_{1}} \to 0$ – см. рис. 2), либо при при С < A стремиться занять положение в экваториальной плоскости эллипсоида инерции (при ${{I}_{1}} \to 0$ угол ${{\delta }_{2}} \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ а угол ${{\delta }_{1}} \to 0$ см. рис. 2).

5. МЕДЛЕННАЯ ДИССИПАТИВНАЯ ЭВОЛЮЦИЯ

Рассмотрим случай медленной диссипативной эволюции КА. Будем считать быструю эволюцию (в случае C > A) закончившейся, и примем ${{I}_{1}} = {{I}_{2}},$ ${{\varphi }_{1}} = 0.$ Вычислим явно координаты вектора ${{O}^{{ - 1}}}{\mathbf{R}} = {{({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}})}^{T}}.$ По формулам (12):

(24)

$\left( {\begin{array}{*{20}{c}} {{{\gamma }_{1}}} \\ {{{\gamma }_{2}}} \\ {{{\gamma }_{3}}} \end{array}} \right) = {{({{{\Gamma }}_{{\text{3}}}}({{\varphi }_{3}}){{{\Gamma }}_{{\text{1}}}}({{\delta }_{1}}){{{\Gamma }}_{{\text{3}}}}({{\varphi }_{2}}){{{\Gamma }}_{{\text{1}}}}({{\delta }_{2}}){{{\Gamma }}_{{\text{3}}}}({{\varphi }_{1}}))}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {\cos \vartheta } \\ {\sin \vartheta } \\ 0 \end{array}} \right).$

Заметим, что ${{{\Gamma }}_{{\text{3}}}}({{\varphi }_{1}}) = {{{\Gamma }}_{{\text{3}}}}(0) = E,$ ${{{\Gamma }}_{{\text{1}}}}({{\delta }_{2}}) = {{{\Gamma }}_{{\text{1}}}}(0) = E,$ где E – единичная матрица. Поскольку ${{\delta }_{2}} = 0$ после завершения быстрой эволюции, то

(25)

$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{\gamma }_{1}}} \\ {{{\gamma }_{2}}} \\ {{{\gamma }_{3}}} \end{array}} \right) = {{({\Gamma }_{{\text{3}}}^{T}({{\varphi }_{2}}){\Gamma }_{{\text{1}}}^{T}({{\delta }_{1}}){\Gamma }_{{\text{3}}}^{T}({{\varphi }_{3}}))}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {\cos \vartheta } \\ {\sin \vartheta } \\ 0 \end{array}} \right) = \\ = \left( {\begin{array}{*{20}{c}} {\cos {{\varphi }_{2}}\cos \alpha + \sin {{\varphi }_{2}}\sin \alpha \cos {{\delta }_{1}}} \\ { - \sin {{\varphi }_{2}}\cos \alpha + \cos {{\varphi }_{2}}\sin \alpha \cos {{\delta }_{1}}} \\ { - \sin {{\delta }_{1}}\sin \alpha } \end{array}} \right). \\ \end{gathered} $

Здесь введен вспомогательной угол α:

$\alpha = \vartheta - {{\varphi }_{3}}.$

Вследствие справедливости формул $\frac{{\partial{ \tilde {R}}{\text{*}}}}{{\partial {{\varphi }_{2}}}}$ = $ = \frac{{\partial{ \tilde {R}}{\text{*}}}}{{\partial {{\varphi }_{3}}}} = 0,$ уравнения (18) для ${{I}_{2}},{{I}_{3}}$ упрощаются и принимают вид

(26)

$\begin{gathered} {{{\dot {I}}}_{i}} = \mu {{R}^{{ - 3}}}\left\{ {\int\limits_{{{\Omega }_{2}}} {3({{\nabla }_{{{{\varphi }_{i}}}}}({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}}),{\mathbf{r}})({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{u}}){{\rho }_{2}}dx} } \right. + \\ + \,\,\left. {\int\limits_{{{\Omega }_{2}}} {3({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}},{\mathbf{r}})({{\nabla }_{{{{\varphi }_{i}}}}}({{O}^{{ - 1}}}{{{\mathbf{R}}}^{0}}),{\mathbf{u}}){{\rho }_{2}}dx} } \right\},\,\,\,\,i = 2,3. \\ \end{gathered} $

Перепишем еще раз уравнения (26), преобразовав их к виду:

(27)

$\begin{gathered} {{{\dot {I}}}_{i}} = 3\mu {{R}^{{ - 3}}}\left\{ {\int\limits_{{{\Omega }_{2}}} {\frac{\partial }{{\partial {{\varphi }_{i}}}}[\gamma _{1}^{2}{{x}_{1}}{{u}_{1}} + \gamma _{2}^{2}{{x}_{2}}{{u}_{2}} + \gamma _{3}^{2}{{x}_{3}}{{u}_{3}}} } \right. + \\ + \,\,{{\gamma }_{1}}{{\gamma }_{2}}({{x}_{2}}{{u}_{1}} + {{u}_{2}}{{x}_{1}}) + {{\gamma }_{1}}{{\gamma }_{3}}({{x}_{3}}{{u}_{1}} + {{u}_{1}}{{x}_{3}}) + \\ \left. {{{ + }^{{^{{^{{^{{^{{}}}}}}}}}}}{{\gamma }_{2}}{{\gamma }_{3}}({{x}_{3}}{{u}_{2}} + {{u}_{2}}{{x}_{3}})]{{\rho }_{2}}dx} \right\},\,\,\,\,i = 2,3. \\ \end{gathered} $

Теперь надо вычислить значения нормальных координат для случая медленной диссипативной эволюции и подставить их в уравнения (27). Будем искать нормальные координаты, используя (6) и при их вычислении имея в виду, что выполняются условия ${{I}_{1}} = {{I}_{2}},$ ${{\varphi }_{1}} = 0,$ ${{I}_{2}} = {\text{const}},$ ${{\delta }_{1}} = {\text{const}}.$ Для кинетического момента G получим

(28)

${\mathbf{G}} = (0,0,{{C}^{{ - 1}}}{{I}_{2}}),\,\,\,\,{\mathbf{\omega }} = J_{0}^{{ - 1}}{\mathbf{G}},\,\,\,\,{\mathbf{\dot {\omega }}} = 0.$

Из (6) выведем выражения для нормальных координат

(29)

$\begin{gathered} {{q}_{0}} = 0,\,\,\,\,{{p}_{0}} = 0, \\ {{q}_{1}} = 3\nu _{1}^{{ - 2}}\left[ {{{b}_{{123}}} + {{b}_{{132}}}} \right]\left( {\mu {{R}^{{ - 3}}}{{\gamma }_{2}}{{\gamma }_{3}} - \chi b{{{\left[ {\mu {{R}^{{ - 3}}}{{\gamma }_{2}}{{\gamma }_{3}}} \right]}}^{\centerdot }}} \right), \\ {{p}_{1}} = 3\nu _{1}^{{ - 2}}\left[ {{{b}_{{123}}} + {{b}_{{132}}}} \right]\left( {\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{3}} - \chi b{{{\left[ {\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{3}}} \right]}}^{\centerdot }}} \right), \\ {{q}_{2}} = 6\nu _{2}^{{ - 2}}{{b}_{{212}}}\left( {\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{2}} - \chi b{{{\left[ {\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{2}}} \right]}}^{\centerdot }}} \right), \\ {{p}_{2}} = 3\nu _{2}^{{ - 2}}{{b}_{{212}}}\left( {\mu {{R}^{{ - 3}}}(\gamma _{1}^{2} - \gamma _{2}^{2}) - \chi b{{{\left[ {\mu {{R}^{{ - 3}}}(\gamma _{1}^{2} - \gamma _{2}^{2})} \right]}}^{\centerdot }}} \right). \\ \end{gathered} $

Подставим формулы (29) в уравнения (27). Для изучения эволюционных процессов оставим в уравнениях (29) только диссипативные члены (пропорциональные χ). В результате уравнения (27) перепишутся в виде

(30)

$\begin{gathered} {{{\dot {I}}}_{i}} = 3\chi b\mu {{R}^{{ - 3}}}{{\rho }_{2}}\left\{ {3{{\mu }_{1}}\left[ {[\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{3}}){{]}^{\centerdot }}\frac{{\partial ({{\gamma }_{1}}{{\gamma }_{3}})}}{{\partial {{\varphi }_{i}}}}} \right.} \right. + \\ + \,\,\left. {[\mu {{R}^{{ - 3}}}{{\gamma }_{2}}{{\gamma }_{3}}){{]}^{\centerdot }}\frac{{\partial ({{\gamma }_{2}}{{\gamma }_{3}})}}{{\partial {{\varphi }_{i}}}}} \right] + 3{{\mu }_{2}}\left[ {{{{[\mu {{R}^{{ - 3}}}(\gamma _{1}^{2} - \gamma _{2}^{2})]}}^{\centerdot }}_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}^{{^{{^{{^{{}}}}}}}}} \right. \times \\ \times \,\,\frac{{\partial (\gamma _{1}^{2} - \gamma _{2}^{2})}}{{\partial {{\varphi }_{i}}}} + \left. {\left. {4[\mu {{R}^{{ - 3}}}{{\gamma }_{1}}{{\gamma }_{2}}){{]}^{\centerdot }}\frac{{\partial ({{\gamma }_{1}}{{\gamma }_{2}})}}{{\partial {{\varphi }_{i}}}}} \right]} \right\},\,\,\,\,k = 2,3. \\ \end{gathered} $

Здесь введены обозначения

${{\mu }_{1}} = \nu _{1}^{{ - 2}}{{\left[ {{{b}_{{123}}} + {{b}_{{132}}}} \right]}^{2}} > 0,\,\,\,\,{{\mu }_{2}} = {{\lambda }_{2}}.$

Уравнения (30) все еще слишком сложны, поэтому усредним их по быстрой переменной ${{\varphi }_{{20}}} = {{\dot {\varphi }}_{{20}}}t$ (угол ${{\varphi }_{2}}$ описывает прецессию оси симметрии спутника вокруг вектора кинетического момента G). После весьма громоздких вычислений получим:

(31)

Уравнения (31) описывают эволюцию вращений спутника на минимальном промежутке времени порядка одного оборота центра масс спутника по орбите. Эти уравнения сложны для анализа, поэтому для выделения главных эффектов медленной диссипативной эволюции, проведем еще одно усреднение уравнений (31) по переменной $\tau = {{\omega }_{0}}t.$ При усреднении следует иметь в виду равенства

$\begin{gathered} dt = \omega _{0}^{{ - 1}}d\tau ,\,\,\,\,d\tau = \frac{{{{{\left( {1 - {{e}^{2}}} \right)}}^{{3/2}}}}}{{{{{\left( {1 + e\cos \vartheta } \right)}}^{2}}}}d\vartheta , \\ \dot {R} = {{\left( {\frac{p}{{1 + e\cos \vartheta }}} \right)}^{\centerdot }} = \frac{{pe}}{{{{{(1 + e\cos \vartheta )}}^{2}}}}\sin \vartheta \cdot \dot {\vartheta }, \\ p = a\left( {1 - {{e}^{2}}} \right). \\ \end{gathered} $

Вычислим

$\begin{gathered} {{\left\langle {{{R}^{{ - 6}}}{{{\cos }}^{2}}\alpha {{{\sin }}^{2}}\alpha } \right\rangle }_{\tau }} = {{p}^{{ - 6}}}{{\Phi }_{1}}(e), \\ {{\Phi }_{1}}(e) = \frac{1}{4}{{(1 - {{e}^{2}})}^{{3/2}}}\left[ {\frac{1}{2} + \frac{{3{{e}^{2}}}}{2} + \frac{{{{e}^{4}}}}{{32}}(5 + 2{{{\sin }}^{2}}2{{\varphi }_{3}})} \right], \\ {{\left\langle {{{R}^{{ - 6}}}{{{\sin }}^{2}}\alpha } \right\rangle }_{\tau }} = {{p}^{{ - 6}}}{{\Phi }_{2}}(e), \\ {{\Phi }_{2}}(e) = \frac{1}{4}{{(1 - {{e}^{2}})}^{{3/2}}} \times \\ \times \,\,\left[ {\frac{1}{2} + \frac{{3{{e}^{2}}}}{4}(1 + 2{{{\sin }}^{2}}{{\varphi }_{3}}) + \frac{{{{e}^{4}}}}{{16}}(1 + 4{{{\sin }}^{2}}{{\varphi }_{3}})} \right], \\ {{\left\langle {{{R}^{{ - 6}}}} \right\rangle }_{\tau }} = {{p}^{{ - 6}}}{{\Phi }_{3}}(e), \\ \end{gathered} $

(32)

$\begin{gathered} {{\Phi }_{3}}(e) = {{(1 - {{e}^{2}})}^{{3/2}}}\left( {1 + 3{{e}^{2}} + \frac{3}{8}{{e}^{4}}} \right), \\ {{\left\langle {{{R}^{{ - 6}}}\dot {\vartheta }{{{\sin }}^{2}}\alpha } \right\rangle }_{\tau }} = {{\omega }_{0}}{{p}^{{ - 6}}}{{\Phi }_{4}}(e), \\ {{\Phi }_{4}}(e) = \frac{1}{2} + \frac{{15}}{8}{{e}^{2}}(1 + 2{{\sin }^{2}}{{\varphi }_{3}}) + \\ + \,\,\frac{{15}}{{16}}{{e}^{4}}(1 + 4{{\sin }^{2}}{{\varphi }_{3}}) + \frac{5}{{128}}{{e}^{6}}(1 + 6{{\sin }^{2}}{{\varphi }_{3}}), \\ {{\left\langle {{{R}^{{ - 6}}}\dot {\vartheta }} \right\rangle }_{\tau }} = {{\omega }_{0}}{{p}^{{ - 6}}}{{\Phi }_{5}}(e), \\ {{\Phi }_{5}}(e) = 1 + \frac{{15}}{2}{{e}^{2}} + \frac{{45}}{8}{{e}^{4}} + \frac{5}{{16}}{{e}^{6}}, \\ {{\left\langle {{{R}^{{ - 7}}}\dot {R}\sin 2\alpha {{{\cos }}^{2}}\alpha } \right\rangle }_{\tau }} = {{\omega }_{0}}{{p}^{{ - 6}}}{{\Phi }_{6}}(e), \\ \end{gathered} $

$\begin{gathered} {{\Phi }_{6}}(e) = \\ = \frac{1}{8}\left[ {5\left( {{{e}^{2}} + {{e}^{4}} + \frac{{{{e}^{6}}}}{{16}}} \right)\cos 2{{\varphi }_{3}} + \left( {\frac{5}{4}{{e}^{4}} + \frac{{{{e}^{6}}}}{8}} \right)\cos 4{{\varphi }_{3}}} \right], \\ {{\left\langle {{{R}^{{ - 7}}}\dot {R}\sin 2\alpha } \right\rangle }_{\tau }} = {{\omega }_{0}}{{p}^{{ - 6}}}{{\Phi }_{7}}(e), \\ {{\Phi }_{7}}(e) = \frac{5}{4}\left( {{{e}^{2}} + {{e}^{4}} + \frac{{{{e}^{6}}}}{{16}}} \right)\cos 2{{\varphi }_{3}}, \\ {{\left\langle {{{R}^{{ - 7}}}\dot {\vartheta }{{{\sin }}^{2}}\alpha {{{\cos }}^{2}}\alpha } \right\rangle }_{\tau }} = {{\omega }_{0}}{{p}^{{ - 6}}}{{\Phi }_{8}}(e), \\ {{\Phi }_{8}}(e) = \frac{1}{4}\left[ {\frac{1}{2} + \frac{{15}}{4}{{e}^{2}} + } \right. \\ + \,\,\left. {\frac{{15}}{{32}}{{e}^{4}}(5 + 2{{{\sin }}^{2}}2{{\varphi }_{3}}) + \frac{{{{e}^{6}}}}{{64}}(7 + 6{{{\sin }}^{2}}2{{\varphi }_{3}})} \right]. \\ \end{gathered} $

Используя (32) выпишем результирующие усредненные уравнения

(33)

где обозначено

$k = 9\chi b{{\mu }^{2}}{{p}^{{ - 6}}}{{\rho }_{2}}{{C}^{{ - 1}}}.$

Уравнения (33) позволяют изучать эволюцию вращений на временах порядка периода прецессии вектора G вокруг нормали к плоскости орбиты центра масс.

Получим из уравнений невозмущенного движения (14) уравнение для угла ${{\varphi }_{3}}.$ Подставляя выражение для ${{\gamma }_{3}}$ и дифференцируя, имеем

${{\dot {\varphi }}_{3}} = 3\mu {{R}^{{ - 3}}}(A - C)I_{2}^{{ - 1}}\cos {{\delta }_{1}}{{\sin }^{2}}\alpha .$

Усредняя по переменной $\tau = {{\omega }_{0}}t,$ получаем приближенное уравнения для ${{\varphi }_{3}}{\text{:}}$

(34)

${{\dot {\varphi }}_{3}} = \frac{3}{2}\mu {{p}^{{ - 3}}}{{(1 - {{e}^{2}})}^{{3/2}}}(A - C)I_{2}^{{ - 1}}\cos {{\delta }_{1}}.$

Из выражения для производной угла ${{\delta }_{1}}$

${{\dot {\delta }}_{1}} = \frac{{{{{\dot {I}}}_{2}}{{I}_{3}} - {{{\dot {I}}}_{3}}{{I}_{2}}}}{{I_{2}^{2}\sqrt {1 - I_{3}^{2}I_{2}^{{ - 2}}} }}$

и формул (34), (33) видно, что она пропорциональна, в отличие от ${{\dot {\varphi }}_{3}},$ малому параметру χ, то есть угол ${{\delta }_{1}}$ изменяется значительно медленнее угла ${{\varphi }_{3}}.$ Кроме того, из формул (32) видно, что в течение одного оборота вектора G вокруг нормали к плоскости орбиты, угол ${{\delta }_{1}}$ совершает колебания с частотами $2{{\dot {\varphi }}_{3}}$ и $4{{\dot {\varphi }}_{3}}$ относительно некоторого среднего значения ${{\tilde {\delta }}_{1}}.$ Будем рассматривать эволюцию вращений на временах существенно превышающих период прецессии вектора G, для чего усредним уравнения (33) по углу ${{\varphi }_{3}}$ на периоде π. Имеем

(35)

$\begin{gathered} {{\left\langle {{{\Phi }_{1}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = \frac{1}{8}{{(1 - {{e}^{2}})}^{{3/2}}}\left( {1 + 3{{e}^{2}} + \frac{{3{{e}^{4}}}}{8}} \right), \\ {{\left\langle {{{\Phi }_{2}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = 4{{\left\langle {{{\Phi }_{1}}(e)\,} \right\rangle }_{{{{\varphi }_{3}}}}},\,\,\,\,{{\left\langle {{{\Phi }_{3}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = 8{{\left\langle {{{\Phi }_{1}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}}, \\ {{\left\langle {{{\Phi }_{4}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = \frac{1}{2}\left( {1 + \frac{{15}}{2}{{e}^{2}} + \frac{{45}}{8}{{e}^{4}} + \frac{5}{{16}}{{e}^{6}}} \right), \\ {{\left\langle {{{\Phi }_{5}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = 2{{\left\langle {{{\Phi }_{4}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}},\,\,\,\,{{\left\langle {{{\Phi }_{6}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = {{\left\langle {{{\Phi }_{7}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = 0, \\ {{\left\langle {{{\Phi }_{8}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}} = \frac{1}{4}{{\left\langle {{{\Phi }_{4}}(e)} \right\rangle }_{{{{\varphi }_{3}}}}}. \\ \end{gathered} $

С учетом (35) усредненные уравнения (33) запишутся в виде

(36)

$\begin{gathered} {{{\dot {I}}}_{2}} = - k\left\{ {{{I}_{2}}{{\Phi }_{1}}(e)\left[ {{{\mu }_{1}}(1 + 2{{x}^{2}} - 3{{x}^{4}})} \right.} \right. + 4{{\mu }_{2}}(3 + 2{{x}^{2}} + \\ \left. { + \,\,3{{x}^{4}})} \right] - C{{\omega }_{0}}{{\Phi }_{4}}(e)x\left[ {4{{\mu }_{2}}(1 + {{x}^{2}})} \right. + \left. {{{\mu }_{1}}(1 - {{x}^{2}})} \right\}, \\ {{{\dot {I}}}_{3}} = - k\left\{ {4{{I}_{2}}{{\Phi }_{1}}(e)x} \right. \times \\ \times \,\,\left[ {(4{{\mu }_{2}} - {{\mu }_{1}})(1 - {{x}^{2}}) - 8{{\mu }_{2}}} \right] + C{{\omega }_{0}}{{\Phi }_{4}}(e) \times \\ \times \,\,\left. {\left[ {({{\mu }_{2}} - {{\mu }_{1}}){{{(1 - {{x}^{2}})}}^{2}} + 2\left[ {(4{{\mu }_{2}} - {{\mu }_{1}}){{x}^{2}} + {{\mu }_{1}}} \right]} \right]} \right\}, \\ x = \cos {{{\tilde {\delta }}}_{1}}. \\ \end{gathered} $

Заметим, что у нас выполняется предположение о том, что орбитальная угловая скорость много меньше угловой скорости вращения спутника ${{\varepsilon }_{1}} = \frac{{C{{\omega }_{0}}}}{{{{I}_{2}}}} \ll 1,$ то есть $C{{\omega }_{0}} = {{\varepsilon }_{1}}{{I}_{2}}.$ С учетом вышесказанного получим еще уравнение для x:

$\dot {x} = {{(\cos {{\tilde {\delta }}_{1}})}^{\centerdot }} = {{({{I}_{3}}{\text{/}}{{I}_{2}})}^{\centerdot }} = \frac{{{{{\dot {I}}}_{3}} - x{{{\dot {I}}}_{2}}}}{{{{I}_{2}}}},$

откуда следует

(37)

$\begin{gathered} \dot {x} = - k\left\{ {4{{\Phi }_{1}}x[4{{\mu }_{2}}(1 - {{x}^{2}} - 2) - {{\mu }_{1}}(1 - {{x}^{2}})]} \right. - \\ - \,\,{{\Phi }_{1}}x[4{{\mu }_{2}}(3 - 2{{x}^{2}} + 3{{x}^{4}}) + {{\mu }_{1}}(1 + 2{{x}^{2}} - 3{{x}^{4}})] + \\ + \,\,{{\varepsilon }_{1}}{{\Phi }_{4}}\left[ {{{{(1 - {{x}^{2}})}}^{2}}({{\mu }_{2}} - {{\mu }_{1}}) + 2\left[ {{{x}^{2}}(4{{\mu }_{2}} - {{\mu }_{1}}) + {{\mu }_{1}}} \right]} \right] - \\ - \,\,\left. {{{\varepsilon }_{1}}{{\Phi }_{4}}{{x}^{2}}\left[ {4{{\mu }_{2}}({{x}^{2}} + 1) + {{\mu }_{1}}(1 - {{x}^{2}})} \right]} \right\}. \\ \end{gathered} $

Функция $f(x) = 1 + 2{{x}^{2}} - 3{{x}^{4}}$ имеет корни 1, –1 и положительна при –1 < x < 1, а функция ${{f}_{1}}(x) = 3 + 2{{x}^{2}} + 3{{x}^{4}} > 0$ всегда. Поэтому ${{\dot {I}}_{2}} < 0$ и ${{I}_{2}}$ убывает – осевое вращение спутника замедляется. Из уравнения (37) следует, что знак $\dot {x}$ определяется двумя первыми слагаемыми (37). Перепишем их в виде

$ - {{\Phi }_{1}}x[4{{\mu }_{2}}(1 + 2{{x}^{2}} - 3{{x}^{4}}) + 3{{\mu }_{1}}{{(1 - {{x}^{2}})}^{2}}].$

Выражение в квадратных скобках положительно при –1 < x < 1, поэтому знак выражения определяется знаком x. Если x > 0, следовательно, $\dot {x} < 0,$ и $\cos {{\tilde {\delta }}_{1}}$ убывает, то есть угол ${{\tilde {\delta }}_{1}}$ растет, значит растет угол между G и нормалью к плоскости орбиты, вектор G наклоняется к плоскости орбиты. Если же x < 0, то $\dot {x} > 0,$ следовательно, $\cos {{\tilde {\delta }}_{1}}$ возрастает и угол ${{\tilde {\delta }}_{1}}$ уменьшается. Поскольку угол ${{\tilde {\delta }}_{1}}$ – тупой, то при убывании угла происходит переворот из обратного вращения в прямое. Определим стационарные значения угла ${{\tilde {\delta }}_{1}},$ обозначив его через ${{\tilde {\delta }}_{{10}}}.$ В этом случае ${{\dot {I}}_{3}} - x{{\dot {I}}_{2}} = 0,$ и считая ${{x}_{0}} = \cos {{\tilde {\delta }}_{{10}}} \sim {{\varepsilon }_{1}},$ в первом приближении получим:

${{x}_{0}} \approx {{\varepsilon }_{1}}\frac{{{{\Phi }_{4}}(e)[{{\mu }_{1}} + {{\mu }_{2}}]}}{{{{\Phi }_{1}}(e)[4{{\mu }_{2}} + 3{{\mu }_{1}}]}},\,\,\,\,{{\tilde {\delta }}_{{10}}} \approx {\text{arccos}}({{x}_{0}}).$

Заметим, что уравнение (37) имеет еще два стационарных значения ${{x}_{1}} = - 1,$ ${{x}_{2}} = 1.$ Из уравнений в вариациях следует, что оба стационарных решения – неустойчивы.

Список литературы

Вильке В.Г. Аналитическая механика систем с бесконечным числом степеней свободы. Ч. I, II. М.: Изд-во мех.-мат. ф-та МГУ, 1997.
Стретт Дж.В. (Лорд Рэлей). Теория звука. Т. 1, 2. М.: ГИТТЛ, 1955.
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Изд-во МГУ, 1975.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал