Космические исследования, 2019, T. 57, № 3, стр. 163-176

1. ВВЕДЕНИЕ

Под быстрыми корональными выбросами массы (КВМ) имеются в виду КВМ, скорости которых V_КВМ > 1500 км/с. Динамика ударной волны, возбуждаемой КВМ со скоростями V_КВМ ≤ 1500 км/с, была исследована достаточно подробно. Первая попытка регистрации ударной волны перед КВМ в короне была предпринята в [1]. В ряде работ существование ударного фронта перед КВМ отождествлялось с наличием всплеска радиоизлучения II типа (например, [2, 3]).

В работе [4] для одного события, а затем в [5, 6] для 15 быстрых КВМ, скорости которых превышали 1500 км/с, была сделана попытка отождествить с ударным фронтом слабо видимую в белом свете резкую границу в передней части КВМ на расстояниях R > 10R₀ от центра Солнца (R₀ – радиус Солнца). Выполнено это было путем сравнения результатов с численным моделированием обтекания трехмерного тела в МГД приближении. Однако корректность этих сравнений в существенной степени зависит от величины показателя адиабаты γ, значения которого для бесстолкновительного ударного фронта может составлять 5/3 ≤ γ ≤ 2 [7].

В работе [8] был предложен метод отождествления и регистрации фронта поршневой ударной волны впереди КВМ на расстояниях R < 30R₀ от центра Солнца и в различных направлениях относительно оси движения КВМ. Физической основой этого метода является понятие возмущенной зоны, которая возникает впереди КВМ в результате его взаимодействия с невозмущенным солнечным ветром (СВ). Анализ с использованием этого метода нескольких десятков лимбовых (с долготой места возникновения более 60^○) КВМ с различными скоростями менее 1500 км/с с использованием данных инструмента AIA на космическом аппарате SDO, наземного коронографа Mark 4, коронографов LASCO C2 и C3 на КА SOHO и коронографа COR2 на КА STEREO позволил установить следующие закономерности формирования поршневой ударной волны перед КВМ [8]:

1) Формирование ударной волны может происходить в передней части возмущенной зоны КВМ в узкой окрестности (диапазон по позиционному углу δРА ≈ ±3°) относительно оси его распространения и на различных расстояниях R от центра Солнца. Ее возникновение определяется выполнением локального неравенства u(R) = = V_КВМ – V_SW > V_А(R), где u(R) – скорость КВМ относительно окружающего СВ, V_SW – скорость СВ, V_A(R) – локальная альвеновская скорость.

2) На расстояниях R < 6R₀ ширина ударного фронта δ_F порядка длины свободного пробега протонов λ_р и механизм диссипации энергии во фронте столкновительный.

3) На расстояниях R ≥ 10–15R₀ в передней части столкновительного ударного фронта наблюдается формирование нового разрыва с шириной $\delta _{{\text{F}}}^{*} \ll {{\lambda }_{{\text{p}}}}.$ В пределах погрешности величина $\delta _{{\text{F}}}^{*}$ не зависит от расстояния R и примерно равна разрешению инструментов, которое составляет ≈0.1–0.2R₀ для LASCO C3 и ≈0.03R₀ для COR2. Это означает, что истинная величина $\delta _{{\text{F}}}^{*}$ должна быть существенно меньше измеренной этими инструментами. Данный разрыв был отождествлен с бесстолкновительной ударной волной [7].

В направлении перпендикулярном к оси движения КВМ на расстояниях менее 6R₀ от центра Солнца условие для формирования ударного фронта выражается неравенством V_КВМ/2 > V_A. Это связано с тем, что скорость расширения КВМ в поперечном направлении примерно в 2 раза меньше скорости V_КВМ [9]. Вследствие этого для КВМ со скоростями менее 1500 км/с ударный фронт регистрируется в основном в узкой области в направлении движения КВМ, где условия его формирования выполняются. Для более быстрых КВМ ситуация может быть иной.

Целью данной работы является исследование, на примере события 27.I.2012, особенностей динамики формирования ударной волны, возбуждаемой быстрым КВМ, а также проверка справедливости закономерностей, ранее установленных при анализе более медленных КВМ.

2. ДАННЫЕ И МЕТОДЫ АНАЛИЗА

При анализе использовались калиброванные данные полной яркости Р (в единицах средней яркости Солнца, P_MSB) изображений короны Солнца в белом свете, получаемых на коронографах LASCO С2 и C3 КА SOHO. Временное разрешение ≈12 мин, поля зрения относительно центра Солнца ≈2.1–6.0R₀ для LASCO C2 и ≈3.8–30R₀ для LASCO С3 [10]. Использовались также данные инструмента AIA на КА SDO [11] с изображениями Солнца в УФ канале 131 Å. Временное разрешение инструмента около 12 с, внешняя граница поля зрения на расстоянии 1.3–1.4R₀ от центра Солнца.

Изображения короны в белом свете и в УФ представлялись в виде разностной яркости с фиксированным начальным моментом времени ΔP = P(t) – P(t₀), где P(t₀) – невозмущенная яркость в момент t₀ до возникновения рассматриваемого события, Р(t) – возмущенная яркость в любой момент времени t > t₀. По разностным изображениям (пример на рис. 1) исследовалась динамика КВМ. Для этого строились распределения ΔP(R) из центра Солнца вдоль радиуса на фиксированном позиционном угле PA в различные моменты времени. Позиционный угол РА отсчитывается на изображениях Солнца от северного полюса против часовой стрелки. В отдельных случаях использовались изображения “бегущей” разностной яркости ΔP_R = P(t_i) – P(t_{i – 1}) двух соседних по времени изображений.

Рис. 1.

Изображения бегущей разностной яркости в последовательные моменты времени, отражающие начальную стадию развития КВМ 27.I.2012. Данные AIA/SDO, канал 131 Å. На рис. 1а показана геометрия при построении распределений разностной яркости ΔP: из точки “О” (на расстоянии R_C = 1R₀ от центра Солнца в направлении PA = 300°) в направлении α = –30° относительно PA = 300° с усреднением по углу δα. На рис. 1б–1е прямые пунктирные линии показывают основные направления, которые использовались при построении распределений ΔP. По осям отложены солнечные координаты в радиусах Солнца.

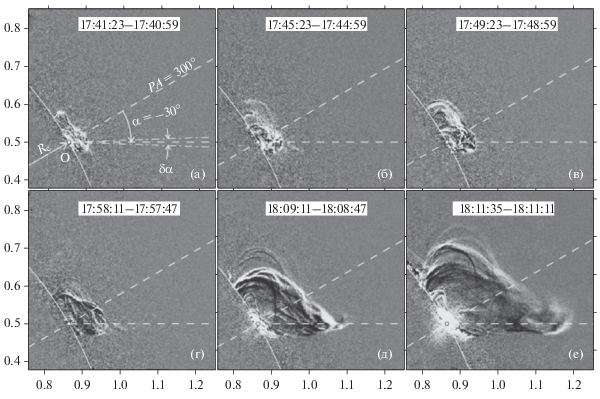
Для корректного измерения размера ударного фронта по изображениям разностной яркости строились распределения ΔP(r) или ΔP_R(r) под различными углами α относительно оси движения КВМ (направленной вдоль определенного РА), с углом усреднения δα в различные моменты времени (отсчет угла α положительный против часовой стрелки, рис. 1а). Расстояние r отсчитывалось от примерного центра КВМ “O”, расположенного на оси движения КВМ на расстоянии R_C от центра Солнца (в случае, показанном на рис. 1а, R_C = 1R₀). Величины расстояний R до центра Солнца и r до центра КВМ связаны соотношением R = ($R_{{\text{C}}}^{2}$ + r² + 2rR_Ccosα)^1/2. Для исследований строились распределения ΔP(r) и ΔP_R(r), направленные примерно по нормали к фронтальной структуре (FS) КВМ и к расположенному перед ней фронту ударной волны.

3. АНАЛИЗ НАЧАЛЬНОЙ СТАДИИ СОБЫТИЯ 27.I.2012 ПО ДАННЫМ AIA/SDO В КАНАЛЕ 131 Å

Как показал предварительный анализ данных AIA/SDO, детали развития рассматриваемого события хорошо видны в “горячих” каналах 94 и 131 Å и малозаметны в остальных, более холодных каналах. Это означает, что на начальной стадии процесса развиваются высокие температуры, которые для канала 131 Å составляют ≈(1–2) ⋅ 10⁷ К [12, 13].

На рис. 1 представлены изображения бегущей разностной яркости в последовательные моменты времени начальной стадии развития КВМ в событии 27.I.2012 по данным AIA/SDO в канале 131 Å. Из рис. 1а видно, что процесс начинается с усиления яркости и увеличения поперечного размера, сначала, низко расположенных сложных арочных структур, а затем структур внешней оболочки, наиболее удаленной от Солнца (рис. 1б, 1в). Все это происходит в течение ≈20 мин. Средняя точка “O” места возникновения этих арочных структур располагается на поверхности Солнца вблизи PA ≈ 300° (рис. 1а). При этом самая внешняя арочная структура с усиленной яркостью остается практически неподвижной на высоте h ≤ 0.1R₀ в течение нескольких минут (рис. 1б–1г). В последующие моменты времени начинается ее постепенное движение от Солнца с возрастающей скоростью. При этом на начальном этапе движение этой граничной структуры неоднородно, а наибольшая скорость ее движения реализуется в направлении угла α ≈ –30° (рис. 1д, 1е).

Изложенная картина развития начальной стадии КВМ аналогична развитию “постепенного” КВМ 19.VII.2012, который ранее был детально исследован в [14]. Согласно этим исследованиям наблюдаемая область сложных арочных структур представляет собой поперечное сечение магнитного жгута, ось спиральной структуры которого расположена примерно вдоль луча зрения. Жгут расположен вблизи поверхности Солнца на высоте h₀ ≤ 0.12R₀, вероятной причиной начала его эрупции является “тороидальная” неустойчивость (torus instability). При этом предполагается, что перед эрупцией происходит медленный квазистатический подъем и раздувание корональных структур. По мнению авторов [14] эрупция начинается, когда медленно поднимающийся магнитный жгут достигнет высот с большим градиентом магнитного поля. По аналогии с [14] можно предположить, что в рассматриваемом событии 27.I.2012 наблюдаемые явления связаны с тем, что нижняя часть жгута за несколько минут до этого была существенно “подогрета” процессами, связанными с магнитным пересоединением. Постепенно в течение десятков минут перед эрупцией удаленная от Солнца часть жгута становится видимой на разностных изображениях из-за возрастания в ней яркости оставаясь при этом неподвижной (см. рис. 1б, 1в). Причиной этого возрастания, согласно [14], могут быть процессы в структурах жгута, вызванные вращательными движениями в основаниях магнитного жгута, укорененных на фотосфере.

Более детально динамика граничной структуры в направлении ее наибольшей скорости (при α ≈ –30°) представлена на рис. 2 распределениями разностной яркости ΔP(R) в последовательные моменты времени при t₀ = 17:30:11 UT. Из него видно, что после постепенного возрастания яркости внешней структуры (крестики и черные кружки на рис. 2а) медленное движение ее внешней границы (показана вертикальной штриховкой на рис. 2а–2д) от Солнца постепенно начинается после ≈17:56:35 UT (этот момент на рис. 2 не показан). Указанная граница фактически является токовым слоем, ограничивающим фронтальную структуру (FS) будущего КВМ. На рис. 2б, 2в профиль ΔP токового слоя аппроксимирован наклонной прямой. Пространственный размер этого слоя δ_I (рис. 2б) определен как удвоенное расстояние спадания яркости внутри токового слоя от максимального значения ΔP_I вдвое (рис. 2в). Средняя точка токового слоя FS показана знаком “+".

Рис. 2.

Распределения разностной яркости ΔP в зависимости от расстояния R для последовательных моментов времени при t₀ = 17:30:11 UT. Распределения строились из точки “О” в направлении α = –30° относительно позиционного угла РА = 300° (см. рис. 1а). Усреднение по углу δα = 2°. Данные AIA/SDO, канал 131 Å.

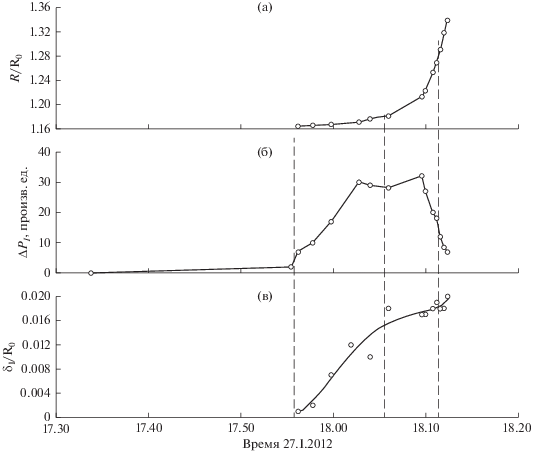
Количественно характер изменения параметров токового слоя FS представлен на рис. 3. Кинематика токового слоя FS на рис. 3а, т.е. зависимость его расстояния R от времени t, характеризует данное событие как КВМ “постепенного” типа, а именно: его движение начинается из состояния покоя с постепенно увеличивающейся со временем скоростью. При этом величина скачка разностной яркости ΔP_I в слое (см. определение на рис. 2в) на начальной стадии движения растет, а затем после момента времени ≈18:10 UT по мере удаления от Солнца начинает резко падать (рис. 3б). Поперечный размер токового слоя δ_I на начальной стадии формирования покоящейся граничной структуры по мере увеличения ее яркости сначала растет до момента ≈18:05 UT, что связано с процессом формирования и уширения самой структуры. После момента ≈18:10 UT по мере удаления от Солнца на участке R ≈ 1.18–1.36R₀ величина δ_I остается практически постоянной (рис. 3в). Постоянство размера δ_I является главным свидетельством в пользу того, что наблюдаемая граница структуры не может быть фронтом ударной волны ширина δ_F которого, согласно [8], должна возрастать при движении в этом интервале примерно в 15 раз.

Рис. 3.

Зависимости от времени в направлении угла α = –30° относительно позиционного угла РА = 300°: (а) – расстояния R средней точки фронта FS КВМ относительно центра Солнца (отмечены знаком “+" на профилях разностной яркости на рис. 2), (б) – скачка разностной яркости ΔP_I на токовом слое FS КВМ (см. рис. 2в); (в) – ширины δ_I токового слоя FS КВМ (см. рис. 2а, 2б, 2г). Данные AIA/SDO, канал 131 Å.

4. ДИНАМИКА УДАРНОГО ФРОНТА В СОБЫТИИ 27.I.2012 НА R > 2R₀ ПО ДАННЫМ КОРОНОГРАФОВ LASCO C2 И C3

Дальнейшая динамика КВМ в рассматриваемом событии хорошо прослеживается на изображениях бегущей разностной яркости короны в белом свете по данным коронографов LASCO C2 и С3 примеры которых для двух выбранных моментов времени представлены, соответственно, на рис. 4а, 4б. Видно, что в проекции на картинную плоскость КВМ имеет вид близкий к окружности. Указаны положения фронтальной структуры КВМ и ударного фронта, которые далее более точно будут определены по распределениям разностной яркости ΔP на рис. 7а, 7б.

Рис. 4.

Изображения бегущей разностной яркости короны в белом свете по данным коронографов LASCO C2 (а) и LASCO C3 (б) в событии 27.I.2012. Пунктирными линиями, проведенными из точки “О”, показаны направления, в которых строились распределения разностной яркости ΔP: (а) R_C = 3R₀, РА = 300°, α = –50°…+40°; (б) R_C = 6R₀, РА = 310°, α = –90°…+90°. По осям отложены солнечные координаты в радиусах Солнца.

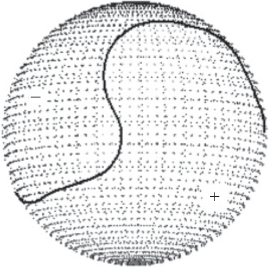
Здесь следует отметить, что кроме большой скорости КВМ важной особенностью данного события является следующее обстоятельство. В течение рассматриваемого события, согласно расчетам Г.В. Руденко (http://bdm.iszf.irk.ru/), выполненным в потенциальном приближении, нейтральная линия глобального магнитного поля Солнца располагалась вдоль западного лимба на широтах от экватора (N0°) до ≈ N70° (сплошная кривая на рис. 5). Место возникновения КВМ располагалось на широте N27° и вблизи западного лимба на долготе W71°. Это означает что пояс стримеров, вдоль которого распространяются КВМ, в данном случае располагался в плоскости неба. Согласно работе [15] квазистационарный пояс стримеров (т.е. в отсутствие КВМ) на расстояниях R > 2–3R₀ от центра Солнца представляет собой последовательность пар радиальных лучей повышенной яркости. Расстояние между лучами в каждой паре порядка размера луча, а направление магнитного поля в них противоположное. Это означает, что нейтральная линия радиальной компоненты глобального магнитного поля Солнца проходит вдоль пояса между лучами каждой из пар. Если пояс стримеров располагается в плоскости неба (как в нашем случае), то ориентация этих лучей повышенной яркости будет отражать направление невозмущенного коронального поля в поясе стримеров. Это может позволить оценить тип ударного фронта, возбуждаемого впереди КВМ.

Рис. 5.

Результаты расчетов Г.В. Руденко (http:// bdm.iszf.irk.ru/) в потенциальном приближении положения нейтральной линии глобального магнитного поля Солнца. Расчет сделан для 16:09:20 UT 27.I.2012. Плюс – направление магнитного поля от Солнца, минус – к Солнцу. Нейтральная линия показана сплошной кривой.

Лучевая структура пояса стримеров в событии 27.I.2012 явно видна на рис. 6, на котором приведены изображения белой короны по данным LASCO C2 в полярных координатах (по горизонтали – позиционный угол PA, по вертикали – расстояние R от центра Солнца). Для выделения лучевых структур, имеющих преимущественно радиальную направленность, из изображения построчно были вычтены строки, полученные скользящим усреднением по позиционному углу 5°.

Рис. 6.

Изображения яркости короны в белом свете по данным коронографа LASCO C2 в полярных координатах (по горизонтали – позиционный угол PA, по вертикали – расстояние R от центра Солнца). Из изображений построчно вычтены строки, полученные скользящим усреднением по позиционному углу 5°. Последовательность изображений отражает развитие КВМ.

На рис. 6а видно, что непосредственно перед появлением КВМ в момент 17:48:05 UT невозмущенная корона представляет собой последовательность радиально ориентированных лучей повышенной яркости с характерным размером по позиционному углу ~2°–3° и расстоянием между ними ~5°–10°, что типично, как уже упоминалось выше, для лучевой структуры пояса корональных стримеров [15]. Эти лучи и связанное с ними невозмущенное корональное магнитное поле ориентированы практически радиально к поверхности Солнца на R > 2–3R₀. В следующий момент времени 18:27:52 UT над поверхностью Солнца появляется фронтальная структура (FS) КВМ (рис. 6б). Она состоит из изогнутых лучей примерно того же углового размера (~2°–3°). Они отражают собой сложную внутреннюю магнитную структуру КВМ, который представляет собой магнитный жгут. На изображении мы видим его поперечное сечение [14]. В то же время на границе с обеих сторон КВМ видны искривленные под действием КВМ лучи пояса стримеров. Несмотря на наличие определенной мелкомасштабной неоднородности вдоль передней границы КВМ, можно отметить следующее: в диапазоне позиционных углов δРА ≈ 275°–330° граница фронтальной структуры КВМ в среднем перпендикулярна лучам пояса стримеров, а значит радиальному корональному магнитному полю. Это означает, что в указанном интервале РА ударный фронт, возбуждаемый впереди КВМ, должен быть “параллельного” типа [16], т.е. на его формирование не должна влиять поперечная к направлению движения КВМ составляющая коронального магнитного поля. Этот диапазон углов δРА примерно сохраняется и в следующий момент времени 18:38:43 UT (рис. 6в).

По мере движения от Солнца КВМ расширяется в обе стороны по позиционному углу РА. Это приводит к боковому воздействию КВМ на лучевые структуры. В результате последние изгибаются вдоль границы КВМ (рис. 6б, 6в). Это искажает профиль возможного ударного фронта перед КВМ вне области позиционных углов δРА ≈ 275°–330°, а, следовательно, затрудняет его регистрацию и исследование в этих направлениях относительно оси движения КВМ. Поэтому на расстояниях R < 6R₀ в поле зрения LASCO C2 все приведенные ниже результаты исследований получены в диапазоне позиционных углов 275°–330°.

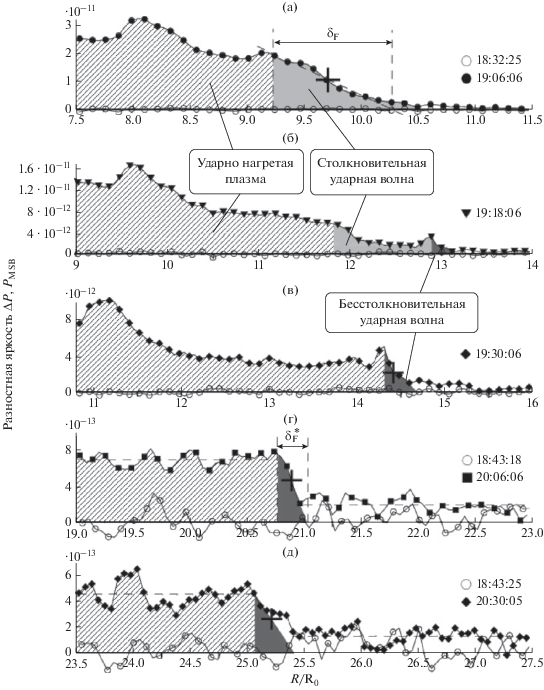
Для более четкого выделения фронтальной структуры КВМ и связанной с ней ударной волны были построены пространственные распределения разностной яркости ΔP(R) по данным LASCO C2 в направлении РА = 310° при t₀ = 17:12:05 UT и по данным LASCO C3 в направлении РА = 300° при t₀ = 17:18:05 UT. Эти распределения представлены, соответственно, на рис. 7 и 8 . Светлыми кружками показаны распределения ΔP(R) непосредственно перед появлением КВМ. Из рис. 7а видно что в первый момент появления КВМ в поле зрения LASCO С2 выделяются три области: фронтальная структура (обозначена FS и показана вертикальной штриховкой), ударно-нагретая плазма (наклонная штриховка) и ударный фронт (серый фон). Правая граница FS на рис. 7а определяется как расстояние R, на котором максимальная разностная яркость ΔP_max FS уменьшается в 2 раза [8]. По мере удаления от Солнца расстояние между ударным фронтом и FS возрастает от ≈0.5R₀ до 2.5R₀ (рис. 7а–7в). На рис. 7а1–в1 бо-лее детально показывающих область ударного фронта профиль ΔP на ударном фронте усреднен наклонной прямой. Ширина фронта δ_F определена как удвоенная ширина на полувысоте скачка яркости ΔP_F на фронте волны (рис. 7а1). По мере движения размер δ_F возрастает примерно в 4 раза в поле зрения LASCO С2 (рис. 7а1–в1), достигая в поле зрения LASCO С3 на R ≈ 9.5R₀ значения δ_F≈ 1R₀ (рис. 8 а). При дальнейшем движении на расстоянии R ≈ 13R₀ в передней части фронта δ_F возникает новый разрыв шириной $\delta _{{\text{F}}}^{*} \ll {{\delta }_{{\text{F}}}}$ (темно-серый фон на рис. 8 б), размер которого практически не меняется при дальнейшем удалении от Солнца. Надежность регистрации этого фронта ограничивалась влиянием следующих двух факторов:

Рис. 7.

(а)–(в) – распределения разностной яркости белой короны ΔP в зависимости от расстояния R для последовательных моментов времени при t₀ = 17:12:05 UT в направлении позиционного угла РА = 310° с усреднением δα = 1°. (а1)–(в1) повторяют графики (а)–(в) на более растянутом пространственном масштабе. Данные LASCO C2.

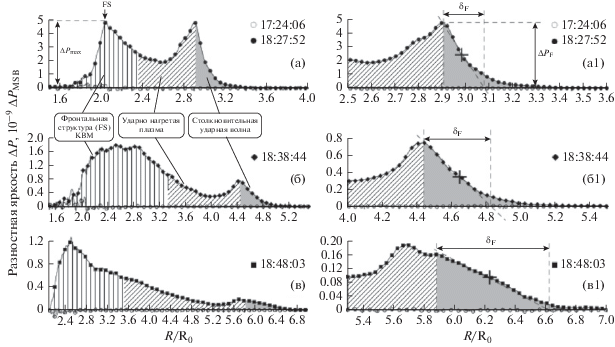
Рис. 8.

Распределения разностной яркости белой короны ΔP в зависимости от расстояния R для последовательных моментов времени при t₀ = 17:18:05 UT в направлении позиционного угла РА = 310° с усреднением δα = 1°. Данные LASCO C3.

1) Наличие на изображениях короны ярких точек и штрихов, вызванных мощным потоком солнечных энергичных частиц, сопровождавших это событие.

2) Некоторые изменения нулевого уровня сигнала от изображения к изображению сравнимые с уровнем шума и скачком ΔP_F на фронте волны.

Отдельные импульсы, связанные с яркими точками и штрихами на изображениях коронографа LASCO С3, легко выделяются на распределениях разностной яркости и исправлялись путем замены на среднее значение вокруг импульса.

На рис. 8 можно видеть, что впереди скачка $\delta _{{\text{F}}}^{*}$ регистрировалось небольшое отклонение среднего сигнала от нулевого уровня (на рис. 8 г, 8д средний уровень разностной яркости впереди и позади скачка показан горизонтальными пунктирными линиями). Светлыми кружками на этих рисунках показаны распределения разностной яркости ΔP(R) для моментов времени перед появлением КВМ в поле зрения LASCO С3, которые отражают уровень шума в разностном сигнале. Из их сравнения с распределениями, полученными в присутствии КВМ (черные кружки на рис. 8 г, 8д), видно, что уровень шума перед скачком может испытывать колебания на масштабе ≈0.5–1.0R₀ сравнимые по амплитуде с регистрируемым отклонением от нулевого уровня ΔP ~ 1.5 ⋅ 10^–13P_MSB. Анализ изображений яркости короны в белом свете на расстояниях R > 10R₀ по данным LASCO C3, представленных в виде аналогичном рис. 6, показал, что эти колебания, скорее всего, результат проявления лучей пояса стримеров, колебания яркости в которых здесь сравнимы с уровнем шума. Это означает, что небольшое отличие среднего сигнала от нулевого уровня впереди скачка $\delta _{{\text{F}}}^{*}$ не связано с самим фронтом.

Обобщение результатов исследования события 27.I.2012, на основе изложенного выше анализа изображений в канале 131 Å и изображений короны в белом свете, приведено на рис. 9. Рисунок отражает условия образования ударного фронта перед КВМ и характера диссипации энергии во фронте на основе сравнения с результатами предыдущих исследований КВМ со скоростями менее 1500 км/с.

Рис. 9.

Зависимости от расстояния R от центра Солнца. (а) – скорости u = V – V_SW средней точки FS КВМ (светлые кружки), ударного фронта (темные кружки и крестики) относительно окружающего СВ в направлении позиционного угла РА = 300° (кружки) и РА = 310° (крестики). Пунктирная кривая – скорость V_SW квазистационарного медленного СВ в поясе стримеров из работы [17]. Сплошная кривая – рассчитанная альвеновская скорость в поясе корональных стримеров из [18, 19]; (б) – ширины δ_F (темные кружки) и $\delta _{{\text{F}}}^{*}$ (крестики) ударных фронтов. Сплошной кривой и горизонтальным пунктиром показаны зависимости ширин фронтов, соответственно, столкновительной (δ_F) и бесстолкновительной ($\delta _{{\text{F}}}^{*}$) ударных волн из [8], полученных на основе усреднения данных около десяти КВМ со скоростями менее 1500 км/с.

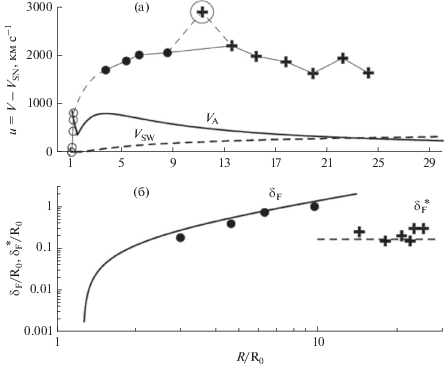
На рис. 9а показана зависимость от расстояния R скоростей u(R) = V(R) – V_SW(R) относительно окружающего СВ средней точки FS КВМ (светлые кружки) и средней точки ударного фронта (темные кружки или крестики) в направлении позиционного угла РА = 300° (темные кружки) и РА = 310° (крестики). Здесь V_SW – скорость квазистационарного медленного СВ в поясе стримеров (жирная пунктирная кривая) из работы [17], а V_A – рассчитанная альвеновская скорость в поясе корональных стримеров (жирная сплошная кривая) из [18] (на R > 1.6R₀) и из [19] (на R < 1.6R₀).

Из рис. 9а видно, что на начальной стадии движения КВМ на R < 1.4R₀, когда ударный фронт перед КВМ отсутствует, относительная скорость u фронтальной структуры КВМ меньше или близка к V_A. При u > V_A перед КВМ всегда существует ударный фронт либо с шириной δ_F (темные кружки), либо с шириной $\delta _{{\text{F}}}^{*}$ (крестики). Это подтверждает вывод работы [8], сделанный на основе анализа около десяти КВМ со скоростями менее 1500 км/с, что условием формирования поршневой ударной волны перед КВМ в короне является неравенство u > V_A.

На рис. 9б приведены зависимости от расстояния R ширины ударного фронта δ_F (темные кружки) и $\delta _{{\text{F}}}^{*}$ (крестики) перед КВМ. Сплошной кривой и горизонтальным пунктиром показаны усредненные зависимости ширины ударных фронтов, соответственно, δ_F(R) и $\delta _{{\text{F}}}^{*}$(R) (по данным LASCO С3) из работы [8]. Они были получены путем усреднения данных около десяти КВМ, имеющих относительные скорости u менее чем 1500 км/с. Из рис. 9б видно, что значения δ_F и $\delta _{{\text{F}}}^{*},$ измеренные для события 27.I.2012, близки к усредненным результатам, полученным в работе [8]. Это означает, согласно [8], что на расстояниях R < 10R₀ ширина фронта δ_F порядка длины свободного пробега протонов в короне λ_р относительно парных протон-протонных соударений и механизм диссипации энергии в ударном фронте столкновительный. На расстояниях R > 10R₀ величина $\delta _{{\text{F}}}^{*} \ll {{\lambda }_{{\text{p}}}},$ поэтому ударная волна бесстолкновительная и механизм диссипации энергии в ней носит коллективный характер. Измеренная ширина $\delta _{{\text{F}}}^{*}$ на несколько порядков больше истинной ширины бесстолкновительного фронта, поскольку определяется пространственным разрешением инструмента LASCO С3 и поэтому практически не зависит от R, так же как в [8].

5. ОСОБЕННОСТИ ДИНАМИКИ УДАРНОГО ФРОНТА БЫСТРОГО КВМ В СОБЫТИИ 27.I.2012 ПО СРАВНЕНИЮ С КВМ СО СКОРОСТЯМИ МЕНЕЕ 1500 КМ/С

При анализе данного события была предпринята первая попытка более детального рассмотрения процесса перехода от столкновительного к бесстолкновительному ударному фронту. Это тем более важно, что данный процесс до сих пор не предсказывался теоретически и не исследовался экспериментально (за исключением отдельных попыток в работах [7, 8]). Поэтому до сих пор до конца не ясно как может осуществляться этот переход. Как видно на рис. 8 а, 8б в течение времени движения на участке от R ≈ 10.5R₀ до R ≈ 13R₀ в передней части столкновительного ударного фронта δ_F возникает новый скачок $\delta _{{\text{F}}}^{*} \ll {{\delta }_{{\text{F}}}}.$ Если оценивать скорость его распространения по положению средней точки фронта δ_F в момент 19:06:06 UT и по положению средней точки фронта $\delta _{{\text{F}}}^{*}$ в следующий момент 19:18:06 UT, то можно получить резкое возрастание относительной скорости u почти до ≈3000 км/с на расстоянии R ≈ 10R₀ (на рис. 9а крестик, выделенный кружком). На самом деле истинная скорость u фронта $\delta _{{\text{F}}}^{*}$ не превышает 2000 км/с и далее мало меняется (слегка уменьшается). Резкое увеличение u на R ≈ 10R₀ до ≈3000 км/с – это суммарный эффект движения и одновременного перехода от столкновительного δ_F к бесстолкновительному фронту $\delta _{{\text{F}}}^{*}$ средние точки которых в момент 19:18:06 UT отстоят друг от друга на ≈1R₀ (рис. 8 б).

Вторая особенность данного события связана с двумя следующими факторами:

а) достаточно большой относительной скоростью ударного фронта (u ≈ 2000 км/с);

б) КВМ и ударная волна в течение времени регистрации двигаются вблизи плоскости неба, вдоль которой был вытянут пояс корональных стримеров.

Дело в том, что согласно анализу в [8] ударная волна впереди КВМ со скоростью u ≤ 1500 км/с обычно наблюдается в узком диапазоне позиционных углов δPA ≈ ±2° относительно основного направления распространения КВМ. Связано это с тем, что исследуемые КВМ распространяются вдоль пояса стримеров, который обычно ориентирован под заметным углом, а иногда даже перпендикулярно к картинной плоскости, которую, обычно, называют плоскостью неба или плоскостью лимба, т.к. она перпендикулярна лучу зрения. Известно, что в поясе стримеров значения альвеновской скорости V_A и скорости квазистационарного солнечного ветра V_SW меньше, чем в окружающей плазме. А это значит, что условие возникновение ударного фронта u(R) = V(R) – V_SW(R) > V_A в нем может выполняться на поперечном масштабе пояса стримеров (δPA ≈ 5°) и не выполняться вне пояса в окружающем СВ.

В событии 27.I.2012 пояс стримеров лежит в картинной плоскости и в этой плоскости происходит распространение КВМ. Поэтому условие u > V_A возбуждения ударной волны выполняется в большем диапазоне позиционного угла РА. Кроме того, скорость u достаточно велика, больше 1500 км/с. Вследствие этого, можно ожидать заметного отличия в рассматриваемом событии протяженности фронтов δ_F и $\delta _{{\text{F}}}^{*}$ в зависимости от угла α или, соответственно, от позиционного угла PA.

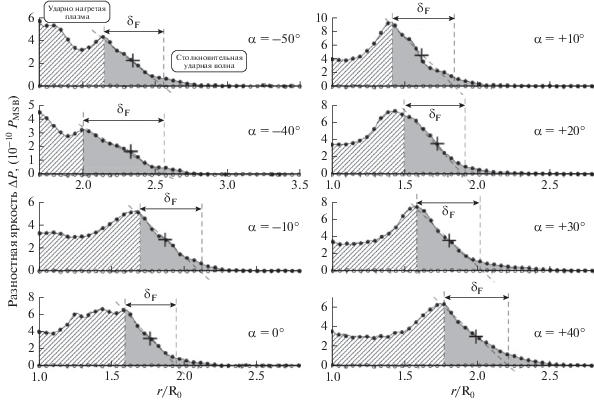
На рис. 4а приведено изображения бегущей разностной яркости белой короны для разности моментов времени t₂ – t₁= 18:38:43 – 18:27:52 UT по данным LASCO C2. Из точки “О” (координаты РА = 300°, R_C = 3R₀) под различными углами α относительно РА = 300° (направление распространения КВМ) были построены распределения разностной яркости ΔP_R(r) (рис. 10). Из рис. 10 следует, что столкновительный ударный фронт с примерно постоянной шириной δ_F ≈ 0.4–0.6R₀ ~ λ_р надежно регистрируется в диапазоне угла α от –50° и до +40°. Эта область соответствует передней “уплощенной” части FS КВМ на рис. 6б в в диапазоне позиционного угла РА ≈ 275°–330°. Таким образом δPA = 55°, что более чем в 10 раз превышает широтную протяженность δPA ≈ 5° ударного фронта для КВМ с u < 1500 км/с [8]. Вероятными причинами такого увеличения δPA являются:

Рис. 10.

Распределения разностной яркости белой короны ΔP в зависимости от расстояния r для разности моментов времени до появления КВМ 17:42:05 UT–17:12:05 UT (светлые кружки) и во время КВМ 18:38:43 UT–18:27:52 UT (черные кружки) при различных направлениях угла α = –50°…+40° (R_C = 3R₀, РА = 300°, δα = 1°). Данные LASCO C2. Событие 27.I.2012.

а) большая скорость рассмотренного КВМ по сравнению со случаями с u < 1500 км/с;

б) регистрация движения КВМ практически в плоскости пояса корональных стримеров, которая совпадает с картинной плоскостью.

Причем последний пункт (б) имеет решающее значение, т.к. в поясе стримеров, как уже отмечалось выше, условие u > V_A для возбуждения ударной волны выполняется лучше, чем вне пояса из-за более низкой альвеновской скорости V_A.

Следует отметить еще одну возможную причину того, что столкновительный ударный фронт с шириной δ_F ~ λ_р на R < 6R₀ формируется именно перед “уплощенной” частью КВМ. Как уже отмечалось выше, в этой области КВМ невозмущенное магнитное поле B преимущественно направлено по нормали к FS КВМ и к ударному фронту, т.е. В_⊥ ≈ 0. Это соответствует случаю, когда угол между B и нормалью к фронту θ_BN ≈ 0° и тип ударного фронта называют “параллельным”. Возрастание угла θ_BN, а значит появление и усиление компоненты поля B_⊥ в боковых направлениях КВМ, должно приводить к изменению ширины ударного фронта δ_F в сторону уменьшения. Это связано с тем, что для значений коронального поля В (и его составляющей B_⊥ ~ B для боковых направлений КВМ) величина ларморовского радиуса ионов ρ_i$ \ll $ λ_р и ионы удовлетворяют условию замагниченности. При значениях θ_BN > 45° тип фронта называют “квазиперпендикулярным” [21, 22]. Достоверно проверить этот процесс изменения δ_F в боковых направлениях в нашем случае не представляется возможным из-за искажений распределений яркости, связанных с появлением изгибов лучей пояса стримеров, возникающих под действием КВМ.

На больших расстояниях в поле зрения LASCO C3 яркость лучей существенно уменьшается и колебания яркости, вызванные их изгибами, становятся сравнимыми с уровнем шума. Это позволило для разности моментов времени t₂ – t₁ = = 19:30:06 – 19:18:05 UT по данным LASCO C3 проанализировать распределения ΔP_R(r) для направлений угла α в диапазоне –90°…+80° относительно направления РА = 310° при R_C = 6R₀ (см. рис. 4б). Анализ этих распределений показал, что бесстолкновительный ударный фронт $\delta _{{\text{F}}}^{*}$ уверенно регистрируется в значительно большем диапазоне углов α = –90°…+80°. Это соответствует протяженности фронта по позиционному углу РА от ≈250° до ≈370°, т.е. δPA ≈ 120°. Измеренная величина $\delta _{{\text{F}}}^{*}$ изменялась от ≈0.2R₀ до ≈0.5R₀. Минимальное значение $\delta _{{\text{F}}}^{*}$ сравнимо с пространственным разрешением LASCO С3, которое составляет ≈0.1R₀. Увеличенное значение $\delta _{{\text{F}}}^{*}$ по сравнению с пространственным разрешением может быть связано как с влиянием шумов, так и с усреднением измеряемого сигнала вдоль луча зрения.

ВЫВОДЫ

1. Исследование особенностей динамики формирования ударной волны, возбуждаемой быстрым КВМ, на примере события 27.I.2012 показало справедливость закономерностей, полученных для сравнительно медленных КВМ (со скоростями <1500 км/c):

а) Формирование ударного фронта происходит при условии u(R) = V(R) – V_SW(R) > V_A, что соответствует явлению “перехода через скорость звука” для замагниченной плазмы в короне.

б) Изменение ширины ударного фронта и, соответственно, механизма диссипации энергии во фронте происходит от “столкновительного” на расстояниях R < 10R₀ к “бесстолкновительному” на расстояниях R > 10R₀.

в) Удалось более детально исследовать процесс перехода от столкновительного к бесстолкновительному ударному фронту.

2) Было обнаружено, что долготная протяженность ударного фронта, возбуждаемого быстрым КВМ, на расстояниях R < 6R₀ увеличена почти в 10 раз по сравнению с более медленными КВМ. Одной из главных причин этого возрастания кроме большой скорости является тот факт, что регистрация движения КВМ происходило в плоскости пояса корональных стримеров, которая совпадала с картинной плоскостью.

3) Сделан вывод о том, что на расстояниях R < 6R₀ ударная волна перед КВМ “параллельного” типа, т.е. угол между вектором невозмущенного магнитного поля B и нормалью к фронту θ_BN ≈ 0°.

Авторы признательны Г.В. Руденко за расчет нейтральной линии глобального магнитного поля Солнца. Авторы благодарят команды инструментов AIA/SDO и LASCO/SOHO данные которых использовались в работе. Работа выполнена в рамках базового финансирования программы ФНИ II.16.