Космические исследования, 2019, T. 57, № 4, стр. 308-320
Оптимизация траектории выведения космического аппарата на геостационарную орбиту с целью снижения поглощенной дозы космической радиации
А. Е. Старченко *
Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
* E-mail: aleksandr.starchenko@phystech.edu
Поступила в редакцию 25.05.2018
После доработки 01.08.2018
Принята к публикации 20.09.2018
Аннотация
Рассматривается метод снижения дозовой нагрузки от заряженных частиц радиационных поясов Земли на многоразовый межорбитальный буксир, который выводится с низкой круговой орбиты на геостационарную орбиту с помощью ядерной электроракетной двигательной установки. Суть метода состоит в численном продолжении решения задачи оптимального быстродействия по накопленной на конец перелета дозе ионизирующей радиации. Для этого к уравнениям движения межорбитального буксира добавляется дополнительное уравнение для дозы радиации, и вводится краевое условие на дозу на правом конце. При расчете дозы использовались модели потоков заряженных частиц радиационных поясов Земли AE8/AP8 MIN, AE8/AP8 MAX и AE9/AP9. За счет изменения формы траектории выведения удалось снизить дозу радиации на 25–38% относительно траектории оптимального быстродействия. При этом время перелета увеличилось не более, чем на 7% от минимального времени выведения на геостационарную орбиту, а затраты характеристической скорости увеличились на 320–560 м/с.
ВВЕДЕНИЕ
Рассматривается задача доставки полезной нагрузки на геостационарную орбиту (ГСО) с помощью многоразового межорбитального буксира (ММБ) с ядерной электроракетной двигательной установкой (ЭРДУ) мегаваттного класса мощности [1]. Одним из назначений рассматриваемого варианта ММБ является транспортировка полезных грузов до 13.3 тонн с низкой круговой орбиты с ненулевым наклонением на ГСО. А также последующее возвращение ММБ на начальную орбиту за следующим модулем полезной нагрузки, выведение этого модуля на ГСО и т.д. Во время многовитковых перелетов между низкой круговой орбитой и ГСО бортовые системы ММБ будут поглощать большую дозу космической радиации, поскольку траектория оптимального быстродействия проходит через области больших потоков заряженных частиц радиационных поясов Земли (РПЗ). Большая радиационная нагрузка на элементы бортовой электроники приводит к усложнению проектирования отказоустойчивых бортовых систем и увеличению их стоимости. В частности, накопление большой дозы приводит к таким эффектам как деградация проектных характеристик электронной компонентной базы, единичные события при прохождении тяжелых заряженных частиц, а также накопление статического заряда на корпусе аппарата. Большой накопленный статический заряд при разряде в плазму собственной атмосферы или на элементы конструкции ММБ может также вывести из строя некоторые электронные системы ММБ.
Помимо задач, связанных с ММБ, проблема большой дозовой нагрузки может возникнуть при комбинированном выведении космических аппаратов на ГСО с использованием химического разгонного блока (ХРБ) и солнечной ЭРДУ. При этом воздействие заряженных частиц РПЗ приводит к деградации электрической мощности солнечных батарей (СБ) и необходимости закладки избытка площади СБ при проектировании КА для покрытия нужд ЭРДУ и других бортовых систем. Задача снижения радиационной нагрузки на СБ с помощью изменения формы траектории при комбинированном выведении рассмотрена в работе [2].
В данной работе представлен способ снижения дозы радиации, полученной бортовыми системами при перелете ММБ с низкой круговой орбиты на ГСО с помощью ядерной ЭРДУ. Данный способ связан со специальным выбором управления движением центра масс ММБ, которое позволяет снизить суммарное количество заряженных частиц РПЗ, поглощаемых бортовыми системами за время перелета. Для перелета с низкой круговой орбиты на ГСО существенная часть накопленной дозы является дозой радиации, полученной от поглощения заряженных частиц РПЗ. Известно [3], что распределение заряженных частиц РПЗ в околоземном пространстве неоднородно и, следовательно, поглощенная доза будет зависеть не только от продолжительности перелета, но и от того, где внутри РПЗ проходит траектория перелета. Меняя расположение траектории относительно поясов РПЗ можно снизить дозовую нагрузку на бортовые системы ММБ.
ПОСТАНОВКА ЗАДАЧИ
В работе рассматривались перелеты ММБ с модулем полезной нагрузки (МПН) с низкой круговой орбиты с ненулевым наклонением на ГСО с помощью ЭРДУ и ядерной энергетической установки (ЯЭУ). Рассматривался вариант ММБ, описанный в работе [1], c электрической мощностью ЯЭУ равной 1070 кВт. Все используемые далее значения проектных параметров ММБ соответствуют значениям из работы [1], которые согласно этой работе являются оптимальными для данного варианта ММБ. Предполагалось, что ММБ и МПН выводятся на начальную орбиту отдельно, по двухпусковой схеме. Первым пуском выводится ММБ, который с помощью ХРБ переводится на низкую круговую орбиту с ненулевым наклонением, которую будем далее называть радиационно безопасной орбитой (РБО). Вторым пуском выводится МПН. В составе МПН также есть блок расходных компонентов, который содержит рабочее тело для ЭРДУ ММБ и последующего перелета на ГСО. МПН также с помощью ХРБ переводится на РБО и совершает стыковку к ММБ. Далее связка ММБ + МПН с помощью ЭРДУ и бортового ядерного источника энергии совершает перелет на ГСО.
Будем считать, что ММБ и МПН в совместной фазе полета движутся только под действием силы притяжения Земли и силы тяги ЭРДУ. Потенциал притяжения Земли будем считать центральным ньютоновским. Всеми остальными возмущающими силами пренебрежем. Будем считать, что ЭРДУ всегда работает в режиме максимальной тяги, и тяга в течение всего перелета постоянна и равна $P = 27$ Н. Электрическая мощность, необходимая для работы ЭРДУ, генерируется бортовым ядерным источником энергии. Удельный импульс ЭРДУ также будем считать постоянным в течение всего перелета и равным ${{I}_{{sp}}} = 4762$ с. Кроме того, будем считать, что на возможную ориентацию вектора тяги ЭРДУ не наложено ограничений, и при этом соответствующие развороты связки ММБ + МПН будут происходить без затрат рабочего тела.
Пусть в начальный момент связка ММБ и МПН имеет массу ${{m}_{0}} = 40$ т и находится на РБО, высота которой равна ${{h}_{{{\text{Р Б О }}}}} = 800$ км, а наклонение – ${{i}_{0}} = {{51.6}^{^\circ }}.$ Конечной орбитой будем считать ГСО, параметры которой примем следующими: высота равна ${{h}_{T}} = 35793$ км, эксцентриситет и наклонение равны нулю. Угловое положение на начальной орбите фиксировано, а на конечной – произвольно. Для оценки радиационной нагрузки на бортовые системы ММБ будем рассчитывать дозу космического ионизирующего излучения, поглощенную некоторым чувствительным элементом (ЧЭ), который расположен в приборно-агрегатном отсеке ММБ. Для приближенного расчета поглощенной ЧЭ дозы будем считать, что ЧЭ находится за бесконечной алюминиевой стенкой толщиной $\lambda = 4$ мм. По причинам, описанным в разделе целевой функционал, будем считать, что ЧЭ поглощает только протоны и электроны РПЗ. Будем искать такие программы управления вектором тяги ЭРДУ, что соответствующие траектории многовиткового перелета с начальной орбиты на конечную имели бы наименьшую дозу радиации, поглощенную ЧЭ за время перелета.
УРАВНЕНИЯ ДВИЖЕНИЯ
Введем орбитальную систему координат $OXYZ$ следующим образом. Начало координат $O$ расположено в центре масс связки ММБ и МПН. Радиальная ось $OY$ направлена из центра Земли в начало координат O, бинормальная ось $OZ$ сонаправлена с вектором орбитального кинетического момента ММБ. Трансверсальная ось $OX$ лежит в плоскости оскулирующей орбиты, перпендикулярна оси $OY$ и направлена в сторону движения ММБ по орбите. Будем задавать направление вектора реактивного ускорения, создаваемого ЭРДУ, с помощью угла тангажа и угла рысканья. Углом тангажа $\vartheta $ будем называть угол между проекцией вектора тяги на плоскость $OXY$ оскулирующей орбиты ММБ и трансверсальным направлением $OX.$ Углом рысканья $\psi $ будем называть угол между вектором тяги и плоскостью $OXY$ оскулирующей орбиты ММБ. Тогда проекции реактивного ускорения ММБ на оси орбитальной системы координат будут иметь вид:
Чтобы избежать особенностей в окрестности нулевых эксцентриситета и наклонения будем использовать для описания движения ММБ на орбите уравнения в равноденственных элементах:
(2)
$\begin{gathered} \frac{{d{{e}_{x}}}}{{dt}} = \delta \frac{P}{m}\frac{h}{\xi }\left\{ {\xi \sin F\sin \vartheta \cos \psi } \right. + \\ + \,\,\left. {\left[ {\left( {\xi + 1} \right)\cos F + {{e}_{x}}} \right]\cos \vartheta \cos \psi - {{e}_{y}}\eta \sin \psi } \right\}, \\ \end{gathered} $(3)
$\begin{gathered} \frac{{d{{e}_{y}}}}{{dt}} = \delta \frac{P}{m}\frac{h}{\xi }\left\{ { - \xi \cos F\sin \vartheta \cos \psi } \right. + \\ + \left. {\left[ {\left( {\xi + 1} \right)\sin F + {{e}_{y}}} \right]\cos \vartheta \cos \psi + {{e}_{x}}\eta \sin \psi } \right\}, \\ \end{gathered} $(4)
$\frac{{d{{i}_{x}}}}{{dt}} = \delta \frac{P}{m}\frac{h}{\xi }\frac{1}{2}\tilde {\varphi }\cos F\sin \psi ,$(5)
$\frac{{d{{i}_{y}}}}{{dt}} = \delta \frac{P}{m}\frac{h}{\xi }\frac{1}{2}\tilde {\varphi }\sin F\sin \psi ,$(6)
$\frac{{dF}}{{dt}} = \frac{{{{\xi }^{2}}}}{{{{h}^{3}}}} + \delta \frac{P}{m}\frac{h}{\xi }\xi \eta \sin \psi ,$ЦЕЛЕВОЙ ФУНКЦИОНАЛ
В качестве индикатора интегральных эффектов деградации бортовой электроники будем использовать суммарную за перелет ММБ поглощенную ЧЭ дозу космической радиации. Наибольший вклад в поглощенную дозу радиации в околоземном пространстве дают захваченные магнитосферой Земли энергичные протоны и электроны РПЗ, а также протоны и ионы солнечных космических лучей (СКЛ) [4]. Современные модели СКЛ в основном дают количественное описание спектра потока протонов и ионов, попадающих в магнитосферу Земли во время различных вспышек и выбросов массы на Солнце. При этом в виду сложности процесса проникновения частиц СКЛ в магнитосферу Земли не существует применяемой на практике модели распространения частиц СКЛ в околоземном пространстве. Поэтому будем считать, что ЧЭ поглощает только электроны и протоны РПЗ, распределение которых в околоземном пространстве изучено довольно хорошо.
Для расчета потоков поглощенных ЧЭ электронов и протонов использовались модели AE8/AP8 MIN, AE8/AP8 MAX [5–7] и AE9/AP9 [8]. Расчеты проводились с помощью программного комплекса IRENE (https://www.vdl.afrl.af.mil/programs/ae9ap9/ downloads.php). Согласно рекомендациям работы [9] для расчета магнитных координат при использовании моделей AE8 MIN, AE8 MAX, AP8 MIN в качестве моделей магнитного поля внутренних источников Земли использовалась модель Jensen и Cain [10]. Для модели AP8 MAX использовалась экстраполированная на эпоху 1970 модель магнитного поля внутренних источников GSFC 12/66 [11]. Магнитное поле внешних токов магнитосферы Земли при использовании всех моделей типа AE8/AP8 не учитывалось. При расчете потоков частиц РПЗ при помощи модели AE9/AP9 для вычисления магнитных координат использовалась связка модели внутренних источников IGRF 2015 с моделью внешних токов Olson-Pfitzer Quiet (OPQ77). На основе рассчитанных потоков протонов и электронов РПЗ расчет поглощенной ЧЭ дозы проводился с использованием программы Shieldose2 [12]. Данная программа рассчитывает дозу, поглощенную чувствительным элементом за алюминиевой защитой некоторой толщины и геометрии от всенаправленного потока электронов и протонов произвольного спектра. В данной работе все дозы рассчитывались, предполагая, что чувствительный элемент ММБ состоит из кремния и находится за бесконечной алюминиевой стенкой толщиной $\lambda = 4$ мм (или примерно 1 г/см2).
Суммарную дозу, поглощенную ЧЭ за весь перелет, можно записать следующим образом:
где $T$ – время перелета ММБ с начальной орбиты на ГСО, ${{N}_{{D1}}}\left( {t,{\mathbf{r}}(t)} \right)$ – мощность дозы, поглощаемая ЧЭ в зависимости от текущего времени $t$ и положения ${\mathbf{r}}(t)$ ММБ в околоземном пространстве. Для применения принципа максимума Понтрягина к системе с целевым функционалом (8) необходимо к уравнениям движения добавить следующее уравнение с начальным условием ${{D}_{1}}(0) = 0$. При этом функция ${{N}_{{D1}}}$ рассчитывается численно на каждом шаге интегрирования с помощью программного комплекса IRENE. В таком случае численное интегрирование траекторий сильно осложняется наличием у функции ${{N}_{{D1}}}$ разрывов частных производных и областей с большими градиентами, что сильно увеличивает количество шагов численного интегрирования и повышает жесткость рассматриваемой системы дифференциальных уравнений. Как будет показано в разделе численные результаты, далее можно рассматривать упрощенную зависимость мощности дозы от времени и положения ММБ в околоземном пространстве. Будем считать, что мощность дозы зависит только от расстояния до центра Земли r, наклонения $i$ и истинной долготы F, и не зависит от текущего времени. Для снижения жесткости системы уравнений движения МКБ рассмотрим осредненную по времени за ${{n}_{a}}$ витков на круговой орбите радиусом $r$ и наклонением $i$ функцию мощности дозы(9)
${{\tilde {N}}_{D}}\left( {r(t),i(t)} \right) = \frac{1}{{{{n}_{a}}{{T}_{r}}}}\int\limits_0^{{{n}_{a}}{{T}_{r}}} {{{N}_{{D1}}}\left( {r(t),i(t),F(s)} \right)ds} ,$Тогда систему уравнений движения ММБ нужно дополнить уравнением
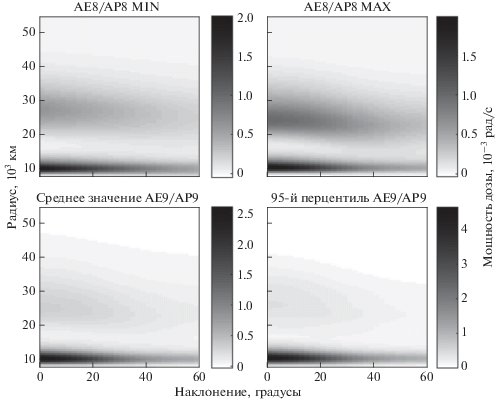
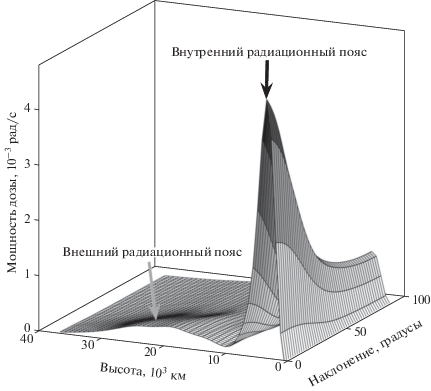
с начальным условием $D(0) = 0,$ где $r = \mu {{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} \xi }} \right. \kern-0em} \xi }$ и $i = \arccos \left( {{{\left( {2 - \tilde {\varphi }} \right)} \mathord{\left/ {\vphantom {{\left( {2 - \tilde {\varphi }} \right)} {\tilde {\varphi }}}} \right. \kern-0em} {\tilde {\varphi }}}} \right).$ Для оценки влияния различных моделей потоков частиц РПЗ на возможность снижения дозы радиации было построено указанным выше способом четыре функции ${{N}_{D}}.$ Три из них являются средними по времени и состоянию магнитосферы мощностями дозы для моделей AE8/AP8 MIN, AE8/AP8 MAX и AE9/AP9. Последняя же функция ${{N}_{D}}$ содержит помимо информации о средних потоках частиц РПЗ еще и информацию о степени неопределенности потоков в областях околоземного пространства, где отсутствуют измерения. При расчете этой функции величины потоков частиц РПЗ в модели AE9/AP9 рассматривались как случайные поля с малой дисперсией в областях, где присутствуют измерения с различных спутников, и с большой дисперсией там, где измерений нет. Четвертая функция ${{N}_{D}}$ является аппроксимацией 95-го перцентиля мощности дозы, рассчитанного по формуле (9) по 40 реализациям случайного поля потоков частиц РПЗ модели AE9/AP9 для каждой из 500 орбит опорной сетки. Все полученные функции мощности дозы представлены на рис. 1. Значения мощности дозы для каждой полученной функции ${{N}_{D}}$ показаны оттенками серого. Подробно четвертая функция ${{N}_{D}}$ показана в виде трехмерной поверхности на рис. 2, где отмечены области, соответствующие внутреннему и внешнему радиационным поясам Земли.ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Будем решать задачу оптимального быстродействия [13] с дополнительным уравнением (11) для накопленной дозы $D$ и дополнительным условием на правом конце:
Рассмотрим серию задач оптимального быстродействия с условием (12), где в каждой задаче ${{D}_{f}}$ постоянно. Последовательно снижая значение ${{D}_{f}}$ от задачи к задаче, начиная от величины поглощенной дозы на траектории оптимального быстродействия ${{D}_{{\min T}}}$, и решая получающиеся краевые задачи, можно найти минимальное значение ${{D}_{f}} = {{D}_{{\min }}}$, при котором еще существует решение краевой задачи. Таким образом, можно найти траекторию перелета с наименьшим конечным значением поглощенной дозы.
Аналогично работе [13] воспользуемся принципом максимума Понтрягина для получения оптимального в смысле времени перелета управления системой (1)–(7), (11). Функция Понтрягина для данной системы будет иметь вид
(13)
$\begin{gathered} H = - 1 - \delta \frac{P}{w}{{p}_{m}} + {{p}_{F}}\frac{{{{\xi }^{2}}}}{{{{h}^{3}}}} + \delta \frac{P}{m}\frac{h}{\xi } \times \\ \times \left( {{{A}_{\tau }}\cos \vartheta \cos \psi + {{A}_{r}}\sin \vartheta \cos \psi + {{A}_{n}}\sin \psi } \right) + {{p}_{D}}{{N}_{D}}, \\ \end{gathered} $(15)
$\begin{gathered} \cos \vartheta = \frac{{{{A}_{\tau }}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }},\,\,\,\,\sin \vartheta = \frac{{{{A}_{r}}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }}, \\ \cos \psi = \frac{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }}{{\sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} }},\,\,\,\,\sin \psi = \frac{{{{A}_{n}}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} }}. \\ \end{gathered} $В таком случае можно исключить из рассмотрения уравнения для массы ММБ $m$ и для сопряженной к ней переменной ${{p}_{m}},$ используя в уравнениях движения явную зависимость массы от времени $m = {{m}_{0}} - \left( {P{\text{/}}w} \right)t.$ Подставим выражения для оптимального управления (14), (15) в равенство (13) и получим выражение для гамильтониана
где $k = {h \mathord{\left/ {\vphantom {h {\left( {m\xi } \right)}}} \right. \kern-0em} {\left( {m\xi } \right)}},$ $A = \sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} ,$ ${{H}_{F}} = {{p}_{F}}{{{{\xi }^{2}}} \mathord{\left/ {\vphantom {{{{\xi }^{2}}} {{{h}^{3}}}}} \right. \kern-0em} {{{h}^{3}}}},$ ${{H}_{D}} = {{p}_{D}}{{N}_{D}}.$ Тогда, если ввести векторные обозначения ${\mathbf{x}} = {{\left( {h,{{e}_{x}},{{e}_{y}},{{i}_{x}},{{i}_{y}}} \right)}^{T}}$ и ${\mathbf{p}} = {{\left( {{{p}_{h}},{{p}_{{ex}}},{{p}_{{ey}}},{{p}_{{ix}}},{{p}_{{iy}}}} \right)}^{T}},$ уравнения оптимального движения запишутся в следующей форме:(16)
$\frac{{d{\mathbf{x}}}}{{dt}} = \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial {\mathbf{p}}}} = Pk\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{p}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{p}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{p}}}}} \right){{A}^{{ - 1}}},$(17)
$\frac{{dF}}{{dt}} = \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial {{p}_{F}}}} = Pk\frac{{{{A}_{n}}}}{A}\frac{{\partial {{A}_{n}}}}{{\partial {{p}_{F}}}} + \frac{{\partial {{H}_{F}}}}{{\partial {{p}_{F}}}},$(18)
$\frac{{dD}}{{dt}} = \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial {{p}_{D}}}} = \frac{{\partial {{H}_{D}}}}{{\partial {{p}_{D}}}} = {{N}_{D}},$(19)
$\begin{gathered} \frac{{d{\mathbf{p}}}}{{dt}} = - \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial {\mathbf{x}}}} = - P\left[ {\frac{{\partial {{k}^{{}}}}}{{\partial {\mathbf{x}}}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{x}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{x}}}}} \right.} \right. + \\ + \left. {\left. {{{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{x}}}}} \right){{A}^{{ - 1}}}} \right] - \frac{{\partial {{H}_{F}}}}{{\partial {\mathbf{x}}}} - {{p}_{D}}\frac{{\partial {{N}_{D}}}}{{\partial {\mathbf{x}}}}, \\ \end{gathered} $(20)
$\begin{gathered} \frac{{d{{p}_{F}}}}{{dt}} = - \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial F}} = - P\left[ {\frac{{\partial k}}{{\partial F}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial F}}} \right.} \right. + \\ + \,\,\left. {\left. {{{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial F}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial F}}} \right){{A}^{{ - 1}}}} \right] - \frac{{\partial {{H}_{F}}}}{{\partial F}} - {{p}_{D}}\frac{{\partial {{N}_{D}}}}{{\partial F}}, \\ \end{gathered} $Из (21) видно, что переменная, сопряженная к поглощенной дозе, постоянна в течение всего перелета ${{p}_{D}} = {\text{const}}$ и имеет смысл множителя Лагранжа в поставленной задаче оптимизации.
Как будет показано ниже к системе уравнений (16)–(20) применяется метод осреднения [13]. Для осредненной системы уравнений оптимального движения гамильтониан не будет зависеть от истинной долготы F, поэтому ${{p}_{F}} = {\text{const}}{\text{.}}$ А поскольку из условий трансверсальности на правом конце ${{p}_{F}}(T) = 0,$ то ${{p}_{F}} \equiv 0$ на всей траектории перелета ММБ. В таком случае для осредненной задачи уравнение для ${{p}_{F}}$ выпадает из рассмотрения, а остальные уравнения оптимального движения (16)–(20) упростятся и примут следующий вид
(22)
$\frac{{d{\mathbf{x}}}}{{dt}} = Pk\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{p}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{p}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{p}}}}} \right){{A}^{{ - 1}}},$(25)
$\begin{gathered} \frac{{d{\mathbf{p}}}}{{dt}} = - \frac{{\partial {{H}_{{{\text{opt}}}}}}}{{\partial {\mathbf{x}}}} = - P\left[ {\frac{{\partial k}}{{\partial {\mathbf{x}}}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{x}}}} + } \right.} \right. \\ + \,\,\left. {\left. {{{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{x}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{x}}}}} \right){{A}^{{ - 1}}}} \right] - {{p}_{D}}\frac{{\partial {{N}_{D}}}}{{\partial {\mathbf{x}}}}. \\ \end{gathered} $Также упростится выражение для гамильтониана, который примет вид
ОСРЕДНЕНИЕ ДВИЖЕНИЯ
Следует отметить, что система уравнений оптимального движения (22)–(25) содержит одну быструю переменную $F$, а все остальные переменные – медленные. Поэтому для повышения численной устойчивости и снижения вычислительной сложности краевой задачи принципа максимума к системе (22)–(25) можно применить метод осреднения [13]. Осреднение дифференциальных уравнений оптимального движения по времени за один виток проводится по следующей формуле
(27)
$\begin{gathered} \frac{{d{\mathbf{y}}(t)}}{{dt}} = \frac{1}{{{{T}_{c}}}}\int\limits_t^{t + {{T}_{c}}} {{{{\mathbf{f}}}_{e}}\left( {{\mathbf{y}},F,s} \right)} \,ds = \\ = \frac{n}{{2\pi }}\int\limits_0^{2\pi } {{{{\mathbf{f}}}_{e}}\left( {{\mathbf{y}},F,s} \right)\frac{{ds}}{{dF}}} \,dF, \\ \end{gathered} $КРАЕВАЯ ЗАДАЧА
Для удовлетворения условий принципа максимума необходимо решить краевую задачу для системы осредненных уравнений оптимального движения (22), (24), (25) со следующими краевыми условиями на левом и правом концах:
(28)
$\begin{gathered} h(0) = {{h}_{0}},\,\,\,\,{{e}_{x}}(0) = 0,\,\,\,\,{{e}_{y}}(0) = 0,\,\,\,\,{{i}_{x}}(0) = {{i}_{{x,0}}}, \\ {{i}_{y}}(0) = 0,\,\,\,D(0) = 0,\,\,\,\,h(T) = {{h}_{f}},\,\,\,\,{{e}_{x}}(T) = 0, \\ {{e}_{y}}(T) = 0,\,\,\,\,{{i}_{x}}(T) = 0,\,\,\,\,{{i}_{y}}(T) = 0, \\ D(T) = {{D}_{f}},\,\,\,\,{{{\bar {H}}}_{{{\text{opt}}}}}(T) = 0, \\ \end{gathered} $(29)
${\mathbf{z}} = \left( {\begin{array}{*{20}{c}} {{\mathbf{p}}(0)} \\ {{{p}_{D}}} \\ T \end{array}} \right).$Таким образом, для решения краевой задачи принципа максимума необходимо подобрать такие значения ${\mathbf{z}}$, что при интегрировании осредненной системы уравнений оптимального движения ММБ удовлетворились условия (28). Тогда краевая задача принципа максимума сводится к задаче решения нелинейной системы уравнений следующего вида:
(30)
${\mathbf{f}}\left( {\mathbf{z}} \right) = \left( {\begin{array}{*{20}{c}} {h(T) - {{h}_{f}}} \\ {{{e}_{x}}(T)} \\ {{{e}_{y}}(T)} \\ {\begin{array}{*{20}{c}} {{{i}_{x}}(T)} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{i}_{y}}(T)} \\ {D(T) - {{D}_{f}}} \end{array}} \\ {{{{\bar {H}}}_{{{\text{opt}}}}}(T)} \end{array}} \end{array}} \end{array}} \right) = 0$РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Для решения нелинейной системы уравнений (30), возникающей из принципа максимума, в данной работе применяется метод продолжения решения по параметру. Описание данного метода и примеры его использования приведены в работах [13–16]. Далее в этом разделе вкратце описана суть данного метода.
Пусть задано некоторое начальное приближение ${{{\mathbf{z}}}_{0}}$ решения системы уравнений (30), и пусть ${\mathbf{f}}\left( {{{{\mathbf{z}}}_{0}}} \right) = {\mathbf{b}}.$ Тогда рассмотрим параметрическое семейство систем нелинейных уравнений, зависящее от скалярного параметра $\tau $ и имеющее вид:
(31)
${\mathbf{F}}\left( {{\mathbf{z}},\tau } \right) = {\mathbf{f}}\left( {\mathbf{z}} \right) - \left( {1 - \tau } \right){\mathbf{b}} = 0.$Начальное приближение ${{{\mathbf{z}}}_{0}}$ является решением системы уравнений (31) при $\tau = 0$ по построению: ${\mathbf{F}}\left( {{{{\mathbf{z}}}_{0}},0} \right) = 0.$ Заметим, что исходная система уравнений (30) содержится в семействе (31) при $\tau = 1{\text{:}}$ ${\mathbf{F}}\left( {{\mathbf{z}},1} \right) = {\mathbf{f}}\left( {\mathbf{z}} \right) = 0.$ Для нахождения семейства решений (31) ${\mathbf{z}} = {\mathbf{z}}\left( \tau \right),$ зависящего от параметра τ, продифференцируем по $\tau $ систему уравнений (31) и, разрешив полученную систему относительно производной по параметру, получим систему обыкновенных дифференциальных уравнений вида
(32)
$\frac{{d{\mathbf{z}}}}{{d\tau }} = - {{\left[ {\frac{{\partial {\mathbf{f}}({\mathbf{z}})}}{{\partial {\mathbf{z}}}}} \right]}^{{ - 1}}}{\mathbf{b}}$Решая полученную систему дифференциальных уравнений каким-либо методом при $\tau \in \left[ {0;1} \right],$ получаем решение исходной системы уравнений (30) как ${\mathbf{z}}* = {\mathbf{z}}(1).$ Таким образом, решение исходной системы нелинейных уравнений сводится к решению задачи Коши для системы обыкновенных дифференциальных уравнений (32), (33). В качестве начального приближения ${{{\mathbf{z}}}_{0}}$ для решения краевой задачи (30) в данной работе использовались значения ${\mathbf{p}}(0),$ $T$ из решения задачи оптимального быстродействия для перелета ММБ между РБО и ГСО. При этом начальное значение${{p}_{D}}$ полагалось равным нулю.
Для вычисления невязок на правом конце траектории перелета ММБ, входящих в (30), при численном интегрировании осредненной системы оптимального движения использовался метод Дорманда–Принса 7(8) порядка [17]. Осреднение правых частей уравнений оптимального движения проводилось согласно (27) с помощью метода трапеций на равномерной сетке из 128 точек. Для вычисления частных производных от функции ${\mathbf{f}}$ по каждому из неизвестных параметров в (32) использовался метод конечных разностей первого порядка. Разрешение относительно производной ${{d{\mathbf{z}}} \mathord{\left/ {\vphantom {{d{\mathbf{z}}} {d\tau }}} \right. \kern-0em} {d\tau }}$ в (32) производилось путем численного решения системы линейных уравнений методом гауссового исключения.
Поскольку наибольшая эффективность использования метода продолжения решения по параметру достигается при использовании методов численного интегрирования высокого порядка [13], в данной работе для интегрирования (32) также использовался метод Дорманда–Принса 7(8) порядка. Однако для еще большего увеличения длины шага по параметру продолжения и для снижения количества отвергнутых шагов в данной работе после каждого принятого шага запускалась процедура коррекции полученного значения вектора неизвестных параметров ${{{\mathbf{z}}}_{1}}.$ Процедура коррекции состояла в решении при фиксированном $\tau {\text{*}}$ уравнения ${\mathbf{f}}\left( {{\mathbf{z}}\left( {\tau {\text{*}}} \right)} \right) = \left( {1 - \tau {\text{*}}} \right){\mathbf{b}}$ относительно вектора ${\mathbf{z}}\left( {\tau {\text{*}}} \right).$ Решение проводилось методом Ньютона с начальным приближением ${\mathbf{z}}\left( {\tau {\text{*}}} \right) = {{{\mathbf{z}}}_{1}}.$
Для проверки насколько отличается полученное управление от оптимального вследствие применения метода осреднения после каждого принятого шага и проведенной процедуры коррекции проводилось интегрирование неосредненных уравнений движения (22)–(25). При этом начальные значения сопряженных переменных и время перелета брались из ${\mathbf{z}}\left( {\tau {\text{*}}} \right),$ сопряженная переменная к истинной долготе полагалась равной нулю в течение всего перелета ${{p}_{F}}(t) \equiv 0,$ а начальное значение истинной долготы полагалось нулевым $F(0) = 0.$ Кроме того, после получения неосредненных траекторий на этих траекториях рассчитывалась неосредненная доза радиации (8) с помощью программного комплекса IRENE. Численное интегрирование неосредненных траекторий оптимального движения также проводилось методом Дорманда–Принса 7(8) порядка.
ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
Практический интерес имеет только снижение конечной дозы ниже ее значения на траектории оптимального быстродействия, то есть когда ${{D}_{f}} < {{D}_{{\min T}}}.$ Но величина максимального снижения поглощенной дозы заранее неизвестна, поэтому проводилась следующая процедура. Сначала требуемое значение поглощенной дозы полагалось ${{D}_{f}} = 0$ и запускалось интегрирование по параметру продолжения системы (32), (33). При некотором значении параметра продолжения $\tau = {{\tau }_{f}} < 1$ наблюдалось существенное увеличение невязок на правом конце. При этом часто либо минимальная высота перицентра на траектории опускалась ниже 300 км, либо максимальная высота апоцентра поднимались выше орбиты Луны. Матрица в правой части (32) при этом оказывалась необратимой. В этот момент интегрирование по параметру продолжения прерывалось. Далее если шаги по $\tau $ были слишком большие и была необходимость получить более подробное решение ${\mathbf{z}}\left( \tau \right),$ $\tau \in \left[ {0;{{\tau }_{f}}} \right],$ то интегрирование системы (32), (33) перезапускалось со значением ${{D}_{f}},$ равным значению осредненной дозы $D(T)$ при $\tau = {{\tau }_{f}}.$ При этом интегрирование проводилось в пределах $\tau \in \left[ {0;{{\tau }_{f}}} \right],$ и выбирался более мелкий шаг по параметру продолжения. Следует отметить, что траектории при $\tau = {{\tau }_{f}}$ полученные таким образом из-за ошибок численных методов необязательно имеют наименьшую в принципе возможную величину конечной поглощенной дозы. Но эти траектории позволяют получить оценку максимального возможного снижения поглощенной дозы радиации на конец перелета.
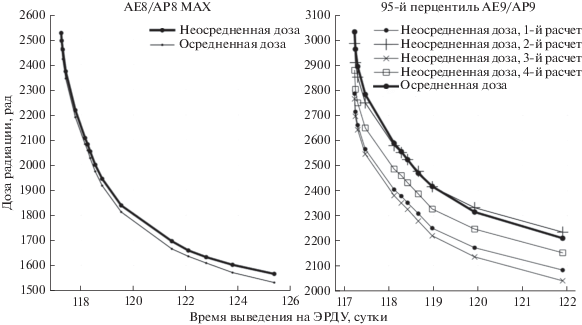
Указанная выше процедура проводилась для всех четырех функций мощности дозы ${{N}_{D}}.$ Далее полученные неизвестные параметры осредненной краевой задачи ${\mathbf{z}}\left( \tau \right)$ использовались для интегрирования неосредненных уравнений оптимального движения (22)–(25) и расчета неосредненной дозы ${{D}_{1}}.$ Зависимость осредненной (10) и неосредненной дозы (8) от времени перелета на полученных траекториях в случае модели AE8/AP8 MAX показана на рис. 3 слева. Каждой точке на графике соответствует траектория при определенном значении параметра продолжения. Видно, что осредненная и неосредненная дозы достаточно хорошо совпадают. Ошибка аппроксимации конечной неосредненной дозы осредненной дозой на полученных траекториях в случае моделей AE8/AP8 MIN, AE8/AP8 MAX и среднего значения AE9/AP9 не превышает 2.2%. Поскольку последняя функция ${{N}_{D}}$ является аппроксимацией 95-го перцентиля мощности дозы, рассчитанного по 40 реализациям случайного поля, то значения этой функции и интеграл от нее по траектории будет зависеть от конкретных реализаций случайного поля потоков частиц РПЗ. Если в набор реализаций попали случаи с низкой мощностью дозы вдоль траектории, то неосредненная доза может существенно отличаться от осредненной дозы. Но все же в большинстве случаев неосредненная доза не будет превосходить осредненную. Поэтому осредненную дозу для четвертой функции ${{N}_{D}}$ можно рассматривать как оценку накопленной дозы в худшем случае. На рис. 3 справа приведена зависимость осредненной и неосредненной дозы от времени перелета на полученных траекториях для четвертой функции ${{N}_{D}}.$ Неосредненная доза рассчитывалась четыре раза с различными начальными значениями генератора случайных чисел модели потоков РПЗ. Видно, что все четыре расчета неосредненной дозы отличаются примерно на константу от осредненной дозы. Но при этом следует отметить, что осредненная доза для всех моделей мощности дозы является хорошим индикатором относительной дозовой нагрузки: если осредненная доза от траектории к траектории снижается, то и, скорее всего, снизится неосредненная доза. Поэтому принятое упрощение о зависимости мощности дозы только от радиуса и наклонения оскулирующей орбиты вполне допустимо в данной работе.
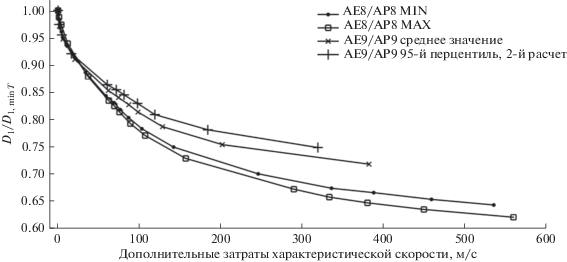
Для сравнения возможностей снижения конечной дозы для каждой функции мощности дозы был проведен расчет отношения неосредненной дозы на полученных траекториях к неосредненной дозе на траектории оптимального быстродействия. Результаты расчетов этого отношения в зависимости от времени перелета показаны на рис. 4 и в зависимости от разности затрат характеристической скорости на полученных траекториях и на траектории оптимального быстродействия – на рис. 5. На этих рисунках видно, что предложенная выше методика снижения дозовой нагрузки на траектории выведения ММБ с помощью специального управления работоспособна и позволяет получить траектории с дозой, меньше чем на траектории оптимального быстродействия. Максимально удается снизить конечную дозу радиации на 25–38% от дозы на траектории оптимального быстродействия в зависимости от модели потоков РПЗ. При этом время выведения увеличивается на 4–7% от оптимального времени выведения, а дополнительные затраты характеристической скорости увеличиваются относительно траектории оптимального быстродействия на 320–560 м/с.
Рис. 4.
Отношение неосредненной дозы на полученных траекториях к неосредненной дозе на траектории оптимального быстродействия в зависимости от времени перелета.
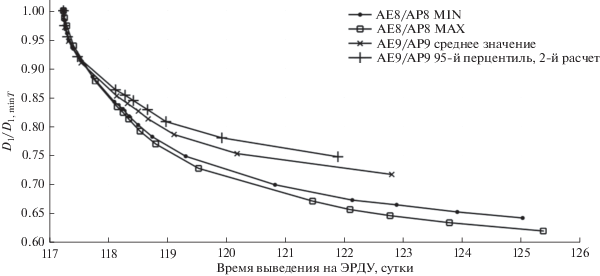
Рис. 5.
Отношение неосредненной дозы на полученных траекториях к неосредненной дозе на траектории оптимального быстродействия в зависимости от дополнительных затрат характеристической скорости на перелет.
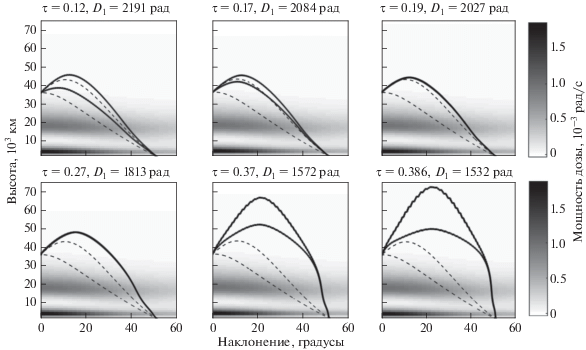
На рис. 6 показано как менялась траектория перелета в случае модели AE8/AP8 MAX по мере увеличения параметра продолжения $\tau $ и, соответственно, снижения конечной дозы радиации. Траектории при каждом значении параметра продолжения представлены в осях “радиус–наклонение”. Две пунктирные линии на каждом графике показывают зависимости высоты перигея и апогея от наклонения на траектории оптимального быстродействия. Две непрерывные линии соответствуют зависимости высоты перигея и апогея от наклонения на траектории, полученной при данном значении параметра продолжения. Оттенками серого на каждом графике показана величина осредненной мощности дозы. Видно, что сначала наблюдается тенденция к увеличению максимальной высоты перигея, чтобы вынести перигейные участки траектории из области высокой мощности дозы. Затем примерно при $\tau \approx 0.19$ высота перигея становится равной высоте апогея и оскулирующая орбита становится круговой во время всего перелета. Далее по мере увеличения параметра продолжения максимальная высота траектории увеличивается, пока примерно при $\tau \approx 0.36$ снова на траектории появляется ненулевой эксцентриситет. Далее по мере увеличения параметра продолжения максимальный эксцентриситет растет вплоть до максимальных полученных значений τ. Также на рис. 6 можно заметить, что по мере снижения конечной дозы радиации изменение наклонения орбиты все меньше происходит в области пересечения траекторией ММБ радиационных поясов Земли и все больше – вне этой области. Этот факт частично подтверждает правильность расчетов, так как видно, что с уменьшением наклонения мощность дозы внутри радиационных поясов растет, и поэтому выгоднее в плане радиационной нагрузки пересекать РПЗ (другими словами набирать высоту) в области больших наклонений.
Рис. 6.
Зависимости высоты перигея и апогея от наклонения на полученных траекториях при различных значениях параметра продолжения $\tau $ для модели потоков частиц РПЗ AE8/AP8 MAX.
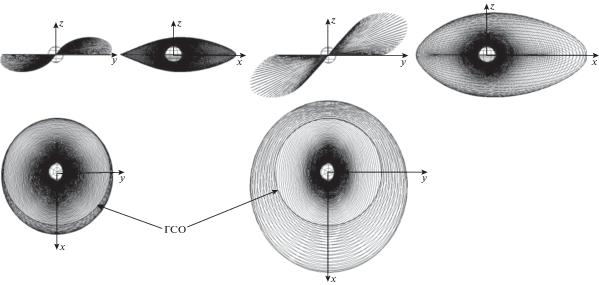
На рис. 7 изображены проекции двух траекторий на координатные плоскости инерциальной геоэкваториальной системы координат. Траектория слева является траекторией оптимального быстродействия. Справа изображена траектория с наименьшей полученной дозой для модели потоков частиц РПЗ AE8/AP8 MAX. Все проекции на рис. 7 изображены в одном масштабе. В центре каждой из проекций условно изображена Земля. Жирной линией в плоскости $Oxy$ показана геостационарная орбита.
Рис. 7.
Форма траектории оптимального быстродействия (слева) и траектории, полученной для модели потоков частиц РПЗ AE8/AP8 MAX при $\tau = 0.386$ (справа).
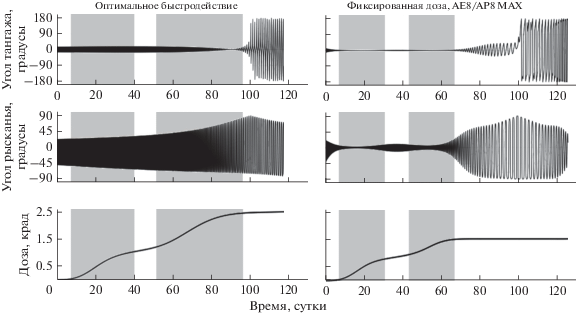
Для траекторий, изображенных на рис. 7, на рис. 8 представлены графики зависимости углов тангажа и рысканья, а также дозы радиации, поглощенной ЧЭ, в зависимости от времени перелета ММБ на ГСО с помощью ЭРДУ. Три графика слева соответствуют траектории оптимального быстродействия, а графики справа относятся к траектории с наименьшей полученной дозой для модели потоков частиц РПЗ AE8/AP8 MAX. На каждом из графиков отмечены серым цветом участки траектории, когда поглощенная ЧЭ доза активно растет. Эти участки примерно соответствуют пересечению ММБ внутреннего и внешнего радиационных поясов. Как видно на графиках угла рысканья для траектории с наименьшей дозой амплитуда угла рысканья снижается внутри серых областей, что приводит к меньшему изменению наклонения внутри РПЗ, наблюдавшемуся на рис. 6.
ЗАКЛЮЧЕНИЕ
В работе были рассмотрены возможности оптимизации поглощенной дозы за счет изменения формы траектории выведения ММБ с низкой круговой орбиты на ГСО с использованием ЭРДУ и ЯЭУ. Математический аппарат построения оптимальных по быстродействию траекторий с фиксированной конечной дозой позволил снизить поглощенную за перелет дозу радиации на 25–38% в зависимости от используемой модели потоков частиц РПЗ. При этом время выведения увеличилось на 4–7% от оптимального времени выведения. Дополнительные затраты характеристической скорости увеличиваются относительно траектории оптимального быстродействия на 320–560 м/с. Для эффективного решения краевых задач принципа максимума, возникающих при решении задач оптимального быстродействия с фиксированной конечной дозой, был предложен метод аппроксимации мощности дозы с помощью осреднения и построения сплайнов 11-го порядка. Полученная аппроксимация является достаточно гладкой для применения в численном интегрировании уравнений движения ММБ интегратором 7(8) порядка и достаточно хорошо отражает характер зависимости накопленной дозы в зависимости от формы траектории выведения ММБ.
Работа выполнена по гранту Российского научного фонда (соглашение № 16-19-10429).
Автор выражает благодарность В.Г. Петухову за ценные замечания, сделанные им при обсуждении данной статьи.
Список литературы
Легостаев В.П., Лопота В.А., Синявский В.В. Перспективы и эффективность применения космических ядерно-энергетических установок и ядерных электроракетных двигательных установок // Космическая техника и технологии. 2013. № 1. С. 4–15.
Старченко А.Е. Оптимизация траектории выведения космического аппарата на геостационарную орбиту с целью снижения уровня радиационной деградации солнечных батарей // Известия РАН. Энергетика. 2017. № 3. С. 128–145.
Радиационные условия в космическом пространстве: учебное пособие / Под ред. Панасюка М.И. М.: Библион–Русская книга, 2006.
Xapsos M.A., O’Neill P.M., O’Brien T.P. Near-Earth Space Radiation Models // IEEE Trans. Nucl. Sci. 2013. V. 60. № 3. P. 1691–1705.
Sawyer D.M., Vette J.I. AP-8 Trapped Proton Environment for Solar Maximum and Solar Minimum. NASA-TM-X-72605. NSSDC/WDC-A-R&S 76-06. 1976.
Vette J.I. Trapped Radiation Environment Model Program (1964–1991). NSSDC/WDC-A-R&S 91-29. November, 1991.
Vette J.I. The AE-8 Trapped Electron Model Environment. NSSDC/WDC-A-R&S 91-24, 1991.
Ginet G.P., O’Brien T.P., Huston S.L. et al. AE9, AP9 and SPM: New Models for Specifying the Trapped Energetic Particle and Space Plasma Environment // Space Sci. Rev 2013. V. 179 P. 579–615.
Heynderickx D. Comparison between methods to compensate for the secular motion of the south Atlantic anomaly // Rad. Meas. 1996. V. 26. № 3. P. 369–373
Jensen D.C., Cain J.C. An Interim Geomagnetic Field // J. Geophys. Res. 1962. V. 67. P. 3568–3569.
Cain J.C., Hendricks S.J., Langel R.A., Hudson W.V. A Proposed Model for the International Geomagnetic Reference Field-1965 // J. Geomag. Geoelec. 1967. V. 19. P. 335–355.
Seltzer S.M. Updated calculations for routine space-shielding radiation dose estimates: SHIELDOSE-2 // NIST Publication, NISTIR 5477. Gaithersburg, 1994.
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. 2004. Т. 42. № 3. С. 260–279. (Cosmic Research. P. 250).
Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. 2012. Т. 50. № 3. С. 258–270. (Cosmic Research. P. 249).
Иванюхин А. В., Петухов В. Г. Задача минимизации тяги и ее приложения // Космические исследования. 2015. Т. 53, № 4. С. 320–331. (Cosmic Research. P. 300).
Шалашилин В.А., Кузнецов Е.Б. Метод продолжения решения по параметру и наилучшая параметризация. М.: Эдиториал УРСС, 1999.
Hairer F., Norsett S.P., Wanner G. Solving Ordinary Differential Equations I. Non-Stiff Problems. Berlin: Springer-Verlag, 1987.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования