Космические исследования, 2019, T. 57, № 5, стр. 386-400
Минимизация деградации трехкаскадных солнечных батарей космического аппарата при выведении на геостационарную орбиту
А. Е. Старченко *
Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
* E-mail: aleksandr.starchenko@phystech.edu
Поступила в редакцию 26.03.2019
После доработки 02.04.2019
Принята к публикации 25.04.2019
Аннотация
В работе рассматривается метод снижения радиационной деградации солнечных батарей (СБ) космического аппарата при комбинированном выведении на геостационарную орбиту с помощью разгонного блока и электроракетной двигательной установки. Суть метода состоит в оптимизации формы траектории перелета и аргумента перигея промежуточной орбиты. Применяется принцип максимума к задаче оптимизации электрической мощности СБ на конец пятнадцатилетнего срока активного существования (САС). Для этого к уравнениям движения КА добавляется уравнение для текущей мощности СБ и ограничение на эту мощность на конец САС. Явно получено решение сопряженного к мощности СБ уравнения. Расчет радиационной деградации СБ проведен с помощью моделей потоков заряженных частиц радиационных поясов Земли AE8 MAX и AP8 MAX. При оптимизации учтена вторая зональная гармоника в разложении гравитационного потенциала притяжения Земли. Удалось увеличить мощность СБ на конец САС на 0.16–0.66% от мощности СБ на начало перелета в зависимости от параметров промежуточных орбит. Дополнительные затраты характеристической скорости увеличились относительно траекторий оптимального быстродействия на 13–1087 м/с в зависимости от параметров промежуточных орбит.
ВВЕДЕНИЕ
Одним из вариантов выведения КА на геостационарную орбиту (ГСО) является комбинированная схема выведения с помощью разгонного блока (РБ) и электроракетной двигательной установки (ЭРДУ). Данная схема обладает преимуществами и недостатками как схемы выведения только с помощью РБ, так и полностью электроракетной схемы. Анализу различных аспектов комбинированной схемы посвящено множество работ [1–5]. Одной из проблем, возникающих во время электроракетной фазы выведения КА на ГСО, является накопление радиационных повреждений в фотоэлектрических преобразователях (ФЭП) СБ при прохождении КА радиационных поясов Земли (РПЗ). Радиационные повреждения ФЭП приводят к существенной деградации его основных характеристик, в том числе и к снижению выходной электрической мощности, необходимой для функционирования бортовых систем, включая ЭРДУ во время выведения. Ситуация осложняется неблагоприятными радиационными условиями на ГСО и длительными сроками активного существования (САС) на целевой орбите, характерными для связных КА, являющихся большинством среди выводимых на ГСО аппаратов. Кроме того, наблюдается эффект “лавинной” деградации характеристик ФЭП [6, 7], когда после некоторого количества повреждений наблюдается экспоненциальное падание характеристик ФЭП. Все эти факторы приводят к необходимости учета радиационной деградации электрической мощности СБ при проектировании КА. Для парирования падения мощности СБ и получения гарантированной выходной мощности на конец САС необходимо при проектировании закладывать избыточную мощность СБ, что приводит к увеличению площади СБ, сложности их конструкции и повышению стоимости КА.
В данной работе рассматривается способ снижения радиационной нагрузки на ФЭП и бортовые системы в целом, связанный с изменением формы траектории выведения. Изменение формы траектории перелета может привести к снижению суммарного количества заряженных частиц (флюенса), поглощенных ФЭП, благодаря тому, что распределение потоков заряженных частиц РПЗ в околоземном пространстве неоднородно [7]. Следовательно, за одно и тоже время пребывания в РПЗ на поверхность ФЭП могут упасть различное количество заряженных частиц в зависимости от того, где внутри РПЗ находится КА.
Данная работа является продолжением работ [8, 9], где рассматривалась оптимизация траекторий комбинированного выведения КА с СБ на основе кремниевых ФЭП. Предполагается, что в данной работе КА оснащен СБ с перспективными трехкаскадными фотоэлектрическими преобразователями ФЭП, обладающими на данный момент самым высоком коэффициентом полезного действия [10].
Помимо задач, связанных с комбинированным выведением, проблема большой радиационной нагрузки может возникнуть при электроракетном выведении полезного груза на ГСО с помощью многоразового межорбитального буксира с ядерной энергетической установкой. В этой задаче перелет начинается с круговой орбиты высотой 800 км, что приводит к еще большей радиационной нагрузке на бортовые системы буксира и полезной нагрузки. Задача снижения поглощенной в РПЗ дозы радиации с помощью изменения формы траектории перелета межорбитального буксира рассмотрена в работе [11].
ПОСТАНОВКА ЗАДАЧИ
Рассматривается следующая схема выведения КА на ГСО. На первом этапе ракета-носитель типа “Союз” выводит КА с разгонным блоком, аналогичным по характеристикам РБ “Фрегат”, на низкую опорную орбиту. Затем РБ выполняет доставку КА на промежуточную орбиту и отделяется от КА. На заключительном этапе КА с помощью ЭРДУ переводится по многовитковой траектории на ГСО.
Будем считать, что КА на этапе выведения с помощью ЭРДУ движется только под действием силы притяжения Земли и силы тяги ЭРДУ. В разложении гравитационного потенциала притяжения Земли будем учитывать только главный член и вторую зональную гармонику. Всеми остальными возмущающими силами пренебрежем. Электрическая мощность, необходимая для работы ЭРДУ, генерируется только бортовыми СБ на основе трехкаскадных ФЭП. Предполагается, что суммарная электрическая мощность СБ выбрана с избытком так, что на конец САС КА (15 лет без учета выведения) генерируемая мощность будет достаточной для функционирования целевой аппаратуры, служебных систем и выполнения КА целевой задачи в целом. Также будем считать, что максимальная тяга ЭРДУ $P$ и удельный импульс ${{I}_{{sp}}}$ в течение всего этапа электроракетного выведения постоянны. Пусть на борту рассматриваемого КА в качестве маршевой ЭРДУ установлены два двигателя СПД-140Д [12] суммарной максимальной тягой $P = 0.58$ Н. Удельный импульс ЭРДУ принимаем равным ${{I}_{{sp}}} = 1780$ с. Кроме того, примем допущение, что на возможную ориентацию вектора тяги ЭРДУ не наложено ограничений, и при этом соответствующие развороты КА будут считаться не требующими затрат рабочего тела. Наконец, будем считать, что деградация СБ происходит только под воздействием на ФЭП протонов и электронов РПЗ, воздействием других источников космической радиации пренебрежем.
Пусть на начало этапа выведения с помощью ЭРДУ КА находится в перицентре промежуточной орбиты и имеет некоторую массу ${{m}_{0}},$ высота перицентра промежуточной орбиты равна ${{h}_{{\pi ,0}}},$ высота апоцентра ${{h}_{{\alpha ,0}}},$ наклонение – ${{i}_{0}} > 0.$ Аргумент перигея и долгота восходящего узла промежуточной орбиты равны ${{\omega }_{{\pi ,0}}}$ и ${{\Omega }_{0}}$, соответственно. Целевой орбитой КА будем считать ГСО: высота ${{h}_{T}} = 35{\kern 1pt} 793$ км, нулевые эксцентриситет и наклонение ${{i}_{T}} = 0.$ Угловое положение КА на конечной орбите не фиксируется. Для заданных фиксированных значений ${{h}_{{\pi ,0}}},$ ${{h}_{{\alpha ,0}}},$ ${{i}_{0}},$ ${{\omega }_{{\pi ,0}}},$ ${{\Omega }_{0}}$ и ${{m}_{0}}$ найдем такие траектории перелета c помощью ЭРДУ, чтобы падение максимальной выходной электрической мощности СБ КА вследствие влияния космической радиации за время перелета с помощью ЭРДУ было наименьшим. Поскольку в течение САС мощность СБ только уменьшается и при проектировании КА необходимо гарантировать достаточный уровень энергоприхода на конец САС, то в целевой функционал для большей наглядности будем включать деградацию СБ за время нахождения КА на ГСО вплоть до конца САС. Тогда рассматриваемую задачу можно записать следующим образом $\Delta N = {{N}_{0}} - {{N}_{{{\text{С А С }}}}} \to \min ,$ где ${{N}_{0}}$ – мощность СБ на начало этапа выведения с помощью ЭРДУ, а ${{N}_{{{\text{С А С }}}}}$ – мощность СБ на конец САС. При фиксированной ${{N}_{{{\text{С А С }}}}}$ эта задача эквивалентна задаче максимизации относительной мощности СБ на конец САС
УРАВНЕНИЯ ДВИЖЕНИЯ
Введем орбитальную систему координат $OXYZ$ следующим образом. Начало координат $O$ расположено в центре масс КА. Радиальная ось $OX$ направлена из начала координат $O$ в направлении от центра Земли, бинормальная ось $OZ$ сонаправлена с вектором орбитального кинетического момента КА. Трансверсальная ось $OY$ лежит в плоскости оскулирующей орбиты, перпендикулярна оси $OX$ и направлена в сторону движения КА по орбите. Чтобы избежать особенностей в окрестности нулевых эксцентриситета и наклонения будем использовать для описания движения КА на орбите уравнения в равноденственных элементах:
(2)
$\frac{{d{{e}_{x}}}}{{dt}} = \frac{h}{\xi }\left\{ {{{a}_{Y}}\xi \sin F\, + \,{{a}_{X}}\left[ {\left( {\xi + 1} \right)\cos F\, + \,{{e}_{x}}} \right]\, - \,{{a}_{Z}}{{e}_{y}}\eta } \right\},$(3)
$\frac{{d{{e}_{y}}}}{{dt}} = \frac{h}{\xi }\left\{ { - {{a}_{Y}}\xi \cos F\, + \,{{a}_{X}}\left[ {\left( {\xi \, + \,1} \right)\sin F\, + \,{{e}_{y}}} \right]\, + \,{{a}_{Z}}{{e}_{x}}\eta } \right\},$(6)
$\frac{{dF}}{{dt}} = \frac{{{{\xi }^{2}}}}{{{{h}^{3}}}} + {{a}_{Z}}{h \mathord{\left/ {\vphantom {h \xi }} \right. \kern-0em} \xi }\eta ,$Будем задавать направление вектора реактивного ускорения, создаваемого ЭРДУ, с помощью угла тангажа и угла рысканья. Углом тангажа $\vartheta $ будем называть угол между проекцией вектора тяги на плоскость $OXY$ оскулирующей орбиты КА и трансверсальным направлением $OY.$ Углом рысканья $\psi $ будем называть угол между вектором тяги и плоскостью $OXY$ оскулирующей орбиты КА. Тогда проекции возмущающего ускорения от работы ЭРДУ и второй зональной гармоники разложения гравитационного потенциала Земли на оси орбитальной системы координат будут иметь следующий вид:
ЦЕЛЕВОЙ ФУНКЦИОНАЛ
Максимальная выходная электрическая мощность СБ КА на орбите зависит от суммарного количества заряженных частиц (флюенса) космической радиации, упавших на единицу площади чувствительной поверхности ФЭП СБ за время от начала перелета до текущего момента. Для расчета флюенсов электронов и протонов РПЗ различных энергий в конкретной точке околоземного пространства будем использовать модели AE8 MAX и AP8 MAX [13–15], реализованные в программном комплексе IRENE (https://www.vdl.afrl. af.mil/programs/ae9ap9/downloads.php). Согласно рекомендациям работы [16] для расчета магнитных координат при использовании модели AE8 MAX в качестве моделей магнитного поля внутренних источников Земли использовалась модель Jensen и Cain [17]. Для модели AP8 MAX использовалась экстраполированная на эпоху 1970 модель магнитного поля внутренних источников GSFC 12/66 [18]. Магнитное поле внешних токов магнитосферы Земли не учитывалось.
Падение максимальной электрической мощности СБ рассчитывалось с помощью метода эквивалентного потока [6]. Его суть состоит в переводе всенаправленного потока протонов и электронов через набор коэффициентов в моноэнергетический нормально падающий поток электронов с энергией 1 МэВ, который создаст то же количество однотипных повреждений ФЭП в единицу времени, что и исходные потоки. Таким образом, уровень повреждений, нанесенных космической радиацией ФЭП, можно измерять в эквивалентном флюенсе нормально падающих на ФЭП электронов с энергией 1 МэВ. Зная величину эквивалентного флюенса электронов с энергией 1 МэВ можно по экспериментальным данным оценить величину деградации различных электрических характеристик ФЭП, в том числе и снижение максимальной электрической мощности ФЭП. Для расчета эквивалентного флюенса по спектрам падающих на ФЭП электронов и протонов РПЗ использовалась программа EQFRUX [6]. Переводные коэффициенты соответствовали трехкаскадному ФЭП производства компании Spectrolab (http://www.spectrolab.com/DataSheets/ TJCell/tj.pdf) и были взяты из программы General EQFlux (https://opensource.gsfc.nasa.gov/projects/ eqflux/index.php). При расчете падения мощности СБ учитывалось, что фоточувствительные элементы ФЭП находятся за слоем защитного стекла, которое частично ослабляет поток энергичных частиц РПЗ падающих на фотоэлектронные преобразователи СБ. Толщина защитного покрытия влияет на переводные коэффициенты для расчета эквивалентного флюенса. В расчетах было принято, что ФЭП находятся за слоем кварцевого стекла толщиной ${{\delta }_{п }} = 150$ мкм плотностью 2.2 г/см3 (как в [6]). Предполагалось, что задняя поверхность ФЭП закрыта элементами конструкции СБ с такими же ослабляющими свойствами как и у кварцевого стекла толщиной ${{\delta }_{{\text{з }}}} = 500$ мкм. Согласно [6] для учета повреждений ФЭП, нанесенных потоком частиц, падающих как с передней, так и с задней поверхности СБ, рассчитывались отдельно эквивалентные флюенсы для частиц, падающих на переднюю и заднюю поверхности СБ, а затем складывались.
Интегральный эквивалентный флюенс электронов 1 МэВ накопленный единицей площади ФЭП от начала перелета и до момента времени $t$ можно рассчитать следующим образом:
(8)
${{\Phi }_{n}}\left( t \right) = \int\limits_0^t {{{{\bar {U}}}_{n}}\left( {s,{\mathbf{r}}\left( s \right)} \right)ds} ,$(9)
${{\beta }_{{{\text{С А С }}}}} \equiv \frac{{{{N}_{{{\text{С А С }}}}}}}{{{{N}_{0}}}} = 1 - C\ln \left( {1 + \frac{{{{\Phi }_{n}}(T) + {{\Phi }_{{{\text{Г С О }}}}}}}{{{{\Phi }_{X}}}}} \right),$(10)
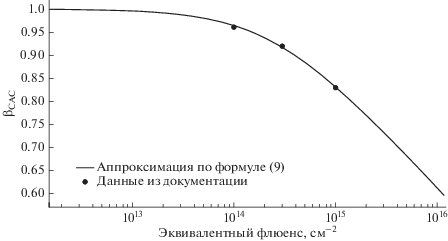
$\begin{gathered} \frac{{d{{\gamma }_{n}}}}{{dt}} = \frac{{{{{\bar {U}}}_{n}}\left( {t,{\mathbf{r}}\left( t \right)} \right)}}{{{{\Phi }_{X}}}} \equiv {{U}_{n}}\left( {t,{\mathbf{r}}\left( t \right)} \right), \\ \frac{{d{{\beta }_{n}}}}{{dt}} = - \frac{{C{{U}_{n}}}}{{1 + {{\gamma }_{n}}(t)}} = - C{{U}_{n}}{{e}^{{ - \frac{{1 - {{\beta }_{n}}}}{C}}}}. \\ \end{gathered} $Рис. 1.
Зависимость относительной мощности трехкаскадного ФЭП Spectrolab GaInP2/GaAs/Ge Triple Junction Solar Cell (КПД = 25.1%) от суммарного эквивалентного флюенса электронов 1 МэВ.
Для применения принципа максимума Понтрягина к системе с целевым функционалом (9) н-еобходимо к уравнениям движения КА добавить уравнение (10) с начальным условием ${{\beta }_{n}}(0) = 1 - С \ln \left( {1 + {{{{\Phi }_{{{\text{Г С О }}}}}} \mathord{\left/ {\vphantom {{{{\Phi }_{{{\text{Г С О }}}}}} {{{\Phi }_{X}}}}} \right. \kern-0em} {{{\Phi }_{X}}}}} \right).$
Но в связи с особенностями реализации расчета спектров частиц РПЗ в программном комплексе IRENE и резким нарастанием величин потоков частиц РПЗ на нижней границе внутреннего радиационного пояса Земли функция ${{U}_{n}}$ имеет разрывы частных производных и области с большими градиентами. Этот факт сильно осложняет численное интегрирование траекторий КА и повышает жесткость рассматриваемой системы дифференциальных уравнений. Аналогично работам [9, 11] для снижения жесткости полученной системы воспользуемся методом осреднения эквивалентного потока. Пусть осредненный эквивалентный флюенс $\Phi $ и осредненная относительная мощность СБ $\beta $ заданы следующим образом:
(11)
$U\left( {r,i} \right) = \frac{1}{{{{n}_{a}}{{T}_{r}}}}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + {{n}_{a}}{{T}_{r}}} {{{U}_{n}}\left( {s,{{{\mathbf{r}}}_{d}}(s)} \right)ds} ,$Чтобы избежать разрывов частных производных функции U, гладкость которых необходима для численного интегрирования систем дифференциальных уравнений методами высокого порядка, аналогично работам [9, 11] построим гладкую аппроксимацию функции $U$ с помощью сплайнов 11-го порядка. Для этого был произведен расчет функции $U$ согласно формуле (11) на опорной сетке из $30 \times 40 = 1200$ круговых орбит в области от 0 до 90 градусов по наклонению и от 7071 до 63 371 км по радиусу. Число витков осреднения выбиралось таким образом, чтобы оно было целым и время движения по круговой орбите осреднения составляло не менее 3 суток. Кроме того, дополнительно ко всем операциям по построению гладкого сплайна $U$ из работ [9, 11] в данной работе применено дополнительное преобразование входных и выходных переменных следующего вида
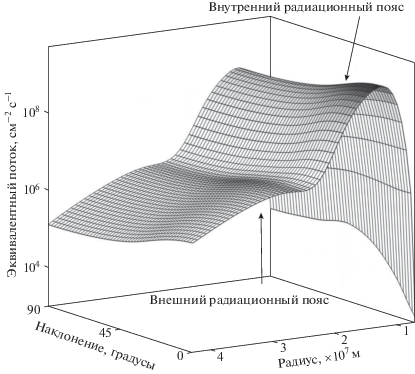
Рис. 2.
Зависимость осредненного эквивалентного потока электронов 1 МэВ от расстояния до центра Земли и наклонения орбиты. Масштаб по оси эквивалентного потока – логарифмический. Стрелками указаны области соответствующие внутреннему и внешнему РПЗ.
После всех преобразований в качестве дополнительного уравнения движения КА, связанного с выходной мощностью СБ, будем рассматривать следующее уравнение
с начальным условием β(0) = 1 – C × $ \times \,\ln \left( {1 + {{{{\Phi }_{{{\text{Г С О }}}}}} \mathord{\left/ {\vphantom {{{{\Phi }_{{{\text{Г С О }}}}}} {{{\Phi }_{X}}}}} \right. \kern-0em} {{{\Phi }_{X}}}}} \right).$ В качестве целевого функционала в данной работе будем рассматривать значение неосредненной относительной мощности СБ на конец САС ${{\beta }_{n}}(T).$ Для упрощения задачи согласно результатам работ [9, 11] допустимо рассматривать в качестве целевого функционала значение осредненной относительной мощности СБ на конец САС $\beta (T).$ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Задачу на максимизацию относительной мощности СБ на конец САС можно формализовать как задачу оптимального быстродействия [19] с дополнительной фазовой переменной $\beta (t),$ удовлетворяющей уравнению (12), и дополнительным ограничением на правом конце следующего вида
Рассмотрим серию задач оптимального быстродействия с ограничением (13), где в каждой задаче ${{\beta }_{T}}$ постоянно. Постепенно увеличивая ${{\beta }_{T}}$ и решая получаемые краевые задачи можно найти максимальное значение $\beta (T),$ при котором еще существует решение краевой задачи. Таким образом, можно найти траекторию перелета с наибольшим возможным конечным значением относительной мощности СБ на конец САС.
Аналогично работе [19] воспользуемся принципом максимума Понтрягина для получения оптимального в смысле времени перелета управления системой (1)–(7), (12). Функция Понтрягина для данной системы будет иметь вид
(14)
$\begin{gathered} H = - 1 - \delta \frac{P}{w}{{p}_{m}} + \delta \frac{P}{m}\frac{h}{\xi }\left( {{{A}_{\tau }}\cos \vartheta \cos \psi } \right. + \\ \left. { + \,\,{{A}_{r}}\sin \vartheta \cos \psi + {{A}_{n}}\sin \psi } \right) + {{H}_{F}} + {{H}_{{J2}}} + {{H}_{\beta }}, \\ \end{gathered} $(16)
$\begin{gathered} \cos \vartheta = \frac{{{{A}_{\tau }}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }},\,\,\,\,\sin \vartheta = \frac{{{{A}_{r}}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }}, \\ \cos \psi = \frac{{\sqrt {A_{\tau }^{2} + A_{r}^{2}} }}{{\sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} }},\,\,\,\,\sin \psi = \frac{{{{A}_{n}}}}{{\sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} }}. \\ \end{gathered} $В таком случае можно исключить из рассмотрения уравнения для массы КА $m$ и для сопряженной к ней переменной ${{p}_{m}},$ используя в уравнениях движения явную зависимость массы от времени $m = {{m}_{0}} - \left( {P{\text{/}}w} \right)t.$ Подставим выражения для оптимального управления (15), (16) в функцию Понтрягина (14) и получим выражение для гамильтониана
где $k = {h \mathord{\left/ {\vphantom {h {\left( {m\xi } \right)}}} \right. \kern-0em} {\left( {m\xi } \right)}},$ $A = \sqrt {A_{\tau }^{2} + A_{r}^{2} + A_{n}^{2}} .$ Тогда, если ввести векторные обозначения ${\mathbf{x}} = {{\left( {h,{{e}_{x}},{{e}_{y}},{{i}_{x}},{{i}_{y}}} \right)}^{T}}$ и ${\mathbf{p}} = {{\left( {{{p}_{h}},{{p}_{{ex}}},{{p}_{{ey}}},{{p}_{{ix}}},{{p}_{{iy}}}} \right)}^{T}}$ уравнения оптимального движения запишутся в следующей форме:(18)
$\frac{{d{\mathbf{x}}}}{{dt}} = Pk\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{p}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{p}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{p}}}}} \right){{A}^{{ - 1}}} + \frac{{\partial {{H}_{{J2}}}}}{{\partial {\mathbf{p}}}},$(19)
$\frac{{dF}}{{dt}} = Pk\frac{{{{A}_{n}}}}{A}\frac{{\partial {{A}_{n}}}}{{\partial {{p}_{F}}}} + \frac{{\partial {{H}_{F}}}}{{\partial {{p}_{F}}}},$(21)
$\begin{gathered} \frac{{d{\mathbf{p}}}}{{dt}} = - P\left[ {\frac{{\partial k}}{{\partial {\mathbf{x}}}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{x}}}}} \right.} \right. + \\ + \,\,\left. {\left. {{{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{x}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{x}}}}} \right){{A}^{{ - 1}}}} \right] - \frac{{\partial {{H}_{F}}}}{{\partial {\mathbf{x}}}} - \frac{{\partial {{H}_{{J2}}}}}{{\partial {\mathbf{x}}}} - \frac{{\partial {{H}_{\beta }}}}{{\partial {\mathbf{x}}}}, \\ \end{gathered} $(22)
$\begin{gathered} \frac{{d{{p}_{F}}}}{{dt}} = - P\left[ {\frac{{\partial k}}{{\partial F}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial F}}} \right.} \right. + \\ + \,\,\left. {\left. {{{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial F}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial F}}} \right){{A}^{{ - 1}}}} \right] - \frac{{\partial {{H}_{F}}}}{{\partial F}} - \frac{{\partial {{H}_{{J2}}}}}{{\partial F}} - \frac{{\partial {{H}_{\beta }}}}{{\partial F}}, \\ \end{gathered} $Как будет показано ниже к системе уравнений (18)–(23) применяется метод осреднения
[19]. Для осредненной системы уравнений гамильтониан не будет зависеть от истинной долготы
F, поэтому ${{p}_{F}} = {\text{const}}{\text{.}}$ А поскольку из условий трансверсальности на правом конце ${{p}_{F}}(T) = 0,$ то ${{p}_{F}} \equiv 0$ на всей траектории перелета КА. В таком случае уравнение для ${{p}_{F}}$ выпадает из рассмотрения. Если заметить, что уравнения (20) и (23) имеют общий множитель 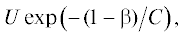 то несложно показать, что уравнение (23) имеет явное решение
то несложно показать, что уравнение (23) имеет явное решение
(24)
${{p}_{\beta }}(t) = {{p}_{\beta }}(0)\exp \left( { - \frac{{\beta (t) - \beta (0)}}{C}} \right).$Подставляя выражение (24) в остальные уравнения оптимального движения (18)–(23) и гамильтониан (17), можно исключить из рассмотрения уравнение (23) и получить систему уравнений оптимального движения КА следующего вида
(25)
$\frac{{d{\mathbf{x}}}}{{dt}} = Pk\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{p}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{p}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{p}}}}} \right){{A}^{{ - 1}}} + \frac{{\partial {{H}_{{J2}}}}}{{\partial {\mathbf{p}}}},$(28)
$\begin{gathered} \frac{{d{\mathbf{p}}}}{{dt}} = - P\left[ {\frac{{\partial k}}{{\partial {\mathbf{x}}}}A + k\left( {{{A}_{\tau }}\frac{{\partial {{A}_{\tau }}}}{{\partial {\mathbf{x}}}} + {{A}_{r}}\frac{{\partial {{A}_{r}}}}{{\partial {\mathbf{x}}}} + {{A}_{n}}\frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{x}}}}} \right){{A}^{{ - 1}}}} \right] - \\ - \,\,\frac{{\partial {{H}_{{J2}}}}}{{\partial {\mathbf{x}}}} + {{p}_{\beta }}(0){{C}_{0}}\frac{{\partial U}}{{\partial {\mathbf{x}}}}, \\ \end{gathered} $ОСРЕДНЕНИЕ ДВИЖЕНИЯ
Следует отметить, что система уравнений оптимального движения (25)–(28) содержит одну быструю переменную F, а все остальные переменные – медленные. Поэтому для повышения численной устойчивости и снижения вычислительной сложности краевой задачи принципа максимума к системе (25)–(28) можно применить метод осреднения [19]. Осреднение дифференциальных уравнений оптимального движения по времени за один виток проводится по следующей формуле
(30)
$\frac{{d{\mathbf{y}}(t)}}{{dt}} = \frac{1}{{{{T}_{c}}}}\int\limits_t^{t + {{T}_{c}}} {{{{\mathbf{f}}}_{e}}\left( {{\mathbf{y}},F,s} \right)} ds = \frac{n}{{2\pi }}\int\limits_0^{2\pi } {{{{\mathbf{f}}}_{e}}\left( {{\mathbf{y}},F,s} \right)\frac{{ds}}{{dF}}} dF,$КРАЕВАЯ ЗАДАЧА
Для удовлетворения условий принципа максимума необходимо решить краевую задачу для системы осредненных уравнений оптимального движения (25), (27), (28) со следующими краевыми условиями на левом и правом концах:
(31)
$\begin{gathered} h(0) = {{h}_{0}},\,\,\,\,{{e}_{x}}(0) = {{e}_{{x,0}}},\,\,\,\,{{e}_{y}}(0) = {{e}_{{y,0}}}, \\ {{i}_{x}}(0) = {{i}_{{x,0}}},\,\,\,{{i}_{y}}(0) = {{i}_{{y,0}}},\,\,\,\beta (0) = 1 - С \ln \left( {1 + \frac{{{{\Phi }_{{{\text{Г С О }}}}}}}{{{{\Phi }_{X}}}}} \right), \\ h(T) = {{h}_{f}},\,\,\,\,{{e}_{x}}(T) = 0,\,\,\,\,{{e}_{y}}(T) = 0, \\ {{i}_{x}}(T) = 0,\,\,\,\,{{i}_{y}}(T) = 0,\,\,\,\,\beta (T) = {{\beta }_{T}},\,\,\,\,{{{\bar {H}}}_{{opt}}}(T) = 0, \\ \end{gathered} $В четвертой строчке (31) под величиной ${{\bar {H}}_{{opt}}}(T)$ имеется в виду выражение для гамильтониана (29), осредненное по схеме (30) на момент конца перелета с помощью ЭРДУ. Условия из третьей и четвертой строчек (31) содержат значения равноденственных элементов, относительной мощности СБ и гамильтониана на правом конце. Для их расчета необходимо проинтегрировать систему уравнений оптимального движения (25), (27), (28) на промежутке $t \in \left[ {0;T} \right]$ с начальными значениями из первой и второй строчек (31) и применением схемы осреднения (30). Для этого необходимо знать время перелета $T$ и недостающие начальные значения сопряженных переменных ${\mathbf{p}}(0)$ и ${{p}_{\beta }}(0),$ которые запишем в виде вектора неизвестных параметров
(32)
${\mathbf{z}} = {{\left( {\begin{array}{*{20}{c}} {{\mathbf{p}}(0)}&{{{p}_{\beta }}(0)}&T \end{array}} \right)}^{T}}.$(33)
${\mathbf{f}}\left( {\mathbf{z}} \right) = \left( {\begin{array}{*{20}{c}} {h(T) - {{h}_{f}}} \\ {{{e}_{x}}(T)} \\ {{{e}_{y}}(T)} \\ {\begin{array}{*{20}{c}} {{{i}_{x}}(T)} \\ {{{i}_{y}}(T)} \\ {\begin{array}{*{20}{c}} {\beta (T) - {{\beta }_{T}}} \\ {{{{\bar {H}}}_{{opt}}}(T)} \end{array}} \end{array}} \end{array}} \right) = 0,$РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Для решения нелинейной системы уравнений (33), возникающей из принципа максимума, в данной работе применяется метод продолжения решения по параметру. Используемый вариант этого метода подробно описан в работах [19–21]. Согласно методу продолжения по параметру решение нелинейной системы уравнений (33) сводится к решению задачи Коши для системы обыкновенных дифференциальных уравнений вида
(34)
$\frac{{d{\mathbf{z}}}}{{d\tau }} = - {{\left[ {\frac{{\partial {\mathbf{f}}({\mathbf{z}},\tau )}}{{\partial {\mathbf{z}}}}} \right]}^{{ - 1}}}\left( {{\mathbf{b}} + \frac{{\partial {\mathbf{f}}({\mathbf{z}},\tau )}}{{\partial \tau }}} \right),$Для непрерывного перехода от задачи оптимального быстродействия, которая решается относительно легко, к задаче с заданной конечной мощностью СБ будем задавать падение мощности на конец САС в зависимости от параметра продолжения $\tau $ следующим образом:
где ${{\beta }_{{\min T}}}$ – падение мощности на конец САС на траектории оптимального быстродействия, а ${{\beta }_{{\max }}}$ – некоторое значение, такое что ${{\beta }_{{\min T}}} < {{\beta }_{{\max }}} < \beta (0) < 1.$ Тогда выражение для производной от ${\mathbf{f}}$ по параметру продолжения можно выписать в явном виде(36)
${{{\mathbf{z}}}_{0}} = {{\left( {\begin{array}{*{20}{c}} {{\mathbf{p}}{\text{*}}(0)}&0&{T{\text{*}}} \end{array}} \right)}^{T}},$Для вычисления невязок на правом конце траектории перелета КА, входящих в (33), при численном интегрировании осредненной системы оптимального движения использовался метод Дорманда–Принса 7(8) порядка [22]. Осреднение правых частей уравнений оптимального движения проводилось согласно (30) с помощью метода трапеций на равномерной сетке из 128 точек. Для вычисления частных производных от функции ${\mathbf{f}}$ по каждому из неизвестных параметров в (34) использовался метод конечных разностей первого порядка. При этом возникает численная ошибка [22], связанная с тем, что при последовательном интегрировании системы дифференциальных уравнений оптимального движения КА с близкими начальными условиями интегратор проходит при разных интегрированиях по разным значениям независимой переменной. Для исключения этой ошибки интегрировались одновременно шесть копий системы уравнений (25), (27), (28) с различными начальными условиями. Разрешение относительно производной ${{d{\mathbf{z}}} \mathord{\left/ {\vphantom {{d{\mathbf{z}}} {d\tau }}} \right. \kern-0em} {d\tau }}$ в (34) производилось путем численного решения системы линейных уравнений методом гауссового исключения.
Поскольку наибольшая эффективность использования метода продолжения решения по параметру достигается при использовании методов численного интегрирования высокого порядка [19], в данной работе для интегрирования (34) также использовался метод Дорманда–Принса 7(8) порядка. Однако для еще большего увеличения длины шага по параметру продолжения и для снижения количества отброшенных шагов в данной работе после каждого принятого шага запускалась процедура коррекции полученного значения вектора неизвестных параметров ${{{\mathbf{z}}}_{1}}.$ Процедура коррекции состояла в решении при фиксированном $\tau {\text{*}}$ следующего уравнения
(37)
${\mathbf{f}}\left( {{\mathbf{z}}\left( {\tau {\text{*}}} \right)} \right) = \left( {1 - \tau {\text{*}}} \right){\mathbf{b}},$Для проверки насколько отличается полученное управление от оптимального вследствие применения метода осреднения после каждого принятого шага и проведенной процедуры коррекции проводилось интегрирование неосредненных уравнений движения (25)–(28). При этом начальные значения сопряженных переменных и время перелета брались из ${\mathbf{z}}\left( {\tau {\text{*}}} \right),$ сопряженная переменная к истинной долготе полагалась равной нулю в течение всего перелета ${{p}_{F}}(t) \equiv 0,$ а начальное значение истинной долготы полагалось нулевым $F(0) \equiv 0.$ Кроме того, после получения неосредненных траекторий на этих траекториях рассчитывались с помощью программного комплекса IRENE неосредненный эквивалентный флюенс на конец перелета на ГСО (8) и неосредненная относительная мощность СБ на конец САС (9). Численное интегрирование неосредненных траекторий оптимального движения также проводилось методом Дорманда–Принса 7(8) порядка.
ОПТИМИЗАЦИЯ АРГУМЕНТА ПЕРИГЕЯ ПРОМЕЖУТОЧНОЙ ОРБИТЫ
Рассмотрим несколько промежуточных орбит, параметры которых указаны в табл. 1. Эта таблица определяет энергетические параметры промежуточных орбит, но не фиксирует для каждой орбиты долготу восходящего узла ${{\Omega }_{0}}$ и аргумент перигея ${{\omega }_{{\pi ,0}}}.$ В задаче оптимального быстродействия (в центральном поле притяжения Земли) для перелета между некомпланарными эллиптической и круговой орбитами оптимальным значением аргумента перигея промежуточной орбиты является ${{\omega }_{{\pi ,0}}} = 0,$ а значение ${{\Omega }_{0}}$ на время выведения не влияет. Для осредненного эквивалентного потока в силу симметрии относительно оси вращения Земли значение ${{\Omega }_{0}}$ не будет влиять на относительную мощность на конец САС. Поэтому далее будем рассматривать задачу оптимального быстродействия с учетом второй зональной гармоники разложения гравитационного потенциала Земли для каждой промежуточной орбиты из таблицы при ${{\Omega }_{0}} = 0$ и различных значениях ${{\omega }_{{\pi ,0}}}.$
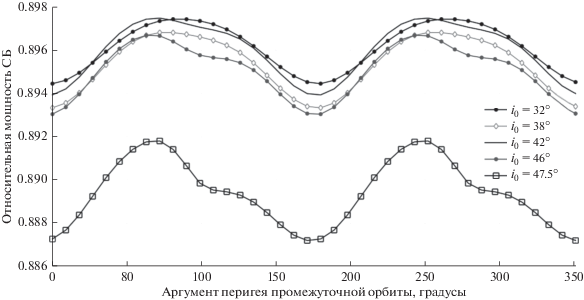
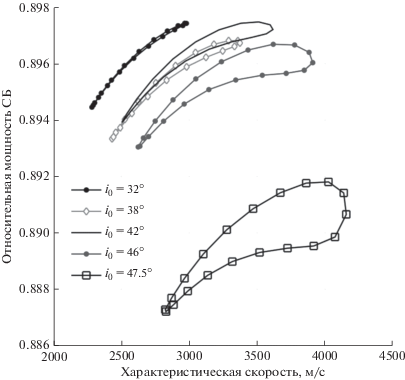
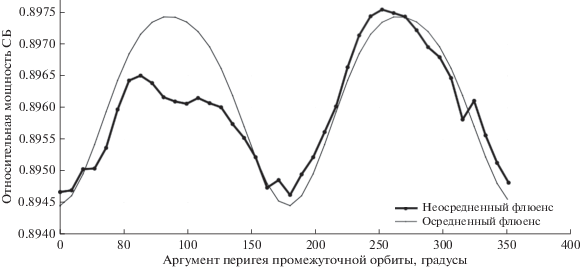
Результаты расчета осредненной и неосредненной относительной мощности СБ на конец САС в зависимости от ${{\omega }_{{\pi ,0}}}$ приведены на рис. 3. Расчеты проведены для перелета на ГСО с промежуточной орбиты №1 из табл. 1. Виден периодический характер зависимости осредненной относительной мощности от аргумента перигея промежуточной орбиты. Период этой зависимости составляет 180 градусов. На рис. 4 изображена зависимость осредненной относительной мощности СБ на конец САС от аргумента перигея для траекторий перелета на ГСО со всех промежуточных орбит из табл. 1. На рис. 5 отложены значения осредненной относительной мощности СБ на конец САС и потребной характеристической скорости для выведения КА по полученным траекториям на ГСО при различных значениях ${{\omega }_{{\pi ,0}}}.$ Точки, соответствующие одной строчке из табл. 1, соединены линиями. Из рис. 5 видно, что в рамках осредненной модели эквивалентного потока существует при одних и тех же затратах характеристической скорости два значения ${{\omega }_{{\pi ,0}}},$ одному из которых соответствует траектория оптимального быстродействия с большим значением $\beta \left( T \right).$
Рис. 3.
Зависимость относительной мощности СБ на конец САС, рассчитанной по осредненному и неосредненному эквивалентному флюенсу для наискорейшего выведения на ГСО с промежуточной орбиты № 1 (см. табл. 1).
ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ
Для каждой орбиты из табл. 1 выбиралось значение аргумента перигея промежуточной орбиты с минимальной и максимальной относительной мощностью СБ на конец САС на траекториях оптимального быстродействия и решалась краевая задача, сведенная выше к задаче Коши (34). Величина ${{\beta }_{{\max }}}$ во всех полученных краевых задачах полагалась равной ${{\beta }_{{\max }}} = 0.906,$ что меньше $\beta (0) = {\text{0}}{\text{.90679615}}{\text{.}}$ При некотором значении параметра продолжения $\tau = {{\tau }_{f}} < 1$ наблюдалось существенное увеличение невязок на правом конце. При этом корректор после каждого шага не мог свести невязки на правом конце к нулю. В этот момент интегрирование по параметру продолжения прерывалось. Следует однако отметить, что подобное прерывание интегрирования системы (34) не гарантирует, что нарастание невязок на правом конце произошло из-за отсутствия решения краевой задачи при $\tau > {{\tau }_{f}}.$ Но тем не менее, полученные траектории позволяют оценить величину максимального возможной мощности СБ на конец САС.
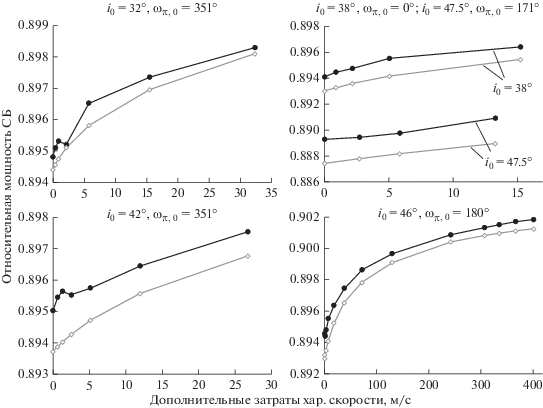
Полученные в ходе решения (34) значения ${\mathbf{z}}(\tau ),$ использовались для интегрирования неосредненных уравнений оптимального движения (25)–(28) и расчета неосредненной относительной мощности СБ на конец САС с помощью программного комплекса IRENE. На рис. 6 представлены результаты расчета осредненной и неосредненной относительной мощности СБ на конец САС на полученных неосредненных траекториях. Все расчеты, представленные на рис. 6, соответствуют выбору ${{\omega }_{{\pi ,0}}}$ с минимальной относительной мощностью СБ на конец САС на траекториях оптимального быстродействия. Осредненная относительная мощность нарисована на всех графиках рис. 6 светлыми линиями, неосредненная – темными. В заголовке каждого графика на рис. 6 указано наклонение и выбранное значение аргумента перигея промежуточной орбиты. На абсциссах графиков отложена величина дополнительных затрат характеристической скорости на перелет с помощью ЭРДУ по сравнению с траекторией оптимального быстродействия для выбранных параметров промежуточной орбиты. Все графики показывают монотонное увеличение относительной мощности с ростом затрат характеристической скорости. Максимальное увеличение мощности СБ на конец САС в этой группе расчетов составляет 0.6% от мощности СБ на начальной орбите. При этом дополнительные затраты характеристической скорости не превышают 400 м/с.
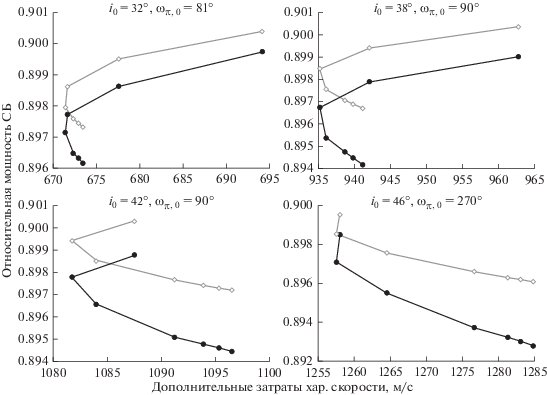
На рис. 7 представлены результаты расчета осредненной и неосредненной относительной мощности СБ на конец САС на полученных неосредненных траекториях, соответствующих ${{\omega }_{{\pi ,0}}}$ с максимальной относительной мощностью СБ на конец САС на траекториях оптимального быстродействия. Все обозначения аналогичны рис. 6. Стоит только отметить, по абсциссе отложены дополнительные затраты характеристической скорости по сравнению с траекторией оптимального быстродействия с соответствующей промежуточной орбиты, но с аргументом перигея соответствующим минимальной относительной мощностью СБ. Такой выбор отсчета дополнительных затрат характеристической скорости позволяет проиллюстрировать результаты оптимизации относительной мощности одновременно по ${{\omega }_{{\pi ,0}}}$ и по ${\mathbf{z}}.$ Следует заметить, что зависимости, представленные на рис. 7 имеют немонотонный характер: относительная мощность растет, а дополнительные затраты характеристической скорости сначала убывают, а потом нарастают. Такой характер изменения характеристической скорости может быть связан с тем, что начальная траектория, с которой запускается метод продолжения по параметру, не является оптимальной по быстродействию в смысле выбора аргумента перигея промежуточной орбиты. Поэтому сначала при оптимизации увеличивается относительная мощность за счет снижения времени перелета и, как следствие, эквивалентного флюенса. Затем в какой-то момент эти возможности исчерпываются и дальнейшее увеличение мощности СБ на конец САС получается только за счет увеличения времени перелета. Максимальное увеличение мощности СБ на конец САС в этой группе расчетов составляет 0.57% от мощности СБ на начальной орбите. При этом дополнительные затраты характеристической скорости не превышают 1258 м/с.
По результатам оптимизации аргумента перигея промежуточной орбиты и применения принципа максимума удалось в зависимости от промежуточной орбиты увеличить мощность СБ на конец САС на 0.16–0.66% от мощности СБ на промежуточной орбите. При этом дополнительные затраты характеристической скорости составили от 13 до 1087 м/с.
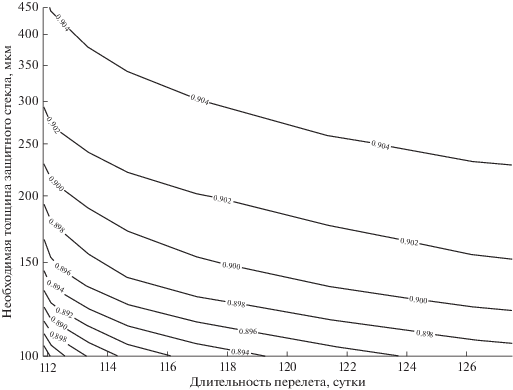
На рис. 8 показаны зависимости необходимой толщины защитного стекла от длительности перелета при различных фиксированных на конец САС относительных мощностях СБ. Значения фиксированной на конец САС относительной мощности указаны на изолиниях. График получен путем варьирования толщины лицевого защитного стекла СБ на траекториях полученных для случая перелета с промежуточной орбиты с наклонением ${{i}_{0}}$ = 46° и аргументом перигея ${{\omega }_{{\pi ,0}}}$ = 180°.
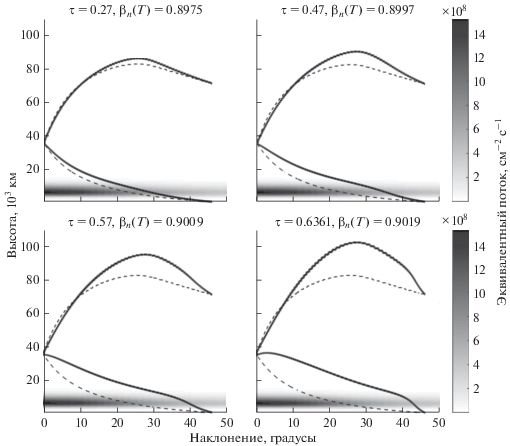
На рис. 9 показано как менялась траектория перелета с промежуточной орбиты с наклонением ${{i}_{0}}$ = 46° и аргументом перигея ${{\omega }_{{\pi ,0}}}$ = 180° по мере увеличения параметра продолжения и, соответственно, увеличения относительной мощности СБ на конец САС. Траектории при каждом значении параметра продолжения представлены в осях “радиус–наклонение”. Две пунктирные линии на каждом графике показывают зависимости высоты перигея и апогея от наклонения на траектории оптимального быстродействия. Две непрерывные линии соответствуют зависимости высоты перигея и апогея от наклонения на траектории, полученной при данном значении параметра продолжения. Оттенками серого на каждом графике показана величина эквивалентного потока электронов 1 МэВ, падающего на СБ. На графиках видна тенденция к вынесению перигейных участков траектории выше границы внутреннего РПЗ, а также к увеличению максимальной высоты апогея. Также на рис. 9 можно заметить, что по мере увеличения конечной относительной мощности СБ изменение наклонения орбиты все меньше происходит в области пересечения траекторией КА внутреннего РПЗ и все больше – вне этой области. Этот факт частично подтверждает правильность расчетов, так как видно, что с уменьшением наклонения эквивалентный поток внутри радиационных поясов растет, и поэтому выгоднее в плане радиационной нагрузки пересекать РПЗ (другими словами набирать высоту) в области больших наклонений.
ЗАКЛЮЧЕНИЕ
В работе рассмотрены возможности снижения радиационной деградации мощности СБ КА на конец САС за счет изменения формы траектории выведения КА с различных промежуточных орбит на ГСО с использованием ЭРДУ и СБ на основе трехкаскадных ФЭП. Математический аппарат построения оптимальных по быстродействию траекторий с фиксированной относительной мощностью СБ на конец САС позволил увеличить мощность СБ на конец САС на 0.16–0.66% от мощности СБ на начало перелета в зависимости от параметров промежуточных орбит. Дополнительные затраты характеристической скорости увеличились относительно траекторий оптимального быстродействия на 13–1087 м/с. При оптимизации учтена вторая зональная гармоника в разложении гравитационного потенциала притяжения Земли. Относительно небольшое увеличение конечной мощности СБ обуславливается большей радиационной стойкостью трехкаскадных ФЭП по сравнению с кремниевыми и тем фактом, что большую часть времени перелета КА находится в области с малым эквивалентным потоком, поскольку существенное влияние на деградацию трехкаскадных ФЭП имеет только внутренний РПЗ. В работе рассмотрена постановка задачи, где к уравнениям движения КА добавляется уравнение для учета радиационной деградации мощности СБ на конец САС. Применен принцип максимума к полученной задаче, получено в явном виде решение сопряженного уравнения к относительной мощности СБ на конец САС.
Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 16-19-10429).
Автор выражает благодарность В.Г. Петухову за ценные замечания, сделанные им при обсуждении данной статьи.
Список литературы
Ceccherini S., Topputo F. System-Trajectory Optimization of Hybrid Transfers to the Geostationary Orbit // AIAA SciTech Forum. 8–12 January 2018. Kissimmee, Florida. 2018 Space Flight Mechanics Meeting.
Macdonald M., Owens S.R. Combined high and low-thrust geostationary orbit insertion with radiation constraint // Acta Astronautica. 2018. V. 142. P. 1–9.
Messenger S.R., Wong F. et al. Low-Thrust Geostationary Transfer Orbit (LT2GEO) Radiation Environment and Associated Solar Array Degradation Modeling and Ground Testing // IEEE Trans. Nucl. Sci. 2014. V. 61. № 6. P. 3348–3355.
Mailhe L.M., Heister S.D. Design of a Hybrid Chemical/Electric Propulsion Orbital Transfer Vehicle // J. Spacecraft Rockets. 2002. V. 39. № 1. P. 131–139.
Петухов В.Г. Квазиоптимальное управление с обратной связью для многовиткового перелета с малой тягой между некомпланарными эллиптической и круговой орбитами // Космич. исслед. 2011. Т. 49. № 2. С. 128–137. (Cosmic Research. P. 121).
Tada H.Y., Carter J.R., Anspaugh B.E., Downing R.G. Solar Cell Radiation Handbook. JPL Publication 82-69, 1982.
Модель космоса: научно-информационное издание / Под ред. М.И. Панасюка, Л.С. Новикова. Т. 1: Физические условия в космическом пространстве. М.: Библион – Русская книга, 2007.
Синицын А.А. Влияние деградации солнечных батарей на эффективность применения электроракетных двигателей // Полет. 2010. № 1. С. 22–29.
Старченко А.Е. Оптимизация траектории выведения космического аппарата на геостационарную орбиту с целью снижения уровня радиационной деградации солнечных батарей // Известия РАН. Энергетика. 2017. № 3. С. 128–145.
Imaizumi M., Nakamura T., Takamoto T., Ohshima T. et al. Radiation degradation characteristics of component subcells in inverted metamorphic triple-junction solar cells irradiated with electrons and protons // Prog. Photovolt: Res. Appl. 2017. V. 25 P. 161–174
Старченко А.Е. Оптимизация траектории выведения космического аппарата на геостационарную орбиту с целью снижения поглощенной дозы космической радиации // Космич. исслед. 2019. Т. 57. № 4. С. 308–320.
Ким В. Стационарные плазменные двигатели в России: проблемы и перспективы // Электронный журнал “Труды МАИ”. 2012. № 60.
Sawyer D.M., Vette J.I. AP-8 Trapped Proton Environment for Solar Maximum and Solar Minimum. NASA-TM-X-72605. NSSDC/WDC-A-R&S 76-06. 1976.
Vette J.I. Trapped Radiation Environment Model Program (1964–1991). NSSDC/WDC-A-R&S 91-29. November, 1991.
Vette J.I. The AE-8 Trapped Electron Model Environment. NSSDC/WDC-A-R&S 91-24, 1991.
Heynderickx D. Comparison between methods to compensate for the secular motion of the south Atlantic anomaly // Rad. Meas. 1996. V. 26. № 3. P. 369–373.
Jensen D.C., Cain J.C. An Interim Geomagnetic Field // J. Geophys. Res. 1962. V. 67. P. 3568–3569.
Cain J.C., Hendricks S.J., Langel R.A., Hudson W.V. A Proposed Model for the International Geomagnetic Reference Field-1965. // J. Geomag. Geoelec. 1967. V. 19. P. 335–355.
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. 2004. Т. 42. № 3. С. 260–279. (Cosmic Research. P. 249).
Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. 2012. Т. 50. № 3. С. 258–270. (Cosmic Research. P. 250).
Шалашилин В.А., Кузнецов Е.Б. Метод продолжения решения по параметру и наилучшая параметризация. М.: Эдиториал УРСС, 1999.
Hairer F., Norsett S.P., Wanner G. Solving Ordinary Differential Equations I. Non-Stiff Problems. Berlin: Springer-Verlag, 2008.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования