Космические исследования, 2020, T. 58, № 1, стр. 40-48

ВВЕДЕНИЕ

Режим гравитационной ориентации спутника обеспечивает благоприятные условия проведения на его борту космических экспериментов в области микрогравитации [1]. Его основные достоинства – малый модуль и малая область вариации вектора квазистатического микроускорения в каждой точке борта. В [1] рассмотрено подержание этого режима гиросистемой, для разгрузки кинетического момента которой часто используют механический момент, создаваемый электромагнитами при их взаимодействии с магнитным полем Земли (МПЗ). Возможности электромагнитов таковы, что их можно использовать для поддержания режима гравитационной ориентации массивных спутников и без использования гиросистемы. Отключение гиросистемы способствует уменьшению уровня микроускорений на борту спутника.

В настоящее время законы управления электромагнитами, обеспечивающие гашение возмущенного движения и стабилизацию режима гравитационной ориентации, разработаны для малых спутников (см., например, [2–4]). Ниже рассмотрен простейший закон такого рода, предназначенный для массивных спутников типа Бион М-1 и Фотон М-4. Чтобы сформировать этот закон, достаточно иметь показания трехосного магнитометра и датчика угловой скорости. Эффективность закона подтверждена математическим моделированием движения спутника относительно центра масс под действием гравитационного и аэродинамического моментов, а также момента, создаваемого электромагнитами.

УРАВНЕНИЯ ДВИЖЕНИЯ СПУТНИКА

Спутник считаем твердым телом, центр масс которого – точка $O$ – движется по геоцентрической орбите. Для записи уравнений движения спутника относительно центра масс и представления результатов математического моделирования, введем три правых декартовых системы координат.

Связанная со спутником система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ образована его главными центральными осями инерции. Несколько упрощая модель, полагаем, что оси этой системы связаны с характерными элементами конструкции спутника: ось $O{{x}_{1}}$ параллельна его продольной оси, ось $O{{x}_{2}}$ перпендикулярна плоскости солнечных батарей. Ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}.$

Начало гринвичской системы $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ находится в центре Земли, плоскость $C{{y}_{1}}{{y}_{2}}$ совпадает с плоскостью экватора, ось $C{{y}_{1}}$ пересекает гринвичский меридиан, ось $C{{y}_{3}}$ направлена к Северному полюсу. Полагаем, что эта система вращается с постоянной угловой скоростью ${{{\omega }}_{E}}$ вокруг оси $C{{y}_{3}}.$

В орбитальной системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ оси $O{{X}_{3}}$ и $O{{X}_{2}}$ направлены соответственно вдоль геоцентрического радиус-вектора точки $O$ и вектора кинетического момента орбитального движения спутника.

Положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно системы $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ зададим нормированным кватернионом $Q = ({{q}_{0}},{{q}_{1}},{{q}_{2}},{{q}_{3}}),$ $\left\| Q \right\| = 1.$ Кватернионная формула перехода между этими системами координат имеет вид $(0,{{y}_{1}},{{y}_{2}},{{y}_{3}})$ = $Q \circ (0,{{x}_{1}},{{x}_{2}},{{x}_{3}}) \circ {{Q}^{{ - 1}}}$. Матрицу перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим $\left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{{\,3}}.$ Здесь ${{b}_{{ij}}}$ – косинус угла между осями $C{{y}_{i}}$ и $O{{x}_{j}}.$ Элементы этой матрицы выражаются через компоненты кватерниона $Q.$

Матрицу перехода от системы координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ обозначим $\left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{{\,3}}.$ Здесь ${{a}_{{ij}}}$ – косинус угла между осями $O{{X}_{i}}$ и $O{{x}_{j}}$. Эту матрицу параметризируем углами ${\gamma ,}$ $\delta $ и $\beta ,$ которые введем с помощью следующего условия [1]. Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ может быть получена из системы $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ тремя последовательными поворотами: 1) на угол $\delta + \pi /2$ вокруг оси $O{{X}_{2}},$ 2) на угол ${\beta }$ вокруг новой оси $O{{X}_{3}},$ 3) на угол $\gamma $ вокруг оси $O{{X}_{1}},$ полученной после первых двух поворотов и совпадающей с осью $O{{x}_{1}}.$

Уравнения движения спутника состоят из двух подсистем. Одна подсистема описывает движение центра масс спутника, другая его движение вокруг центра масс – вращательное движение. Подсистема уравнений движения центра масс записывается в гринвичской системе координат. В ней учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16,16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается согласно модели ГОСТ Р 25645.166-2004. Параметры атмосферы и баллистический коэффициент спутника считаются неизменными на всем интервале интегрирования уравнений движения.

Подсистема уравнений вращательного движения образована уравнениями Эйлера для компонент абсолютной угловой скорости спутника ${\mathbf{\omega }} = ({{{\omega }}_{1}},{{{\omega }}_{2}},{{{\omega }}_{3}})$ и кинематическими уравнениями для кватерниона $Q.$ В уравнениях Эйлера учитываются гравитационный и восстанавливающий аэродинамический моменты, а также управляющий момент, создаваемый электромагнитами. Для гравитационного момента существует простое аналитическое выражение [5]. Аэродинамический момент ${{{\mathbf{M}}}_{a}}$ вычислялся в предположении, что молекулы атмосферы при столкновении с поверхностью спутника испытывают абсолютно неупругий удар [5], спутник имеет форму прямого кругового цилиндра с двумя прикрепленными к нему одинаковыми прямоугольными пластинами солнечными батареями. Ось цилиндра совпадает с осью $O{{x}_{1}},$ радиус цилиндра – ${{R}_{c}},$ высота – ${{L}_{c}}.$ Пластины расположены в плоскости $O{{x}_{1}}{{x}_{3}}$ симметрично относительно оси $O{{x}_{1}}.$ Стороны пластин параллельны осям $O{{x}_{1}}$ и $O{{x}_{3}},$ суммарная площадь пластин – ${{S}_{b}}.$ Координаты геометрических центров масс цилиндра и пластин суть $({{z}_{c}},\;0,\;0)$ и $({{z}_{b}},\;0,\;0).$ Аэродинамический момент имеет вид [1]

где ${{{\rho }}_{a}}$ – плотность атмосферы в точке $O,$ $({{{v}}_{1}},{{{v}}_{2}},{{{v}}_{3}})$ – скорость точки $O$ относительно гринвичской системы координат (но компоненты ${{{v}}_{i}}$ относятся к системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$).

Способы управления космическими аппаратами с использованием МПЗ рассмотрены в [6]. Исполнительный орган – система электромагнитов – создает механический момент

Здесь ${\mathbf{L}} = ({{L}_{1}},\;{{L}_{2}},\;{{L}_{3}})$ – дипольный момент этой системы, ${\mathbf{B}} = ({{B}_{1}},\;{{B}_{2}},\;B{}_{3})$ – магнитная индукция МПЗ в точке $O,$${{B}_{{yi}}}$ – компоненты вектора ${\mathbf{B}}$ гринвичской системе координат, рассчитываемые согласно модели IGRF.

Подсистема уравнений вращательного движения имеет вид

Здесь точка над буквой означает дифференцирование по времени $t,$ ${{I}_{i}}$ – моменты инерции спутника относительно осей $O{{x}_{i}},$ $({{x}_{1}},{{x}_{2}},x{}_{3}) = {\mathbf{r}}$ – геоцент-рический радиус-вектор точки $O,$ $\nu = 3{{{\mu }}_{{\text{E}}}}{{r}^{{ - 5}}},$ ${{{\mu }}_{{\text{E}}}}$ – гравитационный параметр Земли, $r = \;\left| {\mathbf{r}} \right|.$ Чтобы замкнуть подсистему уравнений вращательного движения, к уравнениям (2) надо добавить соотношения, описывающие изменение величин ${{L}_{i}}.$ Явный вид этих соотношений будет указан ниже.

В расчетах использованы следующие числовые значения параметров спутника: ${{I}_{1}} = 2600$ кгм², ${{I}_{2}} = 11{\kern 1pt} 100$ кгм², ${{I}_{3}} = 10{\kern 1pt} 900$ кгм², ${{R}_{c}} = 1.3$ м, ${{L}_{c}}$ = = 5 м, ${{S}_{b}} = 33$ м², ${{z}_{b}} = - 1$ м, ${{z}_{c}} = 0.3$ м. Параметры модели атмосферы: $F = 137.0,$ ${{F}_{{81}}} = 117.09,$ ${{K}_{p}} = 2.333.$

Начальные условия движения центра масс спутника задавались в момент 10:13:07 декретного московского времени 5.V.2013. На этот момент параметры орбиты составляли: высота в апогее 575.2 км, высота в перигее 546.8 км, наклонение $64.87^\circ ,$ аргумент широты перигея $ - 124.65^\circ ,$ долгота восходящего узла (отсчитывается от точки весеннего равноденствия эпохи даты) $ - 16.73^\circ .$ Указанные параметры соответствуют орбите спутника Бион М-1. Начальные условия уравнений (1) задавались в тот же момент времени, что и начальные условия принятой орбиты. Этот момент служил началом отсчета времени – точкой $t = 0.$

СТАБИЛИЗАЦИЯ РЕЖИМА ГРАВИТАЦИОННОЙ ОРИЕНТАЦИИ

Чтобы пояснить стабилизацию режима гравитационной ориентации спутника электромагнитами, рассмотрим более простые уравнения вращательного движения, учитывающие только главные факторы. Пусть орбита спутника круговая и неизменна в абсолютном пространстве, имеет радиус $R$ и наклонение i; на спутник действуют только гравитационный момент и момент, создаваемый электромагнитами; МПЗ представляет собой поле диполя с дипольным моментом m_E, расположенным в центре Земли и направленным по оси $ - C{{y}_{3}}$ (так называемый прямой диполь). Вращательное движение такого спутника описывается уравнениями

Здесь ${{\omega }_{0}} = \sqrt {{{{{\mu }_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{E}}}}} {{{R}^{3}}}}} \right. \kern-0em} {{{R}^{3}}}}} $ – среднее движение спутника (орбитальная частота), $u$ – аргумент широты точки $O.$ Величины ${{a}_{{ij}}}$ выражаются через углы $\gamma ,$ $\delta $ и $\beta .$ Время $t$ входит в уравнения (3) периодически с периодом ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}.$

При ${{L}_{1}} = {{L}_{2}} = {{L}_{3}} = 0$ уравнения (2) автономны и допускают 24 стационарных решения [5]. Ниже будем рассматривать только 4 решения, задаваемые соотношениями

Решения (3) описывают положения равновесия спутника в орбитальной системе координат. В них оси Ox₁ и Ox₂ совпадает с осями ±OX₃ и ±OX₂ соответственно. Выбор знаков здесь произволен. Достаточные условия устойчивости по Ляпунову решений (3) имеют вид [5]: I₁ < I₃ < I₂. Принятые выше значения ${{I}_{i}}$ этим условиям удовлетворяют. Решения (3) реализуют режим гравитационной ориентации спутника в простейшей ситуации.

Из-за разного рода возмущающих факторов (реальная орбита, аэродинамический момент и др.) система (1) не имеет решений, в которых соотношения (3) выполняются точно. Однако она имеет решения, в которых эти соотношения выполнены приближенно на некотором ограниченном отрезке времени. Движения спутника, описываемые такими решениями, представляют собой режим гравитационной ориентации в ситуации, приближенной к реальной. Чтобы обеспечить достаточно точное выполнение соотношений (3) длительное время, т.е. стабилизировать режим гравитационной ориентации, можно использовать управляющий момент, создаваемый электромагнитами.

Дипольный момент электромагнитов, обеспечивающий стабилизацию режима гравитационной ориентации спутника, будем искать из энергетических соображений. Обобщенная энергия механической системы, описываемой уравнениями (2) при ${{L}_{1}} = {{L}_{2}} = {{L}_{3}} = 0,$ выражается формулой [5]

Ее производная по времени в силу уравнений (2) имеет вид

где ${{{\mathbf{E}}}_{2}} = ({{a}_{{21}}},{{a}_{{22}}},{{a}_{{23}}})$ – орт оси $O{{X}_{2}}.$ При ${\mathbf{L}} = 0$ обобщенная энергия является первым интегралом уравнений (2). Этот интеграл использовался в [5] в качестве функции Ляпунова при исследовании устойчивости стационарных решений (3). На этих решениях и только на них $E$ достигает глобального минимума ${{E}_{{\min }}} = {{\omega _{0}^{2}(3{{I}_{1}} - {{I}_{2}})} \mathord{\left/ {\vphantom {{\omega _{0}^{2}(3{{I}_{1}} - {{I}_{2}})} 2}} \right. \kern-0em} 2}.$ Возьмем где $\kappa > 0$ постоянный коэффициент. Система (2), (4) допускает указанные выше 24 стационарных решения и соотношение В силу последнего соотношения и неравенств ${{I}_{1}} < {{I}_{3}} < {{I}_{2}}$ обобщенная энергия спутника убывает. Для почти всех начальных условий движения это убывание заканчивается достижением малой окрестности одного из стационарных решений (3). Эти решения асимптотически устойчивы. Остальные 20 стационарных решений системы (2), (4) экспоненциально неустойчивы, и в них $E > {{E}_{{\min }}}.$ Получили стабилизацию режима гравитационной ориентации.

Строгое доказательство сделанных утверждения опирается на теоремы 14.1 и 15.1 книги [7], условиям которых удовлетворяет система (2), (4). Надо только убедиться, что множество ${\mathbf{B}} \times ({\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}) = 0$ в расширенном фазовом пространстве системы (2) при ${\mathbf{L}} = 0$ не содержит ее целых полутраекторий в окрестности каждого стационарного решения (3).

На закон (4) можно взглянуть и с другой точки зрения. Создаваемый по этому закону управляющий момент представим в виде

Если в правой части этой формулы отбросить последнее слагаемое и в уравнения (2) вместо момента ${\mathbf{L}} \times {\mathbf{B}}$ подставить момент ${{{\mathbf{M}}}_{c}} = - \kappa ({\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}),$ то получим систему с производной обобщенной энергии $\dot {E} = - \kappa {{\left| {{\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}} \right|}^{2}}.$ В окрестности положений равновесия (3) такая система является системой с полной диссипацией, и эти положения равновесия оказываются асимптотически устойчивыми. В окрестности положения равновесия с $\gamma = \delta = 0$ имеем ${{{\mathbf{M}}}_{c}} = - \kappa (\dot {\gamma },\dot {\delta },\dot {\beta }).$ При подходящем выборе $\kappa $ такой момент обеспечивает достаточно быстрое гашение возмущенного движения. Учет отброшенного слагаемого увеличивает время переходного процесса, но в случае большого наклонения орбиты спутника это увеличение не будет значительным.

Асимптотическая устойчивость стационарных решений (3) мотивирует применение закона управления (4) для стабилизации решений системы (1), описывающих режим гравитационной ориентации. В случае системы (1) в (4) следует взять

где ${{{\mathbf{\omega }}}_{{\text{E}}}} = {{\omega }_{{\text{E}}}}({{b}_{{31}}},{{b}_{{32}}},{{b}_{{33}}})$ (${{{\mathbf{\omega }}}_{{\text{E}}}} = (0,0,{{\omega }_{{\text{E}}}})$ в системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Ниже полагаем, что величина ${{\omega }_{0}}$ определена выписанной формулой. Для почти круговой орбиты рассматриваемого спутника на отрезке времени в несколько суток можно взять ${{\omega }_{0}} = {\text{const}}.$ На решениях системы (1), (4) рассмотрим функцию E. Ее производная $\dot {E}$ будет теперь отрицательной лишь при достаточно большом значении $\left| {{\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}} \right|.$ С убыванием $E$ уменьшается и ${\mathbf{\omega }} - {{\omega }_{0}}{{{\mathbf{E}}}_{2}}.$ В результате функция E, не достигнув минимума, начинает колебаться в окрестности некоторого значения, которое при правильном выборе коэффициента $\kappa $ будет близко к ${{E}_{{\min }}}.$ Это значит, соответствующее решение системы (1), (4) будет приближенно удовлетворять одному из соотношений (3).

Для реализации закона (4) необходимо располагать информацией об угловой скорости и ориентации спутника. Ее можно получить, обрабатывая на борту спутника показания датчика угловой скорости и трехосного магнитометра.

Стационарные решения (3) при $\gamma = 0$ можно стабилизировать, используя закон (4), в котором орт ${{{\mathbf{E}}}_{2}}$ оси $O{{X}_{2}}$ заменен ортом ${{{\mathbf{e}}}_{2}}$ оси $O{{x}_{2}}.$ При $\gamma = \pi $ орт ${{{\mathbf{E}}}_{2}}$ надо заменить ортом $( - {{{\mathbf{e}}}_{2}}).$ Новый закон управления обозначим как закон (4'). Его преимущество перед законом (4) состоит в том, что для его реализации необходимо иметь информацию только о векторах ${\mathbf{\omega }}$ и ${\mathbf{B}}$. Эту информацию можно получить непосредственно от бортовых датчиков без сложной обработки.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕЖИМА ГРАВИТАЦИОННОЙ ОРИЕНТАЦИИ СПУТНИКА

Цель моделирования – показать, что закон управления (4') обеспечивает стабилизацию режима гравитационной ориентации реального спутника. Начальные условия движения при моделировании задавались в виде

Полагаем, что такие начальные условия формируются штатной системой управления ориентацией спутника. Решения уравнений (1), (4') при $\kappa $ = 7.5 Нмс с такими начальными условиями вычислялись на отрезке 6 cуток. Результаты интегрирования приведены на рис. 1–3. Здесь представлены графики зависимости от времени углов $\gamma ,$ $\delta ,$ $\beta ,$ компонент угловой скорости ${{\omega }_{i}},$ и компонент ${{L}_{i}}$ дипольного момента системы электромагнитов. В левой части рисунков показан переходной процесс, обусловленный ошибками в задании начальной угловой скорости. Графики величин при переходном процессе охватывают отрезок времени, который примыкает к начальной точке $t = 0$ и имеет длину 6 ч. Графики в правой части рисунков иллюстрируют движение спутника в установившемся режиме после окончания переходного процесса. В этом режиме имеют место колебания рассматриваемых функций с доминирующей орбитальной частотой ${{\omega }_{0}}$ ≈ 0.00109 c^–1. Величина дипольного момента каждого из электромагнитов в установившемся режиме движения ИСЗ не превышает значения 3 Ам². Более подробно результаты моделирования законов стабилизации (4') и (4) приведены в [8, 9].

В [8, 9] показано, что описанную стабилизацию режима гравитационной ориентации нет необходимости выполнять непрерывно. Если после гашения возмущенного движения, которое занимает несколько часов, стабилизацию прекратить, то режим будет сохраняться в течение нескольких суток. После того, как возмущенное движение разовьется до неприемлемых амплитуд, его гашение следует повторить.

Рассматриваемые способы управления электромагнитами могут быть реализованы с помощью отдельной аппаратуры, слабо связанной с остальными системами спутника, подобно аппаратурам Мираж, Гравитон и КСКМ на последних спутниках серии Фотон/Бион.

ПЕРИОДИЧЕСКАЯ АППРОКСИМАЦИЯ ОРИЕНТИРОВАННОГО ДВИЖЕНИЯ СПУТНИКА

Анализ рис. 1–3 показывает, что установившийся режим гравитационной ориентации спутника похож на двухчастотное условно-периодическое движение с частотами ${{\omega }_{0}}$ и ${{\omega }_{{\text{E}}}} \approx {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} {16}}} \right. \kern-0em} {16}}.$ О-сновываясь на этом свойстве, построим аппроксимацию режима гравитационной ориентации спутника набором периодических движений с частотами, близкими ${{\omega }_{0}}.$ На каждом орбитальном витке – между последовательными прохождениями восходящего узла орбиты – построим аппроксимирующее периодическое движение. При построении этого движения гринвичскую систему координат примем инерциальной, зафиксировав ее положение относительно второй геоэкваториальной системы координат на момент прохождения первого восходящего узла орбиты на данном витке. Иными словами, зафиксируем соответствующее среднее звездное время. Орбиту спутника в “замороженной” гринвичской системе примем кеплеровой эллиптической. Элементы этой орбиты вычисляются по фазовому вектору реальной орбиты в начальном восходящем узле. Таким образом, от витка к витку долгота восходящего узла орбиты в “замороженной” гринвичской системе координат меняется, меняется и положение орбиты относительно МПЗ, но внутри витка эта долгота, положение относительно МПЗ остаются неизменными. Уравнения вращательного движения спутника возьмем в виде (1), положив в них ${{\omega }_{{\text{E}}}} = 0$ и приняв в формулах для расчета координат и компонент скорости точки $O$ в “замороженной” гринвичской системе формулы кеплерова движения. Получившуюся систему уравнений обозначим (1'). Время входит в эту систему периодически с орбитальным периодом, поэтому можно поставить задачу об отыскании ее периодических решений. Интерес представляет такое периодическое решение, которое аппроксимирует установившееся решение системы (1) на данном витке.

Построение периодического решения системы (1') сводится к решению для этой системы периодической краевой задачи

Здесь ${{t}_{0}}$ – момент прохождения первого восходящего узла орбиты на витке аппроксимации, $T$ – период используемой в системе (1') кеплеровой орбиты. Задача (1'), (5) решается методом пристрелки. Краевые условия (5) рассматриваются как уравнения для определения неизвестных начальных условий ${\mathbf{\omega }}({{t}_{0}}),$ $Q({{t}_{0}}).$ Кватернион $Q(t)$ должен быть нормированным, в процессе решения задачи (1'), (5) это обстоятельство учитывается следующим образом.

Вариацию решения ${\mathbf{\omega }}(t),$ $Q(t)$ системы (1') на каждой итерации метода пристрелки представим в виде

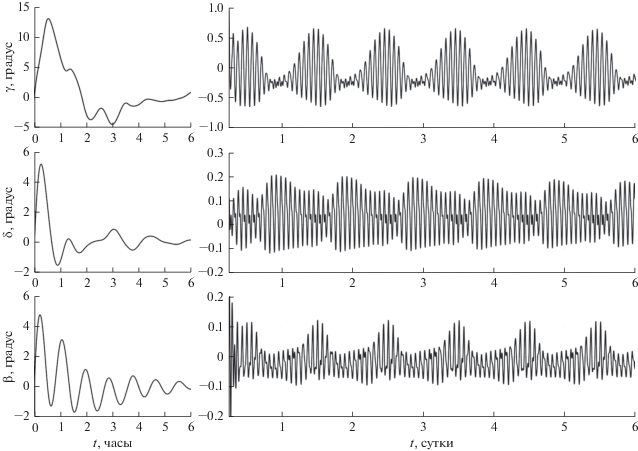
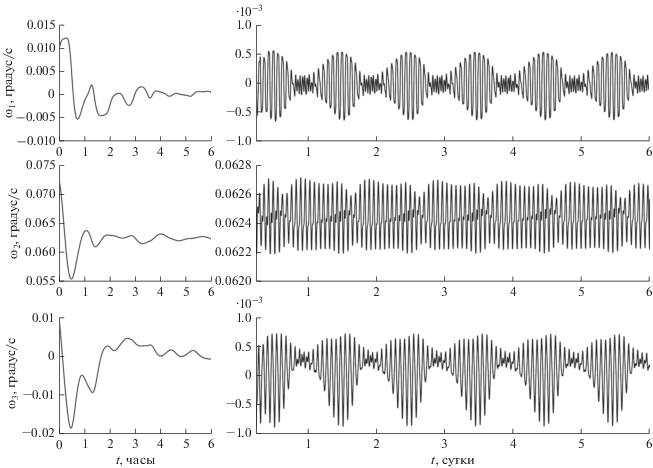
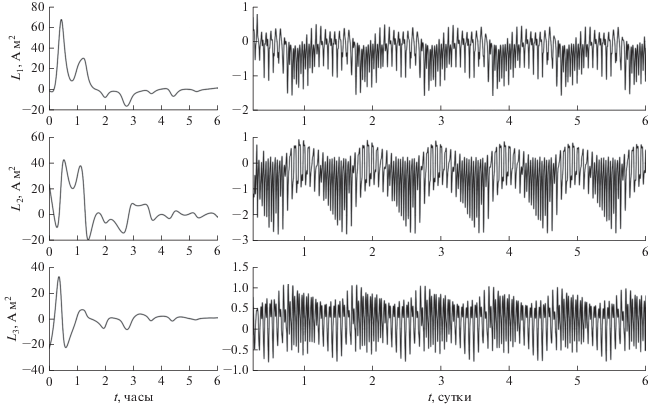
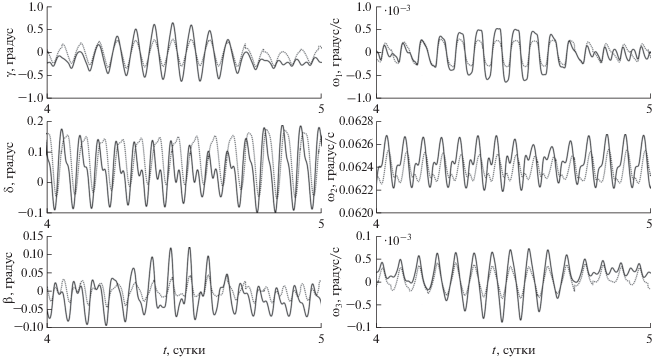
где ${\mathbf{\theta }}(t)$ – вектор бесконечно малого поворота, задающего изменение ориентации спутника в окрестности положения $Q(t).$ Вектор ${\mathbf{\theta }}(t)$ удовлетворяет уравнению ${\mathbf{\dot {\theta }}} + {\mathbf{\omega }}(t) \times {\mathbf{\theta }} = \Delta {\mathbf{\omega }}(t),$ а вектор $\Delta {\mathbf{\omega }}(t)$ – системе уравнений в вариациях для первых трех уравнений (1') (в этой системе вариации векторов ${\mathbf{r}},$ ${\mathbf{v}}$ и ${\mathbf{B}}$ вычисляются по формулам $\Delta {\mathbf{r}} = {\mathbf{r}} \times {\mathbf{\theta }},$ $\Delta {\mathbf{v}} = {\mathbf{v}} \times {\mathbf{\theta }}$ и $\Delta {\mathbf{B}} = {\mathbf{B}} \times {\mathbf{\theta }}$). Подстановка варьируемого решения в краевые условия (5) приводит к соотношениям Величины ${\mathbf{\theta }}({{t}_{0}} + T),$ $\Delta {\mathbf{\omega }}({{t}_{0}} + T)$ входят в эти соотношения в виде линейных комбинаций величин ${\mathbf{\theta }}({{t}_{0}}),$ $\Delta {\mathbf{\omega }}({{t}_{0}})$ (что требует интегрирования 6 экземпляров систем уравнений в вариациях для $\Delta {\mathbf{\omega }}$ и ${\mathbf{\theta }}$ на отрезке $[{{t}_{0}},{{t}_{0}} + T]$). Полученные соотношения рассматриваются как линейные уравнения относительно ${\mathbf{\theta }}({{t}_{0}}),$ $\Delta {\mathbf{\omega }}({{t}_{0}}).$ Эти уравнения выглядят переопределенными, но на самом деле среди них не более шести линейно независимых. Решение этих уравнений находится с помощью процедуры сингулярного разложения их матрицы. Величины ${{[Q({{t}_{0}}) + \Delta Q({{t}_{0}})]} \mathord{\left/ {\vphantom {{[Q({{t}_{0}}) + \Delta Q({{t}_{0}})]} {\left\| {Q({{t}_{0}}) + \Delta Q({{t}_{0}})} \right\|}}} \right. \kern-0em} {\left\| {Q({{t}_{0}}) + \Delta Q({{t}_{0}})} \right\|}}$ и ${\mathbf{\omega }}({{t}_{0}}) + \Delta {\mathbf{\omega }}({{t}_{0}})$ принимаются в качестве новых значений $Q({{t}_{0}})$ и ${\mathbf{\omega }}({{t}_{0}}).$ Итерации заканчиваются, когда поправки $\left| {{\mathbf{\theta }}({{t}_{0}})} \right|,$ $\left| {\Delta {\mathbf{\omega }}({{t}_{0}})} \right|$ станут меньше заданных пределов. Начальным приближением начальных условий периодического решения служат значения переменных системы (1) в точке ${{t}_{0}}.$

На рис. 4 приведены результаты аппроксимации рассмотренного ранее решения системы (1) с законом управления (4') решениями краевой задачи (1'), (5). Результаты приведены на интервале времени 1 сут. Здесь изображены графики зависимости от времени углов $\gamma ,$ $\delta ,$ $\beta $ и компонент угловой скорости ${{\omega }_{i}}$ $(i = 1,\;2,\;3).$ Графики аппроксимируемого решения показаны сплошными линиями, графики аппроксимирующих решений – точками. Аппроксимация построена на участке установившегося движения спутника. Графики аппроксимирующих решений в малых окрестностях моментов прохождения восходящих узлов орбиты налегают друг на друга (кеплеров период несколько больше драконического), но при выбранном масштабе графиков налегания практически не заметны.

Возможность такой аппроксимации обусловлена двумя обстоятельствами. Во-первых, кеплерова аппроксимация орбиты в данной задаче достаточна для построения вращательного движения спутника на орбитальном витке. Во-вторых, МПЗ в “замороженной” системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ в течение витка меняется сравнительно мало, поскольку оно близко к полю диполя, момент которого лежит вблизи точки $C$ и составляет с осью $ - C{{y}_{3}}$ малый угол (~12°). Поле диполя, расположенного в точке $C$ и направленного по $ - C{{y}_{3}}$ в таком случае вообще бы не менялось.

Удобство построенной аппроксимации заключается в том, что, рассмотрев семейство решений краевой задачи (1'), (5) для различных значений долготы восходящего узла орбиты в “замороженной” гринвичской системе координат и вычислив мультипликаторы этого семейства, можно получить детальную информацию о свойствах устойчивости режима гравитационной ориентации спутника, выбрать подходящие параметры законов управления и сами эти законы.

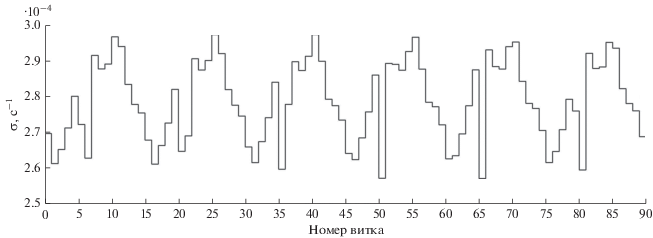
На рис. 5 представлен график степени устойчивости решений краевой задачи (1'), (5), использованных для аппроксимации вращательного движения спутника при управлении (4'). Степень устойчивости рассчитывалась по формуле

где $\rho $ – максимум модулей мультипликаторов системы уравнений в вариациях, для решения задачи (1'), (5). Степень устойчивости вычислена для каждого витка орбиты спутника. График ее зависимости от времени представлен в виде кусочно-постоянной функции. Между восходящими узлами орбиты $\sigma (t) = {\text{const,}}$ а в восходящих узлах она меняется скачком. Как видно из рисунка, все аппроксимирующие периодические решения асимптотически устойчивы.

ЗАКЛЮЧЕНИЕ

1. Показано, что устойчивый режим гравитационной ориентации массивного спутника на достаточно высокой околоземной орбите можно обеспечить с помощью управления электромагнитами.

2. Предложен способ аппроксимации ориентированного движения спутника посредством набора периодических решений, что упрощает параметрическое исследование этого движения.