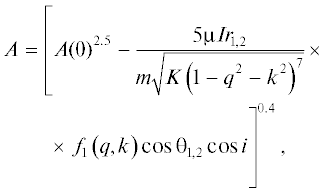Космические исследования, 2020, T. 58, № 1, стр. 61-72
Анализ динамики и выбор параметров электродинамической космической тросовой системы, работающей в режиме генерации тяги
П. С. Воеводин 1, *, Ю. М. Заболотнов 1, **
1 Самарский национальный исследовательский университет им. акад. С.П. Королева
Самара, Россия
* E-mail: p.voevodin@inbox.ru
** E-mail: yumz@yandex.ru
Поступила в редакцию 18.12.2017
После доработки 09.04.2019
Принята к публикации 15.05.2019
Аннотация
Анализируется динамика электродинамической космической тросовой системы, работающей в режиме генерации тяги, на околоземной орбите. Для описания движения тросовой системы относительно центра масс используются математические модели различной сложности без учета и с учетом упругих колебаний невесомого и весомого проводящего ток троса, на который в магнитном поле Земли действует распределенная нагрузка от сил Ампера. Тросовая система предназначена для изменения параметров орбит малых космических аппаратов и наноспутников. Анализируются эволюционные движения системы вокруг центра масс при изменении ее параметров и силы тока. Установлено, что поведение системы в существенной степени зависит от знака момента силы Ампера относительно центра масс системы. Для оценки изменения орбитальных параметров используется система дифференциальных уравнений в оскулирующих элементах, для которой применяется процедура усреднения. Для достаточно малых величин тока получено аналитическое решение усредненной системы, позволяющее произвести предварительный выбор параметров тросовой системы. Результаты вычислений по упрощенным моделям сравниваются с численными расчетами, проведенными по модели с распределенными параметрами, в которой трос представляется совокупностью материальных точек.
ПОСТАНОВКА ЗАДАЧИ
Как известно [1], электродинамические тросовые системы (ЭДТС) могут использоваться для маневров на околоземной орбите. Различают два режима функционирования ЭДТС: генерации электроэнергии и генерации тяги. В последнем случае с помощью управляющей электродинамической силы (ЭДС) индукции по проводящему тросу пропускается ток, определенного направления. В магнитном поле на каждый элементарный участок троса, по которому пропускается ток, действует сила Ампера. Направление тока определяет направление равнодействующей силы Ампера, которая действует на всю механическую систему в целом, изменяя ее орбитальные параметры.
Исследованию динамики ЭДТС посвящено большое количество работ [1–13], в которых рассматриваются различные аспекты применения подобных систем, а также анализируются результаты известных тросовых космических экспериментов с ЭДТС. В работе [3] упоминается двенадцать реальных тросовых экспериментов с ЭДТС, проведенных до настоящего времени. Если управляющая ЭДС отсутствует, то наличие в системе проводящего троса всегда приводит к появлению тормозящей силы Ампера. Подобные режимы движения ЭДТС рассмотрены в работах [3, 4]. Использование бортовых источников энергии дает возможность управлять режимом функционирования ЭДТС [5]. В этом случае ЭДТС может использоваться для перевода системы на более высокие орбиты. Возможно также комбинация режимов торможения и ускорения [6].
При функционировании ЭДТС важным вопросом является обеспечение устойчивости ее движения [1, 7, 8]. Известно, что все относительные положения равновесия ЭДТС на околоземной орбите неустойчивы [1, 7]. В работе [8] проведен подробный асимптотический и численный анализ устойчивости движения ЭДТС и показано, что для наклонных орбит периодические решения вблизи положений равновесия всегда неустойчивы. Отмечено, что при малых величинах тока (малых значений малого параметра ${\varepsilon }$) потеря устойчивости затягивается, так как она определяется слагаемыми, пропорциональными ${{{\varepsilon }}^{3}}.$ В этой работе трос моделируется как жесткий стержень с точечными массами на его концах. В работах [1, 7, 8] рассматривается случай, когда масса одного концевого тела много больше массы остальных частей системы. Для обеспечения функционирования ЭДТС на длительных интервалах времени используются пассивные и активные методы стабилизации их углового движения [9–12].
В настоящей работе тросовая система состоит из двух концевых тел, которые рассматриваются как материальные точки, и проводящего троса. Предполагается, что управляющая ЭДС обеспечивает в тросе постоянный по величине ток необходимого направления. Анализируются эволюционные движения ЭДТС относительно центра масс при изменении ее параметров и силы тока. Показывается, что поведение системы в существенной степени зависит от знака момента, который создает распределенные по тросу силы Ампера относительно центра масс системы. В одном случае неустойчивость движения ЭДТС проявляется в возрастании амплитуды маятниковых колебаний в плоскости орбиты, что приводит к сравнительно быстрому переходу системы во вращение. В другом случае потеря устойчивости движения ЭДТС затягивается. При этом амплитуда маятниковых колебаний в плоскости орбиты уменьшается, а потеря устойчивости происходит вследствие возрастания амплитуд упругих колебаний троса. Оба случая эволюции системы имеют место, как для экваториальных, так и для наклонных орбит. Естественно, информацию о свободных эволюционных движениях ЭДТС надо учитывать при построении алгоритмов стабилизации углового движения системы.
Для приближенного анализа движения ЭДТС относительно центра масс применяются модели различной сложности. Для оценки влияния изгибных колебаний троса используются уравнения движения ЭДТС в орбитальной подвижной системе координат для невесомого троса, в которой форма троса (в проекции на плоскость орбиты) представляет собой часть окружности. Данная модель по сравнению с известной аналогичной моделью [1] не накладывает ограничений на соотношение масс концевых тел и на наклонение орбиты. В этом случае изгибные колебания связаны с переменностью хорды (или радиуса) части окружности, аппроксимирующей форму троса.
Для оценки изменения орбитальных параметров центра масс ЭДТС предлагается процедура усреднения системы уравнений в оскулирующих элементах и получено их приближенное аналитическое решение, которое может быть использовано для предварительного выбора параметров ЭДТС. Для оценки влияния массы троса и других допущений используется математическая модель, в которой трос представляется как совокупность материальных точек. Эту модель можно рассматривать как некоторое приближение к модели с распределенными параметрами в частных производных [1]. Приводятся и анализируются численные результаты сравнения рассматриваемой совокупности математических моделей движения ЭДТС, включая полученное аналитическое решение. Формулируются выводы и приводятся рекомендации по выбору параметров ЭДТС.
МОДЕЛЬ ДВИЖЕНИЯ ЭДТС В ПОДВИЖНОЙ ОРБИТАЛЬНОЙ СИСТЕМЕ КООРДИНАТ
Для получения уравнений движение ЭДТС относительно центра масс в орбитальной системе координат c учетом изгибных колебаний троса используется методика, изложенная в [1], где показано, что если трос невесом, то линия троса в проекции на плоскость орбиты представляет собой часть окружности некоторого радиуса. Уравнения, приведенные в [1], получены для экваториальной орбиты и для случая, когда масса одного концевого тела много больше массы другого. В работе [13] рассматриваемый подход распространен на случай произвольного соотношения масс концевых тел и на орбиты, имеющие наклонение. В этом случае имеем [13]
(1)
$\begin{gathered} \ddot {r} - r\left[ {{{{\dot {\varphi }}}^{2}} + {{{\left( {\dot {\theta } + \omega } \right)}}^{2}}{{{\cos }}^{2}}\varphi + {{\nu }^{{ - 1}}}{{\omega }^{2}} \times } \right. \\ \left. { \times \,\,\left( {3{{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi - 1} \right)} \right] = {{{{Q}_{1}}} \mathord{\left/ {\vphantom {{{{Q}_{1}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}, \\ \end{gathered} $(2)
$\begin{gathered} \ddot {\theta } + \dot {\omega } + 2\left( {\dot {\theta } + \omega } \right)\left( {{{\dot {r}} \mathord{\left/ {\vphantom {{\dot {r}} r}} \right. \kern-0em} r} - \dot {\varphi }{\text{tg}}\varphi } \right) + 1.5{{\nu }^{{ - 1}}}{{\omega }^{2}}\sin 2\theta = \\ = {{{{Q}_{2}}} \mathord{\left/ {\vphantom {{{{Q}_{2}}} {{{m}_{e}}{{r}^{2}}}}} \right. \kern-0em} {{{m}_{e}}{{r}^{2}}}}{{\cos }^{2}}\varphi , \\ \end{gathered} $(3)
$\begin{gathered} \ddot {\varphi } + {{2\dot {\varphi }\dot {r}} \mathord{\left/ {\vphantom {{2\dot {\varphi }\dot {r}} r}} \right. \kern-0em} r} + \left[ {0.5{{{\left( {\dot {\theta } + \omega } \right)}}^{2}} + 1.5{{\nu }^{{ - 1}}}{{\omega }^{2}}{{{\cos }}^{2}}\theta } \right] \times \\ \times \,\,\sin 2\varphi = {{{{Q}_{3}}} \mathord{\left/ {\vphantom {{{{Q}_{3}}} {{{m}_{e}}{{r}^{2}}}}} \right. \kern-0em} {{{m}_{e}}{{r}^{2}}}}, \\ \end{gathered} $Сила Ампера на единицу длины, действующая в магнитном поле Земли, определяется выражением
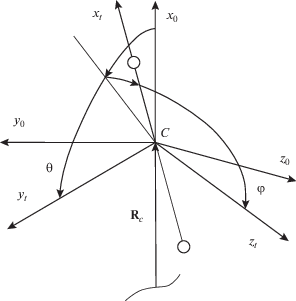
где $\tau = \left( {{{{\tau }}_{x}},{{{\tau }}_{y}},{{{\tau }}_{z}}} \right)$ – единичный вектор, направленный по касательной к тросу; ${{{\tau }}_{x}},{{{\tau }}_{y}},{{{\tau }}_{z}}$ – направляющие косинусы в орбитальной подвижной системе координат $C{{x}_{0}}{{y}_{0}}{{z}_{0}};$ $B$ – вектор магнитной индукции Земли.Используется модель магнитного поля Земли – прямой диполь [1], поэтому
(5)
$B = {{B}_{0}}\left[ {{{e}_{z}} - 3\left( {{{e}_{z}} \cdot {{e}_{R}}} \right){{e}_{R}}} \right],$С учетом допущения о форме троса (часть окружности) обобщенные силы вычисляются из следующих выражений [1, 13]
(6)
$\begin{gathered} {{Q}_{1}} = - 0.5{{B}_{0}}\cos i\left| I \right|r\left( {{\text{ctg}}\psi {{{\cos }}^{2}}\varphi + {{\psi }^{{ - 1}}}{{{\sin }}^{2}}\varphi } \right), \\ {{Q}_{2}} = {{B}_{0}}Ir\Delta \times \\ \times \,\,\left[ {\cos \varphi \cos i - \sin \varphi \sin i\sin \left( {\theta + u} \right)} \right] + \Delta {{Q}_{2}}, \\ {{Q}_{3}} = {{Q}_{{3\psi }}} + {{B}_{0}}Ir\Delta \sin i\left[ {\cos \left( {\theta + u} \right) + 3\sin \theta \sin u} \right], \\ \end{gathered} $Угол ψ определяется из решения нелинейного уравнения [1]
(7)
$r = {{L\,\gamma } \mathord{\left/ {\vphantom {{L\,\gamma } {{{{\left[ {{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\varphi {{{\left( {{\psi \mathord{\left/ {\vphantom {\psi {\sin \psi }}} \right. \kern-0em} {\sin \psi }}} \right)}}^{2}}} \right]}}^{{0.5}}}}}} \right. \kern-0em} {{{{\left[ {{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\varphi {{{\left( {{\psi \mathord{\left/ {\vphantom {\psi {\sin \psi }}} \right. \kern-0em} {\sin \psi }}} \right)}}^{2}}} \right]}}^{{0.5}}}}},$Уравнения (1)–(3) совместно с выражениями (5)–(7) описывают движение ЭДТС относительного своего центра масс с учетом изгибных колебаний троса. Изгибные колебания троса здесь характеризуются изменением расстояния между концевыми точками $r$ и соответственно угла ψ (7), значения которых соответствуют радиусу части окружности ${{r}_{t}} = {r \mathord{\left/ {\vphantom {r {2\sin \psi }}} \right. \kern-0em} {2\sin \psi }}.$
В частном случае, когда $i = 0,$ $e = 0$ и ${{m}_{2}} \gg {{m}_{1}},$ уравнения (1)–(3) совпадают с уравнениями, приведенными в монографии [1].
При выводе уравнений (1)–(3) были приняты следующие допущения: 1) массой троса пренебрегается; 2) плоскость орбиты центра масс считается неподвижной; 3) используется центральное ньютоновское гравитационное поле; 4) расстояние между точками много меньше расстояния центра масс системы до притягивающего центра; 5) концевые тела – материальные точки; 6) вектор магнитной индукции Земли $B$ считается постоянным в пределах ЭДТС; 7) предполагается, что плоскости земного и магнитного экваторов совпадают; 8) в качестве внешних сил учитываются только гравитационные силы и силы Ампера.
Система (1)–(3) включает в себя слагаемые, которые соответствуют более простым уравнениям, в которых трос нерастяжим и приближается прямой линией (жесткий стержень). В этом случае из соотношения (7) имеем ${r \mathord{\left/ {\vphantom {r L}} \right. \kern-0em} L} \to 1,$ когда $\psi \, \to 0$ и $\gamma \, \to 1.$ Если теперь повторить вывод уравнений движения ЭДТС для нерастяжимого троса, то слагаемые в обобщенных силах, соответствующие работе силы натяжения, будут отсутствовать, то есть ${{Q}_{1}} = {{Q}_{{3\psi }}} = 0.$ Оставшиеся обобщенные силы будут соответствовать только работе момента от равнодействующей сил Ампера. В этом случае уравнение (1) не рассматривается, а в других уравнениях полагается $r = L.$
Оценка правомерности некоторых принятых допущений будет сделана ниже в рамках более полной модели, в которой трос представляется как совокупность материальных точек, связанных между собой упругими односторонними связями.
ВЕРТИКАЛЬНЫЕ ПОЛОЖЕНИЯ РАВНОВЕСИЯ ЭДТС
Равновесные положения ЭДТС можно определить для круговой ($e = 0$) и экваториальной ($i = 0$) орбиты из системы (1)–(3) из условий ${{Q}_{{1,2,3}}} = 0.$ При использовании ЭДТС всегда рассматриваются положения равновесия, расположенные в плоскости орбиты вблизи вертикали, так как в этом случае действует естественный стабилизирующий фактор, связанный с гравитационным моментом. Для этих положений равновесия в данном случае имеем
(8)
${{{\theta }}_{1}} = \frac{1}{2}\arcsin \left( {\sigma } \right),\,\,\,\,{{{\theta }}_{2}} = {{{\theta }}_{1}} + {\pi },$Остальные переменные системы (1)–(3) определяются из выражений
(9)
$\begin{gathered} {{\psi }_{k}} = {\text{arctg}}\left[ {\frac{{\mu \left| I \right|}}{{6K{{m}_{e}}{{{\cos }}^{2}}{{\theta }_{k}}}}} \right],\,\,\,\,{{r}_{k}} = L\gamma \frac{{\sin {{\psi }_{k}}}}{{{{\psi }_{k}}}}, \\ {{{\dot {\theta }}}_{k}} = {{{\dot {r}}}_{k}} = \varphi = \dot {\varphi } = 0, \\ \end{gathered} $Для существования рассматриваемых положений равновесия необходимо выполнение условия $\left| {\sigma } \right| < 1.$ При функционировании ЭДТС в режиме генерации тяги использование положений равновесия системы, расположенных вблизи вертикали (8), наиболее рационально, так как в этом случае равнодействующая сил Ампера почти параллельна вектору скорости центра масс системы (с поправкой на колебания по углам ${\theta ,}\,{\varphi }$) и приращение вектора скорости наибольшее.
Из анализа линеаризованной системы следует, что положения равновесия (8) неустойчивы. Причем в линеаризованной системе уравнения для угла ${\varphi }$ отделяются от остальных уравнений и имеют чисто мнимые собственные числа. То же самое было отмечено в работах [1, 7], где рассматривался случай, когда ${{m}_{1}} \ll {{m}_{2}}$ (или ${{m}_{1}} \gg {{m}_{2}}$).
УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС СИСТЕМЫ В ОСКУЛИРУЮЩИХ ЭЛЕМЕНТАХ И ИХ УСРЕДНЕНИЕ
Уравнения движения центра масс ЭДТС записываются в оскулирующих элементах в виде [14]
(10)
$\frac{{dA}}{{dt}} = 2\nu \sqrt {\frac{{{{A}^{3}}}}{{K\left( {1\, - \,{{q}^{2}}\, - \,{{k}^{2}}} \right)}}} \left[ {{{a}_{s}}\frac{{q\sin u - k\cos u}}{\nu } + {{a}_{t}}} \right],$(11)
$\begin{gathered} \frac{{dq}}{{dt}} = \sqrt {\frac{p}{K}} \times \\ \times \,\,\left[ {{{a}_{s}}{\kern 1pt} \sin {\kern 1pt} u\, + \,{{a}_{t}}\left( {1 + \frac{1}{\nu }} \right)\cos u\, + \,\frac{1}{\nu }\left( {q{{a}_{t}} + k{{a}_{w}}{\text{ctg}}i\sin u} \right)} \right], \\ \end{gathered} $(12)
$\begin{gathered} \frac{{dk}}{{dt}} = \sqrt {\frac{p}{K}} \times \\ \times \,\,\left[ { - {{a}_{s}}{\kern 1pt} \cos {\kern 1pt} u\, + \,{{a}_{t}}{\kern 1pt} \left( {1\, + \,\frac{1}{\nu }} \right)\sin u\, + \,\frac{1}{\nu }{\kern 1pt} \left( {k{{a}_{t}}\, - \,q{{a}_{w}}{\text{ctg}}i\sin u} \right)} \right], \\ \end{gathered} $(14)
$\frac{{d\Omega }}{{dt}} = \frac{{{{a}_{w}}}}{\nu }\sqrt {\frac{p}{K}} \frac{{\sin u}}{{\sin i}},$(15)
$\frac{{du}}{{dt}} = \frac{1}{\nu }\nu \sqrt {\frac{p}{K}} \left[ {{{\nu }^{3}}\frac{K}{{{{p}^{2}}}} - {{a}_{w}}{\text{ctg}}i\sin u} \right],$Компоненты ускорения ${{a}_{s}},\,{{a}_{t}},\,{{a}_{w}}$ получаются интегрированием по тросу (части окружности радиусом ${{r}_{t}} = {{L{\gamma }} \mathord{\left/ {\vphantom {{L{\gamma }} {2{\psi }}}} \right. \kern-0em} {2{\psi }}}$) с учетом (4), (5) и в предположении, что в пределах троса вектор $B$ не изменяется (определяется в центре масс системы). Тогда
(16)
$\begin{gathered} {{a}_{s}} = \frac{{{{B}_{0}}Ir}}{m}\left( {\cos {\varphi }\sin {\theta }\cos i - \sin {\varphi }\sin i\cos u} \right), \\ {{a}_{t}} = - \frac{{{{B}_{0}}Ir}}{m}\left( {\cos {\varphi }\cos {\theta }\cos i + 2\sin {\varphi }\sin i\sin u} \right), \\ {{a}_{w}} = \frac{{{{B}_{0}}Ir}}{m}\cos {\varphi }\sin i\left( {\cos {\theta }\cos u + 2\sin {\varphi }\sin u} \right), \\ \end{gathered} $При достаточно малой величине тока и при заданных значениях ${\varphi } = 0,$ ${\theta } = {{{\theta }}_{{1,2}}},$ $r = {{r}_{{1,2}}}$ система (10)–(15) представляет собой систему с вращающейся фазой $u$ и вектором медленно изменяющихся переменных $x = \left( {A,q,k,i,\Omega } \right).$ Тогда, проводя стандартную процедуру усреднения, в первом приближении получим
(17)
$\frac{{dA}}{{dt}} = - 2\frac{{{\mu }I{{r}_{{1,2}}}}}{{m\sqrt {K{{p}^{3}}} {{{\left( {1 - {{q}^{2}} - {{k}^{2}}} \right)}}^{2}}}}{{f}_{1}}\left( {q,k} \right)\cos {{{\theta }}_{{1,2}}}\cos i,$(18)
$\frac{{dq}}{{dt}} = \frac{{{\mu }\,I\,{{r}_{{1,2}}}}}{{8m\sqrt {K\,{{p}^{5}}} }}{{f}_{2}}\left( {q,k,{{{\theta }}_{{1,2}}}} \right)\cos i,$(19)
$\frac{{dk}}{{dt}} = - \frac{{{\mu }\,I\,{{r}_{{1,2}}}}}{{8m\sqrt {K\,{{p}^{5}}} }}{{f}_{3}}\left( {q,k,{{{\theta }}_{{1,2}}}} \right)\cos i,$(20)
$\frac{{di}}{{dt}} = \frac{{{\mu }\,I\,{{r}_{{1,2}}}}}{{8m\sqrt {K\,{{p}^{5}}} }}{{f}_{4}}\left( {q,k,{{{\theta }}_{{1,2}}}} \right)\sin i,$(21)
$\frac{{d\Omega }}{{dt}} = \frac{{{\mu }\,I\,{{r}_{{1,2}}}}}{{4m\sqrt {K\,{{p}^{5}}} }}{{f}_{5}}\left( {q,k,{{{\theta }}_{{1,2}}}} \right),$Правомерность проведения процедуры усреднения можно оценить посредством отношения характерных параметров, определяющих скорость изменения переменных системы (10)–(15). Так, например, скорость изменения любой медленной переменной системы (10)–(15) характеризуется параметром ${{{\eta }}_{m}} = \left| {\frac{1}{{{{x}_{m}}}}\frac{{d{{x}_{m}}}}{{dt}}} \right|$ $\left( {m = 1,2,...5} \right)$ [15]. Величину этого параметра обычно сравнивают с производной фазы ${{{\eta }}_{u}} = {{du} \mathord{\left/ {\vphantom {{du} {dt}}} \right. \kern-0em} {dt}}.$ Отношения этих параметров ${{{\varepsilon }}_{m}} = {{{{{\eta }}_{m}}} \mathord{\left/ {\vphantom {{{{{\eta }}_{m}}} {{{{\eta }}_{u}}}}} \right. \kern-0em} {{{{\eta }}_{u}}}}$ можно рассматривать как величины (безразмерные), пропорциональные малому параметру рассматриваемой задачи. При оценке величин ${{{\varepsilon }}_{m}}$ надо иметь в виду, что наличие наклонения орбиты, когда $i \ne 0,$ приводит к уменьшению производных (17)–(19) в ${1 \mathord{\left/ {\vphantom {1 {\cos i}}} \right. \kern-0em} {\cos i}}$ раз, что соответственно пропорционально уменьшает параметры ${{{\varepsilon }}_{{1,2,3}}}.$ Для исходные данных, соответствующих табл. 1 (при $e = 0.01,$ $\,i = {\pi /}3,$ $I = - 0.1\,{\text{A}}$), оценка максимальных величин параметров ${{{\varepsilon }}_{m}}$ на интервале времени ${\tau } \in \left[ {0,5} \right],$ дает ($3.3 \cdot {{10}^{{ - 5}}},$ $1.8 \cdot {{10}^{{ - 4}}},$ $1.8 \cdot {{10}^{{ - 4}}},$ $1.4 \cdot {{10}^{{ - 5}}},$ $1.9 \cdot {{10}^{{ - 5}}}$). Здесь ${\tau } = {t \mathord{\left/ {\vphantom {t {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$ – безразмерное время, где ${{T}_{0}}$ – период обращения центра масс системы на начальной орбите.
Таблица 1.
Параметры ЭДТС
| Масса концевого тела ${{m}_{1}},{\text{кг}}$ | $2$ |
| Масса концевого тела ${{m}_{2}},{\text{кг}}$ | $6$ |
| Длина недеформированного троса $L,\,\,{\text{км}}$ | $1$ |
| Сила тока $I,\,{\text{A}}$ | $ \pm 0.1$ |
| Жесткость троса $E,\,\,{\text{н}}$ | $7070$ |
| Высота начальной круговой орбиты или высота перицентра $H,\,\,{\text{км}}$ | $1000$ |
| Эксцентриситет орбиты $e$ | $0,\,\,0.01$ |
| Наклонение орбиты $i$ | $0,\pi /6,\pi /3$ |
| Начальные значения ${{{\varphi }}_{0}},\,{{{\dot {\varphi }}}_{0}}$ | $0$ |
| Начальное значение ${{{\theta }}_{0}}$ | $0$ |
| Начальное значение ${{r}_{0}} = {{r}_{1}}$ | $0.992$ |
Анализ решений исходной (10)–(15) и усредненной (17)–(21) систем уравнений при рассматриваемых исходных данных (табл. 1) показывает, что:
1. Погрешность определения всех оскулирующих элементов по усредненной системе монотонно увеличивается и достигает максимума на конце рассматриваемого отрезка.
2. Эволюция эллиптической орбиты происходит в основном за счет изменения большой полуоси ($\Delta A = 7.884\,\,{\text{км}}$), причем эксцентриситет орбиты и параметры, определяющие положение плоскости орбиты центра масс системы изменяются незначительно ($\Delta e = 1.83 \cdot {{10}^{{ - 5}}},$ $\Delta i = - 4.49 \cdot {{10}^{{ - 4}}},$ $\Delta \Omega = 6.00 \cdot {{10}^{{ - 5}}}$).
3. Максимальная относительная погрешность определения приращения большой полуоси (относительно полного приращения $\Delta A$) по усредненной системе составляет $0.012$.
4. Имеют место сравнительно большие колебания эксцентриситета относительно своих средних значений, амплитуда которых существенно превышает величину его полного приращения, что приводит соответственно к погрешности определения высоты центра масс системы.
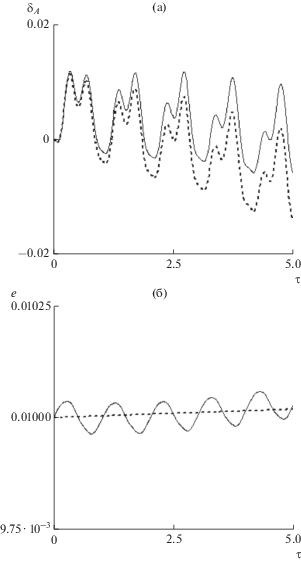
Приведенные выводы иллюстрируются на рис. 2, где приводятся зависимости для относительной погрешности определения большой полуоси ${{{\delta }}_{A}}$ по усредненной системе (рис. 2а, сплошная линия) и эксцентриситета орбиты (рис. 2б; сплошная линия соответствует не усредненной системе) от безразмерного времени ${\tau }{\text{.}}$
Если пренебречь изменением параметров $e,\,i,$ то на сравнительно небольших интервалах времени (несколько витков), интегрируя уравнение (17), нетрудно получить аналитическую оценку для большой полуоси орбиты, которая будет иметь вид
где $A(0)$ – начальное значение большой полуоси.Максимальная погрешность определения изменения большой полуоси при применении формулы (22) для рассматриваемого примера увеличивается незначительно (рис. 2а, штриховая линия).
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ СИСТЕМЫ С ВЕСОМЫМ ТРОСОМ
В общем случае ЭДТС представляет собой систему с распределенными параметрами, движение которой описывается уравнениями в частных производных [1]. Одним из приближений к этой модели являются уравнения движения орбитальной тросовой системы, в которой трос представляется совокупностью материальных точек [16–20]. Запишем эти уравнения в виде
(23)
${{m}_{k}}\frac{{{{d}^{2}}{{r}_{k}}}}{{d{{t}^{2}}}} = {{G}_{k}} + {{F}_{k}} + {{T}_{k}} - {{T}_{{k + 1}}},$Для определенности полагается, что ${{m}_{1}}$ и ${{m}_{n}}$ – массы нижнего и верхнего концевых тел соответственно. Силы ${{F}_{k}}$ вычисляются по алгоритму, который аналогичен алгоритму, используемому для определения аэродинамических сил, действующих на трос [17]. Разница заключается только в определении силы ${{S}_{k}},$ действующей на $k$-ый участок троса. В данном случае имеем
(24)
${{S}_{k}} = {{I}_{k}}\left| {{{r}_{{k + 1}}} - {{r}_{k}}} \right|\left( {{{\tau }_{k}} \times {{B}_{k}}} \right),$Силы ${{S}_{k}}$ распределяются по материальным точкам ЭДТС следующим образом
(25)
${{F}_{k}} = \frac{1}{2}\left( {{{S}_{{k - 1}}} + {{S}_{k}}} \right),\,\,\,\,{{F}_{1}} = \frac{{{{S}_{1}}}}{2},\,\,\,\,{{F}_{n}} = \frac{{{{S}_{{n - 1}}}}}{2},$Силы натяжения троса ${{T}_{k}}$ определяются в соответствии с законом Гука с учетом односторонности механической связи (трос не воспринимает сжимающих усилий) [17, 18, 20]. Для вычисления гравитационных сил ${{G}_{k}}$ используется центральное ньютоновское поле.
Рассматриваемая математическая модель движения ЭДТС (23) позволяет учесть ряд факторов, которыми в более простых моделях пренебрегалось. К этим факторам можно отнести: 1) весомость троса; 2) растяжимость механической связи с учетом того, что трос не воспринимает сжимающих усилий; 3) неравномерность распределенной нагрузки от сил Ампера из-за изменения магнитной индукции $B$ вдоль троса. И как следствие, с учетом этих факторов оценить возможность использования более простых моделей для приближенного определения изменения параметров ЭДТС.
ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
При сравнении результатов, полученных по приведенным выше моделям, предполагалось, что в начальный момент ЭДТС находится в развернутом состоянии на местной вертикали в положении устойчивого относительного равновесия, и по тросу начинают пропускать ток заданной величины. Для модели (23) начальное положение всех точек рассчитывалось из решения системы алгебраических уравнений, которые определялись как совокупность условий равновесия всех материальных точек механической системы. Для всех моделей центр масс ЭДТС в начальный момент находился в перигее орбиты, соответствующей высоте $1000\,\,{\text{км}}$. Для математической модели (1)–(3) система также находилась в начальный момент на вертикали ${{{\theta }}_{0}} = {{{\dot {\theta }}}_{0}} = 0.$ Так как уравнения (1), (3) имеют особенность, когда $r = L$ ($\psi = 0$), то начальные условия для переменной $r$ должны удовлетворять ограничению ${{r}_{0}} < L.$ Поэтому в данном случае полагалось ${{r}_{0}} = 0.999L,$ ${{\dot {r}}_{0}} = 0.$
В табл. 2 приводится сравнение приращений (в км) большой полуоси орбиты, вычисленных по описанным выше математическим моделям, для различных начальных эксцентриситетов орбиты и ее наклонений на интервале ${\tau } \in \left[ {0,5} \right].$ Рассматривается случай подъема высоты орбиты, когда $I = - 0.1,$ другие исходные данные соответствуют табл. 1.
Таблица 2.
Сравнение приращений (в км) большой полуоси орбиты, определенных по различным моделям движения ЭДТС
| Уравнения | $e = 0,\,\,i = 0$ | $e = 0.01,\,\,i = 0$ | $e = 0,i = \pi /3$ | $e = 0.01,i = \pi /3$ |
|---|---|---|---|---|
| (11)–(16) | 15.491 | 15.494 | 7.881 | 7.884 |
| (17)–(21) | 15.491 | 15.502 | 7.786 | 7.791 |
| (23) | 15.038 | 14.819 | 7.619 | 7.486 |
Во всех приведенных в табл. 2 случаях применение модели (23), когда трос представляется совокупностью материальных точек, приводит к меньшим приращениям большой полуоси орбиты. Анализ полученных результатов показывает, что это объясняется большей изгибной деформацией троса при использовании модели (23), что фактически приводит к уменьшению равнодействующей сил Ампера. Учет массы троса в модели (23) также приводит к уменьшению приращений (табл. 2), однако в данном примере ее влияние существенно меньше.
Результаты, приведенные на рис. 2 и в табл. 2 соответствуют сравнительно небольшому интервалу времени ${\tau } \in \left[ {0,5} \right].$ Анализ поведения системы на больших интервалах времени в соответствии с моделями (1)–(3) и (23) показал, что поведение системы в существенной степени зависит от знака параметра ${\sigma }$ (знака момента сил Ампера).
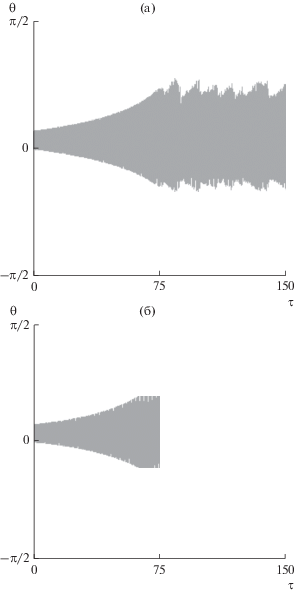
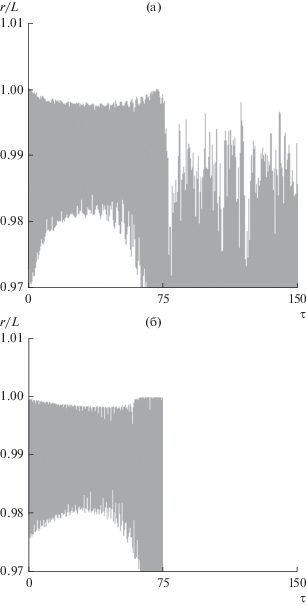
При ${\sigma } > 0$ неустойчивость движения ЭДТС проявляется, прежде всего, в быстром возрастании амплитуды маятниковых колебаний ЭДТС в плоскости орбиты (по углу ${\theta }$). При этом после достижения углом ${\theta }$ некоторых критических значений ${\theta *,}$ которые находятся вблизи $\pi {\text{/}}4,$ система (в зависимости от величины тока) или переходит во вращение, или остается в окрестности $\pi {\text{/}}4,$ в течение длительного времени. Причем модель (1)–(3) можно использовать только когда ${\theta } < {\theta *}.$ Дело в том, что при ${\theta } \to {\theta *}$ амплитуда колебаний по переменной $r$ быстро увеличивается, и ее значения достигают окрестности особой точки $r = L\left( {\psi = 0} \right).$ С другой стороны, моделирование движения системы в соответствии с уравнениями (23) показывает, что трос при ${\theta } \approx {\theta *}$ сжимается (он не натянут) и его движение становится сложным. Далее этот участок движения системы с большой и сложной деформацией троса будем называть переходным участком. Однако если система переходит во вращение, то под действием центробежных сил трос выпрямляется и натягивается (если существовал переходный участок). Рис. 3, 4 иллюстрируют такое поведение системы, когда начальная орбита системы круговая и экваториальная. На рис. 4 отношение ${r \mathord{\left/ {\vphantom {r L}} \right. \kern-0em} L}$ можно считать некоторой мерой деформации троса, так как переменная $r$ в моделях (1)–(3) и (23) это расстояние между концевыми точками системы. Рис. 3а и рис. 4а соответствуют модели (23), а рис. 3б и рис. 4б – модели (1)–(3). На участке, когда ${\theta } < {\theta }*,$ допущение о форме троса (часть окружности) приближенно выполняется, а на переходном участке нет. На рис. 5 показаны несколько положений троса: два левых положения троса соответствуют участку, когда ${\theta } < {\theta }*,$ а два правых положения троса – переходному участку. Здесь надо отметить, что при данной величине тока $I = - 0.1\,{\text{A}}$ система в соответствии с рассматриваемой моделью (23) не переходит во вращение и, следовательно, продолжает выполнять функции по изменению параметров орбиты центра масс, хотя приращения орбитальных параметров центра масс системы уменьшаются.
Когда ${\sigma } < 0$ ($I = 0.1\,{\text{A}}$), поведение системы существенно отличается от предыдущего случая, так как в процессе эволюции амплитуда маятниковых колебаний по углу ${\theta }$ уменьшаются и система приближается к положению равновесия, причем амплитуды колебаний по переменной $r$ остаются приблизительно постоянными. Моделирование движения системы по уравнениям (23) показало, что система остается в окрестности положения равновесия достаточно длительное время без существенного увеличения амплитуд колебаний по переменной $r$ (конечное время ${\tau } = 250$). Таким образом, имеет место существенная асимметрия в поведении системы, так как при ${\sigma } > 0$ система достигает переходного участка, когда ${\tau }* \approx 70$ (рис. 3, 4).
Асимметрия в поведении системы при изменении знака параметра ${\sigma }$ объясняется влиянием переносного движения, связанного с направлением движения центра масс системы по орбите (вращение системы координат $C{{x}_{0}}{{y}_{0}}{{z}_{0}}$). В этом нетрудно убедиться, формально изменив знаки угловой скорости ${\omega }$ и параметра ${\sigma }$ в уравнениях (1)–(3) на противоположные. При этом характерные случаи поведения системы поменяются местами.
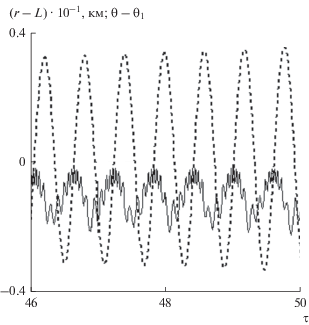
В обоих случаях имеет место синхронизация колебаний по переменным $r$ и ${\theta }$, то есть изгибные колебания троса синхронизируются с маятниковыми движениями системы относительно центра масс. Это иллюстрируется на рис. 6, где сплошной линией показано изменение величины $r - L,$ а штриховой линией – изменение переменной ${\theta } - {{{\theta }}_{1}}.$ Расчет относится к рассмотренному выше случаю ${\sigma } > 0$ и соответствует модели (1)–(3). При использовании модели (23) синхронизация также имеет место, однако не так явно выражена, так как на низкочастотные колебания накладываются высокочастотные продольные колебания троса, которые не учитываются в модели (1)–(3).
Рассмотренные выше примеры относятся к частному случаю движения ЭДТС по экваториальной орбите и когда ${{{\varphi }}_{0}} = 0.$ При наличии малых начальных возмущений по углу ${{{\varphi }}_{0}},$ например, ${{{\varphi }}_{0}} = 0.2$ существенная асимметрия в поведении системы сохраняется. Для ${\sigma } > 0$ момент достижения переходного участка уменьшается ${\tau }* \approx 65$ (было ${\tau }* \approx 70$), причем амплитуды колебаний по переменной ${\varphi }$ также уменьшаются. Для ${\sigma } < 0$ поведение системы становится другим. Как и раньше амплитуды колебаний по углу ${\theta }$ сначала уменьшаются и приближаются к положению равновесия ${{{\theta }}_{1}}$ (8), однако амплитуды колебаний по углу ${\varphi }$ увеличиваются, что приводит в некоторый момент к увеличению амплитуд колебаний переменных ${\theta }$ и $r.$ В этом случае также существует переходный участок, когда амплитуда колебаний ${\theta }$ приближается к ${\pi /}4.$ Время достижения переходного участка в этом случае ${\tau }* \approx 135,$ т.е. приблизительно в 2 раза больше, чем для случая ${\sigma } > 0.$
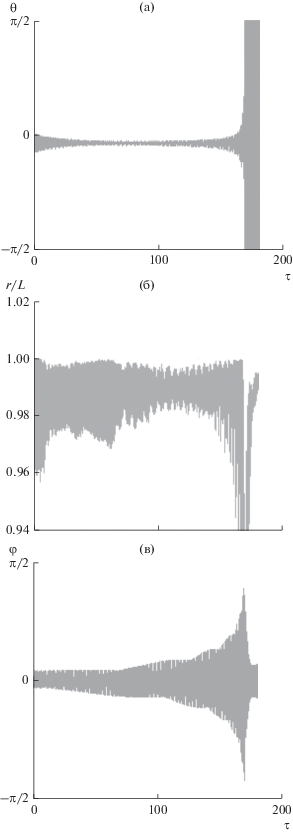
Асимметрия в поведении системы сохраняется и для наклонных орбит. В этом случае движение системы по отношению к плоскости орбиты всегда имеет пространственный характер, даже когда ${{{\varphi }}_{0}} = 0,$ т.е. возмущения по углу ${\varphi }$ всегда имеют место, что характеризуется в модели (1)–(3) существованием связей между уравнениями при $i \ne 0.$ Особенности поведения системы для случаев ${\sigma } > 0$ и ${\sigma } < 0$ также сохраняются. На рис. 7 приводятся характерные зависимости, соответствующие орбите с наклонением ${{i}_{0}} = {\pi /}6$ (${\sigma } < 0,$ ${{e}_{0}} = 0,$ ${{{\varphi }}_{0}} = 0,$ $I = - 0.1\,{\text{A}}$). Эволюция системы происходит также, как для аналогичного случая экваториальной орбиты при ${{{\varphi }}_{0}} = 0.2$. Амплитуды колебаний по переменной ${{{\varphi }}_{0}} = 0$ увеличиваются (рис. 7в). Амплитуды колебаний ${\theta }$ сначала уменьшаются, потом увеличиваются (рис. 7а). Здесь надо отметить, что в этом случае величина тока была увеличена в ${{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{\text{cos}}\left( {{{i}_{0}}} \right)}}} \right. \kern-0em} {{\text{cos}}\left( {{{i}_{0}}} \right)}}$ раз, чтобы сохранить приблизительно те же приращения орбитальных параметров центра масс системы (17)–(19). Данный случай характеризуется тем, что переходный участок практически отсутствует и система переходит во вращение, когда ${\tau } \approx 165.$ Если при этом для тех же данных поменять знак параметра ${\sigma } > 0$ ($I = 0.1\,{\text{A}}$), то характерное время перехода системы во вращение равно приблизительно ${\tau } \approx 42,$ т.е. существенно меньше.
Результаты, представленные на рис. 7, соответствуют модели (23). Для наклонных орбит использование модели (1)–(3), (10)–(15) приводит качественно к тем же результатам, однако моменты времени достижения переходных участков (или моменты времени перехода системы во вращение) увеличиваются на 10–20%.
При движении ЭДТС по эллиптической орбите с достаточно малым эксцентриситетом ($0.01$) рассматриваемая асимметрия в поведении системы сохраняется во всех случаях, причем моменты времени, когда система оказывается в характерных областях ее поведения изменяются не значительно.
Здесь необходимо отметить, что эволюционные движения системы относительно центра масс практически полностью определяются значением параметра ${\sigma }$. Если, например, поменять направление тока на противоположное $I = 0.1\,{\text{A}}$ ($I = - 0.1\,{\text{A}}$) и в то же время поменять местами концевые массы ${{m}_{1}} = 2\,\,{\text{кг,}}$ ${{m}_{2}} = 6\,\,{\text{кг}}$ (${{m}_{1}} = 6\,\,{\text{кг,}}$ ${{m}_{2}} = 2\,\,{\text{кг}}$), то величина параметра ${\sigma }$ (8) не изменится. Соответственно эволюционные движения системы относительно центра масс будут развиваться аналогично. Хотя в первом случае высота орбиты будет уменьшаться, а во втором случае – увеличиваться. Таким образом, при проектировании ЭДТС для конкретной миссии подъема (или торможения) всегда можно выбрать массы концевых тел так, чтобы реализовывался случай ${\sigma } < 0.$ Естественно в любом случае необходимо стремится к минимуму $\left| {\sigma } \right|,$ так как в этом случае влияние сил Ампера на движение системы относительно центра масс будет минимально.
Увеличение массы троса во всех случаях приводит к увеличению времени достижения переходных участков и, соответственно, моментов времени, при которых система переходит во вращение. Так, например, для наклонной орбиты ${{i}_{0}} = {\pi /}6$ (${\sigma } > 0,$ ${{e}_{0}} = 0,$ ${{{\varphi }}_{0}} = 0,$ $I = 0.1\,{\text{A}}$) при увеличении линейной плотности троса в 4 раза $\left( {{\rho } = 0.8\,\,{\text{кг/км}}} \right)$ время перехода системы во вращение увеличивается почти в 2 раза ${\tau } \approx 85$ (было ${\tau } \approx 42$). Понятно, что данный фактор не учитывает математическая модель (1)–(3), построенная для невесомого троса.
Здесь необходимо отметить, что процесс моделирования движения ЭДТС по модели (24) по сравнению с использованием более простых уравнений (1)–(3), (11)–(16) отличается большим объемом вычислений (на несколько порядков). Очевидно, что трудоемкость вычислений зависит от количества отрезков (или материальных точек), на которые разбивается трос. Это связано с тем, что уменьшается масса точек троса, что фактически приводит к увеличению жесткости системы. При больших $n$ появляются малые знаменатели в системе (23), так как для точек троса ${{m}_{k}} = {{\rho L} \mathord{\left/ {\vphantom {{\rho L} {\left( {n - 2} \right)}}} \right. \kern-0em} {\left( {n - 2} \right)}},$ где $k = 1,...n - 1.$ Кроме того, система (23) характеризуется высокочастотными продольными колебаниями троса, которые не учитываются в более простой модели (1)–(3). Поэтому при выборе количества точек, моделирующих трос, необходимо проводить пробные расчеты для различного количества отрезков, характеризующих дискретизацию троса. Пробные расчеты показали, что при количестве отрезков 7 и 14 результаты моделирования с точки зрения оценки характерных моментов времени (с точностью до 0.5 по безразмерному времени) и амплитуд колебаний переменных $r,\,{\theta }\,{\text{,}}\,{\varphi }$ (с точностью до 3%) совпадают. Поэтому все представленные выше расчеты соответствуют $n = 15.$ Понятно, что для более легких тросов при одном и том же количестве отрезков жесткость системы (23) выше. В данных примерах используется сравнительно легкий трос с линейной плотностью ${\rho } = 0.2\,\,{\text{кг/км}}{\text{.}}$
В табл. 3 приводятся значения тока, определенные из условия перехода системы во вращение при ${\tau } \approx 2.$ Система переходит во вращение в направлении угловой скорости орбитального движения ($I = - 0.1\,{\text{A,}}$ $i = 0,$ $e = 0$). В этом случае также имеется асимметрия, соответствующая вариантам ${\sigma } > 0$ и ${\sigma } < 0,$ т.е. при ${\sigma } < 0$ требуется больший по величине ток, чтобы перевести систему во вращение за заданное время. Естественно, когда ${\sigma } = 0,$ то влияние сил Ампера на движение системы относительно центра масс минимально, что приводит к тому, что соответствующие значения тока увеличиваются в несколько раз (табл. 3). Если ${\sigma } = 0$ (${{m}_{1}} = {{m}_{2}}$), то потеря устойчивости сопровождается большой деформацией троса, например, для рассматриваемых данных минимальная величина отношения достигает ${r \mathord{\left/ {\vphantom {r L}} \right. \kern-0em} L} \approx 0.4$ по обеим моделям (1)–(3) и (23). Оценка предельных величин тока из условия статической устойчивости $\left| {\sigma } \right| = 1,$ которая следует из (8), дает $0.45\,{\text{A}}$ для случаев ${{m}_{1}} \ne {{m}_{2}}$ из табл. 3. Причем для варианта ${{m}_{1}} = {{m}_{2}}$ предельные величины тока, определенные из условия статической устойчивости, формально не ограничены, так как ${\sigma } = 0.$
Таблица 3.
Значения тока (в амперах), определенные по различным моделям движения ЭДТС из условия перехода системы во вращение при ${\tau } \approx 2$
| Урав-нения | ${{m}_{1}} = 2\,{\text{кг}}$, ${{m}_{2}} = 6\,{\text{кг}}$, ${{{\theta }}_{1}} < 0\,\,\left( {{\sigma } < 0} \right)$ |
${{m}_{1}} = 6\,{\text{кг}}$, ${{m}_{2}} = 2\,{\text{кг}}$, ${{{\theta }}_{1}} > 0\,\,\left( {{\sigma } > 0} \right)$ |
${{m}_{1}} = 4\,{\text{кг}}$, ${{m}_{2}} = 4\,{\text{кг}}$, ${{{\theta }}_{1}} = 0\,\,\left( {{\sigma } = 0} \right)$ |
|---|---|---|---|
| (1)–(3) | –0.36 | –0.24 | –1.12 |
| (23) | –0.24 | –0.20 | –1.12 |
ВЫВОДЫ
На основании приведенного анализа динамики движения ЭДТС, работающей в режиме генерации тяги, можно сделать следующие выводы.
1. Проведено сравнение математических моделей движения ЭДТС, предназначенных для анализа динамики системы с различной степенью детализации, с учетом действующей распределенной нагрузки от сил Ампера.
2. Показано, что на сравнительно небольших интервалах времени для оценки изменения элементов орбиты можно использовать усредненную систему уравнений (17)–(21) и соответствующее ей аналитическое решение (22).
3. Установлено, что движение ЭДТС под действием распределенной нагрузки от сил Ампера включает в себя ряд характерных участков: 1) участок, где можно использовать допущение о форме троса в виде части окружности и соответственно модель (1)–(3); 2) переходный участок, для которого характерна большая и сложная деформация троса; 3) участок вращательного движения системы.
4. Обнаружена существенная асимметрия в поведении ЭДТС, которая определяется знаком момента от действия распределенных сил Ампера относительно центра масс системы. Если ${\sigma } < 0$ (нижняя концевая точка отклоняется от вертикали по направлению орбитального движения), то процесс перехода системы во вращение затягивается (как правило, в несколько раз) по сравнению с противоположным случаем ${\sigma } > 0.$ Причем это справедливо как для экваториальной, так и для наклонных орбит.
5. Показано, что при малых величинах тока возможно существование длительных переходных участков в движении ЭДТС, когда при увеличении амплитуды маятниковых колебаний система не переходит во вращение и деформируется (трос не натянут).
6. С помощью численного анализа обнаружено существование колебательных режимов движения ЭДТС, при реализации которых изгибные колебания троса синхронизируются с маятниковыми колебаниями системы относительно своего центра масс.
Работа поддержана грантом РФФИ РФ 16-41-630637.
Список литературы
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990.
Levin E.M. Dynamic analysis of space tether missions. San Diego: American Astronautical Society, 2007.
Zhong R., Zhu Z.H. Dynamics of Nanosatellite Deorbit by Bare Electrodynamic Tether in Low Earth Orbit // J. Spacecraft and Rockets. 2013. V. 50. № 3. P. 691–700.
Chen X., Sanmartín J.R. Bare-tether cathodic contact through thermionic emission by low-work-function materials // Physics of Plasmas. 2012. V. 19. P. 1–8.
Zhong R., Zhu Z.H. Optimal Control of Nanosatellite Fast Deorbit Using Electrodynamic Tether // J. Guidance, Control, and Dynamics. 2014. V. 37. № 4. P. 1182–1194.
Fuhrhop K.R. Theory and Experimental Evaluation of Electrodynamic Tether Systems and Related Technologies. PhD Dissertation. University of Michigan. 2007.
Левин Е.М. Устойчивость стационарных положений равновесия электродинамических тросовых систем на орбите // Космические исследования. 1987. Т. 25. № 4. С. 491–501.
Pelaez J., Lorenzini T.C., Lopez-Rebollal O., Ruiz M. A new kind of dynamic instability in electrodynamic tethers // J. Astronautical Sciences. 2000. V. 48(4). P. 449–476.
Iñarrea M., Lanchares V., Pascual A.I., Salas J.P. Attitude stabilization of electrodynamic tethers in elliptic orbits by time-delay feedback control // Acta Astronautica. 2014. V. 96. P. 280–295.
Mantellato R., Pertile M., Colombatti G., Lorenzini E.C. Analysis of Passive System to Damp the Libration of Electrodynamic Tethers for Deorbiting // AIAA SPACE. 2013 Conference and Exposition, San Diego. AIAA 2013-5390. P. 1–9.
Zhou X., Li J., Baoyin H., Zakirov V. Equilibrium control of electrodynamic tethered satellite systems in inclined orbits // J. Guidance, Control, and Dynamics. 2006. V. 29. № 6. P. 1451–1454.
Corsi J., Iess L. Stability and control of electrodynamic tethers for de-orbiting applications // Acta Astronautica. 2001. V. 48. Iss. 5–12. P. 491–501.
Воеводин П.С., Заболотнов Ю.М. Моделирование и анализ колебаний электродинамической тросовой системы на орбите спутника Земли // Математическое моделирование. 2017. Т. 29. № 6. С. 21–34.
Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического полета. М.: Наука, 1990.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 1. Механика. М.: Наука, 1988.
Дигнат Ф., Шилен В. Управление колебаниями орбитальной тросовой системы // Прикладная математика и механика. 2000. Т. 64. Вып. 5. С. 747–754.
Заболотнов Ю.М., Фефелов Д.И. Динамика движения капсулы с тросом на внеатмосферном участке спуска с орбиты // Известия СНЦ РАН. 2006. Т. 8. № 3. С. 841–848.
Асланов B.C., Ледков А.С., Стратилатов Н.Р. Пространственное движение космической тросовой системы, предназначенной для доставки груза на Землю // Полет. 2007. № 2. С. 28–33.
Zhong R., Zhu Z.H. Dynamic Analysis of Deployment and Retrieval of Tethered Satellites using a Hybrid Hinged-Rod Tether Model // International J. Aerospace and Lightweight Structures (IJALS). 2015. V. 5(1). C. 1–21.
Заболотнов Ю.М. Управление развертыванием орбитальной тросовой системы, состоящей из двух малых космических аппаратов // Космич. исслед. 2017. Т. 55. № 3. С. 236–246. (Cosmic Research. P. 224).
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования