Космические исследования, 2020, T. 58, № 2, стр. 138-148
Построение оптимальных траекторий для экспедиции Земля–Астероид–Земля при полете с большой тягой
В. В. Ивашкин 1, 2, *, Аньци Лан 3, **
1 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
2 Московский государственный технический университет им. Н.Э. Баумана
г. Москва, Россия
3 Xi’an Jiaotong University
Shaanxi, China, Xi’an, КНР
* E-mail: Ivashkin@keldysh.ru
** E-mail: langanqi@xjtu.edu.cn
Поступила в редакцию 01.10.2018
После доработки 29.01.2019
Принята к публикации 25.04.2019
Аннотация
В работе построены и проанализированы оптимальные траектории экспедиции к “опасному” астероиду Апофис, предназначенной для изучения астероида, взятия образцов его грунта и возвращения на Землю. Использована схема полета с применением химических двигательных установок “большой” тяги. Для полета к астероиду в 2019–2022 гг. с общей продолжительностью экспедиции до двух лет получены оптимальные по полезной массе трехимпульсные траектории КА. Показана принципиальная возможность осуществления космической экспедиции Земля–Апофис–Земля на основе ракет-носителей (РН) типа “Союз” и разгонного блока “Фрегат” при полете в 2019–2022 гг.
ВВЕДЕНИЕ
Исследование малых тел Солнечной системы (астероидов, комет) с помощью автоматических межпланетных станций, которые позволяют изучать эти тела на близком расстоянии, а также контактным методом, стало одним из главных направлений исследования дальнего космоса. Уже осуществлен ряд миссий для изучения малых тел Солнечной системы, например, “Вега”, “Near”, “Deep Space-1”,“Stardust”,“Rosetta”,“Deep Impact”, “Hayabusa” и др. К основным целям этих исследований можно отнести выявление механизма происхождения и эволюции Солнечной системы, поиск ценных ресурсов, изучение проблемы астероидно-кометной опасности, а также демонстрацию мер по предотвращению угрозы Земле.
Сейчас возрастает роль экспедиций к малым небесным телам с возвращением космического аппарата от этих тел к Земле. К данному моменту реально разработаны 4 космической миссии к малым небесным телам с возвращением к Земле. Из них две миссии (“Stardust”, NASA, и “Hayabusa”, Япония) уже совершили возврат спускаемого аппарата (СА) на Землю [1, 2]. И еще 2 миссии (“Hayabusa-2”, Япония, и “OSIRIS-REx” [3], NASA) осуществляются сейчас.
Такие экспедиции позволяют доставить на Землю образцы вещества небесного тела и исследовать их в условиях Земных лабораторий. Необходимость обеспечения возврата КА к Земле повышает энергетические затраты проекта, тем самым усложняет и удорожает его. Стремление к уменьшению стоимости космических исследовательских миссий, упрощению и повышению надежности их осуществления определяет важность использования отработанных и надежных ракет-носителей среднего класса и обычных химических двигательных установок (ДУ) большой тяги (БТ). Однако эти ДУ приводят к большому расходу топлива, что делает особенно актуальной оптимизацию межпланетных траекторий экспедиции.
Астероид Апофис представляет потенциально серьезную угрозу для безопасности Земли [4, 5]. В России НПО Лавочкина разрабатывает проект полета к этому “опасному” астероиду Апофис [6]. Настоящая работа посвящена разработке алгоритма построения оптимальных орбит КА для экспедиции Земля–астероид–Земля, главными целями которой являются исследование астероида, взятие и доставка образцов его грунта обратно на Землю. В работе сначала рассматривается задача оптимизации траекторий полета к произвольному астероиду с возвратом к Земле, затем результаты анализа будут применены для экспедиции к астероиду Апофис. Данная работа является развитием [7, 8].
Рассмотрена следующая схема экспедиции Земля–астероид–Земля. Ракета-носитель (РН) выводит КА с разгонным блоком (РБ) большой тяги на опорную орбиту искусственного спутника Земли. После пассивного движения по ней в некоторый оптимальный момент t0 двигательная установка РБ со скоростью истечения c1 сообщает КА импульс скорости ∆V1, производится разгон КА, и КА переводится на орбиту полета к астероиду. Затем РБ отделяется от КА, и дальнейшие маневры осуществляются с помощью второй двигательной установки большой тяги, ДУ2, со скоростью истечения газов c2. В момент t1сд аппарат выходит из сферы действия Земли. Далее, в момент t2 КА подлетает к астероиду. С помощью ДУ2 сообщается импульс скорости ∆V2, осуществляется торможение КА, и КА переходит на круговую орбиту искусственного спутника астероида (ИСА) радиусом r2. В окрестности астероида КА пребывает некоторое время ∆t23, это – “время ожидания” [9]. В течение этого времени возможны посадка на поверхность астероида, взятие образцов его грунта и другие исследования. Затем, в момент t3 основному КА сообщается импульс скорости ∆V3, КА разгоняется и переходит на траекторию возвращения к Земле. В момент t4сд КА подлетает к сфере действия Земли. При подлете к Земле от КА отделяется спускаемый аппарат, и в момент tf происходит его гиперболический вход в атмосферу Земли, затем – торможение, посадка. Для уменьшения энергетических затрат в качестве основной принята схема полета, когда тормозной импульс скорости двигателем не сообщается при подлете к Земле, как предлагал К.Э. Циолковский [10] и как сделано в проектах “Stardust”, “Hayabusa”. В этом случае энергетические затраты на экспедицию в номинале определяются тремя величинами импульсов скорости ΔV1, ΔV2, ΔV3.
1. ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ ПО ПОЛЕЗНОЙ МАССЕ ТРАЕКТОРИЙ КА ДЛЯ ЭКСПЕДИЦИИ ЗЕМЛЯ–АСТЕРОИД–ЗЕМЛЯ
Разработана и использовалась двухэтапная методика определения оптимальных межпланетных траекторий полета КА от Земли к астероиду и возврата от астероида к Земле в классе трехимпульсных перелетов. На первом этапе оптимальные гелиоцентрические траектории перелета КА Земля–астероид и астероид–Земля определяются в модели точечных сфер действия Земли и астероида, в импульсной постановке. В основном варианте оптимизации максимизируем полезную массу экспедиции mp, определяемую как конечная масса КА при возвращении к Земле mf минус масса ДУ2 вместе с ее топливными баками, масса которых зависит от массы топлива, т.е. импульсов ΔV1, ΔV2, ΔV3. На втором этапе анализа уточняются характеристики полученных оптимальных межпланетных траекторий в более точной модели с учетом параметров траекторий на геоцентрических и астероидоцентрических участках, возмущений, эфемерид небесных тел и гравитационных потерь на участках маневров.
1.1. ПЕРВЫЙ ЭТАП – ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ КА В ПРИБЛИЖЕННОЙ МОДЕЛИ
На первом этапе гелиоцентрические траектории перелета КА Земля–астероид и астероид–Земля определяются в модели точечных сфер действия Земли и астероида, поэтому орбиты этих перелетов строятся в центральном ньютоновском поле притяжения Солнца. Схема решения задачи будет следующей. При задании граничных времен экспедиции t1 (отлет с орбиты Земли), t2 (подлет к орбите астероида), t3 (отлет с орбиты астероида), t4 (подлет к орбите Земли) гелиоцентрические орбиты перелета между небесными телами определяются путем двукратного решения задачи Эйлера–Ламберта (с учетом возможности совершения одного пассивного витка хотя бы по одной орбите). Это позволяет найти скорости “на бесконечности” V∞1, V∞2, V∞3, V∞4 в граничные времена ti и требуемые импульсы скорости для перелета ΔV1, ΔV2, ΔV3. По этим скоростям можно определить конечную массу mf и полезную mp массу КА [11], с учетом отделяемых масс РБ и ДУ2:
(1)
$\begin{gathered} {{m}_{f}} = {{m}_{1}}{{\mu }_{2}}{{\mu }_{3}},\,\,\,\,{{m}_{1}} = {{m}_{0}}{{\mu }_{1}} - \Delta {{m}_{1}},\,\,\,\,{{\mu }_{1}} = {{e}^{{{{ - \Delta {{V}_{1}}} \mathord{\left/ {\vphantom {{ - \Delta {{V}_{1}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}}}}, \\ {{\mu }_{2}} = {{e}^{{{{ - \Delta {{V}_{2}}} \mathord{\left/ {\vphantom {{ - \Delta {{V}_{2}}} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}}}},\,\,\,\,{{\mu }_{3}} = {{e}^{{{{ - \Delta {{V}_{3}}} \mathord{\left/ {\vphantom {{ - \Delta {{V}_{3}}} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}}}}, \\ \end{gathered} $(1а)
$\Delta {{m}_{2}} = {{m}_{{{\text{2}}0}}} + {{a}_{{T2}}}{{m}_{T}},\,\,\,\,{{m}_{T}} = {{m}_{1}} - {{m}_{f}},$При этом скорости истечения газов с1, с2 из двигательных установок РБ и ДУ2, вообще говоря, различны.
Обычно при оптимизации траекторий рассматривают минимизацию характеристической скорости Vхар, равной сумме величин импульсов скорости (см., например, [12, 13]):
(3)
${{F}_{1}} = {{V}_{{{\text{хар}}}}}\left( {{{t}_{{\text{1}}}},{{t}_{{\text{2}}}},{{t}_{{\text{3}}}},{{t}_{{\text{4}}}}} \right){\text{ }} = \sum\limits_{i = 1}^n {\Delta {{V}_{i}}} \to {\text{min,}}$(4)
${{F}_{2}} = - {{m}_{f}}\left( {{{t}_{{\text{1}}}},{{t}_{{\text{2}}}},{{t}_{{\text{3}}}},{{t}_{{\text{4}}}}} \right) \to {\text{min}}{\text{.}}$Нами при построении оптимальных межпланетных траекторий перелета в основном варианте анализа максимизируется полезная масса экспедиции mp:
(5)
${{F}_{3}} = - {{m}_{p}}\left( {{{t}_{{\text{1}}}},{{t}_{{\text{2}}}},{{t}_{{\text{3}}}},{{t}_{{\text{4}}}}} \right) \to {\text{min}}{\text{.}}$Этот функционал, вообще говоря, лучше отражает требование энергетической эффективности траектории, чем характеристическая скорость Vхар и конечная масса mf.
Тогда задача заключается в выборе времен t1, t2, t3,t4 (при заданных областях для этих времен) для нахождения оптимальных траекторий с максимальной полезной массой.
Классическим способом поиска окна запуска для полета КА к другим планетам является построение графика изолиний функционала с помощью метода прямого перебора (см., например, [14]). При этом время вычисления быстро увеличивается с ростом размерности пространства поиска. Поэтому для уменьшения времени расчета и применения в более сложных задачах разработан комплексный метод, сочетающий несколько методов: метод И.М. Соболя [15–17], генетический алгоритм (ГА) [18] и квазиньютоновский BFGS (Broyden-Fletcher-Goldfarb-Shanno) метод [19].
Сначала для глобальной оптимизации применяется метод И.М. Соболя. В рамках этого метода используется детерминированный подход для построения точек ЛПτ – последовательностей, которые очень равномерно расположены в области поиска. Используя сетку, построенную точками ЛПτ – последовательностей, можно получить много различных решений и одновременно оценить максимумы и (или) минимумы функционала. В итоге, точки ЛПτ – последовательностей позволяют дать хорошее представление о поведении функционала со сравнительно меньшим количеством вычислений, чем в случае прямого перебора. Детальное описание метода построения и свойств точек ЛПτ – последовательностей дано в работах [15–17]. В частности, метод Соболя позволяет быстро найти области, где расположены локальные оптимумы и глобальный оптимум.
Последующий запуск генетического алгоритма (ГА) в этих областях позволяет определить глобальный оптимум с точностью до суток по граничным временам экспедиции. ГА использует принципы и терминологию, заимствованные у биологической науки – генетики. В ГА каждая особь представляет потенциальное решение некоторой задачи. Каждой особи предоставляется определенная пригодность путем вычисления значения фитнесс-функции. Множество этих особей называется популяцией. В процессе эволюции популяции с помощью генетических операторов – репродукции, кроссинговера и мутации, генерируют новые популяции. При этом особи с лучшими значениями целевой функции (пригодности) c большей вероятностью переходят в следующее поколение, т.е. в следующую итерацию. Таким образом, после нескольких поколений (итераций) решения сходятся к оптимальному. Детальное описание метода ГА дано, например, в работе [18]. Для реализации простого ГА использованы следующие основные операторы: репродукция с помощью рулеточного отбора для выбора “родителей”, одноточечный кроссинговер с вероятностью Pc = 0.8, одноточечная мутация с вероятностью Pm = 0.01 и элитарный отбор “особей” в следующее поколение. Метод Соболя и ГА удобны также при решении задач оптимизации с ограничениями, в частности, при ограничениях на граничные времена экспедиции, на скорость входа в атмосферу Земли при возвращении.
В случае внутреннего, по ограничениям, оптимума при необходимости более точного (в пределах суток) его определения, используется квазиньютоновский BFGS метод [19]. В этом методе, как и в других квазиньютоновских методах, матрица Гессе Gk целевой функции f заменяется на ее аппроксимацию Аk с учетом информации о градиенте функции f(x): gk = grad f(xk). При этом производные $\frac{{\partial f}}{{\partial x}}$ определяются численно. Применение BFGS метода позволяет быстро (за 2–8 итераций) уточнить оптимум. Применение этого метода также позволяет снизить требования к точности оптимизации в ГА.
Использование данного комплексного метода позволило быстро и точно проводить оптимизацию траекторий для экспедиции Земля–астероид–Земля. При этом рассмотрено 5 задач:
1) Основная задача оптимизации: при заданной общей продолжительности экспедиции ∆t∑ = = t4 – t1 и заданном времени пребывания КА (времени ожидания) у астероида ∆t23 = t3 – t2 оптимизируются время старта t1 и время перелета от Земли до астероида ∆t12 = t2 – t1, чтобы выполнялось (5). Это близко к постановке, данной в работе [13]. В этой задаче, таким образом, есть два параметра оптимизации.
2) При заданном времени ожидания ∆t23 и при ограничении на общую продолжительность экспедиции ∆t∑ (например, ∆t∑ ≤ 2 года), оптимизируются времена t1, ∆t12 и ∆t∑. Здесь три параметра оптимизации.
3) При заданном суммарном времени экспедиции ∆t∑ оптимизируются времена t1, ∆t12, и ∆t23. Здесь также три параметра оптимизации.
4) Оптимизируются все времена ∆t∑, t1, ∆t12 и ∆t23. Здесь четыре параметра оптимизации.
5) Полная четырехпараметрическая оптимизация времен ∆t∑, t1, ∆t12 и ∆t23 с учетом ограничения на скорость входа КА в атмосферу Земли при возврате от астероида Vвх: Vвх ≤ Vвх max.
1.2. ПРОВЕРКА ОПТИМАЛЬНОСТИ ПОЛУЧЕННЫХ ТРАЕКТОРИЙ КА В КЛАССЕ МНОГОИМПУЛЬСНЫХ ПЕРЕЛЕТОВ
После построения на первом этапе оптимальных гелиоцентрических траекторий перелета КА эти траектории проверяем на выполнение необходимых условий оптимальности в классе многоимпульсных перелетов с помощью сопряженных функций. Получены выражения для базис-вектора Лоудена p (вектора λV, сопряженного к гелиоцентрической скорости КА V) в граничные времена t1, t2, t3, t4 для всех трех указанных выше (3–5) функционалов – как для минимума скорости Vхар, так и для максимума конечной массы mf, и для максимума полезной массы КА mp [20]. При этом было учтено наличие двух двигательных установок с разными скоростями истечения c1, c2 продуктов сгорания, а также наличие отделения массы Δm1 между сообщением импульсов скорости ΔV1, ΔV2. При минимизации характеристической скорости Vхар (3) граничные значения базис-вектора ${{{\mathbf{p}}}_{i}} = {\mathbf{p}}({{t}_{i}})$ определяются выражениями:
(6)
$\begin{gathered} {{{\mathbf{p}}}_{1}} = {{{\mathbf{\lambda }}}_{{v}}}\left( {{{t}_{1}}} \right) = \frac{{{{{\mathbf{V}}}_{{\infty 1}}}}}{{{{V}_{{p1}}}}},\,\,\,\,{{{\mathbf{p}}}_{2}} = {{{\mathbf{\lambda }}}_{{v}}}\left( {{{t}_{2}}} \right) = - \frac{{{{{\mathbf{V}}}_{{\infty 2}}}}}{{{{V}_{{p2}}}}}, \\ {{{\mathbf{p}}}_{3}} = {{{\mathbf{\lambda }}}_{{v}}}\left( {{{t}_{3}}} \right) = \frac{{{{{\mathbf{V}}}_{{\infty 3}}}}}{{{{V}_{{p3}}}}},\,\,\,\,{{{\mathbf{p}}}_{4}} = {{{\mathbf{\lambda }}}_{{v}}}\left( {{{t}_{4}}} \right) = 0. \\ \end{gathered} $(6a)
$\begin{gathered} {{V}_{{p1}}} = \sqrt {V_{{\infty 1}}^{2} + {{2{{\mu }_{E}}} \mathord{\left/ {\vphantom {{2{{\mu }_{E}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} ,\,\,\,\,{{V}_{{p2}}} = \sqrt {V_{{\infty 2}}^{2} + {{2{{\mu }_{A}}} \mathord{\left/ {\vphantom {{2{{\mu }_{A}}} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}} , \\ {{V}_{{p3}}} = \sqrt {V_{{\infty 3}}^{2} + {{2{{\mu }_{A}}} \mathord{\left/ {\vphantom {{2{{\mu }_{A}}} {{{r}_{3}}}}} \right. \kern-0em} {{{r}_{3}}}}} . \\ \end{gathered} $Здесь Vp1 – с корость в перигее орбиты отлета от Земли; Vp2, Vp3 – скорости в перицентрах астероидоцентрических орбит подлета к астероиду и отлета от астероида. Радиусы r2, r3 соответствуют круговым орбитам спутника астероида после подлета к астероиду и при отлете от него. Отметим, что притяжение астероида часто очень мало. Так для астероида Апофис μА ~ 2 м3/с2. В то же время скорости на бесконечность V∞2, V∞3 велики (километры в секунду – сотни метров в секунду). Поэтому вторые слагаемые под знаком радикала для Vp2, Vp3 (4а) малы по сравнению с первыми слагаемыми. Если мы этими вторыми слагаемыми пренебрегаем, т.е. притяжение астероида не учитывается, то в (6) Vp2 ≈ V∞2, Vp3 ≈ V∞3. Для случая максимизации конечной массы (4):
(7)
$\begin{gathered} {{{\mathbf{p}}}_{1}} = \frac{{{{c}_{2}}{{m}_{0}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}}{{{{c}_{1}}{{m}_{f}}}} \cdot \frac{{{{{\mathbf{V}}}_{{\infty 1}}}}}{{{{V}_{{p1}}}}},\,\,\,\,{{{\mathbf{p}}}_{2}} = - \frac{{{{{\mathbf{V}}}_{{\infty 2}}}}}{{{{V}_{{p2}}}}}, \\ {{{\mathbf{p}}}_{3}} = \frac{{{{{\mathbf{V}}}_{{\infty 3}}}}}{{{{V}_{{p3}}}}},\,\,\,\,{{{\mathbf{p}}}_{4}} = 0. \\ \end{gathered} $При максимизации полезной массы КА mp (5):
(8)
$\begin{gathered} {{{\mathbf{p}}}_{1}} = \frac{{{{c}_{2}}{{m}_{0}}{{\mu }_{1}}}}{{{{c}_{1}}{{m}_{f}}}}\left( {{{\mu }_{2}}{{\mu }_{3}} - \frac{{{{a}_{{T2}}}}}{{1 + {{a}_{{T2}}}}}} \right)\frac{{{{{\mathbf{V}}}_{{\infty 1}}}}}{{{{V}_{{p1}}}}},\,\,\,\,{{{\mathbf{p}}}_{2}} = - \frac{{{{{\mathbf{V}}}_{{\infty 2}}}}}{{{{V}_{{p2}}}}}, \\ {{{\mathbf{p}}}_{3}} = \frac{{{{{\mathbf{V}}}_{{\infty 3}}}}}{{{{V}_{{p3}}}}},\,\,\,\,{{{\mathbf{p}}}_{4}} = 0. \\ \end{gathered} $Зная эти граничные сопряженные переменные, можно определить текущие сопряженные переменные по переходной матрице Φ, удовлетворяющей уравнениям:
(9)
$\left[ \begin{gathered} \delta {{{\mathbf{r}}}_{f}} \hfill \\ \delta {{{\mathbf{V}}}_{f}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{{\Phi }_{1}}}&{{{\Phi }_{2}}} \\ {{{\Phi }_{3}}}&{{{\Phi }_{4}}} \end{array}} \right]\left[ \begin{gathered} \delta {{{\mathbf{r}}}_{0}} \hfill \\ \delta {{{\mathbf{V}}}_{0}} \hfill \\ \end{gathered} \right],$где r, V – гелиоцентрические радиус-вектор и вектор скорости КА, индексы “0” и “f” соответствуют началу и концу каждой дуги перелета,
${{\Phi }_{1}} = \frac{{\partial {{{\mathbf{r}}}_{f}}}}{{\partial {{{\mathbf{r}}}_{0}}}},\,\,\,\,{{\Phi }_{2}} = \frac{{\partial {{{\mathbf{r}}}_{f}}}}{{\partial {{{\mathbf{V}}}_{0}}}},\,\,\,\,{{\Phi }_{3}} = \frac{{\partial {{{\mathbf{V}}}_{f}}}}{{\partial {{{\mathbf{r}}}_{0}}}},\,\,\,\,{{\Phi }_{4}} = \frac{{\partial {{{\mathbf{V}}}_{f}}}}{{\partial {{{\mathbf{V}}}_{0}}}}.$ (9а)
Эти матрицы задаются, например, формулами для изохронных производных [12, 13, 21–23 и др.]. Поскольку переходная матрица для (p, p') идентична матрице для вариаций (δr, δV), производная базис-вектора p' = dp/dt в начальный момент:
(10)
${\mathbf{p}}_{0}^{'} = \Phi _{2}^{{ - 1}} \cdot \left( {{{{\mathbf{p}}}_{f}} - {{\Phi }_{1}} \cdot {{{\mathbf{p}}}_{0}}} \right).$Тогда можно определить базис-вектор на всей траектории:
(11)
${\mathbf{р}}\left( t \right) = {{\Phi }_{1}}(t,{{t}_{0}}){{{\mathbf{р}}}_{0}} + {{\Phi }_{2}}(t,{{t}_{0}}){\mathbf{p}}_{0}^{'},$при этом ${{{\Phi }}_{1}},$ ${{\Phi }_{2}}$ пересчитываются по (9а) в каждый момент t. Можно также определить базис-вектор p(t) интегрированием системы уравнений [13]:
(11а)
$\begin{gathered} \frac{{d{\mathbf{r}}}}{{dt}} = {\mathbf{V}};\,\,\,\,\frac{{d{\mathbf{V}}}}{{dt}} = - {{{\mu }}_{{\text{S}}}}\frac{{\mathbf{r}}}{{{{r}^{3}}}},\,\,\,\,\frac{{d{\mathbf{p}}}}{{dt}} = {\mathbf{p}}{\kern 1pt} '; \\ \frac{{d{\mathbf{p}}{\kern 1pt} '}}{{dt}} = - {{{\mu }}_{{\text{s}}}}\frac{{\mathbf{p}}}{{{{r}^{3}}}} + \left( {{\mathbf{p}},{\mathbf{r}}} \right) \cdot \frac{{3{{{\mu }}_{{\text{S}}}}{\mathbf{r}}}}{{{{r}^{5}}}}, \\ \end{gathered} $где μS – гравитационный параметр Солнца. Для оптимальности траекторий в классе многоимпульсных перелетов необходимо выполнение условия [20]:
Если это условие, играющее здесь роль “принципа максимума”, нарушается на некотором участке, то траекторию можно улучшить введением дополнительных импульсов или вариацией граничных времен [20, 24, 25 ].
Также получены производные от функционалов (3–5) по граничным временам траектории [20], они могут быть использованы для проверки выполнения условий трансверсальности и для улучшения траектории по функционалу, например, градиентным или квазиньютоновским методом. Для функционала F3 = –mp (5) имеем [20]:
(13)
$\begin{gathered} \frac{{\partial {{F}_{3}}}}{{\partial {{t}_{1}}}} = - {{d}_{3}}p_{1}^{'}{{V}_{{\infty 1}}},\,\,\,\,\frac{{\partial {{F}_{3}}}}{{\partial {{t}_{2}}}} = {{d}_{3}}p_{2}^{'}{{V}_{{\infty 2}}},\,\,\,\,\frac{{\partial {{F}_{3}}}}{{\partial {{t}_{3}}}} = - {{d}_{3}}p_{3}^{'}{{V}_{{\infty 3}}}, \\ \frac{{\partial {{F}_{3}}}}{{\partial {{t}_{4}}}} = {{d}_{3}}\left( {{\mathbf{p}}_{4}^{'},{{{\mathbf{V}}}_{{\infty 4}}}} \right),\,\,\,\,{{d}_{3}} = {{{{m}_{f}}\left( {1 + {{a}_{{T2}}}} \right)} \mathord{\left/ {\vphantom {{{{m}_{f}}\left( {1 + {{a}_{{T2}}}} \right)} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}, \\ p_{i}^{'} = \frac{{d\left| {{{{\mathbf{p}}}_{i}}} \right|}}{{dt}} = \frac{d}{{dt}}\left[ {{{{({{{\mathbf{p}}}_{i}} \cdot {{{\mathbf{p}}}_{i}})}}^{{\frac{1}{2}}}}} \right] = \frac{{{\mathbf{p}}_{i}^{'} \cdot {{{\mathbf{p}}}_{i}}}}{{\left| {{{{\mathbf{p}}}_{i}}} \right|}},\,\,\,\,i = 1,2,3. \\ \end{gathered} $Если времена ti (i = 1, 2, 3, 4) не зависят друг от друга и лежат внутри допустимых областей, то для оптимальной траектории должно быть ∂F3/∂ti = 0. Если между временами ti есть связи, то переходим к независимым переменным xj.
1.3. ВТОРОЙ ЭТАП – УТОЧНЕНИЕ ХАРАКТЕРИСТИК ПОЛУЧЕННЫХ ТРАЕКТОРИЙ КА
На втором этапе анализа с учетом более точной модели движения КА, гравитационных потерь и ряда технических характеристик проводится корректирование траектории. При этом траектория КА определяется численным интегрированием системы дифференциальных уравнений движения КА
(14)
$\frac{{{{d}^{2}}{\mathbf{r}}}}{{d{{t}^{2}}}} = - \frac{{{{\mu }_{ \odot }}}}{{{{{\left| {\mathbf{r}} \right|}}^{3}}}}{\mathbf{r}} - \sum\limits_i {{{\mu }_{{Gi}}}\left( {\frac{{{{{\mathbf{r}}}_{i}}}}{{{{{\left| {{{{\mathbf{r}}}_{i}}} \right|}}^{3}}}} + \frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{i}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{i}}} \right|}}^{3}}}}} \right)} + {{{\mathbf{\Delta }}}_{1}} + {{{\mathbf{\Delta }}}_{2}},$где r(x, y, z)– радиус-вектор КА в прямоугольной невращающейся системе координат; ri – радиус-вектор i-го небесного тела (из эфемериды DE421); μ⊙, μGi – гравитационные параметры центрального и i-го небесных тел соответственно; Δ1, Δ2 – ускорения за счет сжатия Земли (J2) и давления солнечного света. Данная система (14) рассматривается на двух отрезках t ∈ [t0, t2], t ∈ [t3, tf]. Здесь t0 – момент отлета с опорной орбиты спутника Земли, t2 – момент перехода КА на орбиту спутника астероида, t3 – момент отлета КА с орбиты спутника астероида для полета к Земле, tf – момент вход в атмосферу Земли при возврате c астероида.
Траектория перелета КА уточняется решением двух задач. Внутренняя задача – решение краевых задач. Для перелета от Земли до астероида варьируем три параметра в начальной точке траектории отлета от Земли, например Ω, ω и |V∞1|, с которыми одновременно варьируются и t0, r0, V0. Первоначальные приближения t0, r0, V0 определяются с помощью t1СДЗ (= t1 из первого этапа) и V∞1. Добиваемся выполнения условия, что в момент t2 прицельная дальность в картинной плоскости равняется 1 км. Для перелета от астероида до Земли задача решается в два этапа. Сначала варьируется вектор скорости V∞3, чтобы обеспечить в момент t4СДЗ (в качестве начального приближения t4СДЗ, взято оптимальное время t4 из первого этапа) вход КА в сферу действия Земли с вектором прицельной дальности, соответствующим входу в атмосферу Земли с необходимой высотой условного перигея. Через эту высоту условного перигея орбиты подлета к Земле также обеспечим угол входа в атмосферу Земли. Для численного анализа полагаем, что эта высота равна 50 км. Затем учитываются возмущения до входа в атмосферу, и получается момент tf . Первые решения внутренней задачи называем “квазиоптимальными” траекториями. Внешняя задача – оптимизация возмущенных траекторий по граничным временам t0, t2, t3, tf . В связи с переходом от упрошенной модели к полной модели, оптимальные решения будут слегка отличаться от решений, полученных на первом этапе. Поэтому на втором этапе также выполняется оптимизация – методом покоординатного спуска [30] при малых вариациях. Таким образом, на каждой итерации решаются краевые задачи. После этого уже получаются оптимальные траектории в полной модели.
При коррекции массо-энергетических характеристик экспедиции, прежде всего, был учтен неимпульсный характер разгона КА возле Земли. В этом случае при расчете характеристической скорости отлета КА от Земли $\Delta V_{{\text{1}}}^{*}$ принимаются во внимание “гравитационные потери” δV1gr. Они оценивались численно и аналитически, на основе формулы [26–29]:
(15)
$\delta {{V}_{{gr}}} \approx k({\mu \mathord{\left/ {\vphantom {\mu {{{r}^{3}}}}} \right. \kern-0em} {{{r}^{3}}}})t_{e}^{2}\Delta {{V}_{1}},$где te – время работы двигателя для создания импульса скорости ∆V1 за счет конечной тяги на расстоянии r от центра с гравитационным параметром μ, k ≈ 0.019 [28]. Эта константа немного уточнялась на основе численных расчетов. Для уменьшения этих потерь рассматривается режим разгона с двумя-тремя включениями двигателя. Для коррекции массо-энергетических характеристик также предусмотрены дополнительные импульсы скорости на коррекцию траекторий и т.д.
2. ИССЛЕДОВАНИЕ ОПТИМАЛЬНЫХ ПО ПОЛЕЗНОЙ МАССЕ ТРАЕКТОРИЙ КА ДЛЯ ЭКСПЕДИЦИИ ЗЕМЛЯ–АПОФИС–ЗЕМЛЯ
С помощью разработанного метода, для экспедиции “Земля–Апофис–Земля” построены и исследованы энергетически оптимальные, по максимуму полезной массы КА, межпланетные траектории при полете в течение 2019–2022 гг. Исследованы варианты с использованием РН “Союз-2.1a”, “Союз-2.1б”, “Зенит” и РБ “Фрегат”. Для двигательной установки ДУ2 удельная тяга 304 с; в (1а) постоянная составляющая массы m20 = 100 кг; коэффициент массы топливных баков аT2 = 0.15. Начальная опорная орбита пребывания основного КА у Апофиса взята круговой с радиусом 500 м.
При коррекции массовых характеристик гравитационные потери импульсов скорости ΔV2, ΔV3 не учитываются, т.к. гравитация Апофиса мала (μА ~ 2–3 м3/с2). Для надежности анализа при уточнении траектории предусмотрены дополнительные импульсы скорости на коррекцию: до подлета к астероиду – 50 м/с, возле астероида – 10 м/с и после отлета КА от астероида – 25 м/с. По рекомендации НПО им. С.А. Лавочкина были скорректированы некоторые параметры РБ “Фрегат” и КА, в частности уточнены массовые характеристики отделяемых частей блока; предложены гарантийные запасы топлива; введены отделяемые массы – для небольшого спутника астероида и посадочного устройства – 10 и 20 кг.
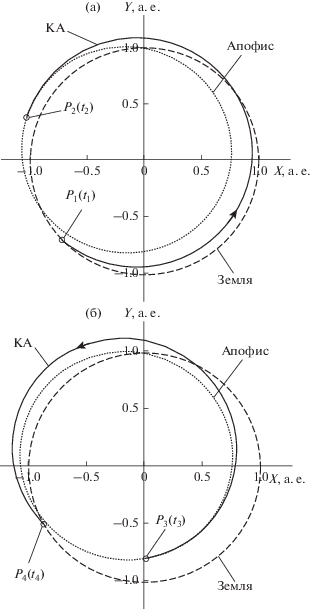
Сначала приведем данные в случае использования РН “Союз-2.1a”. Для задачи оптимизации 1) фиксировано время ожидания ∆t23 = t3 – t2 = 7 сут. При этом суммарное время ∆t∑ выбиралось из множества TS = [390; 420; 450; 510; 540; 570; 600; 630; 660; 690; 730] сут. Решение этой задачи на первом этапе анализа дало оптимальные траектории для разных времен ∆t∑. Среди них максимальная полезная масса КА mp = 272 кг получена для траектории № 1, для которой: ∆t∑ = 690 сут, t1 = 24.V.2019, Δt12 = t2 – t1 = 335 сут, t4 = 13.IV.2021, Vхар = 6.618 км/с, mf = 527 кг, см. рис. 1, где представлены зависимость полезной массы от времен t1 и ∆t12 для варианта Δt∑ = 690 сут, а также изолинии полезной массы в окрестности глобального оптимума. На рис. 2 приведены картины перелета по траектории № 1: здесь рис. 2а – для полета от Земли (P1) до Апофиса (P2); рис. 2б – для полета от Апофиса (P3) до Земли (P4). На второй дуге полета делается пассивный виток, прилет к Земле – у восходящего узла орбиты Апофиса.
Рис. 1.
Зависимость полезной массы от времен t1 и ∆t12 для варианта Δt∑ = 690 сут, ∆t23 = 7 сут: (а) глобальный и локальный оптимумы; (б) изолинии полезной массы в окрестности глобального максимума.
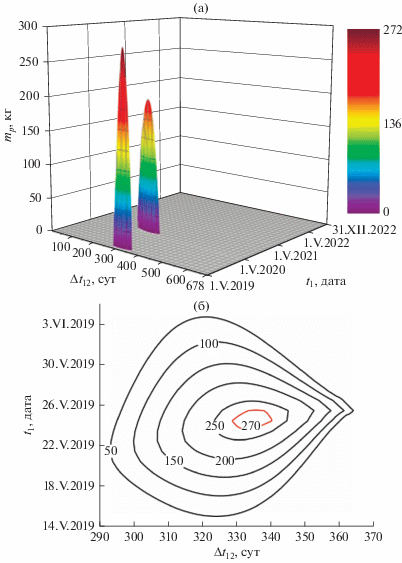
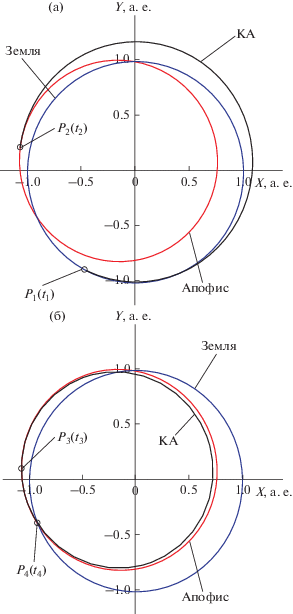
Рис. 2.
Межпланетные перелеты КА для оптимальной траектории № 1: (а) перелет от Земли (P1) до Апофиса (P2); (б) перелет от Апофиса (P3) до Земли (P4).
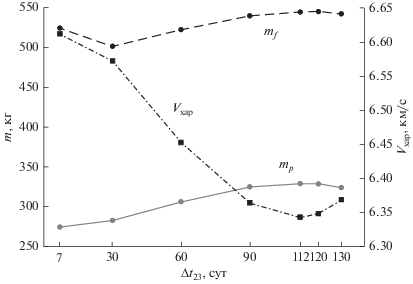
Решена задача 2) трехмерной оптимизации при заданном времени ожидания Δt23 ∈ [7; 30; 60; 90; 120; 130] сут, при ∆t∑ ≤ 2 года. Получено, что оптимальное время ожидания КА у Апофиса ∆t23 opt достигается на интервале 90–120 сут, см. рис. 3. Так, для траектории с Δt23 = 120 сут: t1 = 6.V.2020, Δt12 = 297 сут, ΔtΣ = 716 сут, Vхар = 6.35 км/с, mp = = 328 кг.
В задаче (3) трехмерной оптимизации при задании ∆t∑ = 690 сут, для оптимального решения (траектория № 3): t1 = 23.V.2019, Δt12 = 336 сут, Δt23opt = 93 сут, Vхар = 6.519 км/с, mf = 544 кг, mp = = 293 кг. Картинки траектории № 3 в плоскости эклиптики показаны на рис. 4.
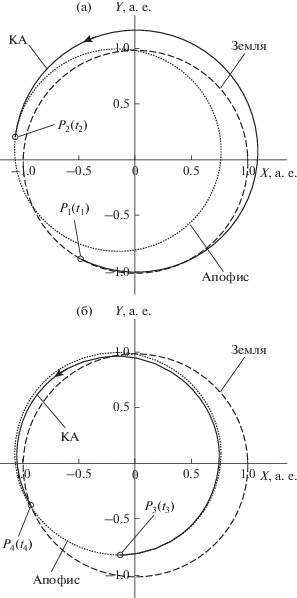
Рис. 4.
Межпланетные перелеты КА для варианта № 3: (а) перелет от Земли (P1) до Апофиса (P2); (б) перелет от Апофиса (P3) до Земли (P4).
Решена также задача 4) полной четырехмерной оптимизации при условиях ∆t∑ ≤ 2 года; Δt23 ≥ 7 сут. Для нее получена траектория № 4 с характеристиками: ∆t∑ = 716 сут, t1 = 05.V.2020, Δt12 = 300 сут, Δt23opt = 112 сут, Vхар = 6.343 км/с, mf = 545 кг, mp = = 329 кг. Картинки траектории перелетов № 4 в плоскости эклиптики показаны на рис. 5. Возврат к Земле происходит также вблизи восходящего узла орбиты Апофиса, как и для траекторий № 1 и 3.
Рис. 5.
Межпланетные перелеты КА для траектории № 4: (а) перелет от Земли (P1) до Апофиса (P2); (б) перелет от Апофиса (P3) до Земли (P4).
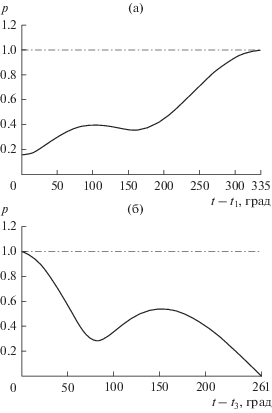
Для полученных траекторий построены сопряженные функции, в частности, модуль базис-вектора. На рис. 6 дано изменение модуля базис-вектора p(t) для основной траектории № 1. Здесь p(t) > 1 на некотором начальном отрезке второй дуги, после приложения импульса ΔV3, условие (12) не выполняется, поэтому траекторию можно улучшить. Поскольку $p_{3}^{'}$ = dp3/dt > 0, из выражений (13) для частных производных от функционала видно, что если dt3 > 0, то уменьшим функционал, dF3 < 0. Это подтверждает улучшение характеристик траектории № 3, у которой большее время t3. И время ожидания у нее, Δt23 = 93 сут, как раз соответствует интервалу оптимального времени ожидания 90–120 сут. На рис. 7 представлено изменение p(t) для этой траектории. Здесь p ≤ 1, условие оптимальности выполняется. Для траектории № 4 условие p(t) ≤ 1 также выполняется.
Рис. 6.
Изменение модуля базис-вектора для траектории № 1: (а) на траектории перелета от Земли до Апофиса; (б) на траектории перелета от Апофиса до Земли.
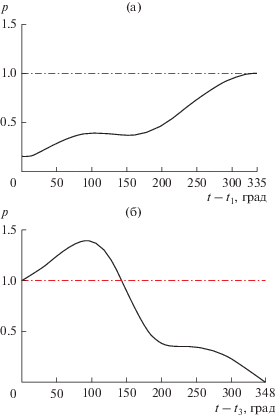
Рис. 7.
Изменение модуля базис-вектора на траектории № 3: (а) перелет от Земли до Апофиса; (б) перелет от Апофиса до Земли.
Далее, на втором этапе анализа, выполнено уточнение полученных на первом этапе характеристик оптимальных траекторий. Проводится интегрирование уравнений движения КА на участках перелета от Земли к Апофису и от Апофиса к Земле, и решаются соответствующие краевые задачи. Система уравнений движения КА (14) интегрируется методом Рунге-Кутта-Фельберга 7-го порядка с контролем ошибки 8 порядка. Затем в окрестности граничных времен полученных траекторий выполнена оптимизация задачи на множестве уточненных траекторий – методом покоординатного спуска. Также сделана коррекция массово-энергетических характеристик экспедиции. Полученные характеристики оптимальных траекторий № 1а, 3а, 4а приведены в табл. 1, где Δts = tf – t0. Уточнение на втором этапе привело к некоторому уменьшению полезной массы. При численном анализе получено также, что если о-птимальное время t0 варьировать в окрестности [t0 – 3 сут, t0 + 3 сут], то полезная масса экспедиции меняется мало, в пределах 1 кг. Это, с одной стороны, обеспечивает большое значение полезной массы КА, и с другой стороны, позволяет при необходимости (плохой погоде, отказе в работе бортовой системы и т.д.) переносить дату запуска в небольшом диапазоне.
Таблица 1.
Характеристики траекторий № 1а, 3а, 4а
| Номер | Δts, сут | t0 | t2 | t3 | tf | Vхар, км/c | mf, кг | mp, кг |
|---|---|---|---|---|---|---|---|---|
| 1а | 692 | 21.V.2019 | 24.IV.2020 | 1.V.2020 | 12.IV.2021 | 6.721 | 492 | 226 |
| 3а | 691 | 21.V.2019 | 24.IV.2020 | 22.VII.2020 | 11.IV.2021 | 6.624 | 509 | 245 |
| 4а | 715 | 6.V.2020 | 2.III.2021 | 23.VI.2021 | 21.IV.2022 | 6.447 | 517 | 290 |
Кроме РН “Союз-2.1а”, рассмотрено использование РН “Союз-2.1б” и “Зенит” с РБ “Фрегат”. При этом для РН “Союз” при разгоне у Земли РБ делается два включения, для РН “Зенит” – три включения РБ, с целью уменьшения гравитационных потерь. В табл. 2 приведены значения масс mf и mp для траекторий № 1a, 3а, 4а при использовании этих РН.
Таблица 2.
Конечная и полезная масса КА для траекторий № 1а, 3а, 4а с использованием разных РН
| № 1a | № 3a | № 4a | |||||||
|---|---|---|---|---|---|---|---|---|---|
| “Союз-2.1а” | “Союз-2.1б” | “Зенит” | “Союз-2.1а” | “Союз-2.1б” | “Зенит” | “Союз-2.1а” | “Союз-2.1б” | “Зенит” | |
| m0, кг | 7130 | 8250 | 14 000 | 7130 | 8250 | 14 000 | 7130 | 8250 | 14 000 |
| Вариант “Фрегата” | “Фрегат-1” | “Фрегат-2” | “Фрегат-СБ” | “Фрегат-1” | “Фрегат-2” | “Фрегат-СБ” | “Фрегат-1” | “Фрегат-3” | “Фрегат-СБ” |
| mf, кг | 492 | 604 | 1193 | 509 | 624 | 1233 | 517 | 611 | 1287 |
| mp, кг | 226 | 301 | 700 | 245 | 325 | 748 | 290 | 362 | 877 |
В основном варианте анализа полагали, что при подлете к Земле тормозной импульс скорости двигателем не сообщается, аналогично [1, 2]. КА в момент t4СД подлетит к сфере действия Земли, и дальше входит в сферу действия Земли со скоростью VСДЗ по гиперболической орбите с некоторым расстоянием условного перигея rp4. Затем КА входит в атмосферу Земли. Для оценки скорости входа Vвх в качестве границы атмосферы Земли берем ha = 125 км [1, 2]. Определена скорость Vвх для полученных оптимальных траекторий. Получается, что Vвх = 12.74, 12.32, 13.26 км/c, для траекторий № 1a, 3а, 4а, соответственно. Для оценки их технологической реализуемости сравниваются их характеристики с теми для миссий “Stardust”, “Hayabusa” и “OSIRIS-REx”, табл. 3. Опыт этих миссий показывает, что современные технологии позволяют успешно приземляться КА, который входит в атмосферу Земли с гиперболической скоростью до 12.9 км/с [1, 2]. Но самая лучшая траектория, полученная нами, № 4а не удовлетворяет этому условию. Поэтому рассмотрена еще одна задача – полная четырехпараметрическая оптимизация с ограничением на скорость входа в атмосферу Земли, Vвх ≤ Vвх max. В табл. 4 приведены результаты анализа зависимости полезной массы от Vвх (12.8–13.26 км/с). Отметим, что при этом при использовании РН “Союз-2.1б” и РН “Зенит” полезная масса остается большей, чем сухая масса КА “Stardust” (300 кг).
Таблица 3.
Характеристики миссий “Stardust”, “Hayabusa” и “OSIRIS-REx”
| Миссия | “Stardust” | “Hayabusa” | “OSIRIS-REx” |
|---|---|---|---|
| Сухая масса КА, кг | 300 | 415 | 880 |
| Скорость входа в атмосферу Земли Vвх, км/c | 12.9 | 12.5 | 12.2 |
Таблица 4.
Изменение полезной массы со скоростью Vвх
| Vвх max, км/с | 12.8 | 12.9 | 13 | 13.1 | 13.2 | 13.26 |
| mp (кг) “Союз-2.1а” | 275.3 | 280 | 284 | 287.5 | 289 | 290 |
| mp (кг) “Союз-2.1б” | 343.6 | 349 | 354 | 358 | 361 | 362 |
| mp (кг) “Зенит” | 839.6 | 852 | 861 | 869.8 | 876 | 877 |
Таким образом, выполненный анализ показывает, что существует принципиальная возможность осуществить экспедицию к астероиду Апофис в течение 2019–2022 гг. на основе существующих ракет типа “Союз”, “Зенит”.
ЗАКЛЮЧЕНИЕ
Разработана методика построения энергетически оптимальных, с максимальной полезной массой КА, траекторий для экспедиции Земля–астероид–Земля при использовании обычных двигательных установок большой тяги. Разработанная методика применена к построению оптимальных траекторий космической экспедиции Земля–Апофис–Земля, предназначенной для изучения этого опасного астероида. Получены оптимальные траектории данной экспедиции при запуске КА в течение 2019–2022 гг. с общей продолжительностью полета до двух лет. Для анализа оптимальности полученных межпланетных траекторий в классе многоимпульсных перелетов разработан алгоритм построения базис-вектора, т.е. вектора, сопряженного к вектору скорости. Построен базис-вектор для ряда решений. Выявлены качественные характеристики оптимальных траекторий: (1) возврат к Земле происходит вблизи восходящего узла орбиты Апофиса; (2) на номинальной траектории нужно не более трех импульсов скорости; (3) получен оптимальный диапазон времени ожидания у Апофиса – в пределах 3–4 мес. Результаты исследования показывают, что существует принципиальная возможность реализации космической экспедиции Земля–Апофис–Земля с использованием обычных двигателей большой тяги и РН типа “Союз”, “Зенит”.
В заключение авторы выражают искреннюю признательность сотрудникам “НПО им. С.А. Лавочкина” к. т. н. В.Г. Полю и к. т. н. А.В. Симонову, а также к.т.н. И.В. Крылову за поддержку и полезные обсуждения работы, а также участникам семинара им. В.А. Егорова в МГУ им. М.В. Ломоносова за очень полезные обсуждения проблемы и настоящей работы. Авторы признательны аспиранту Гуо Пэн за помощь в совершенствовании вычислительной программы и проведении расчетов. В.В. Ивашкин признателен проф. J. Martinez-Garcia, д-ру M. Bello-Mora, д-ру E. Revilla-Pedreira, проф. P. Sanz-Arangues и проф. T. Elices (GMV, Madrid Polytechnic University) за их поддержку исследований проблемы полета к малым небесным телам.
Список литературы
Atkins K.L., Brownlee D.E., Duxbury T. et al. STARDUST: Discovery’s InterStellar dust and cometary sample return mission // Aerospace Conference, 1997. Proceedings, IEEE. № 4. P. 229–245.
Sandford S.A. The Power of Sample Return Missions-Stardust and Hayabusa // Proceedings of the International Astronomical Union, 2011. № 7(S280). P. 275–287.
Ajluni T., Everett D., Linn T. et al. OSIRIS-REx, returning the asteroid sample // Aerospace Conference, 2015 IEEE. IEEE, 2015. P. 1–15.
Астероидо-кометная опасность: вчера, сегодня, завтра / Под ред. Шустова Б.М., Рыхловой Л.В. М.: ФИЗМАТЛИТ, 2010.
Соколов Л.Л., Башаков А.А., Борисова Т.П. и др. Траектории соударения астероида Апофис с Землей в XXI веке // Астрономический вестник. 2012. Т. 46. № 4. С. 311–320.
Автоматические космические аппараты для фундаментальных и прикладных научных исследований / Ред. Полищука Г.М. и Пичхадзе К.М. М.: Изд-во МАИ-ПРИНТ, 2010.
Ивашкин В.В., Лан А. Определение и анализ оптимальных космических траекторий для организации экспедиции Земля–Апофис–Земля с применением двигательных установок большой тяги // Космонавтика и ракетостроение. 2017. Вып 5(98). С. 63–71.
Ивашкин В.В., Лан А. Оптимальные траектории для экспедиции Земля–астероид–Земля при полете с большой тягой // Доклады Академии Наук. Т. 484. № 2. С. 161–166.
Hohmann W. Die Erreichbarkeit der Himmelskörper. München und Berlin. Druck und Verlag R.Oldenbourg. 1926.
Циолковский К.Э. Исследование мировых пространств реактивными приборами [1911–1912 гг.] // Пионеры ракетной техники. Кибальчич. Циолковский. Цандер. Кондратюк. Избранные труды. М.: Наука, 1964.
Лан Аньци. Анализ космических траекторий для экспедиции Земля–Апофис–Земля и движения космического аппарата вокруг астероида Апофис // Инженерный журн.: наука и инновации. 2017. Вып. 7.
Ивашкин В.В. Оптимизация космических маневров при ограничениях на расстояния до планет. М.: Наука, 1975.
Ильин В.А., Кузмак Г.Е. Оптимальные перелеты космических аппаратов с двигателями большой тяги. М.: Наука, 1976.
Кубасов В.Н., Дашков А.А. Межпланетные полеты. М.: Машиностроение, 1979.
Соболь И.М., Статинков Р.Б. Выбор оптимальных параметров в задачах со многим критериями. М.: Наука, 1981.
Numerical recipes in C: The art of Scientific computing / Press W.H., Teukolsky S.A., Vetterling W.T. et al. 2nd ed. Cambridge University Press, 1992.
Sobol’ I.M., Asotsky D., Kreinin A. et al. Construction and Comparison of High-Dimensional Sobol’ Generators // Wilmott J. 2012. V. 2011. Is.56. P. 64–79.
Панченко Т.В. Генетические алгоритмы: учебно-м-етодическое пособие / Под ред. Тарасевича Ю.Ю. Астрахань: Издательский дом “Астраханский университет”, 2007.
Nocedal J., Wright S.J. Numerical Optimization. USA: Springer, 2006.
Ивашкин В.В., Лан А. Анализ оптимальности траекторий экспедиции Земля–астероид–Земля. Препринты ИПМ им. М.В. Келдыша. 2017. № 113. https://doi.org/10.20948/prepr-2017-113
Lawden D.F. Optimal trajectories for space navigation. London, Butterworths. 1963.
Чарный В.И. Об изохронных производных // Искусственные спутники Земли. 1963. Вып. 16.
Pines S. Constants of the Motion for Optimum Thrust Trajectories in a Central Force Field // AIAA. 1964. V. 2. № 11. P. 2010–2014.
Lion P.M., Handelsman M. Primer Vector on Fixed-Time Impulsive Trajectories // AIAA. 1968. V. 6. № 1. P. 127–132.
Jezewski D.J., Rozendaal H.L. An Efficient Method for Calculating Optimal Free-Space N-Impulse Trajectories // AIAA. 1968. V. 6. № 11. P. 2160–2165.
Robbins H.M. An Analytical Study of the Impulsive Approximation // AIAA. 1966. V. 4. № 8. P. 1417–1423.
Захаров Ю.А. Проектирование межорбитальных космических аппаратов. М.: Машиностроение, 1984.
Хохулин В.С., Чумаков В.А. Проектирование космических разгонных блоков с ЖРД. М.: Изд-во МАИ, 2000.
Бычков А.Д., Ивашкин В.В. Проектно-баллистический анализ создания многоразовой транспортной системы Земля–Луна–Земля на основе ядерного ракетного двигателя // Космонавтика и ракетостроение. 2014. № 1. С. 68–76.
Аббасов М.Э. Методы оптимизации. СПб.: Издательство “ВВМ”, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования