Космические исследования, 2020, T. 58, № 3, стр. 199-207

Управление спутником при помощи магнитных моментов: управляемость и алгоритмы стабилизации

В. М. Морозов^1, *, В. И. Каленова¹

¹ Научно-исследовательский институт механики МГУ им. М.В. Ломоносова
г. Москва, Россия

Поступила в редакцию 13.03.2019
После доработки 25.04.2019
Принята к публикации 30.05.2019

DOI: 10.31857/S0023420620030048

Аннотация

Рассматривается стабилизация относительного равновесия спутника на круговой орбите, снабженного магнитной системой ориентации. Показано, что линеаризованная система уравнений движения относится к специальному классу линейных нестационарных систем, приводимых к стационарным. На основе приведенной стационарной системы исследована управляемость и построены работоспособные алгоритмы стабилизации. Проведено моделирование, подтверждающее эффективность предложенной методики.

ВВЕДЕНИЕ

Среди различных типов систем ориентации и стабилизации особое место занимают магнитные системы, принцип действия которых основывается на взаимодействии собственного магнитного момента спутника – управляемого или пассивного – с внешним магнитным полем. Системы магнитной ориентации широко используются в практике космических исследований, в частности, для малых спутников. Большое количество публикаций было посвящено различным аспектам проблем управления и определения ориентации спутников с помощью магнитных катушек и магнитометров (см., например, [1–18]). Обзор работ по управлению ориентацией космических аппаратов при помощи магнитных моментов, выполненных до 2003 года, содержится в [19], а более поздних работ в [20].

Линеаризованные модели рассматриваемых задач представляются линейными нестационарными системами, так как управляющий момент является функцией геомагнитного поля, которое изменяется во время движения спутника по орбите. Зависимость коэффициентов во времени вносит существенные трудности, как в изучение управляемости, так и в разработку алгоритмов управления. Среди подходов к изучению задачи управления ориентацией при помощи магнитных моментов можно выделить два основных направления.

1) Методы, основанные на осредненных моделях (см., например, [4–7, 15, 19]). Преимущество этого подхода в том, что задача управления становится стационарной. Но при этом следует удостовериться, что построенные для приближенной стационарной системы алгоритмы, действительно стабилизируют исходную нестационарную систему.

2) Методы, основанные на периодических моделях (см., например, [1, 3, 4, 10, 11, 19]). Применение этих методов обеспечивает асимптотическую устойчивость замкнутой периодической системы, которая исследуется при помощи теории Флоке. Аналитически эти методы эффективно реализовать трудно и приходится применять численные методы.

В ряде работ, посвященных задаче управления ориентацией при помощи магнитных моментов особое внимание уделено вопросам управляемости линейных нестационарных систем [13, 18, 21, 22].

Цель предлагаемой статьи – представить новый аналитический подход к изучению рассматриваемой проблемы, основанный на приводимости исходной нестационарной системы к стационарной системе большей размерности. Свойство приводимости эффективно используется как при анализе управляемости, так и при построении алгоритмов стабилизации. Для приведенной стационарной системы строится оптимальный алгоритм стабилизации, основанный на ЛКР-методе, А затем это управление при помощи конструктивного преобразования вводится в исходную нестационарную систему. Работоспособность и эффективность предлагаемых алгоритмов подтверждается математическим моделированием.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается движение спутника вокруг центра масс в гравитационном поле Земли. Предполагается, что центр масс спутника движется по круговой орбите.

Системы координат и уравнения движения. Используются две системы координат: $OXYZ$ – орбитальная система координат с началом в центе масс спутника: ось $OZ$ направлена по радиус-вектору центра масс; $OY$ – по нормали к плоскости орбиты, $OX$ дополняет систему до правой тройки; $Oxyz$– связанная система координат, оси которой направлены по главным центральным осям инерции спутника.

Ориентация системы $Oxyz$ относительно орбитальной задается с помощью углов Эйлера ${{\theta }_{1}},{{\theta }_{2}},{{\theta }_{3}}$ (последовательность поворотов 1–2–3). Матрица $\Theta $ направляющих косинусов осей системы $OXYZ$ в системе $Oxyz$ имеет вид [23]

$\begin{gathered} \Theta = \left\| {{{\Theta }_{{ij}}}} \right\|; \\ {{\Theta }_{{11}}} = \cos {{\theta }_{1}}\cos {{\theta }_{3}} - \sin {{\theta }_{1}}\sin {{\theta }_{2}}\sin {{\theta }_{3}}, \\ {{\Theta }_{{12}}} = - \sin {{\theta }_{1}}\cos {{\theta }_{2}},\,\,\,\,{{\Theta }_{{13}}} = \cos {{\theta }_{1}}\sin {{\theta }_{3}} + \\ + \,\,\sin {{\theta }_{1}}\sin {{\theta }_{2}}\cos {{\theta }_{3}},\,\,\,\,{{\Theta }_{{21}}} = \sin {{\theta }_{1}}\cos {{\theta }_{3}} + \\ + \,\,\cos {{\theta }_{1}}\sin {{\theta }_{2}}\sin {{\theta }_{3}},\,\,\,\,{{\Theta }_{{22}}} = \cos {{\theta }_{1}}\cos {{\theta }_{2}}, \\ {{\Theta }_{{23}}} = \sin {{\theta }_{1}}\sin {{\theta }_{3}} - \cos {{\theta }_{1}}\sin {{\theta }_{2}}\cos {{\theta }_{3}}, \\ {{\Theta }_{{31}}} = - \cos {{\theta }_{3}}\sin {{\theta }_{3}},\,\,\,\,{{\Theta }_{{32}}} = \sin {{\theta }_{2}}, \\ {{\Theta }_{{33}}} = \cos {{\theta }_{2}}\cos {{\theta }_{3}}. \\ \end{gathered} $

Компоненты абсолютной угловой скорости спутника ${\mathbf{\omega }}$ в проекциях на оси системы координат $Oxyz$ имеют вид

(1)

$\begin{gathered} {{\omega }_{1}} = - {{{\dot {\theta }}}_{1}}\cos {{\theta }_{2}}\sin {{\theta }_{3}} + {{{\dot {\theta }}}_{2}}\cos {{\theta }_{3}} + {{\omega }_{0}}{{\Theta }_{{21}}}, \\ {{\omega }_{2}} = {{{\dot {\theta }}}_{3}} + {{{\dot {\theta }}}_{1}}\sin {{\theta }_{2}} + {{\omega }_{0}}{{\Theta }_{{22}}}, \\ {{\omega }_{3}} = {{{\dot {\theta }}}_{1}}\cos {{\theta }_{2}}\cos {{\theta }_{3}} + {{{\dot {\theta }}}_{2}}\sin {{\theta }_{3}} + {{\omega }_{0}}{{\Theta }_{{23}}}, \\ \end{gathered} $

где ${{\omega }_{0}}$ – величина орбитальной угловой скорости.

Динамические уравнения движения спутника около центра масс имеют вид [23]

(2)

${\mathbf{J}}\frac{{d{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{J\omega }} = 3\omega _{0}^{2}({{{\mathbf{e}}}_{r}} \times {\mathbf{J}}{{{\mathbf{e}}}_{r}}) + {\mathbf{M}}.$

Здесь ${\mathbf{J}} = {\text{diag(}}\begin{array}{*{20}{c}} {{{J}_{1}}}&{{{J}_{2}}}&{{{J}_{3}}} \end{array}{\text{);}}$ ${{J}_{1}},{{J}_{2}},{{J}_{3}}$ – главные центральные моменты инерции спутника, ${{{\mathbf{e}}}_{r}}$ – единичный вектор оси $OZ$, ${\mathbf{M}}$ – управляющий момент, который создается за счет взаимодействия собственного магнитного момента спутника с магнитным полем Земли.

Управляющий момент ${\mathbf{M}}$ можно представить в виде

${\mathbf{M}} = {\mathbf{m}} \times {\mathbf{b}},$

где ${\mathbf{m}} = {{[\begin{array}{*{20}{c}} {{{m}_{1}}}&{{{m}_{2}}}&{{{m}_{3}}} \end{array}]}^{T}}$ – собственный магнитный момент спутника; ${\mathbf{b}}(t) = \Theta {{{\mathbf{b}}}_{0}}(t),$ ${{{\mathbf{b}}}_{0}}(t)$ – индукция геомагнитного поля, которое аппроксимируется прямым магнитным диполем в орбитальной системе координат [24]

${{{\mathbf{b}}}_{0}}(t) = \frac{{{{\mu }_{{\text{E}}}}}}{{{{a}^{3}}}}\left[ {\begin{array}{*{20}{c}} {\cos {{\omega }_{0}}t\sin I} \\ { - \cos I} \\ {2sin{{\omega }_{0}}t\sin I} \end{array}} \right].$

Здесь $I$ – угол наклона плоскости орбиты спутника к плоскости экватора; ${{\mu }_{{\text{E}}}} = {\text{ }}7.812\,\, \times $ $ \times \,\,{{10}^{6}}\,{\text{к}}{{{\text{м}}}^{3}}\,{\text{кг}}\,{{{\text{с}}}^{{ - 2}}}\,{{{\text{A}}}^{{ - 1}}}$ – постоянная магнитного поля Земли, $a$ – радиус орбиты.

Величины ${{m}_{1}},{{m}_{2}},{{m}_{3}}$ далее считаются управляющими воздействиями.

Линеаризованные уравнения движения. Уравнения движения (1), (2) при ${\mathbf{M}} = 0$ допускают стационарные решения, отвечающие положениям относительного равновесия спутника, в которых оси связанной системы координат $Oxyz$ совпадают с осями орбитальной системы координат $OXYZ$ [23]. Углы поворота ${{\theta }_{i}}(i = 1,2,3)$ выбраны таким образом, что в положении относительного равновесия все углы и относительные угловые скорости равны нулю

(3)

${{\theta }_{i}} = 0,\,\,\,\,{{\dot {\theta }}_{i}} = 0,\,\,\,(i = 1,2,3).$

При линеаризации уравнений движения (1), (2) в окрестности относительного равновесия (3), очевидно, линеаризуются и выражения для моментов ${\mathbf{M}} = {\mathbf{m}} \times \Theta {{{\mathbf{b}}}_{0}}(t)$, в которых управление ${\mathbf{m}}$ формируется в виде линейной обратной связи по компонентам вектора состояния ${{\theta }_{i}},{{\dot {\theta }}_{i}},\,\,(i = 1,2,3)$. Поэтому можно считать (как и в [16, 21]), что $\Theta = {{E}_{3}}$ (${{E}_{k}}$ – единичная матрица ($k \times k$)) и ${\mathbf{M}} = {\mathbf{m}} \times {{{\mathbf{b}}}_{0}}(t).$

Тогда линеаризованные уравнения управляемого движения имеют вид

(4)

$\ddot {x} + D\dot {x} + Kx = B(\tau )u.$

Здесь дифференцирование ведется по безразмерному времени $\tau = {{\omega }_{0}}t;$ $x = {{\left[ {{{x}_{1}}{{x}_{2}}{{x}_{3}}} \right]}^{T}}$ = ${{\left[ {{{\theta }_{2}}{{\theta }_{3}}{{\theta }_{1}}} \right]}^{T}}$ – малые углы рассогласования между осями орбитальной и подвижной системами координат; $m = u = {{\left[ {{{u}_{1}}{{u}_{2}}{{u}_{3}}} \right]}^{T}}.$

$D = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {{d}_{1}}} \\ 0&0&0 \\ {{{d}_{3}}}&0&0 \end{array}} \right],\,\,\,\,K = {\text{diag}}( - {{\kappa }_{1}}, - {{\kappa }_{2}}, - {{\kappa }_{3}}),$

$\begin{gathered} {{\kappa }_{1}} = 4{{({{J}_{3}} - {{J}_{2}})} \mathord{\left/ {\vphantom {{({{J}_{3}} - {{J}_{2}})} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}},\,\,\,\,{{\kappa }_{2}} = 3({{J}_{3}} - {{{{J}_{1}})} \mathord{\left/ {\vphantom {{{{J}_{1}})} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}}, \\ {{\kappa }_{3}} = ({{J}_{1}} - {{{{J}_{2}})} \mathord{\left/ {\vphantom {{{{J}_{2}})} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}},\,\,\,\,{{d}_{i}} = {d \mathord{\left/ {\vphantom {d {{{J}_{i}},}}} \right. \kern-0em} {{{J}_{i}},}}\,\,(i = 1,3), \\ d = {{J}_{2}} - {{J}_{1}} - {{J}_{3}}; \\ \end{gathered} $

$\begin{gathered} B(\tau ) = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} 0&{2{{\beta }_{1}}\sin \tau }&{{{\beta }_{4}}} \\ { - 2{{\beta }_{2}}\sin \tau }&0&{{{\beta }_{2}}\cos \tau } \\ { - {{\beta }_{5}}}&{ - {{\beta }_{3}}\cos \tau }&0 \end{array}} \right], \\ {{B}_{0}} = \frac{{{{\mu }_{{\text{E}}}}}}{{{{a}^{3}}\omega _{0}^{2}}}, \\ \end{gathered} $

$\begin{gathered} {{\beta }_{j}} = {{{\text{sin}}I} \mathord{\left/ {\vphantom {{{\text{sin}}I} {{{J}_{j}}}}} \right. \kern-0em} {{{J}_{j}}}},\,\,(j = 1,2,3); \\ {{\beta }_{4}} = {{\cos I} \mathord{\left/ {\vphantom {{\cos I} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}},\,\,\,\,{{\beta }_{5}} = {{\cos I} \mathord{\left/ {\vphantom {{\cos I} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}. \\ \end{gathered} $

Для круговой орбиты $\omega _{0}^{2} = \frac{\mu }{{{{a}^{3}}}}$, где μ = 3.986 · · 10⁵ км³ с^–2– гравитационный параметр Земли. Тогда параметр ${{B}_{0}} = \frac{{{{\mu }_{{\text{E}}}}}}{\mu }$ не зависит от радиуса орбиты.

Представим систему (4) в виде системы первого порядка

(5)

$\begin{gathered} \dot {\xi } = {{A}_{\xi }}\xi + {{B}_{\xi }}(\tau )u,\,\,\,\,\xi = {{\left[ {{{{\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{3}}}&{{{{\dot {x}}}_{1}}}&{{{{\dot {x}}}_{3}}}&{{{x}_{2}}}&{\dot {x}} \end{array}}}_{2}}} \right]}^{T}}, \\ {{A}_{\xi }} = {\text{diag}}({{A}^{{(1)}}},{{A}^{{(2)}}}), \\ \end{gathered} $

$\begin{gathered} {{A}^{{(1)}}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {{{K}^{{(1)}}}}&{ - {{D}^{{(1)}}}} \end{array}} \right],\,\,\,\,{{K}^{{(1)}}} = {\text{diag}}({{\kappa }_{1}},{{\kappa }_{3}}), \\ {{D}^{{(1)}}} = \left[ {\begin{array}{*{20}{c}} 0&{ - {{d}_{1}}} \\ {{{d}_{3}}}&0 \end{array}} \right], \\ {{A}^{{(2)}}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ {{{\kappa }_{2}}}&0 \end{array}} \right],\,\,\,\,{{B}_{\xi }}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{B}^{{(1)}}}} \\ {{{B}^{{(2)}}}} \end{array}} \right], \\ \mathop {{{B}^{{(1)}}}}\limits_{4 \times 3} = \left[ {\begin{array}{*{20}{c}} {{{O}_{{23}}}} \\ {{{B}_{1}}(\tau )} \end{array}} \right],\,\,\,\,\mathop {{{B}^{{(2)}}}}\limits_{2 \times 3} = \left[ {\begin{array}{*{20}{c}} {{{O}_{{13}}}} \\ {{{B}_{2}}(\tau )} \end{array}} \right], \\ \end{gathered} $

$\begin{gathered} {{B}_{1}} = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} 0&{2{{\beta }_{1}}\sin \tau }&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&{ - {{\beta }_{3}}\cos \tau }&0 \end{array}} \right], \\ {{B}_{2}} = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} { - 2{{\beta }_{2}}\sin \tau }&0&{{{\beta }_{2}}\cos \tau } \end{array}} \right]. \\ \end{gathered} $

Здесь ${{O}_{2}}(2 \times 2),$ ${{O}_{{k3}}}(k\,\, \times 3),(k = 1,2)$ – нулевые матрицы соответствующих размеров.

Требуется построить управление, обеспечивающее асимптотическую устойчивость выбранного положения относительного равновесия, основываясь либо на системе уравнений (4), либо (5). Аналитически построить стабилизирующее управление непосредственно для исходной системы затруднительно из-за существенной нестационарности системы (4) (5).

Предлагается подход к решению этой задачи, ранее применявшийся при исследовании ряда прикладных задач [25–27]. Этот подход состоит из следующих этапов:

1) построить конструктивное преобразование исходной нестационарной системы к стационарной системе;

2) провести анализ управляемости полученной стационарной системы;

3) при наличии управляемости построить для стационарной системы оптимальный алгоритм управления на основе квадратичного критерия качества на бесконечном интервале времени, что позволит получить линейную обратную связь с постоянными коэффициентами;

4) осуществить обратный переход к исходным переменным нестационарной системы, вводя, если это необходимо, дополнительные переменные.

ПРЕОБРАЗОВАНИЕ К СТАЦИОНАРНОЙ СИСТЕМЕ

Системы (4) и (5) относятся к классу линейных нестационарных систем, содержащих управление, которые допускают приведение к стационарным системам большей размерности [25–27]. Напомним, что этот класс систем характеризуется тем, что функции, входящие в выражение для матрицы $B(\tau )$ при управлении, являются решениями линейной однородной системы с постоянными коэффициентами.

Преобразование системы (4). В системе уравнений (4) матрицу коэффициентов при управлении, имеющую вид $B(\tau )$ = ${{B}_{{01}}}cos\tau + {{B}_{{02}}}\sin \tau + {{B}_{{03}}},$ $({{B}_{0}}_{k} = {\text{const)}}$, удобнее представить в комплексной форме

$B(\tau ) = {{\operatorname{e} }^{{i\tau }}}{{C}_{1}} + {{\operatorname{e} }^{{ - i\tau }}}{{C}_{2}} + {{C}_{3}},$

$\begin{gathered} {{C}_{1}} = \left[ {\begin{array}{*{20}{c}} 0&{ - i{\kern 1pt} {{\beta }_{1}}}&0 \\ 0&{ - 0.5{\kern 1pt} {{\beta }_{3}}}&0 \\ {i{\kern 1pt} {{\beta }_{2}}}&0&{0.5{\kern 1pt} {{\beta }_{2}}} \end{array}} \right], \\ {{C}_{2}} = \left[ {\begin{array}{*{20}{c}} 0&{i{\kern 1pt} {{\beta }_{1}}}&0 \\ 0&{ - 0.5{\kern 1pt} {{\beta }_{3}}}&0 \\ { - i{\kern 1pt} {{\beta }_{2}}}&0&{0.5{\kern 1pt} {{\beta }_{2}}} \end{array}} \right],\,\,\,{{C}_{3}} = \left[ {\begin{array}{*{20}{c}} 0&0&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&0&0 \\ 0&0&0 \end{array}} \right]. \\ \end{gathered} $

Введем следующую замену переменных

(6)

$\begin{gathered} x = F_{{}}^{T}(\tau )y,\,\,\,\,\mathop {F_{{}}^{T}(\tau )}\limits_{(3 \times 9)} = {{f}^{T}}(\tau ) \otimes {{E}_{3}}, \\ {{f}^{T}}(\tau ) = \left[ {{{e}^{{i\tau }}}{\text{,}}{{{\text{e}}}^{{ - i\tau }}},1} \right]. \\ \end{gathered} $

Символ $ \otimes $ означает кронекеровское произведение матриц [28].

Вектор новых переменных представим в виде

$\mathop y\limits_{9 \times 1} = \left[ {\begin{array}{*{20}{c}} {{{y}^{{(1)}}}} \\ {{{y}^{{(2)}}}} \\ {{{y}^{{(3)}}}} \end{array}} \right],\,\,\,\,\mathop {{{y}^{{({\text{k}})}}}}\limits_{3 \times 1} = \left[ {\begin{array}{*{20}{c}} {y_{1}^{{({\text{k}})}}} \\ {y_{2}^{{({\text{k}})}}} \\ {y_{3}^{{({\text{k}})}}} \end{array}} \right],\,\,\,\,(k = 1,2,3).$

Дифференцируя дважды соотношения (6), подставляя полученные выражения в систему (4) и приравнивая коэффициенты при независимых функциях ${{\operatorname{e} }^{{i\tau }}},{{\operatorname{e} }^{{ - i\tau }}},1,$ получим следующую стационарную систему

(7)

$\begin{gathered} {{{\ddot {y}}}^{{(k)}}} + {{D}_{k}}{{{\dot {y}}}^{{(k)}}} + {{K}_{k}}{{y}^{{(k)}}} = {{C}_{k}}u, \\ {{D}_{1}} = D{\text{ + 2}}i{{E}_{3}}{\text{;}}\,\,\,\,{{D}_{2}} = D - {\text{2}}i{{E}_{3}}{\text{;}}\,\,\,{{D}_{3}} = D; \\ {{K}_{1}} = K{\text{ + }}iD - {{E}_{3}}{\text{;}}\,\,\,{{K}_{2}} = K - iD - {{E}_{3}}{\text{;}}\,\,\,\,{{K}_{3}} = K. \\ \end{gathered} $

Стационарная система (7) избыточна: каждой компоненте исходного вектора $x$ соответствуют три компоненты расширенного вектора состояния $y$. Система (7) состоит из трех независимых подсистем, относительно переменных ${{z}^{{(1)}}};{{z}^{{(2)}}};{{z}^{{(3)}}}$:

$\begin{gathered} {{z}^{{(1)}}} = {{\left[ {\begin{array}{*{20}{c}} {y_{1}^{{(1)}}}&{y_{2}^{{(1)}}}&{y_{1}^{{(2)}}}&{y_{2}^{{(2)}}} \end{array}} \right]}^{T}}, \\ {{z}^{{(2)}}} = {{\left[ {\begin{array}{*{20}{c}} {y_{3}^{{(1)}}}&{y_{3}^{{(3)}}}&{y_{1}^{{(3)}}}&{y_{2}^{{(3)}}} \end{array}} \right]}^{T}},\,\,\,\,{{z}^{{(3)}}} = y_{3}^{{(3)}}, \\ \end{gathered} $

(8)

${{\ddot {z}}^{{(1)}}} + {{G}_{1}}{{\dot {z}}^{{(1)}}} + {{R}_{1}}{{z}^{{(1)}}} = {{C}^{{(1)}}}{{u}_{2}}$

(9)

${{\ddot {z}}^{{(2)}}} + {{G}_{2}}{{\dot {z}}^{{(2)}}} + {{R}_{2}}{{z}^{{(2)}}} = {{C}^{{(2)}}}\tilde {u},\,\,\,\,\tilde {u} = {{\left[ {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{3}}} \end{array}} \right]}^{{\text{T}}}},$

(10)

${{\ddot {z}}^{{(3)}}} - {{\kappa }_{2}}{{z}^{{(3)}}} = 0,$

$\begin{gathered} {{G}_{1}} = {\text{diag}}({{G}_{{11}}},{{G}_{{12}}}),\,\,\,\,{{R}_{1}} = {\text{diag}}({{R}_{{11}}},{{R}_{{12}}}), \\ {{G}_{{11}}} = \left[ {\begin{array}{*{20}{c}} {2i}&{ - {{d}_{1}}} \\ {{{d}_{3}}}&{2i} \end{array}} \right],\,\,\,\,{{G}_{{12}}} = \left[ {\begin{array}{*{20}{c}} { - 2i}&{ - {{d}_{1}}} \\ {{{d}_{3}}}&{ - 2i} \end{array}} \right], \\ {{R}_{{11}}} = \left[ {\begin{array}{*{20}{c}} { - {{{\bar {\kappa }}}_{1}}}&{ - i{{d}_{1}}} \\ {i{{d}_{3}}}&{ - {{{\bar {\kappa }}}_{3}}} \end{array}} \right],\,\,\,\,{{R}_{{12}}} = \left[ {\begin{array}{*{20}{c}} { - {{{\bar {\kappa }}}_{1}}}&{i{{d}_{1}}} \\ { - i{{d}_{3}}}&{ - {{{\bar {\kappa }}}_{3}}} \end{array}} \right], \\ \end{gathered} $

$\begin{gathered} {{G}_{2}} = {\text{diag}}({{G}_{{21}}},{{G}_{{22}}}),\,\,\,\,{{R}_{2}} = {\text{diag}}( - {{{\bar {\kappa }}}_{2}}, - {{{\bar {\kappa }}}_{2}}, - {{\kappa }_{1}}, - {{\kappa }_{3}}), \\ {{{\bar {\kappa }}}_{j}} = {{\kappa }_{j}} + 1, \\ {{G}_{{21}}} = \left[ {\begin{array}{*{20}{c}} {2i}&0 \\ 0&{ - 2i} \end{array}} \right],\,\,\,\,{{G}_{{22}}} = \left[ {\begin{array}{*{20}{c}} 0&{ - {{d}_{1}}} \\ {{{d}_{3}}}&0 \end{array}} \right], \\ \end{gathered} $

${{С}^{{(1)}}} = \left[ {\begin{array}{*{20}{c}} { - i{\kern 1pt} {{\beta }_{1}}} \\ { - 0.5{\kern 1pt} {{\beta }_{3}}} \\ {i{\kern 1pt} {{\beta }_{1}}} \\ { - 0.5{{\beta }_{3}}} \end{array}} \right],\,\,\,\,{{С}^{{(2)}}} = \left[ {\begin{array}{*{20}{c}} {i{\kern 1pt} {{\beta }_{2}}} \\ { - i{\kern 1pt} {{\beta }_{2}}} \\ 0 \\ { - {{\beta }_{5}}} \end{array}\begin{array}{*{20}{c}} {0.5{\kern 1pt} {{\beta }_{2}}} \\ {0.5{\kern 1pt} {{\beta }_{2}}} \\ {{{\beta }_{4}}} \\ 0 \end{array}} \right].$

Система (8) содержит только компоненту управления ${{u}_{2}}$, система (9) – компоненты ${{u}_{1}},{{u}_{3}}$. Переменная $z_{{}}^{{(3)}}$, очевидно, неуправляема, и можно положить $z_{{}}^{{(3)}}(\tau ) \equiv 0.$

Преобразование системы (5). Введем следующую замену переменных

(11)

$\begin{gathered} \xi = {{e}^{{i\tau }}}{{\eta }^{{(1)}}} + {{e}^{{ - i\tau }}}{{\eta }^{{(2)}}} + {{\eta }^{{(3)}}}, \\ \xi (6 \times 1),{{\eta }^{{(k)}}}(6 \times 1),\,\,\,\,(k = 1,2,3), \\ \end{gathered} $

которая приводит систему (5) к стационарной системе

(12)

$\dot {\eta } = {{A}_{{^{\eta }}}}\eta + {{B}_{\eta }}u.$

Стационарная система (12), аналогично системе (7), может быть записана в виде трех независимых подсистем

(13)

$\begin{gathered} {{{\dot {\zeta }}}^{{(1)}}} = A_{\zeta }^{{(1)}}{{\zeta }^{{(1)}}} + B_{\zeta }^{{(1)}}{{u}_{2}}, \\ \mathop {{{\zeta }^{{(1)}}}}\limits_{8 \times 1} = {{[\eta _{1}^{{(1)}}\eta _{2}^{{(1)}}\eta _{3}^{{(1)}}\eta _{4}^{{(1)}}\eta _{1}^{{(2)}}\eta _{2}^{{(2)}}\eta _{3}^{{(2)}}\eta _{4}^{{(2)}}]}^{{\text{T}}}}, \\ \end{gathered} $

(14)

$\begin{gathered} {{{\dot {\zeta }}}^{{(2)}}} = A_{\zeta }^{{(2)}}{{\zeta }^{{(2)}}} + B_{\zeta }^{{(2)}}\tilde {u}, \\ \mathop {{{\zeta }^{{(2)}}}}\limits_{8 \times 1} = {{[\eta _{5}^{{(1)}}\eta _{6}^{{(1)}}\eta _{5}^{{(2)}}\eta _{6}^{{(2)}}\eta _{1}^{{(3)}}\eta _{2}^{{(3)}}\eta _{3}^{{(3)}}\eta _{4}^{{(3)}}]}^{{\text{T}}}}, \\ \end{gathered} $

(15)

${{\dot {\zeta }}^{{(3)}}} = A_{\zeta }^{{(3)}}{{\zeta }^{{(3)}}},\,\,\,\,{{\mathop \zeta \limits_{2 \times 1} }^{{(3)}}} = {{[\eta _{5}^{{(3)}}\eta _{6}^{{(3)}}]}^{{\text{T}}}},$

$\begin{gathered} A_{\zeta }^{{(1)}} = {\text{diag}}(A_{{11}}^{{(1)}},A_{{12}}^{{(1)}}),\,\,\,\,\mathop {A_{{11}}^{{(1)}}}\limits_{4 \times 4} = - i{{E}_{4}} + {{L}^{{(1)}}}, \\ \mathop {A_{{12}}^{{(1)}}}\limits_{4 \times 4} = i{{E}_{4}} + {{L}^{{(1)}}},\,\,\,\,{{L}^{{(1)}}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right], \\ {{L}_{{21}}} = \left[ {\begin{array}{*{20}{c}} {{{\kappa }_{1}}}&0 \\ 0&{{{\kappa }_{3}}} \end{array}} \right],\,\,\,\,{{L}_{{22}}} = \left[ {\begin{array}{*{20}{c}} 0&{{{d}_{1}}} \\ { - {{d}_{3}}}&0 \end{array}} \right], \\ \end{gathered} $

$\begin{gathered} A_{\zeta }^{{(2)}} = {\text{diag}}(A_{{11}}^{{(2)}},A_{{12}}^{{(2)}}), \\ \mathop {A_{{11}}^{{(2)}}}\limits_{4 \times 4} = {\text{diag}}( - i{{E}_{2}} + {{L}^{{(2)}}},i{{E}_{2}} + {{L}^{{(2)}}}), \\ {{L}^{{(2)}}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ {{{\kappa }_{2}}}&0 \end{array}} \right],\,\,\,\mathop {A_{{12}}^{{(2)}}}\limits_{4 \times 4} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right],\,\,\,\mathop {A_{{}}^{{(3)}}}\limits_{2 \times 2} = {{L}^{{(2)}}}, \\ \end{gathered} $

$\begin{gathered} {{\left( {\mathop {B_{\zeta }^{{(1)}}}\limits_{1 \times 8} } \right)}^{{\text{T}}}} = [\begin{array}{*{20}{c}} 0&0&{ - i{\kern 1pt} {{\beta }_{1}}}&{ - 0.5{\kern 1pt} {{\beta }_{3}}}&0&0&{i{{\beta }_{1}}}&{ - 0.5{\kern 1pt} {{\beta }_{3}}} \end{array}], \hfill \\ {{\left( {\mathop {B_{\zeta }^{{(2)}}}\limits_{2 \times 8} } \right)}^{{\text{T}}}} = \left[ {\begin{array}{*{20}{c}} 0&{i{\kern 1pt} {{\beta }_{2}}}&0&{ - i{\kern 1pt} {{\beta }_{2}}}&0&0&0&{ - {{\beta }_{5}}} \\ 0&{0.5{\kern 1pt} {{\beta }_{2}}}&0&{0.5{\kern 1pt} {{\beta }_{2}}}&0&0&{{{\beta }_{4}}}&0 \end{array}} \right]. \hfill \\ \end{gathered} $

Переменные $\zeta _{{}}^{{(3)}}$, очевидно, неуправляемы, и можно (как и в системе (10)) положить $\zeta _{{}}^{{(3)}}(\tau ) \equiv 0$.

УПРАВЛЯЕМОСТЬ

Управляемость в данной задаче можно исследовать, как исходя из анализа нестационарных систем (4), (5), так и анализируя стационарные системы (8), (9) или (13), (14). Как уже указывалось, стационарные системы являются избыточными по отношению к исходной системе. Если стационарная система управляема, то управляема исходная нестационарная система. Однако неуправляемость стационарной системы может и не повлечь неуправляемость исходной нестационарной системы.

Управляемость стационарной системы (8), (9). Рассмотрим стационарную систему (8), (9). Вектор ${{z}^{{(2)}}}$ содержат компоненты $y_{3}^{{(1)}},y_{3}^{{(3)}},y_{1}^{{(3)}},y_{2}^{{(3)}}$, которые включают в себя все компоненты исходного вектора состояния ${{x}_{1}},{{x}_{2}},{{x}_{3}}$. Поэтому если система (9) окажется управляемой при помощи управлений ${{u}_{1}},{{u}_{3}}$, то систему (8) рассматривать нет необходимости, считая ${{u}_{2}} = 0$. В этом случае можно положить $z_{{}}^{{(1)}}(\tau ) \equiv 0$ и из формул (7) следует

(16)

${{x}_{1}} = y_{1}^{{(3)}},\,\,\,\,{{x}_{3}} = y_{2}^{{(3)}},\,\,\,\,{{x}_{2}} = y_{3}^{{(1)}}{{{\text{e}}}^{{i\tau }}} + y_{3}^{{(2)}}{{{\text{e}}}^{{ - i\tau }}}.$

Предположим, что орбита спутника не является ни экваториальной, ни полярной, т.е. $\sin I \ne 0,$ $\cos I \ne 0$ и исследуем управляемость стационарной системы (9). Необходимым и достаточным условием управляемости является условие [29]

(17)

$\begin{gathered} {\text{rank}}U = 4\,\,\,\,{\text{для}}\,\,\,\,\forall \lambda , \\ U = [{{\lambda }^{2}}{{E}_{4}} + {{G}_{2}}\lambda + {{R}_{2}} \vdots {{C}^{{(2)}}}]. \\ \end{gathered} $

Можно показать, что это условие нарушается при $\lambda = 0$, что имеет место при ${{\kappa }_{2}} + 1 = 0$ и либо ${{\kappa }_{1}} = 0$, либо ${{\kappa }_{3}} = 0$, т.е. при

(18)

$1)\,\,\,\,{{J}_{1}} = {{J}_{2}} = \frac{3}{2}{{J}_{3}}\,\,\,\,{\text{либо}}$

(19)

$2)\,\,{{J}_{2}} = {{J}_{3}} = \frac{3}{4}{{J}_{1}}.$

В этих случаях в системе (9) существуют линейные интегралы, не зависящие от управления, что подтверждает неуправляемость системы [25].

Очевидно, что условия неуправляемости системы (13), (14), эквивалентной системе (8), (9), имеют тот же вид (18), (19).

Управляемость нестационарной системы. Система (5), согласно критерию [30], управляема, если можно указать такую точку $\tau {\text{*}}$, в которой

(20)

${\text{rank}}{{U}_{1}}(\tau *) = 6,$

$\begin{gathered} {{U}_{1}}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{W}_{1}}(\tau )}&{...}&{{{W}_{6}}(\tau )} \end{array}} \right],\,\,\,\,{{W}_{1}}(\tau ) = \tilde {B}(\tau ), \\ {{W}_{k}}(\tau ) = {{A}_{\xi }}(\tau ){{W}_{{k - 1}}}(\tau ) - {{{\dot {W}}}_{{k - 1}}}(\tau ),\,\,\,(k = 2,...,6), \\ \end{gathered} $

$\begin{gathered} \tilde {B}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{{\tilde {B}}}_{1}}} \\ {{{{\tilde {B}}}_{2}}} \end{array}} \right],\,\,\,\,{{{\tilde {B}}}_{1}} = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} 0&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&0 \end{array}} \right], \\ {{{\tilde {B}}}_{2}} = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} { - 2{{\beta }_{2}}\sin \tau }&{{{\beta }_{2}}\cos \tau } \end{array}} \right]. \\ \end{gathered} $

Матрица ${{U}_{1}}(\tau )$ имеет вид

${{U}_{1}}(\tau ) = \left[ {\begin{array}{*{20}{c}} 0&0&0&{{{\beta }_{4}}}&{ - {{d}_{1}}{{\beta }_{5}}}&0&0&{{{l}_{{26}}}{\kern 1pt} {{\beta }_{4}}} \\ 0&{{{\beta }_{4}}}&{ - {{d}_{1}}{{\beta }_{5}}}&0&0&{{{l}_{{26}}}{\kern 1pt} {{\beta }_{4}}}&{{{l}_{{27}}}{{\beta }_{5}}}&0 \\ 0&0&{ - {{\beta }_{5}}}&0&0&{ - {{d}_{3}}{\kern 1pt} {{\beta }_{4}}}&{{{l}_{{45}}}{\kern 1pt} {{\beta }_{5}}}&0 \\ { - {{\beta }_{5}}}&0&0&{ - {{d}_{4}}{{\beta }_{4}}}&{{{l}_{{45}}}{{\beta }_{5}}}&0&0&{{{l}_{{48}}}{{\beta }_{4}}} \\ 0&0&{ - 2{{\beta }_{2}}s}&{{{\beta }_{2}}c}&{4{{\beta }_{2}}c}&{2{{\beta }_{2}}s}&{2{{l}_{{57}}}{{\beta }_{2}}s}&{{{l}_{{58}}}{\kern 1pt} {{\beta }_{2}}c} \\ { - 2{{\beta }_{2}}s}&{{{\beta }_{2}}c}&{2{{\beta }_{2}}s}&{{{\beta }_{2}}s}&{2{{l}_{{65}}}{\kern 1pt} {{\beta }_{2}}s}&{{{l}_{{66}}}{{\beta }_{2}}c}&{2{{l}_{{67}}}{{\beta }_{2}}c}&{{{l}_{{68}}}{\kern 1pt} {{\beta }_{2}}s} \end{array}} \right].$

Здесь $s = sin\tau ,\,\,с = \cos \tau .$

$\begin{gathered} {{l}_{{26}}} = - {{d}_{1}}{{d}_{3}} + {{\kappa }_{1}},\,\,\,\,{{l}_{{45}}} = {{d}_{1}}{{d}_{3}} - {{\kappa }_{3}}, \\ {{l}_{{48}}} = - {{d}_{3}}({{l}_{{26}}} + {{\kappa }_{3}}),\,\,\,\,{{l}_{{65}}} = - {{l}_{{66}}} = 1 - {{\kappa }_{2}}, \\ {{l}_{{27}}} = {{d}_{1}}({{l}_{{45}}} - {{\kappa }_{1}}),\,\,\,\,{{l}_{{57}}} = 2 + {{l}_{{65}}}, \\ {{l}_{{67}}} = {{l}_{{68}}} = 2{{\kappa }_{2}} - {{l}_{{65}}},\,\,\,\,{{l}_{{58}}} = {{l}_{{66}}} - 2. \\ \end{gathered} $

Можно показать, что определитель матрицы, составленный из 6 независимых столбцов ${{U}_{1}}(\tau )$, представляется в виде

$\Delta = {{h}_{0}} + {{h}_{1}}\cos 2\tau ,$

где ${{h}_{0}},{{h}_{1}}$ – постоянные величины, зависящие от параметров системы.

Условием неуправляемости является одновременное выполнение равенств ${{h}_{0}} = 0$ и ${{h}_{1}} = 0.$

При выполнении условия (19) определитель матрицы ${{U}_{1}}(\tau )$, составленной из первых шести столбцов, обращается в нуль. Однако, если выбрать другие 6 независимых столбцов матрицы ${{U}_{1}}(\tau )$, а именно: 1, …, 5, 7, то нетрудно показать, что при выполнении условия (4.4) $\Delta (\tau *) \ne 0.$

Таким образом, нестационарная система (5) управляема при любых значениях моментов инерции спутника, несмотря на то, что соответствующая стационарная система, не является полностью управляемой.

Замечание. В работе [22] указаны лишь достаточные условия управляемости системы (5) для любой неэкваториальной орбиты, имеющие вид

(21)

$\begin{gathered} {{J}_{3}} \ne {{J}_{2}}, \\ {{J}_{2}}({{J}_{1}} - {{J}_{2}} + {{J}_{3}}) \ne 6{{J}_{3}}({{J}_{3}} - {{J}_{1}}). \\ \end{gathered} $

Эти же условия повторены в [13].

Однако, если тензор инерции спутника – шаровой (${{J}_{1}} = {{J}_{2}} = {{J}_{3}}$, т.е. ${{\kappa }_{i}} = 0$), то ${{h}_{0}} \ne 0,{{h}_{1}} \ne 0$, и условия управляемости (20) выполнены, т.е. управляемость имеет место, несмотря на то, что условия (21) нарушаются.

АЛГОРИТМ ПОСТРОЕНИЯ СТАБИЛИЗИРУЮЩЕГО ПРАВЛЕНИЯ

Анализ управляемости, проведенный в п. 4, показал, что система (9) управляема, за исключением случаев (18), (19). Система (14) содержит комбинации всех исходных переменных, и алгоритм стабилизации строится на ее основании, в предположении, что условия (18), (19) не выполнены.

Система (14) записана в комплексной форме. Для построения алгоритма стабилизации удобнее представить ее в действительной форме, вводя следующие переменные

(22)

$\begin{gathered} {{v}_{1}} = \eta _{1}^{{(3)}},\,\,\,\,{{v}_{2}} = \eta _{2}^{{(3)}},\,\,\,\,{{v}_{3}} = \eta _{3}^{{(3)}},\,\,\,\,{{v}_{4}} = \eta _{4}^{{(3)}}, \\ {{v}_{5}} = \eta _{5}^{{(1)}} + \eta _{5}^{{(2)}},\,\,\,\,{{v}_{6}} = \eta _{6}^{{(1)}} + \eta _{6}^{{(2)}}, \\ {{v}_{7}} = i(\eta _{5}^{{(1)}} - \eta _{5}^{{(2)}}),\,\,\,\,{{v}_{8}} = i(\eta _{6}^{{(1)}} - \eta _{6}^{{(2)}}), \\ \end{gathered} $

которые удовлетворяют системе уравнений

(23)

$\dot {v} = {{A}_{v}}v + {{B}_{v}}\tilde {u},$

$\begin{gathered} {{A}_{v}} = {\text{diag}}({{A}_{{v1}}},{{A}_{{v2}}});\,\,\,\,{{A}_{{v1}}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {{{K}^{{(1)}}}}&{ - {{D}^{{(1)}}}} \end{array}} \right], \\ {{A}_{{v2}}} = \left[ {\begin{array}{*{20}{c}} {{{A}^{{(2)}}}}&{ - {{E}_{2}}} \\ {{{E}_{2}}}&{{{A}^{{(2)}}}} \end{array}} \right], \\ {{B}_{v}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}} \\ {{{B}_{2}}} \\ {{{B}_{3}}} \\ {{{B}_{4}}} \end{array}} \right],\,\,\,\,{{B}_{2}} = \left[ {\begin{array}{*{20}{c}} 0&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&0 \end{array}} \right], \\ {{B}_{3}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{{{\beta }_{2}}} \end{array}} \right],\,\,\,\,{{B}_{4}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ { - 2{{\beta }_{2}}}&0 \end{array}} \right]. \\ \end{gathered} $

Задача стабилизации стационарной управляемой системы (23) состоит в том, чтобы построить управление $\tilde {u}$, обеспечивающее стремление к нулю компонент вектора состояния $v(\tau )$ при $\tau \to \infty .$ Стабилизирующее управление строится в виде обратной связи по состоянию, а матрица коэффициентов управления ${{K}_{v}}(2 \times 8) = {\text{const}}$ выбирается из условия минимума квадратичного функционала

$J = \frac{1}{2}\int\limits_0^\infty {\left[ {{{v}^{{\text{T}}}}(\tau )Qv(\tau ) + {{{\tilde {u}}}^{{\text{T}}}}(\tau )\Gamma \tilde {u}(\tau )} \right]} d\tau .$

Здесь $Q\;\;{\text{и}}\;\;\Gamma $ – положительно определенные постоянные матрицы размерности $8 \times 8\,\,{\text{и}}\,\,2 \times 2$ соответственно.

Оптимальное управление имеет вид [31]

(24)

$\tilde {u}(\tau ) = - {{K}_{v}}v(\tau ),\,\,\,\,{{K}_{v}} = {{\Gamma }^{{ - 1}}}{{B}_{v}}P.$

Матрица $P$ размерности $8 \times 8$ является положительно определенным решением матричного алгебраического уравнения Риккати

$P{{A}_{v}} + A_{v}^{{\text{T}}}P - P{{B}_{v}}{{\Gamma }^{{ - 1}}}B_{v}^{{\text{T}}}P + Q = 0.$

Синтезированное управляющее воздействие является функцией переменных $v(\tau )$ стационарной системы (24) более высокого порядка, чем исходная нестационарная система (5). Для введения управления непосредственно в исходную систему (5) следует выразить вектор $v(\tau )(8 \times 1)$ через исходный вектор состояния $\xi (6 \times 1),$ дополненный вектором $\xi {\kern 1pt} ' = {{[{{\xi }_{7}}{{\xi }_{8}}]}^{{\text{T}}}}$ так, чтобы матрица $T$ преобразования [24, 25]

(25)

$\tilde {\xi } = Tv\,\,\,\,\left( {\tilde {\xi } = {{{[\xi \xi {\kern 1pt} ']}}^{{\text{T}}}}} \right)$

была невырожденной.

Компоненты вектора $\tilde {\xi }$ связаны с компонентами вектора состояния стационарной системы (23) соотношениями

(26)

$\begin{gathered} {{x}_{1}} = {{\xi }_{1}} = {{v}_{1}},\,\,\,\,{{x}_{3}} = {{\xi }_{2}} = {{v}_{2}}, \\ {{{\dot {x}}}_{1}} = {{\xi }_{3}} = {{v}_{3}},\,\,\,\,{{{\dot {x}}}_{3}} = {{\xi }_{4}} = {{v}_{4}}, \\ {{x}_{2}} = {{\xi }_{5}} = {{v}_{5}}\cos \tau + {{v}_{7}}\sin \tau , \\ {{{\dot {x}}}_{2}} = {{\xi }_{6}} = {{v}_{6}}\cos \tau + {{v}_{8}}\sin \tau , \\ {{\xi }_{7}} = - {{v}_{5}}\sin \tau + {{v}_{7}}\cos \tau , \\ {{\xi }_{8}} = - {{v}_{6}}\sin \tau + {{v}_{8}}\cos \tau . \\ \end{gathered} $

Матрица преобразования имеет вид

$\begin{gathered} T(\tau ) = {\text{diag}}({{T}_{1}},{{T}_{2}}), \\ {{T}_{1}} = {{E}_{4}},\,\,\,{{T}_{2}}(\tau ) = \left\| {\begin{array}{*{20}{c}} {\cos \tau {{E}_{2}}}&{\sin \tau {{E}_{2}}} \\ { - \sin \tau {{E}_{2}}}&{\cos \tau {{E}_{2}}} \end{array}} \right\|. \\ \end{gathered} $

Уравнения для дополнительного вектора $\xi {\kern 1pt} ' = {{[{{\xi }_{7}}{{\xi }_{8}}]}^{{\text{T}}}}$ имеют вид

(27)

$\begin{gathered} \dot {\xi }{\kern 1pt} ' = {{A}^{{(2)}}}\xi '{\kern 1pt} \,\, + B{\kern 1pt} '(\tau )\tilde {u}, \\ B{\kern 1pt} '(\tau ) = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} { - 2{{\beta }_{2}}\cos \tau }&{{{\beta }_{2}}\sin \tau } \end{array}} \right]. \\ \end{gathered} $

Тогда уравнение для вектора $\tilde {\xi }$ можно записать в виде

(28)

$\begin{gathered} \dot {\tilde {\xi }} = {{{\tilde {A}}}_{\xi }}\tilde {\xi } + {{{\tilde {B}}}_{\xi }}(\tau )\tilde {u}, \\ {{{\tilde {A}}}_{\xi }} = {\text{diag}}({{A}^{{(1)}}},{{A}^{{(2)}}},{{A}^{{(2)}}}),\,\,\,{{{\tilde {B}}}_{\xi }} = {{B}_{0}}\left\| {\begin{array}{*{20}{c}} {{{B}^{{(1)}}}(\tau )} \\ {{{B}^{{(2)}}}(\tau )} \\ {B{\kern 1pt} {\text{'}}(\tau )} \end{array}} \right\|. \\ \end{gathered} $

Нестационарная система (28) включает в себя исходную систему (5), в качестве подсистемы. Управление (24), построенное для стационарной системы (23) можно вводить в систему (28), используя выражения (25), в виде

$\tilde {u} = - {{K}_{v}}{{T}^{{ - 1}}}(\tau )\tilde {\xi }{\kern 1pt} .$

Замкнутая этим управлением система имеет вид

(29)

$\dot {\tilde {\xi }} = \left( {{{{\tilde {A}}}_{\xi }} - {{{\tilde {B}}}_{\xi }}(\tau ){{K}_{y}}{{T}^{{ - 1}}}(\tau )} \right)\tilde {\xi }{\kern 1pt} .$

Решения $\tilde {\xi }(\tau )$ системы (29), содержащие компоненты исходного вектора $\xi (\tau ),$ стремятся к нулю при $\tau \to \infty $, в силу выбора матрицы ${{K}_{v}}$, так как компоненты вектора $\tilde {\xi }$ связаны с компонентами вектора $v$ ограниченным преобразованием (25).

МОДЕЛИРОВАНИЕ

Моделирование проводилось в пакете M-ATLAB 7.1. Коэффициенты вычислялись и использованием стандартной программы ЛКР для стационарной системы восьмого порядка (23). Характеристики квадратичного функционала $\Theta = \gamma {{E}_{8}},$ $\Gamma = \alpha {{E}_{2}}.$

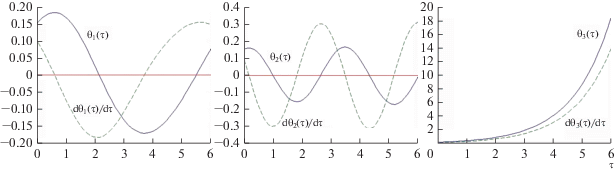
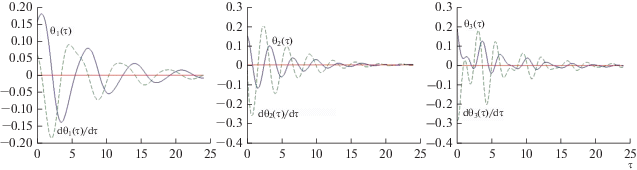
На рис. 1, 2 представлено поведение переменных ${{\theta }_{i}},{{d{{\theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\theta }_{i}}} {d\tau }}} \right. \kern-0em} {d\tau }},\,\,(i = 1,2,3)$ (сплошными линиями описывается поведение углов, пунктирными – скоростей) в отсутствии управления (${{u}_{i}} = 0$) и при его наличии. При следующих значениях параметров ИСЗ: ${{J}_{1}} = 2.5\,\,{\text{кг}}\,{{{\text{м}}}^{2}},$ ${{J}_{2}} = 5.8\,\,{\text{кг}}\,{{{\text{м}}}^{2}},$${{J}_{3}} = 3.6\,\,{\text{кг}}\,{{{\text{м}}}^{2}}$ [11] (неустойчивое положение относительного равновесия). Угол наклона орбиты $I = 60^\circ .$ Величины $\gamma = 1.0,$ $\alpha = 1.0$. Начальные отклонения по углам 0.15, 0.15, 0.2 по скоростям 0.1, 0.1, 0.15.

Рис. 1.

${{u}_{i}} = 0$.

Рис. 2.

${{u}_{i}} \ne 0$.

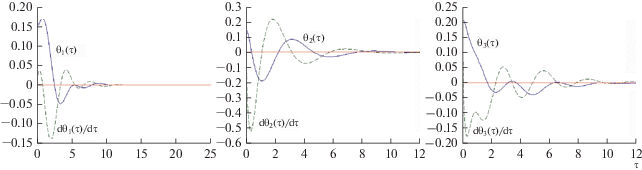
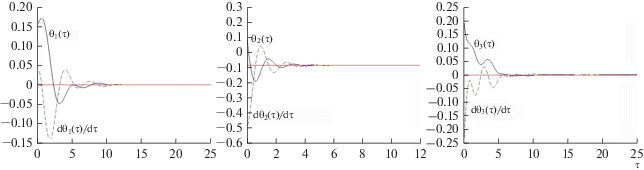
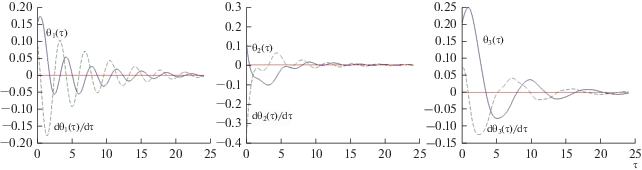
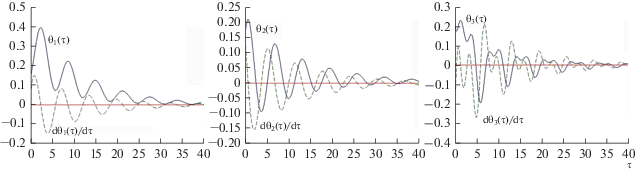
На рис. 3–5 представлено поведение тех же переменных при наличии управления для различных углов наклона орбиты: $I = 60^\circ ,$ $I = 15^\circ ,$ $I = 82.5^\circ .$ При следующих значениях параметров ИСЗ: ${{J}_{1}} = 3.6\,\,{\text{кг}}\,{{{\text{м}}}^{2}},$ ${{J}_{2}} = 5.8\,\,{\text{кг}}\,{{{\text{м}}}^{2}},$ ${{J}_{3}} = 2.5\,\,{\text{кг}}\,{{{\text{м}}}^{2}}$ [11]. Величины $\gamma = 1.0,$ $\alpha = 0.0001.$

Рис. 3.

$I = 60^\circ {\text{.}}$

Рис. 4.

$I = 15^\circ {\text{.}}$

Рис. 5.

$I = 82.5^\circ .$

Анализ приведенных графиков показывает, что время процесса стабилизации увеличивается при движении по орбитам, близким к экваториальным или полярным.

На рис. 6 представлено поведение переменных ${{\theta }_{i}},{{d{{\theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\theta }_{i}}} {d\tau ,}}} \right. \kern-0em} {d\tau ,}}$ $(i = 1,2,3)$ при наличии управления в том случае, когда тензор инерции ИСЗ – шаровой. При следующих значениях параметров: ${{J}_{1}} = {{J}_{2}} = {{J}_{3}} = 130\,\,{\text{кг}}\,{{{\text{м}}}^{2}}$ [15]; $I = 97.8^\circ ;$ $\gamma = 1.0,$ $\alpha = 0.0001.$

Рис. 6.

${{J}_{1}} = {{J}_{2}} = {{J}_{3}}.$

Моделирование показало, что процесс стабилизации практически не зависит от характера устойчивости относительного равновесия спутника.

ЗАКЛЮЧЕНИЕ

Показано, что линеаризованная в окрестности положения относительного равновесия система уравнений движения спутника относится к специальному классу линейных нестационарных систем, допускающих приведение к стационарным системам большей размерности. Указано соответствующее конструктивное преобразование. На основе полученной стационарной системы исследована управляемость и построены работоспособные алгоритмы стабилизации. Проведено моделирование, подтверждающее эффективность предложенной методики.

Список литературы

Pittelkau M.E. Optimal Periodic Control for Spacecraft Pointing and Attitude Determination // J. Guidance, Control, and Dynamics. 1993. V. 16. № 6. P. 1078–1084.
Arduini C., Baiocco P. Active Magnetic Damping Attitude Control for Gravity Gradient Stabilized Spacecraft // J. Guidance, Control, and Dynamics. V. 20. № 1. 1997. P. 117–122.
Psiaki M. Magnetic Torque Attitude Control via Asymptotic Periodic Linear Quadratic Regulation // J. Guidance, Control, and Dynamics. 2001. V. 24. № 2. P. 386–304.
Lovera M., De Marchi E., Bittanti S. Periodic Attitude Control Techniques for Small Satellites With Magnetic Actuators // IEEE Trans. On Control Systems Technology2002. V. 10. № 1. P. 90–95.
Lovera M., Astolfi A. Spacecraft Attitude Control Using Magnetic Actuators // Automatica. 2004. V. 40. P. 1405–1414.
Lovera M., Astolfi A. Global Magnetic Attitude Control of Spacecraft in the Presence of Gravity Gradient // IEEE Trans. On Aerospace and Electronic Sysyems. 2006. V. 12. P. 796–805.
Rehanoglu M., Hervas J.R. Three-axis Magnetic Attitude Control Algorithm for Small Satellites // In Proc. of the 5th Int. Conf. on Recent Advance Technologies. Istanbul. 2011. P. 897–902.
Rodriquez-Vazquez A.L., Martin-Prats M.A., Bernelli-Zazzera F. Spacecraft Magnetic Attitude Control Using Approximating Sequence Riccati Equations // IEEE Trans. Aerospace and Elerctronic Systems. 2015. V. 51 № 4. P. 3374–3385.
Ovchinnikov M.Yu., Roldugin D.S., Ivanov D.S., Penkov V.I. Choosing Control Parameters for Three Axis Magnetic Stabilization in Orbital Frame // Acta Astronau-tica. 2015. V. 116. P. 74–77.
Овчинников М.Ю., Пеньков В.И., Ролдугин Д.С., Иванов Д.С. Магнитные системы ориентации малых спутников. М.: ИПМ им. М.В. Келдыша, 2016. doi:10.20948/mono-2016-ovchinnikov
Ivanov D.S., Ovchinnikov M.Yu., Penkov V.I. et al. Advanced Numerical Study of the Three-axis Magnetic Attitude Control and Determination with Uncertainties // Acta Astronautica. 2017. V. 132. P. 103–110.
Zhou K., Huang H., Wang X., Sun L. Magnetic Attitude Control for Earth-Pointing Satellites in the Presence of Gravity Gradient. 2016. https://doi.org/10.1016/j.ast.2016.11.003
Sutherland R., Kolmanovsky I.K., Girard A.R. Attitude Controlof a 2U Cubesat by Magnetic and Air Drag Torques // IEEE. Trans. Control Systems Technology. 2017. arXiv:1707.04959
Ovchinnikov M.Yu., Penkov V.I. et al. Geomagnetic field models for satellite angular motion studies // Acta Astrona-utica. 2018. V. 144. P. 171–180.
Dipak G., Bijoy M., Bidul T.N., Manoranjan S. Three-axis Global Magnetic Attitude Control of Earth-Pointing Satellites in Circular Orbit // Asian J. Control. 2017. V. 19. № 6. P. 2028–2041.https://doi.org/10.1002/asjc.1506
Yang H. Spacecraft Attitude and Reaction Wheel Desaturation Combined Control Method // IEEE Trans. on Aerospace and Electronic Systems. 2017. V. 53. № 1. P. 286–295.
Kim J., Jung Y., Bang H. Linear Time-Varying Model Predictive Control of Magnetically Actuated Satellites in Elliptic Orbits // Acta Astronautica. 2018. V. 151. P. 791–804.
Yang Y. Spacecraft modeling, attitude determination, and control: quaternion-based approach. Taylor & Francis Group, 2019.
Silani E., Lovera M. Magnetic Spacecraft Attitude Control: a Survey and Some New Results // Control engineering practice. 2005. V. 13. P. 357–371.
Sofyalı A., Jafarov E.M., Wisniewski R. Robust and Global Attitude Stabilization of Magnetically Actuated Spacecraft Through Sliding Mode // Aerosp. Sci.Technol. 2018. https://doi.org/10.1016/j.ast.2018.01.022
Bhat S.P. Controllability of Nonlinear Time-Varying Systems: Application to Spacecraft Attitude Control Using Magnetic Actuation // IEEE Trans. on Automatic Control. 2005. V. 50. № 11. P. 1725–1735.
Yang Y. Controllability of Spacecraft Using Only Magnetic Torques // IEEE Trans. On Aerospace and Electronic System. 2016. V. 52. № 2. P. 955–962.
Белецкий В.В. Движение искусственного спутника относительно центра масс М.: Наука, 1965.
Wertz J. Spacecraft attitude determination and control. Dordrecht, The Netherlands: D. Reidel Publishing Company, 1978.
Каленова В.И., Морозов В.М. Линейные нестационарные системы и их приложения к задачам механики. М.: Физматлит, 2010.
Каленова В.И., Морозов В.М. Приводимость линейных нестационарных систем второго порядка с управлением и наблюдением // ПММ. Т. 76. 2012. Вып. 4. С. 576–588.
Каленова В.И., Морозов В.М. Об управлении линейными нестационарными системами специального вида // Известия РАН. Теория и системы управления. 2013. № 3. С. 6–15.
Беллман Р. Введение в теорию матриц. М.: Наука. 1969.
Laub A.J., Arnold W.F. Controllability and Observability Criteria for Multivariable Linear Second Order Models // IEEE Trans. Automat. Control. 1984. V. AC-29. № 2. P. 163–165.
Красовский Н.Н. Теория управления движением. Линейные системы. М.: Наука, 1968.
Ройтенберг Я.Н. Автоматическое управление. М.: Наука, 1978.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал