Космические исследования, 2020, T. 58, № 4, стр. 284-290
О несимметричных циклах Цейпеля–Лидова–Козаи при резонансах средних движений
С. С. Ефимов 1, В. В. Сидоренко 1, 2, *
1 Московский физико-технический институт
г. Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
* E-mail: sidorenk@keldysh.ru
Поступила в редакцию 09.12.2019
После доработки 09.12.2019
Принята к публикации 19.12.2019
Аннотация
Циклами Цейпеля–Лидова–Козаи называют долгопериодические взаимосвязанные изменения наклонений и эксцентриситетов орбит естественных и искусственных небесных тел, обнаруженные независимым образом X. Цейпелем (1910), М.Л. Лидовым (1961) и Й. Козаи (1962). Первоначально существование циклов Цейпеля–Лидова–Козаи было установлено для нерезонансных движений небесных тел. Подходы, позволяющие изучать подобные вековые эффекты в случае резонанса орбитальных движений, появились существенно позднее. Как оказалось, при резонансе циклы Цейпеля–Лидова–Козаи могут не обладать симметрией, всегда имеющейся у этих циклов в нерезонансных ситуациях в рамках ограниченной задачи трех тел. Более того, результаты численных исследований указывают на наличие несимметричных циклов Цейпеля–Лидова–Козаи в динамике ряда объектов пояса Койпера, движущихся в резонансе с Нептуном.
1. ВВЕДЕНИЕ
Взаимосвязанные долгопериодические колебания наклонения и эксцентриситета, именуемые далее циклами Цейпеля–Лидова–Козаи, впервые были обнаружены Х. фон Цейпелем в начале XX века [1, 2]. Тем не менее, внимание специалистов эти колебания привлекли только через полвека после независимого их переоткрытия в работах М.Л. Лидова [3] и Й. Козаи [4], посвященных преимущественно исследованию предельного случая ограниченной задачи трех тел (ОЗТТ), соответствующего движению пробной частицы по слабо возмущенной кеплеровской орбите с большой полуосью a существенно меньшей полуоси возмущающего тела $a{\kern 1pt} '$ (Хилловской случай по терминологии М.Л. Лидова). Взаимосвязанное изменение эксцентриситета $e$ и наклонения $i$ орбиты частицы обусловлено наличием приближенного интеграла движения
В зависимости от поведения аргумента перицентра орбиты $\omega $ циклы Цейпеля–Лидова–Козаи подразделяются на вращательные и колебательные. Во вращательных циклах $\omega $ монотонно возрастает или убывает, в колебательных циклах значение $\omega $ лежит в некотором ограниченном интервале, имеющем разную величину для разных циклов.
В [5] приведено подробное описание циклов Цейпеля–Лидова–Козаи в круговой ограниченной задаче трех тел (ОЗТТ) при произвольном соотношении значений полуосей частицы и возмущающего тела. Как и в основополагающих работах [3, 4], для анализа вековых эффектов в [5] использовались двукратно осредненные уравнения движения, построенные в предположении отсутствия резонансов в орбитальном движении частицы и возмущающего тела.
Вековая эволюция и, в частности, циклы Цейпеля–Лидова–Козаи в рамках круговой ОЗТТ при наличии резонансов средних движений (РСД) разных типов рассматривались, например, в [6–9]. Тип резонанса определяется отношением двух относительно малых взаимно простых целых чисел $k:l$, где $k$ и $l$ количество орбитальных оборотов, совершаемых примерно за одно и то же время частицей и возмущающим небесным телом; число $\left| {k - l} \right|$ тоже служит важной характеристикой резонансного движения, именуемой порядком резонанса. Как оказалось, свойства движения зависят от типа резонанса столь существенным образом, что каждый резонанс требует фактически отдельного исследования.
Традиционные методы качественного исследования РСД, описанные в [10, 11], применимы только при относительно малых значениях эксцентриситетов и наклонений. Отмеченное Дж. Уиздомом [6] наличие в резонансном случае приближенного интеграла, имеющего смысл адиабатического инварианта при периодических изменениях некой вспомогательной переменной (резонансной фазы), способствовало развитию в последнее время полуаналитических методик изучения вековой эволюции при РСД без каких-либо ограничений на значения элементов оскулирующих орбит. Важной областью применения таких методик является, например, анализ динамики объектов семейств “тутино” и “плутино” в поясе Койпера, находящихся в РСД $1:2$ и $2:3$ с Нептуном соответственно и движущихся по сильно эллиптическим орбитам с большими наклонениями к плоскости эклиптики [12].
В нерезонансных случаях циклы Цейпеля–Лидова–Козаи всегда обладают симметрией [13]: если в некотором цикле изменение аргумента перицентра и эксцентриситета описывается формулами $\omega \left( t \right)$ и $e\left( t \right)$, причем начальный момент времени выбран так, что $\omega \left( 0 \right) = 0{\text{mod}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)$, то тогда
(1.1)
$\begin{gathered} e\left( {{{T}_{{LK}}} - t} \right) = e\left( t \right), \\ \omega \left( {{{T}_{{LK}}} - t} \right) = - \omega \left( t \right){\text{mod}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right). \\ \end{gathered} $Здесь ${{T}_{{LK}}}$ обозначает период цикла.
При РСД циклы Цейпеля–Лидова–Козаи могут не удовлетворять условию (1.1) [7]. В данной статье приведены примеры несимметричных циклов, существование которых было установлено в рамках “адиабатического” приближения Уиздома. Указаны резонансные объекты пояса Койпера с несимметричными циклами Цейпеля–Лидова–Козаи вращательного и колебательного типа, выявленные численным интегрированием уравнений движения с учетом влияния на эти объекты притяжения всех планет Солнечной системы.
2. ПРИМЕНЕНИЕ АДИАБАТИЧЕСКОГО ПРИБЛИЖЕНИЯ ДЛЯ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ ВЕКОВЫХ ЭФФЕКТОВ ПРИ РСД
При РСД в системе “Солнце + планета + + пробная частица” можно выделить “быстрые”, “полубыстрые” и “медленные” динамические процессы. “Быстрыми” динамическими процессами являются движения планеты и частицы по орбитам. “Полубыстрым” процессом будет изменение резонансной фазы $\varphi $, представляющей комбинацию переменных, определяющих положение планеты и частицы в их орбитальном движении, и углов, характеризующих ориентацию орбиты частицы. В пространственной круговой ОЗТТ в качестве резонансной фазы удобно взять
где $\varpi \,\,{\text{ = }}\,{ \Omega }\,\,{\text{ + }}\,\,\omega $ – долгота перицентра орбиты частицы (Ω – долгота восходящего узла), $\lambda $ и $\lambda {\kern 1pt} '$ – средние долготы частицы и планеты соответственно. В резонансных движениях изменение $\varphi $ носит колебательный характер, в нерезонансных движениях $\varphi $ “вращается” – монотонно увеличивается или уменьшается. Наконец, “медленный” процесс состоит в вековой эволюции элементов $e,i,\omega ,{\Omega }$ оскулирующей орбиты частицы.Далее во всех приводимых уравнениях в качестве единиц измерения массы и расстояния используется значение полной массы системы и значение большой полуоси орбиты планеты, единица измерения времени выбрана таким образом, что среднее движение планеты равняется единице. Также предполагается, что масса планеты составляет малую долю $\mu $ от общей массы системы.
Предварительный этап в исследовании медленных процессов методом адиабатической аппроксимации состоит в построении вспомогательной системы, состоящей из подсистемы, описывающей изменение резонансной фазы,
(2.1)
$\frac{{d\varphi }}{{d\tau }} = 3{{\alpha }_{1}}{\Phi },\,\,\,\,~~\frac{{d{\Phi }}}{{d\tau }} = - \frac{{\partial W}}{{\partial \varphi }}$(2.2)
$\begin{gathered} \frac{{d\omega }}{{d\tau }} = \varepsilon {{\alpha }_{2}}\frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial W}}{{\partial e}}, \\ ~~\frac{{de}}{{d\tau }} = - \varepsilon {{\alpha }_{2}}\frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial W}}{{\partial \omega }}, \\ \end{gathered} $Систему (2.1)–(2.2) можно записать в гамильтоновой форме:
В предельном случае $\varepsilon = 0$ исследование поведения решений системы (2.1)–(2.2) сводится к изучению свойств гамильтоновой системы с одной степенью свободы, порождаемой гамильтонианом ${\Xi }$, в котором переменные $\omega ,e$ интерпретируются как параметры. В такой системе от переменных $\varphi ,{\Phi }$ можно перейти к переменным “действие-угол”. Если
(2.3)
$\varphi \left( {\tau ,\omega ,e,H,\xi } \right),~{\Phi }\left( {\tau ,\omega ,e,H,\xi } \right)$то тогда значение переменной “действие” для точек, лежащих на фазовой траектории (2.3), вычисляется по формуле
Здесь $T\left( {\omega ,e,H,\xi } \right)$ обозначает период решения (2.3).
В том случае, когда $\varepsilon \ne 0$, быструю подсистему (2.1) также можно рассматривать как гамильтонову систему с одной степенью свободы, но теперь интерпретировать $\omega ,e$ как медленно меняющиеся параметры. Из такой интерпретации вытекает, что $I\left( {\omega ,e,H,\xi } \right)$ будет адиабатическим инвариантом (АИ) системы (2.1)–(2.2): значение этой величины сохраняется с точностью $\sim {\kern 1pt} \varepsilon $ вдоль решений системы в тех случаях, когда не происходит изменений характера поведения решения (переходов между вращениями и колебаниями резонансной фазы и т.п.). Более того, если для решений с “вращающейся” резонансной фазой в качестве значения АИ брать 2$I\left( {\omega ,e,H,\xi } \right)$, то тогда с точностью $\sim {\kern 1pt} \varepsilon \left| {\ln \varepsilon } \right|$ значение АИ сохраняется и при переходе резонансной фазы от вращений к колебаниям или, наоборот, от колебаний к вращениям.
Таким образом, можно получить представление о вековой эволюции элементов $~\omega ,e$ при заданных значениях $\xi $ и $H$, изучая поведение линий уровня АИ в двумерном диске $D\left( H \right)$, в котором $e$ и $\omega $ используются в качестве полярных координат (параметр $H$ определяет радиус диска: $e < {{e}_{{{\text{max}}}}} = \sqrt {1 - {{H}^{2}}} $).
Полученные в адиабатическом приближении фазовые портреты медленных процессов тождественны фазовым портретам “эволюционной” системы, возникающей после усреднения правых частей медленной подсистемы (2.1) вдоль решений (2.2).
Как уже отмечалось в разд. 1, от других подходов к качественному исследованию вековых эффектов при РСД адиабатическое приближение отличается отсутствием каких-либо ограничений на эксцентриситеты и наклонения изучаемых движений. Опираясь на хорошо изученные свойства АИ, в рамках адиабатического приближения можно установить формирование в фазовом пространстве исходной системы областей хаотической динамики, обусловленных малыми квазислучайными скачками значений $I\left( {\omega ,e,H,\xi } \right)$ при изменении качественного поведения резонансной фазы $\varphi $. Тем не менее, следует принимать во внимание, что для усреднения возмущающей функции по орбитальным движениям и отыскания решений вырожденной системы (2.1) требуется применение численных методов. Достаточно часто встречаются случаи сосуществования нескольких резонансных режимов на одном уровне гамильтониана ${\Xi }$ [15]. Эволюция движения в разных резонансных режимах обычно сильно отличается. Поэтому фазовые портреты медленных процессов в таких ситуациях разделяются на несколько листов. В диске $D\left( H \right)$ эти листы “склеены” вдоль линий, на которых изменяется число сосуществующих режимов.
3. НЕСИММЕТРИЧНЫЕ ЦИКЛЫ ЦЕЙПЕЛЯ–ЛИДОВА–КОЗАИ ПРИ РСД 1 : 2
Длительное время специалисты уделяли основное внимание изучению РСД во внутренней задаче трех тел (т.е., случаю, когда $a < a{\kern 1pt} '$ и, соответственно, $k > l$). Анализ таких резонансов важен для понимания динамической структуры главного пояса астероидов. Несимметричных циклов Цейпеля–Лидова–Козаи в этих исследованиях выявлено не было.
В начале 90-ых годов, после открытия популяции малых тел в занептунной области, начались интенсивные исследования РСД во внешней задаче трех тел. Особенно активно изучаются РСД $1:2$ и $2:3$, формирующие соответственно семейства “тутино” и “плутино” койперовских объектов.
В работе [7] на основе некоторых эмпирических соображений о поведении резонансной фазы было отмечено, что при РСД $1:l$ должны наблюдаться несимметричные циклы Цейпеля–Лидова–Козаи, а также приведен пример несимметричного вращательного цикла в численных расчетах движения гипотетической частицы в резонансе $1:2$. На рис. 1 изображен фазовый портрет для этого резонанса, построенный в рамках адиабатического приближения при $\xi = 0.6$ и $H \approx 0.866$. Помимо несимметричных вращательных циклов Цейпеля–Лидова–Козаи, обнаруженных в [7], на фазовом портрете можно видеть соседствующие с ними циклы колебательного типа, расположенные вблизи краев диска $D\left( H \right)$. Светло-серым цветом выделена область сосуществования двух резонансных режимов на выбранном уровне $\xi = 0.6$ гамильтониана ${\Xi }$. В этой области фазовый портрет, описывающий вековую эволюцию эксцентриситета и аргумента перицентра орбиты пробной частицы, расщепляется на два листа, показанные на рис. 1 отдельно. Видно, что несимметричные циклы есть на обоих листах фазового портрета.
Рис. 1.
Вековая эволюция оскулирующих элементов $\omega $ и $e$ при резонансе $1:2$ в случае $\xi = 0.6$, $H \approx 0.866$ (${{e}_{{{\text{max}}}}} = 0.5)$. На двух частях рисунка изображены траектории с двух разных листов фазового портрета. Черным цветом выделена область “запрещенных” значений $e$ и $\omega $ при указанных значениях величин $\xi $ и $H$: в этой области ${\text{mi}}{{{\text{n}}}_{\varphi }}W\left( {\varphi ,\omega ,e,H} \right) > \xi {\kern 1pt} .$
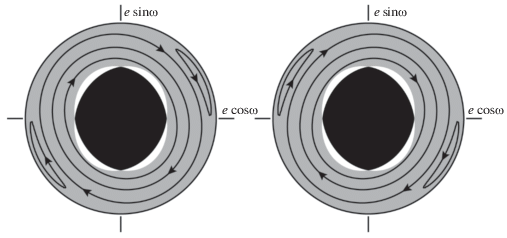
Численные исследования указывают на возможную асимметрию циклов Цейпеля–Лидова–Козаи ряда реальных объектов, находящихся в РСД 1 : 2 с Нептуном. На рис. 2 и на рис. 3 приведены примеры вращательных и колебательных циклов соответственно, полученные численным интегрированием уравнений движения малого небесного тела с учетом влияния всех планет-гигантов Солнечной системы с помощью программного комплекса MERCURY6 [16] на 15 млн лет. В таблице 1 собран полный список “тутино” с выявленной асимметрией вековой эволюции (включая изображенные на рис. 2 и на рис. 3 примеры), а также использованные в численных расчетах значения их оскулирующих элементов.
4. НЕСИММЕТРИЧНЫЕ ЦИКЛЫ ЦЕЙПЕЛЯ–ЛИДОВА–КОЗАИ В РЕТРОГРАДНОМ КООРБИТАЛЬНОМ ДВИЖЕНИИ
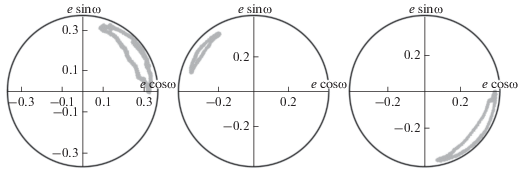
Рис. 2.
Несимметричные циклы Цейпеля–Лидова–Козаи вращательного типа, встречающиеся у принадлежащих семейству “тутино” объектов 2012 XR157, 2012 VR113, 2006 SL371 (слева направо).

Рис. 3.
Несимметричные циклы Цейпеля–Лидова–Козаи колебательного типа, встречающиеся у принадлежащих семейству “тутино” объектов 2013 GW136, 1998 SM165, 2006 SG369 (слева направо).
Для гипотетического наблюдателя, располагающегося в северном полюсе эклиптики, большинство объектов Солнечной системы вращается вокруг Солнца против часовой стрелки. Тем не менее, есть и такие объекты, которые вращаются в противоположную сторону (движение ретроградного типа) [17]. Ретроградное орбитальное движение малого небесного тела может быть в резонансе с орбитальным движением одной из планет Солнечной системы [18]. Например, астероид 2015BZ503 находится в ретроградном резонансе средних движений $1:1$ с Юпитером (ретроградное коорбитальное движение) [19]. Из результатов численного исследования динамики данного астероида следует, что резонанс позволяет ему избегать столкновений с Юпитером и обеспечивает длительное пребывание в указанном режиме движения.
В рамках круговой ОЗТТ вековая эволюция элементов $e$ и $\omega $ для прямого и ретроградного нерезонансного орбитального движения пробной частицы отличается только направлением стрелок на соответствующих фазовых портретах. В случае РСД ситуация другая: некоторое сходство вековой эволюции при прямом и ретроградном движении можно усмотреть только при $\xi \gg 1$, когда ситуация фактически уже не является резонансной.
Детальное исследование вековой эволюции при прямом РСД $1:1$ несимметричных циклов Цейпеля–Лидова–Козаи не выявило [14, 20]. Пример, демонстрирующий существование несимметричных колебательных циклов при ретроградном РСД $1:1$, приведен на рис. 4. Отметим, что несимметричных вращательных циклов Цейпеля–Лидова–Козаи для данного резонанса не обнаружено.
5. НЕСИММЕТРИЧНЫЕ ЦИКЛЫ ЦЕЙПЕЛЯ–ЛИДОВА–КОЗАИ ПРИ ДРУГИХ РСД
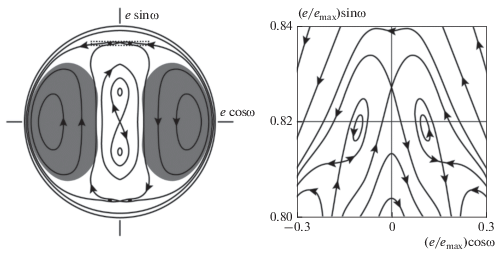
Рис. 4.
Вековая эволюция оскулирующих элементов $\omega $ и $e$ в ретроградном коорбитальном движении в случае $~\xi = 1.29967$, $H \approx - 0.866$ (${{e}_{{{\text{max}}}}} = 0.5)$. Участок с колебательными несимметричными циклами Цейпеля–Лидова–Козаи отмечен слева пунктирной рамкой и показан в увеличенном масштабе справа. Темно-серым цветом выделена область, в которой при указанных значениях $\xi $ и $H$ изменение резонансной фазы носит вращательный характер.
Достаточно большое количество примеров несимметричных циклов Цейпеля–Лидова–Козаи для других резонансов приведено в [9, 21]. Все известные на данный момент несимметричные циклы можно разделить на две группы: циклы в ретроградном движении, обнаруженные при РСД $1:1$ (разд. 4) и при РСД $2:37$ [21], и циклы в прямом орбитальном движении при РСД типа $1:l,~{\text{\;где}}~~l > 2.$ Первая группа характеризуется малым размером циклов, количество которых кратно четырем, причем каждый цикл располагается в своем квадранте, не пересекая линий $\omega = 0{\text{mod}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)$. Все циклы расположены на общем листе фазового портрета. Циклы второй группы встречаются в ситуациях сосуществования двух резонансных режимов и, соответственно, располагаются на разных листах фазового портрета. Поэтому эти циклы могут пересекать границы квадрантов и занимать существенную часть фазового портрета. Количество несимметричных циклов на каждом из листов кратно двум, а траектории на одном из листов могут быть получены из траекторий второго листа зеркальным отображением (рис. 1).
В [7] появление несимметричных циклов Лидова–Козаи при РСД типа $1:l$ связывалось с наличием у этих резонансов несимметричных либраций резонансной фазы. Однако несимметричные либрации могут быть обнаружены и в других резонансах, где их существование не приводит к нарушению симметрии траекторий вековой эволюции. Особенности механизма возникновения несимметричных циклов при РСД $1:l$ связаны, возможно, со вкладом в вековую эволюцию частицы возмущений, определяемых косвенной частью возмущающей функции. Несложно показать, что при РСД типа $2:l,~3:l, \ldots $ среднее значение косвенной части равно нулю. Действительно, выпишем одно из соотношений, позволяющих найти $W\left( {\varphi ,\omega ,e,H} \right)$:
(5.1)
$W\left( {\varphi ,\omega ,e,H} \right) = \frac{1}{{2\pi k}}\int\limits_0^{2\pi k} {R({\mathbf{r}}\left( \lambda \right)} ,{\mathbf{r}}{\kern 1pt} '\left( {\lambda {\kern 1pt} '\left( {\lambda ,\varphi } \right)} \right)d\lambda .$Здесь ${\mathbf{r}}\left( \lambda \right)$ и ${\mathbf{r}}{\kern 1pt} '\left( {\lambda {\kern 1pt} '} \right)$ обозначают положения частицы и планеты при соответствующих значениях их средних долгот, $\lambda {\kern 1pt} '\left( {\lambda ,\varphi } \right)$ = $\frac{1}{k}\left[ {l\lambda - \left( {l - k} \right)\varpi - \varphi } \right],$ функция $R\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} '} \right)$ является деленной на $\mu $ возмущающей функцией круговой ОЗТТ и представляет сумму главной части ${{R}_{D}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} '} \right) = \frac{1}{{\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '} \right|}},$ описывающей непосредственное влияние притяжения планеты на частицу, и косвенной части ${{R}_{E}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} '} \right) = - \left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} '} \right)$, описывающей смещение планетой центра масс системы относительно положения Солнца. При записи косвенной части учтено, что в круговой ОЗТТ при выбранных единицах измерений $\left| {{\mathbf{r}}{\kern 1pt} '} \right| = 1.$
Элементарные преобразования интеграла в правой части формулы (5.1) позволяют привести его к виду
(5.2)
$\begin{gathered} W\left( {\varphi ,\omega ,e,H} \right) = \\ = \frac{1}{{2\pi k}}\int\limits_0^{2\pi } {\left\{ {\mathop \sum \limits_{j = 0}^{k - 1} R\left( {{\mathbf{r}}\left( \lambda \right),{\mathbf{r}}{\kern 1pt} '\left( {\lambda {\kern 1pt} '\left( {\lambda ,\varphi } \right) + \frac{{2\pi j}}{k}} \right)} \right)} \right\}} d\lambda . \\ \end{gathered} $Принимая во внимание структуру подынтегрального выражения в (5.2), эти преобразования можно интерпретировать как переход к системе, в которой частица взаимодействует с $k$ “клонами” планеты, равномерно распределенными по орбите. В круговой задаче трех тел это соответствует расположению “клонов” на равном угловом расстоянии ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } k}} \right. \kern-0em} k}$ друг от друга, и, если $k \geqslant 2$, общий центр масс “клонов” совпадает с положением Солнца. Поэтому вклад косвенной части возмущающей функции в $W\left( {\varphi ,\omega ,e,H} \right)$ в этих случаях оказывается нулевым.
Таблица 1.
Элементы оскулирующих орбит объектов пояса Койпера, с наблюдаемой асимметрией вековой эволюции
| Объект | $a$, а. е. | $e$ | $i$, ° | $\omega $, ° | ${\Omega }$, ° | $M$, ° |
|---|---|---|---|---|---|---|
| Объекты с вращательными асимметричными циклами Цейпеля–Лидова–Козаи | ||||||
| 2006 SL371 | 47.6124787 | 0.2599133 | 22.47454 | 207.37685 | 175.80585 | 13.49792 |
| 2012 VR113 | 47.4575741 | 0.1698337 | 19.2879 | 219.15377 | 120.97277 | 42.2725 |
| 2012 XR157 | 47.6056935 | 0.2249183 | 30.03694 | 276.86916 | 223.66454 | 319.89609 |
| 2014 UW229 | 47.5198496 | 0.1724298 | 14.6365 | 159.96315 | 7.03578 | 236.01215 |
| 2017 FP161 | 47.9918286 | 0.1481168 | 15.2122 | 217.99113 | 123.95334 | 239.71854 |
| Объекты с колебательными асимметричными циклами Цейпеля–Лидова–Козаи | ||||||
| 2006 SG369 | 47.4591679 | 0.3651622 | 13.60574 | 289.76727 | 101.32382 | 12.3743 |
| 2013 GW136 | 48.3167879 | 0.3514135 | 6.64339 | 35.16198 | 219.29938 | 348.38801 |
| 2014 US228 | 47.7589742 | 0.3264617 | 7.17428 | 289.32382 | 3.85454 | 62.4754 |
| 1996 TR66 | 47.6703461 | 0.3995284 | 12.43029 | 308.78934 | 343.07387 | 56.05052 |
| 1997 SZ10 | 47.6030875 | 0.3607708 | 11.81037 | 341.00704 | 9.49134 | 32.27218 |
| 1998 SM165 | 47.4420526 | 0.3708374 | 13.51737 | 130.21855 | 183.19563 | 48.02486 |
Таким образом, в сравнении с другими РСД резонансы $1:l$ имеют принципиально иную структуру усредненной возмущающей функции: есть дополнительное слагаемое, представляющее усредненную косвенную часть. Для резонансов не очень больших порядков косвенная часть по порядку величины равна главной, и поэтому ее наличие существенно изменяет вековую эволюцию частицы.
ЗАКЛЮЧЕНИЕ
Адиабатическое приближение ранее уже неоднократно использовалось для изучения вековых эффектов при РСД разных типов (см., например, [8, 9, 14, 20, 22, 23] ). То, что этот методический прием позволил найти ранее неизвестные примеры несимметричных циклов Цейпеля–Лидова–Козаи, является еще одним подтверждением его универсальности и эффективности.
Список литературы
von Zeipel H. Sur l’application des sèries de M. Lindstedt à l’étude du mouvement des comètes périodiques // Astronomische Nachrichten. 1910. V. 183. P. 345.
Ito T., Ohtsuka K. The Lidov–Kozai Oscillation and Hugo von Zeipel. TERRAPUB, 2019.
Лидов М.Л. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел // Искусственные спутники Земли. 1961. № 8. С. 5.
Kozai Y. Secular perturbations of asteroids with high inclinations and eccentricities // Astronomical Journal. 1962. V. 67. P. 591.
Вашковьяк М.А. Эволюция орбит в ограниченной двукратно осредненной задаче трех тел // Космич. исслед. 1981. Т. 19. № 1. С. 5.
Wisdom J. A perturbative treatment of motion near 3/1 commensurability // Icarus. 1985. V. 63. P. 272.
Gallardo T., Hugo G., Pais P. Survey of Kozai dynamics beyond Neptune // Icarus. 2012. V. 220. P. 392.
Sidlichovsky M. A non-planar circular model for the 4/7 resonance // Celest. Mech. Dyn. Astron. 2005. V. 93. P. 167.
Saillenfest M., Fouchard M., Tommei G. et al. Long-term dynamics beyond Neptune: secular models to study the regular motions // Celest. Mech. Dyn. Astron. 2016. V. 126. P. 369.
Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2009.
Морбиделли А. Современная небесная механика. Аспекты динамики Солнечной системы. М.: ИКИ РАН, 2014.
Morbidelli A., Levinson H.F., Gomes R. The dynamical structure of the Kuiper belt and its primordial origin. In: The Solar system beyond Neptune / Eds. Barucci M.A., Cruikshank D.P., Morbidelli A. Tucson: The University of Arizona press, 2008. P. 275.
Shevchenko I.I. The Lidov-Kozai effect – applications in exoplanet research and dynamical astronomy. Springer, 2017.
Sidorenko V.V., Neishtadt A.I., Artemyev A.V. et al. Quasi-satellite orbits in the general context of dynamics in the 1 : 1 mean motion resonance. Perturbative treatment // Celest. Mech. Dyn. Astron. 2014. V. 120. P. 131.
Beauge C. Asymmetric librations in exterior resonances // Celest. Mech. Dyn. Astron. 1994. V. 60. P. 225.
Chambers J.E. A hybrid symplectic integrator that permits close encounters between massive bodies // Monthly Notices of the Royal Astronomical Society. 1999. V. 304. P. 793.
Kankiewicz P., Włodarczyk I. Dynamical lifetimes of asteroids in retrograde orbits // Monthly Notices of the Royal Astronomical Society. 2017. V. 468. P. 4143.
Li M., Huang Y., Gong S. Survey of asteroids in retrograde mean motion resonances with planets // Astron. Astrophysics. 2019. V. 630. A60. P. 8.
Wiegert P., Connors M., Veillet C. A retrograde co-orbital asteroid of Jupiter // Nature. 2017. V. 543. P. 687.
Сидоренко В.В., Нейштадт А.И., Артемьев А.В. и др. Формирование и разрушение квазиспутникового режима движения небесных тел // Доклады Академии наук. 2013. Т. 450. № 3. С. 286.
Saillenfest M., Lari G. The long-term evolution of known resonant trans-Neptunian objects // Astron. Astrophysics. 2017. V. 603. A79. P. 9.
Сидоренко В.В. Эволюция астероидных орбит при резонансе средних движений 3 : 1 с Юпитером (плоская задача) // Космич. исслед. 2006. Т. 44. № 5. С. 459. (Cosmic Research. P. 440).
Sidorenko V.V. Dynamics of “jumping” Trojans: a perturbative treatment // Celest. Mech. Dyn. Astron. 2018. V. 130. № 67.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования


