Космические исследования, 2020, T. 58, № 4, стр. 261-267
Радиационные пояса в процессе инверсии магнитного поля Земли
О. О. Царева 1, *, Л. М. Зеленый 1, Х. В. Малова 1, 2, В. Ю. Попов 1, 3, 4
1 Институт космических исследований РАН
г. Москва, Россия
2 Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына МГУ им. М.В. Ломоносова
г. Москва, Россия
3 Национальный исследовательский университет “Высшая школа экономики”
г. Москва, Россия
4 Физический факультет МГУ им. М.В. Ломоносова
г. Москва, Россия
* E-mail: olga8.92@mail.ru
Поступила в редакцию 05.10.2018
После доработки 06.09.2019
Принята к публикации 23.10.2019
Аннотация
В рамках осесимметричной модели исследованы изменения формы радиационных поясов Земли и энергетических спектров заряженных частиц в них во время инверсии геомагнитного поля. Области устойчивого существования радиационных поясов получены аналитически обобщением теории Штермера на случай осесимметричного квадруполя. Предложен сценарий инверсии, в котором показано, что может происходить постепенное сокращение радиационных поясов при уменьшении дипольной составляющей современного геомагнитного поля. Получены пространственно-энергетические распределения плотности потоков протонов и электронов, позволившие определить максимальную мощность доз радиации на различных магнитных оболочках в процессе инверсии.
I. ВВЕДЕНИЕ
Геомагнитное поле Земли нестабильно: длительные периоды относительно стабильного геомагнитного поля сменяются сравнительно быстрыми глобальными изменениями его полярности – инверсиями, о чем свидетельствуют палеомагнитные данные. По последним наблюдениям современное магнитное поле ослабевает, его магнитные полюса мигрируют, напряженность магнитного поля в Южно-Атлантической аномалии уменьшается, а ее размер увеличивается. Эти эффекты могут говорить о начале магнитной инверсии.
В работе [1] исследована радиационная обстановка на поверхности Земли и околоземном пространстве в момент инверсии геомагнитного поля. Предложен сценарий процесса инверсии, согласно которому дипольная составляющая поля обратиться в нуль к 3580-ому году, и квадрупольная составляющая станет доминирующей. Остается открытым вопрос о том, будут ли существовать радиационные пояса в период переворота магнитного поля. Целью настоящей работы является исследования формы радиационных поясов Земли и радиационной обстановки в околоземном пространстве на основе сценария уменьшения дипольной компоненты магнитного поля до нуля в рамках осесимметричной модели.
Как известно из теории Штермера [2, 3] о закономерностях движения заряженных частиц в дипольном магнитном поле, устойчивость радиационных поясов обусловлена стационарностью и аксиальной симметрией магнитного поля Земли, откуда следует сохранение двух интегралов движения заряженных частиц, населяющих околоземное пространство: полной энергии $\left| {\text{v}} \right|{\text{ = const}}$ и обобщенного импульса азимутального движения:
(1)
${{{\rm M}}_{{\varphi }}} = R\left( {m{{v}_{{\varphi }}} + e{{{\rm A}}_{{\varphi }}}} \right) = {\text{const}}.$Здесь ${{A}_{{\varphi }}}$ – азимутальный потенциал, $R = r\cos {\lambda }$ – расстояние до оси z и λ – магнитная широта; все переменные рассматриваются в цилиндрической системе координат, в которой ось z направлена на север вдоль оси магнитного диполя. Среди всех возможных топологий поля области устойчивого захвата заряженных частиц существуют только в осесимметричной (или квазиосесимметричной) конфигурации поля, когда его магнитные моменты коллинеарны оси вращения. Представим геомагнитное поле ${{{\mathbf{B}}}_{{{\text{Earth}}}}}$ как суперпозицию магнитного диполя и квадруполя:
(2)
${{{\mathbf{B}}}_{{{\text{Earth}}}}} = {\kappa }{\kern 1pt} {{{\mathbf{B}}}_{{dip}}} + {{{\mathbf{B}}}_{{quad}}},$Мы ограничились рассмотрением двух первых мультиполей, поскольку, чем выше порядок мультиполя, тем быстрее его напряженность затухает с расстоянием. Компоненты современного магнитного диполя ${{{\mathbf{B}}}_{{dip}}}$ определяются аналитически с использованием модели IGRF-12 [4] и в геоцентрической системе координат (r, θ, ϕ) имеют вид:
(3)
$\begin{gathered} B_{r}^{{dip}} = 2{{\left( {\frac{{{{R}_{{\text{E}}}}}}{r}} \right)}^{3}} \times \\ \times \,\,\left( {g_{1}^{0}\cos {\theta } + \left( {g_{1}^{1}\cos {\varphi } + h_{1}^{1}\sin {\varphi }} \right)\sin {\theta }} \right), \\ B_{{\theta }}^{{dip}} = - {{\left( {\frac{{{{R}_{{\text{E}}}}}}{r}} \right)}^{3}} \times \\ \times \,\,\left( { - g_{1}^{0}\sin {\theta } + \left( {g_{1}^{1}\cos {\varphi } + h_{1}^{1}\sin {\varphi }} \right)\cos {\theta }} \right), \\ B_{{\varphi }}^{{dip}} = - {{\left( {\frac{{{{R}_{{\text{E}}}}}}{r}} \right)}^{3}}\left( { - g_{1}^{1}\sin {\varphi } + h_{1}^{1}\cos {\varphi }} \right), \\ \end{gathered} $Области захвата заряженных частиц в осесимметричном дипольном поле подробно исследовались ранее [2, 3]. Современный диполь обладает аксиальной квазисимметрией, т.е. обобщенный импульс азимутального движения частицы не является точным интегралом в современном поле. Таким образом, теория Штермера имеет границу применимости на геомагнитных широтах λ не выше ~65° [4].
В момент переворота, согласно инверсионному сценарию, компоненты диполя ${{{\mathbf{B}}}_{{dip}}}$ обратятся в нуль, и геомагнитное поле будет представлять собой квадрупольное поле. Всевозможные конфигурации такого поля приведены в работе [6], где также было замечено, что зоны устойчивого захвата частиц имеют место лишь в осесимметричной конфигурации. Таким образом, если предполагать, как мы это сделали ранее в работе [1], что оси квадруполя сохранят свою современную, несимметричную относительно оси вращения, ориентацию, то радиационные пояса практически исчезнут, а присутствующие в них низкоэнергичные квазизахваченные частицы не внесут существенного вклада в околоземную радиацию.
Мы будем рассматривать единственную возможную конфигурацию квадруполя, при которой возможно сохранение радиационных поясов Земли – осесимметричный квадруполь. Здесь стоит отметить, что согласно нелинейной модели αΩ-динамо, описанной в работах [7, 8], величина квадрупольного поля в момент хаотической инверсии дипольного поля может носить случайный характер. Таким образом, вероятность реализации предложенного сценария может быть невелика. Однако такой сценарий инверсии удобен для оценки максимально возможной дозы радиации в околоземном пространстве.
Осесимметричный квадруполь определяется старшим квадрупольным коэффициентом Гаусса $g_{2}^{0}$. Компоненты поля ${{{\mathbf{B}}}_{{quad}}}$ при этом имеют вид
(4)
$\begin{gathered} B_{r}^{q} = \frac{3}{2}{{\left( {\frac{{{{R}_{{\text{E}}}}}}{r}} \right)}^{4}}g_{2}^{0}\left( {3{{{\cos }}^{2}}{\theta } - 1} \right), \\ B_{{\theta }}^{q} = \frac{3}{2}{{\left( {\frac{{{{R}_{{\text{E}}}}}}{r}} \right)}^{4}}g_{2}^{0}\sin 2{\theta },\,\,\,\,B_{{\varphi }}^{q} = 0. \\ \end{gathered} $Развитие теории Штермера на случай осесимметричного квадруполя в работе [9] продемонстрировало, что в такой конфигурации области захвата частиц могут представлять собой два отдельных тороида, что приводит к формированию двух поясов и двух кольцевых токов, расположенных симметрично в северном и южном полушариях. Квадрупольные (конусовидные) поверхности центров захвата частиц [6] расположены на ±26.6° магнитной широты и симметричны относительно экваториальной плоскости.
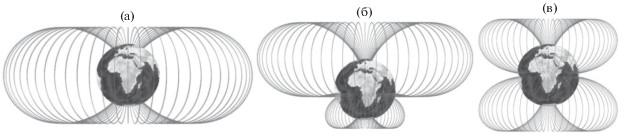
Результаты численных расчетов показывают, что в процессе инверсии магнитное поле Земли представляет собой суперпозицию осесимметричных дипольного и квадрупольного полей (2). Структура радиационных поясов и областей захвата частиц в таком смешанном поле ранее никем не исследовались. С уменьшением дипольной составляющей, тороидальная зона захвата, симметричная относительно экваториальной плоскости ${{{\lambda }}^{{\left( 0 \right)}}} = 0^\circ $, будет уменьшаться в размерах и смещаться на север ${{{\lambda }}^{{\left( - \right)}}} = 26.6^\circ $. В то время как возникшая на юге зона захвата будет расти и двигаться от –90° к ${{{\lambda }}^{{\left( + \right)}}} = - 26.6^\circ $. Таким образом, в процессе инверсии магнитного поля северная внутренняя разрешенная область будет превышать в размерах южную область. А значит, южный радиационный пояс квадруполя наполнит меньшее количество частиц, нежели северный пояс. На рис. 1 изображены магнитные силовые линии этих полей $\left[ {{\mathbf{B}} \times {\mathbf{dr}}} \right] = 0$.
II. СТРУКТУРА И ДИНАМИКА РАДИАЦИОННЫХ ПОЯСОВ
Структура и динамика радиационных поясов определяется соотношением между источниками и потерями заряженных частиц [10]. Заполнение радиационных поясов может протекать медленно и непрерывно в результате распада нейтронов альбедо ГКЛ (с энергиями Ep > 30 МэВ) или же быстро (“импульсно”) в результате переноса и ускорения заряженных частиц в магнитосфере под действием различных нестационарных процессов: возмущений электрических и магнитных полей, квазипериодических возмущений, магнитосферных суббурь, диполизации магнитных силовых линий или же вследствие динамических изменений дневной магнитопаузы.
Для протонов и ионов радиационных поясов основным механизмом гибели на магнитных оболочках L > 4 являются ионизационные потери при взаимодействии с верхней атмосферой. Главной причиной утечек электронов внутреннего пояса на L < 1.5 выступает кулоновское рассеяние, электроны внешнего пояса на L > 3 высыпаются из-за циклотронной неустойчивости, а зазор между поясами обусловлен рассеянием электронов на низкочастотном электромагнитном излучении.
Конфигурацию радиационных поясов хорошо иллюстрируют профили потоков протонов и электронов различных энергий в плоскости экватора в минимум и максимум солнечной активности, представленные на рис. 2, 3. Они построены по данным полуэмпирической модели радиационных поясов АР-8min/max и АE-8min/max [11, 12], которая успешно применяется для электронов и протонов с энергиями в диапазоне 0.1–7 и 0.1–400 МэВ.
Рис. 2.
Дифференциальные спектры протонов радиационного пояса с энергиями 1–400 МэВ в плоскости экватора в минимуме СА. Справа показаны обозначения кривых, соответствующих разным интервалам энергий протонов.
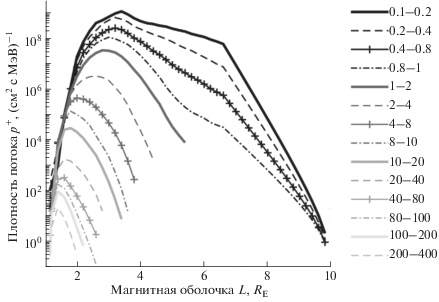
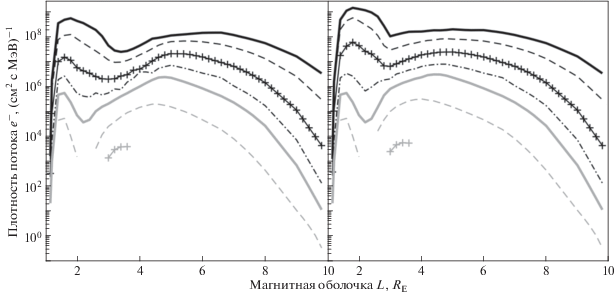
Рис. 3.
Дифференциальные спектры электронов радиационного пояса с энергиями 0.1–7 МэВ в плоскости экватора в минимуме СА (слева) и в максимуме СА (справа). Обозначения кривых такие же, как и на рис. 2.
Как видно из рисунков, основной вклад в радиацию современного протонного пояса вносят протоны с энергией 1–10 МэВ, т.к. спектры протонов больших энергией ниже на 3 и более порядка (рис. 2), а протоны меньших энергией, (их спектр значительно выше), не проникают за самую тонкую защиту (δ = 0.01 г/см2). Разумеется, с увеличением толщины защиты дозы радиации будут снижаться, а вклад в них высокоэнергичных протонов расти.
Ионизационные пробеги электронов в веществе защиты выше, чем у протонов тех же энергий, поэтому основную дозу радиации в электронных поясах будут составлять электроны с энергиями 0.1–1 МэВ (рис. 3). Также, мы увидим, что энергетический спектр этих электронов определяет форму пространственного распределения суммарных доз радиации электронов и протонов в современных естественных радиационных поясах Земли (ЕРПЗ). В процессе инверсии мы увидим, как изменятся значения и распределения доз в радиационных поясах, однако большую их часть будут наполнять частицы упомянутых энергий.
Спектры протонов в максимуме солнечной активности большей частью совпадают со спектрами в минимуме, небольшое расхождение плотностей потоков наблюдается на магнитных оболочках L < 1.5 и не превышает одного порядка. Для нахождения аналогичных профилей частиц в момент инверсии Земли построена следующая численная модель.
III. ОПИСАНИЕ ЧИСЛЕННОЙ МОДЕЛИ
Поскольку учет всех механизмов гибели и возникновения заряженных частиц в радиационных поясах весьма трудоемок, на начальном этапе исследования ограничимся заполнением областей захвата, согласно имеющимся дифференциальным профилям потоков.
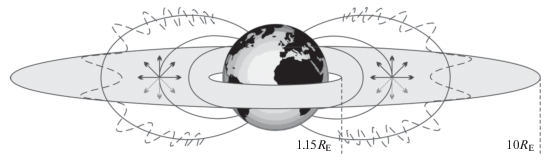
С экваториальной плоскости, множество точек которой удалены от центра Земли на расстояние, не превышающее 10RE (примерное положение сегодняшней магнитопаузы в лобовой части магнитосферы 12RE), во всех направлениях запускаются модельные частицы, имитирующие протоны и электроны радиационных поясов (рис. 4). Начальное распределение потоков частиц по магнитным оболочкам от 1.15 до 10RE соответствует дифференциальным (по энергиям) спектрам радиационных полей, приведенных на рис. 2, 3. Каждая частица трассируется в заданном, постоянном во времени, магнитном поле ${\mathbf{B}}{\text{E}}$ без учета межпланетного $\left( {{{{\mathbf{B}}}_{{IMF}}} = 0} \right)$ и электрического полей. В такой конфигурации модуль скорости частицы сохраняется $\left( {\left| {\mathbf{v}} \right| = {\text{const}}} \right)$, а уравнение движения релятивистской частицы в системе СИ имеет вид:
(5)
$\left\{ \begin{gathered} \frac{{d{\mathbf{r}}}}{{dt}} = {\mathbf{v}}, \hfill \\ m\frac{{d{\mathbf{v}}}}{{dt}} = Ze\sqrt {1 - \frac{{{{{\left| {\mathbf{v}} \right|}}^{2}}}}{{{{c}^{2}}}}} \left[ {{\mathbf{v}} \times {\mathbf{B}}} \right]. \hfill \\ \end{gathered} \right.$Следуя сценарию инверсии, в процессе трассирования частицы в магнитном поле ${\mathbf{B}}{\text{E}}$ мы последовательно уменьшаем его дипольную составляющую ${{{\mathbf{B}}}_{{dip}}}$ в 2, 4, 8 и 16 раз, используя весовой коэффициент диполя κ, в итоге оставляя лишь поле осесимметричного квадруполя ${{{\mathbf{B}}}_{{quad}}}$. На каждом этапе мы снимаем дифференциальный спектр захваченных частиц на заданном энергетическом интервале в зависимости от магнитной оболочки L. Максимальная плотность потоков частиц приходится на экваториальную плоскость ${\lambda } = 0^\circ $ для превалирующей дипольной составляющей поля и на широтах ${\lambda } = \pm 27^\circ $для осесимметричного квадруполя. Что же касается суперпозиции диполя и квадруполя с напряженностями одного порядка, то в связи с разностью скоростей затухания напряженностей диполя и квадруполя максимальная плотность потоков расположена на широтах ${{{\lambda }}^{{\left( \pm \right)}}}$, зависящих от расстояния [15].
Используем полученные спектры для исследования радиационной обстановки в околоземном пространстве осесимметричного квадруполя. Мощность поглощенной дозы радиации в Греях (РД 50-25645.216-90) вычисляется по формуле:
где B – коэффициент перехода от поглощенной энергии к дозе, равный $B = 1.6 \cdot {{10}^{{ - 10}}}$ Гр МэВ–1 см2; ${{dE} \mathord{\left/ {\vphantom {{dE} {\left( {{\rho }{\kern 1pt} dx} \right)}}} \right. \kern-0em} {\left( {{\rho }{\kern 1pt} dx} \right)}}$ – ионизационные потери в веществе защиты, МэВ г–1 см2, описываемые известной формулой [13]; $\Phi (Е)$ – дифференциальный энергетический спектр, E ' – энергия на глубине защиты δ, связанная с энергией падающей на защиту E. Эквивалентная доза от протонов за плоским слоем толщиной δ – это поглощенная доза, умноженная на коэффициент качества ионизирующих излучений Q(E) (ГОСТ 8.496-83 ГСИ). Для гамма-излучения (электронов) коэффициент Q(E) равен единице.Зависимости максимальных мощностей поглощенных доз протонов и электронов в радиационных поясах за слоем тканеэквивалентного (средняя толщина человеческой кожи) вещества толщиной δ = 0.01 г/см2 от магнитных оболочек L (RE) в процессе инверсии магнитного поля Земли изображены на рис. 5, 6. На рис. 5 приведено пояснение для обозначения каждой кривой, которое относится и ко всем последующим рисункам. Все кривые иллюстрируют распределение доз радиации в определенной конфигурации магнитного поля $\left( {\kappa D + Q} \right)$ из ур. (2), (где $D \equiv {{{\mathbf{B}}}_{{dip}}}$, $Q \equiv {{{\mathbf{B}}}_{{quad}}}$, $\kappa $ – разные коэффициенты) и на определенной магнитной широте λ. Выбор магнитной широты λ для каждой конфигурации поля обусловлен выбором максимальных доз на ней, (как это описано выше). На рисунках мы можем проследить, как с последовательным сокращением дипольной компоненты поля $\left( {\kappa D} \right)$ уменьшаются дозы радиации в радиационном поясе, происходит его сжатие, смещение и возникновение второго пояса. Дозы радиации между этими двумя новыми поясами квадруполя (кривые $0.0D + Q$ с маркером “–o”) – северным (${\lambda } = 27^\circ $) и южным (${\lambda } = - 27^\circ $) – перераспределятся несимметрично. Мы приводим один график (рис. 5) для распределений доз протонного радиационного пояса, поскольку энергетические спектры протонов в минимуме и максимуме солнечной активности (СА) не отличаются, и два графика (рис. 6) для доз электронных поясов в минимуме (слева) и максимуме (справа) СА. Как видно, солнечная активность мало влияет на спектры доз радиационных поясов.
Рис. 5.
Распределения максимальных мощностей поглощенных доз протонов (рад/сутки) в радиационных поясах на оболочках L (RE) для разных магнитных широт λ в процессе инверсии магнитного поля Земли. Кривые соответствуют суперпозициям диполя и квадруполя $\left( {\kappa D + Q} \right)$, взятых с разными весовыми коэффициентами κ.
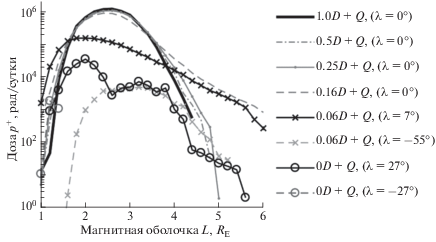
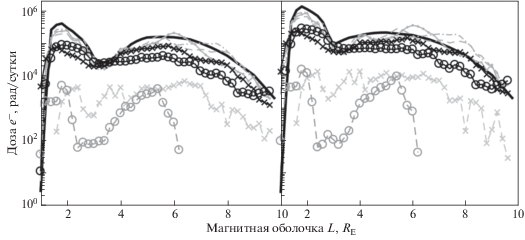
Рис. 6.
Распределения максимальных мощностей поглощенных доз электронов (рад/сутки) в радиационных поясах по оболочкам L (RE) в процессе инверсии магнитного поля Земли в минимум (слева) и максимум (справа) СА. (Обозначения кривых – те же, что и на рис. 5.)
Соответственно суммарные поглощенные и эквивалентные дозы в минимум (слева) и максимум (справа) СА изображены на рис. 7. После суммирования видно, что вклад протонной составляющей в радиацию поясов будет только падать. По этой причине спектры поглощенных (рис. 7) и эквивалентных доз слабо отличаются. Сравнивая имеющиеся в литературе [14] спектры доз ЕРПЗ, найденные с помощью получивших широкое распространение моделей пространственно-энергетического распределения частиц АР-8 и АE-8, с посчитанным распределением доз радиации в современной конфигурации поля, получим хорошую оценку точности расчетов.
Рис. 7.
Распределения максимальных суммарных мощностей поглощенных доз (рад/сутки и Гр/сутки) в радиационных поясах по оболочкам L (RE) в процессе инверсии магнитного поля Земли в минимуме (слева) и максимуме (справа) СА. (Обозначения кривых показаны на рис. 5.)

Таким образом, наши исследования показывают, что в осесимметричной конфигурации магнитного поля, в процессе его инверсии, дозы радиации в квадрупольных радиационных поясах (северном и южном) распределятся несимметрично. Однако со временем можно ожидать, что под действием механизмов гибели и потерь частиц дозы радиации в квадрупольных поясах постепенно сравняются.
ЗАКЛЮЧЕНИЕ
Мы предложили новый сценарий инверсии магнитного поля, согласно которому дипольная и квадрупольная компоненты магнитного поля Земли имеют, соответственно, квазиосесимметричное и осесимметричное распределения. В процессе геомагнитной инверсии дипольная составляющая поля обращается в нуль, в то время как квадрупольная становится доминирующей. В итоге образуются два радиационных пояса и два кольцевых тока. В процессе инверсии области захвата заряженных частиц располагаются несимметрично относительно экваториальной плоскости, что впоследствии приводит к несимметричному распределению доз радиации в поясах квадруполя. Как видно из пространственного распределения максимальных мощностей поглощенных доз (рис. 7), дозы в северном поясе квадруполя превышают дозы в южном более чем на порядок. Основной вклад в радиацию квадрупольных поясов будут вносить электроны (рис. 6). А поскольку протоны слабо влияют на форму спектра (рис. 5), распределения поглощенных и эквивалентных доз мало отличаются. Таким образом, согласно нашим расчетам дозы радиации в современном поле выше доз в южном поясе квадруполе не более чем на два порядка в максимуме СА на магнитных оболочках L = 2–3RE и не менее чем в 3.5 раза на L = 4–8RE в минимуме СА. Заметим, что в данной работе сделаны оценки для максимально возможных доз радиации в момент инверсии магнитного поля Земли без учета нестационарных механизмов гибели и потерь заряженных частиц. Разумеется, возможны и другие сценарии инверсии с асимметричными полями. Так, квадруполь может принять квазиосесимметричную конфигурацию, тогда радиационные пояса сохраняться, но с меньшими дозами. В случае же неосесимметричной конфигурации квадруполя, следуя выводам теории Штермера, можно заключить, что радиационные пояса не смогут устойчиво существовать, а квазизахваченные в них частицы не внесут вклад в околоземную радиацию.
Мы выражаем большую благодарность В.В. Бенгину (НИИЯФ МГУ) за оказанную помощь в расчетах доз радиации.
Список литературы
Царева О.О., Зелёный Л.М., Малова Х.В. и др. Что ожидает человечество при инверсии магнитного поля Земли: угрозы мнимы и подлинные // УФН. 2018. Т. 188. С. 208–220.
Stormer C. The polar aurora. Oxford: Clarendon Press, 1955.
Лонгейр М. Астрофизика высоких энергий. М.: Мир, 1983.
Дорман Л.И., Смирнов В.С., Тясто М.И. Космические лучи в магнитном поле Земли. М.: Наука, 1971.
Thébault E., Finlay C.C., Toh H. International Geomagnetic Reference Field: the 12th generation // Earth, Planets and Space. 2015. V. 67. P. 158.
Vogt J., Glassmeier K.H. On the location of trapped particle populations in quadrupole magnetospheres // J. Geophys. Res. 2000. V. 105. № A6. P. 13,063. https://doi.org/10.1029/2006JA012224
Popova E. Dynamical systems for modeling the evolution of the magnetic field of stars and Earth // J. Phys.: Conf. Series. 2016. V. 681 P. 12.
Попова Е.П. Cовременные результаты асимптотических исследований моделей динамо // УФН. 2016. Т. 186. № 6. С. 577–596.
Urban E.W. Critical Störmer Conditions in Quadrupole and Double Ring-Current Fields // J. Math. Phys. 1965. V. 6.
Тверской Б.А. Динамика радиационных поясов Земли. М.: Наука, 1968.
Sawyer D.M., Vette J.I. AP-8 Trapped proton environment for solar maximum and solar minimum. NASA Report NSSDC/WDC-A-R&S 76-06. 1979.
Vette J.I. AE-8 Trapped electron environment. NASA Report NSSDC/WDC-A-R&S 1-24. 1991.
Антонов Р.А. Модель космоса / Под ред. Панасюка М.И., Новикова Л.С. М.: КДУ. 2007. Т. 1
Гецелев И.В., Зубарев А.И., Пудовкин О.Л. Радиационная обстановка на борту космических аппаратов. ЦИПК, 2001.
Tsareva O.O. Generalization of Störmer theory for an axisymmetric superposition of dipole and quadrupole fields // J. Geophysical Research: Space Physics. 2019. N. 124, P. 2844–2853.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования