Космические исследования, 2021, T. 59, № 1, стр. 78-88

1. ВВЕДЕНИЕ

Первая успешная автоматическая мягкая посадка на поверхность Луны была осуществлена советским космическим аппаратом Луна-9 [1] в 1966 г. Первая пилотируемая успешная посадка на Луну была выполнена американским кораблем Apollo-11 в 1969 г. [2]. В настоящее время в стадии разработки различными космическими агентствами находится ряд новых лунных миссий.

Примеры исследований по траекториям посадки на Луну приведены в [3–21], где рассматривались различные аспекты подобных траекторий: проектирование схем полета, алгоритмы наведения и оптимизация траекторий, проблема перенацеливания и т.д. Многие из ранних работ по оптимизации траекторий посадки на Луну были основаны на непрямых методах, использующих принцип максимума Понтрягина [22]. Решения одномерной задачи вертикального снижения с мягкой посадкой были изложены в [3, 4]. Численный метод оптимизации плоских траекторий посадки был представлен в [5]. В 1971г. получено точное аналитическое решение такой задачи [6]. Рассматривались различные оптимальные стратегии мягкой посадки с окололунной орбиты [10]. Другие численные решения основаны на прямых методах оптимизации использующих, как правило, алгоритмы нелинейного программирования [9, 13, 18]. Ряд работ посвящен разработке алгоритмов управления [7, 12, 15–17]. Практические космические миссии зачастую требуют удовлетворения не только условий по мягкой посадке, но и выполнения специфичных ограничений. Как пример, имеются ограничения во внутренних точках траектории в форме граничных условий или неравенств, ограничения по предпочтительной ориентации и другие операционные ограничения. Траектории посадки с безопасным профилем посадки и ограничениями по ориентации исследовались автором в [14], а ограничение по профилю снижения рассматривались в [18]. Это ограничение связано с двумя целями: посадочная ступень не должна пересекать лунную поверхность (в случае наличия неровностей рельефа вблизи точки посадки) и ограничивает угол видимости этой точки, от которого зависит качество работы системы видеонавигации.

Траектории посадки с окололунных орбит включают три фазы: сход с орбиты, перелет с орбиты и финальную фазу – торможение [11]. Рассматриваются пространственные траектории на фазе торможения. Такие траектории представляют собой интерес для точек посадки, смещенных относительно орбитальной трассы и/или задач перенацеливания. В статье представлен новый приближенный метод двухуровневой прямой оптимизации для заданных конечных продольной и боковой дальностей при свободном времени перелета. Верхний уровень соответствует одномерной оптимизации времени с использованием нелинейного программирования. Нижний уровень – оптимизация посадки при заданном конечном времени и заданных координатах точки посадки, которая базируется на численном методе с использованием дискретных множеств псевдоимпульсов [14, 23]. Этот метод использует дискретизацию траектории на малые сегменты и близкую к равномерной дискретную аппроксимацию пространства управления (т.е. возможные направления вектора тяги и ее величина) множествами псевдоимпульсов с ограничениями неравенствами на каждом сегменте. Краевые условия представляются как линейное матричное уравнение и требуют вычисления частных производных по всем псевдоимпульсам на каждом сегменте. Матричное неравенство для сумм характеристических скоростей псевдоимпульсов используется для преобразования задачи в форму линейного программирования высокой размерности. Ограничение по профилю снижения представляется дополнительной строкой в матрице неравенства. Современные методы линейного программирования используют алгоритмы внутренней точки для решения подобных задач высокой размерности. В общем случае непрерывные маневры включают некоторое число смежных сегментов и необходима обработка решений линейного программирования для формирования последовательности маневров. Итеративный процесс требуется для обновления массы посадочной ступени по сегментам и параметров ограничения по профилю снижения.

Целью работы является разработка метода оптимизации пространственных траекторий посадки на Луну при ограничениях для получения энергетических оценок, которые необходимы для проектирования лунной посадочной ступени (ЛПС).

2. УРАВНЕНИЯ ДВИЖЕНИЯ ЛУННОЙ ПОСАДОЧНОЙ СТУПЕНИ

Трехмерное движение ЛПС переменной массы моделируется в виде точечной массы, движущейся в плоскопараллельном однородном гравитационном поле:

где H – высота; L – дальность; B – боковая дальность; V – скорость; t – время; f_T – безразмерный уровень тяги (для максимальной тяги f_T = 1); a₀ – начальное реактивное ускорение; m – безразмерная масса аппарата (в начальный момент m₀ ≡ 1); $\dot {m}$ – безразмерный массовый расход для максимального уровня тяги; g_M – гравитационное ускорение на поверхности Луны; φ – угол тангажа (между продольной осью ЛПС и плоскостью OLB); ψ – курсовой угол (между проекцией продольной осью ЛПС на плоскость OLB и плоскостью OLH). Для траекторий с изменением высоты на ~15 км и дальности ~200 км эта гравитационная модель имеет ошибки по величине гравитационного ускорения до ~0.85% и до ~2.5° град по его направлению.

Предполагается, что двигатель жестко связан с корпусом аппарата. Таким образом, направление вектора тяги непосредственно определяет ориентацию аппарата.

3. ОПТИМИЗАЦИЯ ТРАЕКТОРИИ ДЛЯ МЯГКОЙ ПОСАДКИ НА ЛУНУ

3.1. Постановка задачи и двухуровневая оптимизация

Рассматривается оптимизация двигательной траектории снижения с минимальными затратами топлива: определить профиль тяги f_T(t) и углы ориентация вектора тяги φ(t) и ψ(t), которые минимизируют следующий функционал:

для уравнений движения (1) и следующих начальных и конечных краевых условий: и ограничении по профилю снижения, при котором посадочный аппарат должен оставаться внутри конуса с максимальным углом γ и вершиной в заданной точке посадки (рис. 1). Уровень тяги должен быть $0 \leqslant {{f}_{T}}(t) \leqslant 1$.

Для представленной постановки конечное время t_f является свободным параметром, которое должно быть определено при оптимизации. Эта задача может быть решена с использованием двухуровневой оптимизации, где верхний уровень соответствует одномерной задаче нелинейного программирования для t_f и нижний уровень – оптимизация траекторий посадки по f_T(t), φ(t) и ψ(t) при фиксированном конечном времени t_f . Для решения задачи верхнего уровня используется функция fminbnd из пакета MATLAB^® [24].

3.2. Оптимизация лунных траекторий посадки при заданном конечном времени

В качестве алгоритма оптимизации на нижнем уровне используется метод, основанный на концепции множеств псевдоимпульсов [14, 23]. Вводится разбиение времени [t₀, t₁, t₂, …,_,t_n], с t₀ = 0 и t_n = t_f, t₀< t₁< t₂ …<t_n, и Δt_i = = t_i + 1 – t_i малый интервал времени для I = 1, 2, .., n.

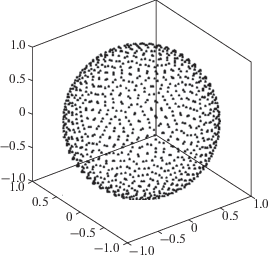
Каждый i-й сегмент рассматривается независимо от других сегментов. Все возможные направления вектора тяги могут быть представлены как k безразмерных псевдоимпульсов $\Delta V_{i}^{{(j)}}$ (являющихся эквивалентом уровня тяги) с близким к равномерному распределением на единичной сфере (рис. 2). Тогда оптимальный импульс можно представить суммой $\Delta {{{\mathbf{V}}}_{{i{\text{ opt}}}}} = \sum\nolimits_1^k {\Delta V_{i}^{{(j)}}{\mathbf{e}}_{i}^{{(j)}}} $ с ограничением на сумму характеристических скоростей псевдоимпульсов: $\sum\nolimits_{j = 1}^{j = k} {\Delta V_{i}^{{(j)}}} \leqslant 1$.

Оптимальный импульс будет суммой ближайших псевдоимпульсов [14, 23].

Для вектора неизвестных неотрицательных переменных размерностью (n × k) X^T = $ = [\Delta V_{1}^{{(1)}},\Delta V_{1}^{{(2)}},$ … $\Delta V_{1}^{{(k)}},\Delta V_{2}^{{(1)}},\Delta V_{2}^{{(2)}},$ … $\Delta V_{2}^{{(k)}}$, … $\Delta V_{n}^{{(k)}}]$, включающего все псевдоимпульсы на всех сегментах, можно записать линейное матричное неравенство:

где: А – матрица размерностью n × (n × k) (показаны только ненулевые элементы):

Вектор ${\mathbf{b}}$ имеет размерность n

Вектор краевых условий при заданном конечном времени t_f

Предположим, что приближенные значения масс на сегментах m_i известны, тогда для постоянного управления на каждом сегменте можно записать:

где ${{{\mathbf{A}}}_{e}}$ – матрица частных производных краевых условий размерностью 6 × (n × k). Вектор краевых условий вдоль пассивной траектории.

Столбцы матрицы частных производных А_е:

где l = (i – 1) × k + j – номер столбца или номер неизвестной переменной, $\Delta t = {{{{t}_{f}}} \mathord{\left/ {\vphantom {{{{t}_{f}}} n}} \right. \kern-0em} n}$.

Для вектора неизвестных переменных X можно записать следующие линейное матричное уравнение:

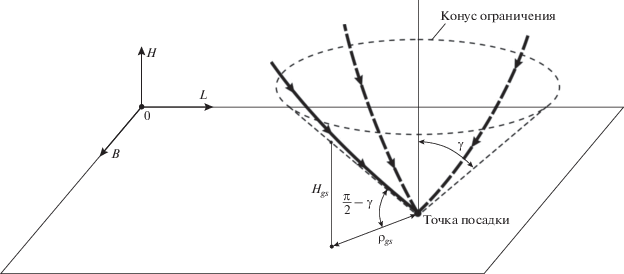
где $\Delta {\mathbf{P}}_{f}^{{}}$ – целевой вектор.

Ограничение по профилю снижения может быть представлено как минимальная высота H_gs в заданный момент t_gs для положения смещенного относительно точки посадки (см. рис. 1).

где ${{\rho }_{{gs}}}({{t}_{{gs}}}) = \sqrt {L{{{({{t}_{{gs}}})}}^{2}} + B{{{({{t}_{{gs}}})}}^{2}}} $. Более строго это требует некоторого числа точек на конусе, но вычислительный опыт показал, что достаточно одной точки. Эта точка соответствует времени t_gs близком к границе конуса. Ограничение высотного профиля является ограничением во внутренних точках траектории и требует введения дополнительной строки в матрице неравенств (3) где ${\mathbf{A}}{\text{*}}$ – базовая матрица в (3), ${{{\mathbf{O}}}_{{(n - l)}}}$ – нулевая строка и

Вектор размерности n + 1 ${{{\mathbf{b}}}^{{\mathbf{T}}}} = \left[ {{{{{\text{(}}{\mathbf{b}}*{\text{)}}}}^{{\text{T}}}}{\text{, }}{{b}_{{gs}}}} \right]$ , где ${{b}_{{gs}}} = - \delta H_{{gs}}^{*} - {{H}_{0}}$; $\delta H_{{gs}}^{*} = {{V}_{{H0}}}{{t}_{{gs}}} - {{{{g}_{M}}t_{{gs}}^{2}} \mathord{\left/ {\vphantom {{{{g}_{M}}t_{{gs}}^{2}} 2}} \right. \kern-0em} 2}$.

Введем вектор весовых коэффициентов размерностью (n × k)

тогда для функционала соответствующего минимальной характеристической скорости можно записать: $J = \Delta {{V}_{x}} = \min \left( {{{{\mathbf{q}}}^{{\mathbf{T}}}} \cdot {\mathbf{X}}{\text{ }}} \right)$.

Это является классической задачей линейного программирования с ограничениями линейного матричного неравенства (2) и линейного матричного равенства (5). Элементы вектора неизвестных переменных X должны быть неотрицательны и ограничены: $0 \leqslant {\text{ }}\Delta V_{i}^{{{\text{(}}j{\text{)}}}} \leqslant 1$ .

Если решение для заданного конечного времени и краевых условий не существует, то в качестве функционала используется штрафная функция. Для решений линейного программирования необходима специальная обработка. Требуется найти все сегменты, соответствующие ненулевым неизвестным переменным. Среди них все смежные сегменты объединяются в маневры.

Такая задача имеет высокую размерность. Современное программное обеспечение такое как MATLAB^® имеет эффективные алгоритмы для вычислений с разряженными матрицами, включая алгоритмы линейного программирования высокой размерности (функция linprog [24]). Типовой процесс решения требует менее 2–4 мин вычислений с процессором Intel^® Core^® 2 Duo.

Поскольку m_i (8), H(t_gs) и ρ_gs(t_gs) из (6) заранее неизвестны, требуется итеративный процесс для обновления масс m_i на всех сегментах (8), частных производных (4) и ${{b}_{{gs}}}$ в (7б). После получения решения линейного программирования выполнения процедуры обработки, рассчитывается новая траектория и определяется новый вектор смещения краевых условий $\delta {\mathbf{P}}_{f}^{{(s)}}$ и смещение $\delta b_{{gs}}^{{(s)}}$. Для второй и последующих итераций обновляется прицельный вектор и смещение $\delta b_{{gs}}^{{}}$: $\Delta {\mathbf{P}}_{f}^{{(s + 1)}} = \Delta {\mathbf{P}}_{f}^{{(s)}} - \delta {\mathbf{P}}_{f}^{{(s)}}$, $b_{{gs}}^{{(s + 1)}} = b_{{gs}}^{{(s)}} - \delta b_{{gs}}^{{(s)}}$, $b_{{gs}}^{{(s)}} = {{H}^{{(s)}}}({{t}_{{gs}}}) - H_{{gs}}^{{(s)}}$ = H^(s)(t_gs) – $ - \,\,\rho _{{gs}}^{{(s)}}({{t}_{{gs}}}){\text{tg}}({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \gamma )$, где s – номер итерации. Как правило, для сходимости параметров в этих вычислениях требуется 3–4 итераций.

4. ЧИСЛЕННЫЕ ПРИМЕРЫ

4.1. Начальные данные и параметры посадочной ступени

Подобно работе [11] для фазы торможения использовались следующие начальные условия: H₀ = 15 км; V_H0 = 0; V_L0 = 1692 м/с. В конце этой фазы ориентация вектора тяги должна быть вдоль вертикали в точке посадки. Соответствующие граничные условия: H_f = 0.05 км; V_Hf = –1 м/с. Для посадочной ступени приняты a₀ = 0.006 км/с² и $\dot {m}$ соответствует удельному импульсу I_sp = 350 с. Траектории разбиты на 100 одинаковых по времени сегментов и используют равномерное распределение псевдоимпульсов на единичной сфере с k = 2000 точек. Таким образом, число неизвестных переменных составляло n × k= 200 000.

4.2. Энергетически достижимые области для фазы торможения

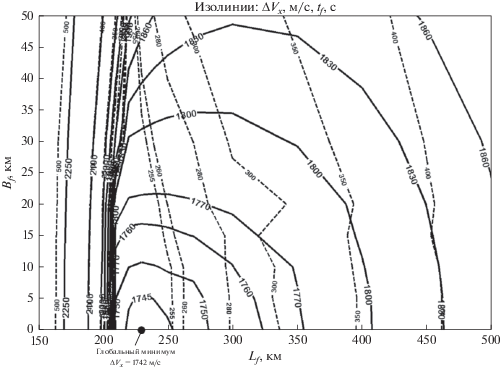
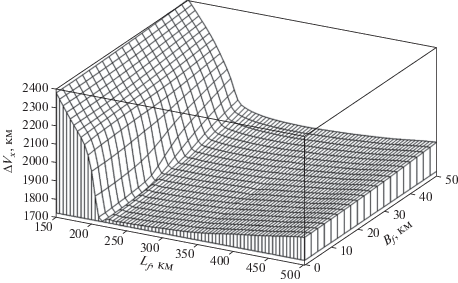
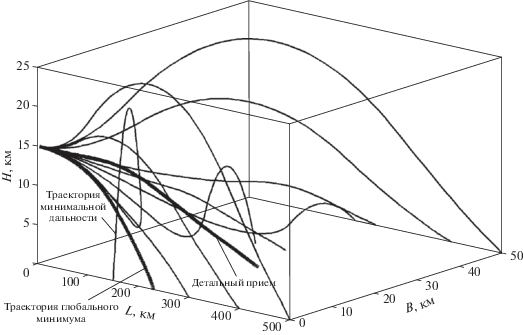
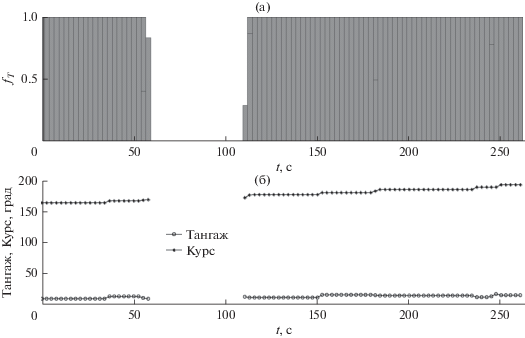
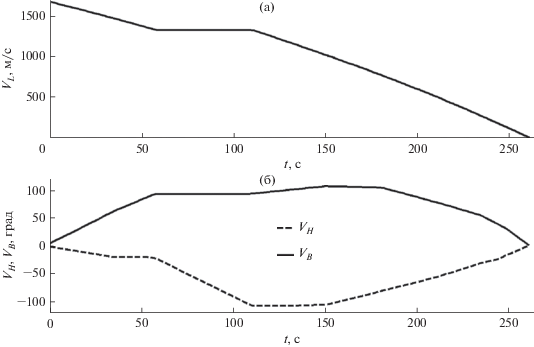
Карты изолиний потребных характеристических скоростей $\Delta {{V}_{x}}({{L}_{f}},{{B}_{f}})$ (сплошные линии) и оптимальные времена посадки ${{t}_{f}}({{L}_{f}},{{B}_{f}})$ (пунктирные линии) для точек посадки как функция продольной и боковой дальности относительно начальной точки представлены на рис. 3. Соответствующая трехмерная поверхность $\Delta {{V}_{x}}({{L}_{f}},{{B}_{f}})$ изображена на рис. 4. Эта поверхность имеет малый наклон за исключением траекторий с минимальной продольной дальностью (${{L}_{f}} < 210{\text{ км}}$), при резком росте значений $\Delta {{V}_{x}}$. Схематические примеры оптимальных пространственных траекторий (оси в разных масштабах) показаны на рис. 5 (толстая линия – траектория глобального минимума). В качестве примера, параметры одной пространственной траектории (толстая линия на рис. 5 – детальный пример) представлены на рис. 6–7. Распределение маневров показано на рис. 6а, где каждый заштрихованный прямоугольник представляет сегмент ненулевой тяги (значение 1 соответствует максимальной тяге). Изменение ориентации вектора тяги представлено на рис. 6б. Углы тангажа и курса фактически близки к линейным зависимостям. Кусочно-постоянными они получаются из-за дискретности представления множеств псевдоимпульсов. На рис. 7 показано изменение компонент скорости по времени. Отметим что боковая скорость на траектории достигает по величине значения ~100 м/с.

Абсолютное большинство траекторий имеет два маневра с максимальной тягой – в начале и в конце траектории (см. пример на рис. 6a). Это соответствует теории базис-вектора Лоудена для однородного гравитационного поля [25]. Имеется глобальный минимум $\Delta {{V}_{x}} = 1742{\text{ }}{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ (для ${{L}_{f}} = 230{\text{ км; }}$ ${{B}_{f}} = 0;$ ${{t}_{f}} = {\text{241}}\,\,{\text{с}}$), который соответствует плоской траектории с непрерывным маневром.

4.3. Достижимая область перенацеливания

Рассмотрены энергетически достижимые области перенацеливания связанные с ограниченными дополнительными характеристическими скоростями. В качестве начальной точки для перенацеливания использованы параметры траектории снижения из предыдущего раздела (для высоты H₀ = 1 км) (L_f = 250 км; B_f = 0; t_f = = 252.6 м/с). Эта траектория близка к глобальному минимуму $\Delta {{V}_{x}}$ с конечным участком, представляющим почти непрерывный маневр. Начальные параметры траектории при перенацеливании: ${{H}_{0}} = 1{\text{ км}};$ ${{L}_{0}} = 242.5{\text{ км;}}$ ${{B}_{{\text{0}}}} = 0;$ ${{V}_{{H0}}} = - 44{\text{ м/с;}}$ ${{V}_{{L0}}} = 317{\text{ м/с}};$ ${{V}_{{B0}}} = 0;$ ${{m}_{0}} = 0.675$.

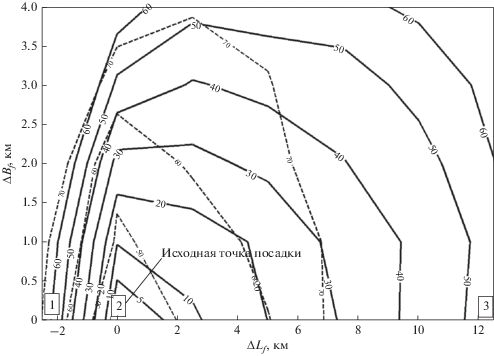
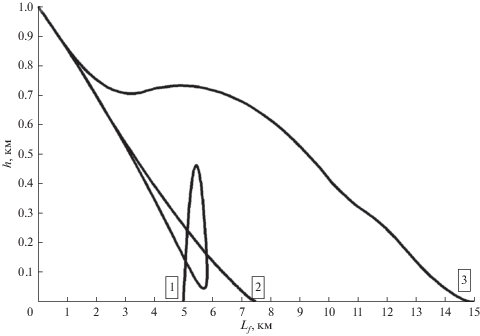
Пример карт изолиний (для полуплоскости) дополнительных характеристических скоростей $\Delta {{V}_{x}}$ (сплошные линии) и времен посадки ${{t}_{f}}$ (пунктирные линии) для перенацеливания показан на рис. 8. Это функция смещений (отклонение дальности $\Delta {{L}_{f}}$ и боковой дальности $\Delta {{B}_{f}}$) для новых точек посадки от исходной точки посадки. На рис. 9 показаны примеры вертикальных профилей для плоских траекторий. Номера маркеров соответствуют точкам посадки на рис. 9. Экзотическая петлевая траектория (№ 1) возможно практического интереса не имеет, но с энергетической точки зрения она возможна.

Очевидно, что перенацеливание предпочтительнее в направлении горизонтальной скорости для ΔL_f = +3 км дополнительная характеристическая скорость $\Delta {{V}_{x}}$ ~ 10 м/с. Такая же $\Delta {{V}_{x}}$ может реализовать боковое смещение ΔB_f ~ 1 км и в направлении противоположном горизонтальной скорости это будет только ΔL_f = –0.4 км.

4.4. Траектория с большой боковой дальностью и ограничением по профилю снижения

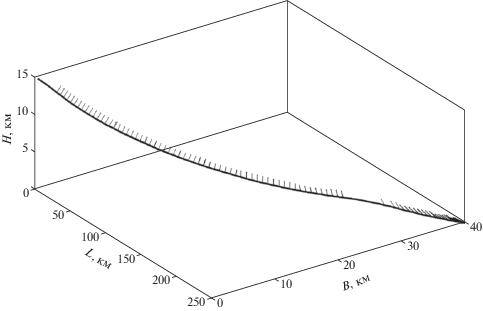
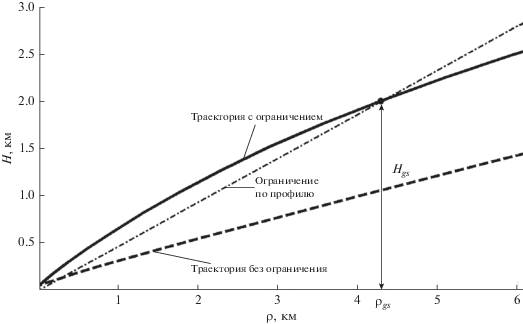
Пример оптимальной траектории посадки для начальной точки $({{H}_{0}} = 15{\text{ км, }}$ ${{L}_{0}} = {{B}_{0}} = 0{\text{)}}$ и точки посадки $({{H}_{f}} = 0.05{\text{ км, }}$ ${{L}_{f}} = 250{\text{ км, }}$ ${{B}_{f}} = 40{\text{ км)}}$, угла наклона профиля ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \gamma = 25^\circ $ и оптимального конечного времени ${{t}_{f}} = 268.3{\text{ с}}$ представлен на рис. 10. Потребная характеристическая скорость ΔV_x = 1838.3 м/с. Для этой траектории имеется два непрерывных маневра. Направления реактивного ускорения на маневрах – непрерывные функции с диапазоном изменения угла тангажа 30°–60° и угла курса 100°–180°. Трехмерный вид траектории показан на рис. 10 (без масштаба). Направления реактивного ускорения для всех сегментов изображены стрелками. Вертикальный профиль траектории на заключительной фазе как функция H(ρ) представлен на рис. 11 (ρ – горизонтальная дальность до точки посадки). Штрихпунктирная линия соответствует ограничению профиля снижения. Для сравнения вертикальный профиль снижения на траектории без ограничения представлен пунктирной линией. Как видно, это ограничение является активным.

Для траектории без ограничений с теми же начальной и конечной точками потребное ΔV_x = = 1825.7 м/с.

4.5. Пространственные траектории с различными углами профиля снижения

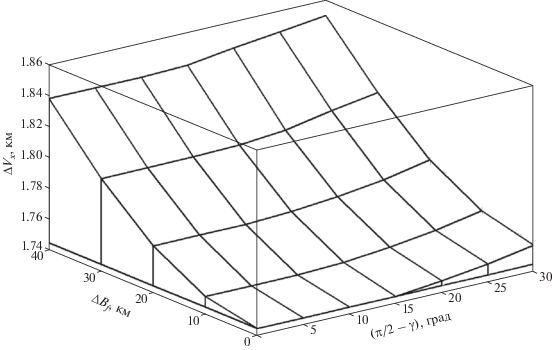
На рис. 12 показано изменение характеристической скорости $\Delta {{V}_{x}}$ как функция угла профиля снижения боковой дальности. Для малых углов $({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \gamma )$ меньших 15° ограничение по профилю снижения неактивно. Для угла $({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \gamma )$ в диапазоне 15°–30° дополнительное $\Delta {{V}_{x}}$ близко к линейной функции угла с производной ${{\partial \Delta {{V}_{x}}} \mathord{\left/ {\vphantom {{\partial \Delta {{V}_{x}}} {\partial \gamma }}} \right. \kern-0em} {\partial \gamma }} \cong (1...1.2)$ (м/c)/град. Как видно основные дополнительные затраты $\Delta {{V}_{x}}$ связаны с боковой дальностью ${{B}_{f}}$.

ЗАКЛЮЧЕНИЕ

В работе предложен новый метод оптимизации траектории мягкой посадки на Луну на фазе торможения. Это решение минимизирующее затраты характеристической скорости основано на двухуровневой процедуре оптимизации для заданных продольной и боковой дальностях при свободном конечном времени. Верхний уровень представляет одномерное решение нелинейного программирования для времени посадки. Нижний уровень соответствует оптимизации для формируемых на верхнем уровне времен посадки и заданных координатах точки посадки на базе линейного программирования высокой размерности. Представлено преобразование этой задачи к форме классического линейного программирования, которое позволяет учитывать ограничение по профилю снижения.

В качестве примеров использования представлены энергетически достижимые траектории для фазы торможения и для перенацеливания, рассмотрены пространственные траектории для различных углов наклона профиля снижения. Описываются детали и вычислительные особенности численного метода.

Представленные результаты позволяют сделать энергетические оценки и могут использоваться при проектировании лунной посадочной ступени.