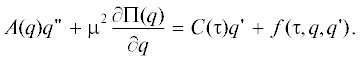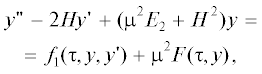Космические исследования, 2021, T. 59, № 2, стр. 135-148
Исследование установившихся движений искусственного спутника Земли в режиме одноосной магнитной ориентации
А. И. Игнатов 1, *, В. В. Сазонов 2
1 Государственный космический научно-производственный центр им. М.В. Хруничева
Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: general_z@mail.ru
Поступила в редакцию 18.02.2020
После доработки 05.04.2020
Принята к публикации 29.05.2020
Аннотация
Исследовано вращательное движение осесимметричного искусственного спутника с постоянным магнитом под действием механического момента, создаваемого влиянием на магнит магнитного поля Земли (МПЗ). Орбитальное движение спутника рассчитывается с учетом нецентральности гравитационного поля Земли и сопротивления атмосферы, собственный магнитный момент спутника параллелен оси симметрии. Построены установившиеся движения спутника, в которых эта ось составляет малый угол с вектором напряженности МПЗ. В качестве модели МПЗ используется модель IGRF. Показана возможность аппроксимации таких движений последовательностью периодических решений модифицированных уравнений движения. Установившиеся движения содержат две базисные частоты – орбитальную и угловую скорость вращения Земли. Периодические решения имеют орбитальный период, но спектр составленной из них аппроксимирующей последовательности практически совпадает со спектром исходного установившегося режима.
1. УРАВНЕНИЯ ДВИЖЕНИЯ СПУТНИКА
Спутник считаем осесимметричным твердым телом, центр масс которого движется по геоцентрической орбите. На спутнике установлен магнит, создающий постоянный дипольный момент, направленный по оси симметрии спутника. Для записи уравнений движения спутника и представления полученных результатов используется гринвичская система координат $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Ее начало находится в центре Земли, плоскость $C{{y}_{1}}{{y}_{2}}$ совпадает с плоскостью экватора, ось $C{{y}_{1}}$ пересекает гринвичский меридиан, ось $C{{y}_{3}}$ направлена к Северному полюсу. Полагаем, что эта система вращается с постоянной угловой скоростью ${{{\mathbf{\omega }}}_{{\text{E}}}} = \left( {0,0,{{\omega }_{{\text{E}}}}} \right)$ вокруг оси $C{{y}_{3}}$. Здесь и ниже компоненты векторов относятся к системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$.
Уравнения движения спутника состоят из двух подсистем. Одна подсистема описывает движение центра масс спутника, другая его движение относительно центра масс – вращательное движение. В подсистеме уравнений движения центра масс учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16.16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается согласно модели ГОСТ Р 25645.166-2004. Параметры атмосферы и баллистический коэффициент спутника считаются неизменными на всем интервале интегрирования уравнений движения.
Подсистема уравнений вращательного движения образована уравнениями, описывающими теорему об изменении кинетического момента спутника в движении относительно центра масс и уравнениями Пуассона для орта оси симметрии спутника. В уравнениях кинетического момента учитываются гравитационный момент, модельный демпфирующий момент и механический момент, обусловленный взаимодействием магнита спутника с магнитным полем Земли (МПЗ). Формулы этих моментов приведены в [1].
Подсистема уравнений вращательного движения имеет вид
(1)
$\begin{gathered} {\mathbf{\dot {\Omega }}} + {{{\mathbf{\omega }}}_{{\text{E}}}} \cdot {\mathbf{\Omega }} + {{k}_{\Omega }}{\mathbf{\Omega }} = \\ = \nu (1 - \lambda )({\mathbf{n}} \cdot {\mathbf{r}})({\mathbf{n}} \cdot {\mathbf{r}}) + {{l}_{0}}({\mathbf{n}} \cdot {\mathbf{B}}), \\ {\mathbf{\dot {n}}} + {{{\mathbf{\omega }}}_{{\text{E}}}} \cdot {\mathbf{n}} = {\mathbf{\Omega }} \cdot {\mathbf{n}},\,\,\,\,\nu = \frac{{3{{\mu }_{{\text{E}}}}}}{{{{{\left| {\mathbf{r}} \right|}}^{5}}}},\,\,\,\lambda = \frac{{{{I}_{1}}}}{{I{}_{2}}}. \\ \end{gathered} $В программе численного интегрировании уравнений (1) использованы следующие единицы измерения физических величин: $[t] = {{10}^{3}}$ с, $[r] = {{10}^{6}}$ м, $[{\mathbf{\Omega }}] = [{{k}_{\Omega }}] = {{10}^{{ - 3}}}$ с–1, $[{\mathbf{B}}] = $ Гс, $[{{l}_{0}}] = {{10}^{{ - 6}}}$ с–2 Гс–1 (в единицах СИ $[{{l}_{0}}] = {{10}^{{ - 2}}}$ А/кг). Параметры уравнений движения: $\lambda = 0.236$, баллистический коэффициент спутника $0.0017$ м2/кг, параметры модели атмосферы: $F$ = 137, ${{F}_{{81}}}$ = 117, ${{A}_{p}} = $ 10. Параметр ${{l}_{0}}$ варьировался в пределах от 2 до 6 А/кг, параметр ${{k}_{\Omega }}$ принимал значения: 0 и 0.00015 с–1.
Начальные условия движения центра масс спутника заданы на момент 10:13:07 декретного московского времени 5.V.2013. На этот момент элементы орбиты составляли: высота в апогее 575.2 км, высота в перигее 546.8 км, наклонение 64.87°, аргумент широты перигея –124.65°, долгота восходящего узла (отсчитывается от точки весеннего равноденствия эпохи даты) –16.73°. Это параметры орбиты спутника Бион-М № 1. Начальные условия уравнений (1) задаются в тот же момент времени, что и начальные условия принятой орбиты. Этот момент служит началом отсчета времени – точкой $t = $ 0.
Ниже рассматриваются движения спутника в режиме одноосной магнитной ориентации [2–4]. В этом режиме ось симметрии спутника совершает малые колебания относительно вектора магнитной индукции МПЗ.
2. ПОСТРОЕНИЕ ОРИЕНТИРОВАННЫХ ДВИЖЕНИЙ СПУТНИКА
При ${{k}_{\Omega }} > 0$ движение спутника в режиме одноосной магнитной ориентации можно искать методом установления – представляющий интерес режим должен быть асимптотически устойчив. В данной работе с этой целью на решениях уравнений (1) минимизировался функционал
(2)
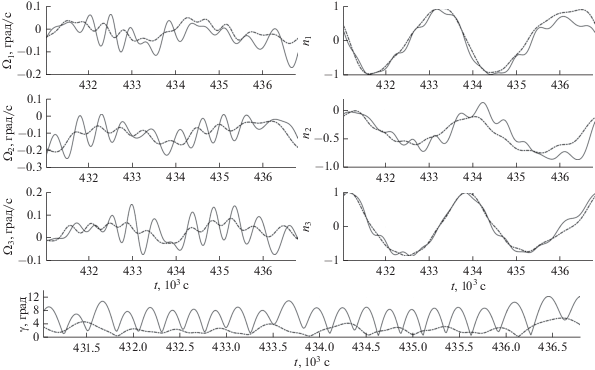
$\Phi = \sum\limits_{s = 0}^S {{{{\left| {{\mathbf{B}}(s\tau ) \cdot {\mathbf{n}}(s\tau )} \right|}}^{2}}} ,$Примеры расчетов решений уравнений (1) с начальными условиями экстремалей функционала (2) приведены на рис. 1–3. Решения вычислены на отрезке времени длиной 20 суток при ${{l}_{0}} = 4$ А/кг. Решение на рис. 1, 2 получено в случае ${{k}_{\Omega }} = 0.00015$ с–1 и $S = 288$. Здесь изображены графики зависимости от времени компонент векторов ${\mathbf{\Omega }} = ({{\Omega }_{1}},{{\Omega }_{2}},{{\Omega }_{3}})$, ${\mathbf{n}} = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ и угла $\gamma = \arccos \,({\mathbf{n}} \cdot {\mathbf{B}})$. Графики построены на отрезках времени $0 \leqslant t \leqslant 3$ сут и $3 \leqslant t \leqslant 20$ сут. Они показывают, что найденное решение можно считать установившимся и описывающим режим одноосной магнитной ориентации. На графиках ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ видны колебания большой амплитуды с периодом 1 сут и колебания малой амплитуды, период которых – примерно половина орбитального периода.
Рис. 1.
Решение системы (1) при ${{k}_{\Omega }} = 0.00015$ с–1, компоненты вектора ${\mathbf{\Omega }}$.
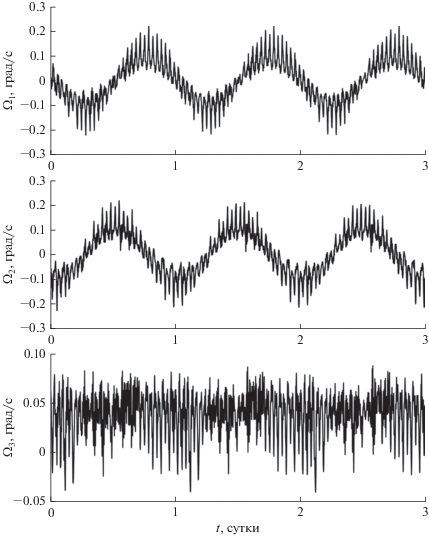
Рис. 2.
Решение системы (1) при ${{k}_{\Omega }} = 0.00015$ с–1, компоненты орта ${\mathbf{n}}$ и угол $\gamma $.
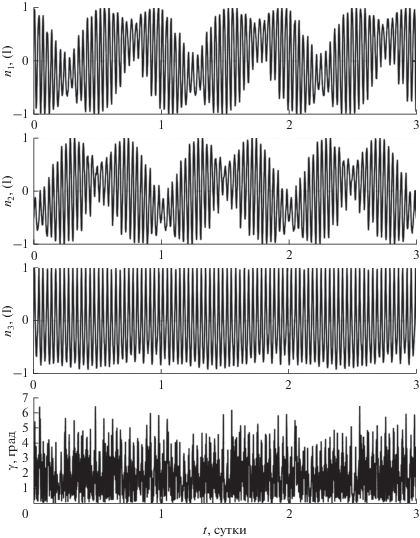
Рис. 3.
Решение системы (1) при ${{k}_{\Omega }} = 0$ и ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$, компоненты вектора ${\mathbf{\Omega }}$ и угол $\gamma $.
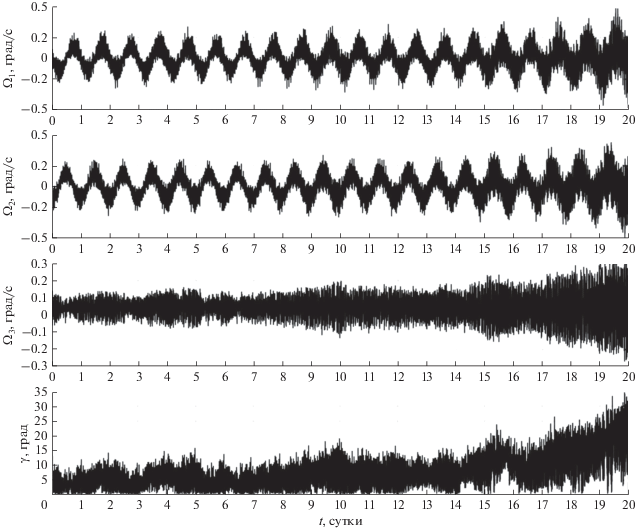
Решение на рис. 3 получено при ${{k}_{\Omega }} = 0$, $S = 1152$ и ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ (в случае ${{k}_{\Omega }} = 0$ система (1) имеет первый интеграл ${\mathbf{n}} \cdot {\mathbf{\Omega }} = {\text{const}}$). Здесь приведены графики компонент вектора ${\mathbf{\Omega }}$ и угла $\gamma $. Это решение первые несколько суток похоже на установившееся, и описывает движение спутника в режиме одноосной магнитной ориентации, но затем оно начинает разрушаться.
3. СПЕКТРАЛЬНЫЙ АНАЛИЗ ОРИЕНТИРОВАННЫХ ДВИЖЕНИЙ
Решение уравнений (1) на рис. 1, 2 выглядит как условно-периодическое. Его частоты были найдены с помощью спектрального анализа, выполнявшегося по следующей схеме [6]. Пусть ${{x}_{n}}$ $(n = 1,\;2,\; \ldots ,\;N)$ – значения какой-либо переменной $x(t)$ исследуемого решения в узлах равномерной временной сетки $\{ \,{{t}_{n}}\} $: ${{x}_{n}} = x({{t}_{n}})$. Во всех рассмотренных ниже примерах шаг сетки $h = {{t}_{{n + 1}}} - {{t}_{n}} = 16$ с. Периодограммой называется функция $I(f)$, рассматриваемая на отрезке $0 \leqslant f \leqslant F = {{(2h)}^{{ - 1}}}$, и определенная соотношениями
Его можно преобразовать к виду
В выражении для $\Delta {{I}_{1}}(f)$ частоты ${{\Omega }_{j}}$ и $\Omega _{j}^{'}$ принадлежат множеству чисел $\{ \pm f_{1}^{^\circ }, \pm f_{2}^{^\circ }, \ldots , \pm f_{M}^{^\circ }\} $, коэффициенты ${{A}_{j}}$ и ${{B}_{j}}$ выражаются через ${{\alpha }_{m}}$ и ${{\beta }_{m}}$ $(m = 1,2, \ldots ,M)$.
Функция $W(f)$ называется функцией окна [6]. Она – четная, периодическая с периодом $2F$ и удовлетворяет соотношениям $0 \leqslant W(f) \leqslant 1$, $W(0) = 1$. Ее наименьший положительный нуль равен ${{(Nh)}^{{ - 1}}}$. Значимые максимумы (пики) функции окна равны 1 и достигаются в точках $f = 2Fl$ $(l = 0,\;1,\;2, \ldots )$. Вне малых окрестностей этих точек $W(f) < 0.01$. С увеличением $N$ ширина пиков этой функции сужается. В силу четности и периодичности функция окна полностью определяется своими значениями на отрезке $0 \leqslant f \leqslant F$.
Для $\Delta {{I}_{1}}(f)$ не удается найти простых эффективных оценок, но при большом $N$ вкладом этого слагаемого в значения функции ${{I}_{1}}(f)$ вблизи точек ее значимых максимумов можно пренебречь и принять
Таким образом, значимые максимумы функций ${{I}_{1}}(f)$ и ${{\tilde {I}}_{1}}(f)$ весьма близки. Отсюда, учитывая вид окна $W(f)$, можно найти точки этих максимумов – они определяются соотношениями $\left| {f \pm f_{m}^{^\circ }} \right| = 2Fl$ $(l = 0,\;1,\; \ldots \;)$. Если $f_{m}^{^\circ } < F$, то периодограмму ${{I}_{1}}(f)$ достаточно исследовать на интервале $0 < f < F$. На нем ее значимые максимумы достигаются в малой окрестности точек $f_{m}^{^\circ }$.
Вернемся к периодограмме $I(f)$. В случае исследуемых решений уравнений (1) ${{\alpha }_{0}} \approx x{\text{*}}$, значимые максимумы периодограммы достигаются в точках $f_{m}^{*} \approx f_{m}^{^\circ }$, и $\alpha _{m}^{2} + \beta _{m}^{2} \approx 4{{N}^{{ - 2}}}I(f_{m}^{*})$ $(m = 1,2, \ldots ,M)$. Точность выписанных соотношений увеличивается с ростом $N$. Таким образом, знание максимумов периодограммы позволяет получить оценки частот и амплитуд гармонических составляющих функции $x(t)$. Ниже вместо графиков периодограммы приводятся графики амплитудного спектра $A(f) = 2{{N}^{{ - 1}}}\sqrt {I(f)} $. Функция $A(f)$ удобна тем, что ее максимальные значения являются оценками амплитуд соответствующих гармоник. Однако ее значимые максимумы выражены менее наглядно значимых максимумов периодограммы.
На рис. 4 (слева) изображены амплитудные спектры ${{A}_{{\Omega {\kern 1pt} i}}}(f)$ переменных ${{\Omega }_{i}}(t)$ $(i = 1,2,3)$, графики которых приведены на рис. 1 (${{k}_{\Omega }} = 0.00015$ с–1). На рис. 4 (справа) изображены амплитудные спектры ${{A}_{{\Omega {\kern 1pt} i}}}(f)$ переменных ${{\Omega }_{i}}(t)$ $(i = 1,2,3)$, графики которых приведены на рис. 2 (${{k}_{\Omega }} = 0$). Амплитудные спектры представлены в диапазоне частот от 0 до $F$ = 0.0008 Гц. Для решения при ${{k}_{\Omega }} = 0.00015$ с–1 частоты и амплитуды наиболее значимых гармоник приведены в табл. 1. Здесь ${{f}_{E}} = {{{{\omega }_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{\omega }_{{\text{E}}}}} {2\pi }}} \right. \kern-0em} {2\pi }}$ – частота вращения Земли, ${{f}_{0}} = {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} {2\pi }}} \right. \kern-0em} {2\pi }}$ – орбитальная частота (${{\omega }_{0}}$ – среднее движение центра масс спутника). Наиболее значимый вклад в установившееся движение вносят гармоники с частотами ${{f}_{{\text{E}}}}$ и $2{{f}_{0}} - {{f}_{E}}$. Присутствие ${{f}_{{\text{E}}}}$ объясняется тем, что переменные уравнений (1) относятся к гринвичской системе координат, частота $2{{f}_{0}} - {{f}_{{\text{E}}}}$ является доминирующей в гринвичских компонентах векторной функции ${\mathbf{B}}$(t) в уравнениях (1). В модели прямого диполя компоненты этой функции в инерциальной системе координат меняются с частотой $2{{f}_{0}}$ [3].
Рис. 4.
Амплитудный спектр компонент вектора ${\mathbf{\Omega }}$: слева – ${{k}_{\Omega }} = 0.00015$ с–1, справа – ${{k}_{\Omega }} = 0$.
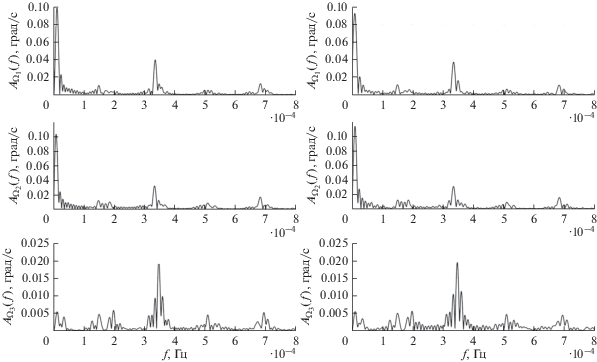
Таблица 1
| № | Частоты | Амплитуды | ||||
|---|---|---|---|---|---|---|
| $f$ | интерпре- тация | ${{A}_{{\Omega 1}}}$ | ${{A}_{{\Omega 2}}}$ | ${{A}_{{\Omega 3}}}$ | ${{A}_{\gamma }}$ | |
| ${{10}^{{ - 4}}}$ Гц | ${{10}^{{ - 3}}}$ град/c | град | ||||
| 1 | 0.1145 | ${{f}_{{\text{E}}}}$ | 99 | 103 | 5.44 | 0.142 |
| 2 | 0.3435 | $3{{f}_{{\text{E}}}}$ | 12 | 14 | 3.99 | 0.232 |
| 3 | 1.506 | ${{f}_{0}} - 2{{f}_{{\text{E}}}}$ | 11 | 12 | 4.71 | 0.184 |
| 4 | 1.621 | ${{f}_{0}} - {{f}_{{\text{E}}}}$ | 1.75 | 8.11 | 0.68 | 0.312 |
| 5 | 1.850 | ${{f}_{0}} + {{f}_{{\text{E}}}}$ | 3.06 | 10 | 3.85 | 0.106 |
| 6 | 1.964 | ${{f}_{0}} + 2{{f}_{{\text{E}}}}$ | 3.84 | 2.64 | 5.84 | 0.076 |
| 7 | 3.356 | $2{{f}_{0}} - {{f}_{{\text{E}}}}$ | 40 | 32 | 9.36 | 0.139 |
| 8 | 3.470 | $2{{f}_{0}}$ | 13 | 12 | 20 | 0.736 |
| 9 | 5.091 | $3{{f}_{0}} - {{f}_{{\text{E}}}}$ | 5.81 | 8.65 | 4.56 | 0.071 |
| 10 | 6.826 | $4{{f}_{0}} - {{f}_{{\text{E}}}}$ | 13 | 17 | 1.40 | 0.043 |
| 11 | 6.940 | $4{{f}_{0}}$ | 7.66 | 5.45 | 5.24 | 0.166 |
| 12 | 8.675 | $5{{f}_{0}}$ | 0.28 | 0.92 | 2.87 | 0.056 |
| 13 | 10.30 | $6{{f}_{0}} - {{f}_{{\text{E}}}}$ | 6.48 | 5.25 | 2.27 | 0.044 |
| 14 | 10.41 | $6{{f}_{0}}$ | 6.05 | 1.67 | 2.06 | 0.139 |
| 15 | 12.15 | $7{{f}_{0}}$ | 1.21 | 1.44 | 2.05 | 0.043 |
| 16 | 13.76 | $8{{f}_{0}} - {{f}_{{\text{E}}}}$ | 2.24 | 2.50 | 1.38 | 0.026 |
| 17 | 13.88 | $8{{f}_{0}}$ | 3.81 | 1.01 | 1.65 | 0.180 |
4. ПЕРИОДИЧЕСКАЯ АППРОКСИМАЦИЯ ОРИЕНТИРОВАННЫХ ДВИЖЕНИЙ
Базисные частоты установившегося режима магнитной ориентации: ${{f}_{0}}$ и ${{f}_{{\text{E}}}} \approx {{{{f}_{0}}} \mathord{\left/ {\vphantom {{{{f}_{0}}} {16}}} \right. \kern-0em} {16}}$. Основываясь на этом свойстве и учитывая соотношение ${{f}_{0}} \gg {{f}_{{\text{E}}}}$, построим аппроксимацию такого режима последовательностью периодических движений с периодом ${1 \mathord{\left/ {\vphantom {1 {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}}$, отличающихся положением орбиты относительно МПЗ.
На каждом орбитальном витке (между последовательными прохождениями восходящего узла орбиты) построим аппроксимирующее периодическое движение. При построении этого движения гринвичскую систему координат примем инерциальной, зафиксировав ее положение в абсолютном пространстве на момент прохождения спутником восходящего узла орбиты на данном витке. Орбиту в “замороженной” гринвичской системе примем кеплеровой эллиптической. Элементы этой орбиты вычисляются по фазовому вектору реальной орбиты в начальном восходящем узле. Таким образом, от витка к витку долгота восходящего узла орбиты в “замороженной” гринвичской системе координат меняется, меняется и положение орбиты относительно МПЗ, но внутри витка эти долгота и положение относительно МПЗ остаются неизменными. Уравнения вращательного движения спутника возьмем в виде (1), положив в них ${{\omega }_{{\text{E}}}} = 0$ и приняв в формулах для расчета координат и компонент скорости центра масс в “замороженной” гринвичской системе формулы кеплерова движения. Получившуюся систему уравнений обозначим (1a). Время входит в эту систему периодически с орбитальным периодом $T$, поэтому можно поставить задачу об отыскании ее периодических решений. Интерес представляет такое периодическое решение, которое можно будет использовать как аппроксимацию установившегося решения исходной системы (1) на данном витке.
Построение периодического решения системы (1a) сводится к решению для этой системы периодической краевой задачи
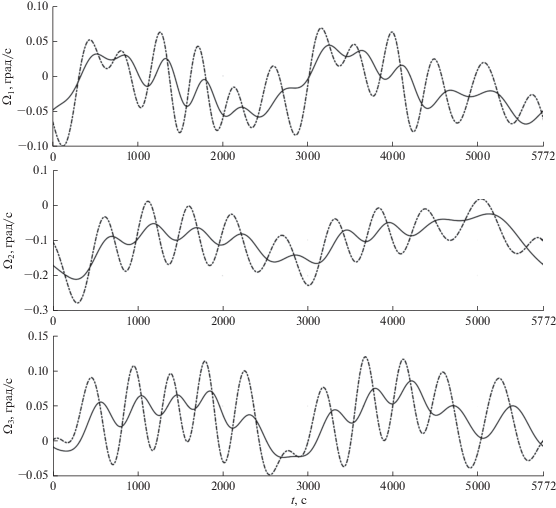
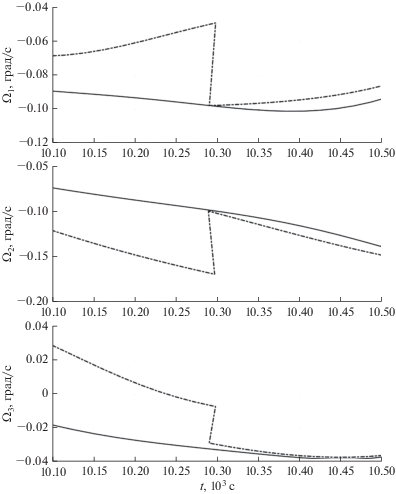
На рис. 5, 6 приведены результаты аппроксимации установившегося решения уравнений (1), рассмотренного в разделе 2 (${{k}_{\Omega }} = 0.00015$, рис. 1, 2). Здесь представлены графики зависимости от времени переменных ${{\Omega }_{i}}$, ${{n}_{i}}$ и угла $\gamma $. Графики аппроксимируемого решения – сплошные линии, графики аппроксимирующего решения – пунктирные. На рис. 5 аппроксимация показана на интервале решения краевой задачи (1a), (3). В принципе, аппроксимацию периодическими решениями можно построить на весьма продолжительном интервале времени, длина которого зависит от наличия подходящей орбиты спутника. На рис. 5 графики аппроксимирующего решения в малых окрестностях моментов прохождения восходящих узлов орбиты налегают друг на друга (кеплеров период несколько больше драконического), но при выбранном масштабе графиков на рис. 5 налегания практически не заметны. На рис. 6 показан стык решений задачи (1a), (3) на соседних витках (пунктирные линии) на фоне аппроксимируемого решения (сплошные линии). Строго говоря, в аппроксимирующую последовательность включается только отрезок периодического решения, расположенный между начальным и конечным на данном витке восходящими узлами. Отрезок решения за конечным восходящим узлом отбрасывается.
Рис. 5.
Аппроксимация решений системы (1) при ${{k}_{\Omega }} = 0.00015$ с–1: компоненты вектора ${\mathbf{\Omega }}$, орта ${\mathbf{n}}$ и угол $\gamma $. Сплошные линии – решения системы (1), пунктирные линии – решения краевой задачи (1a), (3).
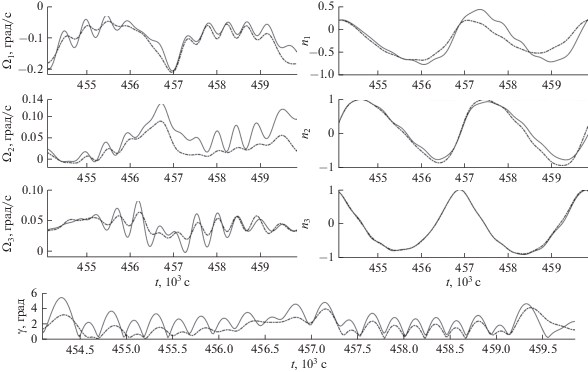
Рис. 6.
Аппроксимация решений системы (1) при ${{k}_{\Omega }} = 0.00015$ с–1: компоненты вектора ${\mathbf{\Omega }}$, орта ${\mathbf{n}}$ и угол $\gamma $. Сплошные линии – решения системы (1), пунктирные линии – решения краевой задачи (1a), (3).
Построенная аппроксимация оказалась достаточно точной. Это обусловлено двумя обстоятельствами. Во-первых, кеплерова аппроксимация орбиты в данной задаче приемлема для построения вращательного движения спутника на орбитальном витке. Во-вторых, МПЗ в “замороженной” системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ в течение витка меняется сравнительно мало, поскольку оно близко к полю диполя, момент которого расположен вблизи точки $C$ и составляет с осью $ - C{{y}_{3}}$ малый угол (~12°). Поле прямого диполя в таком случае вообще не менялось бы.
Последовательность периодических решений уравнений (1a) позволяет сформировать идеальный режим одноосной ориентации спутника в случае ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$. Этот режим обеспечивает те же ошибки ориентации, что и при ${{k}_{\Omega }} > 0$, но не может быть реализован в действительности на продолжительном отрезке времени (см. ниже). Графики переменных ${{\Omega }_{i}}(t)$, ${{n}_{i}}(t)$ и угла $\gamma (t)$ в этом режиме изображены пунктирными линиями на рис. 7 на фоне черных графиков, иллюстрирующих решение уравнений (1) при ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ из раздела 2 (рис. 3).
5. ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ СПУТНИКА
Удобство аппроксимации решений уравнений (1) последовательностью периодических решений заключается в том, что, последние допускают детальное параметрическое исследование. Построив семейства решений краевой задачи (1a), (3) для различных значений ${{l}_{0}}$, ${{k}_{\Omega }}$ и долготы ${{\Omega }_{G}}$ восходящего узла орбиты в “замороженной” гринвичской системе координат можно в сжатом виде получить достаточно полное представление о решениях уравнений (1) на продолжительных интервалах времени, выбрать нужные параметры спутника.
Результаты решения задачи (1a), (3) представлены на рис. 8–10 графиками зависимости начальных условий от параметров ${{l}_{0}}$ и ${{\Omega }_{G}}$. Графики построены при ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ (сплошные линии) и ${{k}_{\Omega }} = 0.00015\,\,{{{\text{c}}}^{{ - 1}}}$ (пунктирные линии). В (3) принято ${{t}_{0}} = 0$, элементы используемой в уравнениях (1a) кеплеровой орбиты (кроме долготы восходящего узла) совпадают с элементами орбиты спутника в момент $t = 0$. Решения найдены методом пристрелки, первое приближение разыскиваемых начальных условий: ${\mathbf{\Omega }}(0) = 0$, ${\mathbf{n}}(0) = {{{\mathbf{B}}(0)} \mathord{\left/ {\vphantom {{{\mathbf{B}}(0)} {\left| {{\mathbf{B}}(0)} \right|}}} \right. \kern-0em} {\left| {{\mathbf{B}}(0)} \right|}}$.
Рис. 8.
Начальные условия решений краевой задачи (1a), (3) при ${{\Omega }_{G}} = 11.67^\circ $: компоненты вектора ${\mathbf{\Omega }}(0)$.
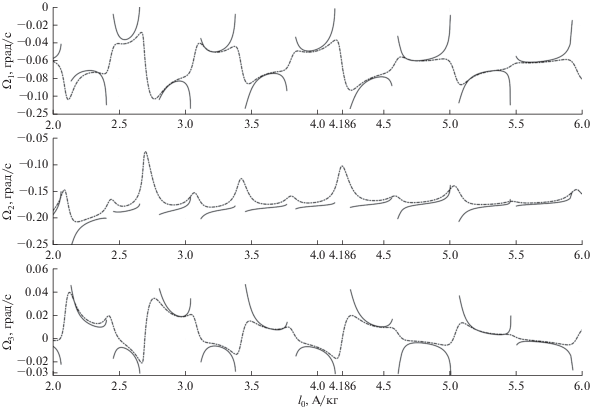
Рис. 9.
Начальные условия решений краевой задачи (1a), (3) при ${{\Omega }_{G}} = 11.67^\circ $: компоненты орта ${\mathbf{n}}(0)$.
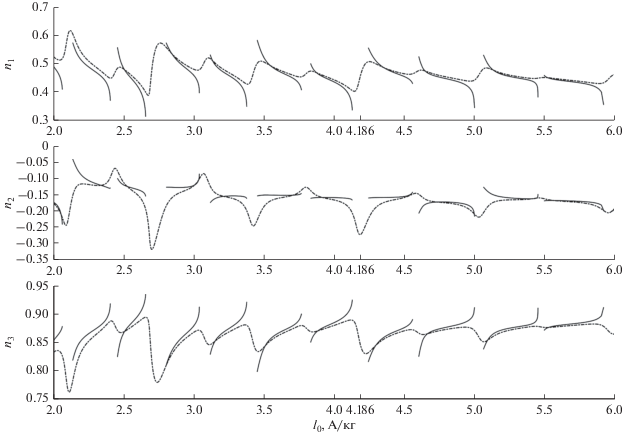
Рис. 10.
Начальные условия решений краевой задачи (1a), (3) ${\mathbf{\Omega }}(0)$ и ${\mathbf{n}}(0)$, сплошные линии – при ${{k}_{\Omega }} = 0$, пунктирные линии – при ${{k}_{\Omega }} = 0.00015$ с–1.
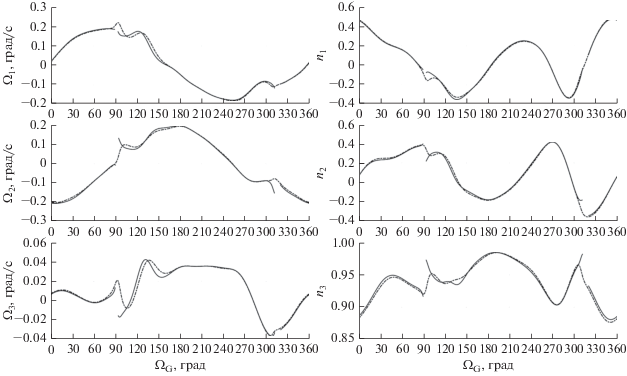
Графики на рис. 8, 9 построены при ${{\Omega }_{G}} = 11.67^\circ $ и $2 \leqslant {{l}_{0}} \leqslant 6$. Здесь $[{{l}_{0}}] = {\text{A}}$/кг. В случае ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ решения задачи (1a), (3) удалось найти не для всех значений ${{l}_{0}}$. Лакуны обусловлены резонансами в системе (1a) и связанным с ними ветвлением периодических решений [2–4, 7]. Резонансы возникают между вращением вектора ${\mathbf{B}}$ вдоль орбиты спутника и колебаниями орта ${\mathbf{n}}$ относительно этого вектора.
Графики на рис. 10 построены при ${{l}_{0}} = 4$ А/кг и $0^\circ \leqslant {{\Omega }_{G}} \leqslant 360^\circ $. В случае ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ решения этой задачи найдены не для всех значений ${{\Omega }_{G}}$. Причина та же, что и у лакун графиков, показанных сплошными линиями на рис. 8, 9 – резонансы в системе (1a). Указанные резонансы проявляются не только в системе (1a), но в системе (1).
Из-за таких резонансов невозможно продолжительное существование режима магнитной ориентации спутника при ${{k}_{\Omega }} = 0$. Изменение режима магнитной ориентации в процессе суточного вращения Земли можно приближенно рассматривать, как изменение периодического решения системы (1a в функции угла ${{\Omega }_{G}}$. Решения задачи (1a), (3) с малым углом ${{\gamma }_{{\max }}} = \max \left| {\gamma (t)} \right|$ ($0 \leqslant t \leqslant T$) образуют однопараметрические семейства с параметром ${{\Omega }_{G}}$. При ${{k}_{\Omega }} > 0$ существует одно такое семейство. Оно непрерывно зависит от ${{\Omega }_{G}}$ на интервале изменения этого параметра, охватывающем многие сутки полета. Как следствие, режим поддерживается продолжительное время. В случае ${{k}_{\Omega }} = 0$, ${\mathbf{n}} \cdot {\mathbf{\Omega }} = 0$ существует достаточно много семейств периодических решений, непрерывных по ${{\Omega }_{G}}$ и имеющих на некоторых отрезках малый угол ${{\gamma }_{{\max }}}$. При каждом ${{\Omega }_{G}}$ существует не более одного решения с ${{\gamma }_{{\max }}} \ll 1$. Лакуны – интервалы значений ${{\Omega }_{G}}$, на которых нет решений задачи (1a), (3) с малым ${{\gamma }_{{\max }}}$, – весьма коротки. Отрезок $0 \leqslant {{\Omega }_{G}} \leqslant 2\pi $ на рис. 10 содержит две таких лакуны. При изменении ${{\Omega }_{G}}$ в течение суток при переходе через лакуны аппроксимирующее периодическое решение перескакивает с одного семейства на другое. Указанные скачки приводят к постепенному нарушению ориентации (рис. 3).
Если в уравнениях (1) и (1a) принять модель МПЗ в виде прямого диполя и подходящее значение ${{l}_{0}}$, то резонансы при изменении ${{\Omega }_{G}}$ не возникают. В этом случае режим магнитной ориентации существует продолжительное время. На интервале времени 20 сут нарастания амплитуды колебаний угла $\gamma $ не наблюдается [8].
Резонансы в задаче (1a), (3) проявляются и при ${{k}_{\Omega }} > 0$. Рис. 11 содержит графики компонент векторов ${\mathbf{\Omega }}(t)$ и ${\mathbf{n}}(t)$, $0 \leqslant t \leqslant T$ решений этой задачи, вычисленных при ${{k}_{\Omega }} = 0.00015$ с–1, ${{\Omega }_{G}} = 11.67^\circ $ и двух значениях ${{l}_{0}}$: 4 А/кг (сплошные линии) и 4.186 А/кг (пунктирные линии). Амплитуды высокочастотных колебаний ${{\Omega }_{i}}$ решений при ${{l}_{0}}$ = = 4.186 А/кг значительно выше, чем при ${{l}_{0}}$= 4 А/кг. Это объясняется наличием в системе (1a) резонанса при ${{l}_{0}} = $ 4.186 А/кг (см. рис. 8, 9). Однако вследствие указанной выше непрерывности по ${{\Omega }_{G}}$ при ${{k}_{\Omega }} > 0$ такие резонансы не приводят к разрушению ориентированного движения.
6. СУЩЕСТВОВАНИЕ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
Чтобы строго доказать существование периодических решений, о которых говорилось разделах 4 и 5, уравнения (1a) запишем иначе. Введем две новые системы координат. Первая система связана с вектором ${\mathbf{B}}$ индукции МПЗ в центре масс спутника – точке $O$. Эту систему обозначим $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$. Орты ${{{\mathbf{e}}}_{i}}$ осей $O{{X}_{i}}$ $(i = 1,\;2,\;3)$ задаются соотношениями
Вторая система координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ образованна осями Резаля спутника. Ее ось $O{{x}_{1}}$ направлена по орту n. Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ получаются из осей системы $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ двумя поворотами. Сначала на угол $\alpha $ вокруг оси $O{{X}_{2}}$, затем на угол $\beta $ вокруг оси $O{{X}_{3}}$, получившейся после первого поворота. Компоненты абсолютной угловой скорости спутника в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ обозначим ${{\omega }_{1}},\;{{\omega }_{2}},\;{{\omega }_{3}}$. Уравнения (1) с использованием введенных систем координат можно записать в виде [3, 9]
(4)
$\begin{gathered} {{{\dot {\omega }}}_{3}} = \left( {\lambda {{\omega }_{1}} - {{\omega }_{2}}{\text{tg}}\beta - \frac{{{{\Phi }_{1}}\cos \alpha - {{\Phi }_{3}}\sin \alpha }}{{\cos \beta }}} \right) \cdot \\ \cdot \,\,{{\omega }_{2}} - {{k}_{\Omega }}{{\omega }_{3}} - {{l}_{0}}B\cos \alpha \sin \beta + \nu (1 - \lambda ){{x}_{1}}{{x}_{2}}, \\ \end{gathered} $Так как ${{\omega }_{1}} = {\text{const}}$ при ${{k}_{\Omega }} = 0$, первое уравнение системы (4) рассматривать не будем, а в остальных ее уравнениях ${{\omega }_{1}}$ будем считать параметром. Введем новую независимую переменную $\tau $ и постоянную $b$, положив
Исключим ${{\omega }_{2}},\;{{\omega }_{3}}$ из последних четырех уравнений (4) и перейдя к независимой переменной $\tau $, получим систему, которую запишем в векторном виде [4]
Здесь штрихом обозначено дифференцирование по $\tau $, $q = {{(\alpha ,\,\beta )}^{{\text{T}}}}$,$B$ и ${{\Phi }_{1}}$ выражаются в функции $\tau $, $\left\| {{\kern 1pt} \cdot {\kern 1pt} } \right\|$ – евклидова норма. Переменная $\tau $ входит в систему (5) периодически с периодом $2b$. Рассмотрим начальную задачу $2Y{\kern 1pt} ' = CY$, $Y(0) = {{E}_{2}} \equiv {\text{diag}}\,(1,\;1)$. Ее решение
Представим его в виде произведения Y(τ) = Y1(τ) · $ \cdot \,\,{{Y}_{2}}(\tau )$, где
Функция $\tilde {\psi }(\tau )$ и матрица ${{Y}_{1}}(\tau )$ – периодические по $\tau $ с периодом $2b$, матрицы ${{Y}_{1}}(\tau )$, ${{Y}_{2}}(\tau )$ удовлетворяют уравнениям
В системе (5) сделаем замену переменных $q \mapsto y$: $q = {{Y}_{1}}(\tau )y$. Получим систему
в которой гладкие $2b$-периодические по $\tau $ функции ${{f}_{1}}$ и $F$ допускают оценкиВведем множество $I(\varepsilon ) = \{ \mu :\mu > 0,$ $\left| {\sin b(\mu + a)\sin b(\mu - a)} \right| \geqslant \varepsilon \} $, $\varepsilon \in (0,\;1)$. Оно не пусто и не ограниченно. При $\varepsilon \ll 1$ оно представляет собой интервал $(0,\; + \infty )$ из которого удалены попавшие в него малые окрестности точек вида $\mu = \pm a + {{\pi m} \mathord{\left/ {\vphantom {{\pi m} b}} \right. \kern-0em} b}$ при целом $m$. Справедлива следующая теорема.
Для любого $\varepsilon \in (0,\;1)$ существуют такие положительные числа $M$, ${{C}_{1}}$ и ${{C}_{2}}$, что при $\mu \geqslant M$, $\mu \in I(\varepsilon )$ система (6) имеет единственное решение ${{y}_{ * }}(\tau ,\mu )$, непрерывно зависящее от $\mu $ и удовлетворяющее неравенствам
К типу таких решений относятся рассмотренные выше решения в случае ${{k}_{\Omega }} = 0$. При ${{k}_{\Omega }} \ne 0$ периодические решения системы (4) могут существовать только при ${{\omega }_{1}} = 0$. Последнее соотношение позволяет отбросить первое уравнение этой системы и перейти к системе вида (5), в матрице $C(\tau )$ которой
Решение начальной задачи $2Y{\kern 1pt} ' = CY$, $Y(0) = {{E}_{2}}$ теперь имеет вид
Представим это решение в виде произведения $Y(\tau ) = {{Y}_{1}}(\tau ){{Y}_{2}}(\tau )$, где
Функции $\tilde {\varphi }(\tau )$ $\tilde {\psi }(\tau )$ и матрица ${{Y}_{1}}(\tau )$ зависят от $\tau $ периодически с периодом $2b$, матрицы ${{Y}_{1}}(\tau )$, ${{Y}_{2}}(\tau )$ удовлетворяют уравнениям
В новой системе (5) сделаем замену переменных $q \mapsto y$: $q = {{Y}_{1}}(\tau )y$. Поучим систему вида (6), в которой $2b$-периодические по $\tau $ функции ${{f}_{1}}$ и $F$ допускают указанные выше оценки.
Введем множество
Множество $I(\varepsilon )$ можно рассматривать в плоскости $(\mu ,{{\Omega }_{G}})$. На этом множестве решение ${{y}_{*}}(\tau ,\mu )$ непрерывно зависит от обоих параметров. Именно такие решения имелись в виду в заключительной части предыдущего раздела, где говорилось о семействах решений задачи (1'), (3), зависящих от ${{\Omega }_{G}}$.
7. УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
Исследование устойчивости сводилось к вычислению мультипликаторов соответствующей системы уравнений в вариациях. Мультипликаторы обозначим ${{\rho }_{k}}$ $(k = 1,\;2,\; \ldots ,\;6)$. Пусть сначала ${{k}_{\Omega }} = 0$. В этом случае система (1a) имеет первый интеграл ${\mathbf{\Omega }} \cdot {\mathbf{n}} = {\text{const}}$ и интегральное соотношение ${\mathbf{n}} \cdot {\mathbf{n}} = 1$, поэтому два ее мультипликатора ${{\rho }_{1}} = {{\rho }_{2}} = 1$. Систему (1a) при ${{k}_{\Omega }} = 0$ можно привести к гамильтоновой форме. Следовательно, необходимые условия устойчивости ее периодических решений выражаются равенствами $\left| {{{\rho }_{k}}} \right| = 1$. Последние равенства проверялись при $k = 3,\;4,\;5,\;6$ вместе с равенствами ${{\rho }_{1}} = {{\rho }_{2}} = 1$ для каждого найденного решения задачи (1a), (3). Необходимые условия устойчивости оказались выполненными для всех таких решений. Но расчеты были сделаны для дискретного набора значений ${{l}_{0}}$ и ${{\Omega }_{G}}$, поэтому малые области неустойчивости в плоскости этих параметров могли быть пропущены. В таких возможных областях $\left| {{{\rho }_{k}}} \right| \approx 1$, и неустойчивость слабая.
При ${{k}_{\Omega }} > 0$ система (1a) имеет интегральное соотношение ${\mathbf{n}} \cdot {\mathbf{n}} = 1$, а скалярное произведение ${\mathbf{\Omega }} \cdot {\mathbf{n}} = \xi $ удовлетворяет соотношению $\dot {\xi } + {{k}_{\Omega }}\xi = 0$. Отсюда находим два мультипликатора ${{\rho }_{1}} = 1$, $\rho {}_{2}\, = \exp ( - {{k}_{\Omega }}T)$. По теореме Лиувилля $\prod\nolimits_{k = 1}^6 {{{\rho }_{k}}} = \exp ( - 3{{k}_{\Omega }}T)$, поэтому $\prod\nolimits_{k = 3}^6 {{{\rho }_{k}}} $ = $ = \exp ( - 2{{k}_{\Omega }}T)$. Достаточные условия устойчивости решений задачи (1a), (3) выражаются неравенствами $\left| {{{\rho }_{k}}} \right| < 1$ ($k = 3,\;4,\;5,\;6$). Эти неравенства, а также выписанные соотношения для ${{\rho }_{1}}$, $\rho {}_{2}$ и $\prod\nolimits_{k = 3}^6 {{{\rho }_{k}}} $ оказались выполненными для всех найденных решений. Во всех этих решениях мультипликаторы ${{\rho }_{k}}$ ($k = 3,\;4,\;5,\;6$) образуют две комплексно-сопряженные пары, причем $\left| {{{\rho }_{k}}} \right| \approx \exp ({{ - {{k}_{\Omega }}T} \mathord{\left/ {\vphantom {{ - {{k}_{\Omega }}T} 2}} \right. \kern-0em} 2})$.
ЗАКЛЮЧЕНИЕ
1. Построены установившиеся движения спутника, в которых его продольная ось симметрии составляет малый угол с вектором напряженности МПЗ. Рассмотрены установившиеся движения спутника при наличии и при отсутствии демпфирования.
2. Предложен способ аппроксимации ориентированного движения спутника посредством набора периодических решений. Такая аппроксимация упрощает параметрическое исследование этого движения. Приведены результаты исследований устойчивости периодических движений спутника при наличии и при отсутствии демпфирования.
Список литературы
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Сарычев В.А., Сазонов В.В., Овчинников М.Ю. Периодические колебания спутника относительно центра масс под действием магнитного момента. Препринт ИПМ им. М.В. Келдыша. 1982. № 182.
Сарычев В.А., Овчинников М.Ю. Магнитные системы ориентации искусственных спутников Земли. Итоги науки и техники. Исследование космического пространства. Т. 23. М.: ВИНИТТИ, 1985.
Сазонов В.В. Одноосная магнитная ориентация искусственных спутников // Механика твердого тела. 1987. № 2. С. 27–32.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985.
Теребиж В.Ю. Анализ временных рядов в астрофизике. М.: Наука, 1992.
Хентов А.А. Влияние магнитного и гравитационного полей Земли на колебания спутника вокруг своего центра масс // Космич. исслед. 1967. Т. 5. № 4. С. 554–572.
Игнатов А.И., Сазонов В.В. Исследование установившихся движений искусственного спутника Земли в режиме одноосной магнитной ориентации. Препринт ИПМ им. М.В. Келдыша. 2019. № 25.
Овчинников М.Ю., Пеньков В.И., Ролдугин Д.С., Иванов Д.С. Магнитные системы ориентации малых спутников. М.: ИПМ им. М.В. Келдыша РАН, 2016.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования