Космические исследования, 2022, T. 60, № 1, стр. 17-25

1. ВВЕДЕНИЕ

За последние немногим более чем шестьдесят лет опубликованы сотни научных статей, обзоров и книг, посвященных генерации магнитосферных ОНЧ хоровых электромагнитных излучений. Хорошо известно, что за плазмопаузой обычно в утреннем и предполуденном секторах средней магнитосферы возбуждаются хоровые излучения свистового диапазона с частотами порядка нескольких килогерц и периодами повторения дискретных элементов в десятые доли секунды.

Согласно экспериментальным данным с космических аппаратов CLUSTER, THEMIS и Van Allen Probes хоровые излучения возбуждаются в области, имеющей форму “сигары” длиной не меньше $l = (1 - 2) \cdot {{10}^{8}}\,\,{\text{см}}$ и средним диаметром $d = 3 \cdot {{10}^{7}}\,\,{\text{см}}$ [1, 2] вблизи локального минимума магнитного поля. Обычно спектрограмма хоровых излучений наблюдается в двух основных спектральных полосах с центром несколько ниже половины минимальной электронной циклотронной частоты для рассматриваемой магнитной трубки. В работе [1] обсуждалась связь области возбуждения хоров в двух спектральных полосах с неоднородной по магнитному полю плотностью фоновой плазмы. Наблюдения на космическом аппарате CLUSTER [3] подтвердили эти предположения.

В обширной литературе основное внимание было уделено циклотронному механизму генерации магнитосферных ОНЧ хоровых электромагнитных излучений. Для объяснения наблюдаемых дискретных спектральных форм обычно обсуждаются различные варианты циклотронной генерации в предположении наличия высокой анизотропии функции распределения энергичных электронов. Однако накопленные экспериментальные данные, не всегда могут быть объяснены в рамках циклотронного механизма генерации электромагнитных излучений. Пучковый механизм усиления импульсов, предложенный авторами [4, 5], позволяет найти ответы на многие вопросы, возникающие при интерпретации ключевых особенностей экспериментальных данных.

В данной работе обсуждаются условия реализации BPA механизма возбуждения хоровых излучений в волноводах плотности шириной порядка 100–300 км с рефракционным отражением. Привлечение волноводной модели соответствует магнитосферным условиям и дает возможность объяснить возбуждение хоровых излучений с малыми углами волновой нормали. В разделе 2 коротко изложены основные особенности BPA механизма. В разделе 3 рассмотрены особенности магнитосферных плоскослоистых волноводов с рефракционным отражением. В разделе 4 сформулированы результаты решения характеристического уравнения для волноводов с модельными профилями плазменной концентрации. В разделе 5 обсуждаются некоторые оригинальные экспериментальные результаты о магнитосферных хоровых излучениях, основанные на данных с космического аппарата Van Allen Probe (http://emfisis.physics.uiowa.edu/Flight/). В разделе ВЫВОДЫ суммированы результаты работы.

2. BPA МЕХАНИЗМ ВОЗБУЖДЕНИЯ ОНЧ ХОРОВЫХ ИЗЛУЧЕНИЙ

Рассмотрим особенности эволюции короткого электромагнитного импульса, падающего на однородный слой намагниченной плазмы. Импульс будет расплываться из-за дисперсии и, если фазовая скорость отличается от групповой скорости, то линии постоянной фазы пересекают границы импульса, что хорошо видно на рисунке, приведенном в статье [6].

Для типичных условий в области возбуждения хоров частота излучений $\omega $ лежит в интервале ${{\omega }_{{LHF}}} < \omega < {{\omega }_{B}} < {{\omega }_{p}},$ где ${{\omega }_{{LHF}}}$ – нижнегибридная частота ${{\omega }_{B}} = {{eB} \mathord{\left/ {\vphantom {{eB} {mc}}} \right. \kern-0em} {mc}},$ ${{\omega }_{p}} = {{({{4\pi {{n}_{p}}{{e}^{2}}} \mathord{\left/ {\vphantom {{4\pi {{n}_{p}}{{e}^{2}}} m}} \right. \kern-0em} m})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – величины электронной циклотронной и плазменной частот, $e$ – величина заряда электрона, $m$ – масса электрона, ${{n}_{p}}$ – концентрация плазмы, $c$ – скорость света. Дисперсионные свойства распространяющихся в указанном диапазоне необыкновенных электромагнитных волн в квазипродольном приближении в холодной сравнительно плотной плазме описываются известным [7] соотношением

где ${{k}_{z}}$ и ${{k}_{x}}$ – компоненты волнового вектора вдоль и поперек магнитного поля. Из дисперсионного уравнения (1) нетрудно видеть, что при $k_{z}^{2} + k_{x}^{2} = {{({{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} c}} \right. \kern-0em} c})}^{2}}$ оно сводится к виду $\omega = ({{c{{\omega }_{B}}} \mathord{\left/ {\vphantom {{c{{\omega }_{B}}} {2{{\omega }_{p}}}}} \right. \kern-0em} {2{{\omega }_{p}}}})\left| {{{k}_{z}}} \right|$ и существует выделенная скорость, отвечающая равенству продольной фазовой и групповой скоростей вдоль магнитного поля (вдоль оси $z$) где $u = {{c{{\omega }_{B}}} \mathord{\left/ {\vphantom {{c{{\omega }_{B}}} {(2{{\omega }_{p}})}}} \right. \kern-0em} {(2{{\omega }_{p}})}}$ скорость Жандрена [8]. При этом линии постоянной фазы “захвачены” внутри импульса и не пересекают его границы.

Рассмотрим кратко особенности эволюции слабого короткого электромагнитного шумового импульса, падающего на однородный слой намагниченной плазмы. Импульс, для спектральных компонент которого выполняются условия (2), представляет собой стационарную волну по координате $z$ и его волновое поле можно записать в виде [6]

Короткий электромагнитный импульс с волновым полем (3) согласно простым кинематическим соображениям [4], лежащим в основе BPA механизма, достаточно долго может взаимодействовать только с малой долей частиц, которые образуют облако активных электронов. Эти электроны влетели в область взаимодействия волн и частиц длиной $l$ вместе с импульсом и для того чтобы они его сопровождали разброс их продольных скоростей $\Delta {{V}_{z}}$ вблизи скорости $u$ должен удовлетворять условию

где ${{t}_{p}}$ – длительность электромагнитного импульса. Для других частиц взаимодействие настолько кратковременно, что они не успевают обменяться энергией с импульсом. Концентрация активных электронов может быть оценена с помощью соотношения где интегрирование функции распределения энергичных электронов $f$ по продольной скорости проводится по интервалу u – (1/2)ΔV_z < V_z < u + $ + \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})\Delta {{V}_{z}}.$ Более тщательный расчет концентрации ${{n}_{b}}$ приведен в работе [9].

Уравнения движения фракции активных электронов и уравнения Максвелла в фоновой плазме образуют самосогласованную систему уравнений. Пространственно-временная эволюция облака активных электронов при их движении в поле электромагнитного импульса (3) описывается уравнениями квазигидродинамики, которые после линеаризации имеют вид

где ${{n}_{{b\sim }}}$ и ${{V}_{\sim }}$ – возмущения концентрации и скорости облака активных электронов. Из уравнений следует, что электромагнитный импульс (3) создает резонансную плотность тока ${{j}_{r}},$ направленную вдоль магнитного поля и ее спектральные компоненты вблизи резонанса Черенкова $\omega = {{k}_{z}}u$ определяются следующим выражением

C учетом резонансного тока (7) из уравнений Максвелла следует обычное уравнение для спектральных компонент электромагнитного импульса

в котором ненулевые компоненты тензора диэлектрической проницаемости плазмы $\hat {\varepsilon }$ определяются следующими выражениями:

Формулы для компонент тензора диэлектрической проницаемости (9) отличаются от хорошо известных выражений для холодной плазмы в магнитном поле только последним слагаемым в компоненте ${{\varepsilon }_{{zz}}},$ обусловленным резонансным током (7). Интересующее нас дисперсионное уравнение представляет собой равенство нулю детерминанта системы (8), которое в квазипродольном приближении сводится к виду (детали расчета приведены в работе [5]):

где знак модуля учитывает возможность распространения волн в двух направлениях, sin θ = $ = {{{{k}_{x}}} \mathord{\left/ {\vphantom {{{{k}_{x}}} {{{{\left( {k_{z}^{2} + k_{x}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left( {k_{z}^{2} + k_{x}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ и $\cos \theta = {{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {{{{\left( {k_{z}^{2} + k_{x}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left( {k_{z}^{2} + k_{x}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$ Дисперсионное уравнение (10) представляет собой кубическое уравнение относительно частоты, свойства решений которого рассмотрены в работе [4]. Например, при выполнении условия (2) $\omega ({{k}_{z}},\theta ) = \left| {{{k}_{z}}} \right|u$ один из корней кубического дисперсионного уравнения (10) соответствует неустойчивому решению.

Инкремент роста волнового возмущения определяется выражением [4, 5]

из которого следует, что максимум инкремента отвечает углу волновой нормали θ ≅ 39° и усиление импульса достаточно для объяснения экспериментальных данных, согласно которым γ_max ≅ ≅ 10² c^–1, хотя концентрация облака активных электронов составляет лишь небольшую часть общей концентрации плазмы.

Таким образом, с коротким импульсом, характеризующимся наличием компоненты электрического поля ${{E}_{z}},$ эффективно взаимодействовать на черенковском резонансе ${{V}_{{phz}}} = u$ могут надтепловые электроны, которые движутся со скоростями близкими к $u$ вдоль магнитного поля, функцию распределения которых при кинетическом расчете можно записать в виде $f = {{n}_{b}}\delta ({{V}_{z}} - u).$ Ранее было показано, что при кинетическом рассмотрении взаимодействия волн и частиц с такой функцией распределения получаются соотношения (9)–(11) [4].

3. РЕФРАКЦИОННЫЙ ВОЛНОВОД ДЛЯ СВИСТОВЫХ ИЗЛУЧЕНИЙ

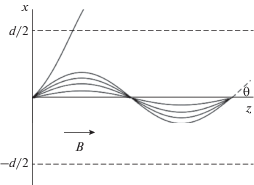
Рассмотрим плоскослоистые волноводы уплотнения и разрежения, которые часто регистрируются в области возбуждения хоров. Для магнитосферных условий в области возбуждения хоров [10] длина λ свистовых волн порядка 15 км, что меньше масштаба неоднородности концентрации плазмы и поперечного размера волновода, d = 100–300 км, и поэтому справедливо WKB приближение [11]. Когда концентрация плазмы неоднородна в направлении перпендикулярном оси волновода, каналирование волн может происходить за счет рефракции. Типичные траектории лучей вдоль оси канала с рефракционным отражением показаны на рис. 1.

Давно известно, что в условиях рефракционного отражения волны с частотами ниже половины электронной циклотронной частоты распространяются в волноводе уплотнения и выше половины циклотронной частоты в волноводе разрежения [7, 11]. Для демонстрации условий волноводного распространения дисперсионное уравнение (1) удобно записать в виде

где $\theta $ – угол между волновым вектором $k$ и магнитным полем $B.$ Частота и продольная составляющая волнового вектора сохраняются в каждой собственной моде плоскослоистого волновода. Поясним, как при этом из-за рефракции изменяется угол волновой нормали θ. Для этого запишем производную ${{\left. {{{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial {{n}_{p}}}}} \right. \kern-0em} {\partial {{n}_{p}}}}} \right|}_{{{{k}_{z}},{{\omega }}}}}$ с фиксированными значениями ${{k}_{z}}$ и ω, используя уравнение (12),

Согласно уравнению (13) для распространения, близкого к продольному, волновой вектор будет повернут в сторону более плотной плазмы, если ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ и в сторону более разреженной плазмы, если ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ Для детализации этой закономерности рассмотрим распространение электромагнитных волн вблизи оси волновода с монотонным профилем плотности от оси к периферии. Допустим, что луч пересекает ось волновода под малым углом ${{\theta }_{^\circ }} \ll 1,$ тогда дисперсионное уравнение (6) на оси волновода можно записать в виде

В области разворота луча $\cos {{\theta }_{r}} = 1$ и поэтому

Исключая из уравнений (14) и (15) ${{k}_{z}},$ получаем

График частотной зависимости относительной концентрации плазмы ${{{{n}_{{pr}}}} \mathord{\left/ {\vphantom {{{{n}_{{pr}}}} {{{n}_{{p \circ }}}}}} \right. \kern-0em} {{{n}_{{p \circ }}}}}$ для угла ${{\theta }_{ \circ }}$ на оси волновода представлен на рис. 2, который показывает, что для частот, меньших половины электронной циклотронной частоты, в точке отражения плотность меньше, чем на оси канала, что соответствует волноводу уплотнения. Для частот, превышающих половину циклотронной частоты электронов в точке отражения концентрация больше, чем на оси волновода, что характерно для волновода разрежения.

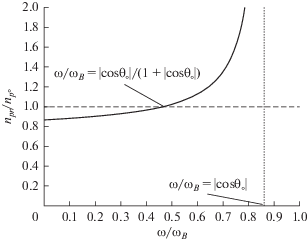
Кроме того, из уравнения (16) следует, что $\left| {\cos {{\theta }_{ \circ }}} \right| > {\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}}.$ Поэтому, например, для волн с частотами ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} \cong 0.5$ распространение волны в волноводе с рефракционным отражением в принципе возможно только при ${{\theta }_{ \circ }} < 60^\circ .$

Рассмотрим количественно рефракцию свистовых волн в приближении геометрической оптики, полагая концентрацию зависящей от поперечной координаты $x,$ а магнитное поле постоянным и однородным. Для корректного описания дисперсионных свойств плоскослоистого волновода важна зависимость поперечной компоненты волнового вектора от частоты и продольной компоненты волнового вектора при различных концентрациях плазмы. Уравнение (1) имеет следующее решение для поперечной компоненты волнового вектора [13]:

Здесь ${{K}_{{x \pm }}} = {{\left\{ {{{{\left( {\frac{{{{\omega }_{B}}{{k}_{z}}}}{{2\omega }}} \right)}}^{2}}{{{\left[ {{{{\left( {1 - \frac{{{{\omega }^{2}}}}{{k_{z}^{2}u_{G}^{2}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \pm 1} \right]}}^{2}} - k_{z}^{2}} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ $H(\varsigma ) = \left\{ {\begin{array}{*{20}{c}} {1,}&{if}&{\varsigma > 0;} \\ {0,}&{if}&{\varsigma < 0} \end{array}} \right.$ – единичная функция Хевисайда.

Будем исследовать волновые уравнения с нулевыми граничными условиями на бесконечности по поперечным координатам. Математически задача сводится к задаче о нахождении собственных функций и собственных значений самосопряженного оператора. Собственные моды волновода соответствуют дискретному спектру собственных значений, которые находятся из характеристического уравнения.

Для определения характеристического уравнения, которое выражает зависимость частоты от продольной компоненты волнового вектора мод плоскослоистого волновода, в приближении WKB необходимо рассчитать полное поперечное изменение фазы за период распространения луча. Изменение фазы $\Phi \left( {\omega ,{{k}_{z}}} \right)$ должно учитывать фазовые сдвиги на каустике и быть кратным $2\pi .$ Таким образом, характеристическое уравнение принимает хорошо известный вид [14]:

где $p$ – натуральное число, а координаты $ \mp {{x}_{{\max }}}$ соответствуют значению ${{k}_{x}} = 0.$

Мы получили решения характеристического уравнения для модельного распределения концентрации фоновой плазмы по поперечной координате, отвечающего волноводам уплотнения ${{{{n}_{{p\infty }}}} \mathord{\left/ {\vphantom {{{{n}_{{p\infty }}}} {{{n}_{{p \circ }}}}}} \right. \kern-0em} {{{n}_{{p \circ }}}}} < 1$ и разрежения ${{{{n}_{{p\infty }}}} \mathord{\left/ {\vphantom {{{{n}_{{p\infty }}}} {{{n}_{{p \circ }}}}}} \right. \kern-0em} {{{n}_{{p \circ }}}}} > 1$

где $d = (1 - 3) \cdot {{10}^{7}}\,\,{\text{cм}}$ – поперечный масштаб волновода (см. рис. 3). Решение характеристического уравнения проводилось в предположении однородного магнитного поля, значение электронной циклотронной частоты принималось равным ${{\omega }_{B}} = 6 \cdot {{10}^{4}}$ рад/с. В результате численного анализа были получены зависимости частоты $\omega $ от продольной составляющей волнового вектора ${{k}_{z}}$ для мод в волноводах обоих типов (см. рис. 4).

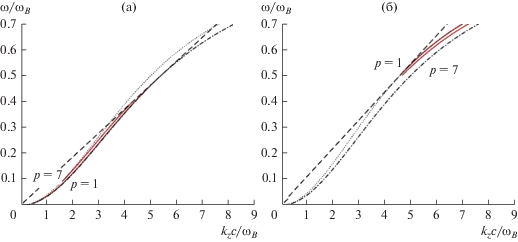
Анализ показал, что важное условие реализации BPA механизма (2) выполняется в волноводе уплотнения, если ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} \cong 0.42$ при ${{{{k}_{z}}c} \mathord{\left/ {\vphantom {{{{k}_{z}}c} {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} \cong 4.7$ и в волноводе разрежения, если ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} \cong 0.51$ при ${{{{k}_{z}}c} \mathord{\left/ {\vphantom {{{{k}_{z}}c} {{{\omega }_{B}}}}} \right. \kern-0em} {{{\omega }_{B}}}} \cong 4.7.$ Указанные частоты часто наблюдаются у хоров в нижней и верхней полосах частот.

В однородной плазме посредством BPA механизма с наибольшим темпом усиливаются подходящие дробовые шумы с углами волновой нормали 39°. Есть данные, что хоры могут иметь такие углы волновой нормали [15]. Однако часто углы волновой нормали имеют величину порядка 20° [16]. Среднее значение угла волновой нормали можно оценить с помощью условия (18), записанного для моды с номером $p{\text{:}}$

Для первых десяти мод средний угол волновой нормали меньше 20°, и при этом инкремент (11) меньше максимального значения инкремента при оптимальном угле волновой нормали только на 20%. Нужно заметить, что мод с высокими номерами вообще может не быть в волноводе со сравнительно малым перепадом концентрации плазмы.

4. НЕКОРЫЕ ПРИМЕРЫ РЕГИСТРАЦИИ ХОРОВ ПО ДАННЫМ С КОСМИЧЕСКОГО АППАРАТА VAN-ALLEN PROBE

Для уточнения условий применимости полученных результатов полезно обратиться к экспериментальным данным с космического аппарата Van Allen Probe, доступных на сайте http://emfisis. physics.uiowa.edu/Flight. На рис. 5, 6 приведены примеры регистрации динамических спектров хоровых излучений (а), магнитного поля (б) и концентрации магнитосферной плазмы (в). Эти типичные примеры подтверждают возможность возбуждения хоров в области локального минимума магнитного поля. Возбуждение происходит в двух спектральных полосах, разделенных белой линией, отвечающей половине минимальной циклотронной частоты электронов вдоль магнитной трубки. Данные о неоднородной концентрации фоновой плазмы указывают на возможность существования волноводов плотности в области возбуждения хоровых излучений. В свою очередь магнитное поле почти однородное в пределах всплеска хоров. Этим обосновывается постановка задачи с однородным магнитным полем и волноводами уплотнения и разрежения в области возбуждения излучений.

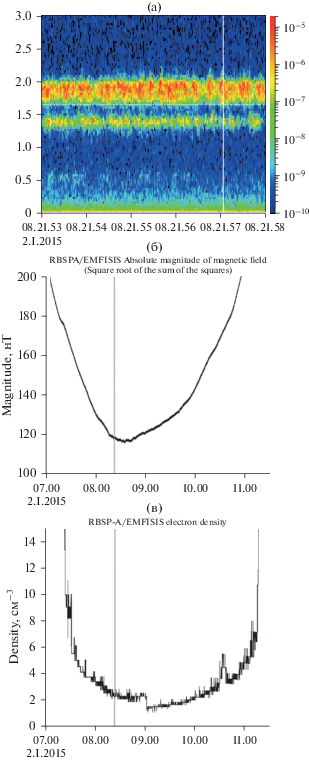
На рис. 5 зарегистрированные 4.I.2015 хоровые элементы в нижней спектральной полосе намного более интенсивные и четкие, чем в верхней. Указанные особенности спектральных форм хорошо согласуются с реализацией BPA механизма возбуждения хоров в рефракционных волноводах уплотнения.

На рис. 6 приведен другой пример зарегистрированных 2.I.2015 динамических спектров хоровых излучений. В этом случае хоровые элементы в верхней спектральной полосе заметно более яркие и четкие, чем в нижней. Указанные спектральные формы хорошо согласуются с реализацией BPA механизма возбуждения хоров в рефракционных волноводах разрежения, которые подчеркивают возбуждение хоров в верхней частотной полосе (см. рис. 4б). Можно отметить, что такого типа излучения не представляется возможным объяснить в рамках нелинейного механизма [17], который предполагает, что верхняя спектральная полоса формируется как вторая гармоника от излучений в нижней спектральной полосе.

На рис. 7 приведен зарегистрированный 11.I.2015 более сложный пример, когда в пределах сравнительно короткого промежутка времени спектральные свойства хоровых излучений довольно сильно изменяются. В какие-то промежутки времени более яркие и четкие хоровые элементы регистрируются в нижней спектральной полосе, а в другие промежутки времени ситуация меняется и хоровые элементы более отчетливы в верхней спектральной полосе. Это возможно, например, если космический аппарат находится вблизи границы между волноводами уплотнения и разрежения.

Таким образом, принятая в данной работе модель с однородным магнитным полем и неоднородностями концентрации в области возбуждения хоров имеет экспериментальное подтверждение. В тоже время надо отметить, что наличие сравнительно сложных примеров динамических спектров хоров указывает на перспективы дальнейших исследований.

ВЫВОДЫ

Отмечено, что предлагаемая модель объясняет возможность возбуждения хоровых излучений с малыми углами волновой нормали. Для мод с относительно низкими номерами угол волновой нормали $\theta \leqslant 20^\circ .$ Важно, что интенсивность и типичный угол волновой нормали для хоровых излучений при наличии волноводов уплотнения и разрежения могут быть разными для нижних и верхних полос излучений.

В работе изучается процесс формирования хоровых излучений в волноводах. На входе в область взаимодействия волн с частицами вблизи вершины магнитной трубки имеется дробовой шум, представляющий собой случайную последовательность слабых коротких электромагнитных импульсов. Короткие электромагнитные импульсы при взаимодействии с попутными надтепловыми электронами эффективно усиливаются, если выполняются необходимые условия (равенство продольных фазовой и групповой скоростей, наличие продольной компоненты волнового возмущения и его достаточно малая длительность). При выполнении указанных условий надтепловые электроны со скоростями вдоль магнитного поля, близкими к скорости Жандрена, которые вместе с импульсом влетают в область взаимодействия волн и частиц в среднем отдают свою энергию импульсу и усиливают его. Шум, не удовлетворяющий условиям такого взаимодействия с частицами, затухает в почти устойчивой плазме.

Проанализировано влияние на пучковый механизм усиления рефракционных волноводов уплотнения и разрежения с поперечным размером 100–300 км. Установлено, что в таких волноводах при типичных параметрах плазмы усиление возможно как в волноводе уплотнения, так и в волноводе разрежения. Например, равенство продольной фазовой и групповой скоростей выполняется на частотах, отвечающих нижней и верхней полосам возбуждения хоров. Для волноводных мод с низкими номерами средний угол волновой нормали меньше чем в однородной плазме и не превышает значения $\theta = 20^\circ .$ Это хорошо соответствует экспериментальным данным [16]. Причем это свойство имеет место только в одной из полос возбуждения хоров. Поэтому спектральные формы хоровых излучений при его возбуждении в рефракционных волноводах должны существенно отличаться в нижней и верхней спектральных полосах. Этот вывод неплохо согласуется с известными экспериментальными данными.

Таким образом, привлечение волноводной модели реализации BPA механизма позволило объяснить возможность возбуждения хоровых излучений с малыми углами волновой нормали и сделать вывод о том, что интенсивность и типичный угол волновой нормали могут быть разными для нижней и верхней спектральных полос в одной реализации.

Исследование П.А. Беспалова, О.Н. Савиной и П.Д. Жаравиной (разделы 3–5) выполнено по проекту РФФИ № 20-02-00206А. Исследование П.А. Беспалова (разделы 1 и 2) выполнено по гранту Российского научного фонда (проект № 20-12-00268). Численные расчеты выполнены в рамках Государственного задания № 0030-2021-0002. Использованные в работе данные с космического аппарата Van Allen Probe доступны на сайте http://emfisis.physics.uiowa.edu/Flight/, которому мы выражаем благодарность.