Космические исследования, 2022, T. 60, № 3, стр. 196-205

Методики расчета влияния электродинамического поля в ионосфере на космический аппарат

Н. И. Сидняев^*

Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

Поступила в редакцию 26.05.2020
После доработки 09.04.2021
Принята к публикации 25.08.2021

EDN: VTIZGS
DOI: 10.31857/S0023420622020066

Аннотация

В статье изучается влияние электромагнитного поля космического пространства на космические аппараты. Получены аналитические зависимости для энергии, излучаемой спутником с учетом направления распространения волн Альвена. Постулируется, что линейный член в уравнении энергии влияет на индукцию при произвольном законе распределения тока в спутнике в электромагнитном поле. Доказано, что при движении спутника на средних высотах распределение тока в магнитосферной плазме может быть удовлетворительно аппроксимировано отрезками прямых линий с максимумом в точке нулевого потенциала, причем индуцированные компоненты магнитного поля можно определить интегрированием. Определена индуцированная компонента магнитного поля. Отмечено, что в отсутствие диссипации энергии, полная энергия излучения выражается в виде произведения скорости спутника на индуктивное сопротивление.

ВВЕДЕНИЕ

В космическом пространстве на КА в полете воздействует обширный комплекс факторов: потоки нейтральных атомов (О): F ≈ 10¹⁸–10²⁰ м^–2 с^–1 при вакууме Р ≈ 10^–4–10^–11 Па вызывает сублимацию материалов, эрозию и потерю массы полимерных материалов загрязнению поверхности, рассеяние света в окрестности КА, снижение прочности и надежности оборудования. Вторичные (индуцированные факторы), как электризация КА (0.1–10^–4 В), объемное заряжение диэлектриков и собственная внутренняя атмосфера КА вызывает электрические заряды, электромагнитные помехи [1–3]. Холодная и горячая космическая плазма в ионосфере, магнитосфере (авроральные области) и плазмосфере Земли, солнечное электромагнитное излучение, электростатическое поле, метеорная материя, твердые частицы искусственного происхождения и другие факторы вызывают разнообразные физико-химические процессы. Некоторые из воздействующих космических факторов, например, космическая плазма и солнечное ультрафиолетовое излучение, оказывают влияние лишь на приповерхностные слои материалов [4–8]. Другие, такие как заряженные частицы высокой энергии вместе с создаваемыми ими в элементах конструкции КА вторичными частицами и квантами, способны проникать глубоко в толщу материалов, а также во внутренние отсеки КА [9–12]. При этом воздействие космических микрочастиц может приводить как к постепенному ухудшению свойств материалов и характеристик бортовых систем и, как следствие, – к отказам в работе КА по истечении некоторого периода эксплуатации, так и к возникновению внезапных отказов в работе бортовой аппаратуры, непосредственно сопровождающих воздействие [13–16].

Следует отдельно учесть электромагнитное солнечное излучения в межпланетном и околоземном пространстве, влияющие на корпус КА корпусе спутника и направлены вниз по потоку [1, 2].

Так, например, течение ионосферы у торцов вызывает поток, направленный над спутником от торцов к плоскости симметрии, а под спутником – от плоскости симметрии к торцам; в результате в спутной струе [3, 4], или следе, за спутником происходит вращение каждой частицы вокруг оси, проходящей через нее и параллельной местному вектору скорости потока ионосферы. Для спутников большого удлинения можно считать, что свободные вихри образуют плоскую вихревую пелену; для корпуса малого удлинения вихревая система является пространственной. Свободные вихри вызывают (индуцируют) в области между торцами корпуса потоки, направленные вниз, которые, налагаясь на набегающий ионосферный поток, отклоняют последний вниз на определенный угол. В результате отклоняющая сила элемента корпуса спутника перпендикулярна к набегающему потоку, отклоняется назад на тот же угол [5–10]. Разлагая эту силу на компоненты вдоль и перпендикулярно вектора скорости, получаем дополнительное индуктивное сопротивление в электростатическом поле.

Необходимо отметить, что индуктивное сопротивление (обусловленное волнами Ван Альвена) спутника, движущегося в электростатическом поле с постоянной скоростью $v$ перпендикулярно линиям постоянного магнитного поля ${{B}_{0}},$ исследовалось в работе [11–14]. Их исследование явилось развитием работы [2], посвященной изучению характеристик спутника заданной формы при переменной величине внутреннего тока. Геомагнитную зону заряженных частиц космического излучения называют радиационным поясом (или поясами) Земли. Электроны с энергией 100 кэВ и больше образуют в геомагнитной области две зоны. Эти зоны получили название внутреннего и внешнего естественного радиационного пояса Земли (ЕРПЗ) [3]. Между внутренним и внешним поясами наблюдается пространство в интенсивности потока электронов. Внутренний пояс располагается на высоте от 1000 км над поверхностью Земли до 13 000 км. Выше 13 000 км и примерно до 65000 км располагается внешний радиационный пояс Земли с максимумом потока электронов (E > 40 кэВ) порядка 500 000 000 частиц/см² с на высоте около 16 500 км. Электростатические пояса представляют собой непрерывно изменяющуюся, динамичную систему, состояние которой зависит от состояния солнечной активности и процессов, которые реализуются в настоящий момент в магнитосфере Земли. Экспериментальные данные указывают на то, что увеличение скорости солнечного ветра приводит к увеличению потока высокоэнергичных электронов на границе магнитосферы, и усиливается диффузия этих электронов внутрь радиационных поясов (см. рис. 1).

Рис. 1.

Схема распределения магнитного и электрического полей вокруг Земли.

Ионосфера, часть атмосферы планеты Земля, содержащая в значительном количестве свободные электроны и ионы, появляющиеся под воздействием идущих от Солнца ультрафиолетового излучения и рентгеновских лучей [4–6]. Степень ионизации в значительной степени зависит от солнечной активности. Протяженность ионосферы Земли – от 80 до 1000 км над земной поверхностью (в пределах атмосферы в радиационных поясах Ван Альвена) [2, 3, 9]. Состоит из нескольких условных слоев, которые отличаются степенью концентрации в них электронов. Их принято обозначать по порядку снизу вверх: D, Е, F1, F2, G. В самых нижних слоях D и Е (слои Хевисайда–Кеннелли) ионизации подвергаются молекулы, в то время как в верхнем слое F ионизируются атомы [3]. На расстоянии 80–100 км над Землей расположен слой, называемый ионосферой, который обладает электропроводимостью (благодаря наличию ионизированных газов).

Целью исследование является выявления механизма возникновения индуцированного сопротивления спутников, а также индуцированных компонент магнитного поля в условиях электризации КА при воздействии вторичных индуцированных факторов.

Поскольку магнитное и электростатическое поля планеты полагаются неподвижными в пространстве, а поверхность спутника вращается относительно геомагнитных и геоэлектрических силовых линий, то униполярная и электродинамическая ЭДС наводится во всех токопроводящих контурах спутника, пересекающих геомагнитные силовые линии. Вполне понятно, что в любом искусственном электропроводном проводнике спутника также будет наводиться униполярная ЭДС. Ее величина зависит от протяжности проводника, параметров геомагнитного поля и от ориентации спутника относительно геомагнитных силовых линий и электростатического поля. Так, при обтекании спутника невозмущенным ионизированным потоком возникает разность давлений над спутником и под ним. В результате часть ионоплазмы на концах спутника перетекает из зоны большего давления в зону меньшего давления. Поток ионосферы перетекает с нижней поверхности спутника на верхнюю и накладывается на ионизированный поток, набегающий на верхнюю часть спутника, что приводит к образованию завихрений массы ионоплазмы за задней кромкой, т.е. образуется вихревой жгут. Ионосфера в вихревом жгуте вращается. Скорость вращения вихревого жгута различна, в центре она наибольшая, а по мере удаления от оси вихря – уменьшается.

ОПРЕДЕЛЕНИЕ ИНДУЦИРОВАННЫХ КОМПОНЕНТ МАГНИТНОГО ПОЛЯ

В работах [1, 2] были выполнены приближенные расчеты величины тока, поступающего в спутник из ионосферы, и на основании полученного распределения тока с использованием закона Био–Савара было рассчитано индуцируемое магнитное поле. Величина сопротивления определялась численной оценкой интегралов, в подынтегральные выражения которых входили также и индуцированные магнитные поля. Значения этих интегралов представляли собой энергию, излучаемую волнами Альвена. Вывод работы [1] состоит в том, что в отсутствие диссипации энергии в следе, полная энергия излучения выражается в виде произведения скорости спутника на электростатическое поле и, что динамика спутника, обусловленное волнами Альвена, входит в величину индукции, а не является дополнительной составляющей.

Энергия излучаемая спутником, определяется уравнением (1), которое приводится здесь (с учетом изменения обозначений осей) [1]:

(1)

$P = {{V}_{A}}{{\mu }}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left[ {h_{x}^{2} + 2{{h}_{y}}\left( {\frac{{{{B}_{0}}}}{{{\mu }}}} \right)\sin {{\alpha }} + h_{y}^{2}} \right]} } dx dy,$

где

(2)

${{h}_{y}} = \frac{1}{{2{{\pi }}}}\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\frac{{j({{\xi }})(x - {{\xi }})}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }}} .$

Здесь ${{h}_{x}}$ выражается аналогичным образом при замене $x - {{\xi }}$ на $ - y,$ а ${{\alpha }}$ – малый угол между направлением поля ${{B}_{0}}$ (осью $z$) и направлением распространения волн Альвена. Рассмотрим предварительно только часть уравнения (1), являющуюся линейной относительно ${{h}_{y}}.$ После подстановки соотношения (2) будем иметь

(3)

$P{\kern 1pt} ' = \frac{{{{B}_{0}}V}}{{{\pi }}} \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\left[ {\frac{{j({{\xi }}) (x - {{\xi }}) d{{\xi }}}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}} \right]} dx dy,} } $

где функция $j({{\xi }})$ является током в крыльях волн Альвена. Предполагается, что эта функция кусочно-непрерывная и может быть определена. Если интегрировать сперва по x, то можно отметить, что интеграл в этом случае не существует. Однако, если интегрировать сперва по y и переписать уравнение (3) в виде

(4)

$\begin{gathered} P{\kern 1pt} ' = \frac{{{{B}_{0}}V}}{{{\pi }}} \times \\ \times \,\,\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\int\limits_{ - \infty }^\infty {\left\{ {\left[ {\int\limits_{ - \infty }^\infty {\frac{{dy}}{{{{y}^{2}} + {{{(x - {{\xi }})}}^{2}}}}} } \right](x - {{\xi }}) dx} \right\} j({{\xi }}) d{{\xi }},} } \\ \end{gathered} $

то можно показать, что интеграл существует.

Рассмотрим несобственный интеграл

(5)

$\int\limits_{ - \infty }^\infty {\frac{{dy}}{{{{y}^{2}} + {{{(x - {{\xi }})}}^{2}}}}} .$

Здесь особые точки $y = \pm \left| {x - {{\xi }}} \right|i$ – простые полюса подынтегральной функции интеграла (5). В верхней полуплоскости располагается точка $y = \left| {x - {{\xi }}} \right|i.$ Тогда по теореме вычетов получаем

$\begin{gathered} \int\limits_{ - \infty }^\infty {\frac{{dy}}{{{{y}^{2}} + {{{(x - {{\xi }})}}^{2}}}}} = 2{{\pi }}i \mathop {{\text{Res}}}\limits_{y = \left| {x - {{\xi }}} \right|i} \frac{1}{{{{y}^{2}} + {{{(x - {{\xi }})}}^{2}}}} = \\ = 2{{\pi }}i \mathop {\lim }\limits_{y \to \left| {x - {{\xi }}} \right|i} \left[ {(y - \left| {x - {{\xi }}} \right|i)\frac{1}{{{{y}^{2}} + {{{(x - {{\xi }})}}^{2}}}}} \right] = \\ = 2{{\pi }}i\mathop {\lim }\limits_{y \to \left| {x - {{\xi }}} \right|i} \frac{1}{{2y}} = \frac{{{\pi }}}{{\left| {x - {{\xi }}} \right|}}. \\ \end{gathered} $

Уравнение (4), следовательно, приобретает вид:

(6)

$P{\kern 1pt} ' = {{B}_{0}}V\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\left[ {\int\limits_{ - \infty }^\infty {\frac{{(x - {{\xi }})}}{{\left| {x - {{\xi }}} \right|}}dx} } \right]} j({{\xi }}) d{{\xi }}.$

Интеграл по x все же не может быть взят, до тех пор, пока не будет определено его главное значение следующим образом:

$\begin{gathered} \int\limits_{ - \infty }^\infty {\frac{{(x - {{\xi }})}}{{\left| {x - {{\xi }}} \right|}}dx} = \mathop {\lim }\limits_{A \to \infty } \left[ {\int\limits_{ - A}^{{\xi }} {( - dx) + \int\limits_{{\xi }}^A {dx} } } \right] = \\ = \mathop {\lim }\limits_{A \to \infty } \left[ {\left. { - x} \right|_{{ - A}}^{{{\xi }}} + \left. x \right|_{{{\xi }}}^{A}} \right] = \mathop {\lim }\limits_{A \to \infty } \left[ { - {{\xi }} - A + A - {{\xi }}} \right] = - 2{{\xi }}. \\ \end{gathered} $

Следовательно, уравнение (6) может быть представлено в форме

(7)

$P{\kern 1pt} ' = - {{B}_{0}}V\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {2{{\xi }}} j({{\xi }}) d{{\xi }},$

но, согласно работе [1],

(8)

$j({{\xi }}) = \frac{d}{{d{{\xi }}}}\frac{{I({{\xi }})}}{2},$

где $I({{\xi }})$ – ток в спутнике. Таким образом, подставляя выражение для $j({{\xi }})$ в уравнение (7), интегрируя его по частям, имея при этом в виду, что $I( \pm l{\text{/}}2) = 0,$ получим:

(9)

$\begin{gathered} P{\kern 1pt} ' = - {{B}_{0}}V\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {{\xi }} \frac{d}{{d{{\xi }}}}I({{\xi }}) d{{\xi }} = \\ = \left. { - {{B}_{0}}V{{\xi }} I({{\xi }})} \right| _{{ - l{\text{/}}2}}^{{l{\text{/}}2}} + {{B}_{0}}V\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {I({{\xi }}) d{{\xi }} = } \\ = V{{B}_{0}}\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} I ({{\xi }}) d{{\xi }} \equiv VD, \\ \end{gathered} $

где D – по определению индуктивное сопротивление.

Этот результат показывает, что линейный относительно ${{h}_{y}}$ член в уравнении (1) дает индуктивное сопротивление космического аппарата при произвольном законе распределения тока $I({{\xi }})$ в спутнике. Два других члена в уравнении, (1) положительны, и поэтому ясно, что полное сопротивление будет больше индуктивного. В работах [1, 2] было показано, что при движении спутника на малых высотах распределение тока может быть удовлетворительно аппроксимировано отрезками прямых линий с максимумом в точке нулевого потенциала, то есть в точке, где потенциал спутника равен потенциалу плазмы. Математически это можно записать в виде:

(10)

$I = \left\{ {\begin{array}{*{20}{c}} {{{I}_{{{\text{max}}}}}\frac{{l{\text{/}}2 + {{\xi }}}}{{l{\text{/}}2 + a}},\,\,\,\, - l{\text{/}}2 \leqslant {{\xi }} \leqslant a;} \\ {{{I}_{{{\text{max}}}}}\frac{{l{\text{/}}2 - {{\xi }}}}{{l{\text{/}}2 - a}},\,\,\,\,a \leqslant {{\xi }} \leqslant l{\text{/}}2.} \end{array}} \right.$

Из соотношения (8) получаем:

(11)

$j({{\xi }}) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{I}_{{{\text{max}}}}}}}{{2(l{\text{/}}2 + a)}},\,\,\,\, - l{\text{/}}2 \leqslant {{\xi }} \leqslant a;} \\ {\frac{{{{I}_{{{\text{max}}}}}}}{{2(l{\text{/}}2 - a)}},\,\,\,\,a \leqslant {{\xi }} \leqslant l{\text{/}}2.} \end{array}} \right.$

Таким образом, индуцированные компоненты магнитного поля можно определить интегрированием. Предварительно рассмотрим компоненту ${{h}_{x}},$ с учетом выражения (11):

$\begin{gathered} {{h}_{x}} = \frac{1}{{2{{\pi }}}}\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\frac{{yj({{\xi }})}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }} } = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}\int\limits_{ - l{\text{/}}2}^a {\frac{y}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }}} } \right. + \\ + \,\,\left. {\frac{1}{{l{\text{/}}2 - a}}\int\limits_a^{l{\text{/}}2} {\frac{y}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }}} } \right] . \\ \end{gathered} $

Произведем замену $t = {{\xi }} - x$

$\begin{gathered} {{h}_{x}} = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}\int\limits_{ - x - l{\text{/}}2}^{ - x + a} {\frac{y}{{{{t}^{2}} + {{y}^{2}}}}dt} + } \right. \\ + \,\,\left. {\frac{1}{{l{\text{/}}2 - a}}\int\limits_{ - x + a}^{ - x + l{\text{/}}2} {\frac{y}{{{{t}^{2}} + {{y}^{2}}}}dt} } \right] = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}} \times \\ \times \left[ { - \frac{1}{{l{\text{/}}2 + a}}\operatorname{arctg} \left. {\frac{t}{y}} \right|_{{t = - x - l{\text{/}}2}}^{{ - x + a}} + \frac{1}{{l{\text{/}}2 - a}}\operatorname{arctg} \left. {\frac{t}{y}} \right|_{{t = - x + a}}^{{x + l{\text{/}}2}}} \right] = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}} \right.\left( {\operatorname{arctg} \frac{{ - x + a}}{y}\left. { - \operatorname{arctg} \frac{{ - x - l{\text{/}}2}}{y}} \right)} \right. + \\ + \,\,\frac{1}{{l{\text{/}}2 - a}}\left( {\operatorname{arctg} \frac{{ - x + l{\text{/}}2}}{y} - \operatorname{arctg} \frac{{ - x + a}}{y}} \right). \\ \end{gathered} $

Для упрощения полученного выражения, возьмем арктангенса тангенса от разности арктангенсов и используем формулу разности тангенсов:

$\begin{gathered} {{h}_{x}} = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}} \right.\operatorname{arctg} {\text{tg}}\left( {\operatorname{arctg} \frac{{ - x + a}}{y}} \right. - \\ - \left. {\operatorname{arctg} \frac{{ - x - l{\text{/}}2}}{y}} \right) + \frac{1}{{l{\text{/}}2 - a}} \times \\ \times \,\,\operatorname{arctg} {\text{tg}}\left( {\operatorname{arctg} \frac{{ - x + l{\text{/}}2}}{y}} \right.\left. {\left. { - \operatorname{arctg} \frac{{ - x + a}}{y}} \right)} \right] = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4\pi }}\left[ { - \frac{1}{{l{\text{/}}2 + a}}} \right. \times \\ \times \,\,\operatorname{arctg} \frac{{{\text{tg}}\operatorname{arctg} \left[ {{{( - x\, + \,a)} \mathord{\left/ {\vphantom {{( - x\, + \,a)} y}} \right. \kern-0em} y}} \right]\, - \,{\text{tg}}\operatorname{arctg} \left[ {{{( - x\, - \,l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x\, - \,l{\text{/}}2)} y}} \right. \kern-0em} y}} \right]}}{{1 + {\text{tg}}\operatorname{arctg} \left[ {{{( - x + a)( - x - l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x + a)( - x - l{\text{/}}2)} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}} \right]}} + \\ + \,\,\frac{1}{{l{\text{/}}2 - a}} \times \\ \times \operatorname{arctg} \left. {\frac{{{\text{tg}}\operatorname{arctg} \left[ {{{( - x\, + \,l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x\, + \,l{\text{/}}2)} y}} \right. \kern-0em} y}} \right]\, - \,{\text{tg}}\operatorname{arctg} \left[ {{{( - x\, + \,a)} \mathord{\left/ {\vphantom {{( - x\, + \,a)} y}} \right. \kern-0em} y}} \right]}}{{1 + {\text{tg}}\operatorname{arctg} \left[ {{{( - x + l{\text{/}}2)( - x + a)} \mathord{\left/ {\vphantom {{( - x + l{\text{/}}2)( - x + a)} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}} \right]}}} \right] = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}} \right.\operatorname{arctg} \frac{{{{( - x + a)} \mathord{\left/ {\vphantom {{( - x + a)} y}} \right. \kern-0em} y} - {{( - x - l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x - l{\text{/}}2)} y}} \right. \kern-0em} y}}}{{1 + {{( - x + a)( - x - l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x + a)( - x - l{\text{/}}2)} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}}} + \\ + \,\,\frac{1}{{l{\text{/}}2 - a}}\operatorname{arctg} \left. {\frac{{{{( - x + l{\text{/}}2)} \mathord{\left/ {\vphantom {{( - x + l{\text{/}}2)} y}} \right. \kern-0em} y} - {{( - x + a)} \mathord{\left/ {\vphantom {{( - x + a)} y}} \right. \kern-0em} y}}}{{{{1 + ( - x + l{\text{/}}2)( - x + a)} \mathord{\left/ {\vphantom {{1 + ( - x + l{\text{/}}2)( - x + a)} {{{y}^{2}}}}} \right. \kern-0em} {{{y}^{2}}}}}}} \right] = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}} \right.\operatorname{arctg} \frac{{y(a + l{\text{/}}2)}}{{{{y}^{2}} + ( - x + a)( - x - l{\text{/}}2)}} + \\ + \,\,\frac{1}{{l{\text{/}}2 - a}}\operatorname{arctg} \left. {\frac{{y(l{\text{/}}2 - a)}}{{{{y}^{2}} + ( - x + l{\text{/}}2)( - x + a)}}} \right]. \\ \end{gathered} $

Внеся минус под знак арктангенса, в итоге получим

$\begin{gathered} {{h}_{x}} = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ {\frac{1}{{l{\text{/}}2 + a}}{\text{arctg}}\frac{{y( - a - l{\text{/}}2)}}{{{{y}^{2}} + (x - a)(x + l{\text{/}}2)}}} \right. - \\ \left. { - \,\,\frac{1}{{l{\text{/}}2 - a}}{\text{arctg}}\frac{{y(a - l{\text{/}}2)}}{{{{y}^{2}} + (x - a)(x - l{\text{/}}2)}}} \right]. \\ \end{gathered} $

Аналогично ищем индуцированную компоненту магнитного поля $h_{y}^{{}}$

(12)

$\begin{gathered} {{h}_{y}} = \frac{1}{{2{{\pi }}}}\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} {\frac{{j({{\xi }})(x - {{\xi }})}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }} } = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ {\frac{1}{{l{\text{/}}2 + a}}\int\limits_{ - l{\text{/}}2}^a {\frac{{x - {{\xi }}}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }}} } \right. - \\ \left. { - \,\,\frac{1}{{l{\text{/}}2 - a}}\int\limits_a^{l{\text{/}}2} {\frac{{x - {{\xi }}}}{{{{{(x - {{\xi }})}}^{2}} + {{y}^{2}}}}d{{\xi }}} } \right] . \\ \end{gathered} $

Делая замену вида $t = {{\xi }} - x,$ получим:

$\begin{gathered} {{h}_{y}} = \frac{{{{I}_{{{\text{max}}}}}}}{{4{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}\int\limits_{ - x - l{\text{/}}2}^{ - x + a} {\frac{t}{{{{t}^{2}} + {{y}^{2}}}}dt} } \right. + \\ \left. { + \,\,\frac{1}{{l{\text{/}}2 - a}}\int\limits_{ - x + a}^{ - x + l{\text{/}}2} {\frac{t}{{{{t}^{2}} + {{y}^{2}}}}dt} } \right]. \\ \end{gathered} $

Используя неопределенный интеграл вида:

$\int {\frac{t}{{{{t}^{2}} + {{y}^{2}}}}dt} = \frac{1}{2}\int {\frac{{d({{t}^{2}})}}{{{{t}^{2}} + {{y}^{2}}}}} = \frac{1}{2}\ln \left[ {{{t}^{2}} + {{y}^{2}}} \right].$

выражение (12) примет вид:

$\begin{gathered} {{h}_{y}} = \frac{{{{I}_{{{\text{max}}}}}}}{{8{{\pi }}}} - \frac{1}{{l{\text{/}}2 + a}}\ln \left. {\left[ {{{t}^{2}} + {{y}^{2}}} \right]} \right|_{{t = - x - l{\text{/}}2}}^{{ - x + a}} + \\ \left. { + \,\,\frac{1}{{l{\text{/}}2 - a}}\ln \left. {\left[ {{{t}^{2}} + {{y}^{2}}} \right]} \right|_{{t = - x + a}}^{{ - x + l{\text{/}}2}}} \right] = \\ = \frac{{{{I}_{{{\text{max}}}}}}}{{8{{\pi }}}}\left[ { - \frac{1}{{l{\text{/}}2 + a}}\ln \frac{{{{{( - x + a)}}^{2}} + {{y}^{2}}}}{{{{{(x + l{\text{/}}2)}}^{2}} + {{y}^{2}}}}} \right. + \\ \left. { + \,\,\frac{1}{{l{\text{/}}2 - a}}\ln \frac{{{{{( - x + l{\text{/}}2)}}^{2}} + {{y}^{2}}}}{{{{{( - x + a)}}^{2}} + {{y}^{2}}}}} \right]. \\ \end{gathered} $

Окончательно получим выражение:

(13)

$\begin{gathered} {{h}_{y}} = \frac{{{{I}_{{{\text{max}}}}}}}{{8{{\pi }}}}\left[ {\frac{1}{{l{\text{/}}2 - a}}{\text{ln}}\frac{{{{{(x - l{\text{/}}2)}}^{2}} + {{y}^{2}}}}{{{{{(x - a)}}^{2}} + {{y}^{2}}}} - } \right. \\ - \,\,\left. {\frac{1}{{l{\text{/}}2 + a}}{\text{ln}}\frac{{{{{(x - a)}}^{2}} + {{y}^{2}}}}{{{{{(x + l{\text{/}}2)}}^{2}} + {{y}^{2}}}}} \right]. \\ \end{gathered} $

Подставляя выражение (13) в (9), получим:

$\begin{gathered} P{\kern 1pt} ' = V{{B}_{0}}\int\limits_{ - l{\text{/}}2}^{l{\text{/}}2} I ({{\xi }}) d{{\xi }} = V{{B}_{0}}{{I}_{{{\text{max}}}}}\left[ {\frac{1}{{l{\text{/}}2\, + \,a}}\int\limits_{ - l{\text{/}}2}^a {(l{\text{/}}2\, + \,{{\xi }})} d{{\xi }} + } \right. \\ \left. { + \,\,\frac{1}{{l{\text{/}}2 - a}}\int\limits_a^{l{\text{/}}2} {(l{\text{/}}2 - {{\xi }})} d{{\xi }}} \right] = \frac{{V{{B}_{0}}{{I}_{{{\text{max}}}}}}}{2} \times \\ \times \left[ {\frac{1}{{l{\text{/}}2 + a}}\left( {al + {{a}^{2}} + \frac{{{{l}^{2}}}}{4}} \right) + } \right. \\ \left. { + \,\,\frac{1}{{l/2 - a}}\left( {\frac{{{{l}^{2}}}}{4} - al + {{a}^{2}}} \right)} \right] = \frac{{V{{B}_{0}}{{I}_{{{\text{max}}}}}}}{2} \times \\ \times \,\,\left[ {\frac{{{{{(l{\text{/}}2 + a)}}^{2}}}}{{l{\text{/}}2 + a}} + \frac{{{{{(l{\text{/}}2 - a)}}^{2}}}}{{l{\text{/}}2 - a}}} \right] = \frac{{{{I}_{{{\text{max}}}}}{{B}_{0}}lV}}{2}. \\ \end{gathered} $

Необходимо отметить, что исследуемая величина, как следует из уравнения (9), тождественно равна произведению индуктивного сопротивления на скорость. При интегрировании сначала по x (при определение главного значения), а затем по y, величина энергии даст другие результаты, что не является необычным, так как это зависит от применения главного значения интеграла к физической проблеме. В работе преобразования сделаны так, чтобы результат имел определенный физический смысл.

Так, например, два члена в уравнении (1), включающие $h_{x}^{2}$ и $h_{y}^{2}$ для типичных условий движения спутника обычно на несколько порядков величины меньше, чем индуктивное сопротивление. Так как в работе [1] результаты были получены на основании только численных расчетов (численной оценки расходящегося интеграла) и оценки каждого из трех членов, по-видимому, не производились, то ясно, почему в [1] пришли к выводу, что волновое сопротивление космического аппарата является частью индуктивного сопротивления. Представленные в статье аналитические исследования дают понять, что их заключение ошибочно.

Дополнительно можно отметить, что в работах [4, 9] предложен механизм генерации узкополосного электромагнитного излучения в ультра низкочастотном диапазоне, сопровождающего полет КА на активном участке горизонтальной траектории полета. Такое излучение многократно регистрировалось как во время запуска, так и во время посадки космических аппаратов наземной сетью электромагнитных обсерваторий на территории США (Rauscher and Van Bise, 1999). Рассмотренный механизм связывает регистрируемые колебания магнитного поля с распространением в нижней ионосфере гиротропных волн, генерируемых когерентными источниками. Такими источниками служат электростатические поля, наведенные фоновым электрическим полем в горизонтальных неоднородностях ионосферной проводимости.

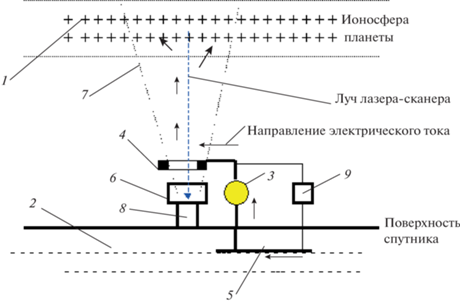
На рис. 2 рассматривается принцип воздействия индуцированных магнитных полей на индуктивное сопротивление КА. Рассматривается способ управления индуктивным полем спутника, естественным подзаряжаемым электрическим конденсатором “ионосфера-спутник” путем подключения одного конца электрической нагрузки 3 к ионосфере планеты 1, заряженной положительно относительно поверхности спутника 2, через ионизирующий луч 7, направленный с поверхности спутника в ионосферу, причем другой конец электрической нагрузки надежно обнуляют устройством 5. В состав установки входит рентгеновский лазер 6 с изолятором 8, кольцевой электрод 4, разрядник 9. Благодаря запасу электроэнергии спутника и наличию механизма его постоянного возобновления данный способ может обеспечить управление индукцией.

Рис. 2.

Схема управления обтеканием спутника ионосферой.

Рис. 3.

Распределение индуцированных зарядов в космическом пространстве между Землей и ионоплазмой.

Аналитические модели дают хорошую оценку этого принципа при условии спокойной геомагнитной обстановки, но в случае возмущенной ионосферы оценка полного электронного содержания становится существенно менее точной, что негативно сказывается на работе различных (в частности магнитных) спутниковых систем [15–18 ].

МЕТОДИКА ОПРЕДЕЛЕНИЯ РАСПРЕДЕЛЕНИЯ ПОТЕНЦИАЛА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В КОСМИЧЕСКОМ ПРОСТРАНСТВЕ

Сложность исследования заключается в том, что все космические тела одновременно взаимодействуют между собой. Известно, что на заряженные частицы, которые движутся в магнитном поле, действует сила Лоренца. Такая же сила действует на заряженный спутник, который движется в магнитном поле Земли. Эта сила зависит от положения спутника и геометрии орбиты. Направление силы всегда перпендикулярно скорости аппарата. При заряжении в магнитосферной плазме характерные величины первичных токов составляют ≈10^–10–10^–8 А ‧ см^–2, ток фотоэлектронной эмиссии для большинства материалов лежит в пределах (–5) ‧ 10^–9 А ‧ см^–2, характерные времена общего заряжения КА составляет 0.3–0.5 с, а дифференциальное заряжение – от единицы до десятков минут.

Для космических аппаратов различной формы учет магнитосферной плазмы для определения сил сопротивления является крайне важным. Простейшая модель такого взаимодействия со спутником представляет собой Землю радиуса ${{r}_{1}},$ который находится в поле двух полусферических ионосферных полей радиуса ${{r}_{2}},$ разделенных между собой узким промежутком и имеющих потенциалы $ + {{V}_{0}}$ и $ - {{V}_{0}}.$ Расчет электромагнитного поля, действующего на космический аппарат в пространстве между Землей и ионосферными полями ${{r}_{1}} < r < {{r}_{2}}$ проведем для случая, когда центры Земли и ионосферных полей совпадают и потенциал Земли предположим не учитывается. В рассматриваемом случае нахождение потенциала ${{\varphi }} = {{\varphi }}\left( {r,{{\theta }}} \right)$ поля в космическом пространстве сводится к решению краевой задачи для уравнения Лапласа, которая с учетом осевой симметрии поля может быть записана в следующем виде:

(14)

(15)

${{\varphi }}\left( {{{r}_{1}},{{\theta }}} \right) = 0;$

(16)

${{\varphi }}({{r}_{2}},{{\theta }}) = U({{\theta }}) = \left\{ \begin{gathered} + {{V}_{0}},\,\,0 \leqslant {{\theta }} \leqslant \frac{{{\pi }}}{2}; \hfill \\ - {{V}_{0}},\,\,\frac{{{\pi }}}{2} \leqslant {{\theta }} \leqslant {{\pi }}. \hfill \\ \end{gathered} \right.$

Используя метод разделения переменных, когда ${{\varphi }}\left( {r,{{\theta }}} \right) = R\left( r \right){{\Phi }}\left( {{\theta }} \right),$ получаем

(17)

$\frac{{\frac{d}{{dr}}\left( {{{r}^{2}}\frac{{dR}}{{dr}}} \right)}}{{R(r)}} = - \frac{{\frac{1}{{\sin {{\theta }}}}\frac{d}{{d{{\theta }}}}\left( {\sin {{\theta }}\frac{{d\Phi }}{{d{{\theta }}}}} \right)}}{{\Phi ({{\theta }})}} = {{\lambda }} = {\text{const}}.$

Отсюда для нахождения функций $R\left( r \right)$ и ${{\Phi }}\left( {{\theta }} \right)$ получаем уравнения

(18)

$\frac{d}{{dr}}\left( {{{r}^{2}}\frac{{dR}}{{dr}}} \right) - {{\lambda }}R = 0;$

(19)

$\frac{1}{{\sin {{\theta }}}}\frac{d}{{d{{\theta }}}}\left( {\sin {{\theta }}\frac{{d\Phi }}{{d{{\theta }}}}} \right) + {{\lambda }}\Phi = 0.$

Если в уравнении (14) сделать замену переменного $\cos ({{\theta }}) = x$ и положить ${{\Phi }}\left( {{\theta }} \right) = X\left( x \right),$ то оно примет вид

(20)

$ - \frac{d}{{dx}}\left[ {\left( {1 - {{x}^{2}}} \right)\frac{{dX}}{{dx}}} \right] = {{\lambda }}X,\,\,\,\, - 1 < x < 1.$

Задача отыскания ограниченного решения уравнения (20), удовлетворяющего условиям $\left| {X\left( { \pm 1} \right)} \right| < \infty ,$ соответствует задаче Штурма–Лиувилля. Эта задача имеет нетривиальное решение ${{X}_{n}}\left( x \right)$ лишь при ${{\lambda }} = {{{{\lambda }}}_{n}} = n\left( {n + 1} \right).$ Эти решения (собственные функции) являются полиномами Лежандра n-го порядка, т.е. ${{X}_{n}}\left( x \right) = {{P}_{n}}\left( x \right)$ или ${{\Phi }}\left( {{\theta }} \right) = {{P}_{n}}\left( {\cos {{\theta }}} \right),$ для $n = 0,~1,~2, \ldots $

Как собственная функция задачи Штурма–Лиувилля полиномы Лежандра удовлетворяют условию ортогональности:

(21)

$\begin{gathered} \int\limits_{ - 1}^1 {{{P}_{n}}(x){{P}_{m}}(x)dx} = \int\limits_0^{{\pi }} {{{P}_{n}}(\cos {{\theta }}){{P}_{m}}(\cos {{\theta }})\sin {{\theta }}d{{\theta }}} = \\ = \left\{ \begin{gathered} 0,\,\,n \ne m; \hfill \\ \frac{2}{{2n + 1}},\,\,n = m. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

При ${{\lambda }} = {{{{\lambda }}}_{n}} = n\left( {n + 1} \right)$ из уравнения (14) находим

$\begin{gathered} R\left( r \right) = {{a}_{n}}{{r}^{n}} + \frac{{{{b}_{n}}}}{{{{r}^{{n + 1}}}}}\,\,\,\,{\text{или}}\,\,\,\,R\left( {{\rho }} \right) = {{A}_{n}}{{{{\rho }}}^{n}} + \frac{{{{B}_{n}}}}{{{{{{\rho }}}^{{n + 1}}}}}, \\ {\text{где}}\,\,\,\,{{\rho }} = \frac{r}{{{{r}_{1}}}};{{A}_{n}},{{B}_{n}} = {\text{const}}. \\ \end{gathered} $

Используя принцип суперпозиции решений для линейного уравнения (14), представим его решение рядом

(22)

$\begin{gathered} {{\varphi }}({{\rho }},{{\theta }}) = \sum\limits_{n = 0}^\infty {\left( {{{A}_{n}}{{{{\rho }}}^{n}} + \frac{{{{B}_{n}}}}{{{{{{\rho }}}^{{n + 1}}}}}} \right){{P}_{n}}(\cos {{\theta }}),} \\ 1 < {{\rho }} < {{\gamma }},\,\,\,\,0 \leqslant {{\theta }} \leqslant {{\pi }}, \\ \end{gathered} $

где ${{\rho }} = \frac{r}{{{{r}_{1}}}};$ ${{\gamma }} = \frac{{{{r}_{2}}}}{{{{r}_{1}}}} > 1.$

Удовлетворяя при ${{\rho }} = 1$ граничному условию (15), получаем ${{A}_{n}} + {{B}_{n}} = 0,$ т.е.

(23)

${{\varphi }}({{\rho }},{{\theta }}) = \sum\limits_{n = 0}^\infty {{{A}_{n}}\left( {{{{{\rho }}}^{n}} - \frac{1}{{{{{{\rho }}}^{{n + 1}}}}}} \right){{P}_{n}}(\cos {{\theta }})} .$

Теперь с учетом граничного условия (16) получаем соотношение

(24)

$\sum\limits_{n = 0}^\infty {{{A}_{n}}{{\Gamma }_{n}}{{P}_{n}}(\cos {{\theta }})} = U({{\theta }}),{{\Gamma }_{n}} = \frac{{{{\gamma }^{{2n + 1}}} - 1}}{{{{\gamma }^{{n + 1}}}}}.$

Теперь найдем коэффициенты разложения Фурье. Заметим, что равенство (24) представляет собой разложение функции $U\left( {{\theta }} \right),$ заданной формулой (16), в ряд Фурье по полиномам Лежандра. Возможность такого разложения по собственным функциям задачи Штурма–Лиувилля (20) следует из теоремы Стеклова. С учетом условия ортогональности (21) находим коэффициенты этого разложения

(25)

$\begin{gathered} {{A}_{n}}{{\Gamma }_{n}} = \frac{{2n + 1}}{2}\int\limits_0^\pi {U({{\theta }}){{P}_{n}}\left( {\cos {{\theta }}} \right)\sin {{\theta }}d{{\theta }}} = \\ = \frac{{2n + 1}}{2}\int\limits_{ - 1}^1 {\widetilde U(x){{P}_{n}}(x)dx} ,\,\,\,\,\widetilde U(x) = \left\{ \begin{gathered} - {{V}_{0}},\,\, - 1 < x < 0; \hfill \\ + {{V}_{0}},\,\,0 < x < 1. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Учитывая правила изменения знака аргумента для полиномов Лежандра ${{P}_{n}}( - x) = {{( - 1)}^{n}}{{P}_{n}}(x),$ из (25) для искомых коэффициентов ${{A}_{n}}$ разложения (22) получим формулы

$\begin{gathered} {{A}_{n}} = 0\,\,\,\,{\text{для}}\,\,\,\,n = 2k; \\ {{A}_{n}} = {{V}_{0}}\frac{{2n + 1}}{{{{\Gamma }_{n}}}}\int\limits_0^1 {{{P}_{n}}\left( x \right)dx} \,\,\,\,{\text{для}}\,\,\,\,n = 2k + 1. \\ \end{gathered} $

Используя известные для полиномов Лежандра формулы

$\begin{gathered} {{P}_{n}}\left( 1 \right) = 1;\,\,\,\,{{P}_{{n + 1}}}\left( 0 \right) = - \frac{n}{{n + 1}}{{P}_{{n - 1}}}\left( 0 \right); \\ {{P}_{n}}\left( x \right) = \frac{1}{{2n + 1}}\left[ {P_{{n + 1}}^{'}\left( x \right) - P_{{n - 1}}^{'}\left( x \right)} \right], \\ \end{gathered} $

можно вычислить квадратуру

$\begin{gathered} \int\limits_0^1 {{{P}_{n}}(x)dx} = \frac{1}{{n + 1}}{{P}_{{n - 1}}}(0);\,\,\,{{P}_{0}}(0) = 1;\,\,\,\,{{P}_{{2k + 1}}}(0) = 0; \\ {{P}_{{2k}}}(0) = {{( - 1)}^{k}}\frac{{1 \cdot 3 \cdot 5 \cdots (2k - 1)}}{{2 \cdot 4 \cdot 6 \cdots 2k}},\,\,\,\,k \geqslant 1. \\ \end{gathered} $

Таким образом, окончательно, решение краевой задачи (14)–(16), описывающее распределение потенциала в космическом пространстве, запишем виде:

(26)

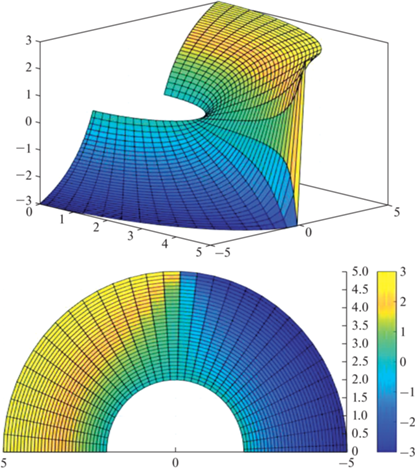
$\begin{gathered} {{\varphi }}({{\rho }},{{\theta }}) = {{V}_{0}}\sum\limits_{k = 0}^\infty {\frac{{(4k + 3){{P}_{{2k}}}(0)}}{{2(k + 1){{\Gamma }_{{2k + 1}}}}}\left( {{{{{\rho }}}^{{2k + 1}}} - \frac{1}{{{{{{\rho }}}^{{2k + 2}}}}}} \right) \times } \\ \times \,\,{{P}_{{2k + 1}}}(\cos {{\theta }}),\,\,\,1 \leqslant {{\rho }} = \frac{r}{{{{r}_{1}}}} \leqslant {{\gamma }},\,\,\,\,0 \leqslant {{\theta }} \leqslant {{\pi }}. \\ \end{gathered} $

Используя известную формулу электродинамики

${{\sigma }} = {{{{\varepsilon }}}_{0}}{{E}_{n}} = - {{{{\varepsilon }}}_{0}}{{\left. {\left( {\frac{{\partial {{\varphi }}}}{{\partial r}}} \right)} \right|}_{{r = {{r}_{1}}}}} = - \frac{{{{{{\varepsilon }}}_{0}}}}{{{{r}_{1}}}}{{\left. {\left( {\frac{{\partial {{\varphi }}}}{{\partial {{\rho }}}}} \right)} \right|}_{{{{\rho }} = 1}}},$

с помощью решения (26) можно определить распределение индуцированных зарядов на определенном участке траектории КА и других произвольных космических объектов. В качестве примера приведено решение распределения потенциала с помощью программы MATLAB для следующих условий: ${{V}_{0}}$ = 5 Мв, ${{r}_{1}}$ = 200 км, ${{r}_{2}}$ = 500 км.

В результате было получено решение краевой задачи для уравнения Лапласа, описывающее распределение потенциала поля в космическом пространстве между Землей и ионосферой.

ЗАКЛЮЧЕНИЕ

Исследована аналитическая зависимость для энергии, излучаемой спутником с учетом направления распространения волн Альвена. Доказано, что порядок интегрирования влияет на существование интеграла для определения индуктивного сопротивления спутника и других удлиненных тел (например, электродинамического троса для уводки с траектории). Отмечено, что линейный член в уравнении энергии влияет на индукцию при произвольном законе распределения тока в спутнике в электромагнитном поле, и, что полное сопротивление будет больше индуктивного. В результате исследований показано, что при движении спутника на средних высотах распределение тока в магнитосферной плазме может быть удовлетворительно аппроксимировано отрезками прямых линий с максимумом в точке нулевого потенциала, то есть в точке, где потенциал спутника равен потенциалу ионоплазмы. Выявлено, что индуцированные компоненты магнитного поля можно определить интегрированием. Определена индуцированная компонента магнитного поля. Необходимо отметить, что сила гравитационного притяжения Земли на три порядка превосходит силу кулоновского взаимодействия. Сила гравитационного притяжения и сила Лоренца, действующая на КА со стороны электромагнитного поля Земли одного порядка. Динамика частиц массой примерно 5–8 г определяется, в первую очередь, не гравитационной силой, а сложным движением в электромагнитном поле Земли. Альвеновская концепция магнитоплазмы справедлива при рассмотрении космических частиц. Для КА можно использовать одночастичное приближение, для массового компонента справедливо представление о континиуме как о сплошной среде. Микрочастица в плазме заряжена отрицательно из-за столкновений с плазменными электронами. Однако она может “утратить” этот заряд за счет фотоэффекта, а также под действием автоэлектронной эмиссии и ударов положительных ионов. Частицы ионосферной плазмы относительно космического пространства имеют положительный или отрицательный потенциал порядка 1…10 В. На частицу, обладающую электрическим зарядом, действует электромагнитная сила и электрическое и магнитное поля. Когда КА попадает в область плазмы с большим количеством надтепловых электронов, ее заряд может резко возрасти примерно в 1000 раз, в результате чего она окажется захваченной плазмой. К основным факторам, приводящим к электризации, следует отнести потоки электронов и ионов околоземной космической плазмы, жесткое ультрафиолетовое излучение Солнца, вакуум, термоциклирование. Все перечисленное особенно существенно для высокоорбитальных космических аппаратов во время суббурь в магнитосфере Земли. В результате происходит общее и дифференциальное заряжение поверхности космического аппарата.

Заряжение элементов КА в космической плазме происходит по причине значительного превышения электронного диффузионного тока над ионным током. При такой плотности тока время электризации КА, имеющего типичные размеры , до потенциала 10 кВ составляет всего 5 мс. Таким образом, общая зарядка КА происходит практически мгновенно в поле.

Список литературы

Chu C.K., Gross R.A. Alfvén Waves and Induction Drag on Long Cylindrical Satellites // AIAA J. Dec. 1966. V. 4. № 12. P. 2209–2214.
Drell S.D., Foley H.M., Ruderman M.A. Drag and Propulsion of Large Satellites in the Ionosphere: An Alfvén Propulsion Engine in Space // J. Geophysical Research. 1965. V. 70. P. 3131–3145.
Воздействие космической среды на материалы и оборудование космических аппаратов. Модель космоса. М.: КДУ, 2007.
Афраймович Э.Л., Перевалова Н.П., Плотников А.В. Регистрация ионосферных откликов на ударно- акустические волны, генерируемые при запусках ракет-носителей // Геомагнетизм и аэрономия. 2002. Т. 42. № 6. С. 790–797.
Денисенко В.В. О проникновении атмосферного электрического поля в ионосферу. Глобальная электрическая цепь. Материалы Всероссийской конференции, 2013.
Пулинец С.А., Давиденко Д.В. Изменчивость ионосферы и глобальная электрическая цепь. Глобальная электрическая цепь. Материалы Всероссийской конференции, 2013.
Sidnyaev N.I. Studi of heat and mass transfer for hypersonic flow past a complex body of revolution // Thermophysics and Aeromechanics. 2006. V. 13. № 1. P. 2–16.
Sidnyaev N.I. Investigation of aerodynamic characteristics of a hypersonic flow around bodies of revolution with a permeable tip // J. Applied Mechanics and Technical Physics. 2007. V. 48. № 2. P. 19–26.
Сорокин В.М. Волновые процессы в ионосфере, связанные с геомагнитным полем // Изв. вузов. Радиофизика. 1988. Т. 31. С. 1169–1180.
Sidnyaev N.I. Aerodynamic Performances of Hypersonic Aircrafts with Surface Mass Transfer // Mathematical Models and Computer Simulations. 2009. V. 1. № 3. P. 343–352.
Сидняев Н.И., Климова Н.С. Изменение поверхностных и объемных свойств космического аппарата при адсорбции и рекомбинация атомов кислорода и азота // Космич. исслед. 2020. Т. 58. № 3. С. 208–222.
Альвен Х. Космическая плазма. М.: Мир, 1983.
Сидняев Н.И., Савченко В.П., Клочкова Д.В. Физические принципы и математическая модель управления индуктивным сопротивлением спутников в ионосфере планеты // Физические основы приборостроения. 2012. Т. 1. № 4. С. 98–105.
Авдуевский В.С., Антонов Б.М., Анфимов Н.А. и др. Основы теории полёта космических аппаратов. М.: Машиностроение, 1972.
Сидняев Н.И., Макриденко Л.А., Геча В.Я. и др. Аэромеханика низкоорбитальных космических аппаратов. Тезисы докладов Четвертой международной научно-технической конференции “Актуальные проблемы создания космических систем дистанционного зондирования Земли”. М.: ВНИИЭМ, 2016.
Сидняев Н.И. Исследование разрушения поверхности КА при контактном взаимодействии с микрочастицами космической среды // Космич. исслед. 2018. Т. 56. № 3. С. 233–242.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал