1. На главную
  2. Электронные версии
  3. Космические исследования
  4. T. 60, № 6, 2022

Космические исследования, 2022, T. 60, № 6, стр. 517-527

Траектории перелета к Луне с минимальной тягой

А. В. Иванюхин 1, *, В. Г. Петухов 1, Юн Сон Ук 2

1 Научно-исследовательский институт прикладной механики и электродинамики Московского авиационного института
Москва, Россия

2 Московский авиационный институт
Москва, Россия

* E-mail: ivanyukhin.a@yandex.ru

Поступила в редакцию 20.05.2022
После доработки 10.06.2022
Принята к публикации 24.06.2022

Полный текст (PDF)

Аннотация

В работе рассматривается задача оптимизации траекторий космического аппарата с малой тягой к окололунным орбитам, точкам либрации системы Земля-Луна и гало-орбитам вокруг них. Целью оптимизации является минимизация тяги. Для решения задачи минимизации тяги используется непрямой подход, основанный на использовании принципа максимума и метода продолжения. Задача оптимизации рассматриваемого класса траекторий приводит к необходимости преодоления ряда проблем, связанных с вычислительной неустойчивостью, ограниченностью области существования решения и необходимостью выбора правильного соотношения угловой дальности и длительности перелета как на геоцентрическом, так и на селеноцентрическом участках. Для преодоления этих трудностей предлагается использовать последовательное решение задачи оптимизации траектории космического аппарата с идеально-регулируемым двигателем и задачи минимизации тяги в постановке с фиксированной угловой дальностью и свободным временем перелета. Точность вычисления производных, необходимых при решении краевой задачи принципа максимума, обеспечивается применением автоматического дифференцирования с использованием комплексных дуальных чисел. Приводятся численные примеры расчета прямых и низкоэнергетических траекторий перелета с включением в траекторию участка движения по устойчивому многообразию.

ВВЕДЕНИЕ

Одним из способов повышения эффективности лунных миссий является использование для их реализации электроракетных двигательных установок (ЭРДУ) с высоким удельным импульсом тяги, что позволяет существенно сократить затраты топлива на перелет. К настоящему времени успешно реализован перелет на окололунную орбиту КА с ЭРДУ SMART-1 [1]. Планируется использовать ЭРДУ для выведения базового модуля лунной орбитальной станции [2], рассматриваются варианты использования космических буксиров с ЭРДУ для обеспечения лунной пилотируемой программы [3].

Теоретические аспекты перелетов к Луне с малой тягой и численные методы для их расчета и оптимизации рассматривались во многих работах, например в [4–9]; однако следует отметить, что до настоящего времени не проведено достаточно полного теоретического исследования особенностей оптимальных лунных траекторий с малой тягой, а разработанные численные методы имеют существенные ограничения по применению.

Использование ЭРДУ приводит к значительному увеличению длительности перелета к Луне, поскольку величина тяги ЭРДУ мала по сравнению с химическими ракетными двигателями. Это также означает, что требуемое число витков может исчисляться десятками и сотнями. Многовитковая задача является многоэкстремальной: для фиксированной длительности перелета существует множество локально-оптимальных решений с разным числом витков. Эта особенность затрудняет обеспечение вычислительной устойчивости применяемых численных методов оптимизации.

Одним из вариантов решения задачи проектирования многовитковых перелeтов к Луне с малой тягой является использование приближенных: локально-оптимальных законов управления на основе функций Ляпунова [10, 11] и квазиоптимального управления с обратной связью (КОУСОС) [12–14].

КОУСОС использовалось в ряде предыдущих исследований [12, 13] для оптимизации траекторий с малой тягой к точке либрации L1 системы Земля-Луна (EML1), на низкую лунную орбиту и гало-орбиты у точек либрации системы Земля-Луна.

Недавно авторами был предложен новый подход к оптимизации траекторий малой тяги с фиксированной угловой дальностью и свободным временем перелeта для оптимизации межорбитальных перелeтов [15–17]. Отличительной особенностью предложенного подхода является использование новой независимой угловой переменной – вспомогательной долготы, которая в невозмущeнном движении совпадает с истинной долготой. Этот подход обеспечивает единственность минимума функционала по длительности перелета в заданном классе экстремалей при фиксированной угловой дальности.

Однако существует еще одна существенная трудность, связанная с использованием методов оптимизации возмущенных траекторий, основанных на применении принципа максимума и метода продолжения. Для их реализации необходимо высокоточное вычисление смешанных производных второго порядка от правых частей дифференциальных уравнений, включающих возмущающие ускорения, по фазовым переменным и неизвестным параметрам краевой задачи. Для решения этой задачи был разработан метод, основанный на использовании комплексных дуальных чисел – автоматическое дифференцирование с использованием комплексных дуальных чисел (CDNAD) [21–24]. CDNAD позволяет существенно облегчить подготовку математической модели, необходимой для оптимизации возмущенной траектории, с помощью автоматизации вычисления производных от возмущающих ускорений по фазовому вектору с использованием комплексных дуальных чисел с последующим вычислением требуемых производных от вектора невязок краевой задачи методом комплексного шага.

Ещe одной проблемой является ограниченность области существования решения задачи оптимизации траектории перелета КА с двигателем малой тяги. Как правило, границы этой области заранее неизвестны. Поэтому, при отказе метода вычисления оптимальной траектории часто бывает трудно установить, связан ли этот отказ с недостатками используемого метода или с попыткой найти решение вне области его существования. Для решения задачи вычисления границы области существования решения задачи оптимизации траектории КА с двигателем ограниченной тяги может быть использована задача минимизации тяги [25–27]. Очевидно, что в случае фиксированной длительности или угловой дальности перелета решение существует только при величине тяги большей некоторого минимального значения. По результатам решения задачи минимизации тяги делается вывод о существовании траектории КА. Решение задачи минимизации тяги существенно облегчается из-за отсутствия разрывов в управлении. Таким образом, задача минимизации тяги может использоваться как инструмент диагностики существования оптимальных траекторий с переключением тяги.

Кроме того, решении задачи минимальной тяги дает много полезной информации, касающейся решения параметрической части задачи [28]. Величина электрической мощности P, доступной для питания ЭРДУ на борту КА, пропорциональна тяге T и скорости истечения c: P = Tc/2. В целом массу энергодвигательной установки (ЭДУ) КА с ЭРДУ можно оценить как mЭДУ = γP = γTc/2, где γ – значение удельной массы ЭДУ. Так как масса ЭДУ почти пропорциональна величине тяги, задача минимизации тяги практически совпадает с задачей минимизации массы ЭДУ.

Траектории перелeта к Луне с малой тягой в отличие от траекторий с большой тягой отличаются медленным изменением константы энергии, поэтому типичная траектория перелета между околоземной и окололунной орбитами входит в сферу Хилла Луны через горловину в окрестности точки либрации EML1. Чем меньше величина реактивного ускорения, тем уже должна быть горловина в окрестности точки либрации из-за необходимости увеличения константы Якоби КА до критического уровня за ограниченное время, пока КА остается в сфере Хилла Луны. Таким образом, траектории с малой тягой к Луне должны проходить вблизи EML1. Следовательно, можно разбить траекторию от околоземной орбиты до окололунной орбиты на две части: геоцентрическую (от околоземной орбиты до EML1) и селеноцентрическую (от EML1 до окололунной орбиты) участков. Отметим, что оскулирующая орбита EML1 является эллиптической как в геоцентрической, так и в селеноцентрической системах координат.

Для расчета траекторий с минимальной тягой будем отдельно рассчитывать геоцентрический и селеноцентрический участки траектории и стыковать их в точке либрации EML1 или использовать для пролета окрестности точки либрации инвариантные многообразия. Для расчета таких траекторий необходимо зафиксировать время прохождения точки либрации (или заданных точек выхода на выбранное устойчивое инвариантное многообразие на геоцентрическом участке и схода с выбранного неустойчивого многообразия на селеноцентрическом участке при использовании инвариантных многообразий для входа в сферу Хилла Луны) и выбрать угловые дальности геоцентрического и селеноцентрического участков такими, чтобы они обеспечивали одинаковое значение минимальной тяги КА на обоих участках траектории. Задача оптимизации траектории перелета к Луне КА с минимальной тягой формулируется как задача независимого вычисления значения минимальной тяги Tmin на геоцентрическом и селеноцентрическом участках траектории с фиксированной угловой дальностью каждого участка с дальнейшим подбором этих угловых дальностей с целью обеспечения равенства минимальной тяги на обеих участках.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ

Рассмотрим задачу оптимизации возмущенной многовитковой траектории с малой тягой. Будем использовать модифицированные равноденственные элементы и вспомогательную долготу K, совпадающую с истинной долготой в невозмущeнном движении, в качестве независимой переменной. Подход к оптимизации траекторий КА, основанный на использовании этой угловой независимой переменной, представлен в [15–17]. Уравнения возмущенного движения КА с малой тягой при использовании вспомогательной долготы K имеют следующий вид:

(1)
$\left\{ \begin{gathered} \frac{{dp}}{{dK}} = \frac{{2{{p}^{3}}}}{{\mu {{q}^{3}}}}{{a}_{t}}, \hfill \\ \frac{{d{{e}_{x}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}}\left[ {\sin L \cdot {{a}_{r}} + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}{{a}_{t}} - \frac{{{{e}_{y}}\xi }}{q}{{a}_{n}}} \right], \hfill \\ \frac{{d{{e}_{y}}}}{{dK}} = \frac{{{{p}^{a}}}}{{\mu {{q}^{2}}}}\left[ { - \cos L \cdot {{a}_{r}} + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}{{a}_{t}} + \frac{{{{e}_{x}}\xi }}{q}{{a}_{n}}} \right], \hfill \\ \frac{{d{{i}_{x}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\cos L \cdot {{a}_{n}},\frac{{d{{i}_{y}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\sin L \cdot {{a}_{n}}, \hfill \\ \frac{{d{{L}_{K}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{3}}}}\xi \cdot {{a}_{n}},\frac{{dm}}{{dK}} = - \frac{\delta }{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}\frac{T}{c}, \hfill \\ \frac{{dt}}{{dK}} = \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}. \hfill \\ \end{gathered} \right.,$
где ${{e}_{x}} = e\cos (\omega + \Omega ),$ ${{e}_{y}} = e\sin (\omega + \Omega ),$ ix = = ${\text{tg}}\frac{i}{2}cos\Omega ,$ ${{i}_{y}} = \operatorname{tg} \frac{i}{2}\sin \Omega ,$ $L = v + \omega + \Omega ,$ s2 = 1 + + $i_{x}^{2} + i_{y}^{2},$ $q = 1 + {{e}_{x}}\cos L + {{e}_{y}}\sin L,$ ξ  = $ = {{i}_{x}}\sin L - {{i}_{y}}\cos L,$ at =  $\delta \frac{T}{m}\cos \vartheta \cos \psi $ + apt, ${{a}_{r}} = \delta \frac{T}{m}\sin \vartheta \cos \psi + {{a}_{{pr}}},$ an =  $\delta \frac{T}{m}\sin \psi + {{a}_{{pn}}},$ T – тяга, c – скорость истечения, m – масса, δ – функция дросселирования, ϑ – тангаж, ψ – рысканье, apt, apr, apn – трансверсальная, радиальная и бинормальная компоненты возмущающего ускорения соответственно, p, e, ω, i, Ω – кеплеровские орбитальные элементы, LK – отклонение истинной долготы L от K, ν – истинная аномалия, μ – гравитационный параметр.

В правой части системы дифференциальных уравнений (1) истинная долгота должна быть представлена как L = K + LK. Рассмотрим перелет из точки начальной орбиты с истинной долготой L0 с угловой дальностью ΔL. В этом случае конечная точка траектории будет иметь истинную долготу Lf = L0 + ΔL.

В [15–17] представлен метод решения задачи оптимизации перелета на околоземную орбиту с малой тягой с фиксированной угловой дальностью перелета и свободным временем перелета. Основное преимущество рассматриваемой формулировки задачи оптимизации траектории с фиксированной угловой дальностью и свободным временем перелета заключается в том, что для однотипных семейств траекторий, судя по проведенному ранее численному анализу, имеется только одно решение, удовлетворяющее необходимым условиям оптимальности. При использовании более традиционной формулировки – оптимизации траектории с фиксированным временем перелета и свободной угловой дальностью – существует множество оптимальных решений с различным числом витков (см., например, рис. 1 в [17]), что ограничивает область сходимости численных методов и затрудняет вычисление глобально-оптимальных решений.

Рис. 1.

Проекции оптимальной траектории на плоскость XY в инерциальной системе координат J2000 (слева) и на мгновенную плоскость орбиты Луны в синодической системе координат (справа), T* = 0.2 Н.

2. ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ: МИНИМИЗАЦИЯ ТЯГИ

Рассмотрим задачу вычисления траектории с минимальной тягой, заданным удельным импульсом, фиксированной угловой дальностью. Аналогично работам [25–27], будем называть ее Tmin-задачей.

В работе [17] уже рассматривалась Tmin-задача для межорбитальных перелeтов с использованием угловой независимой переменной K, но без учета влияния возмущений. Рассмотрим задачу минимизации функционала:

(2)
$\begin{array}{*{20}{c}} {J = \frac{1}{2}\int\limits_{{{L}_{0}}}^{{{L}_{f}}} {{{T}^{2}}dL} = \frac{1}{2}\int\limits_{{{K}_{0}}}^{{{K}_{f}}} {{{T}^{2}}\frac{{dL}}{{dK}}dK} = } \\ \begin{gathered} = \frac{1}{2}\int\limits_{{{K}_{0}}}^{{{K}_{f}}} {{{T}^{2}}\left( {1 + \frac{{d{{L}_{K}}}}{{dK}}} \right)dK = } \\ = \,\,\frac{1}{2}\int\limits_{{{K}_{0}}}^{{{K}_{f}}} {{{T}^{2}}\left[ {1 + {{k}_{1}}{{k}_{2}}\xi \left( {\delta \frac{T}{m}\sin \psi + {{a}_{{pn}}}} \right)} \right]dK} , \\ \end{gathered} \end{array}$
для динамической системы (1), дополненной формальным дифференциальным уравнением для тяги:

(3)
${{dT} \mathord{\left/ {\vphantom {{dT} {dK}}} \right. \kern-0em} {dK}} = 0.$

Очевидно, что при фиксированной угловой дальности перелета минимум функционала (2) достигается при минимальной тяге. Функция Понтрягина рассматриваемой Tmin-задачи в этом случае принимает вид:

(4)
$H = {{H}_{{T\min }}} + {{H}_{p}} + {{H}_{t}},$
(5)
$\left\{ \begin{gathered} {{H}_{{T\min }}} = - \frac{1}{2}{{T}^{2}}\left( {1 + \delta \frac{T}{m}{{k}_{1}}{{k}_{2}}\xi \sin {\kern 1pt} \psi } \right) + \hfill \\ + \,\,\delta T{{k}_{1}}\left[ {\frac{{{{k}_{2}}}}{m}\left( {{{A}_{r}}{\kern 1pt} \sin {\kern 1pt} \vartheta \cos {\kern 1pt} \psi + {{A}_{t}}\cos {\kern 1pt} \vartheta \cos {\kern 1pt} \psi + } \right.} \right. \hfill \\ \left. { + \,\,\left. {{{A}_{n}}\sin {\kern 1pt} \psi } \right) - \frac{{{{p}_{m}}}}{c}} \right] = - \frac{1}{2}{{T}^{2}} + \delta T{{k}_{1}} \times \hfill \\ \times \,\left[ {\frac{{{{k}_{2}}}}{m}\left( {{{A}_{r}}\sin {\kern 1pt} \vartheta \cos {\kern 1pt} \psi + \,{{A}_{t}}\cos {\kern 1pt} \vartheta \cos {\kern 1pt} \psi \, + \,{{A}_{{n1}}}\sin {\kern 1pt} \psi } \right)\, - \frac{{{{p}_{m}}}}{c}} \right], \hfill \\ {{H}_{p}} = {{k}_{1}}{{k}_{2}}\left( {{{A}_{r}}{{a}_{{pr}}} + {{A}_{t}}{{a}_{{pt}}} + {{A}_{{n1}}}{{a}_{{pn}}}} \right), \hfill \\ {{H}_{t}} = \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}{{p}_{t}}, \hfill \\ \end{gathered} \right.$
где ${{H}_{{T\min }}},{{H}_{p}},{{H}_{t}}$ – части функции Понтрягина, зависящие от тяги, возмущающих ускорений и сопряженной к времени переменной pt соответственно,
$\begin{gathered} {{A}_{t}} = 2p{{p}_{p}} + \left[ {\left( {q + 1} \right)\cos {\kern 1pt} L + {{e}_{x}}} \right]{{p}_{{ex}}} + \\ + \,\,\left[ {\left( {q + 1} \right)\sin {\kern 1pt} L + {{e}_{y}}} \right]{{p}_{{ey}}}, \\ {{A}_{r}} = q\left( {\sin {\kern 1pt} L{{p}_{{ex}}} - \cos {\kern 1pt} L{{p}_{{ey}}}} \right), \\ {{A}_{{n1}}} = \xi \left( { - {{e}_{y}}{{p}_{{ex}}} + {{e}_{x}}{{p}_{{ey}}} + {{p}_{{LK}}} - \frac{{{{T}^{2}}}}{2}} \right) + \\ + \,\,\frac{{{{s}^{2}}}}{2}\left( {\cos {\kern 1pt} L{{p}_{{ix}}} + \sin {\kern 1pt} L{{p}_{{iy}}}} \right), \\ \end{gathered} $
pp, pex, pey, pix, piy, pLK, pm – переменные, сопряженные к p, ex, ey, ix, iy, LK и m соответственно.

Максимизируя (4) по управлению ϑ, ψ и δ, получим следующие выражения для оптимального управления:

(6)
$\begin{array}{*{20}{c}} {\sin {\kern 1pt} \vartheta = {{{{A}_{r}}} \mathord{\left/ {\vphantom {{{{A}_{r}}} {{{A}_{{rt}}},}}} \right. \kern-0em} {{{A}_{{rt}}},}}\,\,\,\,\cos {\kern 1pt} \vartheta = {{{{A}_{t}}} \mathord{\left/ {\vphantom {{{{A}_{t}}} {{{A}_{{rt}}},}}} \right. \kern-0em} {{{A}_{{rt}}},}}} \\ {\sin {\kern 1pt} \psi = {{{{A}_{{n1}}}} \mathord{\left/ {\vphantom {{{{A}_{{n1}}}} {{{A}_{1}},}}} \right. \kern-0em} {{{A}_{1}},}}\,\,\,\,\cos {\kern 1pt} \psi = {{{{A}_{{rt}}}} \mathord{\left/ {\vphantom {{{{A}_{{rt}}}} {{{A}_{1}},}}} \right. \kern-0em} {{{A}_{1}},}}} \\ \begin{gathered} \delta = {{\left( {1 + \operatorname{sign} {\kern 1pt} {{S}_{{T\min }}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + \operatorname{sign} {\kern 1pt} {{S}_{{T\min }}}} \right)} 2}} \right. \kern-0em} 2}, \\ {{S}_{{T\min }}} \ne 0;\,\,\,\,\delta \in \left[ {0;1} \right],\,\,\,\,{{S}_{{T\min }}} = 0, \\ \end{gathered} \end{array}$
где ${{S}_{{T\min }}} = \frac{{{{k}_{2}}{{A}_{1}}}}{m} - \frac{{{{p}_{m}}}}{c}$ – функция переключения, ${{A}_{1}} = \sqrt {A_{r}^{2} + A_{t}^{2} + A_{{n1}}^{2}} $. Так как величины k2, A1, m, c положительны на всей траектории, а pm – неположительна (в конечной точке pm = 0 в силу необходимых условий оптимальности, а dpm/dK = –∂H/∂m ≥ 0), то ST min > 0 на всей траектории. Следовательно, на всей траектории с минимальной тягой

(7)
$\delta \left( K \right) \equiv 1.$

Подставляя выражения для оптимального управления (6), (7) в (5), получим следующее выражение для HT min:

${{H}_{{T\min }}} = - \frac{1}{2}{{T}^{2}} + T{{k}_{1}}{{S}_{{T\min }}},$
подставив которое в (4) вместо первого уравнения (5), получим выражение для оптимального гамильтониана H:

$\begin{gathered} H = \underbrace { - \frac{1}{2}{{T}^{2}} + T{{k}_{1}}{{S}_{{T\min }}}}_{{{H}_{{T\min }}}} + \\ + \,\,\underbrace {{{k}_{1}}{{k}_{2}}\left( {{{A}_{r}}{{a}_{{pr}}} + {{A}_{t}}{{a}_{{pt}}} + {{A}_{{n1}}}{{a}_{{pn}}}} \right)}_{{{H}_{p}}} + \underbrace {{{k}_{1}}{{p}_{t}}}_{{{H}_{t}}}. \\ \end{gathered} $

Уравнение для массы КА m, с учетом (7), можно представить в виде:

$m\left( K \right) = m\left( {{{K}_{0}}} \right) - \frac{T}{c}\left[ {t\left( K \right) - t\left( {{{K}_{0}}} \right)} \right].$

В систему дифференциальных уравнений (1) следует добавить дифференциальные уравнения для тяги (3) и сопряженной к ней переменной pT:

(8)
$\begin{gathered} \frac{{d{{p}_{T}}}}{{dK}} = T + {{k}_{1}}\frac{{{{p}_{m}}}}{c} + \\ + \,\,{{k}_{1}}{{k}_{2}}\left[ {\frac{1}{m}\left( { - {{A}_{1}} + \xi {{T}^{2}}\frac{{{{A}_{{n1}}}}}{{{{A}_{1}}}}} \right) + \xi T{{a}_{{pn}}}} \right]. \\ \end{gathered} $

В краевые условия должны быть включены условия трансверсальности для pT на левом и правом концах траектории:

(9)
${{p}_{T}}\left( {{{K}_{0}}} \right) = 0,\quad {{p}_{T}}\left( {{{K}_{f}}} \right) = 0.$

Система обыкновенных дифференциальных уравнений оптимального движения имеет вид:

(10)
$\begin{gathered} \frac{{d{{{\mathbf{x}}}_{1}}}}{{dK}} = \frac{{\partial H}}{{\partial {{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}},\,\,\,\,\frac{{dT}}{{dK}} = 0,\,\,\,\, \\ \frac{{d{{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}}{{dK}} = - \frac{{\partial H}}{{\partial {{{\mathbf{x}}}_{1}}}},\,\,\,\,\frac{{d{{p}_{T}}}}{{dK}} = - \frac{{\partial H}}{{\partial T}}, \\ \end{gathered} $
где ${\mathbf{x}}_{1}^{{\text{T}}}$ = (p, ex, ey, ix, iy, LK, m, t) – фазовый вектор и ${\mathbf{p}}_{{{\mathbf{x}}1}}^{{\text{T}}}$ = (pp, pex, pey, pix, piy, pLK, pm, pt) – вектор сопряженных переменных.

При использовании точки либрации в качестве точки стыковки геоцентрического и селеноцентрического участков, вся траектория разбивается на две части: от околоземной орбиты до EML1 и от EML1 до окололунной орбиты. В этом случае время пролета EML1 фиксируется, а время отлета с начальной околоземной орбиты и время выхода на конечную окололунную орбиту должны удовлетворять необходимым условиям оптимальности.

Краевые условия для геоцентрического участка траектории с учетом возможности установить K0 = 0 без потери общности (см. [15–17]) можно записать в виде

(11)
$\begin{gathered} {{L}_{K}}\left( 0 \right) = {{L}_{0}},\,\,\,\,{\mathbf{x}}\left( 0 \right) = {{{\mathbf{x}}}_{0}}\left( {{{L}_{0}}} \right),\,\,\,\,m\left( 0 \right) = {{m}_{0}}, \\ {{p}_{t}}\left( 0 \right) = 0,\,\,\,\,{{p}_{T}}\left( 0 \right) = 0,\,\,\,\,{{p}_{{LK}}}\left( 0 \right) + H\left( 0 \right) = 0, \\ \end{gathered} $
(12)
$\begin{gathered} {{L}_{K}}\left( {{{K}_{f}}} \right) + {{K}_{f}} = {{L}_{f}},\,\,\,\,{\mathbf{x}}\left( {{{K}_{f}}} \right) = {{{\mathbf{x}}}_{f}}\left( {{{L}_{f}}} \right), \\ t\left( {{{K}_{f}}} \right) = {{t}_{{L1}}},\,\,\,\,{{p}_{m}}\left( {{{K}_{f}}} \right) = 0,\,\,\,\,{{p}_{T}}\left( {{{K}_{f}}} \right) = 0, \\ \end{gathered} $
где xT = (p, ex, ey, ix, iy), а xf, Lf – геоцентрические оскулирующие орбитальные элементы EML1 в заданный момент ее пролета tL1. Подробный вывод условий (11), (12) для задачи перелета между околоземными орбитами приведен в работах [15–17].

Для решения краевой задачи (10)–(12) требуется определить 8 компонент вектора px1(0), конечную вспомогательную долготу Kf и тягу T при которых удовлетворяется последнее уравнение в (11) и 9 уравнений (12).

При оптимизации селеноцентрического участка траектории (от EML1 до окололунной орбиты) фиксируется время начала движения КА от точки либрации EML1t0 = tL1. Таким образом, в этом случае время прилета КА в конечную точку на окололунной орбите tf является неизвестным параметром. К начальным условиям (11) в этом случае необходимо добавить уравнение t(0) = tL1 и исключить уравнение pt(0) = 0, а к конечным условиям (12) необходимо добавить уравнение pt(Kf) = 0 и исключить уравнение t(Kf) = tf.

3. МЕТОД РЕШЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Рассмотрим решение краевой задачи (10)–(12) методом продолжения по параметру в форме, представленной в [21, 22]. Для решения задачи оптимизации геоцентрического участка траектории требуется найти значения неизвестных параметров

${\mathbf{z}} = {{\left[ {{\mathbf{p}}_{{\mathbf{x}}}^{{\rm T}}\left( 0 \right),{{p}_{{LK}}}\left( 0 \right),t\left( 0 \right),T,{{p}_{m}}\left( 0 \right),{{K}_{f}}} \right]}^{{\rm T}}},$
при которых удовлетворяются условия
${\mathbf{f}}\left( {\mathbf{z}} \right) = \left[ \begin{gathered} {\mathbf{x}}\left( {{{K}_{f}}} \right) - {{{\mathbf{x}}}_{f}}\left( {{{L}_{f}}} \right) \hfill \\ {{p}_{{LK}}}\left( 0 \right) + H\left( 0 \right) \hfill \\ {{t}_{f}} - t\left( {{{K}_{f}}} \right) \hfill \\ {{p}_{m}}\left( {{{K}_{f}}} \right) \hfill \\ {{L}_{K}}\left( {{{K}_{f}}} \right) + {{K}_{f}} - {{L}_{f}} \hfill \\ {{p}_{T}}\left( {{{K}_{f}}} \right) \hfill \\ \end{gathered} \right] = 0,$
где $p_{x}^{{\text{T}}}$ = (pp, pex, pey, pix, piy).

Для решения задачи оптимизации селеноцентрического участка траектории требуется найти значения неизвестных параметров

${\mathbf{z}} = {{\left[ {{\mathbf{p}}_{{\mathbf{x}}}^{{\rm T}}\left( 0 \right),{{p}_{{LK}}}\left( 0 \right),{{p}_{t}}\left( 0 \right),T,{{p}_{m}}\left( 0 \right),{{K}_{f}}} \right]}^{{\rm T}}},$
при которых удовлетворяются условия

${\mathbf{f}}\left( {\mathbf{z}} \right) = \left[ \begin{gathered} {\mathbf{x}}\left( {{{K}_{f}}} \right) - {{{\mathbf{x}}}_{f}}\left( {{{L}_{f}}} \right) \hfill \\ {{p}_{{LK}}}\left( 0 \right) + H\left( 0 \right) \hfill \\ {{p}_{t}}\left( {{{K}_{f}}} \right) \hfill \\ {{p}_{m}}\left( {{{K}_{f}}} \right) \hfill \\ {{L}_{K}}\left( {{{K}_{f}}} \right) + {{K}_{f}} - {{L}_{f}} \hfill \\ {{p}_{T}}\left( {{{K}_{f}}} \right) \hfill \\ \end{gathered} \right] = 0.$

Таким образом, задача формально сводится к решению системы уравнений f(z) = 0, причем для вычисления вектора невязок f при текущем значении z необходимо проинтегрировать на отрезке $K \in \left[ {0;{{K}_{f}}} \right]$ систему дифференциальных уравнений (10) с начальными условиями вида (11). В работах [16, 17, 21] для решения подобных задач предлагается использовать методы продолжения, позволяющий свести краевую задачу к задаче Коши для системы вложенных дифференциальных уравнений. Однако, для вычисления правых частей дифференциальных уравнений метода продолжения требуется вычислить частные производные от f по z и параметру продолжения τ.

Частные производные ∂f/∂z и ∂f/∂τ могут быть вычислены с использованием совместного интегрирования дифференциальных уравнений для фазовых и сопряженных переменных с уравнениями для их производных по z и τ:

(13)
$\begin{gathered} \frac{d}{{dK}}\frac{{\partial {{{\mathbf{x}}}_{1}}}}{{\partial {\mathbf{z}}}} = \frac{{{{\partial }^{2}}H}}{{\partial {\mathbf{z}}\partial {{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}},\frac{d}{{dK}}\frac{{\partial {{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}}{{\partial {\mathbf{z}}}} = - \frac{{{{\partial }^{2}}H}}{{\partial {\mathbf{z}}\partial {{{\mathbf{x}}}_{1}}}}, \hfill \\ \frac{d}{{dK}}\frac{{\partial {{{\mathbf{x}}}_{1}}}}{{\partial \tau }} = \frac{{{{\partial }^{2}}H}}{{\partial \tau \partial {{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}},\frac{d}{{dK}}\frac{{\partial {{{\mathbf{p}}}_{{{\mathbf{x}}1}}}}}{{\partial \tau }} = - \frac{{{{\partial }^{2}}H}}{{\partial \tau \partial {{{\mathbf{x}}}_{1}}}}. \hfill \\ \end{gathered} $

Из (13) следует, что необходимо вычислить смешанные производные второго порядка от H по фазовому вектору и z, а также по фазовому вектору и τ. В соответствии с (4), гамильтониан возмущенной задачи может быть представлен в виде H = HTmin + Hp + Ht. Слагаемое гамильтониана Hp зависит от возмущающих ускорений, которые зависят от x1 и вычисляются с использованием сложных алгоритмов, не позволяющих, в общем случае, проводить их вычисление на основе аналитических формул.

Для вычисления смешанных производных второго порядка с высокой точностью был разработан специальный метод, основанный на использовании комплексно-дуальных чисел – метод автоматического дифференцирования с использованием комплексных дуальных чисел (CDNAD) [21–24].

В качестве начального приближения в задаче минимизации тяги используется решение задачи оптимизации траектории КА с идеально-регулируемым двигателем (ОМ-задача) [18]. Управление в ОМ-задаче является гладкой функцией независимой переменной, ограничение на величину реактивного ускорения отсутствует, поэтому получить численное решение этой задачи достаточно просто по сравнению с задачей оптимизации траектории КА с двигателем ограниченной тяги. В [16, 17] представлены методы решения ОМ-задачи, основанные на применении принципа максимума и метода продолжения по параметру. Переход к задаче на минимум тяги, происходит на основе метода продолжения по параметру, реализующим гомотопию между известным решением ОМ-задачи и искомым решением задачи минимизации тяги [23]. Таким образом могут быть получены решения задачи минимизации тяги отдельно на геоцентрическом и селеноцентрическом участках перелeта, после чего необходимо удовлетворить равенство значений минимальной тяги Tmingc на геоцентрическом и Tminsc на селеноцентрическом участках заданному значению тяги T* с помощью подбора угловых дальностей этих участков:

(14)
${{T}_{{\min gc}}}\left( {\Delta {{L}_{{gc}}}} \right) = T*,\,\,\,\,{{T}_{{\min sc}}}\left( {\Delta {{L}_{{sc}}}} \right) = T*,$
где ∆Lgc и ∆Lsc – угловая дальность перелeта на геоцентрическом и селеноцентрическом участках перелeта соответственно.

В результате решения задачи вычисляется оптимальное управление и оптимальная траектория, включая минимальную угловую дальность геоцентрического и селеноцентрического участков перелета с заданной тягой, моменты отлета с околоземной орбиты и прибытия на окололунную орбиту, удовлетворяющие необходимым условиям оптимальности.

4. ЧИСЛЕННЫЕ ПРИМЕРЫ

Рассматривается модель возмущений, включающая притяжение Земли, Луны и Солнца как точечных масс и вторую зональную гармонику геопотенциала. Положение и скорость Земли, Луны и Солнца вычисляются по эфемеридной модели.

Рассмотрим результаты вычисления траекторий с минимальной тягой с эллиптической околоземной орбиты на круговую окололунную орбиту, эллиптическую окололунную орбиту и на устойчивые инвариантные многообразия гало-орбит у точек либрации EML1 и EML2.

В первых двух примерах будем рассматривать начальную орбиту с высотой перигея 4500 км, высотой апогея 50 000 км, наклонением 28°, аргументом перигея 101.409° и долготой восходящего узла 10°. Дата пролeта точки EML1 – 18.IX.2021, 12.00.00 UTC. Начальная масса КА 1000 кг, удельный импульс Isp = 3500 с.

Первая конечная орбита – круговая окололунная орбита с высотой 5000 км, наклонением 35° и долготой восходящего узла 10°. Параметры окололунной орбиты приведены в селеноцентрической геоэкваториальной системе координат. Требуемое минимальное значение тяги T* выбрано равным 0.2 Н.

В табл. 1 представлены орбитальные параметры геоцентрической и селеноцентрической оскулирующей орбиты EML1 для заданного времени.

Таблица 1.

Параметры орбиты геоцентрической и селеноцентрической оскулирующей орбиты EML1 на 12.00.00 UTC 18.IX.2021

Участок траектории Геоцентрический Селеноцентрический
Большая полуось, км 235601.23 33575.53
Эксцентриситет 0.375785 0.714726
Наклонение, град 26.016
Долгота восходящего узла, град 10.383
Аргумент перицентра, град 138.970 316.415
Истинная аномалия, град 176.638 179.193

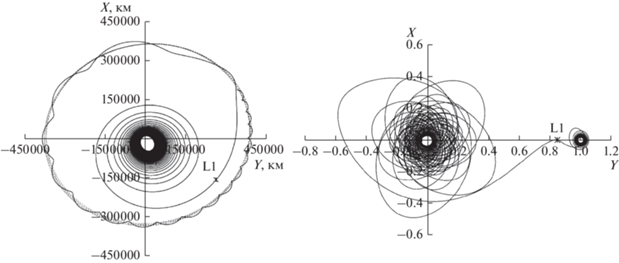
На рис. 1 показаны проекции оптимальной траектории на плоскость XY в инерциальной системе координат J2000 и на мгновенную плоскость орбиты Луны в синодической системе координат.

В результате оптимизации траектории были получены оптимальная длительность перелета Δt = 164.587 суток, конечная масса КА mf = 917.113 кг (масса топлива mp = 82.887 кг), начальное (167.437°) и конечное (4.268°) значения истинной аномалии и угловые дальности геоцентрического (74.09908 витков) и селеноцентрического (20.02767 витков) участков траектории с минимальной тягой. Зависимости углов тангажа и рыскания от времени для рассматриваемой траектории представлены на рис. 2.

Рис. 2.

Зависимости от времени углов тангажа (слева) и рысканья (справа) для перелета на круговую окололунную орбиту.

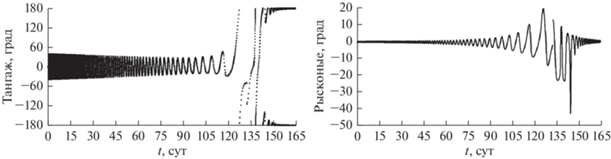
На основной части геоцентрического участка траектории угол тангажа колеблется около нуля, в окрестности EML1 он изменяется от –180° до +180° в течение нескольких витков, а затем, на основной части селеноцентрического участка, колеблется около значения 180° до конца полета. Угол рысканья близок к нулю в начале и в конце перелета, большие углы по рысканья достигаются только на последних витках геоцентрического участка и первых витках селеноцентрического участка.

Вторая рассматриваемая конечная орбита-эллиптическая окололунная орбита с высотой периселения 6000 км и высотой апоселения 10 000 км. Приведем результаты расчета оптимальных траекторий на эту орбиту со значениями требуемой минимальной тяги: 0.3, 0.5 и 0.7 Н. Проекции траекторий с минимальной тягой на плоскость XY инерциальной системы координат J2000 (слева) и синодической системы координат (справа) представлены на рис. 3. В табл. 2 представлены основные параметры оптимальных траекторий с различной минимальной тягой. Требуемые затраты топлива уменьшаются со снижением значения тяги за счет уменьшения гравитационных потерь.

Рис. 3.

Оптимальные траектории с минимальной тягой 0.3 Н (верхний ряд), 0.5 Н (средний ряд) и 0.7 Н (нижний ряд).

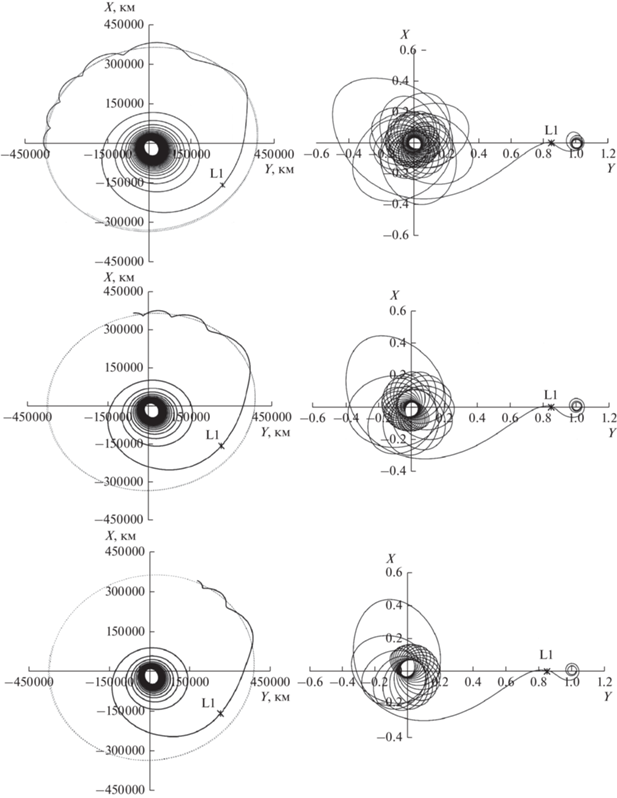
Таблица 2.

Основные параметры оптимальных траекторий с различным значением требуемой минимальной тяги

T*, Н 0.3 0.5 0.7
Δt, сут 105.882 64.429 46.903
mf, кг 920.159 918.915 917.355
ΔLgc 49.30 29.73 21.13
ΔLsc 6.714 3.858 2.774

В качестве третьего примера рассмотрим траектории с минимальной тягой к устойчивым инвариантным многообразиям гало-орбит, ранее рассмотренным в работе [12]:

1) L1HO – северная гало-орбита у точки либрации EML1, обладающая свойством орбитальной устойчивости (максимальный мультипликатор Флоке равен 1), с координатами апоселения в синодической барицентрической безразмерной системе координат (0.8730990324388, 0.0, 0.1906425182060, 0.0, 0.2354475477314, 0.0), периодом 9.677 дня и константой Якоби 3.108604 км2/с2.

2) L1NRHO – северная гало-орбита у точки либрации EML1, относящаяся к классу почти прямолинейных орбит (NRНO) с максимальным по модулю мультипликатором Флоке 5.32, не обладающая свойством орбитальной устойчивости. Ее апоселений имеет координаты (0.9306744714248, 0.0, 0.2304688230602, 0.0, 0.1037746566261, 0.0), период равен 8.047 суткам, а константа Якоби равна 3.1038796 км2/с2.

3) L2HO – северная гало-орбита у точки EML2 достаточно больших размеров, обладающая свойством орбитальной устойчивости, с координатами апоселения (1.0806959653822, 0.0, 0.2023606276413, 0.0, –0.1986289716256, 0.0), периодом 10.265 суток и константой Якоби 3.1266148 км2/с2.

В работе [12] был проведен анализ прямых перелетов к гало-орбитам и точкам либрации и перелетов к ним с выходом на инвариантные многообразия. Для расчета траекторий использовалось квазиоптимальное управление с обратной связью. В качестве начальной околоземной орбиты рассматривалась круговая орбита высотой 42 164 км с наклонением 51.8°. Удельный импульс двигательной установки был принят равным 1770 с, а тяга – 290 мН. Рассматривались перелеты с датой окончания 12.04.2026 00.00 UTС. Для перечисленных выше гало-орбит наиболее эффективными оказались траектории с выходом на инвариантное многообразие.

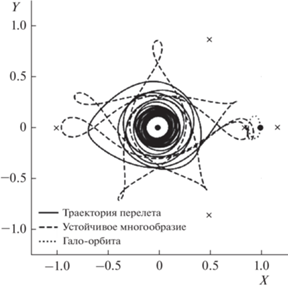
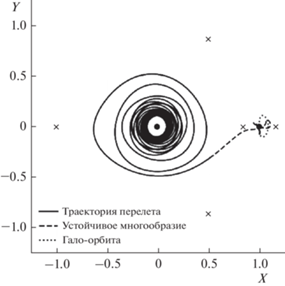
Сравним траектории с квазиоптимальным управлением из работы [12] с траекториями с минимальной тягой, полученными по представленному в этой статье методу. Проекции траекторий перелeта с минимальной тягой к гало-орбитам на мгновенную плоскость орбиты Луны в синодической системе координат представлены на рис. 4, 5 и 6.

Рис. 4.

Траектории перелета на L1HO с минимальной тягой.

Рис. 5.

Траектория перелета на L1NRHO с минимальной тягой.

Рис. 6.

Траектория перелета на L2HO с минимальной тягой.

В табл. 3 представлены основные параметры траекторий к инвариантным многообразиям гало-орбит с использованием КОУСОС [12] и оптимального управления, минимизирующего величину тяги, при одинаковой угловой дальности перелета. В табл. 3 приводятся: длительность движения по многообразию (Δtс), суммарное (ΔtΣ) и моторное (Δtm) время, количество витков (Nrev), тяга (T) и относительная конечная масса КА (µk). Как видно во всех рассмотренных случаях минимальная тяга оказалась меньше тяги, используемой в [12] для расчета траекторий с КОУСОС. Оптимальная длительность перелета на траекториях с минимальной тягой превышает длительность перелета на траекториях с КОУСОС. Конечная масса КА на траекториях с минимальной тягой может быть больше или меньше, чем на траекториях с КОУСОС, так как при использовании КОУСОС долгота восходящего узла конечной орбиты не фиксировалась, а при решении задачи минимизации тяги была задана.

Таблица 3.

Сравнение основных параметров перелета к инвариантным многообразиям гало-орбит с помощью КОУСОС и оптимального управления Tmin-задачи

  Δtс, сут ΔtΣ, сут Δtm, сут Nrev T, Н µk
КОУСОС [12]
L1HO 96.3 183.396 87.096 36.25603 0.290 0.86184
L1NRHO 103.8 193.285 89.485 36.325873 0.290 0.87839
L2HO 21.3 109.051 87.751 35.79731 0.290 0.88832
Tmin-задача
L1HO 96.3 188.391 92.091 36.25603 0.2678 0.89066
L1NRHO 103.8 198.614 94.814 36.325873 0.2688 0.88744
L2HO 21.3 115.177 93.877 35.79731 0.2711 0.88753

ЗАКЛЮЧЕНИЕ

Разработан численный метод решения задачи минимизации тяги для многовитковых траекторий перелета к Луне на основе использования принципа максимума, метода продолжения, автоматического дифференцирования с использованием комплексных дуальных чисел, использования вспомогательной долготы в качестве независимой переменной и постановки задачи с фиксированной угловой дальностью и свободным временем перелета.

Представлены численные результаты оптимизации перелетов с эллиптической околоземной орбиты на круговую и эллиптическую окололунную орбиты, а также с круговой околоземной орбиты на гало-орбиты вокруг точек либрации EML1 и EML2. Проведено сравнение траекторий с квазиоптимальным и оптимальным управлением. В рассмотренных примерах, при одинаковой угловой дальности, оптимальное управление обеспечивает уменьшение величины тяги на 6–8% по сравнению с квазиоптимальным управлением.

Разработанный метод вычисления траекторий перелета к Луне с минимальной тягой может использоваться в качестве средства для диагностики существования решения в задаче оптимизации траекторий с ограниченной тягой: при заданной угловой дальности траектория КА с двигателем заданной тяги существуют только в том случае, если величина заданной тяги не меньше минимальной.

Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 22-19-00329).

Список литературы

  1. Foing B.H., Racca G.D., Marin, A. et al. SMART-1 after lunar capture: First results and perspectives // J. Earth Syst. Sci. 2005. V. 114. № 6. P. 687–697.

  2. McGuire M.L., Burke L.M., McCarty S.L. et al. Low thrust cis-lunar transfers using a 40 kW-class solar electric propulsion spacecraft. AAS/AIAA Astrodynamics Specialist Conference, Washington, 2017, AAS 17-583.

  3. Легостаев В.П., Лопота В.А., Синявский В.В. Перспективы и эффективность применения космических ядерно-энергетических установок и ядерных электроракетных двигательных установок // Космическая техника и технологии. 2013. №. 1 (1). С. 6–17.

  4. Kluever C.A., Pierson B.L. Optimal Low-Thrust Earth-Moon Transfers with a Switching Function // J. Astronautical Sciences. 1994. V. 42. № 3. P. 269–284.

  5. Kluever C.A., Pierson B.L. Optimal Low-Thrust Three-Dimensional Earth-Moon Trajectories // J. Guidance, Control and Dynamics. 1995. V. 18. № 4. P. 830–837.

  6. Ozimek M.T., Howell K.C. Low-Thrust Transfers in the Earth–Moon System, Including Applications to Libration Point Orbits // J. Guidance, Control, and Dynamics. 2010. V. 33. № 2. P. 533–549.

  7. Mingotti G., Topputo F., Bernelli-Zazzera F. Low-energy, low-thrust transfers to the Moon // Celestial Mech. Dyn. Astron. 2009. V. 105. № 1. P. 61–74.

  8. Shimmin R. Trajectory design for a very-low-thrust lunar mission, PhD Thesis, University of Adelaide. 2012. P. 1–204.

  9. Singh S.K., Anderson B.D., Taheri E., Junkins J.L. Exploiting manifolds of L1 halo orbits for end-to-end Earth–Moon low-thrust trajectory design // Acta Astronautica. 2021. V. 183. P. 255–272.

  10. Ельников Р.В. Использование функций Ляпунова для вычисления локально-оптимального управления вектором тяги при межорбитальном перелете с малой тягой // Космич. исслед. 2021. Т. 59. № 3. С. 255–264.

  11. Shannon J., Ozimek M., Atchison J., Hartzell C. Rapid design and exploration of high-fidelity low-thrust transfers to the moon. IEEE Aerospace Conference. 2020. P. 1–12.

  12. Petukhov V.G., Konstantinov M.S. Spacecraft insertion into Earth–Moon L1 and lunar orbit. 60th International Astronautical Congress. 2009. IAC-09. D2.3.11. P. 7423–7431.

  13. Petukhov V.G., Popov G.A., Svotina V.V. Suboptimal low-thrust trajectories for lunar missions. Global Lunar Conference. Beijing, China, 2010, GLUC-2010-2.2.P3.

  14. Иванюхин А.В., Петухов В.Г. Низкоэнергетические квазиоптимальные траектории с малой тягой к точкам либрации и гало-орбитам // Космич. исслед. 2020. Т. 58. № 2. С. 165–176.

  15. Петухов В.Г. Применение угловой независимой переменной и ее регуляризирующего преобразования в задачах оптимизации траекторий с малой тягой // Космич. исслед. 2019. Т. 57. № 5. С. 373–385.

  16. Ivanyukhin A., Petukhov V. Optimization of multi-revolution limited power trajectories using angular independent variable // J. Optimization Theory and Applications. 2021. V. 191. № 2. P. 575–599.

  17. Petukhov V., Ivanyukhin A., Popov G. et al. Optimization of finite-thrust trajectories with fixed angular distance // Acta Astronautica, available online. 2021. P. 14. https://doi.org/10.1016/j.actaastro.2021.03.012

  18. Martins J.R.R.A., Sturdza P., Alonso J.J. The connection between the complex-step derivative approximation and algorithmic differentiation. 39th Aerospace Sciences Meeting and Exhibit. 2001. P. 921.

  19. Dargent T. Automatic minimum principle formulation for low thrust optimal control in orbit transfers using complex numbers. International Symposium on Space Flights Dynamics. Toulouse, France. 2009.

  20. Yu W., Blair M. DNAD, a simple tool for automatic differentiation of Fortran codes using dual numbers // Computer Physics Communications. 2013. V. 184. № 5. P. 1446–1452.

  21. Petukhov V.G. A new approach to low-thrust perturbed trajectory optimization based on the use of complex dual numbers. IAC 2020 Congress Proceedings, 71st International Astronautical Congress (IAC) — IAC CyberSpace Edition. 2020.

  22. Sung W.Y., Petukhov V.G. Perturbed low-thrust trajectory optimization using the algebra of complex dual numbers. 8th International Conference on Astrodynamics Tools and Techniques, ESA, online. 2021.

  23. Petukhov V.G., Sung W.Y. Optimization of perturbed spacecraft trajectories using complex dual numbers. Part 1: Theory and method // Cosmic Research. 2021. V. 59. № 5. P. 401–413.

  24. Petukhov V.G., Sung W.Y. Optimization of perturbed spacecraft trajectories using complex dual numbers. Part 2: Numerical Results // Cosmic Research. 2021. V. 59. № 6. P. 517–528.

  25. Petukhov V.G. Minimum-thrust problem and its application to trajectory optimization with thrust switchings. IAC-13-C1.6.2, Beijing. 2013.

  26. Иванюхин А.В., Петухов В.Г. Задача минимизации тяги и ее приложения // Космич. исслед. 2015. Т. 53. № 4. С. 320–331.

  27. Иванюхин А.В. Область существования решений в задаче оптимального управления космическим аппаратом с ограниченной тягой // Современная математика. Фундаментальные направления. 2016. Т. 62. С. 100–123.

  28. Petukhov V.G., Wook W.S. Joint optimization of the trajectory and the main parameters of an electric propulsion system // Procedia engineering. 2017. V. 185. P. 312–318.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал