1. На главную
  2. Электронные версии
  3. Космические исследования
  4. T. 61, № 2, 2023

Космические исследования, 2023, T. 61, № 2, стр. 163-176

Оптимальное управление вектором тяги воздушного электрореактивного двигателя для наискорейшего изменения высоты апогея орбиты с ультранизким перигеем

А. С. Филатьев 1, 2, О. В. Янова 2, 3, *

1 Московский государственный университет имени М.В. Ломоносова
Москва, Россия

2 Московский авиационный институт
Москва, Россия

3 Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского
Жуковский, Московская обл., Россия

* E-mail: yanova2007@yandex.ru

Поступила в редакцию 20.07.2022
После доработки 04.10.2022
Принята к публикации 08.10.2022

Полный текст (PDF)

Аннотация

Рассмотрена задача оптимального по быстродействию изменения высоты апогея орбит с ультранизким перигеем (высотой 120–250 км). Для компенсации аэродинамического сопротивления космического аппарата используется воздушный электрореактивный двигатель (ВЭРД), топливом для которого служат газы забортной атмосферы. Учтено падение эффективности ВЭРД с увеличением угла атаки и возможность работы ВЭРД только при достаточной концентрации газа в камере ионизации. Задача решена на основе принципа максимума Понтрягина в предположении малости аэродинамического сопротивления и тяги по сравнению с гравитационными силами. Представлены результаты исследований оптимальных программ управления вектором тяги ВЭРД в зависимости от параметров орбиты, компоновки КА, двигателя и мощности источника энергии.

ВВЕДЕНИЕ

Значительное повышение эффективности выполнения космическими аппаратами (КА) целевых задач может быть обеспечено за счет использования ультранизких околоземных орбит высотой 120–250 км (УНОО) [1–3].

Для компенсации аэродинамического сопротивления на таких орбитах могут использоваться воздушные электрореактивные двигатели (ВЭРД), в которых топливом служат газы окружающей атмосферы [4–13]. В общем случае ВЭРД включают: воздухозаборник (ВЗ), обеспечивающий захват атмосферного газа; термализатор (накопитель), в котором частицы газа тормозятся до тепловых скоростей; ионизационную камеру (ИК), в которой газ ионизируется; зону разгона, в которой ионизированный газ ускоряется в электромагнитном поле; и нейтрализатор эжектируемой плазменной струи. Для функционирования последних трех систем необходим источник энергии (ИЭ), в качестве которого предполагается использовать солнечные батареи (СБ).

Отказ от запасенного топлива позволит повысить срок активного существования и эффективность выполнения задач наблюдения земной поверхности и связи. В то же время использование ВЭРД требует решения ряда проблем, связанных с особенностями орбитального полета на ультранизких высотах: значительно возросшим влиянием аэродинамических сил и аномалий гравитационного поля Земли.

Задачи оптимального управления низкоорбитальными КА с ВЭРД рассмотрены в ряде работ. В работах [6, 7] решалась задача оптимального управления тягой ВЭРД за счет изменения скорости истечения реактивной струи для поддержания КА на круговой УНОО, включая оптимизацию высоты орбиты в исследовании [7]. Оптимизация проводилась на основе принципа максимума Понтрягина [14] в предположении постоянных мощности бортового источника энергии и коэффициента аэродинамического сопротивления с учетом несферичности Земли. В работе [9] получены оценки требуемой тяги и предложен алгоритм адаптивного управления тягой электроракетного двигателя (ЭРД) для компенсации возмущений, обусловленных аэродинамическим сопротивлением КА и солнечной радиацией на круговых околоземных орбитах высотой 150–450 км. Работа [10] посвящена анализу реализуемости полета на УНОО на основе статистического моделирования орбитального движения КА с адаптивным управлением тягой ЭРД на околоземных слабоэллиптических орбитах (разность высот апогея и перигея не превышает 9 км) высотой 160 и 225 км. В публикации [11] представлен обзор предложений по управлению аэродинамическим качеством аппарата для поддержания заданной орбиты, стабилизации КА, маневрирования для предотвращения столкновений с различными объектами, фазирования и схода с орбиты.

Оптимизация управления вектором тяги КА c ВЭРД рассматривалась авторами в работах [15–18]. В исследованиях [15–17] задачи максимизации изменения высоты апогея и изменения наклонения орбит сведены к поиску локально оптимального управления, обеспечивающего максимальную скорость изменения максимизируемых параметров в каждый момент времени с учетом малости влияния на функционал возмущающего ускорения по сравнению с гравитационным. Эффективность оптимальности программы управления с подобным критерием при решении задачи в детерминированной постановке может рассматриваться как мера потенциальной возможности компенсации случайных возмущений. Переход к локальной оптимизации управления позволил получить аналитические соотношения для синтеза управления КА с ВЭРД и его эффективности в предположении постоянных скорости истечения и аэродинамического сопротивления без учета зависимости тяги ВЭРД от угла между продольной осью КА и вектором скорости (угла атаки) и ограничения на допустимый уровень концентрации газа в ИК.

Эффективность тяги ВЭРД существенно зависит от угла атаки вследствие уменьшения эффективной площади входа в ВЗ в плоскости, перпендикулярной вектору скорости, и относительного числа молекул, пролетающих через ВЗ без столкновения с его стенками при наличии угла атаки [8, 13, 19, 20]. В работе [18] при “локальной” оптимизации управления учитывалось снижение тяги при ненулевых углах атаки из-за изменения эффективной площади входа в ВЗ.

В настоящей работе рассматривается задача оптимального управления вектором тяги КА с ВЭРД для максимизации изменения высоты апогея орбиты с ультранизкой начальной высотой перигея с учетом ограничения на допустимый уровень концентрации газа в ИК и зависимости тяги ВЭРД и аэродинамического сопротивления от угла атаки КА. Решение задачи получено на основе принципа максимума Понтрягина [14] в предположении малости изменения параметров орбиты в правых частях уравнений движения за один виток. Приведены результаты исследований оптимальных программ управления углом атаки и тягой в зависимости от параметров задачи: начальной высоты перигея и апогея, скорости истечения, параметров компоновки КА.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается движение центра масс КА с ВЭРД в плоскости эллиптической орбиты с начальными высотами перигея hπi и апогея hαi. Задача состоит в определении оптимального управления вектором тяги ВЭРД для максимального изменения высоты апогея hα без изменения высоты перигея hπ с учетом зависимости тяги и аэродинамического сопротивления от угла атаки и ограничения на допустимую концентрацию газа в ИК. Требование равенства конечной высоты перигея ее начальному значению обусловлено ограничениями на высоту полета КА с ВЭРД [16]. Ограничение сверху на высоту полета КА с ВЭРД следует из необходимости создания давления газа в камере ионизации не менее 5 · 10–5 торр для стабильной работы ВЭРД [4]. Ограничение снизу определяется располагаемой мощностью ИЭ (СБ) для компенсации аэродинамического сопротивления КА: ниже некоторой высоты не удается обеспечить требуемую мощность электропитания для создания тяги, так как увеличение площади СБ в свою очередь еще более увеличивает сопротивление.

Движение центра масс КА описывается в геоцентрической инерциальной системе координат с началом координат в центре Земли. Ось Ox направлена в перигей орбиты (в случае круговой орбиты – по начальному радиус-вектору), ось Oy параллельна вектору скорости в перигее орбиты.

Приняты следующие допущения:

1. Нормальная аэродинамическая сила пренебрежимо мала.

2. Скорость с истечения реактивной струи ВЭРД постоянна: c = const.

3. Вектор тяги ВЭРД направлен вдоль продольной оси КА.

4. Масса КА постоянна: m = const.

5. Форма Земли сферическая.

Замечание. Допущение о сферической форме Земли основано на инвариантности аэродинамического сопротивления КА и тяги ВЭРД по отношению к плотности атмосферы (см. далее соотношения для расчета тяги и сопротивления (5), (6)). Это принципиально важное отличие ВЭРД от электроракетного двигателя, поскольку плотность атмосферы даже при движении по круговой орбите может меняться во много раз.

С учетом соотношений [21]

(1)
${{r}_{\pi }} = \frac{p}{{1 + e}},\,\,\,\,{{r}_{\alpha }} = \frac{p}{{1 - e}}$
и уравнений в оскулирующих переменных [22] запишем уравнения для изменения по времени радиуса перигея hπ, радиуса апогея hα, электрической энергии E для создания тяги и истинной аномалии ϑ:
(2)
$\left. {\begin{array}{*{20}{c}} {\frac{{{\text{d}}{{r}_{\pi }}}}{{{\text{d}}t}} = \frac{1}{V}\left[ {{{a}_{t}}\frac{{2p}}{{{{{(1 + e)}}^{2}}}}(1 - {\text{cos}}{\kern 1pt} \vartheta ) + {{a}_{s}}r{\kern 1pt} {\text{sin}}{\kern 1pt} \vartheta } \right],} \\ {\frac{{{\text{d}}{{r}_{\alpha }}}}{{{\text{d}}t}} = \frac{1}{V}\left[ {{{a}_{t}}\frac{{2p}}{{{{{(1 - e)}}^{2}}}}(1 + {\text{cos}}{\kern 1pt} \vartheta ) - {{a}_{s}}r{\kern 1pt} {\text{sin}}{\kern 1pt} \vartheta } \right],} \\ {\frac{{{\text{d}}E}}{{{\text{d}}t}} = {{W}_{P}},} \\ {\frac{{{\text{d}}\vartheta }}{{{\text{d}}t}} = \frac{{\sqrt p }}{{{{r}^{2}}}},} \end{array} } \right\}$
где r – расстояние от центра Земли до центра масс КА, $r = {p \mathord{\left/ {\vphantom {p {\left( {1 + e{\kern 1pt} {\text{cos}}{\kern 1pt} \vartheta } \right)}}} \right. \kern-0em} {\left( {1 + e{\kern 1pt} {\text{cos}}{\kern 1pt} \vartheta } \right)}} = \sqrt {({\mathbf{r}},{\mathbf{r}})} ;$ r – радиус-вектор КА; $V = \sqrt {{{(1 + 2e{\kern 1pt} {\text{cos}}{\kern 1pt} \vartheta + {{e}^{2}})} \mathord{\left/ {\vphantom {{(1 + 2e{\kern 1pt} {\text{cos}}{\kern 1pt} \vartheta + {{e}^{2}})} p}} \right. \kern-0em} p}} = \sqrt {({\mathbf{V}},{\mathbf{V}})} ,$ V – вектор скорости КА, V = (Vr, Vn); Vr – составляющая вектора скорости, направленная по радиус-вектору r, ${{V}_{r}} = {{(e{\kern 1pt} {\text{sin}}{\kern 1pt} \vartheta )} \mathord{\left/ {\vphantom {{(e{\kern 1pt} {\text{sin}}{\kern 1pt} \vartheta )} {\sqrt p }}} \right. \kern-0em} {\sqrt p }};$ Vn – составляющая вектора скорости, направленная по нормали к r в сторону движения, ${{V}_{n}} = {{(1 + e{\kern 1pt} {\text{cos}}\vartheta )} \mathord{\left/ {\vphantom {{(1 + e{\kern 1pt} {\text{cos}}\vartheta )} {\sqrt p }}} \right. \kern-0em} {\sqrt p }};$ p – фокальный параметр; e – эксцентриситет; a – вектор возмущающего ускорения, ${\mathbf{a}} = {{({{a}_{t}},\;{{a}_{s}})}^{T}},$ с компонентами: at – касательная (направлена по вектору скорости), as – нормальная (направлена к центру кривизны траектории в плоскости орбиты); WP – мощность, потребляемая ВЭРД; t – время.

Переменные в выражении (2) и далее используются в безразмерном виде, причем старые обозначения переменных сохраняются:

(3)
$\left. \begin{gathered} r = {{\left( {\frac{r}{{{{R}_{{\text{E}}}}}}} \right)}_{d}},\,\,\,\,V = {{\left( {\frac{V}{{{{V}_{R}}}}} \right)}_{d}},\;\,\,m = {{\left( {\frac{m}{{{{m}_{i}}}}} \right)}_{d}}, \hfill \\ t = {{\left( {\frac{t}{{{{t}_{R}}}}} \right)}_{d}},\,\,\,\,g = {{\left( {\frac{g}{{{{g}_{o}}}}} \right)}_{d}},\,\,\,\,{\mathbf{a}} = {{\left( {\frac{{\mathbf{a}}}{{{{g}_{o}}}}} \right)}_{d}}, \hfill \\ P = {{\left( {\frac{P}{{m{{g}_{o}}}}} \right)}_{d}},\,\,\,\,X = {{\left( {\frac{X}{{m{{g}_{o}}}}} \right)}_{d}},\,\,\,\,{{W}_{P}} = {{\left( {\frac{{{{W}_{P}}}}{{m{{g}_{o}}{{V}_{R}}}}} \right)}_{d}}, \hfill \\ \end{gathered} \right\}$
где нижним индексом d обозначены размерные величины; RE – средний радиус Земли; mi – начальная масса КА (в силу допущения 4. $m = {{\left( {{m \mathord{\left/ {\vphantom {m {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} \right)}_{d}} = 1$); go – ускорение свободного падения на поверхности Земли, ${{V}_{R}} = \sqrt {{{g}_{o}}{{R}_{{\text{E}}}}} ,$ ${{t}_{R}} = \sqrt {{{{{R}_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{E}}}}} {{{g}_{o}}}}} \right. \kern-0em} {{{g}_{o}}}}} ;$ P – тяга ВЭРД; X – аэродинамическое сопротивление КА.

Компоненты возмущающего ускорения создаются тягой ВЭРД P и аэродинамическим сопротивлением X:

(4)
$\left. \begin{gathered} {{a}_{t}} = \frac{{P(\alpha ){\kern 1pt} {\text{cos}}{\kern 1pt} \alpha - X(\alpha )}}{m}, \hfill \\ {{a}_{s}} = - \frac{{P(\alpha ){\kern 1pt} {\text{sin}}{\kern 1pt} \alpha }}{m}, \hfill \\ \end{gathered} \right\}$
где α – угол между вектором скорости и вектором тяги – угол атаки.

Вектор тяги

(5)
${\mathbf{P}} = P{{{\mathbf{e}}}_{P}} = {{\left( {\zeta \frac{{{{\mu }_{{out}}}(\alpha )c}}{{m{{g}_{o}}}}} \right)}_{d}}{{{\mathbf{e}}}_{P}},$
где μout(α) – удельный расход массы топлива, ${{\mu }_{{out}}}(\alpha ) = {{\eta }_{C}}\,{{\mu }_{{in}}}(\alpha );$ μin(α) – скорость поступления массы газа в ВЗ, ${{\left( {{{\mu }_{{in}}}(\alpha )} \right)}_{d}} = \rho (h)V{{A}_{{in}}}{{k}_{p}}(\alpha ){{V}_{R}};$ ηC – эффективность забора газа, $0 \leqslant {{\eta }_{C}} \leqslant 1;$ h – высота полета КА; ρ(h) – плотность атмосферы; kp(α) – коэффициент эффективности ВЗ в зависимости от угла атаки [19, 20]; Ain – площадь входного сечения ВЗ, ζ – параметр включения двигателя, принимающий значение нуль при неработающем двигателе и единица при работающем; eP – единичный вектор тяги.

Потребляемая ВЭРД мощность WP определяется по формуле ${{W}_{P}} = {{{{\mu }_{{out}}}{{c}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{out}}}{{c}^{2}}} {2{{\eta }_{T}}}}} \right. \kern-0em} {2{{\eta }_{T}}}}.$

Вектор силы сопротивления

(6)
${\mathbf{X}} = - X{{{\mathbf{e}}}_{V}} = - {{\left( {\frac{{0.5\rho (h){{A}_{{SC}}}{{{(V{{V}_{R}})}}^{2}}{{c}_{{xa}}}(\alpha )}}{{m{{g}_{o}}}}} \right)}_{d}}{{{\mathbf{e}}}_{V}},$
где cxa(α) – коэффициент аэродинамического сопротивления КА; ASC – площадь поперечного сечения КА; eV = V/V.

Для создания тяги необходимо, чтобы концентрация газа в ИК nIC(α) была не меньше минимально допустимой nmin, при которой возможна его ионизация:

(7)
${{n}_{{IC}}}(\alpha ) = n(h)k{}_{c}{{k}_{p}}(\alpha ) \geqslant {{n}_{{{\text{min}}}}},$
где n(h) – концентрация газа в атмосфере; kc – коэффициент компрессии газа в ИК, определяющий, во сколько раз увеличивается концентрация газа в ИК по сравнению с концентрацией во входном потоке.

Отсюда следует, что $\xi \equiv 0$ при nIC < nmin.

На угол атаки КА наложено ограничение

(8)
$\left| \alpha \right| \leqslant {{\alpha }_{{{\text{max}}}}},$
где αmax – максимально допустимый угол атаки.

Ограничение (8) угла атаки КА с ВЭРД в первую очередь обусловлено снижением эффективности поступления атмосферных газов в ВЗ, что показано далее.

В качестве компонент вектора управления u приняты угол атаки α и параметр включения двигателя ζ:

(9)
$\begin{gathered} {\mathbf{u}} \equiv {{\left\{ {\alpha ,\zeta } \right\}}^{T}},\,\,\,\,{\mathbf{u}} \subset {\mathbf{U}}, \\ {\mathbf{U}} = \left\{ {\left| \alpha \right| \leqslant {{\alpha }_{{{\text{max}}}}},{{n}_{{IC}}}(\alpha ) \geqslant {{n}_{{{\text{min}}}}},\zeta = \left\{ {0,1} \right\}} \right\}. \\ \end{gathered} $

Реализация заданных углов атаки может обеспечиваться известными средствами стабилизации и управления движением КА вокруг центра масс, достоинства и недостатки использования которых для управления вектором тяги рассматривались в исследовании [23]. Отметим, что возрастание аэродинамических моментов на УНОО относительно возмущающих моментов других типов увеличивает влияние аэродинамической компоновки КА и возможности использования специальных аэродинамических поверхностей (например, [24]).

В начальный момент времени ti = 0,

(10)
$\begin{gathered} \vartheta ({{t}_{i}}) = {{\vartheta }_{i}} = 0,\,\,\,\,{{h}_{\pi }}({{t}_{i}}) = {{h}_{{\pi i}}}, \\ {{h}_{\alpha }}({{t}_{i}}) = {{h}_{{\alpha i}}},\,\,\,\,E({{t}_{i}}) = {{E}_{i}} = 0. \\ \end{gathered} $

В силу сделанных допущений достаточно рассмотреть движение КА с ВЭРД на одном витке орбиты $\vartheta \in [0,\;2\pi ].$ В конечный момент времени tf:

(11)
$\vartheta ({{t}_{f}}) = {{\vartheta }_{f}} = 2\pi ,\,\,\,\,{{h}_{\pi }}({{t}_{f}}) = {{h}_{{\pi f}}} = {{h}_{{\pi i}}}.$

Функционал задачи – максимум изменения высоты апогея за виток орбиты при условии равенства начальной hπi и конечной hπf высоты перигея:

(12)
$\Phi = {{\left. {\Delta {{h}_{{\alpha f}}}} \right|}_{{{{h}_{{\pi f}}} = {{h}_{{\pi i}}}}}} \Rightarrow \mathop {{\text{max}}}\limits_{{\mathbf{u}} \in U} ,$

где Δhαf = hαf – hαi, hαf = hα(tf).

Модель аэродинамического сопротивления

Аэродинамическое сопротивление – одно из основных слагаемых возмущающего воздействия на движение КА на высотах менее 300 км. Оценка аэродинамического сопротивления КА зависит от принятой модели взаимодействия молекул с поверхностью, температуры и молекулярного состава атмосферы, температуры и шероховатости материала поверхности и т.д. Обзор различных моделей взаимодействия молекул с поверхностью и сравнение полученных с их использованием коэффициентов аэродинамических сил приведены в публикациях [24–27]. Наиболее простой представляется максвелловская модель взаимодействия, в которой используется единственный коэффициент σ, определяющий долю молекул, испытывающих диффузное отражение от поверхности [28]. Результаты анализа движения аппаратов на высотах менее 300 км показывают, что наиболее точное описание аэродинамических сил может быть получено в предположении практически полностью диффузного отражения молекул (σ ≈ 1) [29–32]. Доминирование диффузного отражения означает возрастание роли поверхностей КА, параллельных потоку, в аэродинамическом сопротивлении.

При оптимизации управления углом атаки КА на основе принципа максимума Понтрягина использование аэродинамического сопротивления КА в форме представленных в работах [24–32] моделей приведет к существенному усложнению математической и численной процедуры решения краевой задачи, к которой сводится оптимизационная. В связи с этим для регуляризации исследований в настоящей работе предложена модель аэродинамического сопротивления КА, позволяющая без существенной потери точности использовать простые аналитические зависимости аэродинамического сопротивления от характеристик атмосферы и угла атаки КА.

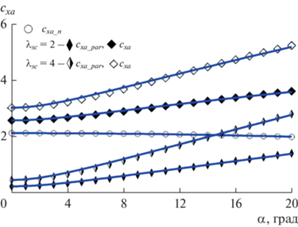
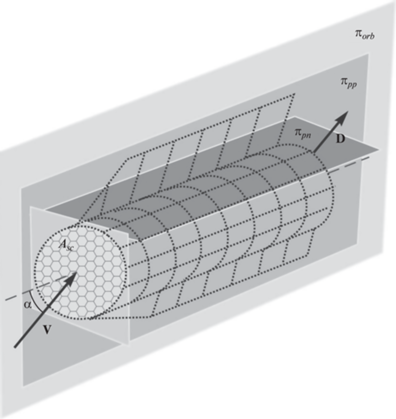
Для наглядности формирования модели аэродинамического сопротивления определим проекции сечений КА плоскостями, параллельными и перпендикулярными продольной оси КА и плоскости орбиты πorb (рис. 1): ASC – площадь и обозначение поперечного сечения КА, Apn – площадь и обозначение проекции сечений КА на плоскость πpn, параллельную продольной оси КА и перпендикулярную πorb, App – площадь и обозначение проекции сечений КА на плоскость πpp, параллельную продольной оси КА и πorb. Тогда, предполагая, что движение КА происходит без скольжения (плоскость симметрии КА проходит через вектор скорости) и, принимая ASC в качестве характерной площади, коэффициент аэродинамического сопротивления КА с учетом исследований [28, 33] представим в виде

(13)
${{c}_{{xa}}} = {{c}_{{xa\_n}}} + {{c}_{{xa\_par}}},$
где cxa_n – коэффициент аэродинамического сопротивления, ${{c}_{{xa\_n}}} = {{c}_{{{{x}_{0}}}}}{\text{cos}}\alpha ,$ характеризующегося проекцией ASC, ${{c}_{{{{x}_{0}}}}}$ – коэффициент аэродинамического сопротивления КА при нулевом угле атаки; cxa_par – коэффициент аэродинамического сопротивления, ${{c}_{{xa\_par}}} = {{c}_{{xa\_pn}}} + {{c}_{{x\_pp}}},$ характеризующегося проекциями Apn и App соответственно: ${{c}_{{xa\_pn}}} = {{k}_{{pn}}}{{c}_{{{{x}_{0}}}}}\left| {{\text{sin}}\alpha } \right|,$ ${{k}_{{pn}}} = {{{{A}_{{pn}}}} \mathord{\left/ {\vphantom {{{{A}_{{pn}}}} {{{A}_{{SC}}}}}} \right. \kern-0em} {{{A}_{{SC}}}}}{\kern 1pt} ,$ ${{c}_{{x\_pp}}} = {{k}_{{pp}}}{{c}_{{{{x}_{{//}}}}}},$ ${{k}_{{pp}}} = {{{{A}_{{pp}}}} \mathord{\left/ {\vphantom {{{{A}_{{pp}}}} {{{A}_{{SC}}}}}} \right. \kern-0em} {{{A}_{{SC}}}}}{\kern 1pt} ,$ ${{c}_{{{{x}_{{//}}}}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {\sqrt \pi {{S}_{\infty }}} \right)}}} \right. \kern-0em} {\left( {\sqrt \pi {{S}_{\infty }}} \right)}}$ – коэффициент аэродинамического сопротивления пластины при нулевом угле атаки; S∞ – скоростное соотношение, равное отношению скорости набегающего потока V к тепловой скорости молекул в ИК.

Рис. 1.

Схема расположения плоскостей, на которые проецируются поверхности КА при создании модели аэродинамических сил, по отношению к продольной оси КА и плоскости орбиты πorb.

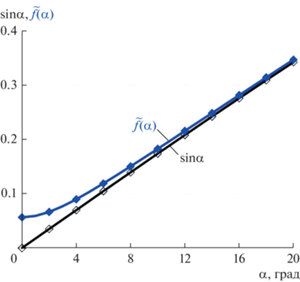
Из приведенных соотношений видно, что cxa_pn = 0 при α = 0, что не соответствует режиму диффузного отражения молекул. Для учета вклада проекций Apn в сопротивление при α = 0 предложена аппроксимация $\left| {{\text{sin}}\alpha } \right|:$

(14)
$\tilde {f}(\alpha ) \approx {{c}_{{{{x}_{{//}}}}}}\sqrt {1 + {{{\left( {{{{\text{sin}}\alpha } \mathord{\left/ {\vphantom {{{\text{sin}}\alpha } {{{c}_{{{{x}_{{//}}}}}}}}} \right. \kern-0em} {{{c}_{{{{x}_{{//}}}}}}}}} \right)}}^{2}}} .$

Как следует из выражения (14), $\tilde {f}(0) = {{c}_{{{{x}_{{//}}}}}},$ а при α > 0 функция $\tilde {f}(\alpha )$ позволяет аппроксимировать $\left| {{\text{sin}}\alpha } \right|$ с достаточной точностью (рис. 2). В результате получаем модель аэродинамического сопротивления КА (6) с коэффициентом cxa(α) в виде

(15)
$\begin{gathered} {{c}_{{xa}}}(\alpha ) = \\ = {{c}_{{{{x}_{0}}}}}\left( {{\text{cos}}\,\alpha + {{k}_{{pn}}}{{c}_{{{{x}_{{//}}}}}}\sqrt {1 + {{{\left( {{{{\text{sin}}\,\alpha } \mathord{\left/ {\vphantom {{{\text{sin}}\,\alpha } {{{c}_{{{{x}_{{//}}}}}}}}} \right. \kern-0em} {{{c}_{{{{x}_{{//}}}}}}}}} \right)}}^{2}}} } \right) + {{k}_{{pp}}}{{c}_{{{{x}_{{//}}}}}}. \\ \end{gathered} $
Рис. 2.

Зависимости sinα и его аппроксимации $\tilde {f}(\alpha )$ от угла атаки.

Для верификации сформированной модели (15) проведено ее сравнение с аэродинамическим сопротивлением, рассчитываемым по широко используемой при исследованиях движения в верхних слоях атмосферы модели “Diffuse Reflection with Incomplete Accommodation” (DRIA) [27, 29, 31]. Результаты сравнения с моделью DRIA для полностью диффузного отражения на рис. 3, рассчитанные для двух значений удлинения КА λSC = 2 и 4 при kpn = kpp, подтверждают возможность применения модели (15) для описания аэродинамического сопротивления аппаратов в свободномолекулярном потоке.

Рис. 3.

Зависимости коэффициентов аэродинамического сопротивления от угла атаки модели (15) показаны сплошными линиями, маркерами отмечены расчеты по модели DRIA.

Модель тяги ВЭРД

Влияние угла атаки на величину тяги ВЭРД определяется уменьшением [18–20]:

1) эффективной площади входа в ВЗ Aincosα,

2) относительного числа молекул, пролетающих через ВЗ без столкновения с его стенками при наличии угла атаки km(α).

Тогда общий коэффициент, характеризующий уменьшение эффективности ВЗ, а, следовательно, и концентрации молекул в ИК и пропорциональной ей тяги (5), равен:

(16)
${{k}_{P}}(\alpha ) = {{k}_{m}}(\alpha )\cos {\kern 1pt} \alpha .$

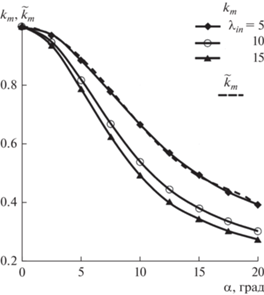
В работе [19] представлены рассчитанные методом Монте-Карло и полученные экспериментально значения km(α) для цилиндрического ВЗ из нержавеющей стали удлинением λin = 9.4, которые практически совпали.

В работе [20] приведены рассчитанные методом Монте-Карло зависимости km(α) для цилиндрических ВЗ удлинением λin = 5, 10, 15 (рис. 4). Для использования в условиях оптимальности там же представлена аппроксимация ${{\tilde {k}}_{m}}(\alpha )$ зависимости km(α) для цилиндрического ВЗ с λin = 5 степенным многочленом с коэффициентами, полученными методом наименьших квадратов:

(17)
${{\tilde {k}}_{m}}(\alpha ) = 1 + \sum\limits_{i = 1}^3 {{{k}_{i}}{{\alpha }^{{2i}}}} ,$
где k1 = –14.8094, k2 = 142.150, k3 = –504.470, радиус апогея α в рад.
Рис. 4.

Относительное снижение эффективности ВЭРД km из-за угла атаки α для цилиндрического канала ВЗ удлинением λin = 5, 10, 15 и аппроксимация ${{\tilde {k}}_{m}}(\alpha )$ для λin = 5.

Модель атмосферы

Используется модель атмосферы ISO/FDIS 14222 (Space environment (natural and artificial) – Earth upper atmosphere. ISO/FDIS 14222, ISO 2013) для средней солнечной активности. Для использования в расчетах построены аппроксимации зависимости плотности и концентрации атмосферы от высоты полиномами 4-й степени.

РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ

Условия оптимальности

Решение задачи (12) основано на применении принципа максимума Понтрягина [14].

В силу малости возмущающего ускорения по сравнению с гравитационным $\left| {\mathbf{a}} \right| \ll \left| {\mathbf{g}} \right|,$ фокальный параметр p и эксцентриситет e орбиты в правых частях системы уравнений (2) будем считать постоянными на протяжении одного витка орбиты:

$p = {\text{const}},\,\,\,\,e = {\text{const}}{\text{.}}$

Гамильтониан H системы (2) с учетом ограничений (7), (8):

(18)
$\begin{gathered} H = {{\psi }_{\pi }}{{{\dot {r}}}_{\pi }} + {{\psi }_{\alpha }}{{{\dot {r}}}_{\alpha }} + {{\psi }_{{\text{E}}}}\dot {E} + \\ + \,\,{{\psi }_{\vartheta }}\dot {\vartheta } + {{\lambda }_{n}}({{n}_{{\min }}} - {{n}_{{IC}}}) + {{\lambda }_{\alpha }}\left( {\left| \alpha \right| - {{\alpha }_{{\max }}}} \right), \\ \end{gathered} $
где λn, λα – множители Лагранжа; ψ – вектор сопряженных переменных, ψ = (ψπ, ψα, ψE, ψϑ)T, удовлетворяющий системе уравнений:

(19)
$ \cdot {{\psi }^{T}} = - \frac{{\partial H}}{{\partial z}},\,\,\,\,{\mathbf{z}} = {{({{r}_{\pi }},{{r}_{\alpha }},E,\vartheta )}^{T}}.$

Из уравнений (19) и условия трансверсальности ${{\left. {\left[ { - \delta {{r}_{\alpha }} - H\delta t + (\psi ,\;\delta z)} \right]} \right|}_{{t = {{t}_{f}}}}} = 0$ следует:

(20)
${{\psi }_{\alpha }} = {\text{const}} = 1,\,\,\,\,\,{{\psi }_{{\text{E}}}} = {\text{const}} = 0.$

В соответствии с условиями оптимальности [14]

(21)
${{{\mathbf{u}}}_{{opt}}} = {\text{arg}}\mathop {{\text{max}}}\limits_{{\mathbf{u}} \in {\mathbf{U}}} H,$
что приводит к определению максимума недифференцируемой функции двух переменных
(22)
$\begin{gathered} \Delta H(\alpha ,\zeta ) = {{\psi }_{\pi }}{{{\dot {r}}}_{\pi }} + {{\psi }_{\alpha }}{{{\dot {r}}}_{\alpha }} + \\ + \,\,{{\lambda }_{n}}({{n}_{{\min }}} - {{n}_{{IC}}}) + {{\lambda }_{\alpha }}\left( {\left| \alpha \right| - {{\alpha }_{{\max }}}} \right), \\ \end{gathered} $
который в данном случае находится в результате сравнения его значений для вариантов ${\mathbf{u}} \in {\mathbf{U}}$ (9), указанных в табл. 1.

Таблица 1.  

Варианты вычислений ΔH(α, ζ)

$\Delta {{H}_{{opt\,H}}} = \Delta H\left( {{{\alpha }_{{opt}}} = {{\alpha }_{{opt\,H}}}:\left\{ {\frac{{\partial \Delta H}}{{\partial \alpha }} = 0,\;\frac{{{{\partial }^{2}}\Delta H}}{{\partial {{\alpha }^{2}}}} < 0} \right\},\;\zeta = 1} \right)$
$\Delta {{H}_{{11}}} = \Delta H({{\alpha }_{{opt}}} = \pm {{\alpha }_{{\max }}},\;\zeta = 1)$
$\Delta {{H}_{{10}}} = \Delta H({{\alpha }_{{opt}}} = \pm {{\alpha }_{{\max }}},\;\zeta = 0)$
$\Delta {{H}_{{00}}} = \Delta H\left( {{{\alpha }_{{opt}}} = 0:\left\{ {\frac{{\partial \Delta H}}{{\partial \alpha }} = 0,\;\frac{{{{\partial }^{2}}\Delta H}}{{\partial {{\alpha }^{2}}}} < 0} \right\},\;\zeta = 0} \right)$
$\Delta {{H}_{{{{n}_{1}}}}} = \Delta H\left( {{{\alpha }_{{opt}}} = {{\alpha }_{{opt\,n}}}:{{n}_{{IC}}}({{\alpha }_{{opt\,n}}}) = {{n}_{{\min }}},\;\zeta = 1} \right)$

В табл. 1 αoptH вычисляется с помощью рекуррентной формулы:

(23)
$\alpha _{{opt\,H}}^{{k + 1}} = \frac{{\partial \Delta {{H}_{{opt\,H}}}}}{{\partial \alpha }}\left( {\alpha _{{opt\,H}}^{k}} \right) + \alpha _{{opt\,H}}^{k},\,\,\,\,k = 0,1, \ldots ,$
где с учетом (2), (5), (6), (15), (17), (18)

(24)
$\left. \begin{gathered} \Delta {{H}_{{opt\,H}}} = \hfill \\ = \,\,{{{\tilde {k}}}_{m}}(\alpha )\cos {\kern 1pt} \alpha (A{\kern 1pt} \cos {\kern 1pt} \alpha + F{\kern 1pt} \sin {\kern 1pt} \alpha ) + B{\kern 1pt} \cos {\kern 1pt} \alpha + C, \hfill \\ A = 2{{\eta }_{C}}{{a}_{\vartheta }}c,\;\,\,B = - {{a}_{\vartheta }}{{c}_{{x0}}}V, \hfill \\ C = {{C}_{0}}{{c}_{{{{x}_{0}}}}}\sqrt {1 + {{{\left( {\frac{{{\text{sin}}\alpha }}{{{{c}_{{{{x}_{0}}}}}}}} \right)}}^{2}}} ,\;\,{{C}_{0}} = - {{k}_{{pn}}}{{a}_{\vartheta }}{{c}_{{x0}}}V, \hfill \\ F = {{\eta }_{C}}{{b}_{\vartheta }}c,\;\,\,{{a}_{\vartheta }} = \frac{{1 + {\text{cos}}{\kern 1pt} \vartheta }}{{{{{(1 - e)}}^{2}}}} + {{\psi }_{\pi }}\frac{{1 - {\text{cos}}{\kern 1pt} \vartheta }}{{{{{(1 + e)}}^{2}}}}, \hfill \\ {{b}_{\vartheta }} = \frac{{{\text{sin}}{\kern 1pt} \vartheta }}{{1 + e{\kern 1pt} {\text{cos}}{\kern 1pt} \vartheta }}(1 - {{\psi }_{\pi }}). \hfill \\ \end{gathered} \right\}$

Начальное приближение $\alpha _{{opt\,H}}^{0} = $ $ = {{(F + {{C}_{0}})} \mathord{\left/ {\vphantom {{(F + {{C}_{0}})} {\left( {4A(1 - {{k}_{1}}) + B} \right)}}} \right. \kern-0em} {\left( {4A(1 - {{k}_{1}}) + B} \right)}}$ в выражении (23) определяется из решения уравнения

(25)
$\frac{{\partial \Delta {{H}_{{appr}}}}}{{\partial \alpha }}\left( {\alpha _{{opt\,H}}^{0}} \right) = 0,$
где ΔHappr – аппроксимация (24) с учетом равенств (14), (17) путем разложения в ряд функций угла атаки α в окрестности α = 0 до α2 включительно.

Для обеспечения требуемой точности численного интегрирования моменты, соответствующие угловым точкам в правых частях систем уравнений (2) и (19), определяются с достаточной точностью из решения в общем случае нелинейных уравнений методом хорд. Появление угловых точек связано с выходом на ограничения (7), (8) и сходом с них и сменой режимов полета в соответствии с условиями оптимальности (21) и табл. 1. Соответствующие невязки ε указаны в табл. 2.

Таблица 2.  

Невязки для отслеживания угловых точек методом хорд

Причина возникновения угловой точки Невязка
Выход на ограничение (7) при ϑ < π и сход с него при ϑ > π $\varepsilon = \left| {1 - \frac{{{{n}_{{IC}}}({{\alpha }_{{opt\,H}}})}}{{{{n}_{{\min }}}}}} \right|$
Сход с ограничения (7) при ϑ < π и выход на него при ϑ > π:  
• при $\Delta H({{\alpha }_{{\max }}},\;0) > \Delta H({{\alpha }_{{opt\,n}}},\;1)$ $\varepsilon = \left| {\Delta H({{\alpha }_{{\max }}},\;0) - \Delta H({{\alpha }_{{opt\,n}}},\;1)} \right|$
• при $\Delta H({{\alpha }_{{\max }}},\;0) \leqslant \Delta H({{\alpha }_{{opt\,n}}},\;1)$ $\varepsilon = \left| {1 - \frac{{{{n}_{{IC}}}(\alpha = 0)}}{{{{n}_{{\min }}}}}} \right|$
Смена режимов полета между $({{\alpha }_{{opt\,H}}},\;\zeta = 1)$ и $\left( {{{\alpha }_{{\max }}},\;\zeta = 0} \right)$ $\varepsilon = \left| {\Delta H({{\alpha }_{{\max }}},\;0) - \Delta H({{\alpha }_{{opt\,H}}},\;1)} \right|$
Смена режимов полета между $\left( {\alpha = 0,\;\zeta = 0} \right)$ и $\left( {{{\alpha }_{{\max }}},\;\zeta = 0} \right)$ $\varepsilon = \left| {\Delta H({{\alpha }_{{\max }}},\;0) - \Delta H(\alpha = 0,\;0)} \right|$

При активном ограничении (7) угол атаки αopt n определяется из решения нелинейного уравнения nIC(α) = nmin методом хорд с невязкой $\varepsilon = \left| {{{k}_{p}}(\alpha ) - \frac{{{{n}_{{{\text{min}}}}}}}{{n(h)k{}_{c}}}} \right|.$

Решение краевой задачи

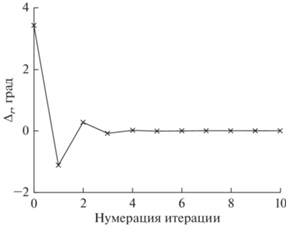
Использование принципа максимума Понтрягина позволяет свести исходную задачу поиска оптимального управления в функциональном пространстве к решению краевой задачи для систем обыкновенных дифференциальных уравнений (2), (19). Для решения двухточечной краевой задачи применяются модифицированный метод Ньютона и метод гомотопии. При сделанных допущениях и с учетом равенств (20) варьируемым параметром выступает сопряженная переменная ψn = const, а соответствующая невязка Δπ следует из условия (11): Δπ = hπf – hπi. Для определения оптимального управления в каждой точке траектории вычисляется оптимальный угол атаки αopt в соответствии с условиями оптимальности (21) и табл. 1. На рис. 5 показано изменение невязки ${{\Delta }_{r}} = \alpha _{{opt\,H}}^{{k + 1}} - \alpha _{{opt\,H}}^{k},$ k = 0, 1, …, по итерациям при применении рекуррентной формулы (23) для вычисления αopt = αopt H = –9.40487 град, полученного при Δr ≤ 10–4 град.

Рис. 5.

Пример изменения невязки Δr по итерациям процедуры поиска оптимального угла атаки по рекуррентной формуле (23).

ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

На основании разработанной методики проведены численные исследования для параметров ВЭРД, КА и орбит, приведенных в табл. 3.

Таблица 3.  

Параметры ВЭРД, КА и орбит

Параметр Значения
Начальная высота перигея hπi, км [140, 180]
Начальная высота апогея hαi, км [160, 1000]
Площадь поперечного сечения КА ASC, м2 0.1
Удлинение КА λSC [2, 8]
Тяговый к.п.д. ВЭРД ηT 0.8
Эффективность забора газа ηc 0.333
Коэффициент компрессии газа в ИК kс 145
Скорость истечения реактивной струи с, км/с [80, 140]
Коэффициент аэродинамического сопротивления КА при нулевом угле атаки ${{c}_{{{{x}_{0}}}}}$ 2.2
Минимально допустимая концентрация молекул газа в ИК nmin, м–3 1018
Скоростное соотношение частиц в набегающем потоке S∞ 10
Максимально допустимый угол атаки $\left| {{{\alpha }_{{{\text{max}}}}}} \right|,$ град 20

Сделаны следующие допущения:

1. КА движется по солнечно-синхронной орбите (ССО) в плоскости терминатора.

2. Площадь входного отверстия ВЗ при α = 0 равна площади поперечного сечения КА Ain = ASC.

3. Apn = App.

4. Ограничение на угловую скорость разворота КА относительно центра масс отсутствует.

Оптимальные программы изменения угла атаки КА и тяги ВЭРД на орбитах с начальной высотой перигея hπi = 160 км в зависимости от начальной высоты апогея hαi и истинной аномалии ϑ приведены на рис. 6, 7. На рис. 6 участки оптимальной программы управления углом атаки при работе ВЭРД с минимально допустимой концентрацией газов в ИК (на границе ограничения (7)) показаны пунктирными линиями. На круговой орбите (начальная высота орбиты horb i = 160 км) концентрация газов в ИК не снижается до минимально допустимой, и участок, соответствующий движению по границе ограничения (7), отсутствует. Функция ΔH10 (табл. 1) — четная, т.е. ΔH(αopt = αmax, ζ = 0) = ΔH(αopt = –αmax, ζ = 0) в соответствии с выражениями (2), (4)–(6), (15), (18), (20), (22). Поэтому выбор αopt = αmax при ϑ ≤ π и αopt = –αmax при ϑ > π на рис. 6а обусловлен минимизацией скачкообразного изменения угла атаки в более плотных слоях атмосферы. В этом случае максимальное изменение угла атаки (переключение с αopt = αmax на αopt = –αmax) происходит в апогее орбиты. В то же время на круговых и слабо эллиптических орбитах это обстоятельство несущественно. С точки зрения минимизации количества резких изменений αopt возможные варианты зависимостей αopt(ϑ) для исходных круговой орбиты с horb i = 160 км и орбиты с hπi = 160 км и hαi = 200 км показаны на рис. 6б: с реализацией αopt = –αmax (сплошные линии) и αopt = αmax (пунктирные линии) на участках движения по границе ограничения на угол атаки (8).

Рис. 6.

Оптимальные программы изменения αopt на орбитах с начальными hπi = 160 км и ${{h}_{{\alpha \,i}}} \in [160,\;1000]\;{\text{км}}$ в зависимости от истинной аномалии ϑ; штриховыми линиями показаны участки, соответствующие граничной концентрации nIC = nmin (а); варианты αopt(ϑ) при реализации αopt = –αmax (сплошные линии) и αopt = αmax (штрихпунктирные линии) на участках движения по границе ограничения (8) (б).

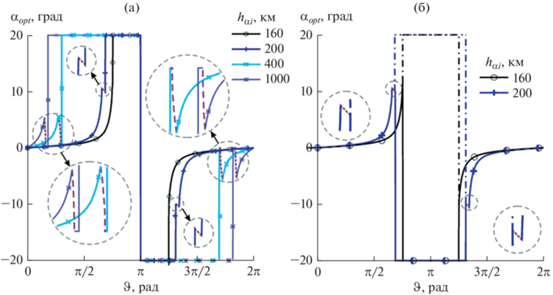
Рис. 7.

Оптимальные программы тяги ВЭРД Popt на орбитах с начальными hπi = 160 км и ${{h}_{{\alpha \,i}}} \in [160,\;1000]\;{\text{км}}$ в зависимости от истинной аномалии ϑ; пунктирными линиями выделены участки, соответствующие граничной концентрации nIC = nmin, штриховыми линиями – участки, соответствующие $\left| {{{\alpha }_{{opt}}}} \right| = {{\alpha }_{{\max }}},$ штрихпунктирными линиями – участки с нулевой тягой.

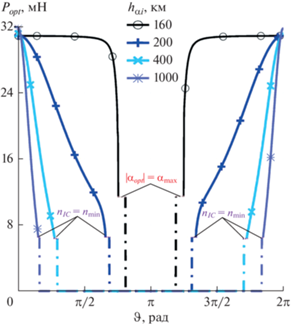
На рис. 7 пунктирными линиями показаны участки работы ВЭРД при минимально допустимой концентрации в ИК (на границе ограничения (7)), штрихпунктирные линии соответствуют участкам пассивного полета КА (с нулевой тягой). Отключается (ζ = 0) и включается (ζ = 1) тяга в соответствии с условиями оптимальности (21). На круговой орбите, где концентрация газов в ИК не снижается до минимальной, штриховой линией указана тяга, реализующаяся при максимальном угле атаки.

На рис. 8 в зависимости от истинной аномалии ϑ показано оптимальное изменение высоты перигея Δhπ (пунктирные линии) и апогея Δhα (сплошные линии) оскулирующих орбит при полете КА с ВЭРД с оптимальным управлением углом атаки и тягой (рис. 6, 7). Как следует из рис. 8, максимум изменения высоты апогея при оптимальном управлении достигается на круговой орбите horb i = 160 км. Но и затраты энергии для работы ВЭРД на круговой орбите также максимальны (рис. 9). Поэтому в условиях ограниченной энергетики благодаря возможности накопления энергии на высотах, где аэродинамическое сопротивление КА практически отсутствует, использование эллиптических орбит для обеспечения длительного существования КА с ВЭРД может оказаться предпочтительнее круговых.

Рис. 8.

Изменение высот апогея Δhα (сплошные линии) и перигея Δhπ (штриховые линии) оскулирующих орбит при оптимальном управлении КА в зависимости от истинной аномалии ϑ с начальными hπi = 160 км, ${{h}_{{\alpha \,i}}} \in [160,\;1000]\;{\text{км}}{\text{.}}$

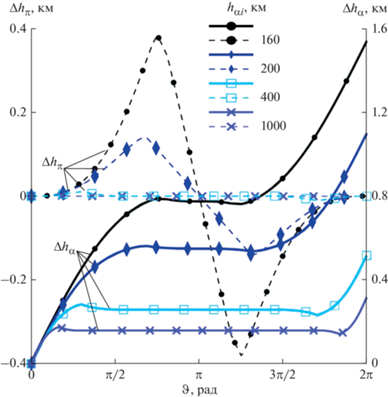
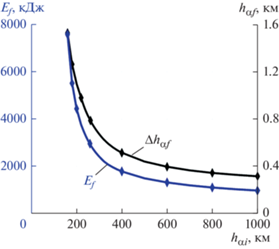
Рис. 9.

Максимально возможное увеличение высоты апогея Δhαf и потребляемая ВЭРД энергия Ef за один виток орбиты с начальной высотой перигея hπi = 160 км в зависимости от начальной высоты апогея hαi.

Результаты численных исследований на рис. 6–9 получены для КА удлинением λSC = 4 с ВЭРД со скоростью истечения с = 100 км/с. Результаты исследования влияния этих параметров представлены на рис. 10, 11. Показаны относительные изменения высоты апогея Δhαf (сплошные линии) и потребляемая ВЭРД энергия Ef (штриховые линии) за один виток орбитального полета с начальной высотой перигея hπi = 160 км в зависимости от начальной высоты апогея hαi, ${{\lambda }_{{SC}}} \in [2,\;8]$ (рис. 10) и скорости истечения $c \in [80,\;140]\;{{{\text{км}}} \mathord{\left/ {\vphantom {{{\text{км}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ (рис. 11). Из рисунков следует, что влияние рассматриваемых параметров (λSC и с) снижается при увеличении эллиптичности орбит с начальными высотами перигея и апогея в рассматриваемом диапазоне.

Рис. 10.

Максимальное изменение высоты апогея Δhαf (сплошные линии) и потребляемая ВЭРД энергия Ef (штриховые линии) за один виток орбиты с начальной высотой перигея hπi = 160 км в зависимости от начальной высоты апогея hαi и удлинения КА λSC при с = 100 км/с.

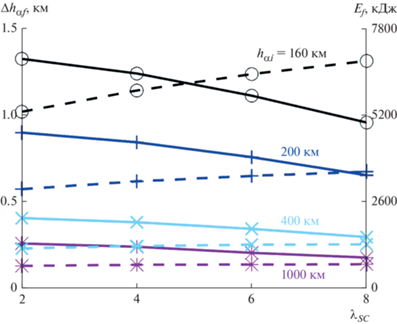
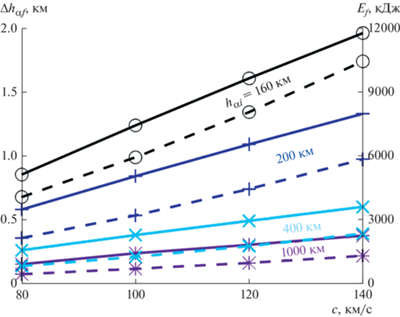
Рис. 11.

Максимальное изменение высоты апогея Δhαf (сплошные линии) и потребляемая ВЭРД энергия Ef (штриховые линии) за один виток орбиты с начальной высотой перигея hπi = 160 км в зависимости от начальной высоты апогея hαi и скорости истечения с при λSC = 4.

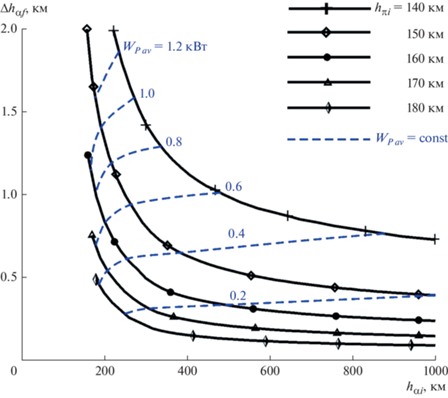
На рис. 12 приведены оптимальные изменения высоты апогея за один виток орбиты Δhαf в зависимости от начальной высоты перигея ${{h}_{{\pi \,i}}} \in \left[ {140,\;180} \right]\;{\text{км}}$ и апогея ${{h}_{{\alpha \,i}}} \in \left[ {140,\;1000} \right]\;{\text{км}}$ при постоянной скорости истечения с = 100 км/с и λSC = = 4. На рис. 12 также показаны линии уровня усредненной мощности ${{W}_{{P\;av}}} = {{{{E}_{f}}} \mathord{\left/ {\vphantom {{{{E}_{f}}} {{{T}_{{orb}}}}}} \right. \kern-0em} {{{T}_{{orb}}}}}$ за период обращения Torb. Приведенные результаты исследований еще раз подтверждают, что для обеспечения длительного активного существования КА с ВЭРД использование эллиптических орбит с ультранизким перигеем может быть предпочтительнее за счет возможности накопления энергии на высотах, где аэродинамическое сопротивление КА пренебрежимо мало.

Рис. 12.

Максимальное изменение высоты апогея Δhαf за один виток орбиты в зависимости от начальных hπi и hαi; штриховыми показаны линии уровня средней за виток потребляемой ВЭРД мощности WPav при с = 100 км/с, λSC = 4.

ЗАКЛЮЧЕНИЕ

На основе применения принципа максимума Понтрягина для системы уравнений в оскулирующих переменных решена задача оптимизации управления вектором тяги ВЭРД для наискорейшего изменения высоты апогея орбиты КА с учетом зависимости тяги от угла атаки и концентрации газа в ионизационной камере.

Получены оценки эффективности разработанных оптимальных программ управления углом атаки и тягой ВЭРД в зависимости от начальных высот перигея и апогея, скорости истечения, параметров компоновки КА.

Показано, что использование эллиптических орбит в условиях ограниченной энергетики может быть предпочтительнее благодаря возможности накопления энергии на высотах, где аэродинамическое сопротивление КА практически отсутствует.

Работа выполнена при поддержке Российского научного фонда, проект № 20-69-46034, Организация – МГУ имени М.В. Ломоносова.

Список литературы

  1. Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета с малой тягой. М.: Наука, 1966.

  2. Маров М.Я., Филатьев А.С. Комплексные исследования электрореактивных двигателей при полетах в ионосфере Земли: К 50-летию Государственной программы “Янтарь” // Косм. исслед. 2018. Т. 56. № 2. С. 137–144. https://doi.org/10.7868/S0023420618020061 (Cosmic Research. 2018. Т. 56. № 2. P. 123–129).10.7868/S0023420618020061

  3. Virgili J., Roberts P.C.E., Palmer K. et al. Very Low Earth Orbit mission concepts for Earth Observation: Benefits and challenges // Proc. 12th Reinventing Space Conf. London, UK. 2014. BIS-RS-2014-37.

  4. Filatyev A.S., Golikov A.A., Nosachev L.V. et al. Spacecraft with air-breathing electric propulsion as the future ultra-speed aircraft // Proc. 71th Intern. Astronautical Congress. The CyberSpace Edition. 1–5 Oct. 2020. IAC-20-C4.6.8.

  5. Dolgich A. Soviet Studies on Low-Thrust Orbital Propellant-Scooping Systems // Foreign Sciebce Bull. 1969. V. 5. № 7. P. 1–9.

  6. Цой Э.П. Выбор оптимальной программы управления тягой накопителя рабочего вещества в нестационарном режиме // Тр. ЦАГИ. 1968. Вып. 1145.

  7. Шумилкин В.Г. Управление тягой орбитального аппарата с двигателем ограниченной мощности при полете с накоплением атмосферного воздуха // Ученые записки ЦАГИ. 1976. Т. 7. № 2. С. 81–87.

  8. Romano F. et al. System Analysis and Test-Bed for an Atmosphere-Breathing Electric Propulsion System Using an Inductive Plasma Thruster // Proc. 68th Intern. Astronautical Congress. Adelaide, Australia, 25–29 Sept. 2017. IAC-17-C4.6.5.

  9. Rock B.St., Blandino J.J., Demetriou M.A. Propulsion Requirements for Drag-Free Operation of Spacecraft in Low Earth Orbit // J. Spacecraft and Rockets. 2006. V. 43. № 3. P. 594–606. https://doi.org/10.2514/1.15819

  10. Marchetti P., Blandino J.J., Demetriou M.A. Electric Propulsion and Controller Design for Drag-Free Spacecraft Operation // J. Spacecraft and Rockets. 2008. V. 45. № 6. P. 1303–1315. https://doi.org/10.2514/1.36307

  11. Becedas J., González G., Domínguez R.M. et al. Aerodynamic Technologies for Earth Observation Missions in Very Low earth Orbit. A: Reinventing Space Conference // Proc. 16th Reinventing Space Conf. (RISpace). London, UK, 30 Oct. – 1 Nov. 2018. P. 1–10.

  12. Filatyev A.S., Erofeev A.I., Yanova O.V. et al. Physical Grounds and Control Optimization of Low-Orbit Spacecraft with Electric Ramjet // Proc. 68th Intern. Astronautical Congress. Adelaide, Australia, 25–29 Sept. 2017. IAC-17-C4.IP.51.

  13. Barral S., Cifali G., Albertoni R. et al. Conceptual Design of an Air-Breathing Electric Propulsion System // Proc. 34th Intern. Electric Propulsion Conf. Kobe, Japan, 4–10 July 2015. IEPC-2015-271.

  14. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969.

  15. Filatyev A.S., Yanova O.V. On the optimal use of electric ramjet for low-orbit spacecraft // Procedia Engineering. 2017. V. 185. P. 173–181. https://doi.org/10.1016/j.proeng.2017.03.299

  16. Filatyev A.S., Erofeev A.I., Nikiforov A.P. et al. Comparative evaluation of the applicability of electrical ramjets // Proc. 58th Israel Annual Conf. Aerospace Science. WeL1T4.3. Tel-Aviv, Haifa, Israel, 14–15 Mar. 2018. P. 503–519. http://toc.proceedings.com/ 37020webtoc.pdf.

  17. Filatyev A.S., Yanova O.V. The control optimization of low-orbit spacecraft with electric ramjet // Acta Astronautica. 2019. V. 158. P. 23–31.

  18. Yanova O.V., Filatyev A.S. Synthesis of the optimal control of spacecraft with air-breathing electric propulsion in orbits with ultra-low perigee in view of dependence of the engine efficiency on angle of attack // Proc. 71th Intern. Astronautical Congress. The CyberSpace Edition. 1–5 Oct. 2020. IAC-20-C1.5.1.

  19. Ерофеев А.И., Никифоров А.П., Плугин В.В. Экспериментальные исследования воздухозаборника в свободномолекулярном потоке газа // Ученые записки ЦАГИ. 2017. Т. 48. № 3. С. 56–69.

  20. Ерофеев А.И., Никифоров А.П., Плугин В.В. Моделирование процессов в воздухозаборнике для низкоорбитальных космических аппаратов в вакуумной аэродинамической трубе // Актуальные вопросы проектирования автомат. космич. аппаратов для фундам. и прикладных науч. исслед.: сб. тр. конф. Вып. 2. Химки: Изд-во “НПО им. С.А. Лавочкина”. 2017. С. 365–374.

  21. Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического полета. М.: Наука. Гл. ред. физ.-мат. лит., 1990.

  22. Мирер С.А. Механика космического полета. Орбитальное движение. М.: Резолит, 2007.

  23. Fearn D.G. Ion thruster thrust vectoring requirements and techniques // 27th Intern. Electric Propulsion Conf. Pasadena, CA. 15–19 Oct. 2001. IEPC-01-115.

  24. Munoz V., González D., Becedas J. et al. Attitude control for satellites flying in VLEO using aerodynamic surfaces // J. British Interplanetary Society. 2020. V. 73. № 3. P. 103–112.

  25. Prieto D.M., Graziano B.P., Roberts P.C.E. Spacecraft drag modelling // Progress in Aerospace Sciences. 2014. V. 64. P. 56–65. https://doi.org/10.1016/j.paerosci.2013.09.001

  26. Livadiotti S., Crisp N.H., Robert P.C.E. et al. A review of gas-surface interaction models for orbital aerodynamics applications // Progress in Aerospace Sciences. 2020. V. 119. Art. № 100675. https://doi.org/10.1016/j.paerosci.2020.100675

  27. Mehta P.M., Walker A., McLaughlin C.A., Koller J. Comparing Physical Drag Coefficients Computed Using Different Gas–Surface Interaction Models // J. Spacecraft and Rockets. 2014. V. 51. № 3. P. 873–883. https://doi.org/10.2514/1.A32566

  28. Koppenwallner G. Satellite Aerodynamics and Determination of Thermospheric Density and Wind // AIP Conf. Proc. 2011. V. 1333. P. 1307–1312. https://doi.org/10.1063/1.3562824

  29. Moe K., Moe M.M. Gas-surface interactions and satellite drag coefficients // Planetary and Space Science. 2005. V. 53. P. 793–801. https://doi.org/10.1016/j.pss.2005.03.005

  30. Koppenwallner G. Comment on special section: new perspectives on the satellite drag environments of Earth, Mars, and Venus // J. Spacecraft and Rockets. 2008. V. 45. № 6. P. 1324–1327. https://doi.org/10.2514/1.37539

  31. Sutton E.K. Normalized Force Coefficients for Satellites with Elongated Shapes // J. Spacecraft and Rockets. 2009. V. 46. № 1. P. 112–116. https://doi.org/10.2514/1.40940

  32. Doornbos E. Thermospheric Density and Wind Determination from Satellite Dynamics. Book Ser.: Springer Theses. 2012. https://link.springer.com/book/10.1007/ 978-3-642-25129-0

  33. Golikov A.A., Filatyev A.S. Integrated optimization of trajectories and layout parameters of spacecraft with air-breathing electric propulsion // Acta Astronautica. 2022. V. 193. P. 644–652. https://doi.org/10.1016/j.actaastro.2021.06.052

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал