Космические исследования, 2023, T. 61, № 3, стр. 215-229

ВВЕДЕНИЕ

Благодаря обтеканию магнитосферы Земли сверхзвуковым потоком плазмы солнечного ветра с вмороженным магнитным полем, она сильно поджата на дневной стороне и вытянута в форме хвоста кометы на ночной стороне [1, 2]. Хвост магнитосферы в низкоширотной части разделен на две примерно симметричные части (так называемые доли) токовым слоем (ТС) плоской формы, в его окрестности плотность плазмы выше, чем в долях. Плоскость симметрии ТС, называемая нейтральной плоскостью, разделяет магнитные потоки противоположного направления. В спокойной невозмущенной магнитосфере толщины токового и плазменного слоев сопоставимы и составляют порядка нескольких десятков тысяч километров. Однако во время геомагнитных возмущений (суббурь), вследствие накопления магнитного потока в хвосте, ТС сильно сжимается, его толщина достигает предельно малой величины порядка одного или нескольких гирорадиусов протонов, т.е. примерно от 200 до 2000 км; также происходит усиление электрического поля поперек хвоста [3–6].

Предельно тонкий токовый слой (ТТС) играет важную роль энергетического резервуара, в котором накапливается магнитная энергия, переносимая из солнечного ветра. Ее избыток может высвобождаться вследствие развития тиринг-неустойчивости (разрывной), приводящей к локальному распаду ТС и трансформации накопленной свободной энергии в энергию нагретых потоков плазмы, распространяющихся в высокие широты вдоль силовых линий магнитного поля [7–10]. Теоретические представления о хвосте магнитосферы Земли и его роли возникли практически одновременно с его открытием. Первые модели токового слоя были аналитическими и описывали его в рамках кинетического рассмотрения. Примером является известная одномерная модель Харриса [11], в которой нормальная (поперечная к слою) компонента магнитного поля не учитывалась. В других моделях (например, в публикациях [12–14]), она учитывалась, и такие токовые равновесия были двумерными. В них давление плазмы считалось изотропным, а профили плотности плазмы повторяли профили плотности тока [15].

Во время магнитосферных суббурь спутниками CLUSTER были зарегистрированы тонкие токовые слои на расстояниях порядка 9–12R_E в хвосте магнитосферы Земли (например, обзор [2]). Стало ясно, что для их описания непригодны старые модели плазменных равновесий, которые хорошо описывали сравнительно толстый ТС хвоста с замагниченной плазмой, характерный для спокойных геомагнитных периодов.

Основными свойствами тонких токовых слоев оказались следующие: 1) предельно малая толщина порядка одного или нескольких протонных (иногда электронных) гирорадиусов; 2) многомасштабность; 3) вложенность, при которой несколько токовых слоев с разными толщинами и разными носителями тока вложены один в другой [16–18]; 4) обогащение ТС ионосферными ионами кислорода во время магнитосферных суббурь, когда плотность тяжелых ионов может сравниваться или даже превышать плотность протонов в хвосте [19, 20]; 5) метастабильность, означающая, что ТТС могут достаточно долго существовать в устойчивом состоянии, а потом спонтанно разрушаться (обзор [10]).

Проведенные теоретические исследования показали, что динамика протонов и электронов в ТТС различна [2, 21, 22]. Так, для электронов масштаб магнитной неоднородности токового слоя (с толщиной L ~ 500–4000 км) намного превышает масштабы их гировращения. Поэтому популяция электронов в ТТС, как правило, является замагниченной [21, 22]. В отличие от электронов, ионы размагничиваются при входе в нейтральную область (z ≈ 0), описывают полуокружность в нормальном к ТТС поле B_z, затем снова замагничиваются и уходят от нейтральной плоскости, как это показано на рис. 1 (красная траектория), или возвращаются к ТС и пересекают его многократно (синяя траектория).

Рис. 1.

Две траектории протонов, рассчитанные в простой аналитической модели ТТС, где магнитное поле задавалось как ${\mathbf{B}} = \{ {{B}_{0}}{\kern 1pt} {\text{tg}}{\kern 1pt} h(z{\text{/}}L),0,{{B}_{z}}\} $ в стандартной геоцентрической солнечно-магнитосферной системе координат GSM. Пролетная траектория обозначена красным цветом, захваченная – синим. Точки запуска частиц обозначены звездочками соответствующих цветов (красная звездочка соответствует протону, запущенному из северного полушария, синяя – из южного). До достижения нейтральной плоскости {XY} пролетная частица совершает гировращение вдоль магнитных силовых линий, показанных штриховыми черными линиями. Захваченная частица многократно возвращается в токовый слой. Плоскость токового слоя обозначена зеленым цветом. Зелеными стрелками показано направление вектора плотности тока в ТС.

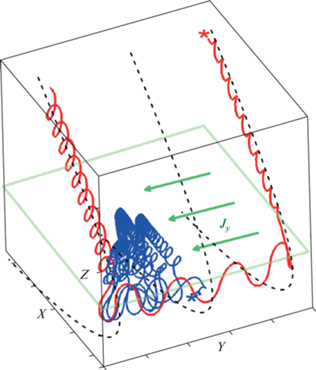
Динамика пролетных протонов, называемая квазиадиабатической, детально рассмотрена в работах [23, 24]. При движении таких частиц их инварианты движения ${{I}_{z}} = {{(2\pi )}^{{ - 1}}}\oint {{{p}_{z}}} dz$ (p_z – обобщенный импульс; z – координата) приближенно сохраняются, однако в момент смены типов движения без пересечения и с пересечением нейтральной плоскости происходят скачки инвариантов, величины которых $\Delta {{I}_{z}}$ много меньше самих инвариантов. Для захваченных частиц величины скачков $\Delta {{I}_{z}}$ оказываются порядка ${{I}_{z}}$. Благодаря приближенному сохранению инвариантов движения пролетные частицы покидают токовый слой без рассеяния, после однократного прохождения через слой, и каждая из них переносит элементарный ток в направлении оси Y. Захваченные частицы, многократно пересекая ТС, испытывают множественные скачки квазиадиабатических инвариантов, вследствие этого их движение хаотизируется; переносимый ими локальный ток оказывается ненулевым, хотя полный ток всегда близок к нулю. Кроме того, траектории захваченных ионов при движении с пересечением нейтральной области сильно петляют, как видно на рис. 1. Из-за этой особенности создаваемый ими локальный ток отрицателен в окрестности нейтральной плоскости z = 0 и положителен на периферии слоя [25, 26].

Таким образом, оказывается, что основными носителями тока в ТТС являются пролетные ионы [2, 21]. В некотором диапазоне параметров системы дрейфовые электронные токи также могут вносить вклад в общую плотность тока [21, 22], но этот вклад может быть невелик по сравнению с ионным, поэтому в настоящей модели эффекты, связанные с электронной популяцией, не рассматриваются.

В тонких слоях плотность тока может иметь большое разнообразие профилей. Так, например, были зарегистрированы слои с двумя или тремя максимумами плотности тока. Встречаются характерные “овершуты” магнитного поля, т.е. локальные максимумы тангенциальной магнитной компоненты ${{B}_{x}}$ на краях слоя в сочетании с расположенными рядом минимумами (см. [2, 17, 27 ] и ссылки там же). Подобные многомасштабные вложенные токовые конфигурации, с одной стороны, плохо описываются в рамках изотропных моделей [12–14]. С другой стороны, возможны противоположные ситуации, когда в спутниковых наблюдениях их многомасштабная структура не просматривается, вопреки известному многокомпонентному составу плазмы. В целом, причины появления подобных эффектов не всегда ясны, данный вопрос рассмотрен, например, в работе [28] и требует дальнейшего исследования.

В настоящей работе, с помощью построенной численной модели, исследуется эволюция токового слоя в хвосте магнитосферы Земли (результаты применимы также к хвостам магнитосфер других планет) и проводится анализ его структуры в плазме, состоящей из протонов ${{p}^{ + }}$ и тяжелых однократно ионизированных ионов кислорода ${{{\text{O}}}^{ + }}$.

1. МОДЕЛЬ ЭВОЛЮЦИИ ДВУХКОМПОНЕНТНОГО ТОКОВОГО СЛОЯ

РЕЗУЛЬТАТЫ

Для начала сравним результаты эволюции токового слоя и структуры равновесной токовой конфигурации в плазме, состоящей только из протонов или только из ионов кислорода. С этой целью нами проведено численное моделирование эволюции и формирования равновесного токового слоя. В обоих случаях была выбрана область моделирования, которая имела одни и те же пространственные размеры для всех расчетов, а для вычислений рассматривалось одно и то же количество макрочастиц. Исходный слой Харриса состоял из 50 тыс. макрочастиц. Температуры харрисовских частиц были выбраны одинаковыми и равными 10 кэВ (что соответствует их энергиям в хвосте магнитосферы Земли), а температуры фоновых частиц были взяты в десять раз ниже. Температуры протонов ${{T}_{{pr}}}$ и ионов кислорода ${{T}_{{ox}}}$ задавались одинаковыми в расчетах (${{T}_{{pr}}} = {{T}_{{ox}}} = 1$). Размер области моделирования был равен шести полутолщинам $L$ исходного слоя Харриса. Моделирование выполнялось за ${{k}_{{max}}} = {\text{8000}}$ шагов по времени. Нормированный временной шаг $k$ составлял 0.1 циклотронного периода ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\Omega }_{i}}}}} \right. \kern-0em} {{{\Omega }_{i}}}}$, который для протонов равен ~16.5 с, а для ионов кислорода – 264.4 с. Исследовалась зависимость процесса формирования ТС от концентраций протонов или тяжелых ионов и их температур.

В левом столбце рис. 2 показаны безразмерные профили тангенциальной компоненты магнитного поля ${{B}_{t}}(z)$ (а) и плотности тока ${{j}_{{_{y}}}}(z)$ (б) для протонного токового слоя в моменты времени $k = 1,\,2000,\,4000,\,6000,\,8000$. В правом столбце показаны аналогичные профили токового слоя в плазме с тяжелыми ионами: тангенциальная магнитная компонента ${{B}_{t}}(z)$ (в) и плотность тока ${{j}_{y}}(z)$ (г). К моменту времени $k = \,8000$ квазистационарные решения в обоих случаях устанавливались, и расчеты останавливались. Сравнение профилей магнитного поля показывает, что процессы эволюции и установления ТС в плазме, содержащей протоны или тяжелые ионы, имеют и сходства, и различия. Так, на рис. 2а,в можно видеть, как проходит процесс формирования очень тонкого протонного токового слоя толщиной порядка двух протонных гирорадиусов (в начале эволюции в момент времени k = 1 сравнительно широкий харрисовский ТС показан черной линией, в конечный момент времени $k = 8000$ – коричневой) с узким и интенсивным максимумом, причем на краях ТС сильные диамагнитные токи приводят к образованию локального минимума магнитного поля. Траекторный анализ показывает, что вблизи токового слоя замагниченные частицы, действительно, дрейфуют в отрицательном направлении по Y. Формирование кислородного токового слоя на рис. 2б сопровождается волнообразным перемещением области диамагнитных токов (овершута) от нейтральной плоскости к периферии токового слоя. Влияние этих токов приводят к уменьшению величины тангенциального магнитного поля на его краях.

Рис. 2.

Профили величин, характеризующих структуру токового слоя: тангенциальной X-компоненты магнитного поля (а, б) и плотностей тока (в, г) в чисто протонном ТС (левый столбец панели рисунков) и в чисто кислородном ТС (правый столбец) в моменты времени $k = 1,\,2000,\,4000,\,6000,\,8000$. Оси абсцисс для этих расчетов нормированы на соответствующие ларморовские радиусы протонов ${{p}^{ + }}$ (левая панель) и ионов кислорода ${{{\text{O}}}^{ + }}$ (правая панель) на краях токового слоя.

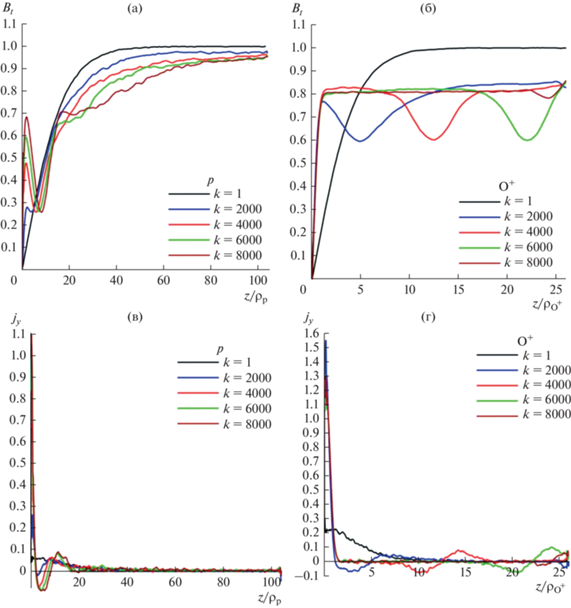
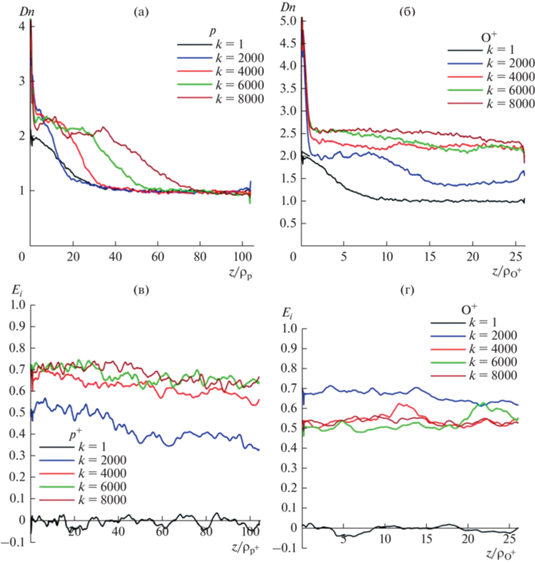
Рис. 3 демонстрирует установление во времени профилей плотности плазмы (а, б) и величины электрического поля (в, г) протонного и кислородного токовых слоев, характеристики которых показаны на рис. 2. На профилях плотности плазмы видно, что в области установившегося тонкого токового слоя наблюдается резкое возрастание, примерно в два раза, плотности плазмы. Хорошо видна двухмасштабная вложенная структура плотности протонов – вокруг тонкого пика располагается более широкий и низкий максимум плотности частиц. На профилях кислородного слоя максимумы плотности плазмы гораздо более широкие. Профили напряженности электрического поля позволяют сделать выводы о временах установления стационарных состояний в слоях. В какой-то момент времени электрическое поле выходит на примерно постоянное значение, тогда эволюция системы прекращается, и можно говорить об установлении квазистационарной конфигурации. За $k$ ~ 4000 временных шагов электрическое поле протонного ТС выходит на постоянное значение, равное примерно 0.65–0.7 (рис. 3в, г). В слое из ионов кислорода стационарное значение устанавливается на более низком уровне ~0.5 за $k$ ≈ 2500 временных шагов, т.е. эволюция кислородного слоя завершается быстрее, чем у слоя из одних протонов.

Рис. 3.

Профили плотности плазмы (а, б) и величины электрического поля (в, г), в чисто протонном (левый столбец панели) и в чисто кислородном (правый столбец) токовых слоях. Параметры расчетов и нормировки осей соответствуют рис. 2.

Ранее было показано, что узкий положительный пик плотности тока в нейтральной плоскости ТТС поддерживается частицами на размагниченных (квазиадиабатических) участках траекторий [23]. Многомасштабная структура ТС может быть обусловлена одновременным существованием в системе квазиадиабатических пролетных частиц (носителей тока) и квазизахваченных частиц (полный ток которых близок к нулю, хотя локальный ток – ненулевой), как это можно видеть на рис. 3а, б. Плотности плазмы и электрического тока в обоих слоях примерно равны по порядку величины. Толщины обоих токовых слоев составляют порядка гирорадиуса токонесущих частиц. Таким образом, установившийся кислородный слой примерно в четыре раза шире протонного слоя вследствие того, что гирорадиусы тяжелых ионов соотносятся с протонными как квадратный корень из отношения их масс: ${{{{\rho }_{{ox}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{ox}}}} {{{\rho }_{p}}\sim }}} \right. \kern-0em} {{{\rho }_{p}}\sim }}\sqrt {{{{{M}_{{ox}}}} \mathord{\left/ {\vphantom {{{{M}_{{ox}}}} {{{m}_{p}}}}} \right. \kern-0em} {{{m}_{p}}}}} \simeq 4$. Напряженности магнитного и электрического полей в кислородном слое устанавливаются на более низком уровне, чем в протонном слое.

На рис. 4 приведены характерные примеры траекторий движения пробных частиц в рассматриваемых протонном и кислородном ТС. Области, где траектории начинаются, обозначены звездочками.

Рис. 4.

Примеры траекторий “горячих” (а, б) и фоновых (в, г) частиц в установившихся конфигурациях: чисто протонном слое (левый столбец (а, в) панели рисунков) и в слое из ионов кислорода (правый столбец (б, г)).

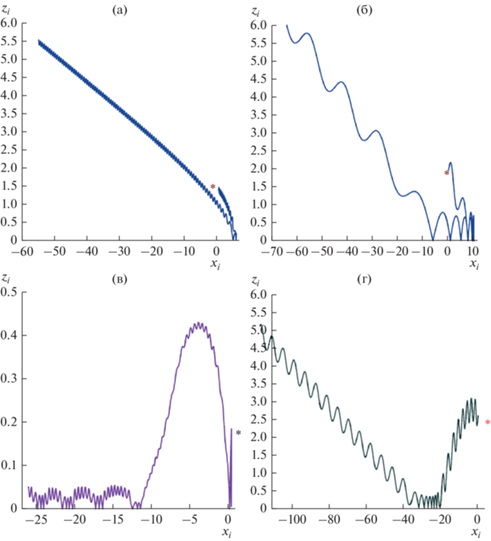
Из рис. 4 видно, что траектории горячих протонов и ионов кислорода в токовых слоях, поддерживаемых только одним сортом ионов, схожи, т.е. в обоих случаях полученные равновесия возникают в результате квазиадиабатической динамики горячих частиц. В то же время более холодная популяция образует вокруг ТС “шубу” из захваченных частиц, которые вклада в ток не вносят, но могут перераспределять профиль плотности тока, делая его расщепленным [25–27] – с двумя симметричными относительной нейтральной плоскости максимумами. Как видно на рис. 4а, б, горячие частицы в системе являются пролетными: за время моделирования протоны однократно взаимодействуют с токовым слоем, после чего уходят из области моделирования. В нейтральной плоскости такие частицы размагничиваются и переносят поперечный к магнитному полю ток в Y-направлении. В то же время холодные ионы, обладающие меньшей энергией, захватываются и движутся в окрестности ТС (рис. 1) вдоль Y. Благодаря дрейфу в скрещенных полях ${{[{\mathbf{E \times B}}]}_{x}}\sim {{E}_{y}}{{B}_{z}}$ они дополнительно смещаются в отрицательном по Х-направлении (вдоль хвоста магнитосферы по направлению к Земле). Многократно взаимодействуя с ТС, они могут перераспределять основной ток, формируя расщепленный профиль плотности тока [25, 26].

Были проведены расчеты конфигураций эволюционирующего ТС, где концентрации ионов ${{{\text{O}}}^{ + }}$ увеличивались в расчетах от ${{\nu }_{{ox}}} = 0.01$ до 1 с шагом 0.1, а далее – с шагом 1.0. Значения относительной температуры ${{T}_{{ox}}}$ были следующими в разных просчетах: ${{T}_{{ox}}} = 0.01,\,\,0.1,\,\,0.5,\,\,1.0,\,\,3.0$. Токовое квазиравновесное решение устанавливалось во всех конфигурациях при $k$ ~ 5000. Установлено, что при малых концентрациях тяжелых ионов в системе ${{\nu }_{{ox}}} = 0.01$ профили равновесных решений практически не зависят от температуры ионов кислорода: небольшие концентрации ионов кислорода не приводят к изменениям эволюции ТС по сравнению с чисто протонным слоем.

При увеличении концентрации кислорода в ТС эволюция токового слоя коренным образом изменяется. Профили всех величин турбулизуются, становятся зашумленными, а процесс вычислений может досрочно обрываться в результате сильных численных шумов. Так, например, при ${{T}_{{ox}}}$ = 0.5 и ${{\nu }_{{ox}}}$ = 0.3 расчеты прекращаются уже на шаге по времени $k = 600$. Затем с увеличением ${{\nu }_{{ox}}}$ время расчетов растет и восстанавливается до значений $k = 8000$ для всех температур ${{T}_{{ox}}}$ в диапазоне ${{\nu }_{{ox}}}\sim 2.0$ и выше. В качестве примера на рис. 5 показаны профили плотностей токов в двухкомпонентной плазме с параметрами ${{T}_{{ox}}}$ = = 0.5 и ${{\nu }_{{ox}}}$ = 2.0 в разные моменты времени: протонный ток (а), ток тяжелых ионов кислорода (б) и полный ток в системе (в). На рис. 5 (г), (д), (е) показаны соответствующие профили магнитного поля, а на рис. 5 (ж), (з), (и) – парциальные и полная плотности плазмы.

Рис. 5.

Зависимости характеристик эволюционирующего токового слоя от времени при ${{\nu }_{{ox}}} = 2.0$ и ${{T}_{{ox}}} = 0.5$. Левая панель рисунков (а, г, ж) относится к только протонным характеристикам в разные моменты времени эволюции системы, центральная (б, д, з) – к ионам кислорода, правая (в, е, и) – к полным характеристикам системы в целом. Три верхних рис. 5а, б, в показывают профили плотности тока, центральные рис. 5г, д, е – профили магнитного поля. На нижней панели рис. 5ж, з, и изображены профили плотности плазмы.

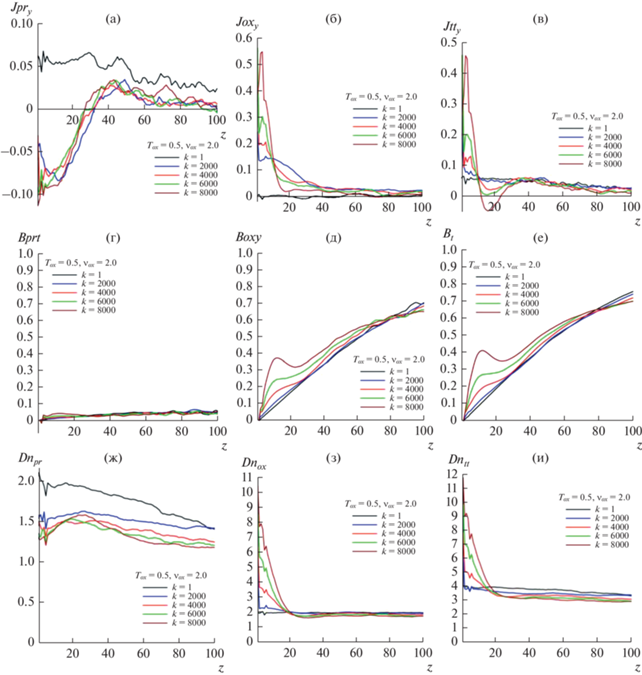
Как видно из сравнения рис. 2, 3 и 5, несмотря на то, что при значениях ${{\nu }_{{ox}}} \geqslant 2.0$ уже можно получить сходящиеся решения, некоторые профили ТС вблизи этой границы еще могут иметь небольшое зашумление. На рис. 5а локальная плотность тока протонов распределена по всей толщине ОМ до z = 100. При этом она отрицательна вблизи нейтральной плоскости и положительна на периферии ТС, а поддерживаемый протонами полный ток и соответствующее магнитное поле много меньше по сравнению с кислородными (ср. рис. 5а, г и 5б, д). Видно, что большая плотность полного тока ${{J}_{{tt}}}$ вблизи нейтральной области (рис. 5в) и магнитное поле ${{B}_{t}}$ поддерживаются за счет высокой плотности квазиадиабатических ионов кислорода в этой области (рис. 5и). При плотностях ионов кислорода ${{\nu }_{{ox}}} \leqslant 1.0$ тонкое токовое равновесие в модели не образуется вообще вследствие хаотизации движения как протонов, так и ионов кислорода.

Рассмотрим, как влияют в целом на эволюцию ТС относительные концентрации ионов кислорода ${{\nu }_{{ox}}} = 2,\,3,4,5,6$. На рис. 6 показаны зависимости установившихся самосогласованных профилей плотности Y-компоненты плотности тока, создаваемого протонами и ионами кислорода, и плотности частиц в слое от параметра относительного содержания ионов кислорода ${{\nu }_{{ox}}}$ при фиксированной относительной температуре ${{T}_{{ox}}} = 0.5$.

Рис. 6.

Зависимости квазиравновесных профилей основных характеристик ТС для разных относительных концентраций O⁺ ионов ${{\nu }_{{ox}}} = 2,\,\,3,\,\,4,\,\,5,\,\,6$ при одинаковой относительной температуре ${{T}_{{ox}}} = 0.5$. На первых двух горизонтальных панелях слева направо показаны профили плотности тока: протонный (а), ионный (б) и полный (в). Аналогичным образом показаны профили плотности плазмы (г, д, е). На нижней горизонтальной панели показаны слева направо: соответствующие верхним рисункам профили магнитного поля, электрического поля, а также эволюция профилей магнитного поля к равновесным решениям при ${{\nu }_{{ox}}} = \,3$ и 9. Видно, что при больших значениях ${{\nu }_{{ox}}} \geqslant 3$ овершут и локальные минимумы на профилях магнитного поля пропадают.

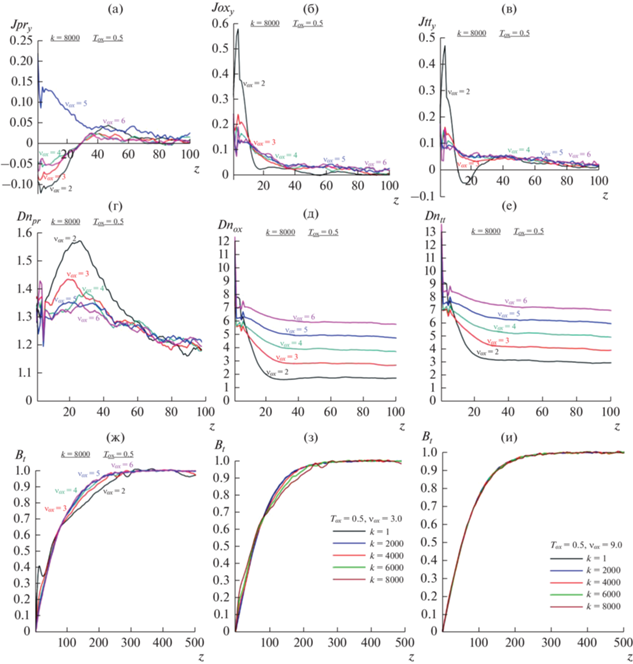
Как следует из рис. 6, в двухкомпонентной плазме плотность тока, поддерживаемого тяжелыми ионами, всегда положительна. На профилях плотности тока в исследуемом диапазоне максимум располагается не симметрично в нейтральной плоскости, а немного смещен по z координате. Это смещение может быть объяснено квазиадиабатическим характером движения ионов кислорода [2, 23]. Мы видим также, что увеличение параметра ${{\nu }_{{ox}}}$ приводит одновременно к утолщению ТС и уменьшению амплитуды плотности тока, равно как и плотности частиц. Профиль плотности тока протонов при всех значениях ${{\nu }_{{ox}}}$ имеет характер небольших осцилляций с выраженным отрицательным током в нейтральной плоскости и положительным – на краях ТС. Благодаря этому эффекту, результирующий профиль плотности тока в смешанной плазме оказывается расщепленным. Величина отрицательного минимума тока с ростом параметра ${{\nu }_{{ox}}}$ уменьшается (рис. 6а), область, занятая положительными протонным и кислородным токами, расширяется, а полная плотность тока при этом уменьшается (рис. 6в). Концентрация протонов вблизи нейтральной плоскости z = 0 с ростом ${{\nu }_{{ox}}}$ уменьшается (рис. 6г). Это связано с уменьшением времени их взаимодействия с токовым слоем. С ростом параметра ${{\nu }_{{ox}}}$ уменьшается также напряженность индуцированного электрического поля (на панелях не показано), эволюция профилей которого означает, что протонный слой как квазиравновесная структура не формируется вообще. Интересным эффектом является практически полное исчезновение отрицательного тока и, соответственно, овершута на профиле магнитного поля при ${{\nu }_{{ox}}} \geqslant {\text{3}}$, наблюдаемого на рис. 6е–к. Расчеты показывают, что при увеличении относительной температуры ионов кислорода растут интенсивность тока и толщина токового слоя за счет влияния обеих плазменных компонент. При этом концентрации частиц в области ТС также увеличиваются

На рис. 7 показаны характерные траектории движения некоторых выбранных частиц в области моделирования, полученные в установившемся токовом слое в двухкомпонентной плазме при параметрах ${{T}_{{ox}}} = 0.05$, ${{\nu }_{{ox}}} = 1$.

Рис. 7.

Пример характерных траекторий движения: (а) горячего протона; (б) холодного “фонового” протона; (в) иона кислорода в токовом слое в двухкомпонентной плазме во время формирования квазистационарной конфигурации ТС. Звездочками отмечено начало движения ионов.

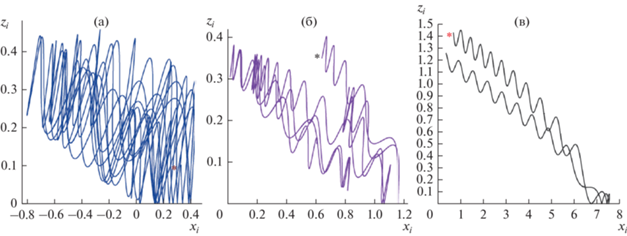
Как горячие, так и более холодные протоны движутся по хаотическим, захваченным вблизи слоя траекториям, они испытывают сильное рассеяние по питч-углам после каждого выхода из токового слоя. Это происходит вследствие больших скачков квазиадиабатического инварианта ${{I}_{z}}$ (аналога магнитного момента). Более холодный протон несколько раз отражается в окрестности ТС на разных расстояниях z от нейтральной плоскости и снова возвращается к ней. Как обсуждалось выше, популяция захваченных протонов, хотя и несет нулевой полный ток, может локально его перераспределять, расщепляя положительный максимум и смещая локальные максимумы к периферии, что мы наблюдаем на рис. 6в. Таким образом, в смешанной двухкомпонентной плазме именно протоны, траектории которых показаны на рис. 7a, б, оказываются источниками отрицательного тока на рис. 5a и 6a.

В отличие от протонов, ионы кислорода в рассматриваемой системе являются квазиадиабатическими носителями тока. На рис. 7в видно, что частица движется по спирали вдоль магнитных силовых линий по направлению к нейтральной плоскости z = 0, где она размагничивается и совершает несколько вертикальных колебаний (cм. также рис. 1). Затем частица замагничивается и уходит от нейтральной области – именно пролетные частицы переносят ток в моделируемом ТТС. Отсюда следует, что в двухкомпонентной плазме как протоны, так и ионы кислорода могут приводить к формированию тонкой токовой конфигурации. В результате утоньшения токового слоя в плазме, состоящей из нескольких компонент, они могут быть единственными носителями тока в ТТС.

При наличии в плазме тяжелых ионов кислорода O⁺ эволюция токового слоя зависит от их концентрации в системе. В небольших концентрациях их влияние на эволюцию незаметно, но при дальнейшем увеличении происходит хаотизация всей системы: траекторий частиц, динамики магнитного и электрического полей, в результате чего токовое равновесие не образуется вообще. При ${{\nu }_{{ox}}}\sim 2.0$ токовое равновесие с ТТС, в котором доминируют ионы кислорода, снова формируется, причем утоньшение слоя является быстрым процессом. Поскольку толщина образуемого ТС велика по сравнению с радиусом гировращения протонов, последние хаотизируются, захватываясь в окрестности ТС. Этот захват сопровождается сильными колебаниями электромагнитных полей, при которых образование вложенного протонного ТС становится невозможным. В результате подобной динамики может образовываться токовый слой с тяжелыми ионами – единственными носителями плотности тока. Данный результат находится в согласии с недавней работой [37], где был получен аналогичный результат, но причины его не были исследованы.

ЗАКЛЮЧЕНИЕ

В настоящей работе построена численная модель эволюции токового слоя, состоящего из протонов и ионов кислорода, в результате которой он утоньшается под действием индукционного электрического поля и соответствующего конвективного движения частиц в направлении нейтрального слоя. В начальном состоянии моделируемая система представляет собой достаточно толстый (по сравнению с гирорадиусами частиц) токовый слой с тангенциальной магнитной компонентой, заданной аналитически согласно модели Харриса [11]. Этот слой при моделировании задается вложенным в более холодную фоновую плазму. В начальный момент времени в системе включается постоянная поперечная к слою магнитная компонента, после чего потоки плазмы начинают распространяться от периферии системы к центру. В результате эволюции ТС самосогласованно утоньшается [38]. Достигая нейтральной плоскости, частицы размагничиваются и переносят электрический ток в поперечном к магнитному полю направлении. Сжатие токового слоя происходит до некоторой предельно малой толщины, после чего его эволюция прекращается.

Данная модель позволяет исследовать процессы сжатия токового слоя хвоста магнитосферы Земли (а также других планет солнечной системы) во время суббурь — крупномасштабных магнитосферных возмущений, когда пересоединенные на дневной стороне магнитосферы магнитные силовые линии перебрасываются в хвост, и магнитный поток в этой области растет. Спутниковые исследования выявили, что в начале магнитных суббурь в хвост из ионосферы поступают потоки холодных ионосферных ионов, концентрация которых может оказаться достаточно большой, сопоставимой с концентрацией протонов. Поступление больших количеств тяжелых ионов в токовый слой магнитосферного хвоста может кардинально менять картину распределения токов в магнитосфере и их устойчивость [19, 20, 33, 37–40]. Изучение структуры и устойчивости образовавшегося нового токового равновесия является важной задачей в исследованиях магнитосферных процессов.

Образующийся ТТС обладает рядом новых свойств по сравнению с исходным “толстым” состоянием [10]. Это новый тип плазменного равновесия. Проведено исследование зависимости формирования этого равновесия от параметров поступающих ионов кислорода: ${{\nu }_{{ox}}}$ – относительной концентрации тяжелых ионов и их относительной температуры ${{T}_{{ox}}}$. Выполнен траекторный анализ движения каждого сорта частиц, участвующих в формировании токового слоя. В рамках рассмотренной численной модели показано:

1) в однокомпонентной плазме, состоящей только из протонов или из ионов кислорода, под действием эволюционирующих электрического и магнитного полей может сформироваться тонкий токовый слой. Носителями тока в таком слое являются, соответственно, протоны или тяжелые ионы на квазиадиабатических орбитах. Вокруг токового слоя образуется широкая область, занятная квазизахваченными частицами, которые не являются носителями тока, но могут его перераспределять, образуя конфигурацию с двумя локальными максимумами плотности тока на периферии;

2) температура ионов кислорода слабо влияет на структуру образующегося ТТС, приводя к его незначительному утолщению;

3) при незначительных относительных количествах ионов кислорода в системе (от 0.01 до примерно 0.1 от концентрации протонов) они не оказывают влияния на формирующийся протонный ТТС;

4) при относительных концентрациях ионов кислорода в системе $0.2 < {{\nu }_{{ox}}} \leqslant 2.0$ от концентрации протонов тонкий токовый слой не образуется из-за сильных флуктуаций в системе. Появление флуктуаций, возможно, связано с большой разностью скоростей движения частиц разных сортов, которая может приводить к флуктуациям концентраций соответствующих частиц в плазме, а, следовательно, и электромагнитных полей.

5) при значениях ${{\nu }_{{ox}}}\sim 2.0$ и более в системе образуется ТТС, основными носителями тока в котором являются тяжелые однозарядные ионы кислорода. При этом протоны не образуют вложенный токовый слой, а захватываются в окрестности ТТС и вносят локальный отрицательный вклад в ток в центральной плоскости ТС, способствуя формированию расщепленного профиля плотности тока.

Анализ траекторий заряженных частиц и развития во времени профилей магнитного и электрического полей показывает, что, в зависимости от параметров модели ТТС формируется горячими протонами или ионами кислорода на квазиадиабатических орбитах. В рассматриваемых условиях, при разных параметрах модели, только одна из плазменных популяций становится носителем тока. При малой концентрации ионов O⁺ ток поддерживается протонами, при большой концентрации – ионами O⁺, в то время как протоны демонстрируют хаотическое поведение с сильным питч-угловым рассеянием; в большинстве своем являются захваченными частицами. Возможно, что формирование многомасштабной токовой конфигурации не может произойти из-за конкуренции носителей тока: тяжелые ионы на квазиадиабатических орбитах доминируют в формировании токового слоя в силу больших массы и гирорадиусов. Им требуется меньше времени на формирование ТТС. В кислородном более широком токовом слое протоны преимущественно переходят на захваченные орбиты, а их вклад в полный ток близок к нулю.

Надо отметить, что в настоящей работе модельные вычисления были определенным образом ограничены вычислительными ресурсами, поэтому авторы далеко не исчерпали все возможности исследования системы в широком диапазоне всех ее параметров и возможностей моделирования, в частности, задания начального состояния системы, которая эволюционирует к “тонкому” токовому равновесию. В рассмотренных условиях ТТС не приобретает свойства пространственной многомасштабности и вложенности, которое многократно было отмечено при многокомпонентном составе плазмы в хвосте магнитосферы и получено в аналитических моделях (например, в [2]). Настоящие результаты позволяют объяснить наблюдения некоторых одномасштабных токовых конфигураций в многокомпонентной плазме магнитосферного хвоста [17, 18]. Но в то же время условия, при которых происходит формирование многомасштабных токовых конфигураций [14, 10, 15–18, 20, 22, 25, 30, 33, 37 ], вызывают большой интерес. Их исследование, несомненно, будет продолжено в рамках наших численных моделей с учетом нестационарных процессов в магнитосферной плазме.

Авторы благодарят В.В. Калегаева и И.И. Алексеева (НИИЯФ МГУ) за внимание к работе и полезные обсуждения.