Космические исследования, 2023, T. 61, № 3, стр. 189-201

ВВЕДЕНИЕ

Магнитосфера Меркурия изучалась при помощи миссии Mariner 10 [1] и MESSENGER (англ. MErcurySurface, SpaceENvironment, GEochemistryandRanging), в результате чего было определено значение внутреннего дипольного момента планеты, составляющее 2.19 · 10¹⁸ А м² [2], что гораздо меньше, чем у Земли. Этот факт, вместе с гораздо более сильным динамическим давлением солнечного ветра на орбите Меркурия (большая полуось орбиты составляет 0.38 а.е.), приводит к возникновению небольшой магнитосферы с расстоянием до подсолнечной точки в 1.45 R_M, где R_M = 2438 км — радиус планеты [3]. Внутренний диполь Меркурия почти совпадает с осью вращения, однако северный магнитный полюс находится на южном планетографическом полюсе планеты [4, 5]. Миниатюрность магнитосферы Меркурия (примерно в 10–12 раз меньше земной магнитосферы) дает нам возможность за сравнительно короткое время собрать большой массив данных, содержащих пересечения космическим аппаратом характерных токовых слоев (скачков вектора магнитного поля) – головной ударной волны и магнитопаузы, которые формируют переходный слой между невозмущенным потоком солнечного ветра и магнитосферой Меркурия. За четыре года (2011–2015) работы на орбите спутника MESSENGER совершил около 4000 витков вокруг планеты и практически на каждом витке его магнитометр дважды фиксировал пересечения как магнитопаузы, так и головной ударной волны. На Земле для того, чтобы собрать такое же количество данных с одного КА потребовалось бы почти полвека.

Под термином пересечение космическим аппаратом бесстолкновительного МГД-разрыва мы понимаем не единичный резкий поворот вектора магнитного поля, а множественные резкие вариации вектора магнитного поля, которые связаны как со смещениями магнитопаузы или головной ударной волны как целого при изменении параметров набегающего потока солнечного ветра, так и с присутствием большого набора колебаний в окрестности разрыва, где происходит релаксация многочисленных локальных плазменных неустойчивостей, которые наблюдаются в этой области. Наша задача – выделить относительно регулярную крупномасштабную структуру этих токовых слоев, которая в свою очередь позволит в дальнейшем исследовать детальную динамику наблюдаемых нелинейных возмущений [6].

В работе [3] был предложен метод идентификации положения головной ударной волны и магнитопаузы у магнитосферы Меркурия для части витков, в результате чего были определены положения 1084 пересечений головной ударной волны и 1065 пересечений магнитопаузы. Впоследствии данный метод был обобщен в работе [7] на полный массив доступных данных. Из-за множественных пересечений головной ударной волны и магнитопаузы авторы исследований [3, 7 ] определяли внутренние и внешние пределы для положения поверхностей. В случаях, когда границу магнитопаузы нельзя было четко определить по повороту вектора направления магнитного поля или изменению дисперсии величины магнитного поля, границы выбирались таким образом, что внутренняя граница явно находится внутри магнитосферы, а внешняя — внутри переходного слоя магнитосферы.

Задача автоматического определения головной ударной волны и/или магнитопаузы и областей между ними по данным магнитометра космического аппарата (КА) не нова и решалась для случая Земли [8, 9] и Марса [10]. Метод в работе [9] основан на измерениях параметров плазмы и магнитного поля одновременно в межпланетном пространстве (на аппарате ACE, англ. AdvancedCompositionExplorer) и в изучаемых областях магнитосферы (на аппарате THEMIS). Нормируя величины параметров в точке положения КА на их значения в межпланетном пространстве, они выделяли три области: солнечный ветер, переходный слой и магнитосфера. При этом головная ударная волна отделяет солнечный ветер от переходного слоя, а магнитопауза выступает границей магнитосферы. Задавая пороговые значения выбранного параметра для каждой из областей, можно определить, где находится КА в данный промежуток времени. Результаты работы предложенного метода затем сравнивались с результатами ручной обработки данных. В работе [10] были разработаны два простых алгоритма для определения положения головной ударной волны по данным, полученным в окрестности Марса. В первом подходе авторы определяли местонахождение аппарата относительно усредненного для многих витков положения головной ударной волны в форме конического сечения. Во втором – добавили данные магнитометра для улучшения работы первого метода. Так как магнитное поле в межпланетном пространстве меньше величины магнитного поля в переходном слое, а также обладает меньшими флуктуациями, используя два пороговых значения для магнитного поля и величины флуктуаций можно определить области пересечения головной ударной волны. Данный метод представляется недостаточно надежным ввиду ручного задания пороговых значений. Можно было бы повысить уровень достоверности, к примеру, путем анализа степени усиления магнитного поля на фронте головной ударной волны.

Цель нашей работы заключается в автоматической обработке массива данных, собранного с помощью КА MESSENGER, для поиска положения головной ударной волны и магнитопаузы магнитосферы Меркурия.

1. ИСПОЛЬЗУЕМЫЕ ДАННЫЕ И ИХ ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА

Анализируются данные по магнитному полю Меркурия с разрешением 1 с и 1 мин, представленные в системе координат MSO (MESSENGERSolarOrbiter), которые были получены при помощи магнитометра КА MESSENGER [11]. В системе MSO ось x направлена на Солнце, ось z сонаправлена с осью вращения Меркурия и имеет положительное направление на север, ось y имеет положительное направление на утро и дополняет правую тройку векторов. Центр системы координат является географическим центром планеты. Исходный массив с данными магнитометра, предоставленный NASA Jet Propulsion Laboratory (по адресу https://pds-ppi.igpp.ucla.edu/search/ view/?f=yes&id=pds://PPI/mess-mag-calibrated) был преобразован для предварительной фильтрации шума и ошибок в данных:

• удалены сигналы калибровки магнитометра;

• измерения координат и магнитного поля объединены в единый файл;

• значения координат в системе MSO пересчитаны с учетом того, что направление на Солнце не совпадает с направлением набегающего солнечного ветра (который для простоты считается направленным радиально от Солнца) из-за достаточно большой орбитальной скорости Меркурия;

• набор данных разделен на файлы по номерам витков, каждый виток центрирован на перигермии;

• данные для ряда частично записанных витков (непригодные к использованию в данной задаче) были удалены.

• полученный итоговый набор данных доступен по ссылке: https://zenodo.org/record/6417492#. Yo4PYqhBzIX.

2. ОПИСАНИЕ ИСПОЛЬЗУЕМОГО МЕТОДА

Мы следуем работам [3, 7] и нашей цель состоит в определении начала и конца каждого пересечения головной ударной волны и магнитопаузы, но уже при помощи автоматических методов. В указанных работах границы головной ударной волны и магнитопаузы определялись вручную визуальным анализом данных магнитометра. Пересечение головной ударной волны идентифицируется по первому резкому возрастанию величины модуля магнитного поля и/или по резкому возрастанию величины ${{\sigma }_{{\left| B \right|}}} = \sqrt {\sigma _{{{{B}_{x}}}}^{2} + \sigma _{{{{B}_{y}}}}^{2} + \sigma _{{{{B}_{z}}}}^{2}} ,$ где ${{\sigma }_{{{{B}_{i}}}}}$ – стандартное отклонение компоненты магнитного поля B_i за 1 с. Пересечения магнитопаузы авторы указанных работ определяли по значительному изменению направления вектора магнитного поля (одновременное резкое изменение двух или трех компонент магнитного поля), либо по возрастанию величины σ_|B|. Если задать определенный пороговый уровень для σ_|B|, можно автоматически выделить случаи сильных вариаций, связанных как раз с пересечениями границ. Другим признаком приближения КА к границе может служить возрастание второй производной величины |B| за 1 с. Однако в зависимости от состояния магнитосферы при большом количестве флуктуаций нахождение порогового уровня может быть затруднено. Данный метод работает лишь при определении пересечения квазиперпендикулярной головной ударной волны, когда происходит резкий скачок магнитного поля относительно уровня межпланетного магнитного поля (ММП). Пример данных магнитометра, амплитуды σ_|B| и величины второй производной модуля |B| для одного из витков КА приведен на рис. 1.

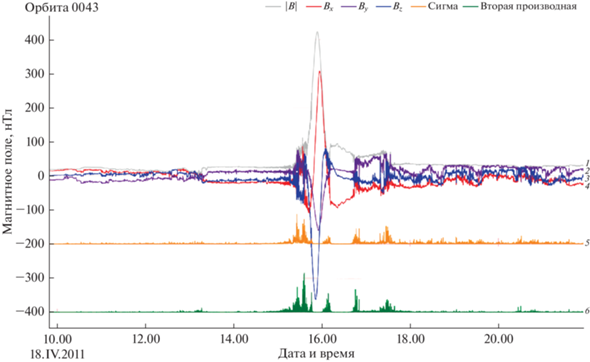
Рис. 1.

Пример данных магнитометра для 43-го витка КА MESSENGER. Серым показано значение модуля магнитного поля (1), три компоненты магнитного поля ${{B}_{x}}$ – красным (4), ${{B}_{y}}$ – фиолетовым (2) и ${{B}_{z}}$ – синим (3). Также показаны оранжевым величина ${{\sigma }_{{\left| B \right|}}}$ (5) и зеленым величина второй производной (6) модуля магнитного поля.

2.1. Определение пересечений головной ударной волны

В зависимости от наклона вектора ММП к поверхности головной ударной волны в данной точке, можно выделить два главных типа головной ударной волны: параллельная (θ_Bn = 0°) и перпендикулярная (θ_Bn = 90°), где θ_Bn – угол между вектором ММП в данной точке и нормалью к поверхности ударной волны. Также говорят о квазиперпендикулярных или квазипараллельных головных ударных волнах, когда θ_Bn не сильно отклоняется от перпендикулярного и параллельного направления соответственно. Типичный профиль магнитограммы при пересечении перпендикулярной ударной волны состоит из областей с меньшей и большей величиной магнитного поля, соединенных крутым скачком в точке пересечения (рис. 2). Перпендикулярные ударные волны перед скачком обычно имеют область, называемую подножием, где магнитное поле возрастает постепенно. Кроме того, уровень магнитного поля в окрестности ударной волны обычно превышает напряженность магнитного поля в области переходного слоя за головной ударной волной. Случай квазипараллельного магнитного поля представляется более сложным, при рассмотрении магнитограммы пересечение головной ударной волны можно обозначить как начало сильных вариаций по |B|, однако в некоторых случаях определить их точное положение затруднительно (рис. 2).

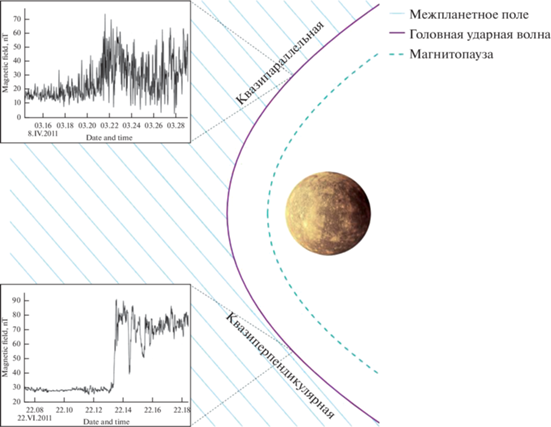
Рис. 2.

Случаи квазипараллельной и квазиперпендикулярной головной ударной волны и соответствующие им магнитограммы для Меркурия и КА MESSENGER. Межпланетное магнитное поле показано косыми линиями, головная ударная волна – сплошной линией, магнитопауза – прерывистой линией.

Для поиска пересечений головной ударной волны на временном ряду необходимо выделить какие-либо особенные точки, в данном случае ими могут служить точки изменения модуля магнитного поля либо его компонент. Согласно работам [3, 7], квазиперпендикулярная головная ударная волна определяется по резкому возрастанию модуля магнитного поля. Такое возрастание достаточно четко наблюдается на подавляющем большинстве витков. Этот случай достаточно просто определять с помощью самых простых методов, в частности, по резкому возрастанию второй производной магнитного поля. Случай квазипараллельной головной ударной волны более сложный, поэтому в итоге для определения пересечений мы использовали библиотеку Kats для анализа данных временных рядов для языка программирования Python (https://github.com/facebookresearch/Kats). Она была разработана сравнительно недавно — первый релиз состоялся 17 июня 2021 г. Ее можно считать первой комплексной библиотекой на языке Python для общего анализа временных рядов, которая предоставляет как классические, так и продвинутые методы моделирования. Библиотека Kats содержит набор алгоритмов и модулей для различных областей анализа временных рядов, из которых нас интересует обнаружение особенностей во временном ряду, в частности модуль RobustStatDetector. Данный алгоритм сглаживает временной ряд с помощью скользящего среднего, рассчитывает разность между значениями сглаженного временного ряда по заданному количеству точек, вычисляет стандартизированную оценку¹¹ и p-значения²² для ранее рассчитанных разностей. Результатом работы метода становится набор точек, в которых p-значение меньше заранее установленного порога. Этот алгоритм определения точек способен фиксировать несколько точек изменения за один прогон по массиву данных. Для того чтобы уменьшить амплитуду максимума магнитного поля в рассматриваемом временном ряду, вычитаем из измеренного вектора магнитного поля поле планетарного диполя Меркурия. Поскольку все орбиты примерно симметричны относительно точки минимального сближения с планетой (перигермия), для удобства обработки делим каждый виток на нисходящую и восходящую части. Кроме того, прежде чем перейти к анализу разрыва, следует исключить стационарные источники поля, а вклад диполя по величине на порядок больше, чем среднее поле в межпланетном пространстве (рис. 1).

Задавая на вход: 1) размер окна скользящего среднего (smoothing_windowsize), 2) количество точек для сравнения (comparison_window) и 3) статистический порог p-значения (p_value_cutoff), в результате работы модуля RobustStatDetector получаем интересующие нас точки, в которых p-значение меньше установленного порога, т.е. изменения велики. В случае если число точек изменения оказывается большим, мы меняем значения входных параметров и повторяем расчет. Полученные точки проходят отсев, исходя из их удаления от прогнозируемого положения разрыва, характера изменения модуля поля в окрестности разрыва (средней величины магнитного поле по обе стороны от разрыва), а также путем анализа тренда изменения магнитного поля в данной точке (восходящий/нисходящий) при помощи модуля MKDetector библиотеки Kats. Для выбранных точек проводится проверка разности значений модуля поля в каждой из точек для их группировки в облако точек, таким образом происходит определение начала и конца зоны пересечения (первая и последняя точка в облаке) области головной ударной волны КА для восходящей и нисходящей частей витка. Пример работы данного метода показан на рис. 3 для случая квазиперпендикулярного случая и рис. 4 для квазипараллельного случая. Из-за постоянно меняющихся условий в межпланетном пространстве положение головной ударной волны в пространстве может довольно быстро изменяться, поэтому могут наблюдаться множественные пересечения космическим аппаратом головной ударной волны. Для квазиперпендикулярной ударной волны, как и для квазипараллельного случая, как правило, фиксируется несколько точек изменения (рис. 3).

Рис. 3.

Пересечение квазиперпендикулярной головной ударной волны Меркурия для витка 1372. Черной линией показан модуль магнитного поля по данным магнитометра, красные точки – выявленные при помощи алгоритма точки изменения, вертикальные линии – определенные по алгоритму итоговые начало и конец пересечения головной ударной волны.

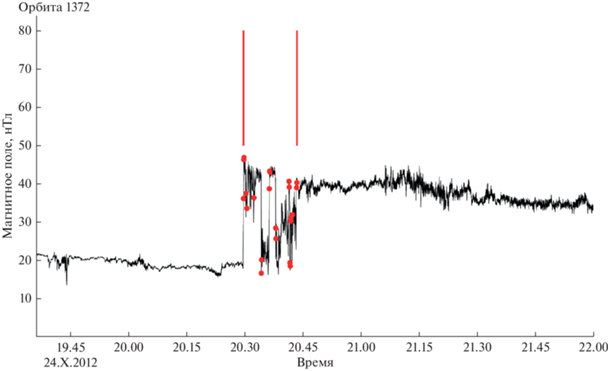
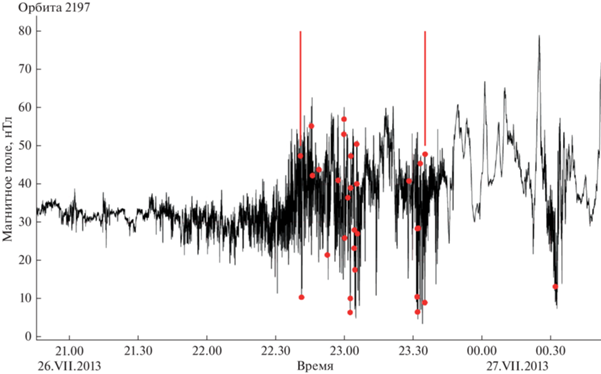
Рис. 4.

Пересечение квазипараллельной головной ударной волны Меркурия для витка 2197. Черной линией показан модуль магнитного поля по данным магнитометра, красные точки – выявленные при помощи алгоритма точки изменения, вертикальные линии – определенные по алгоритму итоговые начало и конец пересечения головной ударной волны.

Зная величину ММП (до начала пересечения головной ударной волны), можно путем последовательных сравнений величин магнитного поля для каждой точки найти момент, когда она стала достаточно большой для того, чтобы считаться пересечением головной ударной волны. Как видно из рис. 3 начало пересечения головной ударной волны и затем множественные пересечения определяются хорошо.

На рис. 4 показаны точки, выделенные красным цветом, которые были выявлены при помощи работы алгоритма. Они определяют моменты, в которые магнитное поле изменялось сильнее всего. Учитывая небольшую разность времени между каждой такой точкой, а также отсутствие уменьшения модуля магнитного поля до значений области ММП, алгоритм достаточно хорошо определяет область пересечения головной ударной волны. Начало пересечения этой области, как видно из рисунка, можно считать определенным хорошо, так как в данной точке заметно сильное возрастание величины модуля магнитного поля. Вместе с тем конец пересечения головной ударной волны определить сложнее из-за гораздо более масштабных флуктуаций. В результате работы алгоритма конец пересечения головной ударной волны определен в 23.30, так как количество флуктуаций после этого времени заметно уменьшается.

Рис. 5.

Пример работы алгоритма по определению пересечений магнитопаузы в невозмущенной магнитосфере. Синей кривой для сравнения показан модуль полного поля без вычета планетарного диполя (1). Красным, зеленым и фиолетовым соответственно показаны ${{B}_{x}}$ (3), ${{B}_{y}}$ (2) и ${{B}_{z}}$ (4) компоненты магнитного поля с вычтенным значением компонент дипольного поля. Красными вертикальными линиями внизу показаны метки, полученные в результате обработки автоматическим методом, черными вверху – после обработки данных вручную [7]. Видно, что исключение дипольного поля уменьшает амплитуду рассматриваемого временного ряда больше чем, в четыре раза – от 380 нТл для исходного поля, до <90 нТл для ΔB = |B_exp – B_dip|. Кроме того, на синей кривой четко видно положение токового слоя хвоста, где регистрируется минимальное значение поля порядка нескольких нТл.

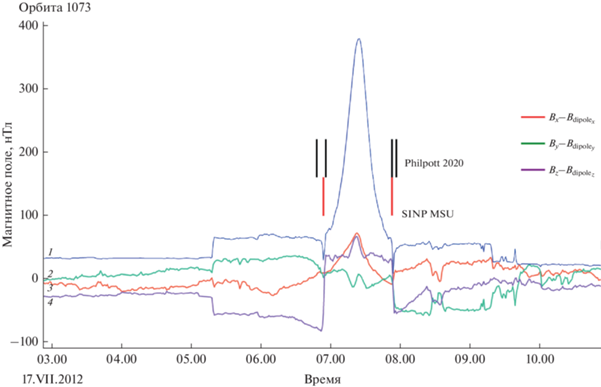
2.2. Определение пересечений магнитопаузы

Пересечения магнитопаузы определить значительно сложнее, чем пересечения головной ударной волны. После пересечения головной ударной волны космический аппарат попадает в область переходного слоя, где наблюдаются значительные флуктуации поля вплоть до пересечения магнитопаузы. При пересечении магнитопаузы направление магнитного поля поворачивается в сторону от направления ММП к направлению внутреннего планетарного поля, после него флуктуации переходного слоя пропадают, и наблюдается гладкое поле планеты. Само пересечение магнитопаузы легче определить не по модулю магнитного поля, а по анализу компонент, так как одна/несколько из компонент при пересечении испытывает сильный скачок (возникающий из-за поворота вектора магнитного поля в пространстве при переходе из переходного слоя в магнитосферу). Также при этом возрастают флуктуации магнитного поля, проявляющиеся в росте второй производной отдельных компонент магнитного поля. В случае возмущенной магнитосферы в результате сильных флуктуаций смена знака одной из компонент может происходить значительное число раз, поэтому для усреднения квазипериодических флуктуаций мы переходим к минутным данным и в результате фиксируем единственное пересечение магнитопаузы (рис. 6).

Рис. 6.

Пример работы алгоритма по определению пересечений магнитопаузы в возмущенной магнитосфере. Синей кривой для сравнения показан модуль полного поля без вычета планетарного диполя (1). Красным, зеленым и фиолетовым соответственно показаны ${{B}_{x}}$ (4), ${{B}_{y}}$ (3) и ${{B}_{z}}$ (2) компоненты магнитного поля с вычтенным значением компонент дипольного поля. Красными вертикальными линиями внизу показаны метки, полученные в результате обработки автоматическим методом, черными вверху — после обработки данных вручную [7].

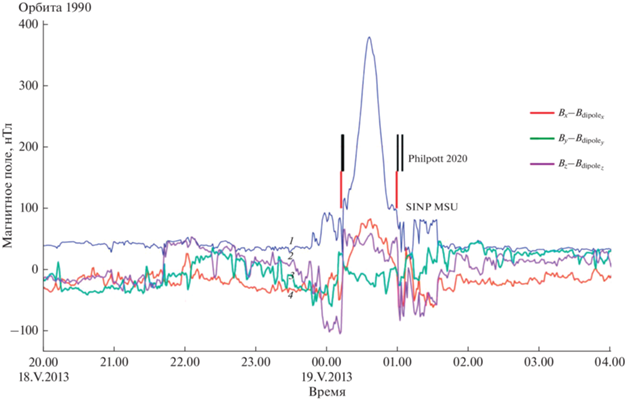
Алгоритм поиска пересечений магнитопаузы отличается от алгоритма поиска пересечений головной ударной волны. На усредненных за минуту данных происходит поиск точек, наиболее близких к точке равенства нулю разности одной из компонент магнитного поля и такой же компонентой планетарного поля. Затем, при помощи библиотеки Ruptures (https://github.com/deepcharles/ruptures) для языка программирования Python для каждой из найденных точек проводится поиск разности значений компонент в двух ближайших к рассматриваемой точках и таким образом определяется поворот вектора магнитного поля. Далее проводится проверка на количество отобранных точек и оценка расстояния между ними. Далее при помощи оценки тренда изменения компонент магнитного поля отсеиваются пересечения токового слоя хвоста магнитосферы (при пересечении токового слоя хвоста x компонента магнитного поля изменяет свой знак, а y и z остаются почти неизменными). Пример работы алгоритма показан на рис. 5. Так как пересечение слоя магнитопаузы длится меньше одной минуты даже в случае возмущенной магнитосферы (рис. 6), на усредненных за минуту данных будет определяться единственная точка пересечения магнитопаузы, в отличие от пересечений головной ударной волны, где для секундных данных определяются начало и конец отрезка пересечения.

Для более точного поиска пересечений используем физические ограничения и соотношения. Зная связь между расстоянием до подсолнечной точки головной ударной волны R_bs и расстоянием до подсолнечной точки магнитопаузы R_ss, которое для Меркурия имеет вид: R_bs = = 1.45R_ss [12], можно ограничить область, в которой необходимо искать соответствующую точку изменения, наложив условие на расстояние до диполя.

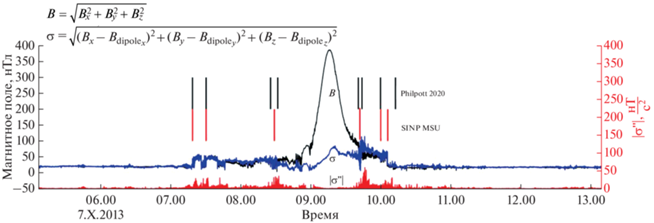
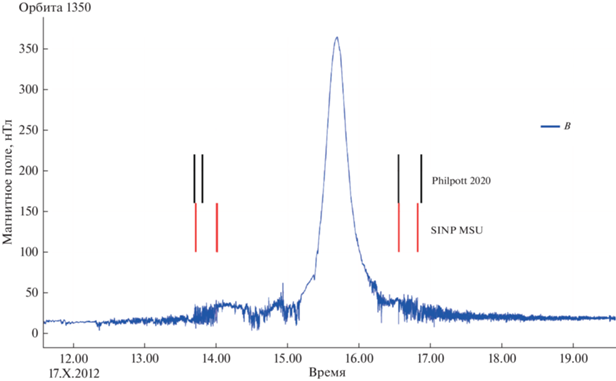
Приведем итоговый пример обработки для всего витка, он показан на рис. 7. На рисунке представлен модуль магнитного поля, измеренный на КА MESSENGER, величина модуля магнитного поля за вычетом поля внутреннего диполя, а также вторая производная магнитного поля. Результаты работы алгоритма хорошо совпадают с результатами ручной обработки данных из работы [7].

Рис. 7.

Пример работы алгоритма для витка 2402 КА MESSENGER. Черная линия показывает измерения модуля магнитного поля на КА MESSENGER, синяя – модуль магнитного поля за вычетом поля диполя, красная линия – вторая производная магнитного поля. Красными вертикальными линиями внизу показаны метки, полученные в результате обработки автоматическим методом, черными – после обработки данных вручную [7]. Модуль полного поля показан для сравнения.

3. СРАВНЕНИЕ РЕЗУЛЬТАТОВ РАБОТЫ АЛГОРИТМА С ПРЕДЫДУЩИМИ РАБОТАМИ

Для того чтобы сравнить полученные нами метки с уже имеющимися метками [7], мы сравнили средние положения пересечений головной ударной волны (середины отрезков между началом и концом области ударной волны), полученные нами и работе [7]. Для магнитопаузы середину отрезка между первым и последним пересечением, найденным авторами исследования [7] сравнивали с точкой пересечения, найденной нами по описанному выше алгоритму. Под средним значением следует понимать точку между началом и концом пересечения токового слоя согласно магнитограмме, равноудаленную от начала и конца. Результаты сравнения представлены в виде гистограмм (рис. 8 и 9), где по оси y указано количество витков, а по оси x – разница во времени между метками разработанного алгоритма и работой [7] (в минутах).

Рис. 8.

Разница между временными метками, полученными в результате работы алгоритма по определению пересечения головной ударной волны и результатами [7], на (а) нисходящей части траектории и (б) восходящей части траектории.

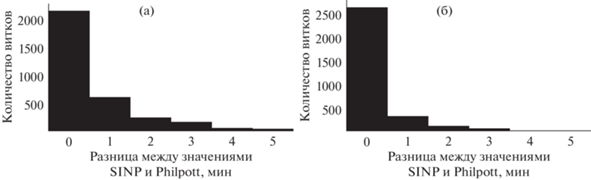
Рис. 9.

Разница между временными метками, полученными в результате работы алгоритма по определению пересечения магнитопаузы и результатами [7], на (а) нисходящей части траектории и (б) восходящей части траектории.

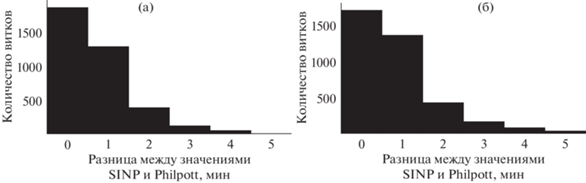
Как видно из рис. 8 и 9, разработанный нами алгоритм определяет пересечения магнитопаузы в пределах одной минуты от значений работы [7] в 83% случаев для магнитопаузы и в 87% для головной ударной волны, что составляет около 100 км.

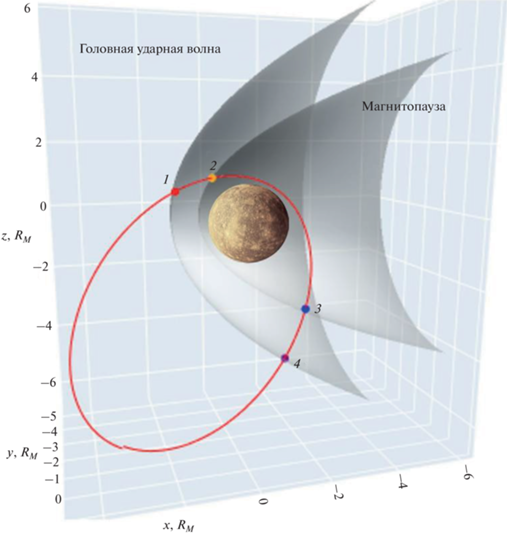
Также для иллюстрации точности результатов, полученных по предложенному методу, на рис. 10 показана траектория 38-го витка КА MESSENGER с найденными точками пересечений и параболоиды, описывающие головную ударную волну и магнитопаузу. Для простоты мы используем аксиально симметричные фигуры параболоидов вращения, оси которых сдвинутых относительно нуля по оси z на 0.2R_M – величину вертикального смещения диполя Меркурия относительно центра планеты.

Рис. 10.

Траектория 38-го витка КА MESSENGER вокруг Меркурия. Координаты выражены в радиусах Меркурия. Показаны средние положения головной ударной волны и магнитопаузы (прозрачно-серым) в приближении параболоида вращения. Красной линией показана траектория КА, красными (1) и фиолетовыми (4) точками обозначены точки пересечения головной ударной волны, оранжевым (2) и синим (3) – магнитопаузы. КА перемещается от красной точки к фиолетовой при своем движении по орбите.

4. ОБСУЖДЕНИЕ

Сравнение результатов работы нашего алгоритма с результатами, полученными в работе [7] показало, что среднее отклонение в 87% случаев меньше ларморовского радиуса протонов солнечного ветра. Ларморовский радиус для протонов со скоростью 400 км/с при средней величине ММП в 23 нТл составляет 180 км. КА MESSENGER, летящий со скоростью ~1.5 км/с преодолевает это расстояние за ~120 с. Большая часть расхождений определенных нами пересечений головной ударной волны с данными работы [7] лежит в пределах одного ларморовского радиуса (рис. 8). Среднее магнитное поле в переходном слое, рассчитанное как сумма измеренных полей на отрезках траектории КА MESSENGER между головной ударной волной и магнитопаузой, деленная на число использованных точек траектории, равно 51 нТл. Поле в переходном слое может быть довольно возмущенным и сильно отличаться от витка к витку. Ларморовский радиус протона с энергией 1 кэВ в поле 51 нТл составляет 89 км. Отношение средних величин магнитного поля в переходном слое B_msh к магнитному полю в межпланетном пространстве B_IMF, так называемый коэффициент сжатия на ударной волне, по нашим данным составляет 2.172, периодически изменяясь за четыре года работы КА от 0 до 5. Речь идет об отношении среднего поля на отрезке траектории внутри переходного слоя к полю выше по потоку от ударной волны, а не об отношении величины магнитного поля по обе стороны от разрыва. Это последнее отношение по законам магнитной гидродинамики должно быть меньше 4 и больше 1. Для сравнения, авторы работы [9] для магнитосферы Земли определили величину ${{{{B}_{{msh}}}} \mathord{\left/ {\vphantom {{{{B}_{{msh}}}} {{{B}_{{IMF}}}}}} \right. \kern-0em} {{{B}_{{IMF}}}}} \approx 4$ по данным КА THEMIS и ACE. Однако флуктуации внутри переходного слоя могут быть значительными, и полученное отношение может сильно отличаться от точки к точке.

При отражении части набегающих на головную ударную волну частиц солнечного ветра выше по потоку в зоне так называемого форшока формируются возмущения, регистрируемые магнитометром как периодические изменения вектора магнитного поля. Эти колебания хорошо видны на данных магнитометра для части витков. Разработанный алгоритм успешно справляется с обработкой форшока и не определяет в этой области точек пересечения разрыва (рис. 11).

Рис. 11.

Пример магнитограммы витка с форшоком. Видны значительные флуктуации перед пересечением головной ударной волны, определенной как в работе [7] (черные линии вверху), так и разработанным алгоритмом (красные линии внизу). Сплошной синей линией показан модуль величины измеренного магнитного поля вдоль витка.

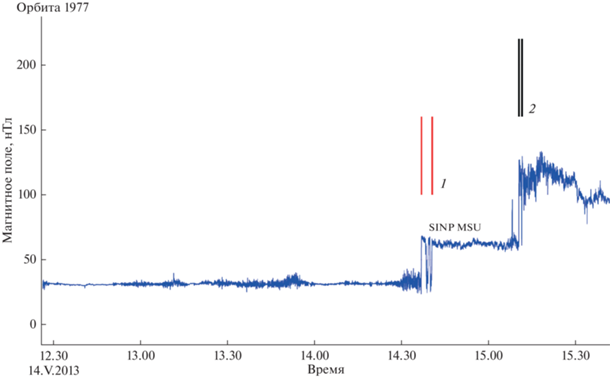
Для небольшой части витков, когда наш метод и точки исследования [7] сильно разнятся, как правило, реализуется необычный сценарий, связанный с экзотическими параметрами потока солнечного ветра. Например, на витке 1977 (рис. 12) разница между нашими метками и авторов [7] составляет чуть более получаса. При этом мы видим двойное пересечение головной ударной волны – аппарат пересек головную ударную волну около 14.35 и зашел в переходный слой. Затем в 15.10 КА догнала движущаяся быстрее первой вторая ударная волна, предположительно возникшая из-за резкого скачка параметров плазмы солнечного ветра. В результате в два раза возросло магнитное поле и плотность. Такие случаи требуют специального рассмотрения и должны быть исключены из массива, который подвергается автоматической обработке.

Рис. 12.

Пример двойного пересечения головной ударной волны в изменившихся условиях в межпланетном пространстве. Красным показаны границы пересечения, определенные в нашей работе (1), черным – границы пересечений, определенные вручную в работе [7] (2).

Повысить возможности разработанного алгоритма можно было бы при переходе к естественным координатам, когда одна из осей лежит в плоскости разрыва и ортогональна направлению тока, а другая перпендикулярна плоскости разрыва и изменение поля в этом направлении меньше, скачков по двум другим осям. Авторы работы [7] использовали этот метод определения минимальной вариации поля для нахождения направления нормали и выделении зоны так называемых каспов в месте разветвления магнитных потоков, выносимых в хвост магнитосферы, и замкнутых силовых линий, формирующих дневную магнитосферу. В нашем случае подобная предобработка с фиксацией нормали к фронту могла бы помочь заранее разделить случаи параллельной и перпендикулярной волны и затем выбрать необходимую методику точного определения пересечения. Однако эти вопросы лежат за пределами данной работы. По этой же причине – стремлению ограничить круг рассмотренных проблем, мы не использовали данные, полученные при помощи плазменного спектрометра на борту MESSENGER. Привлечение плазменных данных в нашем случае неоправданно усложняет задачу и требует применения других методик. Кроме того, угол поля зрения плазменного спектрометра составляет ~1.4 ср [3], что существенно усложняет анализ, делая его очень зависимым от правильного определения направления прибора.

ВЫВОДЫ

Разработан способ автоматической обработки массивов данных магнитометра на борту космического аппарата на примере КА MESSENGER, позволяющий путем выделения особенностей в данных (резких поворотов измеренного вектора поля или вариаций его величины), определять пересечения головной ударной волны и магнитопаузы магнитосферы. Этот способ даетнадежные результаты. Сопоставление с результатами ручной обработки данных работы [7] подтверждает работоспособность разработанного алгоритма и заметно ускоряет процедуру анализа. В некоторых случаях использование объективных критериев дало существенное уточнение результатов ручной обработки и привело к более точному определению положения рассматриваемой границы. Показано, что определение координат головной ударной волны по данным магнитометра КА в 87% случаев происходит с точностью до нескольких десятков километров, а магнитопаузы – в 83% витков. Таким образом, было показано, что определение головной ударной волны возможно только по данным магнитометра без использования данных плазменных измерений.

Координаты точек пересечения траектории КА с головной ударной волной и магнитопаузой можно использовать для определения положения подсолнечной точки и фиксации характерных размеров магнитосферы Меркурия. Это позволяет найти параметры трехмерных глобальных токовых систем, которые определяют границу между открытыми силовыми линиями, куда свободно проникают частицы, например от солнечной вспышки, и замкнутыми линиями, где возможен захват частиц.

Преимуществом данного метода выступает возможность обработки в автоматическом режиме больших объемов данных в короткие сроки. Данная задача актуальна в свете приближающегося выхода на орбиту вокруг Меркурия КА BepiColombo, запланированного на 2025 г. Эта миссия состоит из двух аппаратов, находящихся на полярных орбитах: один будет находиться на эллиптической орбите с периодом 9.3 ч и диапазоном высот 590–11 640 км (0.24–4.77R_M), а второй – на круговой орбите с периодом 2.3 ч. и диапазоном высот в 480–1500 км (0.20–0.61R_M). Таким образом, набор поступающих данных о состоянии магнитосферы Меркурия существенно возрастет.

Данная методика может применяться при анализе данных КА, работающих в окрестности других планеты Солнечной системы. В частности, она может быть использована для анализа данных пересечений космическими аппаратами токовых слоев в магнитосферах других планет, а также разрывов в солнечном ветре.

Работа выполнена при финансовой поддержке РФФИ (проект № 21-52-12025).

Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.