1. На главную
  2. Электронные версии
  3. Космические исследования
  4. T. 61, № 4, 2023

Космические исследования, 2023, T. 61, № 4, стр. 339-352

Исследование движения группы из четырех связанных космических аппаратов под управлением с использованием сил Лоренца

К. С. Чернов 1, *, Д. С. Иванов 1

1 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

* E-mail: chernow.kirill@gmail.com

Поступила в редакцию 10.02.2023
После доработки 10.02.2023
Принята к публикации 11.02.2023

Полный текст (PDF)

Аннотация

В работе рассматриваются четыре космических аппарата, соединенные друг с другом электродинамическими тросами, которые при математическом моделировании движения системы считаются жесткими. В магнитном поле Земли на проводники с током действуют силы Лоренца, с использованием которых производится управление движением центра масс системы и угловым движением. В работе разработан алгоритм расчета величин сил тока для остановки дрейфа центра масс тетраэдральной формации относительно опорной орбитальной системы координат на низкой околоземной орбите и для раскрутки относительно центра масс до постоянной угловой скорости. Проводится численное исследование времени достижения заданного движения в зависимости от максимально возможной силы тока и начальных условий.

ВВЕДЕНИЕ

Групповой полет спутников определяется как полет спутников, движущихся по близким относительным траекториям, которые могут управлять своим относительным положением и/или относительными скоростями, сохраняя близкие расстояния и решая общую задачу. В настоящее время наблюдается взрывное увеличение числа миссий группового полета вследствие миниатюризации космических аппаратов и значительно расширенного спектра решаемых задач по сравнению с миссиями с одиночным аппаратом. Согласно орбитальной динамике, расстояние между двумя аппаратами на околоземной орбите будет увеличиваться за счет действия возмущений естественных сил, даже если изначально относительная скорость равна нулю. Поэтому для сохранения близкого относительного расстояния требуется управление движением аппаратов в группе. Однако если на больших аппаратах для решения этой задачи могут использоваться бортовые двигатели, как, например, в работе [1], то на малых аппаратах за счет ограничений по массе, объему, энергии и стоимости таких двигателей может не оказаться. Поэтому получили развитие способы бестопливного управления относительным движением с использованием естественных сил, например, разницы действующих на аппараты аэродинамических сил [2], сил солнечного давления [3], магнитного взаимодействия [4], обмена импульса [5] или с использованием сил Лоренца на низких околоземных орбитах [6].

Заряженная частица, движущаяся с определенной скоростью относительно магнитного поля Земли, ускоряется в направлении, перпендикулярном вектору ее скорости и локальному вектору магнитного поля, за счет силы Лоренца [7]. Применение этой силы для управления групповым полетом космических аппаратов является относительно новым и потому малоизученным подходом. Первые работы о воздействии силы Лоренца на заряженные тела были выполнены Л. Шаффером и Дж. Бернсом, которые разработали модель, объясняющую влияние плазменного окружения на динамику заряженных пылевых частиц, вращающихся вокруг Юпитера и Сатурна [8]. Эти исследования доказали, что на орбитальное движение большое влияние оказывает сила Лоренца и что эта магнитная сила наряду с гравитационными эффектами, лунными возмущениями и солнечным давлением ответственна за существование щелей в кольцевых резонансах Юпитера и Сатурна. Эти работы представляют собой ценный вклад в проверку моделей, касающихся движения заряженных частиц, и демонстрацию того, что эффекты силы Лоренца приводят к некеплеровым орбитам.

После работы, выполненной Л. Шаффером и Дж. Бернсом, М. Пек провел серию исследований, в которых предлагалось использовать силу Лоренца для разработки бестопливного управления движением группы спутников. В статье [7] М. Пек представляет систему, получившую название Lorentz Augmented Orbit System (LAO), которая могла бы использовать этот эффект для управления орбитальным движением. Он также представляет широкий спектр систем LAO, которые могут быть применены для решения задач увода с орбиты Земли, компенсации аэродинамического сопротивления, управления групповым полетом, изменения наклонения орбиты. Действие силы Лоренца испытывает индивидуально каждый заряженный космический аппарат и, в отличие от кулоновской силы, сила Лоренца не является результатом взаимодействия двух заряженных космических аппаратов. Вместо этого эта сила вызвана магнитным взаимодействием между относительной скоростью заряженного космического корабля и магнитным полем окружающей среды. И направление, и величина силы Лоренца (представляющие разные значения для разных орбитальных положений и, следовательно, чувствительные к геометрии орбиты) зависят от орбитального движения спутника, поскольку ее направление всегда перпендикулярно скорости космического корабля и локальному вектору магнитного поля. В работе [7] М. Пек также представляет возможный дизайн системы LAO. Хотя конфигурации системы LAO не предполагают использования электродинамических тросов, физика работы обоих устройств аналогична. Для LAO тело выступает в роли точечного заряда, движущегося со скоростью тысяч метров в секунду относительно магнитного поля планеты. Движущийся заряд представляет собой ток, аналогичный тому, который действует в электродинамических тросах [9].

Сила, действующая на проводник с током в магнитном поле, в русскоязычной литературе называется силой Ампера, однако в англоязычной она также называется силой Лоренца. В дальнейшем в работе под силой Лоренца будет пониматься именно сила, действующая на проводник с током. В литературе встречается много работ, посвященных динамике орбитальных систем с электродинамическими тросами. В работе [10] предложена схема развертывания и поддержания созвездия аппаратов с электродинамическими тросами. Проблема колебаний электродинамических тросов, расположенных вдоль местной вертикали, затронута в работе [11], где предложена схема асинхронного управления с задержкой для уменьшения амплитуды колебаний. Для обеспечения натянутого состояния троса в статье [12] рассматривается вращающийся электродинамический трос и предложено управление для перехода троса из состояния покоя в состояние вращения, исследуется устойчивость движения. В работе [13] анализируются эволюционные движения системы вокруг центра масс при изменении ее параметров и силы тока в электродинамических тросах космической системы. Большинство опубликованных работ теоретические, но есть и экспериментальные. В частности, в рамках миссии по тестированию подходов увода космического мусора KITE (Kounotori Integrated Tether Experiment) [14] планировалось развернуть электродинамический трос и продемонстрировать эффект его применения, однако этого сделать не удалось из-за отказа системы выпуска троса. Тем не менее системы с электродинамическими тросами имеют большие перспективы для применения к задачам управления околоземных спутников.

В литературе большое количество работ посвящено вопросам управления угловым движением с использованием момента сил Лоренца. Например, в статье [15] исследуется динамика космического аппарата в задаче стабилизации на околокруговой орбите с использованием магнитных катушек и момента сил Лоренца. В работе [16] рассматривается вопрос устойчивости при применении пропорционально-интегрально-дифференцирующего регулятора в системе с распределенными запаздываниями в управлении. Трехосная система ориентации на основе только моментов сил Лоренца рассматривается в [17], показано, что линеаризованная модель углового движения может быть сведена к стационарной системе, управляемость которой исследуется в этой работе.

Для исследования пространственного распределения параметров околоземного пространства требуется запустить минимум 4 аппарата, которые в идеальном случае должны всегда находиться в вершинах правильного тетраэдра. Однако орбитальная динамика такова, что это недостижимо без управления или потребует очень больших затрат характеристической скорости, если использовать бортовые двигатели. Так, миссия MMS (Magnetosphere Multiscale Mission) [18], двигающаяся по сильно эллиптическим траекториям, достигает необходимого качества (близости к правильному) тетраэдра только в заданной области интереса в окрестности апоцентра. В работе [19] получена конфигурация 4 аппаратов, сохраняющая качество тетраэдра на околокруговых орбитах, но получающийся тетраэдр не является правильным. Поэтому возникла идея для создания требуемой конфигурации связать 4 аппарата с помощью тросов равной длины. Но в этом случае встают вопросы устойчивости движения такой системы, они изучены в работе [20]. Без создания центробежных сил, обеспечивающих натяжение тросов, эта тетраэдральная система будет нестабильна и тросы могут перепутаться. В настоящей работе предложен подход с использованием силы Лоренца в электродинамических тросах тетраэдральной формации для обеспечения требуемого углового движения для натяжения тросов с одновременным решением задачи управления движением центра масс тетраэдра в рамках группового полета, когда требуется обеспечить ограниченное движение тетраэдра как целого относительно другого орбитального объекта.

1. УРАВНЕНИЯ ДВИЖЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

В разделе описаны основные допущения, приведены уравнения движения и сформулирована постановка задачи.

1.1. Системы координат и модель движения

В работе используются следующие системы координат:

• OIXYZ – ИСК – инерциальная система координат. Точка OI – в центре Земли, ось OIX направлена в точку весеннего равноденствия, ось OIZ направлена вдоль оси вращения Земли, ось OIY дополняет систему до правой тройки.

• OXrYrZr – ОпСК – опорная система координат. Точка O движется по круговой орбите, система вращается вокруг своей оси с постоянной угловой скоростью.

• Oxyz – ОСК – орбитальная система координат. Точка O движется по круговой орбите, ось Oz направлена вдоль вектора OIO, ось Oy – вдоль вектора орбитального кинетического момента, ось Ox дополняет систему до правой тройки.

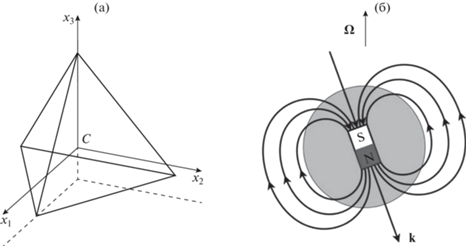
• Cx1x2x3 – ССК – связанная с тетраэдром система координат. Точка C находится в центре масс формации, оси Cx1 и Cx2 лежат в плоскости, параллельной одной из граней тетраэдра, ось Cx3 направлена на четвертый, не лежащий в этой плоскости спутник (рис. 1а).

Рис. 1.

Связанная с тетраэдром система координат (а), магнитный диполь Земли и вектор угловой скорости Земли (б).

При расчете опорной орбитальной траектории формации используется линейная модель движения, которая описывается уравнениями Хилла–Клохесси–Уилтшира [21]:

(1)
$\left\{ \begin{gathered} \ddot {x} + 2{{{{\omega }}}_{{orb}}}\dot {z} = {{f}_{x}}, \hfill \\ \ddot {y} + {{\omega }}_{{orb}}^{2}y = {{f}_{y}}, \hfill \\ \ddot {z} - 2{{{{\omega }}}_{{orb}}}\dot {x} - 3{{\omega }}_{{orb}}^{2}z = {{f}_{z}}. \hfill \\ \end{gathered} \right.$

Здесь ${{[x,y,z]}^{{\text{T}}}} = {\mathbf{r}} = {{{\mathbf{r}}}_{C}} - {{{\mathbf{r}}}_{O}}$ – разность радиус-векторов центров координат ССК и ОпСК, записанных в ОСК; ωorb – орбитальная угловая скорость; ${{[{{f}_{x}},{{f}_{y}},{{f}_{z}}]}^{{\text{T}}}} = {\mathbf{f}}$ – вектор управляющего ускорения. Решение однородной системы имеет вид

(2)
$\left\{ \begin{gathered} x(t) = - 3{{C}_{1}}{{{{\omega }}}_{{orb}}}t + 2{{C}_{2}}\cos ({{{{\omega }}}_{{orb}}}t) - \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,2{{C}_{3}}\sin ({{{{\omega }}}_{{orb}}}t) + {{C}_{4}}, \hfill \\ y(t) = {{C}_{5}}\sin ({{{{\omega }}}_{{orb}}}t) + {{C}_{6}}\cos ({{{{\omega }}}_{{orb}}}t), \hfill \\ z(t) = 2{{C}_{1}} + {{C}_{2}}\sin ({{{{\omega }}}_{{orb}}}t) + {{C}_{3}}\cos ({{{{\omega }}}_{{orb}}}t), \hfill \\ \end{gathered} \right.$
где константы C1, …, C6 зависят от начальных условий следующим образом:

$\begin{gathered} {{C}_{1}} = \frac{{\dot {x}(0)}}{{{{{{\omega }}}_{{orb}}}}} + 2z(0),\,\,\,\,{{C}_{2}} = \frac{{\dot {z}(0)}}{{{{{{\omega }}}_{{orb}}}}}, \\ {{C}_{3}} = - 2\frac{{\dot {x}(0)}}{{{{{{\omega }}}_{{orb}}}}} - 3z(0),\,\,\,\,{{C}_{4}} = - 2\frac{{\dot {z}(0)}}{{{{{{\omega }}}_{{orb}}}}} + x(0), \\ {{C}_{5}} = \frac{{\dot {y}(0)}}{{{{{{\omega }}}_{{orb}}}}},\,\,\,\,{{C}_{6}} = y(0). \\ \end{gathered} $

При численном моделировании интегрирование уравнений движения производится в следующей нелинейной модели

(3)
${\mathbf{\ddot {R}}} = - \frac{{{{{{\mu }}}_{g}}{\mathbf{R}}}}{{{{R}^{3}}}} + {{{\mathbf{f}}}_{\Sigma }},\,\,\,\,{{{\mathbf{f}}}_{\Sigma }} = {{{\mathbf{f}}}_{{{{J}_{2}}}}} + {{{\mathbf{f}}}_{{control}}},$
где μg = 3.986 · 1014 м3 с–2 – гравитационный параметр Земли; ${\mathbf{R}} = {{[X,Y,Z]}^{{\text{T}}}}$ – радиус-вектор точки C в ИСК. В модели (3) учитывается нецентральность гравитационного поля Земли: потенциал раскладывается до второй гармоники, и тогда
$\begin{gathered} {{{\mathbf{f}}}_{{{{J}_{2}}}}} = \left( {\begin{array}{*{20}{c}} {\frac{{{\delta }}}{{{{R}^{5}}}}X\left( {\frac{{5{{Z}^{2}}}}{{{{R}^{2}}}} - 1} \right)} \\ {\frac{{{\delta }}}{{{{R}^{5}}}}Y\left( {\frac{{5{{Z}^{2}}}}{{{{R}^{2}}}} - 1} \right)} \\ {\frac{{{\delta }}}{{{{R}^{5}}}}Z\left( {\frac{{5{{Z}^{2}}}}{{{{R}^{2}}}} - 3} \right)} \end{array}} \right), \\ \,\,{{\delta }} = \frac{3}{2}{{J}_{2}}{{{{\mu }}}_{g}}R_{{\text{E}}}^{2},\,\,{{J}_{2}} = 1082.23 \cdot {{10}^{{ - 6}}}, \\ \end{gathered} $
где средний радиус Земли RE = 6.4 · 106 м.

Угловое движение тетраэдра как твердого тела описывается динамическими уравнениями Эйлера и кинематическими соотношениями в кватернионах

(4)
$\left\{ \begin{gathered} {\mathbf{\dot {\omega }}} = {{{\mathbf{J}}}^{{ - 1}}}\left( { - {\mathbf{\omega }} \times {\mathbf{J\omega }} + {{{\mathbf{M}}}_{\Sigma }}} \right),\,\,\,\,{{{\mathbf{M}}}_{\Sigma }} = {{{\mathbf{M}}}_{{grav}}} + {{{\mathbf{M}}}_{{control}}}, \hfill \\ {\mathbf{\dot {q}}} = {\mathbf{q}} \circ \left[ {0;{\mathbf{\omega }}} \right]{\text{/}}2, \hfill \\ \end{gathered} \right.$
где J – тензор инерции в ССК; ω – полная угловая скорость ССК относительно ИСК; q – кватернион перехода из ИСК в ССК; символ “$ \circ $” обозначает кватернионное умножение. При моделировании учитывается гравитационный момент:

${{{\mathbf{M}}}_{{grav}}} = 3{{{{\mu }}}_{g}}\frac{{{\mathbf{R}} \times {\mathbf{JR}}}}{{{{R}^{5}}}}.$

Как известно, на проводник с током в магнитном поле действует сила Лоренца, определяемая следующим выражением ${\mathbf{F}} = I{\mathbf{L}} \times {\mathbf{B}},$ где I – значение силы тока; L – вектор из начала проводника в его конец вдоль направления тока; B – вектор магнитной индукции.

Для расчета индукции геомагнитного поля используется модель наклонного диполя. Считается, что вектор вдоль направления магнитного диполя Земли k наклонен под углом λ = 12° к оси вращения Земли и вращается с угловой скоростью вращения Земли Ω = 1/24/3600 рад/с (рис. 1б). Тогда индукция магнитного поля определяется следующей формулой:

${\mathbf{B}}(t,{\mathbf{R}}) = \frac{{{{{{\mu }}}_{0}}{{{{\mu }}}_{B}}}}{{4{{\pi }}{{R}^{5}}}}\left( {3\left( {{{{\mathbf{k}}}^{{\text{T}}}}(t){\mathbf{R}}} \right){\mathbf{R}} - {{R}^{2}}{\mathbf{k}}(t)} \right),$
где μ0 = 1.25 · 10-6 Н А–2 – магнитная постоянная и μB = 7.72 · 1022 А м2 – магнитный дипольный момент Земли. Поскольку размеры тетраэдральной формации намного меньше радиуса орбиты, то величина геомагнитного поля во всех точках системы в каждый момент времени считается одинаковой.

1.2. Постановка задачи

Рассматриваются четыре аппарата, каждый из которых соединен с другими электродинамическими тросами. В настоящей работе при построении алгоритма управления движением тетраэдральной формации тросы считаются жесткими, а угловое движение тетраэдра рассматривается как движение твердого тела. Рассматривается движение тетраэдральной формации на низкой околоземной орбите относительно заданной опорной орбитальной системы координат, при этом полный вектор состояния углового и поступательного движения считается известным. Предполагается, что с помощью специальных эмиттеров электронов можно создавать направление и величину требуемого электрического тока, текущего по стержням между аппаратами. При управлении величиной силы тока, текущего по стержням или тросам, можно изменять вектор силы и вектор момента сил, действующих на формацию как на твердое тело, и, таким образом, производится управление орбитальным и угловым движением системы. Предполагается, что величина силы тока ограничена, но существует разность токов, текущих по соседним стержням, таким образом, не рассматривается проблема накопления заряда в каком-либо из четырех аппаратов.

В настоящей работе решается задача построения управления тетраэдральной формацией с помощью силы Лоренца при описанных выше предположениях для остановки дрейфа относительно опорной орбитальной системы при движении на круговой низкой околоземной орбите. Одновременно с управлением поступательным движением решается задача достижения требуемого углового движения с постоянной угловой скоростью вращения формации, что необходимо для поддержания тросов в натянутом состоянии.

2. РАЗРАБОТКА АЛГОРИТМА УПРАВЛЕНИЯ

В разделе представлен разработанный алгоритм управления движением тетраэдральной формации с электродинамическими тросами.

2.1. Требуемое управление

Как видно из первого уравнения в системе (2), если параметр C1 = 0, то движение относительно опорной системы координат будет представлять собой замкнутый эллипс. В этом случае движение центра масс формации будет ограниченным. В начальный момент после развертывания системы это условие может не выполняться. Задача управления – привести систему в состояние, в котором это условие выполняется, а затем поддерживать околонулевое значение параметра C1. В работе [22] показано, что такую задачу решает приложение постоянного управляющего ускорения ${\mathbf{f}} = {{\left[ {{{f}_{x}},{{f}_{y}},{{f}_{z}}} \right]}^{{\text{T}}}}$ за фиксированный период времени Δt, направленного вдоль касательной к орбите:

(5)
$\begin{gathered} {{f}_{x}}(t) = \\ = \left\{ \begin{gathered} - \frac{{{{{{\omega }}}_{{orb}}}}}{{\Delta t}}\left( {\frac{{\dot {x}({{t}_{0}})}}{{{{{{\omega }}}_{{orb}}}}} + 2z({{t}_{0}})} \right),\,\,{\text{если}}\;\;{{t}_{0}} < t < {{t}_{0}} + \Delta t, \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{если}}\,\,t > {{t}_{0}} + \Delta t, \hfill \\ \end{gathered} \right. \\ {{f}_{y}}(t) = 0,\,\,\,\,{{f}_{z}}(t) = 0. \\ \end{gathered} $

Задача достижения требуемого углового движения сводится к приведению углового движения ССК к движению ОпСК, то есть относительная угловая скорость ωrel должна сойтись к окрестности нуля, а относительный кватернион ориентации qrel к кватерниону с единичной скалярной частью и нулевой векторной частью. Относительная угловая скорость и кватернион определяются следующим образом:

${{{\mathbf{\omega }}}_{{rel}}} = {\mathbf{\omega }} - {{{\mathbf{\omega }}}_{{ref}}},$
${{{\mathbf{q}}}_{{rel}}} = {{{\mathbf{\tilde {q}}}}_{{ref}}} \circ {\mathbf{q}},$
где ωref – угловая скорость ОпСК; qref – кватернион ориентации ОпСК. Угловая скорость вращения ОпСК ωref считается постоянной; в начальный момент времени задается кватернион перехода из ИСК в ОпСК qref и интегрируется в соответствии с кинематическими уравнениями:

${{{\mathbf{\dot {q}}}}_{{ref}}} = {{{\mathbf{q}}}_{{ref}}} \circ \left[ {0;{{{\mathbf{\omega }}}_{{ref}}}} \right]{\text{/}}2.$

Закон управления угловым движением получен на основе метода Ляпунова, описанного в работе [23]. Составим кандидат-функцию Ляпунова в следующем виде:

$V = \left( {{\mathbf{\omega }}_{{rel}}^{{\text{T}}}{\mathbf{J}}{{{\mathbf{\omega }}}_{{rel}}}} \right){\text{/}}2 + {{{\mathbf{K}}}_{a}}\left( {1 - {{q}_{{rel,0}}}} \right),$
где Ka – положительно определенная матрица; qrel,0 – скалярная часть кватерниона рассогласования. Продифференцируем эту функцию в соответствии с уравнениями углового движения (4):

$\begin{gathered} \dot {V} = {\mathbf{\omega }}_{{rel}}^{{\text{T}}}\left( { - {\mathbf{\omega }} \times {\mathbf{J\omega }} + {{{\mathbf{M}}}_{{grav}}} + {{{\mathbf{M}}}_{{control}}} + } \right. \\ \left. { + \,\,{\mathbf{J}}{{{\mathbf{\omega }}}_{{rel}}} \times {{{\mathbf{\omega }}}_{{ref}}} - {\mathbf{J}}{{{{\mathbf{\dot {\omega }}}}}_{{ref}}} + {{{\mathbf{K}}}_{a}}{{{\mathbf{q}}}_{{rel}}}} \right). \\ \end{gathered} $

Согласно теореме Барбашина–Красовского [24], для асимптотической устойчивости нулевого положения равновесия, когда ССК совпадает с ОпСК, требуется положительная знакоопределенность функции Ляпунова и неположительная определенность ее производной, притом что область, где $\dot {V} = 0$, не содержит целых траекторий. Первое условие для данной функции V выполнено в силу построения. Второе условие достигается при выполнении следующего равенства:

(6)
$\begin{gathered} - {\mathbf{\omega }} \times {\mathbf{J\omega }} + {{{\mathbf{M}}}_{{grav}}} + {{{\mathbf{M}}}_{{control}}} + {\mathbf{J}}{{{\mathbf{\omega }}}_{{rel}}} \times \\ \times \,\,{{{\mathbf{\omega }}}_{{ref}}} - {\mathbf{J}}{{{{\mathbf{\dot {\omega }}}}}_{{ref}}} + {{{\mathbf{K}}}_{a}}{{{\mathbf{q}}}_{{rel}}} = - {{{\mathbf{K}}}_{w}}{{{\mathbf{\omega }}}_{{rel}}}, \\ \end{gathered} $
если Kw – положительно определенная матрица. При выполнении (6) производная функции Ляпунова имеет следующий вид:

$\dot {V} = - {\mathbf{\omega }}_{{rel}}^{{\text{T}}}{{{\mathbf{K}}}_{w}}{{{\mathbf{\omega }}}_{{rel}}}.$

Отсюда следует, что $\dot {V}$ действительно будет неположительно определена, $\dot {V} = 0$ достигается только при ωrel = 0, что является значением относительной угловой скорости в положении равновесия. Из (6) находим управляющий момент:

(7)
$\begin{gathered} {{{\mathbf{M}}}_{{control}}} = {\mathbf{\omega }} \times {\mathbf{J\omega }} + {\mathbf{J}}{{{{\mathbf{\dot {\omega }}}}}_{{ref}}} - {\mathbf{J}}\left( {{{{\mathbf{\omega }}}_{{rel}}} \times {{{\mathbf{\omega }}}_{{ref}}}} \right) - \\ - \,\,{{{\mathbf{K}}}_{a}}{{{\mathbf{q}}}_{{rel}}} - {{{\mathbf{K}}}_{w}}{{{\mathbf{\omega }}}_{{rel}}} - {{{\mathbf{M}}}_{{grav}}}. \\ \end{gathered} $

Матрицы коэффициентов управления Ka и Kw подбираются исходя из обеспечения желаемых характеристик переходных процессов при заданных ограничениях ресурса управления.

Таким образом, с помощью шести электрических токов в стержнях I1, …, I6 требуется обеспечить такое управление, которое реализует расчетные значения поступательного ускорения fx и момент сил ${\mathbf{M}}_{c}^{{\text{T}}}.$

2.2. Расчет сил тока

В этом разделе приведено описание расчета электрических токов, необходимых для реализации расчетного вектора управления поступательным и угловым движением.

Если по стержням правильного тетраэдра текут электрические токи I1, …, I6, то равнодействующее ускорение fa, действующее на систему, будет равно

(8)
${{{\mathbf{f}}}_{a}} = \sum\limits_{i = 1}^6 {{{I}_{i}}{{{\mathbf{L}}}_{i}} \times {\mathbf{B}}{\text{/}}m} ,$
где Li – вектор из начала i-го стержня в его конец; m – масса всей тетраэдральной формации как твердого тела. Первая компонента этого вектора имеет следующий вид:

${{f}_{{a,x}}} = {{B}_{z}}\sum\limits_{i = 1}^6 {{{L}_{{i,y}}}{{I}_{i}}{\text{/}}m} - {{B}_{y}}\sum\limits_{i = 1}^6 {{{L}_{{i,z}}}{{I}_{i}}{\text{/}}m} .$

Момент, действующий на одно i-е ребро, равен

$\begin{gathered} {{{\mathbf{M}}}_{{a,i}}} = {{{\mathbf{N}}}_{i}} \times \left( {{{I}_{i}}{{{\mathbf{L}}}_{i}} \times {\mathbf{B}}} \right) = {{{\mathbf{L}}}_{i}}\left( {{\mathbf{N}}_{i}^{{\text{T}}}{\mathbf{B}}} \right){{I}_{i}} - \\ - \,\,{\mathbf{B}}\left( {{\mathbf{N}}_{i}^{{\text{T}}}{{{\mathbf{L}}}_{i}}} \right){{I}_{i}} = {{{\mathbf{L}}}_{i}}\left( {{\mathbf{N}}_{i}^{{\text{T}}}{\mathbf{B}}} \right){{I}_{i}}, \\ \end{gathered} $
где Ni – радиус-вектор из центра тетраэдра к середине i-го ребра, в правильном тетраэдре этот вектор перпендикулярен вектору Li. Так как в правильном тетраэдре $\left( {{\mathbf{N}}_{i}^{{\text{T}}}{{{\mathbf{L}}}_{i}}} \right) = 0,$ то второе слагаемое обнуляется и суммарный момент сил относительно центра масс тетраэдра равен

(9)
${{{\mathbf{M}}}_{a}} = \sum\limits_{i = 1}^6 {{{{\mathbf{L}}}_{i}}\left( {{\mathbf{N}}_{i}^{{\text{T}}}{\mathbf{B}}} \right){{I}_{i}}} .$
Таблица 1.

Основные параметры моделирования

Параметр Значение
Масса каждого спутника 10 кг
Длина стержня 10 м
Масса стержня 100 г
Скорость вращения ОпСК 10–2 рад/с
Максимальный ток 10 А
Высота орбиты 550 км
Наклонение орбиты 51.7°
Время моделирования 8 ч
Шаг интегрирования 0.1 с

Итак, силы тока приводят к возникновению ускорения и момента сил со следующими компонентами:

$\begin{gathered} {{\left[ {{{f}_{{a,x}}},{\mathbf{M}}_{a}^{{\text{T}}}} \right]}^{{\text{T}}}} = \left[ {\sum\limits_{i = 1}^6 {\left( {{{B}_{z}}{{L}_{{i,y}}} - {{B}_{y}}{{L}_{{i,z}}}} \right){{I}_{i}}} {\text{/}}m,} \right. \\ {{\left. {\sum\limits_{i = 1}^6 {{\mathbf{L}}_{i}^{{\text{T}}}\left( {{\mathbf{N}}_{i}^{{\text{T}}}{\mathbf{B}}} \right){{I}_{i}}} } \right]}^{{\text{T}}}}. \\ \end{gathered} $

Заметим, что и ускорение, и момент сил зависят от токов линейно, то есть это выражение можно записать в следующем виде:

${{\left[ {{{f}_{{a,x}}},{\mathbf{M}}_{a}^{{\text{T}}}} \right]}^{{\text{T}}}} = {\mathbf{A}}{{\left[ {{{I}_{1}},...,{{I}_{6}}} \right]}^{{\text{T}}}},$
где A – матрица, элементы которой не зависят от токов. Чтобы с помощью тока получить требуемые ускорение и момент сил, необходимо выполнение равенства

${{\left[ {{{f}_{{a,x}}},{\mathbf{M}}_{a}^{{\text{T}}}} \right]}^{{\text{T}}}} = {{\left[ {{{f}_{{c,x}}},{\mathbf{M}}_{c}^{{\text{T}}}} \right]}^{{\text{T}}}}.$

В результате получена следующая система:

${\mathbf{A}}{{\left[ {{{I}_{1}},...,{{I}_{6}}} \right]}^{{\text{T}}}} = {{\left[ {{{f}_{{c,x}}},{\mathbf{M}}_{c}^{{\text{T}}}} \right]}^{{\text{T}}}}.$

Это линейная система из четырех уравнений с шестью неизвестными токами. Для краткости запишем ее в виде

${\mathbf{AI}} = {\mathbf{u}}.$

Так как эта система уравнений переопределена, то целесообразно искать решение с минимальной суммой токов, то есть решать следующую оптимизационную задачу:

$\left\{ \begin{gathered} {{{\mathbf{I}}}^{{\text{T}}}}{\mathbf{I}} \to \min , \hfill \\ {\mathbf{AI}} = {\mathbf{u}}. \hfill \\ \end{gathered} \right.$

Эту задачу можно решить методом квадратичного программирования [25]. Составим функцию Лагранжа вида

$L({\mathbf{I}},{\mathbf{\lambda }}) = {{{\mathbf{I}}}^{{\text{T}}}}{\mathbf{I}} + {{{\mathbf{\lambda }}}^{{\text{T}}}}\left( {{\mathbf{AI}} - {\mathbf{u}}} \right).$

Градиенты по I и по λ соответственно равны

$\frac{{\partial L}}{{\partial {\mathbf{I}}}} = 2{{{\mathbf{I}}}^{{\text{T}}}} + {{{\mathbf{\lambda }}}^{{\text{T}}}}{\mathbf{A}},\,\,\,\,\frac{{\partial L}}{{\partial {\mathbf{\lambda }}}} = {{\left( {{\mathbf{AI}} - {\mathbf{u}}} \right)}^{{\text{T}}}}.$

Приравняем их к нулю. Из первого уравнения получим

${\mathbf{I}} = - {{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{\lambda }}{\text{/}}2,$
подставляем во второе уравнение и находим

${\mathbf{\lambda }} = - 2{{\left( {{\mathbf{A}}{{{\mathbf{A}}}^{{\text{T}}}}} \right)}^{{ - 1}}}{\mathbf{u}}.$

Это приводит к решению

${\mathbf{I}} = {{{\mathbf{A}}}^{{\text{T}}}}{{\left( {{\mathbf{A}}{{{\mathbf{A}}}^{{\text{T}}}}} \right)}^{{ - 1}}}{\mathbf{u}},$
то есть величины токов определяются из следующего выражения:

(10)
${{\left[ {{{I}_{1}},...,{{I}_{6}}} \right]}^{{\text{T}}}} = {{{\mathbf{A}}}^{{\text{T}}}}{{\left( {{\mathbf{A}}{{{\mathbf{A}}}^{{\text{T}}}}} \right)}^{{ - 1}}}{{\left[ {{{f}_{{c,x}}},{\mathbf{M}}_{c}^{{\text{T}}}} \right]}^{{\text{T}}}}.$

В настоящей работе предполагается, что по тросу тетраэдральной формации нельзя пустить ток, превышающий некоторую величину Imax, определяемую техническими возможностями системы. Если в результате нахождения требуемых токов абсолютное значение максимального по модулю рассчитанного значения Ik, $k = \arg \max \left\{ {\left| {{{I}_{1}}} \right|,...,\left| {{{I}_{6}}} \right|} \right\},$ больше некоторого заданного максимально возможного тока Imax, то ток по данному стержню берется максимальным по величине, то есть равным

(11)
${{I}_{k}} = {\text{sign}}({{I}_{k}}) \cdot {{I}_{{\max }}},$
а все остальные токи уменьшаются пропорционально:

${{I}_{i}} \to {{I}_{i}} \cdot {{I}_{{\max }}}{\text{/}}{\kern 1pt} \left| {{{I}_{k}}} \right|.$

Таким образом, расчетное управление может быть реализовано с некоторыми ошибками вследствие аппаратных ограничений.

3. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ

В разделе продемонстрированы примеры работы алгоритма и проведено численное параметрическое исследование характеристик управляемого движения.

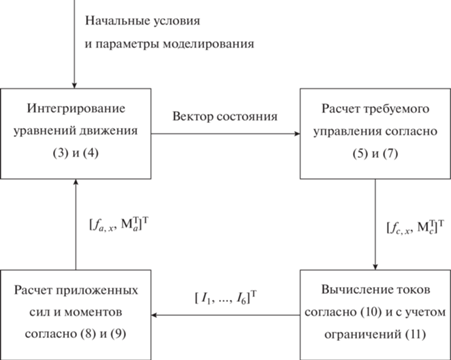
Для исследования управляемого движения тетраэдральной формации с помощью сил Лоренца проводится численное моделирование работы описанного в разделе 2 алгоритма. На рис. 2 представлена общая схема проведения численного моделирования. На входе подаются начальные условия движения, а также все необходимые параметры системы. Проводится численное интегрирование уравнений поступательного и углового движения согласно (3) и (4). Полученный на каждом шаге моделирования вектор состояния системы используется для расчета требуемого управляющего ускорения и момента сил ${{\left[ {{{f}_{{c,x}}},{\mathbf{M}}_{c}^{{\text{T}}}} \right]}^{{\text{T}}}}$ согласно (5) и (7). Далее по формулам (10) вычисляются значения необходимых токов, но они подвергаются модификации в соответствии с аппаратными ограничениями (11).

Рис. 2.

Общая схема проведения численного моделирования.

Получившиеся в результате токи ${{\left[ {{{I}_{1}},...,{{I}_{6}}} \right]}^{{\text{T}}}}$ используются для вычисления приложенного фактически управляющего ускорения и момента сил ${{\left[ {{{f}_{{а,x}}},{\mathbf{M}}_{а}^{{\text{T}}}} \right]}^{{\text{T}}}}$ согласно (8) и (9). Эти значения используются для интегрирования уравнений движения. В табл. 1 представлены основные параметры моделирования.

3.1. Оценка влияния магнитного поля проводников с токами

Вокруг проводника с током создается магнитное поле, величина которого на расстоянии r от него равна

${\mathbf{B}}({\mathbf{r}}) = \frac{{{{{{\mu }}}_{0}}}}{{4{{\pi }}{{r}^{3}}}}Id{\mathbf{l}} \times {\mathbf{r}},$
где dl – длина этого проводника. Оценим магнитное поле, созданное токами, текущими по другим стержням, во всех точках каждого стержня. Для этого разобьем каждый стержень на достаточно большое количество отрезков NL и посчитаем в середине каждого такого отрезка поле от всех остальных 5NL отрезков. Поле от отрезков на этом же стержне равно нулю, так как в этом случае вектор dl параллелен вектору r. Таким образом, магнитное поле в центре p-го отрезка i-го стержня равно

${{{\mathbf{B}}}_{{i,p}}} = \sum\limits_{j \ne i} {\sum\limits_{q = 1}^{{{N}_{L}}} {\frac{{{{{{\mu }}}_{0}}}}{{4{{\pi }}{{{\left| {{{{\mathbf{R}}}_{{i,p}}} - {{{\mathbf{R}}}_{{j,q}}}} \right|}}^{3}}}}{{I}_{j}}d{{{\mathbf{l}}}_{{j,q}}} \times \left( {{{{\mathbf{R}}}_{{i,p}}} - {{{\mathbf{R}}}_{{j,q}}}} \right)} } .$

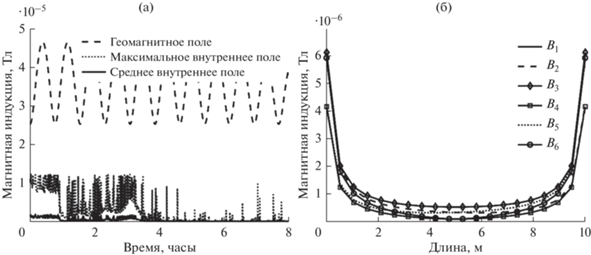
На рис. 3а показаны величина геомагнитного поля, а также максимальная среди всех отрезков и средняя по всем отрезкам величины внутреннего поля. При максимально допустимых токах в 10 А среднее внутреннее магнитное поле на порядок меньше геомагнитного поля и линейно убывает с уменьшением токов. На рис. 3б показано внутреннее поле в точках каждого ребра тетраэдра при токах в 1 А. Около вершин поле значительно больше, чем в середине ребер, поскольку величина магнитной индукции обратно пропорциональна квадрату расстояния между проводниками. При этом максимальное внутреннее поле на порядок меньше геомагнитного поля. Эти оценки позволяют заключить, что при рассматриваемых значениях токов влияние друг на друга магнитных полей пренебрежимо мало и может рассматриваться как дополнительное возмущение при математическом моделировании.

Рис. 3.

Сравнение геомагнитного поля и магнитного поля от других стержней (а), величина внутреннего магнитного поля в точках ребра при Ii = 1 А, i = 1, …, 6 (б).

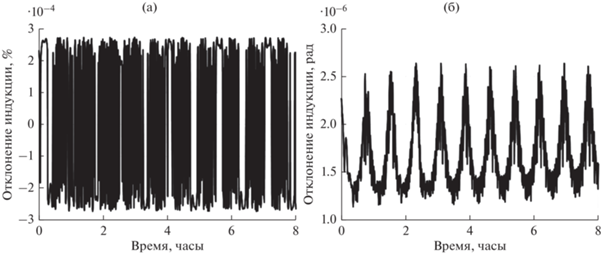
Покажем, насколько сильно отличается геомагнитное поле в различных точках тетраэдра. Вычислим векторы магнитной индукции в центре тетраэдра и в центре каждого отрезка каждого стержня. Сравним величины и направления индукции (рис. 4). Модуль индукции различается на тысячные доли процента, а направление совпадает с точностью до 10–5 рад.

Рис. 4.

Максимальное отклонение модуля (а) и направления (б) геомагнитной индукции.

3.2. Пример результатов моделирования управляемого движения

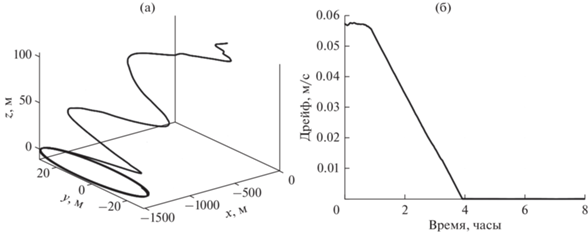
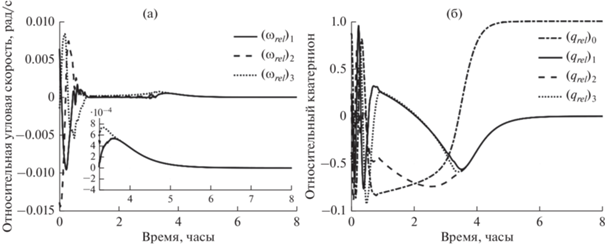
Теперь проанализируем пример результатов моделирования управляемого движения с приведенными в табл. 1 параметрами. На рис. 5а показана траектория движения центра масс тетраэдра относительно опорной орбитальной системы координат; видно, что относительный дрейф был успешно устранен системой управления и траектория движения стала близкой к замкнутой. Из рис. 5б видно, что за 4 ч полностью устраняется дрейф тетраэдра относительно опорной системы координат. Одновременно с этим происходит совмещение углового движения тетраэдра с требуемым угловым движением. Оно достигается примерно за 6 ч, как показано на рис. 6.

Рис. 5.

Относительное орбитальное движение (а), орбитальный дрейф (б).

Рис. 6.

Относительная угловая скорость (а), относительный кватернион (б).

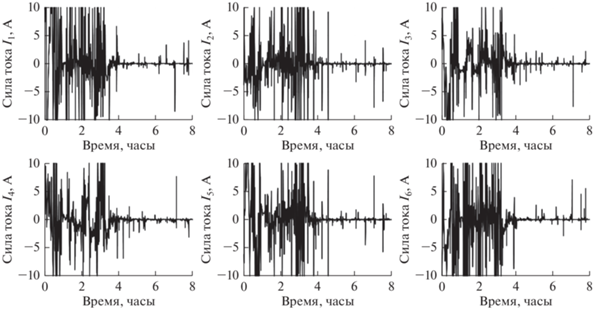
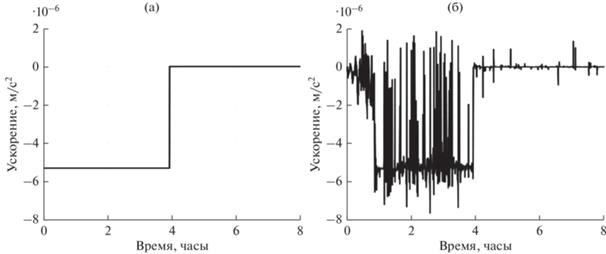
На рис. 7 представлены величины сил токов в 6 стержнях, рассчитанные согласно предложенному алгоритму. Как видно из графика, в первые 4 ч величины часто выходили на ограничения по максимальному значению тока в 10 А, это приводило к значительным ошибкам в реализации расчетного управляющего ускорения и момента сил. На рис. 8 можно увидеть, что в первый час движения расчетное управляющее ускорение отличалось от реализованного почти на его величину и было около нуля. Это привело к тому, что на этом отрезке моделирования уменьшение величины дрейфа (см. рис. 5б) было незначительным. Такая большая ошибка была вызвана тем, что в первый час движения система управления стремилась устранить рассогласование по параметрам углового движения.

Рис. 7.

Силы тока в стержнях.

Рис. 8.

Требуемое (а) и приложенное (б) управление орбитальным движением.

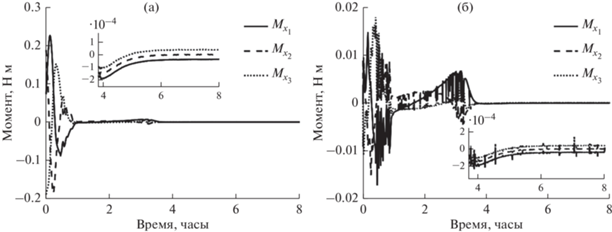
Как видно из рис. 9, в начальный момент времени требуемый управляющий момент был на порядок больше приложенного, опять же из-за ограничений на максимальный ток. Однако спустя час, вследствие устранения большого рассогласования по угловой скорости (рис. 6а), приложенный момент стал близок к требуемому, как и управляющее ускорение. Резкие и значительные ошибки в реализации управления на интервале от часа до конца моделирования вызваны принципиальной невозможностью реализовать направление сил Лоренца вдоль вектора локального геомагнитного поля, что математически выражается в плохой обусловленности матрицы в системе уравнений (10). Однако, вследствие углового движения тетраэдра и изменения направления стержней относительно магнитного поля, такие ситуации вырождения системы уравнений кратковременны и не оказывают значительного влияния на управляемое движение системы.

Рис. 9.

Требуемое (а) и приложенное (б) управление угловым движением.

Представленный пример результатов математического моделирования демонстрирует работоспособность предложенной схемы управления движением тетраэдральной формации. Однако предположение о том, что тросы тетраэдра могут быть заменены стержнями при расчете сил токов, требует верификации, а именно – проведения математического моделирования системы с использованием модели гибких нерастяжимых тросов, что планируется сделать в дальнейшей работе авторов.

3.3. Время сходимости

Проведем численное исследование зависимости времени сходимости от различных параметров моделирования. Будем считать, что достигнуто требуемое относительное поступательное движение, если относительный дрейф стал меньше некоторого порогового значения (в настоящей работе это $\left| {{{С}_{1}}} \right| < $ 0.1 м). Численные расчеты показывают, что примерно это же время требуется и для достижения опорного углового движения (критерий сходимости для углового движения $\left| {{{{\mathbf{\omega }}}_{{rel}}}} \right| < {{10}^{{ - 5}}}$ рад/c).

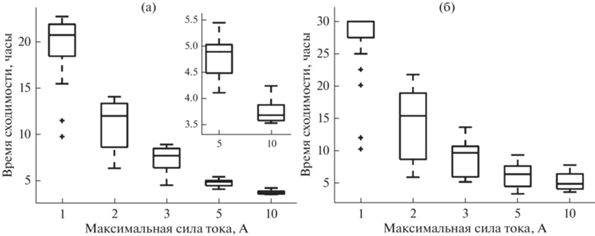
Сначала будем устанавливать различные ограничения на величину максимального допустимого тока. Рассмотрим значения Imax на уровне 1, 2, 3, 5 и 10 А. При каждом значении тока проведем серию численных экспериментов с различными начальными условиями. Начальная угловая скорость тетраэдра как твердого тела равна 10–3 рад/с, но может иметь случайное направление. Результаты показаны на рис. 10 в виде диаграммы размаха случайной величины времени сходимости. На диаграмме горизонтальная линия внутри прямоугольника обозначает медианное значение, выше и ниже нее в прямоугольнике находится 25% результатов, а также по 25% результатов находится выше и ниже прямоугольника. Из рисунка видно, что при более жестких ограничениях на максимальную величину тока время сходимости увеличивается, поскольку ограничения силы тока влияют на величину управляющего ускорения и момента. При дальнейшем уменьшении величины максимального тока время сходимости превышает время моделирования для заданных параметров системы.

Рис. 10.

Время сходимости орбитального (а) и углового (б) движения при различных ограничениях максимального тока.

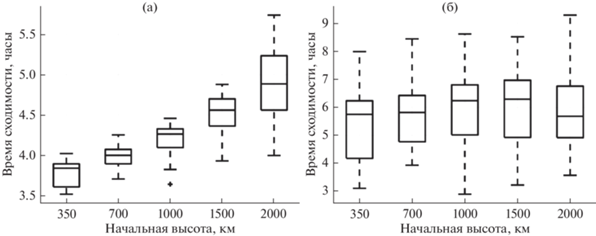
Теперь зафиксируем величину максимального тока величиной 5 А и будем варьировать начальную высоту орбиты от 350 до 2000 км. При каждом значении также рассмотрим различные начальные условия с фиксированной величиной модуля угловой скорости 10–3 рад/с. Результаты приведены на рис. 11, откуда видно, насколько увеличивается время сходимости с увеличением высоты орбиты. Увеличение времени сходимости вызвано уменьшением величины геомагнитного поля, а следовательно, и уменьшением величины реализуемой силы Лоренца, что может приводить к все сильнее отличающимся реализованным управляющим ускорениям и моментам от требуемых. При значениях больше 2000 км система не успевает сойтись за 8 ч.

Рис. 11.

Время сходимости орбитального (а) и углового (б) движения при различных начальных высотах орбиты.

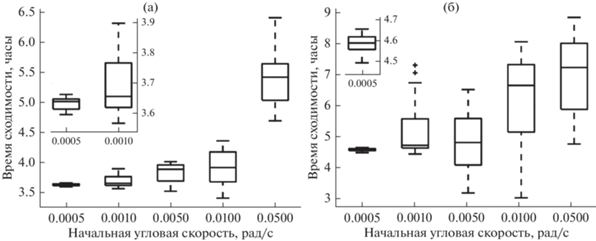
Так как системой управления решается задача одновременного достижения опорной траектории для углового и поступательного движения, то при различных начальных угловых скоростях будут получаться разные времена сходимости. С помощью метода Монте-Карло при фиксированном максимальном токе в стержнях тетраэдра 5 А и при заданной высоте орбиты 350 км проводилось математическое моделирование управляемого движения при различных начальных угловых скоростях, фиксированных по величине, но случайных по направлению. Результаты численного исследования представлены на рис. 12. Так как требуемая угловая скорость составляет 10–2 рад/с, то при начальных угловых скоростях около этого значения, но со случайным направлением в некоторых случаях моделирования требовалось даже несколько меньше времени для сходимости, чем при раскрутке до 10–2 рад/с от меньших значений. Однако при больших угловых скоростях системе управления приходилось прилагать усилия по уменьшению угловой скорости, что занимало больше времени.

Рис. 12.

Время сходимости орбитального (а) и углового (б) движения при различных начальных угловых скоростях.

Таким образом, параметрическое численное исследование требуемого времени сходимости с помощью метода Монте-Карло позволило выявить диапазон значений ряда параметров, при котором предложенное управление справляется с задачей достижения требуемого поступательного и углового движения за фиксированное время 8 ч и при заданных параметрах системы.

ЗАКЛЮЧЕНИЕ

В работе продемонстрирована принципиальная возможность управления поступательным и угловым движением тросовой тетраэдральной формации с использованием силы Лоренца. Предложенный алгоритм управления справляется с задачей даже с учетом аппаратных ограничений на максимально возможную силу тока. Таким образом, подобная система может быть рассмотрена для применения на околоземных миссиях группового полета, в том числе на основе наноспутников, не имеющих бортовых двигателей для управления относительным движением. Однако управляемое движение требует дальнейшей верификации с использованием более детальных моделей с учетом гибкости тросов и сил натяжения в них. Особенный интерес представляет рассмотрение этапа управления при развертывании тросовой формации, представляющий наибольшую техническую сложность. Эти задачи планируется решить в дальнейшей работе.

Список литературы

  1. Shirobokov M.G., Trofimov S.P. Adaptive Neural Formation-Keeping Control for Satellites in a Low-Earth Orbit // Cosmic Research. 2021. V. 59. Iss. 6. P. 501–516. https://doi.org/10.1134/S0010952521060113

  2. Leonard C.L. Formationkeeping of Spacecraft via Differential Drag. Master Thesis. Massachusetts Inst. Technol., 1986. http://hdl.handle.net/1721.1/13358

  3. Mashtakov Y., Ovchinnikov M., Petrova T. et al. Two-satellite formation flying control by cell-structured solar sail // Acta Astronaut. 2020. V. 170. P. 592–600. https://doi.org/10.1016/j.actaastro.2020.02.024

  4. Ivanov D., Gondar R., Monakhova U. et al. Electromagnetic uncoordinated control of a ChipSats swarm using magnetorquers // Acta Astronaut. 2022. V. 192. P. 15–29. https://doi.org/10.1016/j.actaastro.2021.12.014

  5. Shestakov S., Ivanov D., Ovchinnikov M. Formation-Flying Momentum Exchange Control by Separate Mass // J. Guid. Control. Dyn. 2015. V. 38. Iss. 8. P. 1–10. https://doi.org/10.2514/1.G001137

  6. Peck M.A., Streetman B., Saaj C.M., Lappas V. Spacecrat Formation Flying Using Lorentz Forces // J. Br. Interplanet. Soc. 2007. V. 60. Iss. 7. P. 263–267.

  7. Peck M.A. Prospects and challenges for Lorentz-augmented orbits // Collect. Tech. Papers – AIAA Guid. Navig. Control Conf. 2005. V. 3. P. 1631–1646. https://doi.org/10.2514/6.2005-5995

  8. Schaffer L., Burns J.A. Charged dust in planetary magnetospheres: Hamiltonian dynamics and numerical simulations for highly charged grains // J. Geophys. Res. SP. Phys. 1994. V. 99. Iss. A9. P. 17211–17223.https://doi.org/10.1029/94JA01231

  9. Saaj C.M., Lappas V., Richie D. et al. Electrostatic forces for satellite swarm navigation and reconfiguration. Final report for Ariadna Study Id. AO 4919 05. ESA, 2006. 96 p.

  10. Liu J., Gangqiang L., Zhu Z.H. et al. Automatic orbital maneuver for mega-constellations maintenance with electrodynamic tethers // Aerospace Science and Technology. 2020. V. 105. Art. ID. 105910. https://doi.org/10.1016/j.ast.2020.105910

  11. Yang Y.-W., Cai H. Extended time–delay autosynchronization method for libration control of electrodynamic tether using Lorentz force // Acta Astronaut. 2019. V. 159. P. 179–188. https://doi.org/10.1016/j.actaastro.2019.03.038

  12. Lu H., Li A., Wang C., Zabolotnov Y. Stability analysis and motion control of spinning electrodynamic tether system during transition into spin // Acta Astronaut. 2020. V. 177. 2019. P. 871–881. https://doi.org/10.1016/j.actaastro.2019.11.032

  13. Voevodin P.S., Zabolotnov Y.M. Analysis of the Dynamics and Choice of Parameters of an Electrodynamic Space Tether System in the Thrust Generation Mode // Cosm. Res. 2020. V. 58. Iss. 1. P. 42–52. https://doi.org/10.1134/S0010952520010062

  14. Ohkawa Y., Kawamoto S., Okumura T. et al. Review of KITE – Electrodynamic tether experiment on the H-II Transfer Vehicle // Acta Astronaut. 2020. V. 177. 2019. P. 750–758. https://doi.org/10.1016/j.actaastro.2020.03.014

  15. Kalenova V.I., Morozov V.M. Stabilization of Satellite Relative Equilibrium Using Magnetic and Lorentzian Moments // Cosm. Res. 2021. V. 59. Iss. 5. P. 343–356. https://doi.org/10.1134/S0010952521050051

  16. Alexandrov A.Y., Tikhonov A.A. Electrodynamic Control with Distributed Delay for AES Stabilization in an Equatorial Orbit // Cosm. Res. 2022. V. 60. Iss. 5. P. 366–374. https://doi.org/10.1134/S0010952522040013

  17. Kalenova V.I., Morozov V.M. Novel approach to attitude stabilization of satellite using geomagnetic Lorentz forces // Aerospace Science and Technology. 2020. V. 106. Iss. 1. Art. ID. 106105. https://doi.org/10.1016/j.ast.2020.106105

  18. Guzmán J.J., Edery A. Mission design for the MMS tetrahedron formation // IEEE Aerosp. Conf. Proc. 2004. V. 1. P. 533–540. https://doi.org/10.1109/AERO.2004.1367637

  19. Shestakov S., Ovchinnikov M., Mashtakov Y. Analytical approach to construction of tetrahedral satellite formation // J. Guid. Control. Dyn. 2019. V. 42. Iss. 12. P. 2600–2614. https://doi.org/10.2514/1.G003913

  20. Guerman A.D., Smirnov G.V., Paglione P., Seabra A.M.V. Stationary configurations of a tetrahedral tethered satellite formation // J. Guid. Control. Dyn. 2008. V. 31. Iss. 2. P. 424–428. https://doi.org/10.2514/1.31979

  21. Hill G.W. Researches in the Lunar Theory // Am. J. Math. 1878. V. 1. P. 5–26.

  22. Ivanov D., Monakhova U., Ovchinnikov M. Nanosatellites swarm deployment using decentralized differential drag-based control with communicational constraints // Acta Astronaut. 2019. V. 159. P. 646–657. https://doi.org/10.1016/j.actaastro.2019.02.006

  23. Mashtakov Y.V., Ovchinnikov M.Y., Tkachev S.S. Study of the disturbances effect on small satellite route tracking accuracy // Acta Astronaut. 2016. V. 129. P. 22–31. https://doi.org/10.1016/j.actaastro.2016.08.028

  24. Барбашин Е.А. Введение в теорию устойчивости. М.: Наука, 1967.

  25. Кюнци Г.П., Крелле В. Нелинейное программирование. М.: Советское радио, 1965.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал