Кристаллография, 2019, T. 64, № 1, стр. 20-28

ВВЕДЕНИЕ

Лабораторные исследования дифракции рентгеновских лучей в кристаллах в течение многих лет проводили в двух взаимно дополняющих схемах, получивших название “рентгеновская секционная топография” и “рентгеновская двухкристальная дифрактометрия” [1]. В качестве источника использовали рентгеновскую трубку, создающую квазимонохроматическое излучение. Однако полуширина спектра характеристического излучения рентгеновской трубки все же недостаточно мала для того, чтобы иметь необходимую временную когерентность. С другой стороны, относительно большая излучающая поверхность соответствует малому размеру пространственной когерентности.

В методе рентгеновской секционной топографии проблему создания когерентного излучения решают с помощью установки узкой щели перед кристаллом [2], которая ограничивает пространственные размеры пучка. Как показано в [3], в этом случае щель становится вторичным некогерентным источником, но малых размеров, что позволяет наблюдать на фотопленке интерференционные полосы с большим периодом в центральной области засветки кристалла, которые описываются теорией дифракции сферической волны [4].

В методе рентгеновской двухкристальной дифрактометрии проблему решают другим способом. Измеряется интегральная по площади интенсивность излучения после отражения от двух кристаллов в зависимости от угла поворота второго кристалла относительно первого. Первый кристалл называют монохроматором, второй – образцом. При использовании бездисперсионной схемы, когда углы Брэгга для обоих кристаллов совпадают, и асимметричного отражения от монохроматора можно получить “практически собственную” кривую дифракционного отражения (КДО), которая совпадает с теоретической кривой угловой зависимости отражения при дифракции плоской монохроматической волны [1].

При переносе таких экспериментов на источник синхротронного излучения (СИ) возникает несколько новых проблем. Во-первых, использование бездисперсионной схемы и асимметричного отражения от монохроматора не всегда возможно и желательно. С другой стороны, спектр СИ очень широкий, и его необходимо ограничивать дополнительно, поскольку первый кристалл просто работает как призма, разлагая частотный спектр в угловой спектр, так как угол Брэгга почти линейно зависит от частоты в небольшом интервале частот.

Для получения почти параллельного и монохроматического пучка СИ обычно используют две пары кристаллов в дисперсионной схеме (например, [5, 6]). Два кристалла для каждого отражения необходимы для того, чтобы сохранить направление пучка.

В [7] при использовании СИ дополнительно к симметричному монохроматору, состоящему из пары кристаллов, в экспериментальной схеме устанавливали узкую щель перед кристаллом-образцом. Изучали трехволновую компланарную дифракцию в парателлурите TeO₂. Удобство использования СИ в таких экспериментах состоит в том, что монохроматор позволяет выделить любую частоту излучения и тем самым построить двумерную карту (угол−частота), на которой легко зафиксировать многоволновое взаимодействие.

Однако оказалось, что двухволновые КДО как в случае сильного (с малыми индексами Миллера), так и слабого (с большими индексами Миллера) отражения имели полуширину, значительно превосходящую полуширину “собственных” КДО, причем уширение слабого отражения было намного больше. Заметим, что в [8] аналогичные экспериментальные результаты, полученные с лабораторным источником излучения, вполне допускали теоретическое моделирование в рамках существующей теории.

Более того, недавние эксперименты с использованием СИ в указанной выше схеме [9] измерения двухволновых КДО в кремнии для разных индексов отражения от монохроматора и образца и разных размеров щели показали интересные особенности, для объяснения которых необходимо развитие более точной теории, которая бы в явном виде учитывала все параметры экспериментальной схемы, включая не только кристаллы, но и размер источника, расстояния до щели перед кристаллом-образцом и ее размер.

Попытки теоретического описания экспериментальных схем с возможностью численного моделирования эксперимента предпринимались и раньше (например, [5, 10–12]), однако схемы, в которых необходимо одновременно аккуратно учитывать дифракцию в кристалле и дифракцию на щели, не рассматривались.

В настоящей работе представлена последовательная теория, которая впервые аккуратно учитывает размер источника, дифракцию в кристаллах и на щели, а также расстояния между элементами оптической схемы. Расчет проводится из первых принципов с использованием методов, развитых при расчете фазово-контрастных изображений некристаллических объектов в условиях ограничения пространственной и временной когерентности, а также дифракции пространственно неоднородных пучков (например, [13–15]).

Общая формула оказалась весьма сложной для анализа, однако в двух приближениях малого и большого размера щели удалось получить формулы, удобные для численного расчета, из которых также можно сделать физические выводы.

ФОРМУЛИРОВКА ЗАДАЧИ

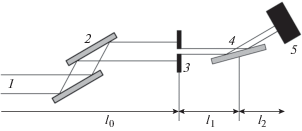
Схема эксперимента показана на рис. 1. Она состоит из источника СИ, двухкристального монохроматора, щели, кристалла–образца и детектора. Как известно, СИ генерируется во время торможения электронов в облаке при его движении по кольцевой орбите. Разные электроны высвечивают короткие цуги волн в разное время, поэтому излучение от них не согласовано по фазе. Хорошей аппроксимацией такого источника является набор точечных источников, расположенных в плоскости, перпендикулярной направлению пучка, которые излучают белый спектр [15].

Разные частоты в спектре излучения некогерентны по той же причине. Детектор регистрирует большой набор коротких цугов из каждой точки источника. Они не согласованы по времени, а время измерения значительно превосходит длительность отдельных цугов [16]. Поэтому уравнения Максвелла необходимо решать для точечного монохроматического источника. Сначала вычисляется интегральная интенсивность такого излучения, регистрируемого детектором. Затем интенсивность суммируется по спектру и по координатам точек на источнике с учетом яркости отдельных точек.

Необходимо вычислить зависимость интегральной интенсивности от угла поворота кристалла–образца и понять, как на нее влияют монохроматор, размер щели и угловой размер источника. Щель можно описать только в прямом пространстве относительно базовой системы координат, поэтому расчет начинается в прямом пространстве.

Рассмотрим волновую функцию монохроматической компоненты излучения с заданной частотой. Выберем произвольную точку на линии пересечения поперечного сечения источника и плоскости дифракции с координатой x_s и базовую траекторию (систему координат), которая начинается в этой точке и идет параллельно оси z. В точке, где она достигает поверхности первого кристалла-монохроматора, она отклоняется на двойной угол Брэгга, соответствующий базовой частоте излучения, и идет по новому направлению до второго кристалла. Там она снова отклоняется на такой же угол в обратную сторону и снова идет параллельно оси z до щели.

При двухволновой дифракции волновая функция излучения изменяется только в плоскости дифракции, образованной направлением распространения пучка и вектором обратной решетки кристалла, представляющим систему атомных плоскостей, от которых этот пучок отражается. В перпендикулярной плоскости кристаллы никак не искажают излучение, и ее можно не учитывать.

Перед щелью амплитуду электрического поля рентгеновского излучения для заданной поляризации можно записать в виде ${\text{exp}}\left( {iKz} \right)A_{0}^{'}\left( {x,{{q}_{{\text{1}}}}} \right)$, где K = ω/c = 2π/λ – волновое число, ω – частота излучения, c – скорость света, λ – длина волны. Ее можно представить в виде суперпозиции плоских волн, если записать функцию $A_{0}^{'}$(x,q₁) в виде следующего интеграла Фурье:

Здесь q – модуль компоненты волнового вектора плоской волны k₀ = K₀ + q в плоскости дифракции в перпендикулярном траектории направлении. Компонента волнового вектора K₀ вдоль траектории точно удовлетворяет условию Брэгга для базовой частоты и дает дополнительный фазовый множитель, который не влияет на интенсивность. Поэтому соответствующий фазовый множитель здесь и далее не выписывается. Вектор q направлен таким образом, что составляет тупой угол с вектором обратной решетки h.

При отражении от кристалла волновой вектор k₀ превращается в волновой вектор k_h = K_h + q_h, где K_h = K₀ + h, а вектор q_h отличается от q на компоненту, параллельную нормали к поверхности кристалла, которая в случае симметричного брэгговского отражения антипараллельна вектору обратной решетки. Модуль этой компоненты находится из условия K_hq_h = 0, т.е. q_h перпендикулярно K_h. Можно показать, что в симметричном случае дифракции модуль вектора q_h равен q и имеет правильное направление. То есть направление плоской волны полностью сохраняется при двойном отражении.

Такое преобразование волнового вектора имеет место при выходе излучения из кристалла из-за преломления на границе, так как модуль волнового вектора в воздухе не может измениться при сохранении частоты излучения. В кристалле волновой вектор другой, он равен ${\mathbf{k}}_{h}^{'}$ = K_h + q, и его модуль не равен модулю исходного вектора k₀. Соответственно параметр отклонения от условия Брэгга равен α = ((k₀ + h)² – K²)/K² = 2hq/K².

В формуле (1) сразу учтено, что фурье-образ пропагатора Френеля

зависит от полного расстояния l₀ вдоль базовой траектории. На самом деле необходимо писать произведение трех пропагаторов: до первого кристалла, между кристаллами и после второго кристалла. Однако из явного вида функции (2) следует, что произведение равно новому пропагатору на суммарном расстоянии.

Пропагатор Френеля есть часть сферической волны в параксиальном приближении без учета базовой плоской волны в направлении пучка. Свертка волновой функции с пропагатором описывает распространение излучения в воздухе. Амплитуды дифракционного отражения (АДО) двух кристаллов монохроматора тоже перемножаются, что приводит к квадрату АДО для одного кристалла P_M(q), так как кристаллы одинаковые. Кристаллы ориентированы произвольным образом, но эффективно работают только на частоте, для которой угол Брэгга соответствует базовой траектории, проходящей через середину щели. Эта частота является базовой частотой.

Рассмотрим ограниченный и относительно малый интервал частот вблизи базовой частоты. В случае произвольного отклонения частоты излучения от базового значения условия Брэгга для кристаллов монохроматора при q = 0 удовлетворяются не точно. Однако при малом изменении частоты можно пренебречь зависимостью параметров дифракции от частоты. Что касается условия Брэгга, то его можно компенсировать поворотом кристаллов на некоторый угол θ₁ = q₁/K.

Чтобы определить этот угол, запишем условие Брэгга в виде 2dsin(θ_B1 + θ₁) = λ + Δλ, где d – межплоскостное расстояние в кристалле, θ_B1 – угол Брэгга для базовой частоты, λ – базовая длина волны. Отсюда находим приближенно, что θ₁ = = (Δλ/λ)tg θ_B1 = –(Δω/ω)tg θ_B1.

Пропагатор Френеля должен зависеть от реальной частоты излучения. Однако небольшое относительное изменение частоты можно компенсировать небольшим относительным изменением расстояния, хотя известно, что результат не очень сильно зависит от небольшого изменения расстояния. То есть можно использовать базовое значение частоты. В результате изменение частоты излучения эффективно определяется только параметром q₁.

Волновую функцию за щелью получаем умножением функции (1) на трансмиссионную функцию щели T(x):

Здесь θ(x) – ступенчатая функция Хевисайда, равная единице в случае положительного аргумента и нулю в случае отрицательного, x₀ – половина ширины щели. При изменении координаты x_s точки на источнике излучения базовая траектория сместится на такое же расстояние. Относительно нее центр щели сместится на обратное расстояние. Используется условие, что базовая траектория проходит через центр щели при координате x_s = 0, т.е. положение щели оптимизировано относительно положения источника.

Для решения задачи нужно представить функцию (3) в виде суперпозиции плоских волн

т.е. вычислить обратное преобразование Фурье:

Окончательно волновая функция на детекторе определяется интегралом

где l₁ – расстояние от щели до кристалла–образца, l₂ – расстояние от кристалла–образца до детектора, P_C(q) – АДО кристалла–образца.

В этой формуле учтены две особенности отражения кристаллом-образцом. Первая состоит в том, что кристалл-образец можно вращать, поэтому его АДО отсчитывается от угла θ_r = q_r/K поворота кристалла относительно его положения, при котором отражение максимально для базовой частоты. При изменении частоты появляется дополнительный угол поворота аналогично тому, как это учитывается в монохроматоре: q₂ = Kθ₂, θ₂ = (Δλ/λ)tg θ_B2.

Важно, что q₂ = q₁M, где M = tg θ_B2/tg θ_B1. Противоположный знак у аргумента функции АДО кристалла–образца объясняется тем, что кристалл-образец ориентирован не параллельно кристаллам монохроматора, а под углом π – θ_B1 – θ_B2 к ним. Если первый кристалл монохроматора отражает горизонтальный пучок вверх, то кристалл-образец отражает его вниз.

Вторая особенность состоит в том, что в кристалле–образце отражение может быть несимметричным, т.е. нормаль к поверхности кристалла не антипараллельна вектору обратной решетки. Кристалл изменяет не только направление пучка, но и его угловую расходимость.

Обычно аргументом АДО принято считать угловое отклонение входящего пучка θ = q/K. Но на выходе из кристалла угловое отклонение относительно базовой траектории будет равно θ' = qb/K, где b = sin θ₀/sin θ_h, θ_0,h – острые углы, которые волновые векторы K_0,h образуют с поверхностью кристалла [1]. Заметим, что θ₀ + θ_h = 2θ_B. В симметричном случае θ₀ = θ_h = θ_B.

В эксперименте измеряется интегральная интенсивность излучения, регистрируемая детектором, как функция угла поворота кристалла θ_r. Соответственно из (6) получаем

Множитель b^–1, если он не равен единице, просто отражает тот факт, что переменные x и q не являются дополнительными. Координата q в обратном пространстве соответствует координате xb на детекторе.

Формула (7) является известным правилом Парсеваля, согласно которому интегралы от интенсивности в прямом и обратном пространствах равны. Так как модуль фурье-образа пропагатора Френеля равен единице, то расстояния от кристалла до детектора не влияют на интегральную интенсивность. Это следствие общего закона сохранения энергии.

Для сравнения с экспериментом нужно вычислить интеграл от этой функции по размеру источника и по спектру излучения. В результате получаем функцию угла вращения кристалла, которую обычно называют КДО. Она определяется формулой

где G_B(x_s) – функция яркости источника в точке x_s, которая обычно аппроксимируется гауссовой функцией. В общем случае задача выглядит достаточно сложной, однако можно рассмотреть предельные случаи, в которых удается получить более простые приближенные формулы.

В последующих расчетах для простоты не будем выписывать множители, которые не влияют на форму КДО. Что касается максимального значения, то в теоретических расчетах обычно используют такую нормировочную константу, которая приводит к “собственной” КДО кристалла–образца в наиболее благоприятном случае. А при сравнении с экспериментом постоянный множитель является подгоночным параметром.

О ВЛИЯНИИ РАЗМЕРА ЩЕЛИ НА КДО

Для вычисления функции A₁(q,x_s,q₁) подставим формулы (1) и (3) в (5) и сдвинем начало координат в интеграле по x. В результате получаем

Подынтегральное выражение содержит быстро осциллирующую экспоненту. Для приближенной оценки интеграла воспользуемся методом стационарной фазы для интеграла по q' внутри интеграла по x.

Аргумент экспоненты (фаза) и точка стационарной фазы соответственно равны

где

В методе стационарной фазы интегрируется экспонента, а остальные части подынтегральной функции выносятся за интеграл в точке стационарной фазы.

В результате приближенно получаем

Здесь не выписан фазовый множитель, так как интересен только модуль этого выражения, а также постоянный множитель, не зависящий от аргументов функции.

В общем случае необходимо вычислять интеграл (12), который эффективно зависит от двух независимых аргументов (q_s – q₁) и (q – q_s). Чтобы получить более простой ответ, рассмотрим два предельных случая.

В первом случае рассматривается щель очень малого размера. Можно пренебречь переменной q_x в аргументе функции $P_{M}^{2}$ и квадратичным по x членом в аргументе экспоненты, так как они малы. В результате формула приобретает более простой вид:

где

Во втором случае рассматривается щель очень большого размера. Наличие в экспоненте члена, квадратичного по координате x, становится существенным и указывает на то, что вся щель все равно не дает вклада в интеграл, а в ней есть участки, которые работают более эффективно, чем остальные. Снова используем приближение стационарной фазы, но уже в интеграле по x. Точка стационарной фазы равна x = r²(q – q_s). Соответственно в этой точке q_x = q – q_s, и, подставляя, получаем более простую формулу в виде

В обоих предельных случаях анализ теоретических формул резко упрощается. Что касается области их применимости, то в первом случае очевидным условием является неравенство x₀ < r. Физический смысл этого условия в том, что размер щели должен быть настолько мал, чтобы можно было пренебречь кривизной поверхности постоянной фазы сферической волны в области щели. То есть перед щелью падающее излучение очень похоже на плоскую волну, направление которой зависит от координаты x_s точечного источника.

Очевидно, что во втором предельном случае необходимо выполнение обратного неравенства x₀ $ \gg $ r. Что касается формулировки условий для ширины “собственных” КДО монохроматора и кристалла–образца, то этот вопрос более сложный. Ответ на него можно получить либо численными экспериментами, либо сравнением с результатами реальных экспериментов.

ПРЕДЕЛЬНЫЙ СЛУЧАЙ ЩЕЛИ МАЛОГО РАЗМЕРА

В этом случае получаем следующее приближение для экспериментальной КДО, переходя от переменной интегрирования x_s к переменной q_s:

где Тройной интеграл удобно вычислять, используя фурье-интегралы функций Подставляя (18) в (16), получаем семикратный интеграл, в котором три интеграла по q равны трем дельта-функциям, которые снимают еще три интеграла по x, и в результате получаем Этот результат интересен с двух точек зрения. Во-первых, он резко сокращает время вычислений, так как существуют эффективные процедуры численного расчета преобразования Фурье. Во-вторых, прямо из формулы можно сделать некоторые физические выводы о влиянии разных элементов экспериментальной схемы на результат.

В случае бездисперсионной схемы, когда M = 1, учет размеров источника сводится к постоянному множителю $G_{B}^{'}\left( 0 \right)$. То есть размер источника никак не влияет на форму КДО. При малых отличиях M от единицы кривая функции источника будет широкой, поэтому источник влиять будет слабо, а при больших отличиях он может существенно влиять на результат. Если аппроксимировать функцию яркости источника G_B(q_s) гауссовой функцией

то функция $G_{B}^{'}\left( x \right)$ вычисляется аналитически и равна

Из полученной формулы также следует, что если кривая $G_{C}^{'}\left( x \right)$ имеет минимальную полуширину из всех четырех функций, то в результате получится “почти собственная” КДО кристалла–образца. Если $G_{B}^{'}\left( x \right)$ имеет минимальную полуширину, то эксперимент покажет угловой размер источника. Аналогично для очень узкой щели эксперимент может показать угловой размер щели. Также можно получить “почти собственную” КДО монохроматора.

Часто “собственные” КДО монохроматора и образца соизмеримы по ширине, а КДО щели может иметь как меньшую, так и большую ширину, причем большая ширина наблюдается в случае узкой щели. Угловая ширина щели, как известно, равна θ_S = λ/D, где D = 2x₀ – ширина щели. Этот результат можно сразу получить из формулы (14). При λ = 10^–10 м, D = 50 мкм получаем θ_S = 2 мкрад. Даже такая узкая щель не должна приводить к сильному уширению экспериментальной КДО.

Рассмотренное приближение соответствует приближению геометрической оптики для кристаллов. Его часто используют при анализе дифракции расходящегося излучения в кристаллах, в том числе в деформированных кристаллах. Часто точно так же описывают щель.

Отметим, что функция $G_{S}^{'}\left( x \right)$ имеет также аналитический вид:

Эту формулу легко получить, если учесть, что эта функция является сверткой двух функций щели θ(x₀ – |x|). То есть она равна площади перекрытия двух прямоугольников единичной высоты и шириной 2x₀. При полном перекрытии она равна 2x₀, при расстоянии между ними, равном или больше 2x₀, она равна нулю (нет перекрытия), а между точками 0 и 2x₀ изменяется линейно.

ПРЕДЕЛЬНЫЙ СЛУЧАЙ ЩЕЛИ БОЛЬШОГО РАЗМЕРА

В этом случае получаем следующее приближение для экспериментальной КДО:

где

Аналогично предыдущему разделу этот трехкратный интеграл методом преобразования Фурье можно свести к однократному интегралу в виде

Самый важный вывод, который следует из формулы (25), состоит в том, что в бездисперсионной схеме, когда M = 1, форма кривой КДО не зависит от размеров источника и размера щели. Она определяется просто сверткой КДО монохроматора и кристалла–образца. Это свойство легко вывести и непосредственно из формулы (23), если в интеграле по q₁ сделать замену переменной q₁ на q – q₁. Функции G_M и G_C перестают зависеть от q, а интегралы по q_s и q превращаются в множители, не зависящие от q_r.

Интересно, что такой же вывод следует из формулы предыдущего раздела при большом размере щели. Размер источника снова не влияет на форму КДО, а широкая щель приводит к большой полуширине функции $G_{S}^{'}(x)$ по сравнению с полуширинами функций монохроматора $G_{M}^{'}(x)$ и кристалла–образца $G_{C}^{'}(x)$.

Однако в дисперсионной схеме, когда M не равно единице, ситуация меняется. Теперь необходимо учитывать функцию $G_{T}^{'}(x)$, которая равна

Полуширина этой функции равна πr²/x₀. Она может быть сколь угодно малой с ростом ширины щели. Соответственно полуширина КДО будет сколь угодно большой и будет определяться только угловой расходимостью излучения в пределах широкой щели. В этом случае кристаллы очень слабо влияют на результат.

КОНКРЕТНЫЕ ПРИМЕРЫ

В численных расчетах по формулам (19) и (25) разумно использовать функции $G_{B}^{'}(x)$, $G_{M}^{'}(x)$, $G_{S}^{'}(x)$ и $G_{T}^{'}(x)$ при нормировке, когда они равны единице для x = 0. В этом случае они никак не искажают “собственную” КДО кристалла–образца, если имеют очень большую полуширину по сравнению с “собственной” КДО. Вопрос о том, насколько эти функции искажают форму “собственной” КДО кристалла–образца, является главным вопросом теории.

Расчет конкретных примеров выполнен для параметров станции “Рентгеновская кристаллография и физическое материаловедение” Курчатовского источника СИ [17], а именно l₀ = 13 м, σ_s = Kσ_x/l₀, где σ_x = 54 мкм – параметр гауссиана, моделирующего поперечный размер источника в реальном пространстве, и для энергии рентгеновских фотонов E = 12 кэВ, K = 6.0812 × 10⁴ мкм^–1.

Компьютерная программа написана на языке ACL [18]. Расчет АДО P_M(q) и P_C(q) проводился с помощью стандартного модуля для общего случая многослойного кристалла по формулам [19]. Использовался один слой достаточно большой толщины. Наиболее интересная ситуация возникает в случае дисперсионной схемы с M < 1. Рассмотрим монохроматор из кремния с симметричным отражением 333 и кристалл–образец из кремния с симметричным отражением 111. В этом случае tg θ_B1 = 29.621°, tg θ_B2 = 9.483°, M = 0.2938.

Расчет интегралов Фурье проводился методом быстрого преобразования Фурье (FFT – Fast Fourier Transformation) на сетке точек с постоянным шагом и с числом точек 2¹⁶ = 65 536. Интервал изменения аргумента x был равен X = 512 мкм. В соответствии с условиями метода FFT шаг сетки точек для аргумента q был равен 2π/X с тем же самым числом точек. Реально функции существенно изменяются на меньших интервалах, поэтому для графиков использовали не все точки сетки, а лишь их центральную часть.

На рис. 2 показаны функции $G_{C}^{'}(x)$, $G_{M}^{'}(Mx)$, $G_{B}^{'}([{\text{1 }} - M]x)$, $G_{S}^{'}(x)$ и $G_{T}^{'}([{\text{1 }} - M]x)$ для указанного выше случая и для ширины щели 50 мкм. Первые две функции являются комплексными и имеют небольшую мнимую часть, так как соответствующие им преобразования Фурье являются несимметричными. Они показаны на рис. 2а и 2б двумя кривыми. Кривая 1 соответствует реальной части, 2 – мнимой. Остальные три функции показаны на рис. 2в и различаются цифрами 1, 2, 3.

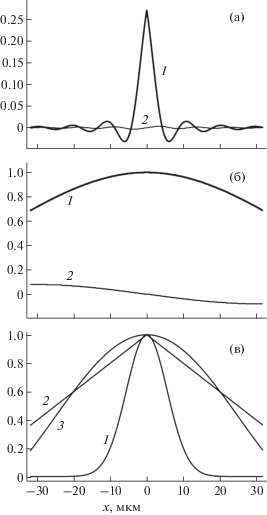
Первые три функции не зависят от ширины щели и используются одинаковым образом в обоих приближениях для щели малого и большого размера. Хорошо видно, что функция $G_{C}^{'}(x)$ имеет наименьшую полуширину, а функции $G_{S}^{'}(x)$ и $G_{T}^{'}([{\text{1 }} - M]x)$, хотя и различаются по форме, но слабо искажают “собственную” КДО кристалла–образца. Поэтому не удивительно, что в обоих приближениях симуляция экспериментальной КДО практически одинакова.

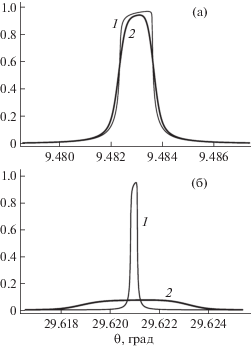
Результат расчета показан на рис. 3а. Здесь кривая 1 соответствует “собственной” КДО кристалла–образца в приближении падающей плоской монохроматической волны, а кривая 2 симулирует результат эксперимента. В соответствии с выбранной нормировкой площади под кривыми равны. Результат показан в приближении щели малого размера, но кривая в приближении щели большого размера практически с ней совпадает, и обе кривые трудно различить.

Особенности двух приближений состоят в том, что щель искажает экспериментальную КДО только при очень малых размерах за счет дифракции излучения на ней, когда угловая ширина щели θ_S = λ/D становится больше угловой ширины “собственной” КДО кристалла–образца. При большом размере щели ее угловая ширина мала, и щель не искажает результат.

С другой стороны, приближение большого размера щели учитывает ее угловой размер, связанный с расходимостью падающего на щель излучения. Исходная расходимость не ограничена, а щель ее ограничивает тем лучше, чем меньше ее размер. Как показывает расчет, существует интервал размеров щели, внутри которого она не искажает экспериментальную КДО.

Легко оценить, что для щели размером D = 1 мкм ее угловая ширина вследствие дифракции будет равна λ/D = 100 мкрад, это больше, чем угловая ширина “собственной” КДО, т.е. ширина экспериментальной КДО будет примерно та же, и будет отлична от нуля вторая производная в центре. С другой стороны, щель размером D = 2 мм будет иметь угловой размер D/l₀ = 154 мкрад. С учетом множителя (1 – M) угловая полуширина экспериментальной КДО будет равна 109 мкрад, или 0.0062°, и будет почти нулевой вторая производная в центре. Эти оценки полностью соответствуют результатам численных расчетов.

Рассмотрим обратную ситуацию, когда в монохроматоре реализуется отражение 111, а в кристалле–образце 333. В этом случае параметр M = = 3.404, а углы Брэгга имеют те же значения, что и в предыдущем случае, только меняются местами. При этом полуширина функции $G_{C}^{'}(x)$ будет больше, а полуширина функции $G_{M}^{'}(Mx)$ во много раз меньше, и результат свертки будет определяться исключительно монохроматором.

Результат расчета показан на рис. 3б. Снова кривая 1 соответствует “собственной” КДО, а кривая 2 симулирует экспериментальную КДО. Интересно, что хотя экспериментальная кривая очень сильно уширена, она все же асимметрична. Эту асимметрию объясняет тот факт, что кривая фактически является уширенной КДО монохроматора. Однако нормировка выбрана такой, что площадь под обеими кривыми одинаковая, поэтому максимум на кривой меньше, чем на КДО монохроматора.

ЗАКЛЮЧЕНИЕ

Теоретически показано, что новая схема рентгеновской двухволновой дифрактометрии с использованием синхротронного излучения, монохроматора с симметричными отражениями, узкой щели и кристалла–образца позволяет получить “почти собственную” кривую дифракционного отражения кристалла–образца, если для монохроматора использовать отражения при большом угле Брэгга, который в 2 раза или более превосходит угол Брэгга для кристалла–образца.

В этом случае размер щели должен иметь оптимальное значение, так как при очень малом размере возможная дифракция излучения на щели увеличивает угловую расходимость пучка, а при большом размере угловая расходимость исходного излучения может быть аномально большой. Оптимальное значение для кристалла кремния равно 50 мкм.

В обратном случае монохроматор не обеспечивает нужную коллимацию и монохроматизацию пучка, и КДО кристалла–образца сильно уширена, причем выбором размера щели ситуацию исправить невозможно. Таким образом, данная схема пригодна для исследования отражений с высокими индексами Миллера только при условии использования отражений в монохроматоре с очень большими индексами.

Теория учитывает все параметры экспериментальной схемы, включая размер источника, расстояния, размер щели. Она позволила объяснить особенности экспериментальных результатов [7, 9].

Автор выражает благодарность П.А. Просекову за проявленный интерес к работе и ценные замечания.