Кристаллография, 2019, T. 64, № 1, стр. 161-166
Рентгеновская томография в условиях полихроматического зондирования: использование знаний о мультикомпонентности в методе реконструкции
В. Е. Прун 1, А. В. Бузмаков 2, М. В. Чукалина 2, 3, *
1 Московский физико-технический институт
Долгопрудный, Россия
2 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия
3 Институт проблем передачи информации РАН
Москва, Россия
* E-mail: chukalinamarina@gmail.com
Поступила в редакцию 28.05.2018
После доработки 05.07.2018
Принята к публикации 05.07.2018
Аннотация
Предложен новый подход к решению задачи томографической реконструкции при сканировании объектов полихроматическим излучением. Применение алгебраического метода реконструкции, в котором заложена возможность учитывать спектральные особенности взаимодействия компонентов объекта с излучением, позволяет восстанавливать карты их распределения. Одновременный анализ полученных карт и результата реконструкции методом свертки и обратной проекции позволяет количественно проинтерпретировать результат реконструкции, несмотря на возникающие искажения. Оптимизационная задача решается в условиях наличия ограничений на локальный состав. Обсуждаются результаты реконструкции для синтетических проекций.
ВВЕДЕНИЕ
Метод томографии позволяет восстанавливать 3D-структуру объекта без его физического разрушения. Это достигается путем математической обработки набора измеренных томографических 2D-проекций. Сканирование полихроматическим излучением в методе рентгеновской томографии позволяет существенно сократить время проведения измерений. Это особенно востребовано в биологических и медицинских приложениях, где зондируемым объектом является живой организм. Помимо потребности снизить дозовую нагрузку проведение измерений за как можно более короткий период продиктовано тем, что живой объект может оставаться неподвижным лишь непродолжительный период времени.
Традиционно используемые алгоритмы реконструкции предполагают, что зондирование ведется монохроматическим излучением. То есть для зондирования используется только одна выделенная каким-либо способом длина волны рождаемого источником рентгеновского излучения спектра. Использование полихроматического излучения (используется весь рожденный источником спектр или какая-то его часть) усложняет интерпретацию результатов реконструкции, если реконструкция проводится классическими (не ориентированными под задачу полихроматического зондирования) методами [1]. Связано это с тем, что восстанавливаемой функцией в классической задаче реконструкции для метода рентгеновской томографии является функция распределения коэффициента линейного ослабления объекта, которая однозначно описывает морфологию зондируемого объекта только в случае монохроматического зондирования. То есть объект сканируется монохроматическим излучением и восстанавливается распределение коэффициента для используемой энергии. При этих условиях прямая задача томографии может быть сведена к преобразованию Радона. Тогда обратная задача или задача реконструкции заключается в восстановлении функции по ее известному преобразованию Радона.
При полихроматическом зондировании модель формирования сигнала меняется, и свести к преобразованию Радона прямую задачу удается лишь с некоторыми допущениями, нарушающими однозначную связь между восстанавливаемой величиной и морфологией зондируемого объекта. Существует несколько способов выстроить такую связь. Например, применять для зондирования не один, а два спектра [2], или использовать априорные знания о составе объекта в методах реконструкции со статистическим подходом [3]. В настоящей работе метод условной минимизации с регуляризацией использован для решения оптимизационной задачи. Описаны постановка задачи, предлагаемый алгоритм реконструкции, обсуждаются результаты модельного эксперимента для нового метода и метода свертки и обратной проекции. Последний метод в основном реализован в серийно выпускаемых томографах. Сходимость предложенного метода подтверждена результатами моделирования.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФОРМИРОВАНИЯ ТОМОГРАФИЧЕСКОЙ ПРОЕКЦИИ ПРИ ПОЛИХРОМАТИЧЕСКОМ ЗОНДИРОВАНИИ
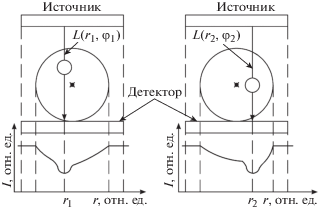
Задача решается в следующей постановке. Пусть двухкомпонентный объект зондируется полихроматическим излучением, спектр которого описывается функцией ${{I}_{0}}(E)$. Для данного спектра ослабляющие свойства одного компонента отличаются от свойств другого. Например, зуб с металлическим включением, допустим, коронкой, зондируется рентгеновским спектром, сформированным молибденовым анодом. Тогда материал зуба – это один компонент, а металлическая коронка – второй. Компоненты объекта пространственно разделены (в одном пикселе одновременно не может быть двух компонентов) и их поглощательные свойства затабулированы [4]. В модели используется приближение параллельной схемы измерения (рис. 1). Оно правомерно, если расстояние источник–образец достаточно велико. Рассмотрим 2D-задачу, т.е. будем восстанавливать распределение компонентов в одном из сечений объекта. Система “источник–детектор” неподвижна. Детектор позиционно-чувствительный. Объект укреплен на гониометре. Величина φ описывает текущий проекционный угол, r – определяет ячейку детектора, для которой будет записано выражение, связывающее величину регистрируемого сигнала и распределение фракций компонентов (рис. 1).
Согласно закону Бугера–Ламберта–Бера наблюдается экспоненциальное ослабление зондирующего излучения при его прохождении через объект:
(1)
$I(\varphi ,r) = \int {dE{{I}_{0}}(E)} \exp \left( { - \int\limits_0^{L(r,\varphi } {\mu (l,E)} } \right)dl.$ОБ ОБРАТНОЙ ЗАДАЧЕ В ДВУХ ПОСТАНОВКАХ
Рассмотрим алгебраический подход к решению обратной задачи, т.е. будем решать алгебраическую систему уравнений [1]. Воспользуемся векторной записью. Введем матрицу весов $W$, размером ${{n}_{\varphi }}n \times {{n}^{2}}$, которая описывает геометрию эксперимента и содержит значения 0 и 1. 1 – если рассматриваемый луч пересекает пиксел, 0 – не пересекает. Здесь ${{n}_{\varphi }}$ – число проекционных углов, $n$ – число ячеек детектора соответственно, $n \times n$ – размер восстанавливаемого сечения. Векторы ${{c}_{1}}$ и ${{c}_{2}}$ размером $n \times n$ есть восстанавливаемые изображения, а компонентами вектора I размером ${{n}_{\varphi }}n$ являются измеренные значения. Рассмотрим только дискретные значения энергий используемого для зондирования спектра. Перепишем математическую модель формирования проекций, применив введенные обозначения:
(3)
$I = \sum\limits_j {I_{0}^{j}\exp \left( { - W\left( {{{c}_{1}}\mu _{1}^{j} - {{c}_{2}}\mu _{2}^{j}} \right)} \right)\Delta E} ,$(4)
$Q({{c}_{1}},{{c}_{2}}) = \frac{{{{{\left\| {{{I}^{{{\text{exper}}}}} - {{I}^{k}}} \right\|}}_{2}}}}{{\sum\limits_j {I_{0}^{j}\Delta E} }}.$(5)
$\left\{ \begin{gathered} {{с }_{1}} \geqslant 0, \hfill \\ {{с }_{1}} \leqslant 1, \hfill \\ {{с }_{2}} \geqslant 0, \hfill \\ {{с }_{2}} \leqslant 1 \hfill \\ \end{gathered} \right.$(6)
$F({{c}_{1}},{{c}_{2}}) = Q({{c}_{1}},{{c}_{2}}) + \beta {{\left\| {{{c}_{2}} \circ {{c}_{2}}} \right\|}_{2}}.$(7)
$\begin{gathered} F({{c}_{1}},{{c}_{2}}) = Q({{c}_{1}},{{c}_{2}}) + \beta {{\left\| {{{c}_{2}} \circ {{c}_{2}}} \right\|}_{2}} - \\ - \;\frac{1}{t}\left( {\lg ( - {{c}_{1}}) + \lg ( - {{c}_{2}}) + \lg (1 - {{c}_{1}}) + \lg (1 - {{c}_{2}})} \right). \\ \end{gathered} $В серийных томографах для решения задачи реконструкции применяется метод свертки и обратной проекции (Filtered Back Projection (FBP)) [1]. Метод выбирается производителями за его быстродействие. Результат работы метода есть пространственное распределение некоторого усредненного коэффициента линейного ослабления зондируемого объекта. Рассмотрим приближения, без которых метод не применим, и обсудим последствия их влияния на результат реконструкции. Обратимся к выражению (1) и перепишем его, введя оператор преобразования Радона:
где ${{\mu }_{E}}(\varphi ,r)$ – точки, лежащие на траектории луча $(\varphi ,r)$. Дальнейшая работа ведется с результатом логарифмирования $P(\varphi ,r)$. Согласно [7], это(9)
$P(\varphi ,r) = - \ln \left( {\int {dE{{I}_{0}}(E)\exp \left( { - R{{\mu }_{E}}(\varphi ,r)} \right)} } \right).$(10)
$P(\varphi ,r) = - \ln \left( {\frac{{\int {dE{{I}_{0}}(E)\exp \left( { - R{{\mu }_{E}}(\varphi ,r)} \right)} }}{{\int {dE{{I}_{0}}(E)} }}} \right).$В следующем разделе описан предлагаемый подход к интерпретации результатов компьютерной томографии при полихроматическом зондировании двухкомпонентных объектов, позволяющий в будущем автоматизировать интерпретацию результата. Карты распределения компонентов анализируются совместно с результатом, полученным методом FDK [11].
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
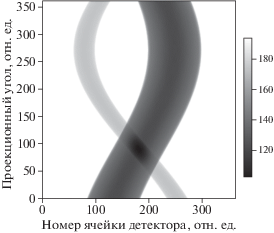
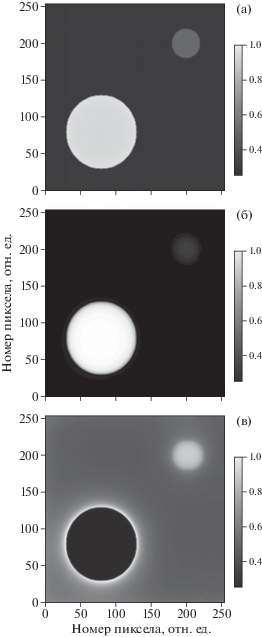
Приведенные результаты модельного эксперимента получены для двухкомпонентного фантома. Пространственные распределения компонентов ${{c}_{1}}$ и ${{c}_{2}}$ приведены на рис. 2. Зависимости коэффициентов ослабления от энергии для каждого из компонентов и спектр, использованные при расчете синограммы, представлены на рис. 3. На рис. 4 приведена синограмма, рассчитанная с использованием выражения (1). Реконструкция проводилась двумя методами: FBP (рис. 5а) и алгебраическим (рис. 5б, 5в). При решении оптимизационной задачи использовались следующие значения параметров: β = 0.05, t = 1. Процедура выбора значений состоит в нахождении таких величин, чтобы выполнялись сразу два условия: значение градиентов по всем трем слагаемым выражения (6) соизмеримы, т.е. ни одно из слагаемых в суммарном шаге не доминирует; суммарный шаг не выводит за границы целевого множества. В экспериментах параметры подбирались экспертом вручную, в дальнейшем их подбор планируется осуществлять автоматически. Если за 20 итераций значение функционала (6) изменялось меньше чем на 0.001, то величина параметра $t$ удваивалась. Начальное значение функционала – 2011.815, значение на момент остановки – 19.232. Использованное для реконструкции число итераций равно 1800. Результаты реконструкции ${{c}_{1}}$ и ${{c}_{2}}$ алгебраическим методом представлены на рис. 5б и 5в соответственно. Отметим, что три изображения, приведенные на рис. 5, дополняют друг друга. Результат реконструкции методом FDK предъявляет весь объект целиком, не давая никаких указаний к интерпретации. В то время как рис. 5б точно указывает местоположение первого компонента, а распределение ${{c}_{2}}$ (рис. 5в) показывает в дополнение к местоположению второго место отсутствия первого. Однако вывод о том, что гало вокруг места отсутствия первого есть артефакт, можно сформулировать лишь после сравнения результатов на рис. 5в и 5а. В дальнейшем планируется продолжить исследования с целью уменьшения величины артефактов и создания метода совместной интерпретации получаемых разными методами результатов.
Рис. 2.
Вид фантома, использованного для расчета синограммы; распределение первой (а) и второй (б) компоненты. Белый цвет соответствует объекту, черный – фону.
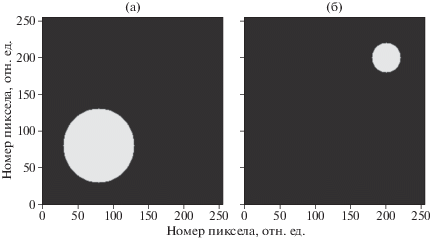
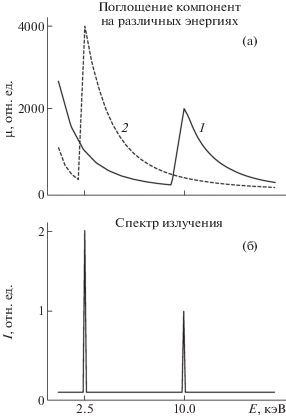
Рис. 3.
Зависимость коэффициентов ослабления рентгеновского излучения компонентами фантома от энергии. Края поглощения для первого – 10 кэВ и второго – 2.5 кэВ (а). Спектр, использованный для расчета синограммы (б).
ЗАКЛЮЧЕНИЕ
Описан новый подход к решению задачи томографической реконструкции при сканировании объектов полихроматическим излучением. Поскольку результат реконструкции при использовании традиционных алгоритмов в таких условиях представляет собой распределение некоторого усредненного коэффициента ослабления рентгеновского излучения, полученное распределение не всегда удается легко связать с морфологией объекта. Предложено решать задачу реконструкции в постановке, когда восстанавливаются распределения компонентов объекта. Задача реконструкции решается алгебраическим методом. Функционал, содержащий невязку и регуляризирующий член, минимизируется на наборе ограничений. Обсуждаются результаты модельного эксперимента с двухкомпонентным объектом, в котором продемонстрирована потенциальная возможность разделения компонент. Дополнение ансамбля интерпретируемых изображений результатом реконструкции методом FBP позволяет выделить на восстановленных распределениях компонентов сомнительные области. Одним из направлений дальнейшей работы будет создание алгоритма совместного анализа результатов реконструкции двумя методами. Во время работы над текстом статьи была опубликована работа [11], в которой приведен обзор последних аппаратных и программных подходов к решению задачи, возникающей в томографии в условиях полихроматического зондирования. Это подчеркивает необходимость создания отдельных инструментов при работе в таких условиях и актуальность представленных в данной статье работ.
Авторы выражают благодарность Н.П. Власовой за техническое содействие в подготовке материалов (ФИЦ ИУ ИСА РАН).
Исследования, посвященные способу модификации алгебраического метода томографии для работы с мультикомпонентными данными, и численная реализация использованных алгоритмов проводились при финансовой поддержке Российского научного фонда (проект № 14-50-00150). Реализация модельных расчетов, включая оптимизацию используемых распределений, выполнялась при поддержке Федерального агентства научных организаций (соглашение № 007-ГЗ/Ч3363/26).
Список литературы
Наттерер Ф. Математические аспекты компьютерной томографии. М.: Мир, 1990. 288 с.
Maaß C., Meyer E., Kachelrieß M. // Med. Phys. 2011. V. 38. № 2. P. 691.
Elbakri I.A., Fessler J.A. // IEEE Trans. Med. Imaging. 2002. V. 21. № 2. P. 89.
Schoonjans T., Brunetti A., Golosio B. et al. // Spectrochim. Acta. B. 2011. V. 66. № 11–12. P. 776.
Boyd S., Vandenberghe L. Convex optimization. Cambridge: Cambridge University press, 2004. 730 p.
Прун В., Николаев Д., Чукалина М., Ингачева А., Бузмаков А. // Тез. докл. “Информационные технологии и системы 2015” 39-я междисциплинарная школа-конференция, Сочи, 7–11 сентября 2015. С. 536.
Park H.S., Hwang D., Seo J.K. // IEEE Trans. Med. Imaging. 2016. V. 35. № 2. P. 480.
Bock R., Hoppe S., Scherl H., Hornegger J. // Proc. Workshop Bildverarbeitung fur die Medizine, Munchen, 25–27 Marz 2007. P. 46.
Nikolaev D.P., Buzmakov A., Chukalina M. et al. // 9-th Int. Conf. Machine Vision (ICMV 2016). France, Nice. 2016, Proc. SPIE 10253. P. 102530B.
Chukalina M., Ingacheva A., Buzmakov A. et al. // Proc. 31-st Europ. Conf. Modelling and Simulation, Budapest, Hungary, 23–26 May 2017. P. 270.
Feldkamp L.A., Davis L.C., Kress J.W. // J. Opt. Soc. Am. A. 1984. V. 1. № 6. P. 612.
Kazantsev D., Jorgensen J., Andersen M. et al. // Inverse Problems. 2018. V. 34. P. 064001.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография