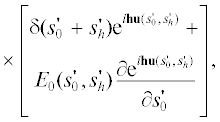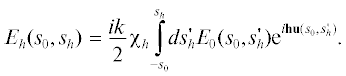Кристаллография, 2019, T. 64, № 2, стр. 173-183
К решению обратной задачи дифракционной рентгеновской топо-томографии. компьютерные алгоритмы и 3D-реконструкция на примере кристалла с точечным дефектом кулоновского типа
П. В. Конарев 1, 2, *, Ф. Н. Чуховский 1, **, В. В. Волков 1
1 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия
2 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: konarev@crys.ras.ru
** E-mail: f_chukhov@yahoo.ca
Поступила в редакцию 06.04.2018
После доработки 17.04.2018
Принята к публикации 17.04.2018
Аннотация
На основе полукинематического решения уравнений Такаги–Топена для амплитуды дифрагированной σ-поляризованной волны предложен последовательный подход к решению обратной задачи дифракционной рентгеновской топо-томографии. Рассмотрен пример точечного дефекта кулоновского типа в кристаллической пластине Si(111) в условиях симметричной лауэ-дифракции и набора наклонных двумерных топографических проекций, отвечающих вращению плоскопараллельного кристалла-образца вокруг вектора дифракции [$\bar {2}20$]. Для компьютерной реконструкции трехмерной функции поля смещений вокруг точечного дефекта использованы итерационные алгоритмы моделирования отжига и квазиньютоновского типа. Представлены результаты компьютерного моделирования функции поля смещений по данным одной 2D-проекции, отвечающей изображению точечного дефекта на рентгеновской топограмме в классическом смысле рентгеновской дифракционной топографии.
ВВЕДЕНИЕ
Как известно [1–6], дифракционная рентгеновская топография (ДРТ) является высокочувствительным неразрушающим инструментом диагностики различных дефектов кристаллической решетки, таких как полосы роста, границы зерен, дефекты упаковки, отдельные включения и дислокации различного типа. Все эти дефекты приводят к изменению положений отдельных атомов кристаллической структуры относительно их правильного положения. При этом в схемах лауэвской и/или брэгговской дифракции реальная структура кристалла изучается по его 2D-проекциям. Как правило, для интерпретации и анализа экспериментальных ДРТ-изображений дефектов на 2D-проекциях они сопоставляются с 2D-проекциями, рассчитанными на основе компьютерного моделирования изображений дефектов с использованием численных методов решения динамических уравнений Такаги–Топена [1–3, 6–8].
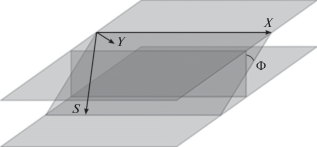
В последние 20 лет в структурном анализе реальных кристаллов широко применяется метод дифракционной рентгеновской топо-томографии (ДРТТ). В методе ДРТТ кристалл-образец поворачивается вокруг оси, перпендикулярной семейству отражающих плоскостей кристалла (ось вращения выбирается вдоль вектора дифракции $h$). Поэтому при различных значениях соответствующего угла поворота получается набор дифракционных 2D-проекций, каждая из которых отвечает разным ориентациям плоскости дифракционного рассеяния рентгеновского излучения по отношению к собственной системе координат кристалла-образца (рис. 1).
Рис. 1.
Схема взаимного расположения плоскопараллельной пластины кристалла-образца и тригональной системы координат XYS, связанной с наклонной плоскостью дифракционного рассеяния. Φ – угол поворота образца вокруг вектора дифракции h.
Первые ДРТТ-эксперименты были успешно выполнены на синхротронных источниках рентгеновского излучения ESRF [9] и SPring-8 [10], а затем и в России на лабораторных установках с использованием характеристического рентгеновского излучения [11, 12]. При этом для компьютерной 3D-реконструкции дефекта в кристалле по соответствующему набору 2D-проекций ДРТ использовались различные модификации алгоритмов поглощающей томографии [13].
Особый интерес, напрямую связанный с применением метода ДРТТ, представляет идея компьютерной реконструкции пространственного положения дефектов в кристалле, а также, что особенно важно, локальных полей смещений (напряжений) вокруг дефектов в кристаллических веществах.
И здесь компьютерная 3D-реконструкция по экспериментальным данным ДРТТ в равной, если не в большей, степени связана с теми же трудностями, что и интерпретация картин изображения дефектов на 2D-проекциях ДРТ (топограммах) из-за сложного механизма формирования дифракционного контраста, отвечающего различным областям вокруг дефектов в кристаллах [1, 2].
В этой связи представляются важными нахождение и использование аппроксимационных аналитических решений уравнений Такаги–Топена, которые позволили бы с достаточной точностью описать особенности контраста дефектов на ДРТ-топограммах, связанные с формированием контраста в той или иной области кристалла вблизи дефекта, что стало бы ключевым моментом для решения обратной задачи ДРТТ, в частности компьютерной 3D-реконструкции функции поля смещений вокруг дефектов.
Настоящая работа посвящена построению аппроксимационного аналитического решения уравнений Такаги–Топена, на базе которого строится решение обратной задачи ДРТТ.
Затем с использованием полукинематического приближения для амплитуды дифрагированной σ-поляризованной волны Eh(r) построена теория 3D-реконструкции функции поля упругих статических смещений u(r – r0) точечного дефекта кулоновского типа (r0 – радиус-вектор положения точечного дефекта в кристалле).
На примере одной 2D-проекции с вектором дифракции h = [$\bar {2}20$] для кристалла Si(111) с применением итерационных алгоритмов моделирования отжига [14] и квазиньютоновского спуска [15, 16] найдено решение обратной задачи ДРТТ, а именно, проведена компьютерная реконструкция трехмерной функции поля смещений точечного дефекта, $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}}) = {\mathbf{h}} \cdot {\mathbf{u}}({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$.
Отметим, что первая попытка трехмерной реконструкции статического поля точечного дефекта в кристалле была предпринята в [17], где использовался алгоритм модифицированного алгебраического метода (алгоритм SART [11]), широко применяемого в поглощающей рентгеновской томографии. К сожалению, оказалось, что трехмерные решения для функции поля смещений точечного дефекта, полученные с использованием алгоритма SART, сходятся только при ограниченном количестве разбиений области кристалла вокруг точечного дефекта (не более чем 5 × 5 × 5 = 125 вокселей).
2D-ИЗОБРАЖЕНИЕ ТОЧЕЧНОГО ДЕФЕКТА В КРИСТАЛЛЕ В УСЛОВИЯХ НАКЛОННОЙ СИММЕТРИЧНОЙ ЛАУЭ-ДИФРАКЦИИ. ПОЛУКИНЕМАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ
Целью данного раздела является построение решения динамических уравнений Такаги–Топена в полукинематическом приближении, которое будет использовано в качестве базового для трехмерной реконструкции поля статических смещений по наклонным 2D-проекциям ДРТ.
Как известно [1–3], и это подтверждается неоднократными численными расчетами [16], прямое изображение дефекта в кристалле, если оно есть, обусловлено межветвевым рассеянием блоховских рентгеновских волн в сильно искаженной области кристалла непосредственно вблизи дефекта, что можно интерпретировать как кинематическое рассеяние блоховских волн, распространяющихся в совершенном кристалле вдали от центральной области дефекта.
Для наглядности, а также с целью избежать громоздких формул и вычислений ограничимся рассмотрением распространения σ-поляризованного рентгеновского волнового поля внутри искаженного кристалла, который “в среднем” находится в точном брэгговском положении.
В рассматриваемом случае распространение рентгеновского волнового поля внутри искаженного кристалла в условиях симметричной двух-волновой лауэ-дифракции описывается уравнениями Такаги–Топена [7, 8]:
(1)
$\begin{gathered} - \frac{{2i}}{k}\frac{{\partial {{E}_{0}}}}{{\partial {{s}_{0}}}} = {{{\chi }}_{0}}{{E}_{0}} + {{{\chi }}_{{\bar {h}}}}{{{\text{e}}}^{{ - i{\mathbf{hu}}\left( {\mathbf{r}} \right)}}}{{E}_{h}} - \frac{{2i}}{k}{\delta }\left( {{{s}_{0}} + {{s}_{h}}} \right), \\ - \frac{{2i}}{k}\frac{{\partial {{E}_{h}}}}{{\partial {{s}_{h}}}} = {{{\chi }}_{0}}{{E}_{h}} + {{{\chi }}_{h}}{{{\text{e}}}^{{i{\mathbf{hu}}\left( {\mathbf{r}} \right)}}}{{E}_{0}} \\ \end{gathered} $(2)
$\begin{gathered} {{E}_{0}}( - {{s}_{h}},{{s}_{h}}) = 1, \\ {{E}_{h}}( - {{s}_{h}},{{s}_{h}}) = 0. \\ \end{gathered} $Граничные условия (2) можно непосредственно учесть, модифицируя уравнения (1), в частности добавляя в правую часть первого уравнения дополнительный член $ - \frac{{2i}}{k}{\delta }({{s}_{0}} + {{s}_{h}})$.
Ипользуя известные подстановки ${{E}_{0}}\, \to \,{{E}_{0}}{{{\text{e}}}^{{ik{{{\chi }}_{0}}\frac{{{{s}_{0}} + {{s}_{h}}}}{2}}}}$, ${{E}_{h}} \to {{E}_{h}}{{{\text{e}}}^{{ik{{{\chi }}_{0}}\frac{{{{s}_{0}} + {{s}_{h}}}}{2}}}}$ и сохраняя для амплитуд проходящей и дифрагированной волн $\quad{{E}_{0}}({{s}_{0}},{{s}_{h}})$, ${{E}_{h}}({{s}_{0}},{{s}_{h}})$ прежние обозначения, легко показать, что амплитуда дифрагированной волны ${{E}_{h}}({{s}_{0}},{{s}_{h}})$ удовлетворяет неоднородному дифференциальному уравнению гиперболического типа в частных производных второго порядка
(3)
$\begin{gathered} \frac{{{{\partial }^{2}}{{E}_{h}}}}{{\partial {{s}_{0}}\partial {{s}_{h}}}} + \frac{{{{{\chi }}_{h}}{{{\chi }}_{{\bar {h}}}}{{k}^{2}}}}{4}{{E}_{h}} = \frac{{ik{{{\chi }}_{h}}}}{2}{{{\text{e}}}^{{i{\mathbf{hu}}\left( {\mathbf{r}} \right)}}}{\delta }({{s}_{0}} + {{s}_{h}}) + \\ + \;\frac{{ik{{{\chi }}_{h}}}}{2}{{E}_{0}}\frac{{\partial {{{\text{e}}}^{{i{\mathbf{hu}}\left( {\mathbf{r}} \right)}}}}}{{\partial {{s}_{0}}}}. \\ \end{gathered} $Интересует поле упругих статических смещений точечного дефекта кулоновского типа u(r – r0), которое имеет следующий вид:
(4)
${\mathbf{u}}({\mathbf{r}} - {{{\mathbf{r}}}_{0}}) = \frac{{\text{С }}}{{4{\pi }}}\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{0}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{0}}} \right|}}^{3}}}},\quad {\text{С }} = {\text{const}},$В качестве модельного кристалла выбрана плоскопараллельная пластина Si(111), вектор дифракции h = [$\bar {2}20$], длина волны падающего рентгеновского характеристического излучения λ = = 0.071 нм. Использовалась лабораторная рентгеновская трубка с молибденовым анодом, энергия излучения 17.48 КэВ; Λ – длина экстинкции, равная 36.287 ммк, угол Брэгга θB = 10.65°.
Отметим, что второй член в правой части первого из двух уравнений Такаги–Топена отвечает плоской волне ${{E}_{0}}({\mathbf{r}}) = {{{\text{e}}}^{{i{{{\mathbf{k}}}_{0}}{\mathbf{r}}}}}$, падающей на входную поверхность кристалла z = 0.
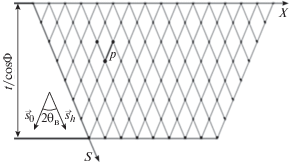
На рис. 2 показана дискретная треугольная сетка, построенная на векторах ${{{\mathbf{s}}}_{0}}$, ${{{\mathbf{s}}}_{h}}$ с одинаковым шагом $p$, которая может быть использована для компьютерного моделирования и анализа наклонных 2D-проекций ДРТ на основе численного решения уравнений Такаги–Топена (1) с граничными условиями (2) в переменных S, X [11].
Рис. 2.
Косоугольные координаты X, S в наклонной плоскости дифракционного рассеяния; t – толщина образца, ${{{\theta }}_{{\text{B}}}}$ – угол Брэгга.
Отметим, что S, X – координаты косоугольной системы координат SXY (ось Y перпендикулярна плоскости (SX)), связаны с координатами s0, sh линейными соотношениями
Уравнение (3) можно записать в интегральной форме, вводя в рассмотрение функцию Грина, описывающую
распространение дифрагированного излучения в идеальном кристалле от точечного источника
в треугольной области (треугольник Бормана) с вершиной в точке 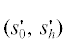 характеристиками вдоль направлений ${{{\mathbf{s}}}_{0}} = \frac{{{{{\mathbf{k}}}_{0}}}}{k}$, ${{{\mathbf{s}}}_{h}} = \frac{{{{{\mathbf{k}}}_{h}}}}{k}$ ${\text{(}}k = {{k}_{0}} = {\text{ }}{{k}_{h}})$, а именно:
характеристиками вдоль направлений ${{{\mathbf{s}}}_{0}} = \frac{{{{{\mathbf{k}}}_{0}}}}{k}$, ${{{\mathbf{s}}}_{h}} = \frac{{{{{\mathbf{k}}}_{h}}}}{k}$ ${\text{(}}k = {{k}_{0}} = {\text{ }}{{k}_{h}})$, а именно:
(5)
$ \times \;(k\quad\sqrt {{{{\chi }}_{h}}{{{\chi }}_{{\bar {h}}}}({{s}_{0}} - s_{{0\quad}}^{'})({{s}_{h}} - s_{h}^{'})} ) \times $Дальнейшее рассмотрение компьютерной реконструкции 3D-поля статических смещений точечного дефекта (4) основывается на утверждении, что в области сильных искажений вблизи дефекта рассеяние носит кинематический характер, что обусловлено межветвевым рассеянием блоховских волн вблизи дефекта [1–6]. При этом волновое поле, формирующее так называемое “прямое” изображение дефекта на 2D-проекциях ДРТ, распространяется вдоль направления поля дифрагированной волны ${\text{ }}{{{\mathbf{s}}}_{h}} = \frac{{{{{\mathbf{k}}}_{h}}}}{k}$.
Математически это означает, что для описания прямого ДРТ-изображения дефекта соответствующее выражение для амплитуды дифрагированной волны может быть найдено в результате интегрирования по частям второго члена в квадратных скобках в правой части интегрального уравнения (5).
Кроме того, ограничиваясь только первым членом двойного интеграла в правой части (5), находим
Далее, следуя предположению, что прямое изображение дефекта на 2D-проекциях ДРТ отвечает кинематическому рассеянию проходящей волны в области сильных искажений вблизи дефекта, в правой части интегрального уравнения (6) амплитуду проходящей волны в первом приближении можно заменить на соответствующее выражение для идеального кристалла, т.е. ${{E}_{0}}({{s}_{0}},{\text{ }}s_{0}^{'}) \to E_{0}^{{(id)}}({{s}_{0}},{\text{ }}s_{h}^{'}),$ где $E_{0}^{{(id)}}({{s}_{0}},s_{h}^{'})$ есть не что иное, как решение для амплитуды проходящей волны в идеальном кристалле соответственно:(7)
${{E}_{h}}\left( {{{s}_{0}},{{s}_{h}}} \right) = \frac{{ik}}{2}{{{\chi }}_{h}}\mathop \smallint \limits_{ - {{s}_{0}}}^{{{s}_{h}}} ds_{h}^{'}E_{0}^{{\left( {i{\text{d}}} \right)}}({{s}_{0}},s_{h}^{'}){{e}^{{i{\mathbf{hu}}({{s}_{0}},s_{h}^{'})}}}.$Формула (7) для амплитуды $\quad{{E}_{h}}({{s}_{0}},{{s}_{h}})$ описывает кинематическое рассеяние проходящей волны $E_{0}^{{\left( {i{\text{d}}} \right)}}({{s}_{0}},s_{h}^{'})$ сильно искаженной области вблизи дефекта, которая представляет собой фазовый объект. При этом волна ${{E}_{h}}({{s}_{0}},{{s}_{h}})$ распространяется вдоль направления дифрагированной волны ${{{\mathbf{s}}}_{h}} = \frac{{{{{\mathbf{k}}}_{h}}}}{k}.$ Таким образом, формула (7), полученная в полукинематическом приближении, будет использоваться для описания 2D-проекций ДРТ в той части, которая формируется за счет рассеяния рентгеновской волны в сильно искаженной области кристалла вблизи дефекта.
Для проведения численных расчетов выберем начало системы координат ${{s}_{0}}$, ${{s}_{h}}$ в левой верхней вершине трапеции (рис. 2) и введем косоугольную аффинную систему координат XYS (ср. с рис. 1), в которой ось Х направлена вдоль вектора дифракции h, а ось S вдоль вектора ${{s}_{h}}$, ось Y перпендикулярна плоскости XS.
При этом связь между координатами ${{s}_{0}}$, ${{s}_{h}}$ и X, S задается соотношениями
(8)
${{s}_{0}} = - \frac{X}{{2\sin {{{\theta }}_{{\text{B}}}}}},\quad {{s}_{h}} = S + \frac{X}{{2\sin {{{\theta }}_{{\text{B}}}}}}.$Кроме соотношений (8) потребуются соотношения между координатами ${{s}_{0}}$, ${{s}_{h}}$ и x, Z, а именно:
(9)
$\begin{gathered} {{s}_{0}} = \frac{1}{2}\left( {\frac{Z}{{\cos {{{\theta }}_{{\text{B}}}}}}{\text{--}}\frac{x}{{\sin {{{\theta }}_{{\text{B}}}}}}} \right){\text{,}} \\ {{s}_{h}} = \frac{1}{2}\left( {\frac{Z}{{\cos {{{\theta }}_{{\text{B}}}}}} + \frac{x}{{\sin {{{\theta }}_{{\text{B}}}}}}} \right). \\ \end{gathered} $(10)
$\begin{gathered} {{E}_{h}}(X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi }) = \frac{{ik}}{{2\cos {{{\theta }}_{{\text{B}}}}\cos {\Phi }}}{{{\chi }}_{h}} \times \\ \times \;\mathop \smallint \limits_0^{\text{T}} dz\cos \left[ {k\surd \left( {{{{\chi }}_{h}}{{{\chi }}_{{ - h}}}} \right)\frac{z}{{2\cos {{{\theta }}_{{\text{B}}}}}}} \right]{{{\text{e}}}^{{if\left( {{\mathbf{r}} - {{{\mathbf{r}}}_{0}}} \right)}}}, \\ \end{gathered} $(11)
$f({\mathbf{r}} - {{{\mathbf{r}}}_{0}}) = G\frac{{X - {{X}_{0}} + \frac{{\operatorname{tg} {{{\theta }}_{{\text{B}}}}}}{{\cos {\Phi }}}(z - {{z}_{0}})}}{{{{{\left( {{{{\left( {X - {{X}_{0}} + \frac{{\operatorname{tg} {{{\theta }}_{{\text{B}}}}}}{{\cos {\Phi }}}(z - {{z}_{0}})} \right)}}^{2}} + {{{(y - {{y}_{0}} + \operatorname{tg} {\Phi }(z - {{z}_{0}}))}}^{2}} + {{{(z - {{z}_{0}})}}^{2}}} \right)}}^{{3/2}}}}},\quad G = {\text{const}}.$Отметим, что координаты x, y, z “жестко” связаны с декартовыми координатами в кристалле.
В формуле (11) в явной форме учтена зависимость функции поля смещений точечного дефекта (4) в переменных X, y, z от угловых параметров θB, Φ.
Теоретическая формула (10) для амплитуды дифрагированной волны ${{E}_{h}}(X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi })$ наряду с формулой (11) для функции поля смещений точечного дефекта $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в области сильных искажений является основным выражением для решения обратной задачи ДРТТ.
Имея в виду компьютерную 3D-реконструкцию функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ на основе минимизации целевой χ2-функции вида
(12)
$\begin{gathered} {{\chi }^{2}}\{ f\left( {{\mathbf{r}} - {{{\mathbf{r}}}_{0}}} \right)\} = \frac{1}{{N(X,y,z)}} \times \\ \times \;\mathop \sum \limits_{\left\{ {X,y,z} \right\}} \mathop \sum \limits_{\Phi } ({{I}_{{h,obs}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi }\} - \\ - \;{{I}_{{h,calc}}}{{\{ X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi })}^{2}} = {\text{Min,}} \\ \end{gathered} $В (12) $\quad{{I}_{{h,obs}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi }\} $ есть модельная (наблюдаемая) ДРТ-проекция, отвечающая значению угла наклона Ф, а ${{I}_{{h,calc}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},{\Phi }\} $ рассчитывается по формуле (10) в соответствии с выбранным итерационным алгоритмом, начиная с некоторой стартовой функции поля смещений ${{f}_{{in}}}({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$.
КОМПЬЮТЕРНАЯ 3D-РЕКОНСТРУКЦИЯ ФУНКЦИИ СМЕЩЕНИЙ ТОЧЕЧНОГО ДЕФЕКТА НА ОСНОВЕ ПРИМЕНЕНИЯ МЕТОДОВ СИМУЛИРОВАННОГО ОТЖИГА И КВАЗИНЬЮТОНОВСКОГО СПУСКА
Моделирование на основе алгоритма симулированного отжига. Как известно [14], алгоритм симулированного отжига (SA) широко применяется для минимизации нелинейных целевых функций и является одним из эффективных методов для решения задачи с большим количеством переменных и комбинаторной природой итерационных вычислений.
Стартуя с заданной в качестве начального приближения модели и варьируя ее параметры псевдослучайным образом, программа SA работает до достижения наилучшей сходимости расчетной модели с наблюдаемыми данными ДРТ-проекции дефекта (минимум целевой χ2-функции (12)).
Будем различать два состояния системы – функции поля смещений f(r – r0): текущее и пробное значения функции $f(r\quad--\quad{{r}_{0}})$. В итерационном процессе текущее состояние, становясь пробным, служит в дальнейшем в качестве нового текущего состояния системы.
Псевдослучайное изменение системы применяется к текущему состоянию, которое затем становится пробной функцией $f(r - {{r}_{0}})$. Вероятность принятия пробной функции в качестве новой текущей определяется значением больцмановской функции exp(–Δχ2/T), где Δχ2 – изменение целевой функции, T – параметр, называемый температурой отжига. Выбор нового текущего состояния системы существенно зависит от значения T. Легко видеть, что более высокая температура означает более высокую вероятность exp(–Δχ2/T)), это позволяет принять пробную модель в качестве новой текущей даже в случае худшего пробного приближения в сравнении с текущим, когда Δχ2 > 0. Но если Δχ2 < 0, то пробная модель всегда принимается в качестве новой текущей. В начале итерационной минимизации целевой χ2-функции температура T выбирается достаточно высокой, так что частота принятия худшего состояния системы в качестве текущего в 10–100 раз превышает частоту обновления лучших состояний системы (другими словами, изменения системы носят почти случайный характер). Это заставляет программу SA “блуждать” по пространству поиска минимальных значений функции системы f. В принципе, программа SA может преодолевать локальные минимумы целевой χ2-функции, которые являются одним из главных препятствий для многих других нелинейных методов минимизации целевой χ2-функции, например, для градиентных методов спуска [15, 16].
В итерационном процессе минимизации целевой χ2-функции температура Tn + 1 на следующем после предыдущего n-шага (внешний цикл по n) снижается монотонно как Tn + 1 = FTn, где коэффициент отжига F равен 0.9–0.95, а значение целевой χ2-функции уменьшается аналогично тому, как снижается внутренняя энергия системы в процессе понижения температуры (так называемая машина Больцмана). По этой причине программа-алгоритм SA получила название “симулированного отжига” (алгоритм Метрополиса [18]). В табл. 1 представлены детали протокола итерационной программы SA согласно [14, 18].
Таблица 1.
Протокол использования итерационной программы-алгоритма SA
| Последовательные стадии протокола SA | Программа-алгоритм SA – функциональные стадии |
|---|---|
| Инициализация число элементов системы {i, j, k}температура Т1 = Тin целевая функция $\chi _{{1,1}}^{2} = \chi _{{in}}^{2}$ | N– номер итерации внешнего цикла по температуре Tn m – номер итерации внутреннего цикла (при фиксированном значении температуры Tn система f1,1({i, j, k}) = fin({i, j, k}), n = (1, 2, .., N), N = 200 – число внешних циклов по T m = (1, 2, .., M), M = 500 000 – число внутренних циклов Tn + 1 = $T_{n}^{*}$F, F = 0.95 |
| Итерации n = (1, 2, .., N), N = 200 для каждого номера итерации n и номера в цикле по m | fm + 1,n = fm,n({i, j, k}) | U{i, j, k} → ${\hat {U}}${i, j, k} для одного произвольно выбранного элемента U{i, j, k}; изменение энергии системы Δm,n = $\chi _{{m + 1,n}}^{2}$(fm + 1,n) – $\chi _{{m,n}}^{2}$(fm,n) |
| Алгоритм SA внутренний цикл по m = (1, 2, .., M), M = 500 000 | Δm,n < 0: безусловно принимается пробная модель fm + 1,n; Δm,n > 0: принимается пробная модель fm + 1,n, если вероятность Wm,n = exp(–Δm,n/Tn) больше случайно генерируемого числа в единичном интервале чисел [0, 1]. В обратном случае принимается модель fm,n |
| Внешний цикл по n = (1, 2, .., N), если N = 200 – остановка работы программы SA | Если частота ν успешных изменений системы fm,n на данной температуре Tn такая, что ν > M/10, программа переходит на следующий шаг по температуре Tn+1 внешнего цикла. Если частота ν < 50 при значении текущей температуры Tn и/или n = N, программа SA выходит из режима работы, сохраняя последнее состояние системы fm,n |
Для простоты все последующие результаты расчетов приводятся в безразмерных координатах. Положение точечного дефекта задается радиус-вектором r0, r0 = nt/2, n – внутренняя нормаль к входной поверхности кристалла z = 0. Толщина t модельного кристалла Si(111) выбрана такой, что поглощением рентгеновского излучения в образце можно пренебречь.
На первом этапе решения обратной задачи ДРТТ программа SA была протестирована на примере минимизации целевой χ2-функции в случае одной 2D-проекции, когда в формуле (12) остается одно слагаемое с Φ = 0, а именно:
(13)
$\begin{gathered} {{\chi }^{2}} = 1{\text{/}}N\{ X,y,z\} \mathop \sum \limits_{\{ X,y,z\} } ({{I}_{{h,obs}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} - \\ - \;{{I}_{{h,calc}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} {{)}^{2}} = {\text{Min}}, \\ {{I}_{{h,calc}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} = {{\left| {{{E}_{h}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} } \right|}^{2}}, \\ \end{gathered} $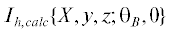 рассчитывается по формуле (10) с пробными функциями смещений в процессе итерационной минимизации целевой χ2-функции (13).
рассчитывается по формуле (10) с пробными функциями смещений в процессе итерационной минимизации целевой χ2-функции (13).
Отметим, что масштабирующий коэффициент G в формуле (11) можно выбрать равным единице за счет соответствующего выбора шага дискретной пространственной сетки координат в кристалле, на которой задается функция поля смещений $f(r - {{r}_{0}})$.
Кроме того, преследуя цель оценить степень сходимости итерационного процесса минимизации целевой χ2-функции к правильной (теоретической) функции fobs(r – r0) (см. (11)), будем использовать контрольный параметр (CP), который определяется как
(14)
$\begin{gathered} {\text{CP}} = 1{\text{/}}N\{ X,y,z\} \times \\ \times \;\mathop \sum \limits_{\{ X,y,z\} } \begin{array}{*{20}{c}} {\frac{{\left| {{{f}_{{obs}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} - {{f}_{{calc}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} } \right|}}{{\left| {{{f}_{{obs}}}\{ X,y,z;{{{\theta }}_{{\text{B}}}},0\} } \right|}}} \end{array}\quad \\ \end{gathered} $Для случая наблюдаемой 2D-проекции ДРТ (рис. 3) результаты компьютерной 3D-реконструкции функции смещений $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ для различных пространственных сеток, на которых она определена, а также ее различных линейных комбинаций в качестве стартовых функций с индексами убывания {pi} в интервале значений i = 1–4 представлены в табл. 2.
Рис. 3.
Наблюдаемая 2D-проекция ДРТ кристалла Si(111) с точечным дефектом. Теоретическая функция поля смещений f(r – r0) с индексом убывания p = 1.5 задана в узлах пространственной сетки {15, 15, 15}.
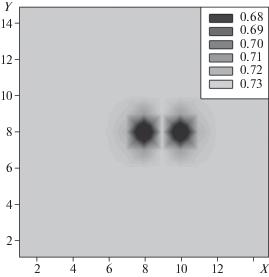
Таблица 2.
Компьютерная 3D-реконструкция функции поля смещений f(r – r0) для точечного дефекта кулоновского типа в кристаллах с использованием алгоритма SA. Входные данные и результаты расчетов
| Простран-ственная сетка {i, j, k} | Стартовые значения | Конечные значения | ||||
|---|---|---|---|---|---|---|
| pi, {i = 1–4} | Целевая χ2-функция | CP | pi, {i = 1–4} | Целевая χ2-функция | CP | |
| {21, 21, 21} | {0.9} | 0.77 | 0.79 | {1.5} | 1 ×.10–7 | 6 × 10–7 |
| {21, 21, 21} | {0.5, 1.0, 1.8} | 0.48 | 0.95 | {1.51, 1.47, 1.52} | 3 × 10–4 | 5 × 10–3 |
| {21, 21, 21} | {0.9, 1.2, 1.8, 2.1} | 1.43 | 0.99 | {1.51, 1.50, 1.49, 1.50} | 6 × 10–3 | 1 × 10–2 |
| {41, 41, 41} | {0.9} | 0.79 | 1 | {1.5} | 8 × 10–7 | 4 × 10–7 |
| {41, 41, 41} | {0.5, 1.0, 1.8} | 0.48 | 0.96 | {1.49, 1.49, 1.52} | 3 × 10–4 | 1 × 10–2 |
| {41, 41, 41} | {0.9, 1.2, 1.8, 2.1} | 1.44 | 1 | {1.48, 1.54, 1.49, 1.49} | 3 × 10–3 | 1.4 × 10–2 |
Диапазон поиска каждого индекса убывания {pi}, i = 1–4, в части действия алгоритма SA (внутренний цикл, табл. 1) задавался с равной вероятностью в интервале чисел 0.0–3.0.
Как видно из табл. 2, в случае одного индекса убывания {pi}, i = 1, в качестве стартового значения теоретическое решение для функции смещений $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ с индексом убывания p = 1.5 достигается с точностью, по крайней мере CP = 10–6, в то время как для большего, чем единица, числа индексов убывания {pi}, i = 1–4, теоретическое решение достигается с точностью порядка CP = 10–2.
На практике представляет интерес 3D-реконструкция функции поля смещений $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ деффекта в кристалле без необходимости его описания в аналитической форме. В отличие от случая, описанного выше, будем рассматривать функцию $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в каждом узле дискретной пространственной сетки как искомый параметр. При этом будут использованы только свойства симметрии функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ по координатам x – x0, y – y0, z – z0, а также “включено” требование монотонного убывания с увеличением расстояний |y – y0| и/или |z – z0|.
Наблюдаемая 2D-проекция ДРТ от тонкого (непоглощающего) кристалла Si(111) (рис. 3) рассчитана на основе формулы (10) с учетом (11) на пространственной сетке, состоящей из 15 × 15 × × 15 узлов. Видно, что проекция является симметричной относительно координаты y и в направлении распространения дифрагированной волны сдвигается от центра вдоль координаты x как целое на величину t/2 × tg θB (в данном случае этот сдвиг равен 4/3 в безразмерных координатах x и z).
Входные данные и результаты компьютерной 3D-реконструкции функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ по данным наблюдаемой 2D-проекции ДРТ представлены в табл. 3. В первом столбце указаны пространственные сетки, на которых проводятся расчеты, жирным шрифтом (здесь и далее) выделены номера плоскостей вдоль оси z, в которых значения функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ варьируются, в то время как в остальных плоскостях они фиксированы в соответствии с теоретическим индексом убывания p = = 1.5.
Таблица 3.
Компьютерная 3D-реконструкция функции поля смещений f(r – r0) для точечного дефекта кулоновского типа в кристалле с использованием алгоритма SA. Входные данные и результаты расчетов
| Пространственная сетка {i, j, k} | Стартовые значения | Конечные значения | |||
|---|---|---|---|---|---|
| Pini | Целевая χ2-функция | CP | Целевая χ2-функция | CP | |
| {15, 15, 1–6 | 7–9 | 10–15} | 1.55 | 1.67 × 10–2 | 0.0161 | 1.31 × 10–5 | 0.0171 |
| {15, 15, 1–5 | 6–10 | 11–15} | 1.55 | 1.56 × 10–2 | 0.0273 | 2.94 × 10–6 | 0.029 |
| {15, 15, 15} | 1.55 | 1.42 × 10–2 | 0.0658 | 2.63 × 10–8 | 0.118 |
Из табл. 3 видно, что в случае пространственной сетки {15, 15, 15} удается снизить значение целевой χ2-функции более чем на 6 порядков, в то время как контрольный параметр СР растет до 0.118 против стартового значения, равного 0.0658.
Вероятно, это может происходить по двум причинам, первая из которых – неоднозначность решения обратной задачи ДРТТ. Такой вывод следует, в частности, из того факта, что в случае перехода к пространственным сеткам с меньшим числом узлов по толщине кристалла контрольный параметр СР уменьшается.
Вторая причина заключается в эффективности работы самого алгоритма SA для минимизации целевой χ2-функции. Расчеты показывают, что, если вместо минимизации целевой χ2-функции (13) применяется алгоритм SA для минимизации CP-функции, согласно (14), значение параметра CP уменьшается только примерно в 2 раза, например, для пространственной сетки {15, 15, 15} параметр CP изменяется от 0.0658 до 0.0371, в то время как его значение должно было бы снизиться до нуля в предположении, что алгоритм SA работает эффективно.
Моделирование на основе алгоритма квазиньютоновского спуска. Для сравнения с результатами, полученными с использованием алгоритма SA, был применен для минимизации целевой χ2-функции (13) алгоритм квазиньютоновского спуска по схеме Левенберга–Маркварда. Был использован программный код NL2SNO, имеющийся в открытом доступе (подробнее в [15, 16, 19], вариант NL2SOL с расчетом градиентов по методу конечных разностей).
Результаты минимизации целевой χ2-функции (13) c использованием алгоритма квазиньютоновского спуска для различных пространственных сеток и различных стартовых значений индекса убывания рini функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ представлены в табл. 4. Обозначения для идентификации пространственных сеток приняты аналогично тому, как это сделано в табл. 3. Видно, что для двух пространственных сеток {15, 15, 1–6 | 7–9 | 10–15} и {15, 15, 1–5 | 6–10 | 11–15} удается достичь значений контрольного параметра CP ∼ 5 × 10–5 при конечных значениях целевой χ2-функции порядка 10–22.
Таблица 4.
Результаты компьютерной 3D-реконструкции функции поля смещений f(r – r0) для точечного дефекта кулоновского типа в кристалле с использованием алгоритма квазиньютоновского спуска
| Пространственная сетка {i, j, k} | Стартовые значения | Конечные значения | |||
|---|---|---|---|---|---|
| Pini | Целевая χ2-функция | CP | Целевая χ2-функция | CP | |
| {15, 15, 1–6 | 7–9 | 10–15} | 5.0 | 8.24 × 10–3 | 8.30 × 10+2 | 3.76 × 10–6 | 1.374 |
| 3.0 | 4.54 × 10–5 | 2.581 | 4.46 × 10–9 | 8.07 × 10–2 | |
| 2.0 | 6.32 × 10–9 | 0.211 | 5.27 × 10–14 | 4.37 × 10–2 | |
| 1.55 | 2.52 × 10–11 | 1.77 × 10–2 | 5.67 × 10–14 | 1.81 × 10–2 | |
| 1.45 | 1.21 × 10–11 | 1.71 × 10–2 | 6.88 × 10–21 | 4.90 × 10–6 | |
| 1.00 | 8.79 × 10–11 | 0.112 | 5.74 × 10–13 | 0.116 | |
| 0.50 | 7.21 × 10–11 | 0.155 | 3.67 × 10–13 | 0.132 | |
| 0.05 | 7.02 × 10–11 | 0.174 | 3.45 × 10–13 | 0.128 | |
| 5.0 | 8.24 × 10–3 | 8.30 × 10+2 | 3.76 × 10–6 | 1.374 | |
| 3.0 | 4.54 × 10–5 | 2.581 | 4.46 × 10–9 | 8.07 × 10–2 | |
| {15, 15, 1–5 | 6–10| 11–15} | 5.0 | 1.71 × 10–2 | 2.09 × 10+3 | 3.39 × 10–5 | 3.066 |
| 3.0 | 6.29 × 10–5 | 5.291 | 3.01 × 10–8 | 0.249 | |
| 2.0 | 8.47 × 10–9 | 0.408 | 1.57 × 10–14 | 6.69 × 10–2 | |
| 1.55 | 2.82 × 10–11 | 2.92 × 10–2 | 2.14 × 10–22 | 2.70 × 10–3 | |
| 1.45 | 1.47 × 10–11 | 2.79 × 10–2 | 9.56 × 10–28 | 6.00 × 10–4 | |
| 1.00 | 1.29 × 10–10 | 0.185 | 5.61 × 10–13 | 0.212 | |
| 0.50 | 1.07 × 10–10 | 0.260 | 2.32 × 10–13 | 0.226 | |
| 0.05 | 1.00 × 10–10 | 0.291 | 1.74 × 10–12 | 0.231 | |
| {15, 15, 15} | 5.0 | 1.94 × 10–02 | 2.46 × 10+3 | 9.74 × 10–06 | 46.2 |
| 3.0 | 4.92 × 10–05 | 1.047 | 1.20 × 10–08 | 8.771 | |
| 2.0 | 5.39 × 10–09 | 1.011 | 9.59 × 10–16 | 0.692 | |
| 1.55 | 2.42 × 10–11 | 7.06 × 10–2 | 5.03 × 10–24 | 0.119 | |
| 1.52 | 3.31 × 10–12 | 2.82 × 10–2 | 3.33 × 10–17 | 4.46 × 10–2 | |
| 1.48 | 2.46 × 10–12 | 2.72 × 10–2 | 6.38 × 10–27 | 4.24 × 10–2 | |
| 1.45 | 1.24 × 10–11 | 6.65 × 10–2 | 7.99 × 10–17 | 0.107 | |
| 1.00 | 1.36 × 10–10 | 0.476 | 4.30 × 10–14 | 0.694 | |
| 0.50 | 1.48 × 10–10 | 0.704 | 1.40 × 10–13 | 0.778 | |
| 0.05 | 1.49 × 10–10 | 0.814 | 1.87 × 10–12 | 0.659 | |
Отметим, что в случае пространственной сетки {15, 15, 15} и различных стартовых значениях индекса убывания рini контрольный параметр CP практически не уменьшается по сравнению со стартовым CP, а в некоторых случаях даже растет.
Как показывают расчеты, последнее обстоятельство можно преодолеть, если последовательно использовать итерационную схему, корректируя при каждой итерации значения функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в периферийной области от центра точечного дефекта. Детали расчетов с использованием корректировки значений функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ периферийных областях пространственной сетки выходят за рамки данной работы и являются отдельной темой будущего исследования.
На рис. 4 приведены сечения трехмерной функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в плоскостях z = const для значений z = 6, 8, 10 (z = 8 – центральное сечение).
Рис. 4.
Сечения 3D-функции поля смещений точечного дефекта f(r – r0) в плоскостях z = const. В безразмерных единицах: z = 6 (а), z = 8 (центральное сечение (б)), z = 10 (в). Верхняя панель – сечения теоретической 3D-функции поля смещений f(r – r0), индекс убывания p = 1.5; нижняя панель – сечения 3D-функции поля смещений f(r – r0), восстановленной в узлах пространственной сетки {15, 15, 15} с использованием алгоритма квазиньютоновского спуска.
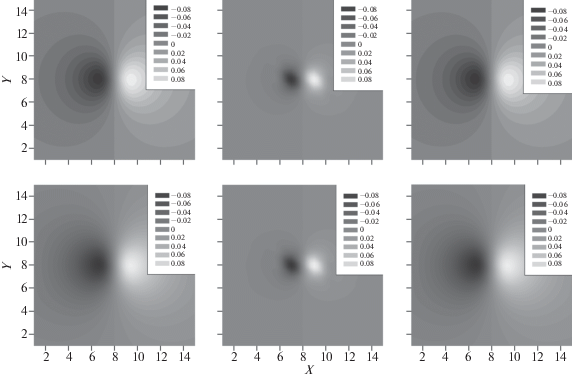
Верхние рисунки 4а, 4б, 4в – сечения теоретической 3D-функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$, индекс убывания р = 1.5, нижние – сечения 3D-функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ как результат компьютерной 3D-реконструкции с использованием метода квазиньютоновского спуска. Наилучшее согласие соответствующих изображений имеет место для центрального сечения z = 8. В принципе, это может означать, что наилучшим образом удается восстановить 3D-функцию $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в области непосредственно вблизи центра дефекта.
ЗАКЛЮЧЕНИЕ
Развит последовательный подход к решению обратной задачи ДРТТ. Предложено полукинематическое приближение для решения уравнений Такаги–Топена, соответствующего дифракционному рассеянию рентгеновских лучей в сильно искаженной области вблизи дефекта в кристалле.
Для решения обратной задачи ДРТТ были использованы итерационные алгоритмы моделирования отжига и квазиньютоновского спуска, приведены результаты компьютерной 3D-реконструкции функции поля смещений точечного дефекта $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$. Показано, что использованные в работе алгоритмы при определенных ограничениях на класс функций, на котором ищется функция $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$, работают в случае одной 2D-проекции ДРТ, что позволяет восстановить теоретическую 3D-функцию поля смещений $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$, заданную как в аналитической форме, так и в численном виде в узлах пространственной сетки кристаллической пластины.
Проведенные предварительные расчеты показали, что алгоритм квазиньютоновского спуска допускает определенную возможность улучшить работу итерационной схемы, корректируя при каждой итерации значения 3D-функции $f({\mathbf{r}} - {{{\mathbf{r}}}_{0}})$ в узлах пространственной сетки в периферийной области на некотором расстоянии от центра точечного дефекта.
Представляется весьма вероятным, что сходимость процесса минимизации целевой χ2-функции с использованием алгоритма квазиньютоновского спуска также должна улучшиться в случае использования набора наблюдаемых наклонных 2D-проекций (общая формула (12)), что является немаловажным обстоятельством для фильтрации шумов и практической обработки 2D-проекций в условиях ДРТТ.
Авторы выражают благодарность В.Е. Асадчикову за обсуждения и полезные замечания, сделанные им в ходе выполнения данной работы.
Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН в области развития методов исследования структуры с помощью рентгеновского и синхротронного излучений.
Список литературы
Инденбом В.Л., Чуховский Ф.Н. // УФН. 1972. Т. 107. Вып. 2. С. 229.
Epelboin Y. // Acta Cryst. A. 1975. V. 31. P. 591.
Authier A. Dynamical theory of X-ray diffraction. Oxford: University press, 2003. 513 p.
Смирнова И.А., Суворов Э.В., Шулаков Е.В. // ФТТ. 2007. Т. 49. Вып. 6. С. 1050.
Шульпина И.Л., Прохоров И.А. // Кристаллография. 2012. Т. 57. № 5. С. 740.
Беседин И.С., Чуховский Ф.Н., Асадчиков В.Е. // Кристаллография. 2014. Т. 59. № 3. С. 365.
Takagi S. //Acta Cryst. 1962. V. 15. P. 1311.
Taupin D. // Bull. Soc. Fr. Mineral. 1961. V. 84. P. 51.
Ludwig W., Cloetens P., Härtwig J. et al. // J. Appl. Cryst. 2001. V. 34. P. 602.
Kawado S., Taishi T., Iida S. et al. // J. Synchrotron Rad. 2004. V. 11. P. 304.
Золотов Д.А., Бузмаков А.В., Асадчиков В.Е. и др. // Кристаллография. 2011. Т. 56. № 3. С. 426.
Золотов Д.А., Бузмаков А.В., Елфимов Д.А. и др. // Кристаллография. 2017. Т. 62. № 1. С. 12.
Календер В. Компьютерная томография. Основы, техника, качество изображений в области клинического использования. М.: Техносфера, 2006. 344 с.
Kirkpatrick S., Gelatt C.D., Vecci M.P. // Science. 1983. V. 220. P. 671.
Gill P.E., Murray W., Wright M.H. Practical Optimization. London: Academic Press. 1981. 401 p.
Dennis J., Gay D., Welsch R. // ACM Trans. Math. Soft. 1981. V. 7. P. 348.
Asadchikov V., Besedin I., Buzmakov A. et al. // Acta Cryst. A. 2014. V. 70. P. C1132.
Metropolis N., Rosenbluth A.W., Rosenbluth M.N. et al. // J. Chem. Phys. 1953.V. 21(6). P. 1087.
More J.J. // The Levenberg-Marquardt algorithm, implementation and theory. Springer Lecture Notes in Mathematics № 630 / Ed. Watson G.A. Berlin; New York: Springer-Verlag, 1978. P. 105.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография