Кристаллография, 2019, T. 64, № 3, стр. 351-361
Исследование разбиения Пенроуза методом параметризации
А. В. Шутов 1, А. В. Малеев 1, *
1 Владимирский государственный университет
Владимир, Россия
* E-mail: andr_mal@mail.ru
Поступила в редакцию 03.11.2016
После доработки 27.05.2017
Принята к публикации 08.06.2017
Аннотация
Получено новое описание разбиения Пенроуза, основанное на параметризации ромбов разбиения. Разработан метод, позволяющий описывать кластеры и координационные окружения в разбиении Пенроуза на языке параметров. Найдены параметры всех возможных типов первых координационных окружений в разбиении Пенроуза. Получено новое доказательство того, что формой послойного роста разбиения Пенроуза является правильный десятиугольник, и вычислены его вершины.
ВВЕДЕНИЕ
Одной из наиболее распространенных математических моделей структур квазикристаллов являются модельные множества, введенные Муди [1]. Данные множества получаются проектированием в физическое пространство многомерных решеток с дополнительным условием принадлежности некоторой двойственной проекции заданному множеству в фазовом пространстве, называемому окном. Модельные множества хорошо описывают расположение атомов в квазикристалле. На их основе хорошо моделируются результаты дифракции на квазикристаллических структурах [2, 3].
Основной недостаток модельных множеств состоит в том, что в них не содержится информации о связях между элементами квазикристаллической структуры. Для получения этой информации требуется переходить к таким математическим моделям, как графы и разбиения.
В случае графов связи между элементами структуры задаются ребрами, соединяющими вершины графа. В случае разбиений связи описываются примыканием друг к другу соседних фигур разбиения. При этом существует несколько различных понятий соседства фигур. В общем случае отношение соседства задается при помощи аксиом, введенных в [4, 5].
Отметим, что подходы к описанию структур, связанные с графами и разбиениями, во многом являются двойственными. В частности, хорошо известна конструкция, ставящая в соответствие разбиению его двойственный граф. Кроме того, поскольку любое разбиение также содержит вершины и ребра, его можно непосредственно рассматривать как граф.
Наиболее известным разбиением плоскости, связанным с квазикристаллическими структурами, является разбиение Пенроуза. Его роль обусловлена тем, что оно обладает запрещенной в кристаллах симметрией пятого порядка, наблюдаемой и в реальных квазикристаллах. Это разбиение можно также рассматривать как граф. В [6–8] было проведено подробное исследование соответствующего графа, названного графом вершин разбиения Пенроуза. При этом были получены результаты, связанные с описанием кластеров и координационных окружений соответствующего графа [7], а также найдена форма его послойного роста [8]. С другой стороны, более традиционным является рассмотрение разбиения Пенроуза именно как разбиения, а не как графа его вершин. В настоящей работе покажем, как получить для разбиения Пенроуза результаты, аналогичные полученным ранее для соответствующего графа вершин.
КОНСТРУКЦИЯ ГРАФА ВЕРШИН РАЗБИЕНИЯ ПЕНРОУЗА
Вначале построим множество вершин разбиения Пенроуза, используемая конструкция предложена в [9–11]. Рассмотрим схему
(1)
$\begin{gathered} {\mathbf{С }}\;\xleftarrow{{{{\pi }_{1}}}}\;{{{\mathbf{R}}}^{4}}\;\xrightarrow{{{{\pi }_{2}}}}\;{\mathbf{С }} \times {{{\text{С }}}_{{\text{5}}}} \hfill \\ \quad \quad \;{\kern 1pt} \cup \hfill \\ \quad \quad \;{\kern 1pt} {{{\mathbf{Z}}}^{4}} \hfill \\ \end{gathered} $Для перехода от множества вершин к графу, или к разбиению Пенроуза, требуется задать ребра. Для этого используется следующее правило: вершины соединены ребром тогда и только тогда, когда расстояние между ними равно единице.
ПАРАМЕТРИЗАЦИЯ РОМБОВ РАЗБИЕНИЯ ПЕНРОУЗА
Для перехода к изучению разбиения Пенроуза нужно получить параметризацию ромбов, т.е. поставить в соответствие каждому ромбу некоторый параметр из фазового пространства.
Отметим, что идея параметризации фигур разбиения ранее рассматривалась авторами для разбиений Рози [12–15], а также разбиений, получаемых на основе ступенчатых поверхностей [16]. При этом было показано, что нужно рассмотреть определенные точки, однозначно определяющие фигуры разбиения, и в качестве параметров фигур выбрать параметры этих точек. В случае разбиения Пенроуза в качестве подобных точек естественно рассмотреть центры ромбов – точки пересечения диагоналей ромбов.
Напомним, что вершины разбиения Пенроуза имеют вид $h + j\zeta + k{{\zeta }^{2}} + l{{\zeta }^{3}}$ с целыми индексами h, j, k, l и $\zeta = {{e}^{{\frac{{2\pi i}}{5}}}}$. Определим отображение $x \to x{\text{*}}$ из физического пространства в фазовое по формуле
Комплексная координата центра ромба получается как полусумма комплексных координат любой пары его противоположных вершин и поэтому имеет вид $h + j\zeta + k{{\zeta }^{2}} + l{{\zeta }^{3}}$, но числа h, j, k, l могут быть не только целыми, но и полуцелыми. Возникает вопрос, как определить отображение $x \to x{\text{*}}$ для таких точек. Очевидно, что данное отображение условно разбивается на два
Для второго отображения аналогичное продолжение также может быть определено, если определить $\frac{x}{2}\bmod 5$ как единственное целое y такое, что $0 \leqslant y < 5$ и $2y \equiv x(\bmod 5)$. С другой стороны, можно просто заметить, что все ромбы разбиения Пенроуза с точки зрения вершин, которые в них входят, можно разбить на два типа. В каждом из ромбов первого типа вторые части параметров одной пары противоположных вершин равны 1 и 3, а вторые части параметров обеих вершин другой противоположной пары равны 2. В ромбах второго типа вторые части параметров одной пары противоположных вершин равны 2 и 4, а вторые части параметров обеих вершин другой противоположной пары равны 3. Используя правило полусуммы, для точки пересечения диагоналей получаем вторые части параметров $\frac{{1 + 3}}{2} = \frac{{2 + 2}}{2} = 2$ и $\frac{{2 + 4}}{2} = \frac{{3 + 3}}{2} = 3$ соответственно. Таким образом, вторая часть параметра ромба корректно определена.
Ромбы с острым углом 36° будем называть малыми, а ромбы с острым углом 72° – большими. Существуют по пять ориентаций больших и по пять ориентаций малых ромбов каждого из типов. При этом ориентации ромбов связаны между собой поворотной осью симметрии пятого порядка.
Алгоритм получения параметров ромбов заданного типа и ориентации состоит в следующем:
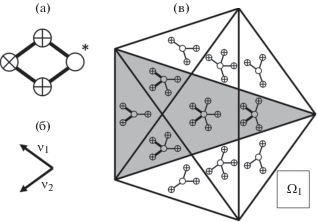
– зафиксируем одну из вершин ромба. Например, для ромба, изображенного на рис. 1а, зафиксируем вершину, вторая часть параметра которой равна единице (правая вершина, помеченная звездочкой);
– пусть ${{\text{v}}_{1}}$ и ${{\text{v}}_{2}}$ – векторы, ведущие из зафиксированной вершины в соседние вершины (рис. 1б). Рассмотрим все возможные первые координационные окружения вершин, в которые входят векторы ${{\text{v}}_{1}}$ и ${{\text{v}}_{2}}$, и найдем объединение параметров соответствующих вершин. Отметим, что параметры всех возможных первых координационных окружений вершин были найдены в [7]. Для рассматриваемого ромба полученное множество будет иметь вид выделенного серым треугольника на рис. 1в;
– пусть $\text{v}$ – комплексное число, полученное как полусумма комплексных координат векторов ${{\text{v}}_{1}}$ и ${{\text{v}}_{2}}$. В рассматриваемом примере $\text{v} = \frac{{{{\zeta }^{2}} + {{\zeta }^{3}}}}{2}$. Комплексная часть множества параметров ромба получается сдвигом полученного на предыдущем шаге множества (серого треугольника) на вектор $\text{v}{\kern 1pt} {\text{*}}$. При этом в данном множестве необходимо рассматривать комплексные числа вида $h + j\zeta + $ $ + \;k{{\zeta }^{2}} + l{{\zeta }^{3}}$ с целыми или полуцелыми индексами h, j, k, l. Причем целость или полуцелость h, j, k, l определяется целостью или полуцелостью соответствующего индекса вектора $\text{v}{\kern 1pt} {\text{*}}$. Так, в рассматриваемом примере индексы вектора $\text{v}{\kern 1pt} {\text{*}}$ есть $\left( {0;0;\frac{1}{2};\frac{1}{2}} \right)$. Следовательно, для всех ромбов рассматриваемого типа индексы h, j должны быть целыми, а индексы k, l – полуцелыми;
– вторая часть параметров ромба равна 2 для ромбов первого типа и 3 для ромбов второго типа.
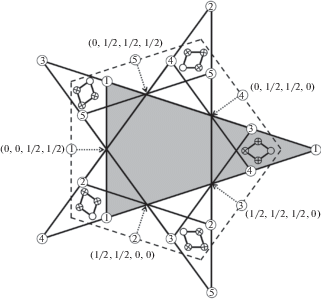
На рис. 2, 3 изображены множества параметров больших и малых ромбов первого типа соответственно. Цифрами в кружочках помечены вершины треугольников, соответствующих одной из ориентаций ромба, а также начало соответствующего вектора сдвига ${{v}^{*}}$, рядом с которым указаны его индексы. Штриховой линией на обоих рисунках изображен пятиугольник ${{\Omega }_{1}}$. Серым цветом выделен на каждом рисунке треугольник, соответствующий одной из ориентаций ромба.
Множество параметров ромбов второго типа (за исключением граничных точек) получается из рассмотренных множеств параметров ромбов первого типа инверсией, т.е. поворотом вокруг начала координат на 180°. Принадлежность граничных точек множеству параметров определяется выбором границ окна W.
Из рассматриваемой конструкции не ясно, являются ли множества центров ромбов разбиения Пенроуза модельными множествами. На самом деле ответ на этот вопрос положителен, но требует изменения фазового пространства. Схема (1) заменяется на схему
КЛАСТЕРЫ В РАЗБИЕНИИ ПЕНРОУЗА
Кластером в разбиении Пенроуза будем называть пару (R, TR), в которой R – некоторый ромб, а TR – конечное подмножество ромбов разбиения Пенроуза, содержащее ромб R. Кластеры (R, TR) и (R ', TR′) будем называть эквивалентными, если параллельный перенос, переводящий R в R ', переводит также TR в TR'. Данное отношение разбивает все множество кластеров на множество классов эквивалентности. Параметром кластера $(R,{{T}_{R}})$ будем называть параметр ромба R. Задача состоит в том, чтобы для произвольного кластера (R, TR) описать множество параметров эквивалентных ему кластеров.
Пусть V – множество векторов, ведущих из центра ромба R в центры ромбов из TR. В случае модельных множеств и соответствующих им графов в [7] была доказана формула, позволяющая эффективно вычислять множества параметров произвольных кластеров
Здесь * – естественное отображение из физического пространства в фазовое, в данном случае определяемое равенством Данная формула применима и к кластерам модельного множества, образованного центрами ромбов разбиения Пенроуза. Обоснование применимости формулы непосредственно к кластерам разбиения Пенроуза требует дополнительных рассуждений.Пусть R и R ' – два ромба, параметры которых принадлежат найденному множеству W(C). Обозначим через x(R) и x(R ') их центры. Выберем вектор $\text{v} \in V$. Тогда рассуждения из [7] гарантируют, что точки x(R) + $\text{v}$ и x(R ') + $\text{v}$ являются центрами некоторых ромбов, принадлежащих разбиению, но не гарантируют эквивалентность этих ромбов. Однако в случае разбиения Пенроуза легко видеть, что части параметров этих ромбов, принадлежащие множеству ${{{\text{С }}}_{{\text{5}}}} \times {{{\text{С }}}_{{\text{2}}}} \times {{{\text{С }}}_{{\text{2}}}} \times {{{\text{С }}}_{{\text{2}}}} \times {{{\text{С }}}_{{\text{2}}}}$, совпадают. При этом проверяется, что по соответствующей части параметра определяются тип и ориентация ромба, что и обосновывает применимость формулы (2) к разбиению Пенроуза.
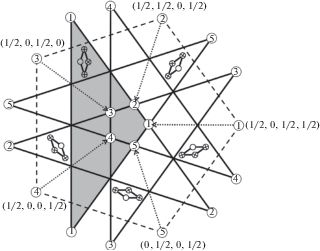
На рис. 4 показаны множества параметров шести типов кластеров, встречающихся в разбиении Пенроуза. Отметим, что пять множеств параметров являются двумерными, а одно одномерным. Кластеры с одномерным множеством параметров имеют нулевую частоту появления в разбиении (так как частота появления кластера может быть найдена по формуле $\rho (C) = \frac{{\left| {W(C)} \right|}}{{\left| W \right|}}$). Такие кластеры называются исключительными. Их возникновение очень сильно зависит от выбора границ множеств параметров. Подробности даны в [7].
КООРДИНАЦИОННЫЕ ОКРУЖЕНИЯ
Существуют два естественных способа ввести понятие соседства на множестве ромбов разбиения Пенроуза:
– ромбы являются соседними тогда и только тогда, когда они имеют общее ребро;
– ромбы являются соседними тогда и только тогда, когда они имеют хотя бы одну общую точку.
При желании можно рассматривать более сложные отношения соседства, удовлетворяющие введенным в [4, 5] аксиомам. В настоящей работе рассмотрим только первое из предложенных отношений соседства. При этом используемая техника может быть применена и в остальных случаях.
Отношение соседства позволяет ввести метрику на множестве ромбов разбиения Пенроуза. Последовательность соседних ромбов разбиения будем называть цепью. Длиной цепи будем называть число входящих в цепь ромбов минус 1. Расстоянием d(R, R') между ромбами R и R' будем называть наименьшую из длин цепей, соединяющих данные ромбы. Легко проверяется, что введенная функция d(R, R') действительно удовлетворяет всем аксиомам расстояния.
Для произвольного ромба R разбиения Пенроуза и целого числа n определим координационную сферу порядка n:
а также координационное окружение порядка n: Данные понятия были введены в [17, 18] и подробно исследовались в [12, 14–16] для других квазипериодических разбиений.Аналогично случаю кластеров можно определить классы эквивалентности координационных окружений, а также поставить вопрос об описании ромбов заданного класса эквивалентности координационного окружения в терминах фазового пространства.
В общем случае задача описания параметров координационных окружений квазипериодических структур является более сложной, чем задача описания параметров кластеров. Это объясняется тем, что класс эквивалентности координационного окружения элемента не только гарантирует появление некоторых элементов в заданной окрестности исходного, но и запрещает появление других элементов.
Например, рассмотрим первые координационные окружения графа вершин разбиения Пенроуза, изображенные на рис. 5. Легко видеть, что координационное окружение A является подмножеством координационных окружений B, C, D. Данные координационные окружения отличаются друг от друга наличием или отсутствием дополнительных вершин. Это означает, что множество параметров конфигурации А, рассматриваемой как кластер, не совпадает с множеством параметров той же самой конфигурации, рассматриваемой как первое координационное окружение. Более того, можно показать, что множество параметров кластера А является объединением множеств параметров всех четырех координационных окружений A–D (на рис. 5 выделено серым).
Рис. 5.
Множество параметров кластера А в графе вершин разбиения Пенроуза как объединение множеств параметров четырех координационных окружений A–D.
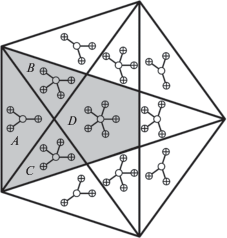
Оказывается, что в случае разбиения Пенроуза подобная ситуация невозможна и множество параметров произвольного координационного окружения совпадает с множеством параметров той же самой конфигурации, рассматриваемой как кластер. Это позволяет использовать формулу (2) для эффективного вычисления параметров координационных окружений.
Данное утверждение нетрудно доказать индукцией по номеру координационного окружения n. При n = 1 утверждение доказывается непосредственным перебором первых координационных окружений. Предположим, что имеются два класса эквивалентности координационных окружений с представителями $E{{q}_{n}}(R)$ и $E{{q}_{n}}(R{\text{'}})$ такие, что $E{{q}_{n}}(R) \subset E{{q}_{n}}(R{\text{'}}) - \text{v}$ для вектора $\text{v}$, соединяющего точки пересечения диагоналей ромбов R и R′. Это означает, что существует ромб $T{\kern 1pt} {\text{'}} \in E{{q}_{n}}(R{\text{'}})$ и такой, что $T{\kern 1pt} {\text{'}} - \text{v} \notin E{{q}_{n}}(R)$. Выберем ромб $S{\kern 1pt} {\text{'}} \in E{{q}_{{n - 1}}}(R{\text{'}})$ так, чтобы $T{\kern 1pt} {\text{'}} \in E{{q}_{1}}(S{\text{'}})$. По предположению индукции $E{{q}_{{n - 1}}}(R) = E{{q}_{{n - 1}}}(R{\text{'}}) - \text{v}$. Отсюда легко получить, что ромб S = S′ – v корректно определен и содержится в координационном окружении $E{{q}_{{n - 1}}}(R)$. При этом $E{{q}_{1}}(S) \subset E{{q}_{1}}(S{\text{'}}) - \text{v}$. Получаем противоречие с ранее рассмотренным случаем n = 1.
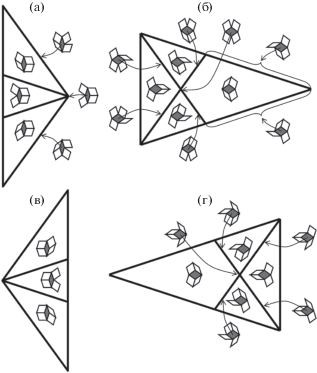
На рис. 6 приведены параметризации первых координационных окружений малых и больших ромбов первого и второго типов разбиения Пенроуза для одной ориентации ромбов. Для остальных четырех ориентаций аналогичные параметризации получаются умножением на ζ2, т.е. поворотами на $\frac{{4\pi }}{5}$ в фазовом пространстве, что соответствует умножению на ζ (повороту на $\frac{{2\pi }}{5}$) координационных окружений в физическом пространстве.
Рис. 6.
Параметризации первых координационных окружений одной ориентации малых (а) и больших (б) ромбов первого типа, малых (в) и больших (г) ромбов второго типа разбиения Пенроуза.
Так же, как и в случае кластеров, можно выделить типичные координационные окружения с двумерным множеством параметров и исключительные координационные окружения, множества параметров которых имеют меньшую размерность. При этом наличие тех или иных исключительных координационных окружений, а также конкретный вид соответствующего множества параметров зависят от выбора границы окна при определении множества вершин разбиения Пенроуза.
Отметим, что множества исключительных координационных окружений не обязаны обладать симметрией, связывающей типичные координационные окружения и их параметры. Также отметим, что кроме исключительных координационных окружений с одномерным множеством параметров имеются три исключительных координационных окружения, множества параметров которых нульмерны и представляют собой одну точку. Каждое из таких первых координационных окружений встречается в разбиении ровно один раз. Интересно, что для координационных окружений графа вершин разбиения Пенроуза подобного эффекта не возникает.
ФОРМА ПОСЛОЙНОГО РОСТА РАЗБИЕНИЯ ПЕНРОУЗА
Рассмотрим предел последовательности вложенных координационных сфер
Если данный предел существует, то он называется формой послойного роста разбиения Пенроуза. В [5] доказано, что из существования формы роста следует ее независимость от выбора начального ромба.Понятие формы послойного роста впервые было введено в [17, 18] и рассматривалось в [4, 5, 8, 12, 14–16, 19, 20] для различных периодических и квазипериодических структур, а также структур с элементами случайности. В частности, в [8] доказано, что форма послойного роста графа вершин разбиения Пенроуза существует и представляет собой правильный десятиугольник, координаты вершин которого вычислены в явном виде. В [21] также доказано, что форма роста разбиения Пенроуза существует и представляет собой правильный десятиугольник, однако координаты вершин данного десятиугольника не были явно вычислены, хотя, на наш взгляд, метод рассматриваемой работы позволял сделать это. Метод [21] основывается на существовании в разбиении Пенроуза специальной структуры, называемой полосами Амманна [22], и не годится для большинства других квазипериодических структур (за исключением, возможно, разбиения Амманна–Бинкера и некоторых его аналогов).
Приведем набросок другого доказательства теоремы о форме роста разбиения Пенроуза, аналогичный доказательству теоремы о форме роста для графа вершин разбиения Пенроуза из [8]. Идеи данного доказательства могут быть перенесены на другие квазипериодические графы и разбиения, получаемые на основе модельных множеств.
Теорема. Форма послойного роста разбиения Пенроуза существует и представляет собой правильный десятиугольник γ, вершинами которого на комплексной плоскости являются числа вида $R{{e}^{{\frac{{2\pi ik}}{{10}}}}}$, где k = 0, 1, …, 9 и $R = \left( {{{\tau }^{{ - 1}}}\sin \frac{{2\pi }}{5} + {{\tau }^{{ - 2}}}\sin \frac{\pi }{5}} \right)i$.
Замечание. Формы послойного роста разбиения Пенроуза и его графа вершин совпадают. Другими примерами разбиений с подобным свойством являются правильные разбиения плоскости на квадраты/шестиугольники. В общем случае подобное утверждение, разумеется, неверно. Авторам неизвестно простое объяснение совпадения рассматриваемых форм роста.
Доказательство теоремы о форме роста состоит из двух частей: доказательство нижней и верхней границы.
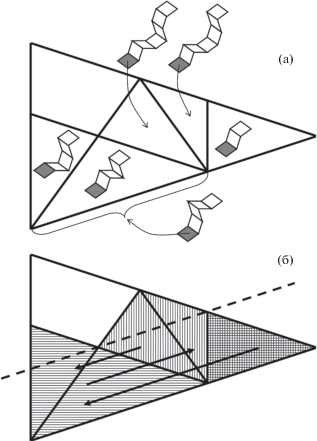
Для доказательства нижней границы достаточно построить цепи длины n, ведущие в точки, расположенные в окрестности размера o(n) множества nγ. На самом деле достаточно для произвольного начального ромба построить цепи, направление которых определяется лучами, ведущими из начала координат в вершины многоугольника γ. Будем называть такие цепи вершинными. Их значение объясняется тем, что все остальные цепи могут быть получены как комбинации вершинных цепей [5, 8]. Более того, в силу наличия симметрии 10 порядка достаточно научиться строить вершинные цепи, соответствующие одной выбранной вершине.
Рассмотрим произвольную прямую на разбиении Пенроуза и выделим множество ромбов какого-либо одного типа и одной ориентации, пересекаемых данной прямой. Для любой пары соседних ромбов рассмотрим соединяющую их кратчайшую цепь. Тогда легко видеть, что этим цепям соответствует конечное число типов кластеров $\{ {{C}_{i}}\} $. Обозначив через ${{C}_{i}}$ вектор, соединяющий точки пересечения диагоналей начального и конечного ромбов кластера ${{C}_{i}}$, получаем, что средняя скорость движения вдоль построенной цепи $\bar {R} = \bar {s}{\text{/}}\bar {n}$ будет определяться как отношение среднего сдвига $\bar {s} = \sum\nolimits_i^{} {\nu ({{C}_{i}})} \left| {{{C}_{i}}} \right|$ на среднюю длину цепей ${{C}_{i}}$ $\bar {n} = \sum\nolimits_i^{} {\nu ({{C}_{i}})} \left| {{{C}_{i}}} \right|$, где $\nu ({{С }_{i}})$ – частота появления ${{С }_{i}}$ в строящейся цепи, $\left| {{{C}_{i}}} \right|$ – длина вектора ${{C}_{i}}$, а $\left| {{{С }_{i}}} \right|$ – длина цепи ${{С }_{i}}$.
Для вычисления частот $\nu ({{С }_{i}})$ необходимо перейти к параметрам кластеров. При этом исходной прямой в разбиении Пенроуза будет соответствовать отрезок, полученный пересечением окна с двойственной прямой в пространстве параметров. При этом параметризация кластеров $\{ {{C}_{i}}\} $ порождает разбиение данного отрезка на части, соответствующие отдельным кластерам. Переход от одного кластера к следующему будет соответствовать сдвигу на некоторый эффективно вычисляемый вектор в пространстве параметров. Таким образом, движение вдоль цепи соответствует некоторому перекладыванию отрезков в пространстве параметров. Во многих случаях удается доказать, что орбита данного перекладывания равномерно распределена. Это означает, что частоты появления кластеров становятся пропорциональными длинам соответствующих отрезков, что дает эффективный способ получения частот, а следовательно, и нижних границ (в общем случае не обязательно точных).
Применяя данную схему к разбиению Пенроуза, вернемся к рис. 4. На рис. 4а представлена параметризация пяти типов кластеров, встречающихся в вершинных цепях, соответствующих вершине $R{{e}^{{\frac{{9\pi i}}{5}}}}$ десятиугольника роста, а на рис. 4б различной штриховкой выделены три области, включающие в себя параметры кластеров, которым соответствуют три различных вектора сдвига. Если взять любой из указанных пяти кластеров, параметр которого попадает ниже штриховой линии, то рис. 4б задает перекладывание трех отрезков в фазовом пространстве, которому в физическом пространстве соответствует вершинная цепь, ведущая в вершину $R{{e}^{{\frac{{9\pi i}}{5}}}}$. Критерии равномерной распределенности орбиты для таких перекладываний хорошо известны [23]. Непосредственное вычисление показывает, что полученное перекладывание является равномерно распределенным и действительно дает цепь, скорость роста которой доказывает требуемую нижнюю границу.
На самом деле приведенная конструкция позволяет строить вершинные цепи с требуемой скоростью роста не из произвольного начального ромба, а только из начального множества ромбов положительной плотности. Однако для произвольного начального ромба можно построить цепь, ведущую в допустимый. Более того, легко показать, что длина такой цепи не превосходит некоторой постоянной, не зависящей от выбора начального ромба. Это соображение позволяет построить вершинные цепи с требуемой скоростью роста, выходящие из любого начального ромба, и завершает доказательство нижней границы.
Для доказательства верхней границы рассмотрим граф G, двойственный разбиению Пенроуза. Множество вершин данного графа совпадает с множеством центров ромбов разбиения Пенроуза. Две вершины соединены ребром тогда и только тогда, когда соответствующие им ромбы являются соседними. Очевидно, что форма роста данного графа совпадает с формой роста разбиения Пенроуза. Поэтому можно доказывать верхнюю границу для формы роста графа G.
Общая идея доказательства верхних оценок формы роста квазипериодических графов G, множество вершин которых является модельным множеством, основана на их вложении в периодические графы более высокой размерности.
Определим граф $\bar {G}$ следующим образом. Множество вершин $\bar {G}$ есть $\{ \pi _{1}^{{' - 1}}(x):x \in G\} $. Две вершины соединены ребром тогда и только тогда, когда соединены их прообразы в графе $\bar {G}$. Пусть $\hat {G}$ – периодический граф, содержащий все вершины и ребра графа $\bar {G}$. Из общих результатов теории послойного роста [5, 18] следует, что граф $\hat {G}$ имеет самоподобный рост, причем форма роста эффективно вычислима и представляет собой выпуклый центрально симметричный многогранник $\overline {Pol} $. Пусть $P = \{ x \in {{{\mathbf{R}}}^{n}}:\pi _{2}^{{''}}(x) = 0\} $, где проекция $\pi _{2}^{{''}}(x)$ определяется соотношением $\pi _{2}^{{''}}({{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}})$ = = $\frac{{{{x}_{1}} + {{x}_{2}}{{\zeta }^{2}} + {{x}_{3}}{{\zeta }^{4}} + {{x}_{4}}\zeta }}{2}$. Тогда методы [8] показывают, что имеет место верхняя оценка $\gamma \subseteq \pi _{1}^{'}(\overline {Pol} \cap P)$, и доказательство верхней границы сводится к выбору подходящего графа $\hat {G}$, вычислению его формы, а также расчету соответствующего сечения и проекции.
В случае разбиения Пенроуза в качестве $\hat {G}$ использовался периодический граф в четырехмерном пространстве, фундаментальная область (примитивная ячейка решетки трансляций) которого определяется базисом ${{{\mathbf{e}}}_{1}} = (5;0;0;0)$, ${{{\mathbf{e}}}_{2}} = ( - 1;1;0;0)$, ${{{\mathbf{e}}}_{3}} = ( - 1;0;1;0)$, ${{{\mathbf{e}}}_{4}} = ( - 1;0;0;1)$. Все возможные в графе $\hat {G}$ ребра определяют 30 векторов, которые приведены в табл. 1. В табл. 2 представлены 20 трансляционно независимых вершин графа $\hat {G}$, а также номера векторов из табл. 3, определяющих ребра, выходящие из каждой вершины.
Таблица 1.
Векторы, определяющие ребра в графе $\hat {G}$
| Вектор | h | j | K | l |
|---|---|---|---|---|
| 1 | 0 | 0 | –0.5 | –0.5 |
| 2 | 0.5 | 0.5 | 0.5 | 0 |
| 3 | 0 | 0.5 | 0.5 | 0.5 |
| 4 | –0.5 | –0.5 | 0 | 0 |
| 5 | 0 | –0.5 | –0.5 | 0 |
| 6 | 0.5 | 1.0 | 0.5 | 0.5 |
| 7 | –0.5 | 0 | 0.5 | 0 |
| 8 | 0 | –0.5 | 0 | 0.5 |
| 9 | –0.5 | –0.5 | –1.0 | –0.5 |
| 10 | 0.5 | 0 | 0 | –0.5 |
| 11 | 0 | 0 | 0.5 | –0.5 |
| 12 | 0.5 | 0.5 | 0.5 | 1.0 |
| 13 | –1.0 | –0.5 | –0.5 | –0.5 |
| 14 | 0.5 | –0.5 | 0 | 0 |
| 15 | 0 | 0.5 | –0.5 | 0 |
| 16 | 0 | 0 | 0.5 | 0.5 |
| 17 | –0.5 | –0.5 | –0.5 | 0 |
| 18 | 0 | –0.5 | –0.5 | –0.5 |
| 19 | 0.5 | 0.5 | 0 | 0 |
| 20 | 0 | 0.5 | 0.5 | 0 |
| 21 | –0.5 | –1.0 | –0.5 | –0.5 |
| 22 | 0.5 | 0 | –0.5 | 0 |
| 23 | 0 | 0.5 | 0 | –0.5 |
| 24 | 0.5 | 0.5 | 1.0 | 0.5 |
| 25 | –0.5 | 0 | 0 | 0.5 |
| 26 | 0 | 0 | –0.5 | 0.5 |
| 27 | –0.5 | –0.5 | –0.5 | –1.0 |
| 28 | 1.0 | 0.5 | 0.5 | 0.5 |
| 29 | –0.5 | 0.5 | 0 | 0 |
| 30 | 0 | –0.5 | 0.5 | 0 |
Таблица 2.
Координаты независимых вершин периодического графа $\hat {G}$ и номера векторов из табл. 1, определяющих выходящие из этих вершин ребра
| Вершина | Координаты вершин | Число ребер вершины | Номера векторов, определяющих ребра | |||
|---|---|---|---|---|---|---|
| h | j | k | l | |||
| 1 | 1 | 0 | 0.5 | 0.5 | 8 | 8, 9, 10, 17, 20, 22, 23, 24 |
| 2 | 3.5 | 0.5 | 0.5 | 0 | 8 | 6, 9, 10, 16, 18, 23, 24, 25 |
| 3 | 3 | 0.5 | 0.5 | 0.5 | 8 | 6, 7, 10, 17, 19, 21, 24, 25 |
| 4 | 1.5 | 0.5 | 0 | 0 | 8 | 6, 7, 8, 18, 20, 21, 22, 25 |
| 5 | 1 | 0.5 | 0.5 | 0 | 8 | 7, 8, 9, 16, 19, 21, 22, 23 |
| 6 | 2 | 0 | 0.5 | 0.5 | 8 | 2, 5, 7, 8, 9, 23, 24, 25 |
| 7 | –0.5 | 0.5 | 0.5 | 0 | 8 | 1, 3, 8, 9, 10, 21, 24, 25 |
| 8 | –1 | 0.5 | 0.5 | 0.5 | 8 | 2, 4, 6, 9, 10, 21, 22, 25 |
| 9 | 2.5 | 0.5 | 0 | 0 | 8 | 3, 5, 6, 7, 10, 21, 22, 23 |
| 10 | 2 | 0.5 | 0.5 | 0 | 8 | 1, 4, 6, 7, 8, 22, 23, 24 |
| 11 | 3.5 | 0 | 0.5 | 0.5 | 6 | 8, 12, 18, 19, 24, 30 |
| 12 | 1.5 | 0 | 0.5 | 0 | 6 | 9, 13, 19, 20, 25, 26 |
| 13 | 1 | 0.5 | 0 | 0.5 | 6 | 10, 14, 16, 20, 21, 27 |
| 14 | 3.5 | 0.5 | 0 | 0.5 | 6 | 6, 15, 16, 17, 22, 28 |
| 15 | 1.5 | 0 | 0 | 0.5 | 6 | 7, 11, 17, 18, 23, 29 |
| 16 | –0.5 | 0 | 0.5 | 0.5 | 6 | 3, 4, 9, 15, 23, 27 |
| 17 | 2.5 | 0 | 0.5 | 0 | 6 | 4, 5, 10, 11, 24, 28 |
| 18 | 2 | 0.5 | 0 | 0.5 | 6 | 1, 5, 6, 12, 25, 29 |
| 19 | –0.5 | 0.5 | 0 | 0.5 | 6 | 1, 2, 7, 13, 21, 30 |
| 20 | 2.5 | 0 | 0 | 0.5 | 6 | 2, 3, 8, 14, 22, 26 |
Таблица 3.
Координаты вершин многогранника $\overline {Pol} $
| Вершина | h | j | k | l | Вершина | h | j | k | l |
|---|---|---|---|---|---|---|---|---|---|
| 1 | –1/2 | –1/2 | –1 | –1/2 | 11 | –1/7 | –2/7 | –3/7 | –4/7 |
| 2 | 1/2 | 1/2 | 1 | 1/2 | 12 | 1/7 | 2/7 | 3/7 | 4/7 |
| 3 | 0 | 1/2 | 0 | –1/2 | 13 | 1/7 | 2/7 | –2/7 | –1/7 |
| 4 | 0 | –1/2 | 0 | 1/2 | 14 | –1/7 | –2/7 | 2/7 | 1/7 |
| 5 | 1/2 | 0 | –1/2 | 0 | 15 | –1/7 | –2/7 | –3/7 | 1/7 |
| 6 | –1/2 | 0 | 1/2 | 0 | 16 | 1/7 | 2/7 | 3/7 | –1/7 |
| 7 | –1/2 | –1 | –1/2 | –1/2 | 17 | 1/7 | –3/7 | –2/7 | –1/7 |
| 8 | 1/2 | 1 | 1/2 | 1/2 | 18 | –1/7 | 3/7 | 2/7 | 1/7 |
| 9 | –1/2 | 0 | 0 | 1/2 | 19 | 4/7 | 3/7 | 2/7 | 1/7 |
| 10 | 1/2 | 0 | 0 | –1/2 | 20 | –4/7 | –3/7 | 2/7 | –1/7 |
Согласно [5, 18] многогранник $\overline {Pol} $ представляет собой выпуклую оболочку множества векторов, получаемых нормированием цепей, для которых начало и конец сравнимы по модулю решетки периодов и которые не содержат промежуточных вершин, сравнимых по модулю решетки. Для вычисления данных векторов использовался программный комплекс [24]. Расчет выпуклой оболочки осуществлялся при помощи программы QHULL [25, 26]. Вычисления показали, что $\overline {Pol} $ – выпуклый центрально-симметричный многогранник, содержащий 60 трехмерных граней, представляющих собой тетраэдры, 120 двумерных треугольных граней, 80 ребер и 20 вершин. Непосредственное вычисление сечения и его проекции дало требуемую верхнюю границу.
ВЫВОДЫ
В результате проведенного исследования получено новое описание разбиения Пенроуза, основанное на сопоставлении каждому ромбу разбиения Пенроуза некоторого параметра. Данное описание порождает новый алгоритм построения разбиения Пенроуза.
Разработан метод, позволяющий описывать конфигурации (кластеры и координационные окружения) в разбиении Пенроуза на языке параметров. В качестве приложения найдены параметры всех возможных типов первых координационных окружений в разбиении Пенроуза.
Показано, что существуют типичные координационные окружения, имеющие положительную плотность (частоту появления), и исключительные координационные окружения с нулевой плотностью. Также показано, что существуют исключительные координационные окружения, встречающиеся в разбиении как бесконечное, так и конечное число раз.
Получено новое доказательство того факта, что формой послойного роста разбиения Пенроуза является правильный десятиугольник γ с вершинами $R{{e}^{{\frac{{2\pi ik}}{{10}}}}}$ на комплексной плоскости, где k = 0, 1, …, 9 и $R = \left( {{{\tau }^{{ - 1}}}\sin \frac{{2\pi }}{5} + {{\tau }^{{ - 2}}}\sin \frac{\pi }{5}} \right)i$. При этом обнаружено, что формы послойного роста разбиения Пенроуза и его графа вершин совпадают.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты № 14-01-00360-a, 17-02-00835-a, 17-42-330787-ра).
Список литературы
Moody R.V. // From Quasicrystals to More Complex Systems. V. 13 of the series Centre de Physique des Houches. Springer, 2000. P. 145.
Hof A. // Commun. Math. Phys. 1995. V. 169. P. 25.
Schlottmann M. // Quasicrystals and Discrete Geometry / Ed. Patera J. Fields Institute Monographs. V. 10. AMS, Providence, 1998. P. 247.
Шутов А.В., Малеев А.В., Журавлев В.Г. // Тр. V Всерос. науч. школы “Математические исследования в естественных науках”. Апатиты: K & M, 2009. С. 126.
Шутов А.В., Малеев А.В. Модель послойного роста разбиений, упаковок и графов. Владимир: Транзит-Х, 2011. 107 с.
Shutov A.V., Maleev A.V. // Crystallography Reports. 2015. V. 60. № 6. P. 797.
Шутов А.В., Малеев А.В. // Кристаллография. 2017. Т. 62. №4. С. 535.
Шутов А.В., Малеев А.В. // Кристаллография. 2017. Т. 62. № 5. С. 707.
Baake M., Kramer P., Schlottman M., Zeidler D. // Int. J. Mod. Phys. B. 1990. V. 04. P. 2217.
Baake M., Huck C. // Philos. Mag. 2007. V. 87. P. 2839.
Baake M., Grimm U. Aperiodic order. V. 1. A Mathematical Invitation. Cambridge University Press, 2013. 552 p.
Журавлев В.Г., Малеев А.В. // Кристаллография. 2007. Т. 52. № 2. С. 204.
Журавлев В.Г. // Алгебра и анализ. 2010. Т. 22. № 4. С. 21.
Shutov A.V., Maleev A.V., Zhuravlev V.G. // Acta Cryst. A. 2010. V. 66. P. 427.
Shutov A.V., Maleev A.V. // Classification and Application of Fractals: New Research / Eds. Eric W. et al. Nova Science Publishers, 2012. P. 55.
Shutov A.V., Maleev A.V. // Acta Cryst. A. 2008. V. 64. P. 376.
Рау В.Г., Журавлев В.Г., Рау Т.Ф., Малеев А.В. // Кристаллография. 2002. Т. 47. № 5. С. 793.
Журавлев В.Г. // Алгебра и анализ. 2001. Т. 13. № 2. С. 69.
Журавлев В.Г., Малеев А.В., Рау В.Г., Шутов А.В. // Кристаллография. 2002. Т. 47. № 6. С. 976.
Шутов А.В. // Чебышевский сборник. 2003. Т. 4. Вып. 2. С. 109.
Akiyama S., Imai K. // Cellular Automata and Discrete Complex Systems. V. 9664 of the series Lecture Notes in Computer Science. Springer, 2016. P. 35.
Grunbaum B., Shephard C.G. Tiling and Patterns. N.Y.: Freemann, 1986. 700 p.
Keane M. // Mathematische Z. 1975. B. 141. № 1. S. 25.
Малеев А.В., Журавлев В.Г., Шутов А.В., Рау В.Г. // Программный комплекс для исследования координационных окружений в модели послойного роста графов связности. Свидетельство о регистрации программы для ЭВМ № 2013619399. М.: Федеральная служба по интеллектуальной собственности (Роспатент). 2013.
Barber C.B., Dobkin D.P., Huhdanpaa H.T. // ACM Transactions on Mathematical Software. 1996. V. 22. № 4. P. 469.
http://www.qhull.org.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография