Кристаллография, 2019, T. 64, № 4, стр. 509-520
Акустические волны и надмолекулярные структуры в жидких кристаллах
1 Акустический институт им. Н.Н. Андреева РАН
Москва, Россия
* E-mail: oakapustina@yandex.ru
Поступила в редакцию 11.01.2019
После доработки 11.01.2019
Принята к публикации 17.01.2019
Аннотация
Рассмотрены и обобщены достижения в области изучения надмолекулярных структур, возникающих в жидких кристаллах (ЖК) под воздействием акустических волн, начало которому положила выполненная более 50 лет назад работа профессора А.П. Капустина. Основное внимание уделено обсуждению проблемы “пороговой” дестабилизации текстуры слоя ЖК при разных видах механических деформаций, порождаемых акустическими волнами, что проявляется в образовании разнообразных надмолекулярных структур. Рассмотрены не только факторы, определяющие пороговые характеристики этих структур в широкой области частот для нематических и холестерических ЖК, но и динамика этих структур за порогом, а также особенности их искажения при акустическом бинарном воздействии.
ОГЛАВЛЕНИЕ
Введение
1. Надмолекулярные структуры, возникающие под действием акустических колебаний на звуковых частотах
2. Надмолекулярные структуры, индуцированные воздействием УЗ-волн
3. Надпороговая динамика надмолекулярных структур в акустических полях
4. Надмолекулярные структуры при бинарном акустическом воздействии на НЖК
Заключение
ВВЕДЕНИЕ
В августе 2019 г. исполняется 115 лет со дня рождении профессора Александра Павловича Капустина, известного российского ученого, первооткрывателя одного из уникальных явлений в современной физике жидких кристаллов (ЖК) – так называемых “доменов Капустина–Вильямса”, индуцированных электрическим полем [1]11. А.П. Капустину принадлежит приоритет и в открытии доменов иной природы. В его опытах начала 70-х гг. в акустических полях МГц-диапазона впервые наблюдались упорядочение поликристаллической текстуры тонкого слоя ЖК (n-азоксифенетол) и образование некой новой надмолекулярной структуры, получившей название “акустические домены” (рис. 1) [2]. Эта работа стала основополагающей для становления нового направления в акустике ЖК – науки об акустических доменах. Сегодня приняты два подхода при анализе устойчивости структуры ЖК к акустическому воздействию: классическая гидродинамика Лесли–Эриксена [3] и неравновесная гидродинамика. При рассмотрении данных выделяют [3] два типа надмолекулярных структур, свойственных частотам звукового или УЗ-диапазона, вводя своеобразный критерий: соотношение толщины d слоя ЖК и длины вязкой волны λv как частотно зависимого параметра среды.
НАДМОЛЕКУЛЯРНЫЕ СТРУКТУРЫ, ВОЗНИКАЮЩИЕ ПОД ДЕЙСТВИЕМ АКУСТИЧЕСКИХ КОЛЕБАНИЙ НА ЗВУКОВЫХ ЧАСТОТАХ
Интерес к проблеме акустически индуцированных надмолекулярных структур в ЖК первыми проявили физики университетов Орсе (Франция) [4–7] и Глазго (Англия) [8, 9]. В начале 80-х годов они провели опыты в области звуковых частот (${{\lambda }_{v}}$ $ \gg $ d), изучая действия периодического сдвига и сжатия на гомеотропные и планарные слои НЖК, и описали свойства доменов на пороге неустойчивости. Обобщая наиболее значимые результаты этих работ, получившие объяснение в рамках классической гидродинамики [3], можно выделить ряд ситуаций, различающихся типом текстуры и видом воздействия.
Планарный слой НЖК и периодический линейный сдвиг. Реакция структуры слоя на такое воздействие зависит от расположения директора n НЖК и вектора скорости осциллирующего потока, созданного колебаниями сдвига. Рассмотрим ситуацию в следующей геометрии: одна из пластин ячейки с ЖК колеблется по закону ${{v}_{y}} = {{v}_{0}}_{y}$sin ωt (${{v}_{y}}{\text{ и }}{{v}_{0}}_{y}$ – компоненты колебательной скорости и ее амплитуды по оси Y), индуцируя поток с профилем скорости вида: Vx = Vz = 0, Vy (t) = S(t) z (S(t) – градиент скорости в потоке, t – время, ω = 2πf – круговая частота колебаний, f – число полных циклов колебаний за одну секунду. Директор n лежит в плоскости XY и составляет угол φ с вектором скорости потока Vy(t) (рис. 2а). При ортогональном расположении векторов n и Vy(t) в слое возникает система одномерных доменов, оси которых совпадают с направлением сдвига. Механизм этого явления, известного как ролл-неустойчивость Гюйона–Перанского [4–7], объясняют усилением случайного ориентационного начального искажения структуры при взаимодействии поля скоростей и директора n. Впервые его наблюдали на частотах 0.4–0.7 Гц при наложении стабилизирующих электрического или магнитного полей [4].
Рис. 2.
К анализу одномерных доменов в планарном слое НЖК в осциллирующем линейном потоке,
вызванном сдвиговыми колебаниями одной из пластин ячейки: а – геометрия задачи; б
– связь пороговых волновых чисел qх,th доменов с углом φ между директором n и вектором колебательной скорости ${{v}_{y}}$; d = 40 мкм, (обозначения ×, $\blacktriangle $, $\blacksquare $,  отвечают частотам, равным 1, 5, 15 и 20 Гц соответственно).
отвечают частотам, равным 1, 5, 15 и 20 Гц соответственно).
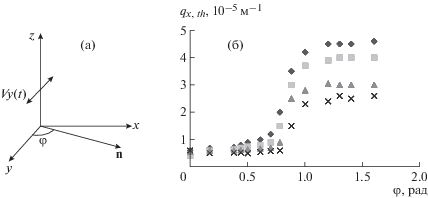
Упрощенная теория этого явления, построенная без учета инерции среды [6, 7], утверждает, что в зависимости от напряженности поля и частоты возможно появление двух типов искажения: Y-моды (〈ny〉 = 0, 〈nz〉 ≠ 0) и Z-моды (〈ny〉 ≠ 0, 〈nz〉 = 0) с разными временами релаксации. Здесь 〈ny〉 и 〈nz〉 – средние по периоду колебаний отклонения директора n от исходного положения в плоскости слоя и в направлении нормали к ней. Согласно этой теории пороговое волновое число искажения qх,th, периодического по оси Х, и круговая частота колебаний связаны соотношением вида qх,th ~ ω1/3.
Более точная модель, учитывающая влияние инерции среды, была построена значительно позднее [10]. Она предсказывает многообразие возможных конфигураций искажений типа (j, 1) и (j, 2) (j = 1, 2). Эти типы различаются поведением постоянной и переменной компонент углов отклонения директора n в возмущенной структуре. Согласно [10] связь пороговых характеристик надмолекулярной структуры с частотой колебаний и толщиной слоя НЖК определяется соотношением ωd2 ~ ωτ, где τ = γ1d2/К33, γ1 – коэффициент вращательной вязкости, K33 – упругая постоянная Франка. Диаграмма состояния, приведенная в [10], построена в координатах (ωτ, α3/γ1) и предсказывает иерархию возможных структурных искажений слоя НЖК (α3 – коэффициент вязкости Лесли [3]). Оказалось, что на шкале частот можно выделить области, разделенные значениями (ωτ)1 ≈ 35 и (ωτ)2 ≈ 19 000, где возникают неустойчивости разного типа: однородные искажения (1, 2) (область I), домены (1, 1) с периодом Lth ~ 1/ω (область II) и домены (1, 2) с периодом Lth ≈ 2d (область III). Согласно теории в области II волновое число искажения qх, th при повышении частоты растет от 4.5 до 13.5, что согласуется с данными опытов [11], проведенных в области частот 1–20 Гц на слоях толщиной 30–80 мкм при φ = π/2.
При параллельном положении директора n и вектора скорости потока Vy(t) в слое возникают домены, вытянутые ортогонально Vy(t). Их появление в НЖК объясняют [8, 9] влиянием инерции среды, вызывающей запаздывание скорости вторичных осциллирующих потоков от скорости потока, который инициирует эффект. Пока эта гипотеза требует проверки.
Наиболее полные сведения о свойствах доменов, возникающих в НЖК при произвольном положении директора n и скорости потока, приведены в [11–13]. Наблюдаемое в опытах увеличение пороговых градиентов скорости сдвига и волнового числа искажения при снижении угла между векторами n и Vy(t) связывают с изменением коэффициентов вязкости НЖК. Типичная картина деформации при частотах 1–20 Гц, представленная в координатах (qх,th, φ), показывает, что наиболее заметные изменения qх,th происходят в области значений φ ∈ [0.7, 0.88 рад] (рис. 2б) [13]. Это согласуется с предсказанием [12] о существовании критического угла φcr ~ arctg[1 + (α5/α4 – – 2α3/α6)/3], разделяющего области, где развиваются различные моды неустойчивости. Для НЖК типа МББА (N-(n-метоксибензилиден)-n'-бутиланилин) при значениях коэффициентов вязкости Лесли αi, отвечающих температуре 23°С, согласно расчетам угол φcr ≈ 0.77 рад близок к найденному в опытах. По теории [12] в области I (φ < < φcr) развивается мода I, которой сопутствуют домены с волновыми числами, слабо зависящими от частоты, а при снижении угла до значения φ = = 0 рад влияние частоты исчезает. В области II (φcr < φ ≤ 1.57 рад), где возникает мода II, волновое число qх,th зависит как от частоты колебаний, так и угла φ, что характерно для неустойчивости Гюйона–Перанского [4]. По данным [13] связь порогового волнового числа qх,th с толщиной слоя d не зависит от типа моды и при d, равных 10–150 мкм, следует закономерности qх,th ~ 1/d, что соответствует результатам численного расчета [12]. Заметим, что анализ искажений в [12] был упрощен (учитывалось малое число гармоник в зависимости угловых переменных от времени, не рассматривался вклад инерции). Для полной апробации модели нужны данные опытов в более широкой области частот.
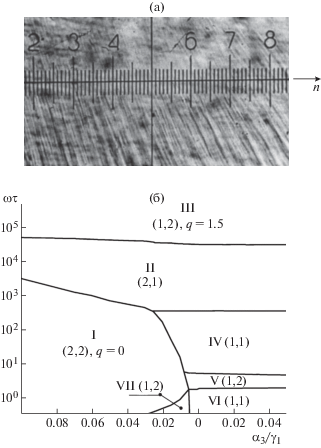
Планарный слой НЖК в условиях периодического сжатия. Первые данные об искажении планарного слоя НЖК в осциллирующем потоке с параболическим профилем скорости, созданном в плоском капилляре перепадами давления, в области частот 0.005–0.8 Гц (d = 200 мкм) приведены в [14]. В [11, 13] был расширен диапазон частот (до 30 Гц) и изменена геометрия опыта: одна из пластин ячейки совершала поршневые колебания вдоль оси Z, что вызывало периодическое сжатие слоя НЖК и растекание жидкости от его центра к концам. Радиальная симметрия такого осциллирующего потока позволила реализовать в набор значений угла φ между векторами n и V(r, t). Эти одномерные домены “лежат” вдоль линий тока, а их период зависит от угла φ и при его снижении растет [13]. Теория явления пока разработана только для ортогонального расположения векторов n и V(r, t) [15]. Диаграмма состояния, приведенная в [15], демонстрирует многообразие возможных конфигураций искажений (j, 1), (j, 2) структуры, наблюдаемое в областях I–VII, которые представляют ситуацию при разных сочетаниях вязкости среды и параметра ωτ (рис. 3б). Данных для апробации этой теории нет. Отметим вывод [16] об общности закономерностей, которые описывают домены, наблюдаемые в потоке с параболическим или линейным профилем скорости, ибо в первом из них неустойчивость возникает в приграничной зоне слоя НЖК, где имеет место сдвиг, свойственный линейному потоку.
Рис. 3.
Планарный слой НЖК в осциллирующем потоке, созданном поршневыми колебаниями пластины ячейки: а – картина одномерных доменов; f = = 30 Гц, d = 100 мкм, φ = 1.6–1.3 рад; стрелка показывает исходную ориентацию молекул в слое (положение директора n); цена деления шкалы окуляра – 6.6 мкм; б – диаграмма состояния, которая представляет конфигурации искажений в областях I–VII, отвечающих разным видам неустойчивости НЖК: тип (2, 2), q = 0 (область I); тип (2, 1), q(ω) (область II); тип (1, 2), q = 1.5 (область III); тип (1, 1), q = 4.6–7.5 (область IV); тип (1, 2), q ≈ 4.5 (область V); тип (1, 1), q ≈ 5 (область VI); тип (1, 2), q ≈ 4.5 (область VII).
Гомеотропный слой НЖК при периодическом линейном сдвиге. Известно, что в такой ситуации в НЖК возникает система одномерных доменов, расположенных ортогонально вектору колебательной скорости сдвига. Попытки [17–22] дать описание их свойств, адекватное результатам опытов, оказались весьма неудачными. Пока наиболее точную модель явления удалось построить в [23], где анализ эффекта проведен в рамках классической гидродинамики при сохранении в ее уравнениях квадратичных слагаемых, пропорциональных произведению угла поворота молекул и скорости жидкости. Оказалось, что стационарные напряжения и моменты, способные дестабилизировать исходную структуру НЖК, отличны от нуля, если скорость жидкости в осциллирующих вихревых потоках запаздывает по фазе от ее скорости в линейном потоке, индуцированном колебаниями сдвига. Найдены факторы, ответственные за запаздывание, – это пограничные эффекты и инерция среды. Они “работают” на низких или высоких частотах и поэтому дают разные представления для пороговой амплитуды сдвига (ξ0,th) и периода доменов на пороге эффекта (Lth), а именно: ξ0,th ~ 1/(ωd 2)1/4 и Lth ~ ~ 0.6d или ξ0,th ~ 1/(ωd2) и Lth ~ 1.01d. В современной литературе достаточно данных о пороговых характеристиках доменов в областях частот 0.01–200 Гц [18, 20] и 0.1–100 кГц [24]. Однако большинство из них не только различается в несколько раз, но и противоречит друг другу. Так, следующая из теории связь пороговой амплитуды с параметром ωτ согласуется с данными [19, 21], но не коррелируют с результатами [24]. Также не совпадают значения пороговой амплитуды, приведенные в [18, 20, 24]. Корреляция теоретической зависимости периода Lth/d от параметра ωτ с результатами [18, 21] установлена только в области высоких частот, а на низких частотах его расчетные значения в 1.5 раза выше наблюдаемых. В этой связи сделать однозначный вывод об адекватности теории [23] пока не удается.
Гомеотропный слой НЖК и периодический эллиптический сдвиг. В опытах по изучению действия периодического эллиптического сдвига на НЖК-пластины ячейки совершали колебания в плоскости XY по осям X и Y со сдвигом по фазе π/2, при этом в слое возникала система одномерных доменов, ориентированных под углом к оси X [25–29]. Согласно [25] период доменов при частотах 200–500 Гц пропорционален толщине слоя, а вид диаграммы порогов, построенной в координатах амплитуд колебаний ξ0х и ξ0у, зависит от толщины слоя [28]. На первом этапе исследований в рамках классического подхода удалось построить теорию явления для толстых слоев НЖК [26, 28], а позднее предложить ее уточненную модель [27], которая дает адекватное описание данных опытов [29] и в тонких слоях ЖК.
НАДМОЛЕКУЛЯРНЫЕ СТРУКТУРЫ, ИНДУЦИРОВАННЫЕ ВОЗДЕЙСТВИЕМ УЛЬТРАЗВУКОВЫХ ВОЛН
Впервые образование надмолекулярных структур под действием УЗ наблюдали в поликристаллической текстуре НЖК более полувека назад [2]. Первые сведения об одномерных доменах, возникающих в этой области частот на пороге неустойчивости в планарном слое НЖК, появились значительно позднее [30]. В те же годы были открыты двумерные домены в холестерических жидких кристаллах (ХЖК) [31]. Однако дать адекватное результатам опытов описание таких структур удалось, только отказавшись от классического подхода [3, 32] и переходя на позиции неравновесной гидродинамики, которая учитывает зависимость коэффициентов вязкости мезофазы от ее упорядочения. Концепция Е.Н. Кожевникова о релаксационной природе дестабилизации структуры планарного слоя при воздействии УЗ привела к созданию моделей ориентационной неустойчивости НЖК [33] и ХЖК [34] на этих частотах, учитывающих процессы релаксации параметра ориентационного порядка ЖК в УЗ-поле. Эти модели постулируют гипотезу о двух независимых механизмах явления (вихревом и релаксационном) и дают его описание, адекватное результатам [30, 33, 35–38]. Рассмотрим эти два варианта моделирования в соответствии с типом ЖК.22
Планарный слой НЖК. Модель [33] построена на основе гипотезы о вихревом механизме дестабилизации планарной структуры для случая, когда директор n НЖК и волновой вектор k упругой волны ортогональны, а одномерные домены выстроены перпендикулярно исходной ориентации молекул. Рассмотрена двумерная картина деформации слоя в предположении, что поворот молекул ЖК и движение жидкости происходят в плоскости XZ, направление оси X и директора n совпадают, а ось Z перпендикулярна плоскости слоя. Все переменные не зависят от координаты Y. Волновое поле в слое представляет стоячая волна сжатия $v = {\text{2}}{{v}_{0}}$ sinkz cosωt, где ${{v}_{0}}$ – амплитуда колебательной скорости, k = ω/с, с – скорость распространения УЗ. Согласно [33] при сжатии ЖК в поле УЗ-волн случайно возникшее и периодическое вдоль слоя отклонение его молекул от исходной ориентации ведет к появлению сдвиговых напряжений и моментов, которые рождают осциллирующие с частотой УЗ вихревые потоки и искажения структуры, имеющие тот же пространственный период.
Конвективное взаимодействие поля УЗ-волн, осциллирующих углов поворота молекул и вихрей приводит к появлению стационарных моментов и потоков, которые усиливают начальное искажение структуры. При достаточно высокой интенсивности УЗ дестабилизирующие моменты превысят упругие моменты Франка, и в слое возникнет система доменов, расположенных перпендикулярно начальной ориентации молекул. Анализ этого эффекта в [33] проведен в рамках представлений неравновесной гидродинамики в предположении, что релаксационные процессы в среде ведут к появлению анизотропных напряжений, определяемых тензором вязко-упругих напряжений вида
(1)
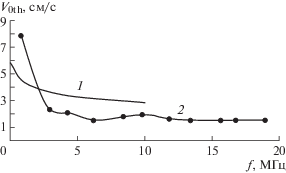
$\begin{gathered} {{v}_{{0th}}} = [(\pi {\text{c/2}}d)[{{({{K}_{{{\text{33}}}}}\eta F({{s}_{{{\text{min}}}}}){\text{/}}\gamma \Delta {\rm E}]}^{{{\text{1}}/{\text{2}}}}}, \\ {{L}_{{th}}} = d{\text{/}}{{({{s}_{{{\text{min}}}}})}^{{{\text{1}}/{\text{2}}}}}. \\ \end{gathered} $Упрощенные представления ${{v}_{{0th}}}$ и Lth для случая толстого или тонкого слоев НЖК можно найти в [33]. Рисунок 4 иллюстрирует сравнение значений ${{v}_{{0th}}}$(f), рассчитанных по формуле (1) (график 1) и полученных опытным путем (график 2) [33], в диапазоне частот 0.1–10 МГц, где справедливо ограничение ${{\lambda }_{v}}$ < d < λ на частоту УЗ. Видно, что при повышении частоты УЗ в области f < fr (fr ~ 5.3 МГц – частота релаксации) график 2 демонстрирует более глубокий “спад”, который сохраняется вплоть до частот, близких к частоте fr. При f > fr оба графика выходят на плато, где зависимость ${{v}_{{0th}}}$ от частоты УЗ исчезает. Отметим, что следующие из опытов [33] изменения ${{v}_{{0th}}}$(f) коррелируют с предсказаниями теории как качественно, так и по порядку величины. Введенное при построении модели [33] ограничение на частоту УЗ таково, что о тенденции изменения пороговой амплитуды ${{v}_{{0th}}}$ при частотах, отвечающих условию ωτ $ \gg $ 1, можно судить пока только по результатам наблюдений. Здесь τ – время релаксации параметра ориентационного порядка. На таких частотах значимость процессов структурной релаксации в макроскопических явлениях только усиливается [39], и это обстоятельство необходимо учитывать при моделировании механизма явления. Такая задача выходит за рамки [33]. Заметим, что согласно теории [33] период доменов не зависит от частоты, а представления о его связи с толщиной слоя для толстых и тонких слоев близки: Lth = 0.52d и Lth = 0.48d соответственно. Это подтверждают данные опытов при частотах 0.9–18.5 МГц [33] и 2.8–10 МГц [35]. В свете результатов анализа, приведенных выше, данная гипотеза о вихревой природе неустойчивости НЖК представляется вполне обоснованной для частот, не превышающих частоту структурной релаксации.
Рис. 4.
Сопоставление теоретических и экспериментальных данных о связи пороговой амплитуды
колебательной скорости и частоты УЗ для планарного слоя НЖК. График 2 функции ${{v}_{{0th}}}$(f) рассчитан для частот 0.1–10 МГц, экспериментальные значения ${{v}_{{0th}}}$ (график 1,  ) соответствуют диапазону частот 0.9–18.9 МГц. λ – длина упругой волны, d = 100 мкм.
) соответствуют диапазону частот 0.9–18.9 МГц. λ – длина упругой волны, d = 100 мкм.
Планарный слой ХЖК. Среди известных моделей ориентационной неустойчивости ХЖК в УЗ-полях [34, 40, 41] наиболее достоверными представляются модели, построенные в рамках методологии, учитывающей вклад релаксационных процессов и концепцию о двух независимых механизмах дестабилизации структуры планарного слоя ЖК [34]. Моделирование вихревого механизма образования доменов в области частот ω < < 1/τ проведено в геометрии, описанной выше, на основе уравнений гидродинамики, где тензор вязкоупругих напряжений содержит анизотропное слагаемое, обусловленное релаксацией параметра порядка и дисперсионным скачком анизотропии модуля упругости ХЖК. По сценарию, описанному выше для НЖК, в слое ХЖК при периодическом сжатии в поле УЗ-волн происходит образование двумерных доменов, возникающих при уравнивании действия упругих и дестабилизирующих моментов.
Представление для пороговой амплитуды сжатия в области частот ω1 < ω < ω2 имеет вид
(2)
$\begin{gathered} \varepsilon _{{th}}^{{({\text{1}})}} = \{ \rho {{K}_{{{\text{33}}}}}({\text{3}} + \kappa )({\text{1}} - \delta )q_{0}^{2}{\text{/4}} \times \\ \times \;[{\text{1}} + {\text{sin}}({\text{2}}kd){\text{/2}}kd]\gamma \tau {{q}^{{\text{2}}}}{\text{DE}}]{{\} }^{{{\text{1}}/{\text{2}}}}}, \\ \end{gathered} $За пределами указанной выше области частот порог эффекта и период доменов соответственно определяются как ${{\varepsilon }_{{th}}} = \varepsilon _{{th}}^{{({\text{1}})}}{{({\text{2}}а {\text{/}}\omega \tau )}^{{{\text{1}}/{\text{2}}}}}$, L0th при ω < < ω1 и ${{\varepsilon }_{{th}}} = \varepsilon _{{th}}^{{({\text{1}})}}\omega \tau {{a}^{{{\text{1}}/{\text{2}}}}}$, L0th/(аωτ)1/2 при ω > ω2, где L0th = $\sqrt 2 $πq0 [40]. Соотношение (2) справедливо в области частот ω1 < ω < ω2, где действие вихревого механизма наиболее эффективно и слабо зависит от частоты, а период доменов Lth = L0th.
Модель [34], постулирующая нелинейный релаксационный механизм неустойчивости ХЖК, учитывает изменения коэффициентов вязкости Лесли при деформации среды в упругих и вязких волнах. Релаксационное запаздывание этих изменений от деформации ЖК под воздействием УЗ индуцирует стационарные напряжения и моменты релаксационной природы. Для их определения впервые использован статистический подход, основанный на микромодели ЖК [42, 43], уточненной в [44]. Этот механизм неустойчивости рождает двумерные домены при пороговой амплитуде сжатия $\varepsilon _{{th}}^{{({\text{2}})}}$, равной [34]:
(3)
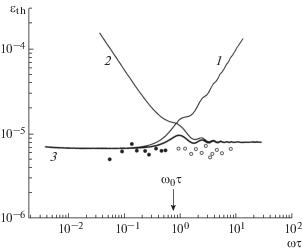
$\begin{gathered} \varepsilon _{{th}}^{{({\text{2}})}} = \{ {{K}_{{{\text{33}}}}}({\text{3}} + b)({\text{1}} - \delta )q_{0}^{2}{\text{/2}}\gamma F(\omega ,\tau ) \times \\ \times \;({\text{2}}B{{\Omega }_{{\text{1}}}} + {{\Omega }_{{\text{2}}}}){{\} }^{{{\text{1}}/{\text{2}}}}}, \\ \end{gathered} $Рис. 5.
Зависимость пороговых амплитуд сжатия $\varepsilon _{{th}}^{{({\text{1}})}},{\text{ }}\varepsilon _{{th}}^{{({\text{2}})}}$, εth от параметра ωτ: 1 и 2 – вихревой и релаксационный механизмы, 3 – совместное действие обоих механизмов. Расчет проведен для d = 100 мкм, δ = 0.8, P0 = 10 мкм в области частот 0.1–50 МГц; стрелка отмечает значение ω0τ = 0.75, определяющее частоту f0 = 3.9 МГц, при которой пороговые амплитуды $\varepsilon _{{th}}^{{({\text{1о
}})}}{\text{ }}\;{\text{и
}}\;{\text{ }}\varepsilon _{{th}}^{{({\text{2}})}}$, отвечающие разным механизмам неустойчивости, совпадают;  и $\bigcirc $ – значения порогов в опытах для областей частот 0.3–3 и 4–45 МГц соответственно.
и $\bigcirc $ – значения порогов в опытах для областей частот 0.3–3 и 4–45 МГц соответственно.
НАДПОРОГОВАЯ ДИНАМИКА НАДМОЛЕКУЛЯЫХ СТРУКТУР В АКУСТИЧЕСКИХ ПОЛЯХ
В нелинейном мире хорошо известны ситуации, когда при изменении управляющего параметра система теряет устойчивость, демонстрируя разные варианты дальнейшего существования. Поэтому всегда встает вопрос, какой из вариантов реализуется. Первые данные о надпороговой динамике доменов получены в опытах А.П. Капустина [2] на n-азоксифенетоле, когда при повышении интенсивности УЗ наблюдался переход доменов в динамическую систему ячеек, созданных акустическими потоками. Физики Орсе первыми описали поведение одномерных доменов за порогом эффекта на частотах звукового диапазона в условиях действия на гомеотропный слой НЖК эллиптического сдвига [25, 29, 45]. Оказалось, что при критическом значении параметра ω ξ0х ξ0y/D домены искажаются, образуя систему, состоящую из квадратных и гексагональных элементов (D – коэффициент ориентационной диффузии ЖК) [45]. Дальнейший рост амплитуды колебаний вызывает разнообразные трансформации двумерных структур, которые заканчиваются образованием в слое НЖК поликристаллической текстуры. Процесс такого перехода на частотах в десятки кГц подробно описан в [46]. Важный этап развития этого направления исследований в начале XXI в. инициировал Е.Н. Кожевников. Ему удалось создать первые модели динамики доменов за порогом неустойчивости для НЖК [47] и ХЖК [48]. Экспериментальному изучению проблемы посвящены работы [11, 49–51].
Планарный слой НЖК в условиях периодического линейного сдвига. Модель [47] описывает надпороговую динамику системы одномерных доменов, возникающих в слое НЖК под воздействием осциллирующего гидродинамического потока, созданного колебаниями сдвига. Анализ этого эффекта проведен на основе нелинейных уравнений гидродинамики, где сохранены кубические по возмущениям слагаемые, для области звуковых частот, определяемой двумя условиями 2ρωd2/α4 < < 1 и γ1ωd2/К33 < 2 × 104.33 Рассмотрены искажения за порогом дестабилизации планарного слоя НЖК для конфигурации (1, 1) (Y-мода в терминах [4]) при ортогональном расположении директора n и вектора скорости потока Vy(t) и вычислен угол стационарного поворота молекул, определяющего переход ЖК в новое ориентационное состояние при внешнем воздействии. Принято, что в исходном состоянии директор n‖Х, а в возмущенной структуре он отклоняется от нее на углы θ в плоскости ХΖ и ψ в плоскости ХΥ, при этом в слое возникают замкнутые потоки. Деформация структуры слоя за порогом неустойчивости определена через амплитуду θ0 постоянной составляющей угла θ, а именно: θ0 ~ [Q(s0 – s0th)]1/2 [47]. Здесь Q – функция частоты колебаний и параметров слоя, s0 – безразмерная амплитуда сдвига (s0 = = ξ0y/d), s0th – пороговая амплитуда сдвига, при которой возникает устойчивое искажение структуры, а молекулы колеблются около нового равновесного направления. Конечные искажения угла θ0, нарастающие по мере движения за порог, возникают при амплитуде s0 > s0th, при этом растет и амплитуда осцилляций постоянной составляющей ψ0 угла ψ. Следуя модели [10], обсудим динамику доменов применительно к конфигурации искажения (1, 1), имеющей определенные особенности. На низких частотах при s0 = s0th,1 появляются лишь однородные по x искажения (волновое число qth,1 = 0), а в области более высоких частот при s0 = s0th,2 возникают модулированные искажения, и постоянная составляющая угла θ меняется: θ0 ~ cos(qth,2x). Согласно [47] нарастание искажений в надпороговом режиме зависит от приведенной частоты ωτ и волнового числа q, а непосредственно за порогом возможно появление искажений лишь с волновыми числами qth, которые соответствуют минимальному значению порога s0th. По сценарию [47] спектр возмущений расширяется по мере движения за порог, и возникают пространственные гармоники искажений углов θ и ψ с волновыми числами в интервале q ∈ ∈ (0, q1) вблизи qth,1 = 0 и интервале q ∈ (q2, q3) вблизи qth,2 ≠ 0, причем ширина ∆qi этих интервалов с повышением амплитуды сдвига растет. Здесь i = = 1, 2; ∆q1 = q1 и ∆q2 = q3 – q2 соответственно. Результаты наложения этих возмущений определяют оптическую картину искажения структуры.
Теория [47] предсказывает, что на низких частотах, например при ωτ = 10, деформация структуры, периодическая вдоль слоя, возникает только при значении s0 > s0th, 2, а картину искажения задает распределение функции квадрата угла θ2(x). Здесь θ(x) ≈ θ01 + θ02cos(4.24x)44, θ01 и θ02 – интегральные амплитуды искажения, относящиеся к интервалам ∆q1 и ∆q2. Результаты расчета этой функции при s0 = 1.02s0th,2 < s0tr и s0 = 1.3s0th,2 > > s0tr показывают графики 1 и 2 (рис. 6а). Расстояние между соседними максимумами этих графиков отличается в 2 раза. Это означает, что при превышении амплитудой сдвига значения s0tr возможен масштабный переход в системе доменов, при котором их период меняется с L на L/2. В области высоких частот, где s0th,2 < s0th,1, за порогом эффекта амплитуда θ01 = 0, и в слое возникают домены с периодом π/qth,2, определяемым волновым числом qth,2. Рост амплитуды сдвига s0 до значения s0th,1 приведет лишь к увеличению амплитуды θ02, но как только амплитуда s0 превысит значение s0th,1, появятся дополнительные однородные искажения с амплитудой θ01. По численным оценкам [47] соотношение амплитуд θ01 < θ02 сохраняется вплоть до значений амплитуды s0 ≈ 102, поэтому в этой области частот при амплитудах s0 > s0th,1 должна формироваться система доменов с постоянным периодом π/qth,2 и чередующейся прозрачностью соседних полос.
Рис. 6.
Сопоставление теоретических и экспериментальных данных об эволюции одномерных доменов в планарном слое НЖК за порогом эффекта; а – графики 1 и 2 – результаты численного расчета функции θ2(x) при ωτ = 10 для значений амплитуды сдвига s0 = = 1.02s0th,2 и s0 = 1.3s0th,2; оптические картины искажения в слое НЖК на пороге эффекта (б) и при его превышении (в) и (г); d = 30 мкм, f = 0.21 Гц (ωτ = = 11.54). Цена деления шкалы окуляра –6.6 мкм.
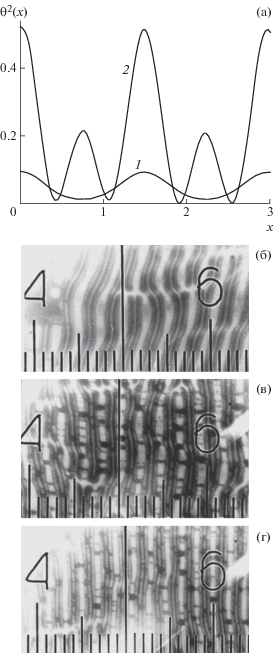
Данные опытов [11, 49] подтверждают вывод теории для низких частот о снижении периода доменов с L до L/2 уже при амплитуде колебаний ξ0 ≈ 1.3ξ0th. Полагают, что это вызвано нарастанием за порогом высших гармоник искажения по амплитуде так, что постоянная составляющая угла отклонения директора n принимает следующий вид: θ0 ≈ θ0cosqx + b${\theta }_{{\text{0}}}^{{\text{2}}}$cos(qx + ψ) [47], где второе слагаемое “отвечает” за изменения картины доменов. Этот переход в опыте выглядит так: в центре домена возникает светлая полоса, которая делит его надвое (рис. 6б–6г) [49].
Планарный слой ХЖК в поле УЗ-волн. До сих пор одной из наиболее сложных задач проблемы неустойчивости ЖК в акустических полях остается создание теории надпороговой динамики надмолекулярных структур на частотах УЗ-диапазона. Пока ее удалось решить только для ХЖК. Обсудим модель [48], построенную в рамках неравновесной гидродинамики для частот ω > ω0 = τ‒1d/P0, когда “работает” только нелинейный релаксационный механизм дестабилизации структуры ХЖК, а шаг спирали P0$ \ll $ d. Анализ степени деформации с ростом интенсивности УЗ проведен в описанной выше геометрии задачи. В возмущенной структуре положение директора n задают угловые переменные θ и ψ = (2π/Р)z + φ:
где θ – угол между директором n и плоскостью XY, φ – угол отклонения вектора n от равновесной ориентации молекул в плоскости слоя. Деформация структуры слоя ХЖК за порогом определена через амплитудные значения углов θ и ψ, а именно: θ0 ~ ψ0 ~ (ε2 – $\varepsilon _{{th}}^{2}$)1/2 [48]. Значение εth имеет смысл порогового сжатия слоя ЖК в УЗ-волне. Геометрия структуры, возникающей при этом в слое ХЖК, определяется волновым числом q0, а период доменов Lth = $\sqrt 2 $π/q равен периоду доменов L0th = $\sqrt 2 $π/q0, которые образуются при статическом растяжении этого слоя [34, 40]. За порогом эффекта, согласно [48], при относительном сжатии s = ε/εth > 1 искажения структуры ХЖК представляет спектр волновых чисел из интервала, определяемого условием(4)
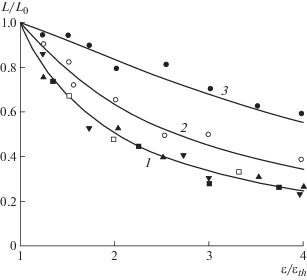
${{L}_{{th}}} = {{L}_{{0th}}}{\text{/}}{{[{{s}^{{\text{2}}}}({\text{1}} - \delta ) + \delta ]}^{{{\text{1}}/{\text{2}}}}}.$На рис. 7 представлены результаты численного анализа [48] в виде графиков 1–3 зависимости приведенного периода доменов L/L0 от относительной амплитуды сжатия ε/εth в поле УЗ-волн при различных растяжениях δ холестерической структуры слоя. Они показывают уменьшение соотношения L/L0 с подъемом амплитуды сжатия для значений параметра δ в интервале 0–0.85. Данные опытов [50] с раствором холестерилхлорид–НЖК и слоями ЖК с равновесной или растянутой холестерической структурой в области частот 1–4 МГц подтверждают именно такой характер динамики доменов. Оказалось [51], что за порогом эффекта при постоянных значениях Р, Р0, d, δ период доменов действительно падает в 2 раза независимо от состояния структуры ХЖК, но при ее предварительном растяжении скорость спада понижается с повышением δ, что указывает на снижение влияния УЗ на динамику доменов.
Рис. 7.
Сравнение данных о динамике доменов в планарных слоях ХЖК с равновесным (δ = 0) и
вынужденным (δ 1 ≠ 0) шагом спирали. 1–3 – данные расчета изменений приведенного периода доменов L/L0 за порогом по мере увеличения относительной амплитуды сжатия ε/εth среды в поле УЗ-волн для δ, равных 0, 0.5, 0.85 соответственно. Результаты опытов
с плоской (при d ∈ [20, 100
]
мкм и клинообразной ячейками в области частот 1–4 МГц: $\blacktriangle $, $\blacktriangledown $ ⇒ δ = 0, Р0 = 4 мкм, d = 80 мкм, f = 1.2 и 2.95 МГц соответственно, $\blacksquare $, $\square $ ⇒ δ = 0, Р0 = 2 и 10 мкм соответственно, d = 80 мкм, f = 1.2 МГц), $\bigcirc $ ⇒ δ = 0.5, Р0 = 2.2 мкм, d ≈ 21.5 мкм, f = 3.65 МГц,  Þ δ = 0.84, Р0 = 4.3 мкм, d ≈ 20.4 мкм, f = 3.65 МГц.
Þ δ = 0.84, Р0 = 4.3 мкм, d ≈ 20.4 мкм, f = 3.65 МГц.
НАДМОЛЕКУЛЯРНЫЕ СТРУКТУРЫ ПРИ БИНАРНОМ АКУСТИЧЕСКОМ ВОЗДЕЙСТВИИ НА НЖК
Сведения о переходных процессах в системе одномерных доменов, индуцированных в планарном слое НЖК его периодическим сжатием на частотах звукового диапазона, опубликованы в [11]. Приведены результаты наблюдения “рождения” вторичных двумерных надмолекулярных структур с периодом, несоразмерным по отношению к периоду исходной системы. Этот процесс “складывается” из двух этапов. На первом периодический сдвиг в осциллирующем линейном потоке создает в слое НЖК одномерные домены, расположенные вдоль потока. На втором этапе дополнительный поток с параболическим профилем скорости, созданный периодическим сжатием слоя, действует на уже деформированную структуру и вызывает по достижении порогового градиента скорости ее вторичные искажения. При дальнейших исследованиях этого явления удалось наблюдать и описать сценарий перехода одномерных, “вытянутых” в направлении колебаний сдвига (ось Y) доменов во вторичные, двумерные в плоскости XY структуры разнообразной формы (рис. 8а, 8б) [13, 52].
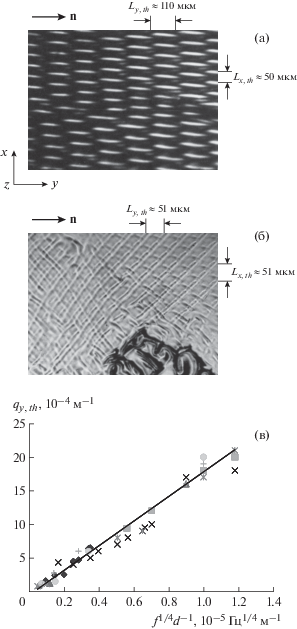
Рис. 8.
К анализу вторичной неустойчивости в планарном слое НЖК в условиях бинарного воздействия
для области частот 3–20 Гц, когда исходная система одномерных доменов с периодом Lx,th ≈ 180 мкм, “вытянутых” вдоль оси Y, предварительно создана в слое НЖК колебаниями сдвига, φ = 0 рад, d = 60 мкм: а – картина несоразмерной структуры, возникшей при ξ0z = 0.1ξ0x,th и f = 3 Гц (система черточек, сгруппированных в “столбцы”, с периодом Lx,th ≈ 50 мкм и Lу,th ≈ 110 мкм по осям X и Y соответственно); б – сетчатая структура при ξ0z = 0.3ξ0х и f = 20 Гц; размеры сторон квадратной ячейки сетки на пороге эффекта Lу,th = Lx,th ≈ 51 мкм; в – сопоставление экспериментальных и теоретических данных о связи толщины
слоя и частоты колебаний с пороговым волновым числом несоразмерных структур qу,th, показанных на рис. а; $\blacksquare $, ×,  ,
,  , $\blacktriangle $, *, + – значения qу,th для слоев толщиной 10, 30, 60, 80, 100, 120, 150 мкм соответственно в области частот
0.1–20 Гц.
, $\blacktriangle $, *, + – значения qу,th для слоев толщиной 10, 30, 60, 80, 100, 120, 150 мкм соответственно в области частот
0.1–20 Гц.
Пока нет теории этого явления, а задача ее построения сложна и требует привлечения полной системы уравнений гидродинамики НЖК. В этой связи определенный интерес представляет модель В.Н. Решетова [53], предложенная для феноменологического описания образования несоразмерной структуры (рис. 8а) [13]. В модели [53] исходная система доменов рассматривается как некая структура с определенной жесткостью, массой, вязкостью, а затем интерпретируется ее возможное поведение в условиях, определяемых геометрией задачи. Предполагается, что в исходном состоянии директор n‖Y и в том же направлении колеблется одна из пластин ячейки, а колебания ее второй пластины происходят вдоль оси Z, вызывая периодическое сжатие слоя, при котором изменяется его толщина d (t) = d0(1 + δсоs ωt). Здесь δ = ξ0z/d0 – степень сжатия слоя, d0 – его толщина. При заданных значениях d0 и ω исходная система доменов имеет одно допустимое (оптимальное) волновое число qxopt искажения, созданного колебаниями сдвига, которое при периодической перемене толщины слоя меняется так, что qxopt = qx0(1 + δсоs ωt). В [53] постулируются два способа подгонки волновых чисел qxopt и qx у этой системы доменов: уплотнение и разуплотнение в расположении доменов по плоскости слоя; волнообразный изгиб доменов вдоль своих осей и их осцилляции по углу изгиба α, что энергетически более выгодно. Чтобы определить пороговые характеристики вторичной неустойчивости, вводятся эффективные модули доменов, которые связаны с их возможными деформациями (рассогласование реального и оптимального волнового числа qx (C1), изгиб в направлении своих осей (C2), поворот относительно оси Y на угол α (C3)) [53]. Далее решается уравнение Id2α/dt2 = Me + + ${{M}_{v}}$, описывающее динамику доменов, и определяется связь степени сжатия δ слоя с волновым числом qy вторичного искажения. Здесь Mv = = –ηefdα/dt(qz/qy)2 – вязкий момент, I = $\rho {\text{/}}q_{y}^{2}$ – момент инерции, ηef – эффективная вязкость, qy и qz – волновые числа вторичного искажения по осям Y и Z, qz = π/d. Представления для пороговых характеристик вторичной неустойчивости, найденные из условия минимума функция ${{\delta }^{{\text{2}}}}(q_{y}^{2})$ по волновому числу qy, имеют следующий вид [53]:
(5)
$\begin{gathered} {{\delta }_{{th}}} = \sqrt 2 {{({{q}_{z}}{\text{/}}{{q}_{х }})}^{{\text{2}}}}{{[{{({{С }_{{\text{3}}}}{\text{/}}{{С }_{{\text{1}}}})}^{{\text{2}}}} + {\text{2}}{{({{С }_{{\text{2}}}}{\text{/}}{{С }_{{\text{1}}}})}^{{\text{2}}}}(\omega {\text{/}}{{\omega }_{0}})]}^{{{\text{1}}/{\text{2}}}}} \\ {\text{и }}\quad {{q}_{{у ,th}}} = {{q}_{z}}{{(\omega {\text{/}}{{\omega }_{0}})}^{{{\text{1}}/{\text{4}}}}}, \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
История науки знает немало примеров того, как интерес к проблеме возрождается спустя многие десятилетия. Яркая тому иллюстрация – это работы А.П. Капустина, которые оказывали и продолжают оказывать влияние на развитие физики ЖК и идей физиков в XXI в. Сегодня интересно отметить не только то, что сделал А.П. Капустин в физике ЖК, но и показать, к чему привели результаты его исследований. Так, до конца остается ключевой проблема устойчивости упорядочения ЖК в акустических полях [2]. Продолжает расти количество посвященных ей публикаций, а на грани XX–XXI вв. был преодолен кризис классической гидродинамики, связанный с ее неспособностью описать природу доменов на высоких частотах, и наконец, был найден иной адекватный подход к анализу явления – нелинейной релаксационной гидродинамики. Этой перемене физика ЖК обязана работе [2].
В ряду научных событий, знаменующих научно-техническую революцию в области акустического приборостроения на ЖК, решающим стало открытие Капустина [54]. Обнаружив уникальную способность слоя НЖК “рождать” адекватный оптический отклик на механический импульс, он построил первый в мире акустический датчик на НЖК и получил авторское свидетельство на изобретение [55]. К исследованиям по этому направлению в конце ХХ в. подключились специалисты ряда научных центров страны (Акустический институт, ИК РАН, НИКФИ, Самарский государственный университет, Институт физики Земли РАН, НПО Атолл, Центр БОС, ЦНИИ “Морфизприбор”). Разработана методология построения акустических приборов на НЖК для инфразвуковых и звуковых частот [39, 56, 57] и созданы их действующие макеты, способные считывать сигналы по электрическому и волоконно-оптическому кабелю, управлять чувствительностью устройства, выполнять автокалибровку. Круг задач, которые эти приборы способны решать, относится к различным сферам: сейсмология, гидроакустика, электроакустика, метеорология, виброметрия, навигация, криминалистика, медицина [58]. Так, уникальный многоканальный комплекс “Сенсор” на НЖК [59] ведет непрерывный контроль векторных характеристик движения среды и состояния атмосферы в широком частотном и динамическом диапазоне, что позволяет эффективно решать задачи геомониторинга. Актуальность идей внедрения таких перспективных систем имеет особую значимость. Будем верить, что время воплощения идей, базирующихся на одном из открытий А.П. Капуcтина [55], еще впереди.
Список литературы
Капустин А.П., Зверева Г.Е. // Применение ультраакустики к исследованию вещества. М.: Изд-во Московского обл. педагог. института, 1961. Т. 15. С. 69.
Капустин А.П., Дмитриев Л.М. // Кристаллография. 1962. Т. 7. Вып. 2. С. 332.
Handbook of Liquid Crystals. Weinheim: Wiley-VCH, 1998. V. I. 914 p.
Pieransky P., Guyon E. // Phys. Rev. A. 1974. V. 9. № 1. P. 404.
Pieransky P., Guyon E. // Phys. Rev. Lett. 1977. V. 39. № 2. P. 1280.
Manneville P., Dubos-Violette E. // J. Phys. (Fr.). 1976. V. 37. № 7. P. 285.
Guyon E., Janossy I., Pieransky P. // J. Mech. (Fr.). 1977. V. 16. № 7. P. 733.
Hogan S.J., Mullen T., Woodford P. // Proc. Roy. Soc. A. 1993. V. 441. P. 559.
Clark M., Saunders F., Shenks I., Leslie F. // Mol Crst. Liq. Cryst.1981. V. 70. P. 195.
Кожевников Е.Н. // Кристаллография. 2006. Т. 51. № 4. С. 714.
Аникеев Д.И., Капустина О.А. // ЖЭТФ. 1996. Т. 110. № 4(10). С. 1328.
Решетов В.Н. // Акуст. журн. 1985. Т. 31. № 5. С. 639.
Капустина О.А. // Кристаллография. 2019. Т. 64. № 3. С. 419.
Guyon E., Pieransky P. // J. Phys. (Fr.). 1975. V. 36. № 3. Coll. 1. P. 203.
Кожевников Е.Н. // Акуст. журн. 2007. Т. 53. № 4. С. 478.
Manneville P. // J. Phys. (Fr.). 1979. V. 49. № 7. P. 713.
Кожевников Е.Н. // ЖЭТФ. 1986. Т. 64. № 5. С. 793.
Borsonyi T., Buka A., Krekhov A.P., Kramer L. // Phys. Rev. E. 1998. V. 58. P. 7419.
Тарасов О.С., Крехов А.П. // Кристаллография. 1999. Т. 44. № 6. С. 1121.
Krekhov A.P., Kramer L. // Phys. Rev. E. 1996. V. 53. № 5. P. 4925.
Borsonyi T., Krekhov A.P., Totch P. et al. // Phys. Rep. 2000. V. 337. P. 171.
Чабан И.А. // Акуст. журн. 1985. Т. 31. С. 132.
Кожевников Е.Н. // Вестн. Пермск. ун-та. Физика. 2002. № 1. С. 63.
Белова Г.Н., Ремизова Е.И. // Акуст. журн. 1985. Т. 31. С. 171.
Pieransky P., Guyon E. // Phys. Rev. Lett. 1977. V. 39. № 2. P. 1280.
Rothen F., Dubos-Violette E. // J. Phys. (Fr.). 1978. V. 38. P. 1034.
Sadik J., Roothen F., Bestgen W. // J. Phys. (Fr.). 1981. V. 42. P. 915.
Dreyfus J.M., Guyon E. // J. Phys. (Fr.). 1981. V. 42. P. 283.
Guyon E., Guazzelli E. // J. Phys. (Fr.). 1982. V. 43. № 4. P. 985.
Капустина О.А., Лупанов В.Н. // ЖЭТФ. 1976. Т. 71. № 6. С. 2324.
Gurova I., Kapustina O., Loupanov V. // Abstracts 7-eme Congres International sur les cristeaux liquids. Bordeaux. 1978. P. 51.
Physical Properties of Liquid Crystals. Weinheim: Wiley-VCH, 1999. P. 447.
Капустина О.А., Кожевников Е.Н., Чумакова С.П. // Акуст. журн. 2014. Т. 60. № 3. С. 243.
Кожевников Е.Н. // Акуст. журн. 2002. Т. 48. С. 777.
Аникеев Д.И., Капустина О.А., Лупанов В.Н. // ЖЭТФ. 1991. Т. 100. № 1. С. 197.
Гурова И.Н., Капустина О.А. // Письма в ЖЭТФ. 1996. Т. 63. № 11. С. 866.
Капустина О.А. // Письма в ЖЭТФ. 2005. Т. 81. № 8. С. 481.
Капустина О.А. // Кристаллография. 2014. Т. 59. № 4. С. 627.
Капустин А.П., Капустина О.А. // Акустика жидких кристаллов. М.: Наука, 1986. 247 с.
Кожевников Е.Н. // ЖЭТФ. 1987. Т. 92. № 4. С. 1306.
Кожевников Е.Н. // Акуст. журн. 2001. Т. 47. № 4. С. 501.
Osipov M.A., Terentjev T.M. // Phys. Lett. A. 1989. V. 134. № 5. P. 301.
Семенов А.Н. // ЖЭТФ. 1983. Т. 85. № 2(8). С. 549.
Кожевников Е.Н. // Изв. Самар. гос. ун-та. Сер. Механика. 2008. Т. 2. С. 1.
Guyon E., Guazzelli E. // C. R. Acad. Sci. 1981. V. 282. P. 142.
Bertolotti M., Scudieri F., Sturla E. // J. Appl. Phys. 1978. V. 49. P. 3922.
Кожевников Е.Н. // Акуст. журн. 2008. Т. 54. С. 25.
Кожевников Е.Н. // Акуст. журн. 2004. Т. 50. С. 562.
Капустина О.А. // Акуст. журн. 2015. Т. 61. № 3. С. 361.
Капустина О.А. // Письма в ЖЭТФ. 2014. Т. 100. № 4. С. 256.
Капустина О.А. // Акуст. журн. 2015. Т. 61. № 1. С. 49.
Капустина О.А. // Письма в ЖЭТФ. 2006. Т. 83. № 1. С. 12.
Решетов В.Н. // Акустически инициируемые ориентационные явления в нематических жидких кристаллах: автореф. дис. … канд. физ.-мат. наук: 01.04.06. Москва, Акустический институт. 1986. 28 с.
Bocharov Yu.V., Gurova I.N., Kapustina O.A. et al. // Sensors Actuators. 1991. V. 28. P. 178.
Bocharov Yu.V., Gurova I.N., Kapustina O.A. et al. // Sensors Actuators. 1991. V. 28. P. 178.
Капустин А.П. // Способ обнаружения механических импульсов. А.с. на изобретение № 224102. М. 23.05.1968 г.
Бочаров Ю.В., Капустина О.А., Решетов В.Н. // Акуст. журн. 1992. Т. 38. № 4. С. 616.
Капустина О.А. // Кристаллография. 2014. Т. 59. № 5. С. 685.
Bocharov Yu.V., Gurova I.N., Kapustina O.A. et al. // Mol. Cryst. Liq. Cryst. 1993. V. 209. P. 19.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография



