Кристаллография, 2020, T. 65, № 1, стр. 160-168

ВВЕДЕНИЕ

До недавнего времени казалось вполне очевидным, что в результате длительного свободного роста кристалла в изотропных условиях питания все симметрично-эквивалентные грани кристаллографической простой формы {hkl}, обладающие наименьшей скоростью роста по сравнению с гранями других простых форм, должны быть представлены в полном количестве, а кратчайшие расстояния от зародыша кристалла до данных граней должны быть равными. Этот вывод приписывается закону симметрии и явно следует из второго начала термодинамики с учетом практически неограниченного времени существования отдельного кристалла минерала в масштабах так называемого “геологического времени”. Однако симметрично-эквивалентные грани на свободно выросших кристаллах минералов всегда имеют разные площади и форму, а центральные расстояния значительно варьируют. И этот факт статистически не связан с нарушением условий изотропного питания кристалла.

Объяснение кроется в неравновесных условиях кристаллизации. Можно утверждать, что свободный рост кристаллов в природе чаще всего происходит в неравновесной открытой системе. Остановка роста кристалла, как и инициация нового этапа кристаллизации, происходит чаще всего в результате быстрых катастрофических событий, связанных, например, с тектоническими движениями горных пород. При этом времени для равновесного преобразования формы кристаллов согласно принципу Гиббса–Кюри недостаточно. Во-первых, макроскопические размеры кристалла не позволяют осуществить преобразование его формы в направление минимума поверхностной энергии из-за крайне медленных скоростей равновесного процесса. Во-вторых, активная кристаллообразующая среда в открытой системе может быть удалена от поверхности кристалла и заменена на другую, в которой обменные потоки вещества крайне незначительны. Даже факт присутствия естественной свободной формы у редких природных кристаллов в недрах литосферы свидетельствует о катастрофических явлениях для системы кристалл–среда. Примером может служить природный гидротермальный кварц. Если рост кристаллов кварца в горячих гидротермальных растворах, протекающих по системе тектонических трещин в горных породах, не прекращается, то в итоге формируется жильный кварц, полностью заполняющий трещины в породе без образования гранных форм индивидов, но если новые разрывные нарушения останавливают движение раствора и он заменяется на паровую фазу, то процесс роста прерывается. В этом случае сохраняется естественная огранка кристаллов кварца, демонстрирующая их свободный рост. Именно такие кристаллы, процесс роста которых был внезапно прерван, иллюстрируют гранные формы в экспозициях минералогических музеев.

В рамках термодинамических представлений о неравновесной открытой системе, для которой предельным является принцип минимума функции принуждения по Дьярмати [1] или принцип минимума производства энтропии [2], построена адсорбционно-флуктуационная модель дислокационного роста кристалла [3]. В условиях стационарного роста грани кристалла величина прироста вещества на грани удовлетворяет гамма-распределению (закону Эрланга):

где f – плотность вероятности значения носителя распределения h, которое соответствует высоте пирамиды роста конкретной грани – центральное или кратчайшее расстояние от зародыша кристалла до грани, и может принимать любое положительное значение. Закон (1) описывается двумя параметрами: λ – параметр масштаба, определяющий среднее значение прироста вещества за все время процесса, n – параметр формы, связанный с длительностью физического процесса. Если на кристалле присутствуют несколько симметрично-эквивалентных граней, принадлежащих данной кристаллографической простой форме, то распределение кратчайших расстояний до них в изотропных условиях кристаллизации будет также описываться данным выражением. Уравнение получено в приближении стационарного неравновесного процесса роста, в котором явления адсорбции–десорбции примесей на растущей поверхности кристалла, не участвующие в фазовом переходе, и связанные с ними флуктуации свободной энергии можно рассматривать с равновесных позиций.

Распределение (1) обладает важным свойством. Любой макроскопический неравновесный и даже нестационарный процесс роста кристалла можно представить как серию последовательных стационарных процессов приращения вещества согласно модели (1) на том основании, что сумма случайных величин, подчиняющихся гамма-распределениям, будет также распределена по закону гамма-распределения, но с некими “обобщенными” параметрами масштаба – λ и формы – n [4].

Главным параметром процесса кристаллизации согласно адсорбционно-флуктуационной модели является коэффициент вариации кратчайших расстояний от зародыша до симметрично-эквивалентных поверхностей растущего кристалла – k = n^–1/2. Количество отдельных независимых актов послойного нарастания вещества к растущей грани зависит от общего времени процесса и величины отклонения от термодинамического равновесия, связанного со скоростью роста [3].

РАЗНООБРАЗИЕ МНОГОГРАННИКОВ

Еще в XIX в. было известно, что произвольные сочетания плоских граней могут приводить к заметно различающимся многогранникам. Перечисление всех возможных разновидностей полиэдров от 4- до 8-гранника включительно дает 300 топологических вариантов [5]. Однако если учесть не только число, форму и способ сопряжения граней, но и углы между ними, чего требует кристаллография, то, например, для кристаллографических граней с индексами Миллера {111} в рамках наивысшей кристаллографической группы симметрии $m\bar {3}m$ оказываются возможны только 33 типа многогранников [6]. Если также принять во внимание, что формирование каждой грани на реальном кристалле происходит независимо, то в природе могут встречаться только простые многогранники, в вершинах которых соединяются три ребра и грани. Следовательно, для описания природных кристаллов имеет смысл рассматривать только 14 морфологических вариантов октаэдров [7]. Каждый морфотип характеризуется набором восьми центральных расстояний, пронумерованных в определенном порядке и меняющихся в рамках некоторых индивидуальных интервалов вариации. Среди них встречается по одному варианту 4-гранника (тетраэдра) и 5-гранника, три 6-гранника, четыре 7-гранника и пять 8-гранников (рис. 1).

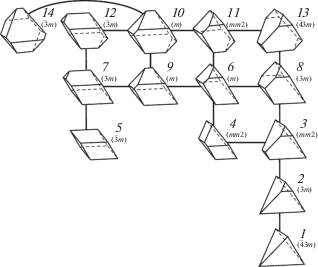
Заметим, что наложенное ограничение на углы между гранями сокращает множество топологических типов полиэдров на порядок, но в некоторых случаях одновременно расширяет многообразие кристаллографических морфотипов полиэдров. Например, если простой гексаэдр с восемью вершинами имеет всего два топологических типа [5], то 6-гранник, образованный кристаллографическими гранями {111} с учетом кристаллографического закона постоянства углов, демонстрирует уже три разновидности. Такой комбинаторный анализ полиэдров можно называть симметрийно-топологическим, поскольку из топологических свобод, допускающих любые непрерывные преобразования объекта, не приводящие к новому качеству, возможен только параллельный перенос определенно ориентированных поверхностей (граней) вдоль направления вектора нормали к грани в соответствии с группой симметрии кристаллической структуры. Если учесть, что формы растворения кристаллов тоже можно представить многогранниками [8, 9], образованными симметрично-эквивалентными гранями, пусть и не всегда плоскими, то для них также применим симметрийно-топологический анализ.

Распределение (1) позволяет вычислить методом Монте-Карло вероятности (частоты встречаемости) всех симметрийно-топологических типов многогранников, образованных гранями данной простой формы при фиксированном коэффициенте вариации. Полученные вероятности представляют собой мгновенные значения вероятностей состояний в марковском процессе преобразования формы кристалла в ходе его роста. Кристаллографические разновидности многогранников как состояния динамической системы всегда образуют единый, неразложимый, непериодичный и возвратный процесс Маркова. Если вероятности морфологических типов многогранников не зависят от коэффициента вариации и времени, следовательно, и переходные вероятности между морфотипами не зависят от времени, то марковский процесс можно считать дополнительно однородным, стационарным и эргодичным [10]. Перечисленный набор свойств марковского процесса эволюции свободной формы кристалла, обладающей комбинаторно-топологическим разнообразием, характерен не только для роста, но и для растворения кристаллов. В ходе неравновесного роста или растворения переходы между морфотипами (дискретными состояниями динамической системы) происходят случайно.

В ходе физического стационарного роста кристалла коэффициент вариации центральных расстояний будет зависеть от времени, уменьшаясь как t^–1/2. Соответственно зная вероятности всех состояний как функции от коэффициента вариации k, можно теоретически рассчитать зависимости вероятностей морфотипов от времени. Однако если природный процесс роста не является стационарным, что чаще всего и происходит в природе, то распределение (1) будет отражать некое стационарное приближение, обобщенные значения параметров которого не позволяют рассчитать зависимость вероятности каждого морфотипа многогранника от времени.

СВОБОДНЫЕ ФОРМЫ КРИСТАЛЛОВ МИНЕРАЛОВ

Эмпирически установлено, что на формах роста кристаллов искусственного или природного алмаза всегда встречается по восемь граней октаэдра, которые формируют пять различных многогранников, относящихся к полногранному классу кристаллографических морфотипов октаэдра (рис. 1). Измеренный для выборки из 500 искусственных алмазов единого происхождения средний коэффициент вариации кратчайших расстояний оказался равным 0.05 [7]. Октаэдрические алмазы текущей добычи из кимберлитовых трубок Мир и Заполярная (Якутия), насчитывающие 46 и 60 кристаллов в выборках, имеют коэффициенты вариации центральных расстояний – 0.11 и 0.12 [11].

Моделированием роста кристалла методом Монте-Карло по стационарной модели (1) было установлено, что статистически достоверное появление морфотипов простой формы {111}, не входящих в класс 8-гранников при количестве кристаллов более 1000, происходит только при коэффициентах вариации, превышающих 0.2. Поэтому становится вполне понятно, почему среди тысяч просмотренных октаэдров алмаза Якутии, Урала и Бразилии не был встречен ни один из девяти возможных неполногранных морфотипов полиэдров простой формы {111}. Моделированием установлено, что постепенное повышение коэффициента вариации до значения 0.6, что эквивалентно сокращению времени роста кристалла, приводит к появлению всех 14 морфологических разновидностей октаэдра в модельной выборке [7]. Таким образом, эволюция форм октаэдра со временем происходит строго в направлении полногранных морфотипов. Одновременно при коэффициентах вариации центральных расстояний менее 0.2 вероятности морфотипов перестают зависеть от коэффициента вариации и соответственно от времени.

Аналогичное явление наблюдается для природного α-кварца. Головка свободно растущего кристалла кварца в основном огранена гранями положительного $\{ 10\bar {1}1\} $ и отрицательного $\{ 01\bar {1}1\} $ ромбоэдров, а ограничена обычно шестью гранями гексагональной призмы 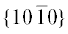. К такому открытому многограннику комбинированной формы, состоящей из двух простых кристаллографических форм, был применен симметрийно-топологический подход [12]. Шесть граней ромбоэдров, контактирующих между собой без учета вариантов сопряжения с гранями призмы, но ограниченных ими по периметру, образуют 17 комбинаторных типов головки, на которой ребра между гранями ромбоэдров (в 16 вариантах) образуют связный граф (рис. 2) [12]. Многогранники изображены в проекции на плоскость пинакоида {0001}. Полногранный класс открытых многогранников, насчитывающих по шесть граней ромбоэдров, включает в себя только первые три морфологических варианта (рис. 2), которые в абсолютном большинстве случаев наблюдаются на природных кристаллах кварца. По выборкам природных кристаллов кварца из жил Приполярного Урала, Памира и агатовых секреций Тимана и Бразилии установлено, что коэффициент вариации центральных расстояний до граней ромбоэдров варьирует от 0.02 до 0.05 [12].

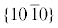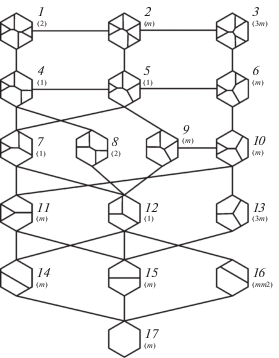
Согласно расчетам Монте-Карло по адсорбционно-флуктуационной модели (1) при коэффициентах вариации до 0.1 и близких скоростях роста граней ромбоэдра и призмы на кристалле должны встречаться только три полногранных морфотипа головки. Если скорость роста граней призмы замедляется до 0.8 от скорости роста ромбоэдра, то при коэффициенте вариации 0.1 уже до 4% кристаллов будут представлены неполногранными морфотипами головки. С другой стороны, в случае понижения коэффициента вариации до 0.05 первые неполногранные морфотипы головки появляются при отношении скоростей роста граней призмы и ромбоэдров 0.5. Таким образом, эмпирически установлено, что природные условия кристаллизации кварца в гидротермальных жилах и базальтовых секрециях обеспечивают существование только трех полногранных морфотипов головки, а их вероятности, согласно модельным экспериментам, также не зависят от коэффициента вариации и времени.

Третий случай связан с цирконом. Восемь граней дипирамиды {101} или {111} в группе симметрии циркона 4/mmm образуют 20 морфологических типов многогранников, которые можно получить комбинаторным перебором вариантов соединения всех симметрично-эквивалентных граней. Этот же результат легко получить с помощью теории групп. Если выделить одну из осей четвертого порядка кубического кристалла, симметрия которого представлена группой $m\bar {3}m$, например, растянув кристалл вдоль данной оси, то остальные две четверные оси превратятся в оси второго порядка, а оси третьего порядка исчезнут. Следовательно, группа симметрии кристалла снизится до 4/mmm. Для такого кристалла кристаллографическая простая форма {111} является дипирамидой. Идеальная группа симметрии каждого морфологического типа дипирамиды будет подгруппой соответствующей группы симметрии исходного морфотипа октаэдра. Таким образом, преобразуя группу симметрии $m\bar {3}m$ в 4/mmm, из известных 14 вариантов многогранников простой формы октаэдра {111} получим 20 морфотипов дипирамиды {111}. Причем полногранный класс 8-гранников дипирамиды насчитывает уже семь морфотипов (рис. 3а), а не пять, как для октаэдра. Те же морфотипы характерны для всех тетрагональных дипирамид – {hhl} и {h0l} – в данном классе симметрии.

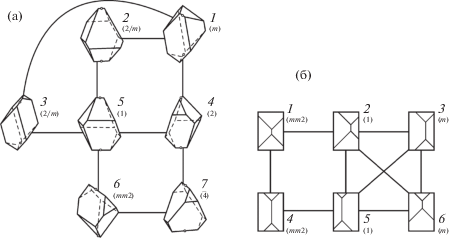
Однако в природе трудно найти полногранные кристаллы циркона и установить их морфологический тип. Кроме того, на кристаллах часто представлены грани призм {110} и {100}. Например, из 35 кристаллов циркона, собранных из элювия на одной из копей Ильменских гор, только 20 демонстрировали обе головки. На всех кристаллах присутствовали грани {110} и {100}.

Легко убедиться, что комбинаторные варианты сочетания граней дипирамиды {111} и призмы {110} на головке кристалла циркона образуют 16 симметрийно-топологических типов открытых тетрагональных многогранников, а полногранных среди них будет только шесть (рис. 3б). Эти же морфологические разновидности должны быть свойственны головкам циркона, образованным комбинациями всех дипирамид {hhl} и призмы {110}, а также любой из дипирамид {h0l} и призмы {100}. Анализ 55 головок на 35 кристаллах циркона Ильменских гор подтвердил, что встречаются только шесть полногранных морфологических типов головок, образованных гранями дипирамиды {101} и призмы {100}. При этом коэффициент вариации центральных расстояний до граней дипирамиды природных кристаллов из Ильменских гор составляет 0.19 при близких значениях средних скоростей роста граней дипирамиды и призмы. В результате моделирования Монте-Карло до тысячи кристаллов установлено, что неполногранные разновидности головки циркона, образованные гранями дипирамиды {101} и призмы {100}, появляются только при коэффициентах вариации, превышающих 0.2, и отношении скоростей роста граней призмы и дипирамиды не ниже 0.8. Таким образом, природные условия роста циркона при метасоматических преобразованиях миаскитов Ильменских гор [13] находятся на границе интервала, допускающего существование исключительно полногранных морфотипов открытого тетрагонального многогранника, образованного гранями дипирамиды и призмы. Как и в двух описанных выше случаях, установлено, что вероятности полногранных морфотипов дипирамиды при k < 0.2 не зависят от коэффициента вариации.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Таким образом, можно сформулировать принцип полного огранения: множество многогранников, которыми можно описать динамическую свободную форму макрокристаллов в ходе процесса минералообразования, стремится к классу полногранных морфологических разновидностей, образованных преобладающими на кристалле симметрично-эквивалентными поверхностями, а вероятности многогранников (их частоты встречаемости) перестают зависеть от времени процесса.

Принцип полного огранения является обобщением наблюдаемых фактов и выполняется даже для комбинированной формы кристалла, состоящей из двух кристаллографических простых форм, преобладающих в данных условиях минералообразования, а также для открытых многогранников.

Данный принцип применим и для форм растворения. Была построена адсорбционно-флуктуационная модель стационарного процесса нормального растворения и получен аналогичный уравнению (1) закон распределения толщины растворенного слоя кристаллического вещества с участка элементарной поверхности кристалла, геометрия которой сохраняется во времени в ходе растворения. Преобразуя его в закон распределения кратчайших расстояний от некоторого геометрического центра кристалла до симметрично-эквивалентных поверхностей кристалла, получаем гамма-распределение

где H₀ – среднее значение кратчайшего расстояния от геометрического центра кристалла до начальной элементарной поверхности формы растворения, H – значение кратчайшего расстояния до поверхности. Законы (1) и (2) различаются не только знаком асимметрии, но и выражениями для коэффициента вариации. Для модели растворения (2) коэффициент вариации определяется выражением

Геометрический центр кристалла, не обязательно совпадающий с его зародышем, определяется минимумом функции, имеющей также смысл коэффициента вариации кратчайших расстояний от данной точки до симметрично-эквивалентных поверхностей:

где H_i – расстояния от искомой точки геометрического центра до симметрично-эквивалентных поверхностей кристалла, N – число симметричных граней данной простой кристаллографической формы кристалла. Показать факт существования геометрического центра кристалла можно численными методами, но единственность обосновать сложнее. Легко понять, что в пределе при коэффициенте вариации, стремящемся к нулю, для замкнутой кристаллографической формы геометрический центр кристалла будет совпадать с центром единственного вписанного шара, касающегося одновременно всех симметрично-эквивалентных граней кристалла, и являться точкой, максимально удаленной от них (H₀ = max). Заметим, что геометрический центр не совпадает с центром масс кристалла.

Однако для практики морфологических измерений информация о положении геометрического центра в теле кристалла не является остро необходимой. Обычно достаточно знать минимальное значение коэффициента вариации кратчайших расстояний k, соответствующее такому центру.

Форма растворения природного алмаза (алмаз уральского типа) описывается выпуклым тетрагексаэдроидом. Из 24-гранников тетрагексаэдроида можно сконструировать 12-гранники, похожие на ромбододекаэдры, которыми можно представить реальные тетрагексаэдроиды. У тетрагексаэдра {hk0} как простой кристаллографической формы, существующей в трех точечных группах симметрии кубических кристаллов $m\bar {3}m$, 432 и $\bar {4}3m$, присутствуют два типа ребер – 〈100〉 и 〈khh〉. Если не принимать во внимание ребра первого типа, то получим обобщенные тетрагексаэдроиды (12-гранники), в полногранном классе которых существует всего семь симметрийно-топологических разновидностей (рис. 4). Оказалось, что округлые кристаллы алмаза уральского типа, добытые из россыпей Анабарского бассейна и из трубки Удачной Якутии, подразделяются строго на семь указанных морфотипов обобщенных тетрагексаэдроидов и таким образом тоже подчиняются принципу полного огранения.

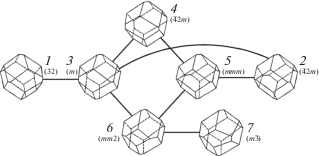
Согласно адсорбционно-флуктуационным моделям дислокационного роста (1) и нормального растворения (2), а также эмпирическому принципу полного огранения коэффициент вариации центральных расстояний до симметрично-эквивалентных граней кристалла в ходе природных процессов минералообразования всегда устремляется ниже определенного значения, свойственного многогранникам симметрийно-топологического типа. Ниже этого порога вероятности полногранных морфологических типов многогранников перестают зависеть от времени процесса и представляют собой предельное состояние минералообразующей системы.

Если учесть, что предельным состоянием открытой термодинамической системы является стационарное состояние, в котором достигается минимум производства энтропии и теряется зависимость производства энтропии от времени [2], то нетрудно заметить аналогию. Можно утверждать, что принцип полного огранения является макроскопическим следствием основного принципа неравновесной термодинамики.

При длительном стационарном росте кристалла параметр формы n в распределении (1) непрерывно увеличивается, что приводит к уменьшению коэффициента вариации кратчайших расстояний. В результате все центральные расстояния до симметрично-эквивалентных граней приближаются к среднему значению. В этом случае отношение

рассчитанное для любого морфотипа замкнутого многогранника, образованного одной кристаллографической простой формой, стремится к единственному минимальному значению. Здесь S_i – площадь отдельной грани кристалла, и суммирование выполняется по всей поверхности, V – объем кристалла. Например, для октаэдра алмаза M = 5.7191, для ромбододекаэдра – 5.3454, а для куба, который не обладает морфологическим разнообразием, M = 6.

Кроме того, численными экспериментами для куба, октаэдра и ромбододекаэдра в интервале значений k (0, 0.10) с точностью до критерия достоверности R² = 0.999 установлена линейная зависимость

где параметр А для перечисленных выше многогранников соответственно принимает значения 1.123, 1.387, 2.600.

Принципиально важным является то обстоятельство, что при наличии симметрийно-топологических разновидностей многогранников все морфологические типы полногранного класса сохраняются с их постоянными значениями вероятности, несмотря на то, что они одновременно устремляются к пределу (4) по линейному закону (5). Поэтому, в частности, октаэдр Платона для алмаза, идеальный куб для пирита или галита, а также идеальный 14-вершинный ромбододекаэдр для гранатов в природе никогда не будут обнаружены.

Обсуждаемый принцип полного огранения связан с понятием габитусной формы реального кристалла: “Характеристика габитуса основывается на преобладании тех или иных кристаллографических форм в кристаллах данного минерала” [14]. То есть габитусные грани определяются простой кристаллографической формой (формами), симметричные грани которой преобладают на кристалле при его свободном росте в данных условиях кристаллизации. Однако принцип полного огранения не заменяет понятия габитусной формы. Следует учитывать, что габитус кристалла не обязательно должен быть представлен на кристалле полным числом симметрично-эквивалентных граней. Описание габитуса предполагает только констатацию типов многогранников и подразумевает согласно симметрийно-топологическому анализу максимально возможный спектр многогранников по сравнению с той выборкой морфологических разновидностей, которая обычно реализуется в природе. В природе наблюдается только вершина этого многообразия. Именно этот эмпирический факт отражает суть принципа полного огранения.

Заметим, что понятие габитусной формы может быть применимо к формам растворения и центральным поверхностям второго порядка [15]. При этом габитусная форма остается индикатором определенного природного процесса [14].

Габитусные грани, слагающие реальный кристалл-многогранник, согласно принципу наименьшего производства энтропии должны также обладать минимальной плотностью поверхностной энергии в данной термодинамической обстановке, поэтому выражение (4) с точностью до сомножителя эквивалентно принципу Гиббса–Кюри для граней замкнутой простой формы. Однако это совпадение случайно, поскольку закономерности (4) и (5) записаны для открытой системы, тогда как принцип Гиббса–Кюри выводится для замкнутой термодинамической системы из второго начала термодинамики. Закономерность (4) является следствием интегрального свойства центрального расстояния в ходе естественного процесса роста или растворения, принципа минимума производства энтропии и закона больших чисел – устойчивости средних значений независимых случайных величин определенного случайного процесса.

Вся история минералогической кристалломорфологии свидетельствует о том, что наблюдаемые эмпирические закономерности в развитии свободной макроскопической формы различных кристаллов минералов подтверждают эволюционный тренд (4). Причиной данного явления практически единодушно признавался принцип Гиббса–Кюри. Поэтому до недавнего времени важнейшей задачей кристалломорфологии минералов был поиск равновесной формы природных кристаллов как предельного состояния природной кристаллообразующей термодинамической системы, являющегося типоморфным признаком более крупного рудообразующего геологического процесса [16]. Однако такую интерпретацию природных закономерностей, как показано выше, можно считать ошибочной.

Если в выборке природных кристаллов единого генезиса их свободная форма описывается множеством симметрично-топологических многогранников, принадлежащих исключительно полногранному классу, то отсюда следует:

1. Неравновесная открытая макроскопическая минералообразующая система достигла стационарного состояния, в котором вероятности морфотипов полногранного класса не зависят от времени и одновременно коэффициент вариации кратчайших расстояний не превышает определенного для данного типа многогранников критического значения.

2. Даже если в истории кристаллов преобладали нестационарные условия кристаллизации, в качестве эталона могут быть применимы вероятности полногранных морфологических типов многогранников, рассчитанные по адсорбционно-флуктуационным моделям и отражающие стационарный изотропный рост или растворение. На основе модельных теоретических распределений вероятностей становится возможным оценить характер и степень воздействия наложенных диссимметризующих природных процессов.

3. Адсорбционно-флуктуационные модели (1) и (2) применимы для роста или растворения кристаллов, развивающихся по двум разным сценариям: первый – непрерывный рост (растворение) кристаллов от зарождения (начальной формы растворения) до момента остановки свободного роста (растворения), второй – импульсный процесс, состоящий из множества нерегулярных этапов роста (растворения), каждый из которых незначительно отличается от других и вклад отдельного этапа несопоставимо меньше интегрального вклада всех остальных этапов роста (растворения). В разных геологических процессах для одного минерала могут реализоваться эти разные механизмы. В рамках первого типа процесса, характерного чаще всего и для физического эксперимента, можно предсказать связь пересыщения с параметрами модели. Чем выше пересыщение и скорость роста, тем меньше характерное время τ отдельного независимого акта десорбции примесей и прироста вещества на грань кристалла и тем большее значение может принимать целочисленный параметр n. Соответственно должен уменьшаться коэффициент вариации центральных расстояний. Второй вариант не позволяет установить величину неравновесности термодинамической системы, поскольку параметры модели λ и n являются статистическим обобщением суммы независимых этапов роста (или растворения) кристалла. Данный случай характерен чаще для природных кристаллов, и представление об изотропии или анизотропии питания употребляется в статистическом смысле в полном согласии с исходными идеями П. Кюри о дисимметрии в применении к природным объектам.

Принцип полного огранения в ряде практических случаев может нарушаться. При особых условиях кристаллизации в природе и тем более в эксперименте могут реализоваться условия предельно медленного и направленного роста при сохранении стационарных термодинамических условий или исключительно кратковременного роста (эксперимент или природные импактные события). Тогда в выборке кристаллов могут быть представлены морфотипы с меньшим количеством симметричных граней и, более того, может происходить смена преобладающих на кристалле простых кристаллографических форм, например появление или исчезновение граней куба и ромбододекаэдра на искусственных алмазах или природных алмазах на ранних бурных этапах развития литосферы Земли. Подчеркнем, что неполногранность в обсуждаемом смысле особенно характерна для экспериментальных условий кристаллизации, в которых время процесса кратко (параметр n в аппроксимирующем распределении (1) недостаточно велик [3]) и присутствует анизотропия питания. Однако природные процессы отличаются тем, что в общем случае радикальные изменения свободной формы кристаллов в ходе единого процесса на данном исследуемом объекте большинству минералов не свойственны, а сумма очень большого количества этапов анизотропного роста (растворения) статистически может интерпретироваться как изотропный процесс. Природный алмаз в данном случае не является примером, поскольку история его роста в межзеренном пространстве гранулированной горной породы [11] затрагивает значительную часть истории развития Земли. Тем не менее последние этапы его развития (рост или растворение) находятся в полном согласии с обсуждаемым принципом.

Метасоматический рост циркона приближается к описанной ситуации, но даже для циркона Ильменогорского массива не был преодолен теоретический порог полного огранения. Если в форме многогранника кроме габитусных граней учитывать редко встречающиеся грани, не относящиеся к габитусным, например тригональный трапецоэдр для α-кварца, полное огранение в обсуждаемом смысле будет скорее исключением, чем правилом.

ЗАКЛЮЧЕНИЕ

Принцип полного огранения может рассматриваться как признак выхода неравновесной минералообразующей системы на стационарный режим, являющийся предельным режимом развития открытой неравновесной системы. Он является макроскопическим следствием предельного принципа минимума производства энтропии по И. Пригожину [2] или принципа наименьшего принуждения по И. Дьярмати [1]. Принципы Пригожина и Дьярмати справедливы в локальном случае, а принцип полного огранения является макроскопическим, тем не менее он иллюстрирует для свободной формы кристаллов направление минералообразования в литосфере Земли в масштабе длительных геологических процессов. Он справедлив также в закрытой по отношению к обмену веществом системе при коллективном росте кристаллов. Как прямой процесс роста, так и обратный процесс растворения кристалла в равной степени подчиняются данному принципу и напоминают о принципе обратимости В. Косселя.